Skip to main content
PMC home page
PLOS ONE logoLink to PLOS ONE
. 2011 May 31;6(5):e20650. doi: 10.1371/journal.pone.0020650

Scaling Behavior of Human Locomotor Activity Amplitude: Association with Bipolar Disorder

Premananda Indic 1,*, Paola Salvatore 2,3,4, Carlo Maggini 4, Stefano Ghidini 4,5, Gabriella Ferraro 4, Ross J Baldessarini 2,3, Greg Murray 6
Editor: Matjaz Perc7
PMCID: PMC3105113  PMID: 21655197

Abstract

Scale invariance is a feature of complex biological systems, and abnormality of multi-scale behaviour may serve as an indicator of pathology. The hypothalamic suprachiasmatic nucleus (SCN) is a major node in central neural networks responsible for regulating multi-scale behaviour in measures of human locomotor activity. SCN also is implicated in the pathophysiology of bipolar disorder (BD) or manic-depressive illness, a severe, episodic disorder of mood, cognition and behaviour. Here, we investigated scaling behaviour in actigraphically recorded human motility data for potential indicators of BD, particularly its manic phase. A proposed index of scaling behaviour (Vulnerability Index [VI]) derived from such data distinguished between: [i] healthy subjects at high versus low risk of mood disorders; [ii] currently clinically stable BD patients versus matched controls; and [iii] among clinical states in BD patients.

Introduction

Scale invariance is a feature of biological complexity arising from interactions of various physiological control nodes operating at multiple time scales [1]. Loss of scale invariance can indicate pathophysiological states as it represents a shift to fewer control nodes [2]. In humans, the hypothalamic suprachiasmatic nucleus (SCN) is a major node in neural networks responsible for multi-scale regulation of biological rhythms. In particular, the SCN is responsible for scale-invariant properties of temporal fluctuations in locomotor activity [3]. Multi-scale properties of activity data can be important clinically, and are readily detected non-invasively and recorded by wrist-worn, microprocessor-controlled, piezoelectric actigraphic devices. Multi-scale features of physiological data have proved useful in understanding various clinical states as diverse as heart disease [4], [5], asthma [6], schizophrenia [7], and clinical depression [7], [8], [9].

Bipolar (manic-depressive) disorder (BD) is a relapsing, major psychiatric disorder with poorly understood neurobiology, typically incomplete treatment responses, and often unsatisfactory clinical outcomes, with a high risk of premature mortality due to suicide and other causes. BD may be particularly well suited to the investigation of multi-scale properties of motility data. Its complex manifestations include marked disturbances of locomotor activity [10], [11] as well as major changes in mood, thinking, and many aspects of behavior. Furthermore, the SCN may be involved in the regulation of behavior and mood in BD patients [12]. Development of non-invasive, objective correlates or predictors of morbid states in BD patients may support more timely and efficient clinical interventions aimed at limiting risk of recurrence of major episodes of illness.

Based on this background, we sought biologically plausible correlates of BD in multi-scale characteristics of daily motility rhythms in human subjects, including patients with reliably diagnosed BD in a range of ill and remitted clinical states, healthy controls, and subjects showing a range of potential vulnerabilities for BD based on standardized and validated behavioural and symptomatic ratings. We hypothesized that multi-scale behavior in motility rhythms recorded over several days would: [1] distinguish between high and low vulnerability to BD in apparently healthy young adults, [2] distinguish BD patients from healthy, sex- and age-matched controls, and [3] distinguish among different psychopathological states of BD patients.

We tested these hypotheses using data collected with wrist-worn actigraphs in three experimental protocols. Study 1 involved healthy young adults with no history of mental illness, in Melbourne, Australia. Their potential risk of future BD was assessed using the well-validated General Behavior Inventory (GBI) [13], [14]. We divided subjects by highest versus lowest deciles of resulting GBI scores into those with apparently low risk (n = 35; 77.1% women; mean±SD, age  = 20.9±2.3) versus high risk for BD (n = 35; 65.7% women; age 22.3±3.0 years). Subjects wore an actigraph continuously on the nondominant wrist for seven days. For Study 2, in Australia, we recruited currently clinically euthymic, medicated patients diagnosed with type-I BD by DSM-IV criteria (n = 15; 46.7% women; age 46.8±12.4) and healthy controls with no history or current clinical evidence of mental illness, low GBI scores, and matched approximately for sex and age (n = 15; 46.7% women; age  = 46.7±14.1), who also wore an actigraph for seven days. In Study 3, at the University of Parma, Italy, patients with a DSM-IV diagnosis of type-I BD (n = 51; 70.6% women; age 43.8±10.5 years) were actigraphically monitored prospectively for 3 days during acute manic (n = 21) or mixed manic-depressive states (n = 13), episodes of major depression (n = 13), and during full clinical recovery (n = 46) sustained for at least 60 days (total of 90 observations).

Measures of output variables representing underlying dynamics of a biological system can exhibit complex fluctuations across different time scales. Based on nonlinear system theory, the multi-scale features of these measures can be characterized [4], [5], [15]. The past decade has seen growing interest in nonlinear dynamical analysis of physiological data [16], [17], and a range of computational approaches have been used to seek hidden signals of pathology from the measures of the time series [18], [19], [20]. In the present study, we focused on amplitude behavior since amplitude of motility data is physiologically grounded as a measure of strength of physiological oscillations regulated by the SCN [21], [22].

Results

Probability distribution of multi-scale amplitudes

To understand the multi-scale characteristics of amplitude measures of motility data collected with actigraphy, we considered data from Study 1. A wavelet transform[23] (see Methods) was used to extract amplitude of motility rhythms at different time scales ranging from 0.2 to 26 h. Motility data are highly non-stationary due to various extrinsic and intrinsic factors [24], and wavelet transform is a powerful method for obtaining amplitude at multiple time scales from such non-stationary biological signals [15].

Rhythms were observed at circadian (∼24 h) as well as other temporal ranges (minutes or hours). Figure 1 represents an example of motility data along with the multi-scale rhythms obtained using wavelet analysis. The amplitude of rhythms at shorter time scales appeared to be random; to check whether such fluctuation was simply due to noise in the data, we plotted the distribution of amplitudes at a range of time-scales. The distribution of amplitudes obtained at very short time-scales (≤2.0 h) had an apparent long-tail and was nearly collapsed (Figure 2 (a–d)). Such a long-tail distribution is characteristic of nonlinear complex systems near critical points, and the collapse of amplitude distribution represents the scale-invariant feature of such systems [25].

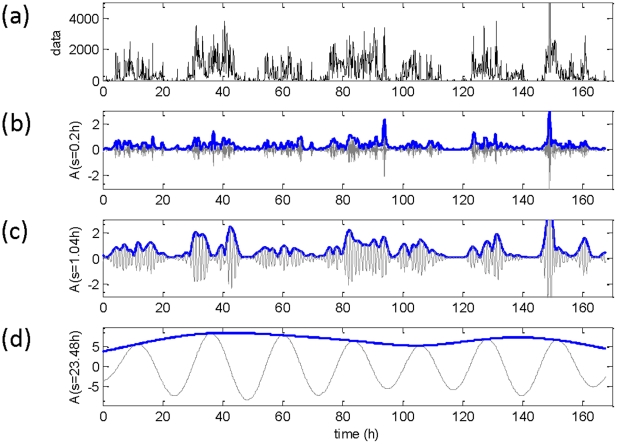
Figure 1. Estimated multi-scale rhythms of motility data obtained by wavelet analysis.

Figure 1

Open in a new tab

(a) Raw data in arbitrary units (a.u) along with the rhythms detected at three different time scales. (b) The detected rhythm (grey line) along with its amplitude (blue line) for a scale of 0.2 h. (c) The corresponding rhythm and amplitude for a scale of 1.04 h. (d) The same measure at a scale of 23.48 h. Wavelet amplitudes are in normalized arbitrary units.

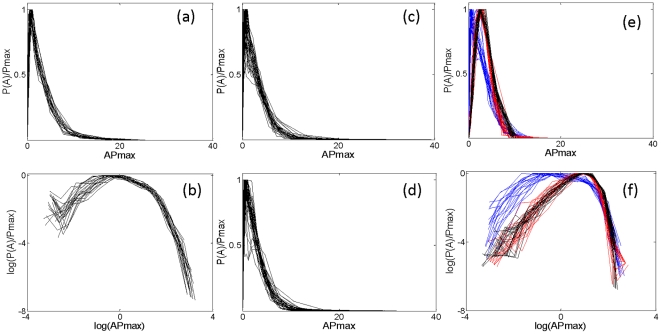
Figure 2. Probability distribution P(A) of amplitude, A, obtained by wavelet analysis of motility data.

Figure 2

Open in a new tab

(a) Rescaled distributions, normalized to provide unit area by rescaling using Pmax, of amplitude at a range of time-scales up to 2 h from a subject considered to be at low risk for BD by GBI criteria. (b) The same data, log-transformed and showing a long-tail, which share most of the values of log (APmax). (c) Amplitude distribution at a specific scale (s = 0.54 h) for 35 subjects considered to be at low risk for BD by GBI criteria. (d) The same for 35 other subjects at high risk for BD. (e) Amplitude distribution up to 2 h for a subject at high risk for BD (blue line) and the corresponding surrogate data (red line); the amplitude distribution (black line) obtained from the wavelet analysis of data derived from a Gaussian distribution follows the amplitude distribution of surrogate data. (f) Log-transformed amplitude from panel e; here, wavelet amplitudes of Gaussian as well as surrogate data have identical distributions without a long-tail, and differ from the distribution of the original data.

To confirm that the observed long-tail distribution was an intrinsic nonlinear property of the motility data rather than an artifact of wavelet analysis, we performed surrogate data analysis, a standard test to confirm nonlinearity of the data [26]. Surrogate data were obtained by Fourier transform of the original motility data, preserving the amplitude, randomizing the phases, and then computing inverse Fourier transforms. Since both amplitude and the power spectrum were preserved in the surrogate data, it might be expected that the amplitude distribution for the surrogate and original data would be identical.

However, wavelet analysis indicated that the amplitude distribution for the surrogate data followed a Gaussian distribution without a long tail. In addition, we generated artificial data with values obtained from a Gaussian distribution, and repeated the wavelet analysis. The amplitude distribution of such artificial data at lower time scales had a similar distribution to that of the surrogate data (Figure 2 (e–f)). These observations imply the presence of nonlinear interactions in the original motility data and that the long-tail distribution of amplitude was an intrinsic property.

Derivation of Vulnerability Index (VI) of BD

To characterize the long-tail distribution, we sought the distribution function that best fit the observed amplitude distribution. Although Gamma functions are considered optimal for characterizing such long-tail distributions [27], we compared the goodness-of-fit of the amplitude distribution for both Gamma and Rayleigh [28] distributions. Theoretically, based on the central limit theorem, amplitude at different time-scales for data derived from a Gaussian distribution should follow a Rayleigh distribution, whereas a long-tail distribution characterized by a Gamma distribution should reveal the presence of nonlinear interactions [15]. We found that for scales up to 2.0 h, the fit of the Gamma distribution was better than the Rayleigh distribution based on Akaike Information Criteria (AIC) [29].

To look for any scale-invariant feature in the amplitude distribution at multiple time scales, we plotted the estimated shape parameter, γ, of the Gamma distribution fit at different time scales. We found that the shape parameter exhibited multi-scale behavior (Figure 3). If the shape parameter of the individual distribution showed a constant value for time scales up to 2.0 h, this would indicate scale-invariance. However, the shape parameter decreased at short time scales and gradually increased at longer time scales. Although the long-tail distribution was a property of the data, the amplitude distribution lacked a scale-invariant feature. Since such a non-collapsed nature of the distribution may represent an abnormality of the system, we investigated plausible correlates of this multi-scale behavior to the illness of BD. To quantify the observed behavior, we integrated the shape parameter up to 2.0 h time scales for each subject as 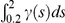Inline graphic. The derived integral, termed a vulnerability index (VI), was used in hypothesis-testing analyses.

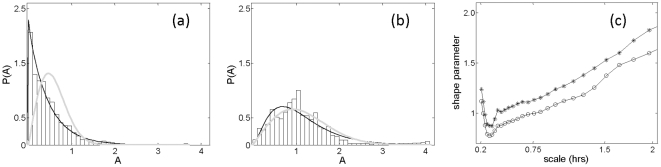
Figure 3. Characterization of the probability distribution of amplitudes using Gamma and Rayleigh functions.

Figure 3

Open in a new tab

(a) Probability distribution P(A) for a subject considered to be a low risk for BD at a scale s∼0.59 h, along with Gamma (black line) and Rayleigh (grey line) best-fit functions: based on AIC, the Gamma distribution yields a better fit. (b) Probability distribution P(A) at a scale of s∼3.0 h for the same subject: the fit of the Rayleigh distribution function (gray line) is superior to the Gamma function at this scale, by AIC criteria. (c) Average value of the shape parameter, Inline graphic, at different scales (hours) for 35 subjects considered to be low risk for BD by GBI criteria (open circles) and another 35 at high risk (filled circles).

VI as a marker for detecting trait of BD

Hypothesis 1 was tested with data from Study 1, in which the low risk group, based on lowest decile GBI ratings, had 12% lower mean VI scores (2.11±0.45) than the high risk group (2.39±0.42). Logistic regression modeling indicated that VI was significantly associated with presumptive high risk for BD (F [df = 1; 66] = 8.69, p = 0.004), but that sex and age were not. Similarly, testing of Hypothesis 2 with data from Study 2 found 17% higher VI scores among patients diagnosed with BD (2.53±0.49) than in healthy control subjects (2.17±0.40), and that VI score was associated with the diagnosis of BD, based on logistic regression modelling (F[df = 1;26] = 4.65, p = 0.04).

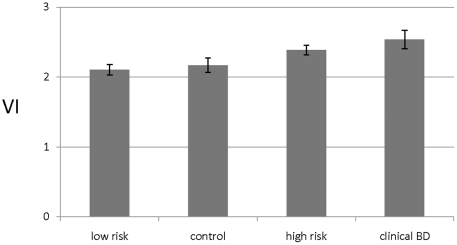
When all subjects from Studies 1 and 2 were included in a multivariate linear regression modelling, with GBI score as the dependent measure, and controlling for sex and age, the VI score was significantly and independently associated with either high risk for, or diagnosis of BD, and was the only factor associated (F [df = 3; 96] = 4.94, p = 0.001). Likewise, we found a significant linear trend in the mean magnitude of VI measures, ranking: low-GBI score < healthy controls ≤ non-BD patients with high GBI scores < BD patients (Figure 4), with control for sex and age (F [df = 3; 94] = 4.28, p = 0.007, β = 0.32, p = 0.01).

Figure 4. Estimated means (±SEM) computed vulnerability index (VI) values in four groups of human subjects of increasing risk or presence of BD.

Figure 4

Open in a new tab

Low risk by GBI criteria (n = 35), healthy controls (n = 15), high-risk by GBI criteria (n = 35), and patients diagnosed with DSM-IV type-I BD who are currently clinically stable or euthymic (n = 15). Curve-fitting found that mean VI increased linearly across these groups (F [df = 3; 94] = 4.28, p = 0.007, controlling for sex and age).

These findings indicate the presence of a consistent and significant association between VI scores and GBI scores as an indication of trait for BD in healthy subjects with high versus low GBI scores, and in comparison of BD patients with sex- and age-matched healthy controls.

Circadian amplitude and detrended fluctuation measure of motility data

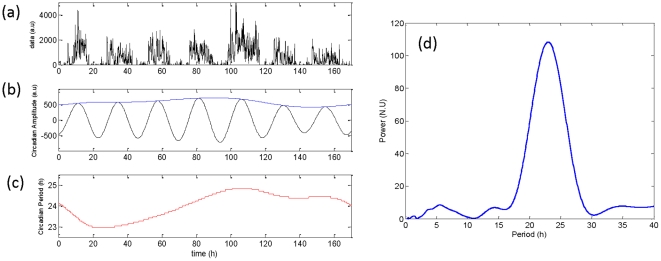
To check whether vulnerability to BD would typically be inferred from more common analyses of ∼24-hour (circadian) features of actigraphic data, we estimated the predominant component using wavelet transform along with a ridge extraction algorithm [30]. Figure 5 represents an example of the estimated predominant amplitude and the period from a representative human subject. The predominant component of motility data was in the circadian range. However the predominant amplitude in arbitrary units (mean ± SD ranked for low risk: 446±150, versus high risk: 411±145 subjects, BD patients: 332±132, versus healthy controls: 435±146) and the predominant period in hours (mean ± SD ranked for low risk subjects: 24.0±0.20, high risk subjects: 23.9±0.3, BD patients: 24.0±0.05, healthy controls: 24.0±0.1) of the circadian component did not show significant differences among the subject-groups.

Figure 5. Estimated predominant component of motility data.

Figure 5

Open in a new tab

(a) The raw data in arbitrary units (a.u). (b) The estimated circadian rhythm (black line) with its amplitude (blue line). (c) The estimated circadian period (red line) in hours. Due to the non-stationary nature of the data, the estimated amplitude and the period show cycle-to-cycle variability. (d) Normalized scalogram at a specific time of 32 hr. The peak power occurred at a period of 23 h

Detrended fluctuation analysis has indicated that motility data have long range correlations with a scale-invariant feature in temporal fluctuations ranging up to 24 h, and that these correlations can distinguish elderly persons diagnosed with Alzheimer's disease from healthy elderly controls[31]. By application of detrended fluctuation analysis [31] of the present motility data, we considered whether such fluctuations were different among the various groups of test subjects. Although we found a scale-invariant feature in temporal fluctuations, its characterizing parameter, scaling exponent, (mean ± SD) did not differ significantly among subject-groups. This measure ranked: low risk subjects, 0.98±0.07 = high risk subjects, 0.98±0.06> healthy controls, 0.96±0.05> BD patients, 0.94±0.09.

VI as a marker for detecting different morbid phases of BD

We used data from Study 3 to test whether differences in VI values were associated with varying clinical states of BD (Hypothesis 3). Statistical findings are shown based on linear correlations (Table 1), which were supported by nonparametric Spearman rank-correlations (not shown). Regression modelling, with control for sex and age indicated that VI was significantly and uniquely associated with both self- (β = 0.31, t = 2.76) and clinician-rated mania (β = 0.33, t  = 3.07, both p = 0.01), whereas age was a lesser covariate (β = 0.239, p = 0.05). The pattern of findings was replicated with multi-level modelling to account for nesting of assessments within subjects: and a significant relationship was found between VI and both self- (t [df = 78] = 2.97, p = 0.004) and clinician-rated mania (t [df = 81] = 2.54, p = 0.013).

Table 1. Correlations of individual values of vulnerability index (VI) with self- and clinician-ratings of manic and depressive symptom-severity.

Correlate r-value p-value
Manic Symptoms
Clinician-rated with YMRS +0.304 0.005
Self-rated +0.305 0.006
Depressive Symptoms
Clinician-rated with HDRS) −0.017 0.877
Self-rated) −0.114 0.313
Open in a new tab

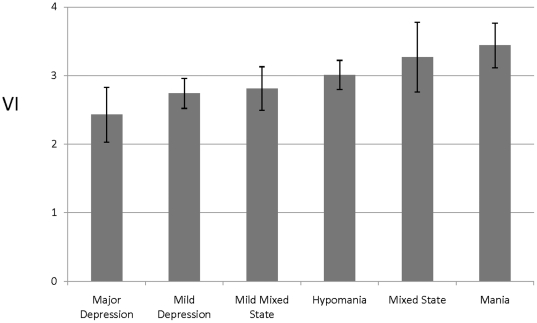
Importantly, regression analyses found no correlation of VI with depressive symptom ratings (Hamilton Depression Rating Scale [HDRS] score or self-rated depression F [df = 3;79] = 2.32, and F [df = 3;76] = 1.21 both p>0.05). However, there was a significant increase in mean VI values across mood-states, ranking: major depression < minor depression < euthymia < minor mixed-states < hypomania < major mixed-states < mania (Figure 6).

Figure 6. Mean (±SEM) computed vulnerability index (VI) values associated with various mood states of patients meeting DSM-IV diagnostic criteria for type-I BD.

Figure 6

Open in a new tab

VI rises consistently and significantly with increasing manic features, from major depression, through mild depression or dysthymia, subclinical or mild mixed manic-depression, hypomania, mixed major manic-depressive states, to current mania-all in BD patients.

Discussion

We identified a novel scaling behaviour of the amplitude measures of locomotor activity in human subjects. Importantly, an index of this multi-scale behaviour, the “vulnerability index” (VI), is found to be clinically meaningful. That is, higher VI scores were found in subjects with apparently high versus low vulnerability to BD (high versus low GBI scores), and in BD patients versus healthy, matched controls. We propose that an elevated value of VI can serve as a novel and effective indicator of trait for BD as well as being characteristic of subjects with clinically diagnosed BD. In these subject-groups vulnerability for BD manifested in the amplitude characteristics of activity data at lower time scales, which appeared as noise to the naked eye, and were unrelated to the temporal long-range correlations or typically-analysed circadian features of motility rhythms.

The VI is specifically sensitive to mania and manic symptoms, which distinguish BD from other mood disorders. However, VI is insensitive to depression, consistent with the view that mania and depression in BD have dissimilar pathophysiologies [32]. Furthermore, the increasing variations of VI across different mood states, as shown in Figure 6, suggest that the VI might be a specific and sensitive indicator of a gradually emerging component of psychomotor activation from predominantly inhibited or psychomotorically retarded depressive states towards mixed or manic states.

The VI may reflect SCN function, which has been implicated in the pathophysiology of BD [33]. Of various SCN-related rhythms, human motility can easily be monitored noninvasively and inexpensively, either intermittently for short times, or continuously for long periods under naturalistic conditions, making it particularly well-suited to longitudinal tracking of illness-course and treatment responses in BD patients. Further research is warranted to investigate the biological substrate of VI and to confirm its potential utility as an objective marker of risk for, or presence of BD, and of its selectivity for manic versus depressive features. It might also bear testing as early indicator of impending clinical relapse into manic or mixed states of BD arising from depression or euthymia.

Methods

Ethics Statement

All subjects provided written informed consent for aggregate and anonymous reporting of data arising from their clinical and actigraphic assessments. Study 1 was approved by Swinburne University Human Research Ethics Committee; Study 2 was approved by Bendigo Health Care Group Ethics Committee and Study 3 was approved by the Ethics Committee of the University of Parma Medical Center, in full accordance with international standards for the ethical use of human subjects in research.

Psychiatric measures

The 73-item GBI is a reliable and validated self-report measure with stable between-subject differences that are reported to reflect vulnerability to BD. [34], [35]. In Study 3, clinician ratings of symptom-status were made with the Young Mania Rating Scale (YMRS) [36] and the Hamilton Rating Scale for Depression (HDRS) [37]. Subjects in Study 3 also self-rated symptoms on a series of 10-cm visual analog scales (29 items) based on items of the YMRS and HDRS as well as the Bonn Scale for the Assessment of Basic Symptoms (BSABS) [38].

Subjects

Study 1. Exclusion criteria included past history of mania/hypomania, working shift work, or having a physical condition that would confound activity measurement. The highest versus lowest deciles of the distribution of GBI scores, identified 35 subjects considered to be at high-risk, and 35 at low-risk for BD from an initial sample of 358. Mean GBI score differed by more than ten-fold between subjects with low versus high apparent risk for BD (10.5±6.20 vs. 109±26.3, F [df = 1; 68]) = 465, p<0.001). Study 2: Clinical subjects were recruited from an outpatient public mental health service in Victoria, Australia, who met DSM-IV criteria for a diagnosis of type-I BD as determined by an experienced research psychiatrist. Sex- and age-matched healthy controls were recruited through network of researchers. Study 3: Patients were recruited as inpatients at the Section of Psychiatry of the University of Parma, Italy, whose DSM-IV diagnosis of type I BD was supported by semi-structured interviews by a research psychiatrist over prolonged (7.43±2.24 years) follow-up as outpatients.

Activity measurement

Actigraphy is commonly used to document rest/activity cycles under naturalistic conditions and to characterize abnormal sleep/wake behaviour and altered circadian rhythms amongst ill or euthymic BD patients. In the present studies, subjects wore an actigraph continuously on the non-dominant wrist under naturalistic conditions for 3–7 days. The Mini-Mitter Actiwatch® 64 (Respironics, Inc. Bend, OR, USA) was used in Studies 1 and 2, and AMA-128K Mini-Motionlogger® Actigraph (Ambulatory Monitoring, Inc. [AMI], Ardsley, NY, USA) in Study 3. Activity data were obtained at 32 Hz and integrated at every 0.1 h.

Data Analysis

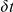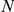The continuous wavelet transform of digitally acquired motility data, Inline graphic with Inline graphic is obtained by the convolution of the data with a scaled and translated version of a mother wavelet [23], as:

graphic file with name pone.0020650.e005.jpg (1)

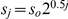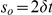where Inline graphic = 0.1 hr, Inline graphic is the total number of data points, Inline graphic is the scale defined in a dyadic representation as Inline graphic with Inline graphic and 4 sub-octave per octave of the dyadic scale to obtain a total number of 57 scales with 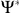Inline graphic. Inline graphic represents the complex conjugate of the normalized wavelet function, where:

graphic file with name pone.0020650.e013.jpg (2)

We performed this convolution with a Morlet wavelet, a plane wave modulated by a Gaussian function defined as

graphic file with name pone.0020650.e014.jpg (3)

Since the Morlet wavelet is a complex function, the obtained wavelet transformation of the data, 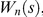Inline graphic is also complex with a real part and an imaginary part. Therefore, corresponding to each scale the amplitude is defined as 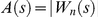Inline graphic. The obtained amplitudes are in normalized units.

To determine the predominant component of the motility data we employed the wavelet transform with an increased resolution of scale with 256 sub-octaves per octave in the dyadic representation. At each time point, using a ridge extraction algorithm[30], the scale at which the normalized scalogram has a peak value is detected. The corresponding amplitude multiplied by the appropriate de-noising factor [23] at this scale is the predominant amplitude and the corresponding period is the predominant period. Our approach for determining the predominant component is similar to the method employed for estimating circadian oscillations from bioluminescence data [39], [40].

Acknowledgments

We thank Ben Bullock and Fiona Judd for assistance with Studies 1 and 2, Kun Hu and Steven A Shea for kindly providing their detrended fluctuation analysis software.

Footnotes

Competing Interests: The authors have declared that no competing interests exist.

Funding: This research was supported, in part, by grants from Swinburne University of Technology and Beyond Blue: National Depression Initiative (to GM), a grant from the Bruce J Anderson Foundation and by the McLean Private Donors Bipolar Disorder Research Fund (to RJB). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. No additional external funding was received for this study.

References

  • 1.Gisiger T. Scale invariance in biology: Coincidence or footprint of a universal mechanism? Biological Reviews. 2001;76:161–209. doi: 10.1017/s1464793101005607. [DOI] [PubMed] [Google Scholar]
  • 2.Goldberger AL, Amaral LAN, Hausdorff JM, Ivanov PC, Peng CK, et al. Fractal dynamics in physiology: Alterations with disease and aging. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:2466–2472. doi: 10.1073/pnas.012579499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Hu K, Scheer FA, Ivanov P, Buijs RM, Shea SA. The suprachiasmatic nucleus functions beyond circadian rhythm generation. Neuroscience. 2007;149:508–517. doi: 10.1016/j.neuroscience.2007.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Peng CK, Havlin S, Stanley HE, Goldberger AL. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos. 1995;5:82–87. doi: 10.1063/1.166141. [DOI] [PubMed] [Google Scholar]
  • 5.Costa M, Goldberger AL, Peng CK. Multiscale entropy analysis of complex physiologic time series. Physical Review Letters. 2002;89 doi: 10.1103/PhysRevLett.89.068102. [DOI] [PubMed] [Google Scholar]
  • 6.Frey U, Brodbeck T, Majumdar A, Taylor DR, Town GI, et al. Risk of severe asthma episodes predicted from fluctuation analysis of airway function. Nature. 2005;438:667–670. doi: 10.1038/nature04176. [DOI] [PubMed] [Google Scholar]
  • 7.Hauge ER, Berle JO, Oedegaard KJ, Holsten F, Fasmer OB. Nonlinear Analysis of Motor Activity Shows Differences between Schizophrenia and Depression: A Study Using Fourier Analysis and Sample Entropy. PLoS One. 2011;6(1):e16291. doi: 10.1371/journal.pone.0016291. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Nakamura T, Kiyono K, Yoshiuchi K, Nakahara R, Struzik ZR, et al. Universal scaling law in human behavioral organization. Phys Rev Lett. 2007;99:138103. doi: 10.1103/PhysRevLett.99.138103. [DOI] [PubMed] [Google Scholar]
  • 9.Nakamura T, Takumi T, Takano A, Aoyagi N, Yoshiuchi K, et al. Of mice and men–universality and breakdown of behavioral organization. PLoS ONE. 2008;3:e2050. doi: 10.1371/journal.pone.0002050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Henry BL, Minassian A, Young JW, Paulus MP, Geyer MA, et al. Cross-species assessments of motor and exploratory behavior related to bipolar disorder. Neuroscience & Biobehavioral Reviews. 2010;34:1296–1306. doi: 10.1016/j.neubiorev.2010.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Murray G. Circadian and sleep/wake considerations in the practical management of bipolar disorder. In: Young A, Ferrier N, Michalak EE, editors. Practical management of bipolar disorder. Cambridge: Cambridge University Press; 2010. pp. 152–162. [Google Scholar]
  • 12.Roybal K, Theobold D, Graham A, Dinieri JA, Russo SJ, et al. Mania-like behavior induced by disruption of CLOCK. Proceedings of the National Academy of Science USA. 2007 doi: 10.1073/pnas.0609625104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Depue RA, Krauss S, Spoont MR, Arbisi P. General behavior inventory identification of unipolar and bipolar affective conditions in a nonclinical university population. J Abnorm Psychol. 1989;98:117–126. doi: 10.1037//0021-843x.98.2.117. [DOI] [PubMed] [Google Scholar]
  • 14.Reichart CG, van der Ende J, Wals M, Hillegers MHJ, Nolen WA, et al. The use of the GBI as predictor of bipolar disorder in a population of adolescent offspring of parents with a bipolar disorder. Journal of Affective Disorders. 2005;89:147–155. doi: 10.1016/j.jad.2005.09.007. [DOI] [PubMed] [Google Scholar]
  • 15.Ivanov PC, Rosenblum MG, Peng CK, Mietus J, Havlin S, et al. Scaling behaviour of heartbeat intervals obtained by wavelet-based time-series analysis. Nature. 1996;383:323–327. doi: 10.1038/383323a0. [DOI] [PubMed] [Google Scholar]
  • 16.Kantz H, Schreiber T. Cambridge: Cambridge university press; 2004. Nonlinear time series analysis. [Google Scholar]
  • 17.Hegger R, Kantz H, Schreiber T. Practical implementation of nonlinear time series methods: The TISEAN package. Chaos. 1999;9:413–435. doi: 10.1063/1.166424. [DOI] [PubMed] [Google Scholar]
  • 18.Kodba S, Perc M, Marhl M. Detecting chaos from a time series. European Journal of Physics. 2005;26:205–215. [Google Scholar]
  • 19.Perc M. The dynamics of human gait. European Journal of Physics. 2005;26:525–534. [Google Scholar]
  • 20.Perc M. Nonlinear time series analysis of the human electrocardiogram. European Journal of Physics. 2005;26:757–768. [Google Scholar]
  • 21.Vitaterna MH, Ko CH, Chang AM, Buhr ED, Fruechte EM, et al. The mouse Clock mutation reduces circadian pacemaker amplitude and enhances efficacy of resetting stimuli and phase-response curve amplitude. Proc Natl Acad Sci U S A. 2006;103:9327–9332. doi: 10.1073/pnas.0603601103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Indic P, Forger DB, St Hilaire MA, Dean DA, 2nd, Brown EN, et al. Comparison of amplitude recovery dynamics of two limit cycle oscillator models of the human circadian pacemaker. Chronobiol Int. 2005;22:613–629. doi: 10.1080/07420520500180371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Torrence C, Compo GP. A practical guide to wavelet analysis. Bulletin of the American Meteorological Society. 1998;69:61–78. [Google Scholar]
  • 24.Hu K, Ivanov P, Chen Z, Hilton MF, Stanley HE, et al. Non-random fluctuations and multi-scale dynamics regulation of human activity. Physica A. 2004;337:307–318. doi: 10.1016/j.physa.2004.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Barbasi A-L, Stanley HE. Cambridge: Cambridge University Press.; 1995. Fractal concepts in surface growth.366 [Google Scholar]
  • 26.Theiler J, Eubank S, Longtin A, Galdrikian B, Farmer JD. Testinng for nonlinearity in time-series- The method of surrogate data. Physica D. 1992;58:77–94. [Google Scholar]
  • 27.Stauffer D, Stanley HE. Heidelberg: Springer; 1996. From Newton to Mandelbrot: A primer in theoretical physics. [Google Scholar]
  • 28.Papoulis A, Pillai SU. 2002 Probability, random variables and stochastic processes: McGraw Hill Higher Education. [Google Scholar]
  • 29.Priestley MB. 1981 Spectral Analysis and Time series: Academic Press. [Google Scholar]
  • 30.Carmona RA, Hwang WL, Torresani B. Multiridge detection and time-frequency reconstruction. Ieee Transactions on Signal Processing. 1999;47:480–492. [Google Scholar]
  • 31.Hu K, Van Someren EJW, Shea SA, Scheer FAJL. Reduction of scale invariance of activity fluctuations with aging and Alzheimer's disease: Involvement of the circadian pacemaker. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:2490–2494. doi: 10.1073/pnas.0806087106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.McGuffin P, Rijsdijk F, Andrew M, Sham P, Katz R, et al. The heritability of bipolar affective disorder and the genetic relationship to unipolar depression. Archives of General Psychiatry. 2003;60:497–502. doi: 10.1001/archpsyc.60.5.497. [DOI] [PubMed] [Google Scholar]
  • 33.Mansour HA, Monk TH, Nimgaonkar VL. Circadian genes and bipolar disorder. Ann Med. 2005;37:196–205. doi: 10.1080/07853890510007377. [DOI] [PubMed] [Google Scholar]
  • 34.Depue RA, Krauss S, Spoont MR, Arbisi P. General Behavior Inventory identification of unipolar and bipolar affective conditions in a nonclinical university population. Journal of Abnormal Psychology. 1989;98:117–126. doi: 10.1037//0021-843x.98.2.117. [DOI] [PubMed] [Google Scholar]
  • 35.Reichart CG, van der Ende J, Wals M, Hillegers MHJ, Nolen WA, et al. The use of the GBI as predictor of bipolar disorder in a population of adolescent offspring of parents with a bipolar disorder. Journal of Affective Disorders. 2005;89:147–155. doi: 10.1016/j.jad.2005.09.007. [DOI] [PubMed] [Google Scholar]
  • 36.Young RC, Biggs JT, Ziegler VE, Meyer DA. A rating scale for mania: reliability, validity and sensitivity. Br J Psychiatry. 1978;133:429–435. doi: 10.1192/bjp.133.5.429. [DOI] [PubMed] [Google Scholar]
  • 37.Williams JBW, Link MJ, Rosenthal NE, Terman M. NY: New York State Psychiatric Institute; 1988. Structured Interview Guide for the Hamilton Depression Rating Scale- Seasonal Affective Disorder Version (SIGH-SAD). [Google Scholar]
  • 38.Klosterkotter J, Gross G, Huber G, Wieneke A, Steinmeyer EM, et al. Evaluation of the ‘Bonn Scale for the Assessment of Basic Symptoms BSABS’ as an instrument for the assessment of schizophrenia proneness: A review of recent findings. Neurology Psychiatry and Brain Research. 1997;5:137–150. [Google Scholar]
  • 39.Price TS, Baggs JE, Curtis AM, FitzGerald GA, Hogenesch JB. WAVECLOCK: wavelet analysis of circadian oscillation. Bioinformatics. 2008;24:2794–2795. doi: 10.1093/bioinformatics/btn521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Etchegaray JP, Yu EA, Indic P, Dallmann R, Weaver DR. Casein Kinase 1 Delta (CK1 delta) Regulates Period Length of the Mouse Suprachiasmatic Circadian Clock In Vitro. PLoS One. 2010;5(4):e10303. doi: 10.1371/journal.pone.0010303. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from PLoS ONE are provided here courtesy of PLOS

RESOURCES