Abstract
It is well established that short-term synaptic plasticity (STP) of neocortical synapses is itself plastic – e.g., the induction of LTP and LTD tend to shift STP towards short-term depression and facilitation, respectively. What has not been addressed theoretically or experimentally is whether STP is “learned”; that is, is STP regulated by specific learning rules that are in place to optimize the computations performed at synapses, or, are changes in STP essentially an epiphenomenon of long-term plasticity? Here we propose that STP is governed by specific learning rules that operate independently and in parallel of the associative learning rules governing baseline synaptic strength. We describe a learning rule for STP and, using simulations, demonstrate that it significantly enhances the discrimination of spatiotemporal stimuli. Additionally we generate a set of experimental predictions aimed at testing our hypothesis.
Keywords: timing, temporal processing, short-term synaptic plasticity
Introduction
Since Donald Hebb's famous postulate that if neuron A connects to neuron B and “repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased” (Hebb, 1949) decades of research have revealed much about the rules and mechanisms underlying the long-term changes in synaptic strength thought to underlie learning and memory (Brown et al., 1990; Dan and Poo, 2004; Malenka and Bear, 2004). But one issue that was not addressed by Hebb, or in current learning rules, is the temporal dimension; specifically, what, if anything, determines when within a train of presynaptic action potentials should a synapse be at its strongest?
Since Eccles et al. (1941) described short-term synaptic plasticity (STP) at the neuromuscular junction over 60 years ago, hundreds of studies demonstrated that synaptic efficacy is not a constant but varies dramatically over the course of hundreds of milliseconds as a result of recent activity (Zucker, 1989; Zucker and Regehr, 2002; Abbott and Regehr, 2004). However, in contrast to long-term synaptic plasticity, which is embedded in a solid theoretical framework, the computational function of changes in synaptic strength on the order of tens to hundreds of milliseconds is not known. On theoretical grounds STP has been proposed to contribute to a number of different functions including temporal processing (Buonomano and Merzenich, 1995; Buonomano, 2000; Fortune and Rose, 2001), gain control (Abbott et al., 1997; Chance et al., 1998; Rothman et al., 2009), network stability (Galarreta and Hestrin, 1998; Sussillo et al., 2007), and working memory (Maass and Markram, 2002; Mongillo et al., 2008). But there has been little discussion regarding long-term plasticity of STP as a means to enhance the underlying neuronal computations (see however Seung, 2003).
Associative forms of synaptic plasticity, including spike-timing-dependent plasticity (STDP; Abbott and Nelson, 2000; Dan and Poo, 2004), state that if neuron A consistently fires 10 ms before neuron B the synapse between them will be a strong one. However, current synaptic learning rules, such as STDP, do not speak effectively to the processing of temporal information. Consider two scenarios: (1) presynaptic neuron A fires twice 100 ms apart and post-synaptic neuron B consistently fires only immediately after the second spike in A; (2) again neuron A fires twice 100 ms apart, but now neuron B fires only after the first spike in A and never after the second one. By most accounts STDP predicts that in both scenarios LTP of baseline synaptic strength will be induced (note that the pre1–post relationship in scenario #2 should dominate over potential LTD induced by the post–pre2 relationship). At neocortical synapses this LTP is expected to be accompanied by a change in STP toward increased depression. But in scenario #1 increased depression is computationally counterproductive if the computation being performed is temporal in nature. That is, if the goal is to detect the second spike in A it is important for the post-synaptic neuron to discriminate between Afirst and Asecond. This would be best achieved by preferentially increasing the strength of the second EPSP from A – changing STP towards facilitation.
It is often implicitly assumed that STP is essentially an epiphenomenon of baseline synaptic strength – strong synapses favor short-term depression and weak synapses favor short-term facilitation. However, there is evidence that while CA1 and neocortical LTP are both NMDA-dependent they differ in their effects on STP. Although LTP results in little or no alteration in STP in CA1 synapses, STP of neocortical synapses changes after the induction of LTP or LTD (Markram and Tsodyks, 1996; Buonomano, 1999; Selig et al., 1999; Bender et al., 2006; Hardingham et al., 2007). Additionally, neocortical STP also undergoes developmental and experience-dependent changes, and varies from one cortical area to another (Finnerty et al., 1999; Reyes and Sakmann, 1999; Atzori et al., 2001; Zhang, 2004; Speed and Dobrunz, 2008). While these observations suggest that the changes in STP are not simply an epiphenomenon, it remains possible that the observed changes in STP are all secondary to the control of initial synaptic strength. An issue that has not been addressed experimentally or theoretically is whether STP itself is governed by learning rules that operate independently and in parallel of those governing long-term plasticity of baseline synaptic strength.
Given the inherent temporal complexity of neuronal firing patterns and the importance of temporal information to cortical computation (Mauk and Buonomano, 2004), we suggest that synapses may have mechanisms in place to control the dynamics of STP. For example, given a train of presynaptic spikes, synapses may come to express short-term depression or facilitation depending on whether the post-synaptic cell consistently fires early or late in the train, respectively.
Materials and Methods
To examine the contribution of STP to the discrimination of spatiotemporal stimuli we used a simple feed-forward network, in which the afferents convey the time-varying patterns generated by the stimuli. These inputs synapse onto post-synaptic neurons which act as classifiers. Initially these post-synaptic units were simulated as integrate-and-fire neurons (Figures 1 and 2), and latter as a multi-compartmental model with active conductances (Figure 4).
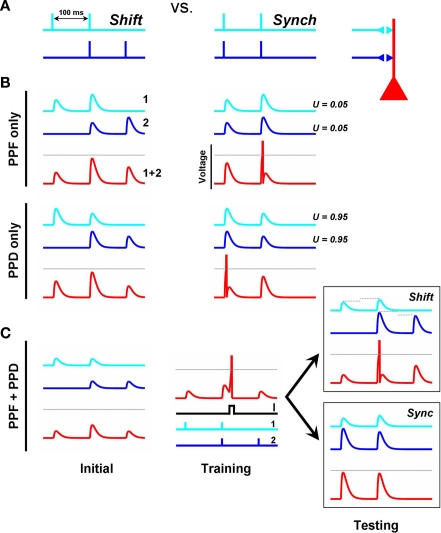
Figure 1.
Metaplasticity of short-term plasticity. (A) Shift Problem. The goal is for the post-synaptic unit (red) to fire to the shift pattern (left), but not to the synchronous pattern (right). (B) If both input synapses exhibit the same type of STP the shift problem cannot be solved. The traces depict the voltage contribution of each input (light and dark blue) to the total post-synaptic voltage (red). PPF or paired-pulse depression in both inputs cannot solve the problem because the neuron's peak response (red trace) will always be to the second or first pulse of the Synch pattern, respectively. Each input exhibits PPF or PPD depending on whether the inputs have a low or high U, respectively. (C) A simple learning rule that adjusts the variable U (“Pr”) at each synaptic terminal can solve the shift problem. . S is a variable that reflects the number of presynaptic spikes (see Materials and Methods). Training: Pairing post-synaptic depolarization (I) – which generates a spike and acts as the “supervisor” – with the coincident presynaptic spikes of the Shift pattern results in PPF at synapse 1 and PPD at synapse 2, in addition to conventional post-synaptic LTP at both synapses (driven by STDP). The rationale is that the time of the post-synaptic spike in relation to a presynaptic spike train determines whether those synapses will show PPD (early pairing) or PPF (late pairing). By pairing post-synaptic depolarization with either the first or second spikes of the synchronous pattern the post-synaptic neuron will also learn to respond selectively to the synch pattern.
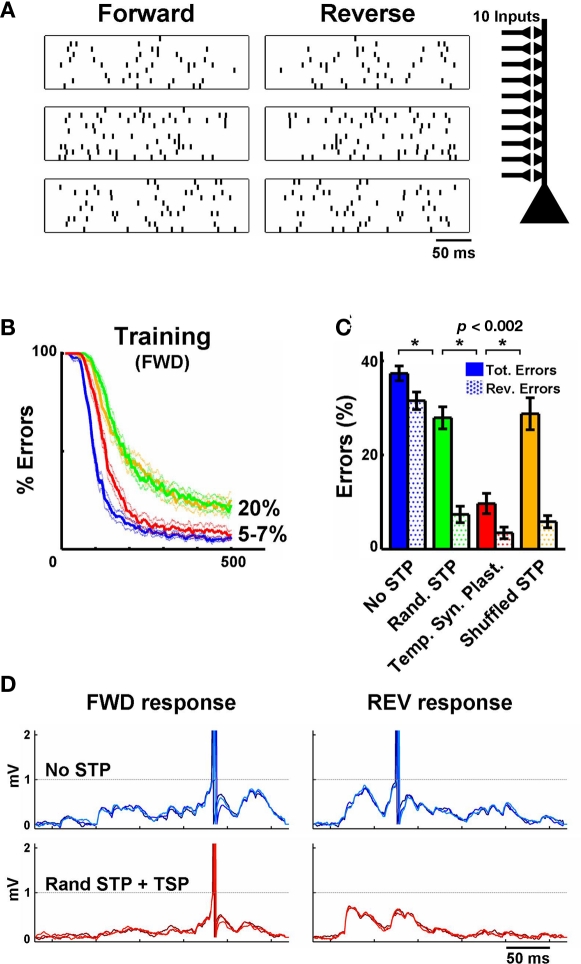
Figure 2.
Temporal synaptic plasticity enhances the discrimination of complex spatiotemporal patterns. (A) Sample of three (out of five) spike patterns of one stimulus set – three forward patterns and their reverses are shown. Each pattern is composed of 10 inputs. (B) Performance during training on the FWD patterns in an IAF neuron. The blue line depicts learning without short-term plasticity and the green line depicts training when synapses were assigned random but fixed STP values. In the red line condition synapses were “metaplastic,” i.e., U underwent long-term plasticity, guided by the temporal synaptic plasticity learning rule. The yellow line depicts retraining with the shuffled STP values obtained from the simulations shown in red again in the absence of STP plasticity. The tempotron learning rule alone (no STP) performed well (blue), yielding 5–7% errors. Here an error is a failure to detect the target (forward) pattern or firing to any of the non-target patterns. Training for longer periods (2000 trials) or stopping training when a fixed error level is achieved (e.g., 20%) yields results similar to the ones shown in (C). (C) Performance during testing. Filled bars represent total errors (FWD + REV), and the dotted bars represent the REV errors (e.g., an output unit trained to recognize pattern #1 responded to pattern #1 presented backwards). Notice that the inclusion of synapses with random (but “fixed”) STP values before training improves performance significantly (green). However, using temporal synaptic plasticity to tune STP (starting with random values) further decreases the number of errors (red). (D) Top row: Response of IAF neuron trained to recognize the stimulus shown in the first row of A (three overlaid test presentations are shown). Synapses do not exhibit short-term plasticity. Bottom row: as above, but synapses exhibit STP, whose parameters were adjusted by the temporal synaptic plasticity learning rule during training. Notice the effectiveness of temporal synaptic plasticity in preventing the neuron to fire to the reverse pattern. Each plot shows three trials represented in different shades of blue or red.
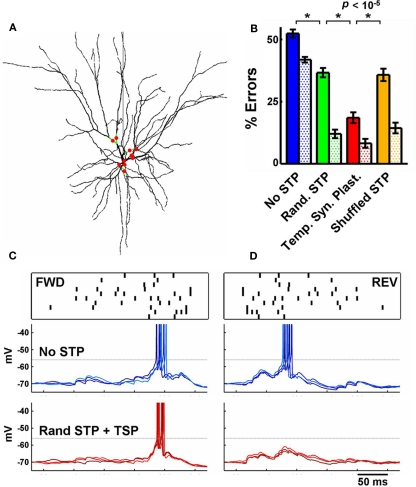
Figure 4.
Temporal synaptic plasticity applied in realistic conditions and background synaptic input. (A) 3D reconstruction of the modeled realistic multicompartment neuron. The location of the driving input synapses is indicated by the red circles (branches in green). (B) Performance of the realistic neuron under the same conditions described in Figure 2C, and as in Figure 2C the filled bars represent total errors, and the dotted bars the REV errors. The presence of STP + temporal synaptic plasticity outperformed the other conditions. (C) Top row: a sample pattern (FWD and REV). Middle row: response of the realistic neuron (C and D) to three repeated presentations of the stimulus above. Synapses do not exhibit short-term plasticity. Bottom row: as above, but synapses exhibit STP, whose parameters were adjusted by the temporal synaptic plasticity learning rule during training. Notice the effectiveness of temporal synaptic plasticity in preventing the neuron to fire to the reverse pattern. This neuron fires in short bursts of doublets and the horizontal dotted line indicates the approximate action potential threshold.
Model neuron (simple)
Post-synaptic neurons were modeled as conductance based integrate-and-fire (IAF) units:
| (1) |
where gL = 0.1 μS, EEx = 3 mV, and EInh = −3 mV. If V(t) > 1 mV a spike was elicited and V(t + dt) was reset to 0. Upon arrival of a presynaptic action potential gEx and gInh increase by the effective synaptic efficacy (see below) and decay exponentially back to 0 with time constant τEx = τInh = 5 ms. For the simulations shown in Figure 2 a “noise current” withdrawn from a normal distribution with mean 0 and SD 0.015 was also present.
Model neuron (complex)
In Figure 4 we implemented temporal synaptic plasticity in a reconstructed layer 3 pyramidal neuron, which includes a variety of passive and active membrane mechanisms (described in detail in Mainen and Sejnowski, 1996). The model neuron was obtained from the SenseLab Project database at http://senselab.med.yale.edu/ (ModelDB database, accession number #2488). The model incorporates the following currents:
low density Na+ channels in the soma and dendrites, and high density Na+ channels in the axon hillock and initial segment (Hodgkin and Huxley kinetics);
fast K+ channels in the axon and soma (Hodgkin and Huxley kinetics);
slow non-inactivating K+ channels responsible for spike afterhyperpolarization;
calcium-dependent K+ channels;
high-threshold Ca2+ channels.
This model was also implemented using the NEURON simulation environment (Hines and Carnevale, 1997) and it contained 104 dendritic compartments. Each compartment was comprised by an odd number of segments, each of which no longer than 50 μm, which resulted in a total of 242 dendritic segments. The total number of segments being simulated, including soma and myelinated axon, was 283. The resting membrane potential was approximately −70 mV, the observed action potential threshold was approximately −56 mV and the input resistance in response to 0.1 nA of injected current was 95 MΩ. The densities and distribution of the current mechanisms were based on the original publication. This implementation resulted in a model neuron that would frequently fire action potentials as small bursts of doublets in response to evoked inputs (as originally reported). All the simulations were performed with an integration time step of 0.1 ms, at a temperature of 37°C.
In vivo neurons are constantly bombarded by ongoing background synaptic activity which causes significant instantaneous fluctuations in the membrane potential and resistance. To mimic these effects, we simulated noise by adding background synaptic activity, which we modeled by randomly distributing 1000 synapses (800 Ex and 200 Inh) on the dendritic tree. Excitatory and inhibitory synapses, respectively, were spontaneously active at rates of 1 and 5.5 Hz (Poisson statistics; Ho and Destexhe, 2000), had reversal potentials of 0 and −80 mV, respectively, and upon activation their conductance would increase instantaneously and decay exponentially with time constants of 5 and 10 ms (Chance et al., 2002). Background synaptic weights were adjusted such that background excitation and inhibition were “balanced” (Chance et al., 2002), i.e., background synaptic activity did not alter the model neuron's average resting membrane potential compared to rest. The empirically determined background excitatory and inhibitory synaptic weights were 0.12 and 0.35 pA, which caused a decrease in the input resistance of the cell to 74 MΩ (note that the inhibitory synapses were part of the “background” noise, they carried no signal and were not plastic). Moreover, background synaptic activity caused significant variations in the membrane potential as expected, resulting in a “basal” Vm SD of 0.5 mV (Figure 4C). This SD value is on the low end of the values observed in vivo but in this model an SD of just 2.3 mV, and zero weight on the “driving inputs” (Chance et al., 2002), would be sufficient to cause spontaneous firing at 0.4 Hz, essentially leaving no room for an increase in the weights of the excitatory synaptic inputs. The “driving” input synapses had the same characteristics as the excitatory background synapses, except that they were active at the times specified by the Poisson input patterns, their synaptic weight was plastic and, when indicated, they exhibited short-term dynamics.
Simulation of short-term synaptic plasticity
Short-term synaptic plasticity was simulated as described previously (Markram et al., 1998a; Maass and Markram, 2002; Mongillo et al., 2008). Briefly, STP is characterized by three parameters: U (fraction of synaptic efficacy used by the first action potential), τD (time constant of recovery from depression) and τF (time constant of synaptic facilitation). High values of U, which is bounded between 0 and 1, favor depression and low values facilitation. U together with τD and τF control the time-varying values of depression (D) and facilitation (F) variables. D is best thought of as a recovery variable, and the kinetics of D and F at each synapse are described by:
| (2) |
| (3) |
The presynaptic spike train at each synapse is represented by ΣnΔ(t − tn), where the Dirac function Δ(t) equals 0 at all values except when there is a presynaptic spike at time t, when it equals 1. The initial values of D and F are 1 and U, respectively. When there is a presynaptic spike, immediately after synaptic release, D is decreased by DF, and recovers thereafter to 1 with time constant τD. Similarly, upon a presynaptic spike, F is increased by U(1 − F) and subsequently recovers back to U with time constant τF. Hence, F is related to the degree of facilitation and its initial value (U) represents an unfacilitated synapse. Presynaptic efficacy is determined by the product of D and F. Total effective synaptic efficacy was obtained by multiplying the presynaptic efficacy with the post-synaptic weight, w (see below). In Figure 1 τD = 100 ms, τF = 200 ms, and the weights w were 1.00 and 0.08 for the “PPF only” and “PPD only” conditions, respectively. In all simulations U was bounded between 0.1 and 0.9 (except in Figure 1, where U was bounded between (0.05 and 0.95) to improve visualization. Unless otherwise noted the values of τD and τF were selected from a uniform distribution between 1 and 1200 ms.
Stimuli
Stimuli were composed of 10 inputs, and the duration of each pattern was 250 ms. The inputs followed random Poisson statistics: at each time point the presence or absence of a spike was drawn from a uniform distribution set to yield an average rate of 20 Hz. A refractory period of 5 ms was imposed, which recovered with a time constant of 2 ms. Each stimulus set consisted of five spike patterns which were presented randomly, for a total of 5 × 500 presentations (Figure 2) or 5 × 200 presentations (Figure 4). During testing the stimuli were presented in the forward direction (which was used for training), and in the reverse direction. A total of 20 different stimulus sets were built from different random number seeds, each set was tested on a different simulated neural network, each also based on different random number generator seeds.
Supervised learning rule
We used the tempotron learning rule (Gutig and Sompolinsky, 2006) to train each neuron to respond exclusively to one target (positive) Poisson pattern but not the others (negative patterns). In brief, in this supervised learning rule, if the post-synaptic neuron did not fire to the target (“positive”) stimulus the weights of the synapses whose activity contributed to the maximum voltage are increased in a manner proportional to that contribution. On the other hand, if the post-synaptic neuron fires at any point during a “negative” stimulus the synaptic weights of each synapse are decreased in proportion to their contribution to the incorrect spike.
Neurons had 10 incoming synapses, with initial strengths [0 0.01] (Figures 1, 2) or [0 10−4] μS (Figure 4) drawn from an uniform distribution. To determine the change in the post-synaptic weight (Δw) at each learning step the tempotron learning kernel was normalized to 1 and multiplied by a constant of 10−3 (Figures 1 and 2) or 2 × 10−4 (Figure 4), which determines the learning rate. Δw was divided by U to normalize the changes in synaptic strength (U alters the temporal profile of the PSP, which can slow the effectiveness of the tempotron learning rule) and the synaptic weights were bounded between [10−9 and 0.15] μS.
Temporal synaptic plasticity
There are a number of different potential implementations for the plasticity of the U, τD, and τF variables (previously discussed in abstracts: Carvalho and Buonomano, 2008; Gutig et al., 2008). Here we focus on a rule that changes the U parameter. We have explored similar types of rules to control τD and τF, however they did not generally improve performance significantly compared to U plasticity alone (see below), and since plasticity of the time constants is more speculative these results are not included here.
Since the value of U should be dependent on the timing and number of presynaptic spikes in relation to the post-synaptic spike, a variable that tracks the presynaptic spike train is required. Thus we defined a variable S that reflects the number of spikes at each presynaptic terminal, and can be thought of as a saturating presynaptic Ca2+ sensor:
| (4) |
where τS (1 s) and Smax Eq. 4 represent the decay time constant and maximal value of S, respectively.
Since low and high values of U favor facilitation and depression, respectively, we used an equilibrium based equation (Eq. 4) to control U. At the time of the post-synaptic spike the presynaptic variable U (which in this model relates to Pr) of each synapse i was updated by:
| (5) |
where tpre represents the time of the last presynaptic spike to precede tpost, and corresponds to a reasonable equilibrium or default value of F (recall that F is essentially the running value of U Eq. 2) at the time of the post-synaptic spike (in all simulations shown here a value of 0.5 was used, Table 1). Thus if the post-synaptic spike occurs after one presynaptic spike (S < 1; or well after the last presynaptic spike) U will converge towards Umax (0.9) and favor paired-pulse depression (PPD). If the post-synaptic spike occurs after more than one presynaptic spike (S > 1) U will converge towards an appropriate value that will yield at the time of the last presynaptic vesicle release to precede the post-synaptic spike. Note that the value of F at the time of the last presynaptic spike is used because it reflects the degree of facilitation the last time the synapse was used – which is ultimately what contributes to the behavior of the post-synaptic neuron. This results in a more efficient learning rule in part because ΔU is adjusted according to the potential strength before the synapses was used (for after release F can be high either because there was significant facilitation or because there was many presynaptic pulses that drove F towards its asymptote). While more effective computationally, this implementation is less biologically plausible as it requires temporarily “storing” the value of F. An implementation that relies on the running value of F, however, is also effective, but slower in converging. Note additionally, that although we propose that the trigger for plasticity of U is a post-synaptic spike – which must be retrogradely communicated to the presynaptic terminal – that because of the nature of the tempotron learning rule it is actually the peak post-synaptic voltage that triggers STP plasticity. We further stress that the current implementation is meant as a proof of principle that plasticity of STP improves temporal processing, not as a mechanistic hypothesis as to how exactly such plasticity would be implemented.
Table 1.
Values of the constants used in the computer simulations.
| Umax | 0.9 |
| 0.5 | |
| 0.1 | |
| 0.4 | |
| 0.2 | |
| 0.2 | |
| αU | 0.05 |
| ατD+ | 10 |
| ατF+ | 10 |
| ατD− | 25 |
| ατF− | 20 |
| τK | 10 ms |
| τS | 1000 ms |
| Smax | 4 |
As with the tempotron, presynaptic plasticity was modulated with a kernel that equals 1 at tpost and decays to 0 for the preceding time points (with time constant τK) – thus preventing plasticity of short-term plasticity at synapses that fired significantly before the post-synaptic spike.
The desired steady-state values and gain constants used in the simulations presented here were determined empirically and are presented in Table 1.
Spike-timing-dependent plasticity
In Figure 1 we used STDP to change the post-synaptic weights. STDP was implemented according to (Song et al., 2000):
| (6) |
Where wi is assumed to be controlling the synaptic weight and Δt = tpost − tpre. In Figure 1 initial weights were 0.05 and Ap = Ad = 5 × 10−4, τp = 30, and τd = 40 ms. During training the post-synaptic neuron was depolarized 20 ms after the last spike of pathway P1 (Figure 1C) or 5 ms after the last spike of the target interval.
Results
To provide a simple demonstration of the computational value of plasticity of short-term plasticity (which we will refer to as temporal synaptic plasticity) we describe a toy problem that cannot be solved unless STP is “learned.” Consider a post-synaptic neuron that receives inputs from two presynaptic neurons. Each of the presynaptic neurons fires a pair of spikes separated by 100 ms, but there are two possible global patterns of activity. In the “synch” pattern both inputs spike in synchrony; in the “shift” pattern only one of the spikes is synchronous (Figure 1A). The task is to discriminate between both patterns by having the post-synaptic neuron fire to the shift but not the synch pattern (we will refer to this as the shift problem) – implicit here is that it must also discriminate between “Input1 first” and an “Input2 first” shift patterns, making this a true spatiotemporal task. One can see that this task is impossible to solve if the synapses are static (no STP), because the sum of the synchronous EPSPs will be the same independent of the global pattern. Additionally one can see that the task is also impossible if both synapses exhibit the same type and magnitude of STP (Figure 1B). Specifically, if both synapses exhibit paired-pulse facilitation (PPF) any set of synaptic strengths that result in firing to the shift pattern must also produce a spike in response to the second pulse of the synch pattern. Similarly, if both synapses exhibit PPD, the maximal response must occur at the first pulse of the synch pattern (assuming no temporal summation, but the argument holds taking temporal summation into account). However, the post-synaptic neuron can respond selectively to the shift pattern if input 1 exhibits PPF and input 2 PPD (Figure 1C, right panels). Thus the mere presence of STP does not allow this simple circuit to solve the shift problem, but if there were a learning rule that guided synapses toward facilitation or depression, depending on the global temporal structure of pre- and post-synaptic activity, the shift problem can be solved.
Experimental and theoretical studies indicate that STP is generally a presynaptic phenomenon that relies on the balance of two opposing variables, one controlling depression and the other facilitation (Gingrich and Byrne, 1985; Varela et al., 1997; Markram et al., 1998a; Zucker and Regehr, 2002; Abbott and Regehr, 2004). Depression is viewed as arising from the depletion of the readily releasable pool of synaptic vesicles (Schneggenburger et al., 2002), while facilitation is associated with the accumulation of residual calcium in the presynaptic terminal, which can enhance subsequent transmitter release (Katz and Miledi, 1968; Burnashev and Rozov, 2005). In a quantitative description of STP by Tsodyks and Markram (Markram et al., 1998a) a parameter U determines in part whether a synapse exhibits depression or facilitation. U reflects the fraction of presynaptic efficacy that is used by the first spike, and if one were to assume the presence of many synaptic boutons U would be related to the probability of vesicle release (Pr), which is known to be one of the determinants of whether a synapse exhibits short-term facilitation or depression. In addition to U, this description of STP assumes the presence of two time constants that govern the time course of depression and facilitation (τD and τF) and, together, these three variables can be used to fit a wide range of different flavor of STP (Markram et al., 1998b; Gupta et al., 2000), here we will assume these time constants are fixed.
It is possible for the simple circuit presented in Figure 1A to solve the shift problem if we assume the presence of a learning rule that controls U (“Pr”). If the post-synaptic cell fires after the first presynaptic action potential, high U values are desirable (causing PPD); whereas if it fires after the second presynaptic action potential low U values should be preferred (so that not too much presynaptic efficacy is used in the first pulse, allowing for PPF). To mimic a potential experimental protocol, during training we depolarized the output neuron to make it fire in the middle of the shift pattern, and implemented a rule that altered U (see Figure 1C). The rule assumes the presence of a parameter S that tracks the number of presynaptic spikes and can be thought of as a saturating Ca2+-sensor (see Materials and Methods). If the presynaptic neuron only spiked once before the post-synaptic spike (S ≤ 1) U increases (favoring PPD), in contrast, if it spiked more than once (S > 1) U decreases (favoring PPF). This simple rule was able to solve the shift problem (Figure 1C), demonstrating that a STP learning rule can solve an otherwise unsolvable spatiotemporal problem.
In these simulations we implemented pre- and post-synaptic learning rules in an essentially independent manner (see Materials and Methods). The presynaptic learning rule, temporal synaptic plasticity, governs the dynamics of STP – determining whether short-term depression or short-term facilitation is induced and the temporal profile of the effective synaptic strength. The post-synaptic learning rule was STDP, which is responsible for governing the traditional “weight” of the synapse associated with AMPA receptor number and conductance. However, since the mechanisms of STP are not fully understood, and because post-synaptic mechanisms may contribute to STP (Rozov and Burnashev, 1999; Bagal et al., 2005) it should be stressed that our approach represents a simplification.
Temporal synaptic plasticity: discrimination of complex spike patterns
We next examined whether plasticity of STP enhances the ability of feed-forward networks to discriminate complex spatiotemporal patterns (Figure 2A; see Materials and Methods). Output neurons were trained to discriminate the input patterns by adjusting the post-synaptic weights according to a previously described supervised learning rule (Gutig and Sompolinsky, 2006). In brief, if the post-synaptic neuron did not fire to the target (“positive”) stimulus the weights of the synapses whose activity contributed to the maximum voltage are increased in a manner proportional to that contribution. On the other hand, if the post-synaptic neuron fires at any point during a “negative” stimulus the synaptic weights of each synapse are decreased in proportion to their contribution to the incorrect spike. At each trial during training we randomly presented one of five spike patterns (each pattern consisted of 10 inputs) with average firing rates of 20 Hz. During testing we included the reverse (backward) version of the spike patterns to ensure that the output units were discriminating the spatiotemporal structure of the patterns.
The goal of the output neuron is to adjust its 10 synaptic weights in a manner that it fires an action potential selectively to its target pattern. In the absence of STP, the tempotron learning rule performed well, yielding 5–7% errors (Figure 2B). However, when we tested performance not only in response to the original stimuli, but to their reverse patterns as well, performance degraded to 40 ± 1% errors (an error is a failure to detect the positive pattern or firing to any of the non-target patterns, Figure 2C, blue solid bar). Analyzing the errors in more detail reveals that the output units are generally firing to the reverse of their target pattern. The lack of selectivity to the forward versus reverse patterns indicates that discrimination relies in large part not on the temporal structure of the stimulus, but on the detection of synchronous spike sets that are exclusive to a particular stimulus. The presence of non-plastic (“fixed”) STP significantly increased the discrimination of forward versus reverse spatiotemporal patterns. Specifically, when the parameters controlling STP were randomly assigned, discrimination improved to 28 ± 2% total errors (green bars in Figure 2C). Interestingly in the presence of static STP most of the errors were now produced by between pattern confusion – indicating that the presence of STP improved direction selectivity. Next we incorporated the temporal synaptic plasticity learning rule, which resulted in a highly significant improvement in performance (10 ± 2%, red bar). These results establish that plasticity of STP improves the discrimination of complex temporal stimuli. Importantly, the differences in performance during testing were not an outcome of the asymptote during training (i.e., training different groups to the same value did not alter the improvement produced by STP plasticity). As a further control we shuffled the U parameter of each synapse obtained at the end of training across synapses, and then retrained the output units with the tempotron alone (i.e., the STP parameters were held constant during training). This procedure resulted in increased percentage of errors (29 ± 3%, orange bar in Figure 2C), similar to the levels of the “Random STP” condition (green bar). This control shows that if STP at each synapse is “tunable” there is a significant improvement in performance, which is not a result of the statistical distribution of different flavors of STP.
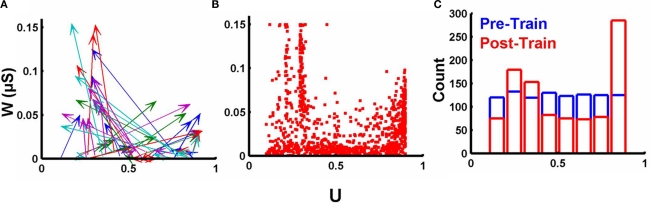
Implicit in the notion that synapses may adjust their short-term plasticity to better process the temporal features of stimuli is that U should not be correlated with post-synaptic weights in any simple fashion. To examine the changes in U we plotted the pretraining and posttraining values of U and w (for a single experiment) in Figure 3A. The plot reveals that changes in U and w do not simply reflect initial values or a uniform shift. Across all synapses and experiments there was a complex relationship between U and w, after training (Figure 3B). Additionally, training resulted in a significant change in the distribution of U, the final distribution was bimodal with a peak around 0.2–0.3 and one at the upper boundary (Figure 3C). Note that in Eq. 5, there are two equilibrium points, and when the post-synaptic spike occurs after multiple presynaptic spikes U should be driven towards a value that results in (0.5) at the time of the “last” presynaptic spike. The two neighboring “peaks” in Figure 3B (around 0.22 and 0.3) reflect this. For example, in the case of two presynaptic spikes, followed by a post-synaptic spike, a value of U = 0.3 will yield a value of approximately 0.51 (U + U (1 − U); assuming the time constant τF is very large relative to the presynaptic interspike interval) at the time of the second presynaptic spike. Similarly in the case of three presynaptic spikes, Eq. 5 will drive U to values around 0.22. The presence of these multiple “peaks” demonstrates that the final values are strongly dependent on the structure of the temporal patterns. And the absence of a simple relationship between U and w, indicates that in these simulations STP is not an epiphenomenon of baseline synaptic strength determined by the post-synaptic terminal.
Figure 3.
Complex relationship between final synaptic weights and values of U. (A) Change in both w and U over the course of training for one simulation. The origin of each arrow marks the initial value of w (initially all weak) and U; the arrowhead marks the values of w and U for each synapse after training. Arrow colors reflect each of the five output units (each trained to recognize a different pattern). (B) Final values of w and U for all synapses across all 20 experiments. (C) Initial (blue) and final (red) distribution of U values across all 20 experiments.
Spatiotemporal selectivity in a realistic neuron
The above results establish that STP and its plasticity have the potential to significantly enhance the ability of a simple feed-forward circuit to discriminate complex spatiotemporal patterns. However, the above simulations relied on single compartment integrate-and-fire units, and real neurons have a number of critical features that could impact the above results. Particularly, different synaptic inputs can have different delays, amplitudes, and interact non-linearly with their neighbors depending on their location on the dendritic tree. Thus, to examine the robustness of plasticity of STP under more realistic conditions we used a reconstructed layer 3 pyramidal cortical model neuron containing passive and active conductances (Mainen and Sejnowski, 1996) and significant spontaneous background activity (Figure 4).
We distributed the driving inputs randomly on the dendritic branches around the soma (specifically, on 10 of the 16 quaternary branches, Figure 4A), and followed a similar training protocol as in Figure 2. With the tempotron learning rule alone governing the synaptic weights, the performance on testing was 48 ± 1% (no STP). Random STP significantly improved the discrimination of FWD versus REV patterns (32 ± 2%), but synapses with temporal synaptic plasticity of STP provided the biggest decrease in the number of errors (17 ± 2%; the percentage of errors of the shuffled control was 31 ± 2%; Figure 4B).
The above results establish a dramatic increase in the ability of a single output unit to discriminate complex spatiotemporal stimuli patterns when STP is governed by a simple learning rule that controls the parameter U. Little experimental data is available as to whether the time constant parameters of STP are plastic, but since they seem to be governed by a network of Ca2+-dependent proteins it is a possibility. To examine whether plasticity of τD and τF further enhance discrimination we incorporated separate and more complex (and less biologically plausible) learning rules for τD and τF. Our results revealed that inclusion of time constant plasticity did not significantly increase performance (data not shown).
Nevertheless, there are clear situations in which time constant plasticity would be beneficial. One such scenario is a purely temporal internal discrimination task in which a post-synaptic neuron would be required to respond selectively to a specific interval of spikes from a single presynaptic neuron. In order for the post-synaptic neuron to fire specifically to the second of a pair of presynaptic spikes separated by 100 ms, but not to an interval of 50 or 200 ms, τD and τF need to be tuned accordingly. This can be achieved by learning rules that take into account not only the number of presynaptic spikes at the time of the post-synaptic spike, but of the current values of the parameters controlling both facilitation and depression. However, plasticity of τD and τF is both more speculative in nature and more complex in regard to biological plausibility. Since plasticity of U (or Pr) is computationally effective and more biologically plausible (see below), we would suggest that if STP specifically adapts to the temporal features of stimuli the probability of release would be the primary target of such a rule.
Discussion
It has been proposed that STP may play a role in timing (Buonomano and Merzenich, 1995; Buonomano, 2000; Maass et al., 2002) and the filtering of time-varying patterns of activity (Dobrunz and Stevens, 1999; Fortune and Rose, 2001), a hypothesis consistent with experimental data suggesting that STP contributes to interval selective responses in the frog auditory system (Edwards et al., 2007). In these previous models, STP contributed to spatiotemporal processing by altering the internal state of complex recurrent neural networks. Here we show that even in a simple feed-forward network STP dramatically improves the discrimination of time-varying stimuli. Whether in simple or complex networks, STP provides a built-in temporal asymmetry that ensures that forward and reverse stimuli are distinguishable. This is a critical observation because forward versus reverse selectivity is a defining characteristic of spatiotemporal selective cells (Margoliash, 1983; Doupe, 1997; Wang and Kadia, 2001; Kilgard and Merzenich, 2002). Some models of the discrimination of spatiotemporal patterns rely largely on the synchrony of subsets of inputs (Gutig and Sompolinsky, 2006; Masquelier et al., 2008) and thus do not easily discriminate between forward and reverse stimuli; yet, perceptually, forward and reverse stimuli are thoroughly distinct. Indeed, the mechanisms the brain uses to recognize spatiotemporal stimuli appear to be inherently time asymmetric because robust forward versus reverse selectivity is present even if the reverse stimuli were never experienced – humans and songbirds do not confuse forward and reverse vocalizations even if they were never exposed to the latter.
Biological plausibility
Here it is proposed that the relative timing of the pre- and post-synaptic spikes do not simply modulate long-term plasticity, as established by associative rules such as STDP (Debanne et al., 1994; Markram et al., 1997; Bi and Poo, 1998), but may serve as a “teacher” signal to determine whether the synapse should be depressing or facilitating. Temporal synaptic plasticity would require mechanisms to be in place that regulate STP independently of baseline synaptic transmission – a process that would likely rely on changes in the regulation of presynaptic Ca2+.
Within the same type of synapse, STP can range from strong short-term depression to significant short-term facilitation (Reyes and Sakmann, 1999; Cheetham et al., 2007; Hardingham et al., 2007). Although probability of release or initial synaptic strength are often a predictor of whether a synapse exhibits depression or facilitation, these correlations are often not very strong and not always significant (Reyes and Sakmann, 1999; Atzori et al., 2001; Sippy et al., 2003; Cheetham et al., 2007). One explanation for the heterogeneity of STP is that the presynaptic mechanisms of STP may be partially independent of the learning rules controlling baseline PSP strength – as the current model predicts. Here the change in STP was implemented through modulation of the probability of release, simulated as the parameter U. But, absent from our implementation is the fact that synaptic release is probabilistic and that a high percentage of synaptic events are “failures.” Although the stochastic nature of synaptic transmission was not included in our simulations it should not alter our overall conclusions, with the exception that it may alter the speed of convergence of the learning rule.
Since short-term plasticity is primarily governed by presynaptic mechanisms, and because our model relies heavily on the number of presynaptic spikes, we propose the mechanisms underlying temporal synaptic plasticity would be presynaptic in nature. Specifically, that a retrograde signal triggered by a post-synaptic spike interacts with the level of Ca2+ (determined by the number of presynaptic action potentials) in the presynaptic terminal: low levels of Ca2+ at the time of the retrograde messenger would shift short-term plasticity towards depression, conversely high levels of Ca2+ would favor facilitation. While there is little evidence for such an interaction, there is evidence that there is indeed retrograde communication between post- and presynaptic terminals: in the neocortex it has been shown that retrograde messengers seem to contribute to the induction of the long-term depression component of STDP (t-LTD) – both endocannabinoids and nitric oxide are candidate retrograde messengers (Sjostrom et al., 2003; Bender et al., 2006; Sjostrom et al., 2007). One potential problem with this interaction is delays in the arrival of the retrograde messenger; although little is known about the timing of retrograde signals, this problem might be solved by built-in delays in the presynaptic Ca2+ trace. In parallel with interactions happening at the presynaptic terminal responsible for potential changes in short-term synaptic plasticity, synapses still must keep track of the order of the pre- and post-synaptic spikes, as required for STDP. It has been proposed that order sensitivity for STDP is a post-synaptic computation, that relies on one or two coincidence (e.g., Karmarkar and Buonomano, 2002; Shouval and Kalantzis, 2005). But we remain somewhat agnostic regarding the interaction between the mechanisms of STDP and those underlying temporal synaptic plasticity. As mentioned, the major novel mechanistic prediction from our model is that retrograde signals must be generated by the post-synaptic spike, diffuse to the presynaptic terminal, and interact with the level of presynaptic Ca2+. To the best of our knowledge there is no data to support this prediction. However, given the large number of presynaptic proteins involved in Ca2+ regulation (Zucker and Regehr, 2002; Burnashev and Rozov, 2005; Mochida et al., 2008), it seems possible that such mechanisms are in place. Indeed, there is evidence that presynaptic mechanisms are in place to regulate short-term plasticity. For example, it has been shown that presynaptic increases in a neural Ca2+ sensor (NCS1) can switch synapses from a PPD to a PPF mode without changing baseline synaptic strength (Sippy et al., 2003). Additional evidence that there may be as yet undiscovered mechanisms in place to regulate short-term facilitation is that recently identified presynaptic NMDA receptors play a role in modulating STP (Larsen et al., 2011).
Experimental predictions
The simplest experimental prediction of the hypothesis proposed here is that when pairing post-synaptic activity with a train of presynaptic spikes, the position of the post-synaptic spikes should shape short-term plasticity in a predictable manner. For example, a post-synaptic spike paired with the first (early pairing) or last (late pairing) of a pair of presynaptic spikes should both induce LTP. However, the former should favor PPD and the latter PPF because the contribution of the EPSP to the post-synaptic spike would be optimized by short-term depression if the post spike occurs early, and by short-term facilitation if the post spike occurs late. It should be noted that this prediction has been indirectly examined experimentally in CA1 synapses with negative results (Buonomano et al., 1997). However, as mentioned previously, it is possible that CA1 and neocortical LTP have distinct properties relating to STP; indeed the same induction protocol can induce similar magnitudes of LTP in both CA1 and L-II/III pyramidal neurons, yet a dramatic change in STP is only observed in the neocortical synapses (Buonomano, 1999). Related experiments were performed by Froemke et al. (2006), who confirmed that pairing a single post-synaptic spike with spikes that were early or late in a presynaptic train both produced LTP (although progressively less), however, changes in STP were not examined.
Although to the best of our knowledge no experimental studies have explicitly examined the effects of “early” and “late” paring on the induction of long- and short-term synaptic plasticity it is still relevant to ask if there are reasons why any potential directed changes in STP may have been missed. We would suggest that one possible reason is because in contrast to the rapid induction of long-term plasticity of baseline synaptic strength, plasticity of STP may require protein synthesis and take place over the course of hours. This view is supported by an observation in the mossy fiber pathway, where it is typically reported that LTP changes STP (increasing depression). Interestingly, however, at the mossy fiber → CA3 synapse the initial decrease in the paired-pulse ratio slowly reverses over the course of hours, bringing STP close to baseline levels while the first EPSP remains more or less stable over this same window (Huang et al., 1994). Although LTP at these synapses relies on different mechanisms than in the neocortex (and CA1), this result suggests that at least in the mossy fiber synapses STP is independent of initial synaptic strength and plasticity of STP occurs over a time course of hours. Thus, an experimental test of our prediction may require examining the late-phase of synaptic plasticity.
The notion of temporal synaptic plasticity extends traditional Hebbian plasticity into the temporal domain by proposing that synapses learn not only whether they should be strong or weak, but when they should be strong or weak. Leading to the suggestion that presynaptic learning rules may be in place to primarily control STP, and a post-synaptic learning rule may control “baseline” synaptic strength. The presence of two learning rules operating in parallel at the same synapse may help explain the complexity of neocortical associative plasticity and why in some instances the same induction protocol can induce either LTD or LTP (Ismailov et al., 2004; Hardingham et al., 2007). Additionally, the presence of two independent learning rules governing pre- and post-synaptic efficacy provides a framework to understand neocortical plasticity data that indicates the presence of parallel pre- and post-synaptic changes under control of a complex network of biochemical processes (Bender et al., 2006; Sjostrom et al., 2007; Rodriguez-Moreno and Paulsen, 2008).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Supported by NIMH (MH60163), and Tiago P. Carvalho was supported by the Portuguese Science and Technology Foundation. We would like to thank Weixiang Chen, Hope Johnson, Jian Liu, and Felix Schweizer for their comments on earlier versions of this manuscript.
References
- Abbott L. F., Nelson S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183 [DOI] [PubMed] [Google Scholar]
- Abbott L. F., Regehr W. G. (2004). Synaptic computation. Nature 431, 796–803 10.1038/nature03010 [DOI] [PubMed] [Google Scholar]
- Abbott L. F., Varela J. A., Sen K., Nelson S. B. (1997). Synaptic depression and cortical gain control. Science 275, 220–224 10.1126/science.275.5297.221 [DOI] [PubMed] [Google Scholar]
- Atzori M., Lei S., Evans D. I., Kanold P. O., Phillips-Tansey E., McIntyre O., McBain C. J. (2001). Differential synaptic processing separates stationary from transient inputs to the auditory cortex. Nat. Neurosci. 4, 1230–1237 [DOI] [PubMed] [Google Scholar]
- Bagal A. A., Kao J. P., Tang C. M., Thompson S. M. (2005). Long-term potentiation of exogenous glutamate responses at single dendritic spines. Proc. Natl. Acad. Sci. U.S.A. 102, 14434–14439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender V. A., Bender K. J., Brasier D. J., Feldman D. E. (2006). Two coincidence detectors for spike timing-dependent plasticity in somatosensory cortex. J. Neurosci. 26, 4166–4177 10.1523/JNEUROSCI.0176-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi G. Q., Poo M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown T. H., Kairiss E. W., Keenan C. L. (1990). Hebbian synapses: biophysical mechanisms and algorithms. Annu. Rev. Neurosci. 13, 475–511 [DOI] [PubMed] [Google Scholar]
- Buonomano D. V. (1999). Distinct functional types of associative long-term potentiation in neocortical and hippocampal pyramidal neurons. J. Neurosci. 19, 6748–6754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonomano D. V. (2000). Decoding temporal information: A model based on short-term synaptic plasticity. J. Neurosci. 20, 1129–1141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonomano D. V., Hickmott P. W., Merzenich M. M. (1997). Context-sensitive synaptic plasticity and temporal-to-spatial transformations in hippocampal slices. Proc. Natl. Acad. Sci. U.S.A. 94, 10403–10408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonomano D. V., Merzenich M. M. (1995). Temporal information transformed into a spatial code by a neural network with realistic properties. Science 267, 1028–1030 10.1126/science.7863330 [DOI] [PubMed] [Google Scholar]
- Burnashev N., Rozov A. (2005). Presynaptic Ca2 (dynamics, Ca2(buffers and synaptic efficacy. Cell Calcium 37, 489–495 10.1016/j.ceca.2005.01.003 [DOI] [PubMed] [Google Scholar]
- Carvalho T. P., Buonomano D. V. (2008). Short-term plasticity enhances recognition of spatiotemporal stimuli in neural network models. Soc. Neurosci. Abstr. 136, 18 [Google Scholar]
- Chance F. S., Abbott L. F., Reyes A. D. (2002). Gain modulation from background synaptic input. Neuron 35, 773–782 10.1016/S0896-6273(02)00820-6 [DOI] [PubMed] [Google Scholar]
- Chance F. S., Nelson S. B., Abbott L. F. (1998). Synaptic depression and the temporal response characteristics of V1 cells. J. Neurosci. 18, 4785–4799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheetham C. E. J., Hammond M. S. L., Edwards C. E. J., Finnerty G. T. (2007). Sensory experience alters cortical connectivity and synaptic function site specifically. J. Neurosci. 27, 3456–3465 10.1523/JNEUROSCI.5143-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dan Y., Poo M. M. (2004). Spike timing-dependent plasticity of neural circuits. Neuron 44, 23–30 10.1016/j.neuron.2004.09.007 [DOI] [PubMed] [Google Scholar]
- Debanne D., Gahwiler B. H., Thompson S. M. (1994). Asynchronous pre- and postsynaptic activity induces associative long-term depression in area CA1 of the rat hippocampus in vitro. Proc. Natl. Acad. Sci. U.S.A. 91, 1148–1152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrunz L. E., Stevens C. F. (1999). Response of hippocampal synapses to natural stimulation patterns. Neuron 22, 157–166 10.1016/S0896-6273(00)80687-X [DOI] [PubMed] [Google Scholar]
- Doupe A. J. (1997). Song- and order-selective neurons in the songbird anterior forebrain and their emergence during vocal development. J. Neurosci. 17, 1147–1167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles J. C., Katz B., Kuffler S. W. (1941). Nature of the “Endplate Potential” in curarized muscle. J. Neurophysiol. 4, 362–387 [Google Scholar]
- Edwards C. J., Leary C. J., Rose G. J. (2007). Counting on inhibition and rate-dependent excitation in the auditory system. J. Neurosci. 27, 13384–13392 10.1523/JNEUROSCI.2816-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finnerty G. T., Roberts L. S., Connors B. W. (1999). Sensory experience modifies the short-term dynamics of neocortical synapses. Nature 400, 367–371 10.1038/22553 [DOI] [PubMed] [Google Scholar]
- Fortune E. S., Rose G. J. (2001). Short-term synaptic plasticity as a temporal filter. Trends Neurosci. 24, 381–385 10.1016/S0166-2236(00)01835-X [DOI] [PubMed] [Google Scholar]
- Froemke R. C., Tsay I. A., Raad M., Long J. D., Dan Y. (2006). Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95,1620–1629 10.1152/jn.00910.2005 [DOI] [PubMed] [Google Scholar]
- Galarreta M., Hestrin S. (1998). Frequency-dependent synaptic depression and the balance of excitation and inhibition in the neocortex. Nat. Neurosci. 1, 587–594 [DOI] [PubMed] [Google Scholar]
- Gingrich K. J., Byrne J. H. (1985). Simulation of synaptic depression, posttetanic potentiation, and presynaptic facilitation of synaptic potentials from sensory neurons mediating gill-withdrawal reflex in Aplysia. J. Neurophysiol. 53, 652–669 [DOI] [PubMed] [Google Scholar]
- Gupta A., Wang Y., Markram H. (2000). Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science 287, 273–278 10.1126/science.287.5451.273 [DOI] [PubMed] [Google Scholar]
- Gutig R., Sompolinsky H. (2006). The tempotron: a neuron that learns spike timing-based decisions. Nat. Neurosci. 9, 420–428 [DOI] [PubMed] [Google Scholar]
- Gutig R., Sompolinsky H., Tsodyks M. (2008). Temporal processing with plastic short term synaptic dynamics. Soc. Neurosci. Abstr. 432, 5 [Google Scholar]
- Hardingham N. R., Hardingham G. E., Fox K. D., Jack J. J. (2007). Presynaptic efficacy directs normalization of synaptic strength in layer 2/3 rat neocortex after paired activity. J. Neurophysiol. 97, 2965–2975 10.1152/jn.01352.2006 [DOI] [PubMed] [Google Scholar]
- Hebb D. O. (1949). Organization of Behavior. New York: Wiley [Google Scholar]
- Hines M. L., Carnevale N. T. (1997). The NEURON simulation environment. Neural Comput. 9, 1179–1209 10.1162/neco.1997.9.6.1179 [DOI] [PubMed] [Google Scholar]
- Ho N., Destexhe A. (2000). Synaptic background activity enhances the responsiveness of neocortical pyramidal neurons. J. Neurophysiol. 84, 1488–1496 [DOI] [PubMed] [Google Scholar]
- Huang Y. Y., Li X. C., Kandel E. R. (1994). cAMP contributes to mossy fiber LTP by initiating both a covalently mediated early phase and macromolecular synthesis-dependent late phase. Cell 79, 69–79 10.1016/0092-8674(94)90401-4 [DOI] [PubMed] [Google Scholar]
- Ismailov I., Kalikulov D., Inoue T., Friedlander M. J. (2004). The kinetic profile of intracellular calcium predicts long-term potentiation and long-term depression. J. Neurosci. 24, 9847–9861 10.1523/JNEUROSCI.0738-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karmarkar U. R., Buonomano D. V. (2002). A model of spike-timing dependent plasticity: one or two coincidence detectors? J. Neurophysiol. 88, 507–513 [DOI] [PubMed] [Google Scholar]
- Katz B., Miledi R. (1968). The role of calcium in neuromuscular facilitation. J. Physiol. (Lond.) 195, 481–492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilgard M. P., Merzenich M. M. (2002). Order-sensitive plasticity in adult primary auditory cortex. Proc. Natl. Acad. Sci. U.S.A. 99, 3205–3209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen R. S., Corlew R. J., Henson M. A., Roberts A. C., Mishina M., Watanabe M., Lipton S. A., Nakanishi N., Perez-Otano I., Weinberg R. J., Philpot B. D. (2011). NR3A-containing NMDARs promote neurotransmitter release and spike timing-dependent plasticity. Nat. Neurosci. 14, 338–344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maass W., Markram H. (2002). Synapses as dynamic memory buffers. Neural Netw. 15, 155–161 10.1016/S0893-6080(01)00144-7 [DOI] [PubMed] [Google Scholar]
- Maass W., Natschläger T., Markram H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14, 2531–2560 10.1162/089976602760407955 [DOI] [PubMed] [Google Scholar]
- Mainen Z. F., Sejnowski T. J. (1996). Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363–366 10.1038/382363a0 [DOI] [PubMed] [Google Scholar]
- Malenka R. C., Bear M. F. (2004). LTP and LTD: an embarrassment of riches. Neuron 44, 5–21 10.1016/j.neuron.2004.09.012 [DOI] [PubMed] [Google Scholar]
- Margoliash D. (1983). Acoustic parameters underlying the responses of song-specific neurons in the white-crowned sparrow. J. Neurosci. 3, 1039–1057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H., Lubke J., Frotscher M., Sakmann B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 10.1126/science.275.5297.213 [DOI] [PubMed] [Google Scholar]
- Markram H., Tsodyks M. (1996). Redistribution of synaptic efficacy between neocortical pyramidal neurons. Nature 382, 807–810 10.1038/382807a0 [DOI] [PubMed] [Google Scholar]
- Markram H., Wang Y., Tsodyks M. (1998a). Differential signaling via the same axon of neocortical pyramidal neurons. Proc. Natl. Acad. Sci. U.S.A. 95, 5323–5328 10.1073/pnas.95.9.5323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H., Wang Y., Tsodyks M. (1998b). Differential signaling via the same axon of neocortical pyramidal neurons. Proc. Natl. Acad. Sci. U.S.A. 95, 5323–5328 10.1073/pnas.95.9.5323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masquelier T., Guyonneau R., Thorpe S. J. (2008). Spike timing dependent plasticity finds the start of repeating patterns in continuous spike trains. PLoS ONE 3, e1377. 10.1371/journal.pone.0001377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauk M. D., Buonomano D. V. (2004). The neural basis of temporal processing. Ann. Rev. Neurosci. 27, 307–340 [DOI] [PubMed] [Google Scholar]
- Mochida S., Few A. P., Scheuer T., Catterall W. A. (2008). Regulation of presynaptic Ca(V)2.1 channels by Ca2+ sensor proteins mediates short-term synaptic plasticity. Neuron 57, 210–216 10.1016/j.neuron.2007.11.036 [DOI] [PubMed] [Google Scholar]
- Mongillo G., Barak O., Tsodyks M. (2008). Synaptic theory of working memory. Science 319, 1543–1546 10.1126/science.1150769 [DOI] [PubMed] [Google Scholar]
- Reyes A., Sakmann B. (1999). Developmental switch in the short-term modification of unitary EPSPs evoked in layer 2/3/ and layer 5 pyramidal neurons of rat neocortex. J. Neurosci. 19, 3827–3835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Moreno A., Paulsen O. (2008). Spike timing-dependent long-term depression requires presynaptic NMDA receptors. Nat. Neurosci. 11, 744–745 [DOI] [PubMed] [Google Scholar]
- Rothman J. S., Cathala L., Steuber V., Silver R. A. (2009). Synaptic depression enables neuronal gain control. Nature. 457, 1015–1018 10.1038/nature07604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rozov A., Burnashev N. (1999). Polyamine-dependent facilitation of postsynaptic AMPA receptors counteracts paired-pulse depression. Nature 401, 594–598 10.1038/44151 [DOI] [PubMed] [Google Scholar]
- Schneggenburger R., Sakaba T., Neher E. (2002). Vesicle pools and short-term synaptic depression: lessons from a large synapse. Trends Neurosci. 25, 206–212 10.1016/S0166-2236(02)02139-2 [DOI] [PubMed] [Google Scholar]
- Selig D. K., Nicoll R. A., Malenka R. C. (1999). Hippocampal long-term potentiation preserves the fidelity of postsynaptic responses to presynaptic bursts. J. Neurosci. 19, 1236–1246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seung H. S. (2003). Learning in spiking neural networks by reinforcement of stochastic synaptic transmission. Neuron 40, 1063–1073 10.1016/S0896-6273(03)00761-X [DOI] [PubMed] [Google Scholar]
- Shouval H. Z., Kalantzis G. (2005). Stochastic properties of synaptic transmission affect the shape of spike time-dependent plasticity curves. J. Neurophysiol. 93, 1069–1073 10.1152/jn.00504.2004 [DOI] [PubMed] [Google Scholar]
- Sippy T., Cruz-Martin A., Jeromin A., Schweizer F. E. (2003). Acute changes in short-term plasticity at synapses with elevated levels of neuronal calcium sensor-1. Nat. Neurosci. 6, 1031–1038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjostrom P. J., Turrigiano G. G., Nelson S. B. (2003). Neocortical LTD via coincident activation of presynaptic NMDA and cannabinoid receptors. Neuron 39, 641–654 10.1016/S0896-6273(03)00476-8 [DOI] [PubMed] [Google Scholar]
- Sjostrom P. J., Turrigiano G. G., Nelson S. B. (2007). Multiple forms of long-term plasticity at unitary neocortical layer 5 synapses. Neuropharmacology 52, 176–184 10.1016/j.neuropharm.2006.07.021 [DOI] [PubMed] [Google Scholar]
- Song S., Miller K. D., Abbott L. F. (2000). Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926 [DOI] [PubMed] [Google Scholar]
- Speed H. E., Dobrunz L. E. (2008). Developmental decrease in short-term facilitation at Schaffer collateral synapses in hippocampus is mGluR1 sensitive. J. Neurophysiol. 99, 799–813 10.1152/jn.00625.2007 [DOI] [PubMed] [Google Scholar]
- Sussillo D., Toyoizumi T., Maass W. (2007). Self-tuning of neural circuits through short-term synaptic plasticity. J. Neurophysiol. 97, 4079–4095 10.1152/jn.01357.2006 [DOI] [PubMed] [Google Scholar]
- Varela J. A., Sen K., Gibson J., Fost J., Abbott L. F., Nelson S. B. (1997). A quantitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J. Neurosci. 17, 7926–7940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Kadia S. C. (2001). Differential representation of species-specific primate vocalizations in the auditory cortices of marmoset and cat. J. Neurophysiol. 86, 2616–2620 [DOI] [PubMed] [Google Scholar]
- Zhang Z. W. (2004). Maturation of layer V pyramidal neurons in the rat prefrontal cortex: intrinsic properties and synaptic function. J. Neurophysiol. 91, 1171–1182 10.1152/jn.00855.2003 [DOI] [PubMed] [Google Scholar]
- Zucker R. S. (1989). Short-term synaptic plasticity. Annu. Rev. Neurosci. 12, 13–31 [DOI] [PubMed] [Google Scholar]
- Zucker R. S., Regehr W. G. (2002). Short-term synaptic plasticity. Annu. Rev. Physiol. 64, 355–405 10.1146/annurev.physiol.64.092501.114547 [DOI] [PubMed] [Google Scholar]