Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data

Abstract

Developments in whole genome biotechnology have stimulated statistical focus on prediction methods. We review here methodology for classifying patients into survival risk groups and for using cross-validation to evaluate such classifications. Measures of discrimination for survival risk models include separation of survival curves, time-dependent ROC curves and Harrell’s concordance index. For high-dimensional data applications, however, computing these measures as re-substitution statistics on the same data used for model development results in highly biased estimates. Most developments in methodology for survival risk modeling with high-dimensional data have utilized separate test data sets for model evaluation. Cross-validation has sometimes been used for optimization of tuning parameters. In many applications, however, the data available are too limited for effective division into training and test sets and consequently authors have often either reported re-substitution statistics or analyzed their data using binary classification methods in order to utilize familiar cross-validation. In this article we have tried to indicate how to utilize cross-validation for the evaluation of survival risk models; specifically how to compute cross-validated estimates of survival distributions for predicted risk groups and how to compute cross-validated time-dependent ROC curves. We have also discussed evaluation of the statistical significance of a survival risk model and evaluation of whether high-dimensional genomic data adds predictive accuracy to a model based on standard covariates alone.

INTRODUCTION

Statistical regression methods have traditionally been used for problems where the number of cases (n) exceeds the number of candidate variables (p). For time-to-event modeling, the effective sample size n is the number of events. n/p ratios of 10 or even 20 are frequently recommended for the development of stable models. With the development of biotechnology that enables genome-wide measurement of DNA sequence, RNA abundance and gene copy number, there has been an explosion of interest in predictive modeling where the number of candidate variables (p) greatly exceeds n. Predictive modeling is of importance in medical applications and most of the work on p > n modeling has been in the context of predictive classification; i.e. predicting the class of a sample based on the measurement of its p vector of variables (i.e. features).

For predictive classification in p > n settings it has been recognized that the ‘apparent error’ of a model, computed on the same data used to develop the model, is a highly biased estimator of the true error of the model for classifying new samples [1]. The apparent error is also called the re-substitution error estimate. The split sample method and complete cross-validation are widely used for estimating prediction error in p > n classification modeling. With the sample splitting approach, a model is completely developed on a training set and then the samples in a separate test set are classified to determine the error rate. The samples in the test set should not be used for any aspect of model development including variable selection. For many studies, the number of samples (n) is too small to effectively separate the data into a training set and a test set [2] and re-sampling methods provide more accurate estimates of predictive accuracy [3]. With complete K-fold cross-validation, for example, the full data set D is partitioned into K approximately equal parts D₁, … , D_K, a predictive classification model M_k is developed on training set D–D_k and used to classify cases in D_k, for k = 1, … , K. The models are developed from scratch, repeating variable selection and calibration, for each loop of the cross-validation. The classification error is estimated from the discrepancies between the predictive classifications of the n cases and their true classes.

For many applications of predictive modeling using high-dimensional gene expression data, survival time or disease-free survival (DFS) time is the primary endpoint and the re-sampling methods used for evaluating classification models are not directly available. Dupuy and Simon [4] and Subramanian and Simon [5] have reviewed the literature of such applications in oncology and identified serious deficiencies in the validation of survival risk models. Many of these studies involved too few cases to have adequate sized separate training and test sets. Consequently, they frequently presented Kaplan–Meier curves of high- and low-risk groups estimated using the same data employed to develop the models. In some publications, in order to utilize the cross-validation approach developed for classification problems, they dichotomized their survival or disease-free survival data. How to cross-validate the estimation of Kaplan–Meier curves has not been intuitively obvious. Another problem identified in this literature was failure to adequately evaluate whether prediction models based on high-dimensional genomic variables added predictive accuracy to those based on standard clinical and histopathological covariates.

Our objective here is to describe re-sampling based methods for estimating predictive accuracy of survival risk models in p > n modeling settings. We will describe the calculation of cross-validated Kaplan–Meier curves of high- and low-risk groups and the estimation of cross-validated time-dependent receiver-operating characteristic (ROC) curves. We will also describe the use of permutation methods to test the hypotheses that survival is independent of all p variables and the hypothesis that the genomic variables do not add predictive accuracy to a survival risk model developed using a smaller number of standard covariates. This approach does not require that the outcome data be pre-divided into classes of good and poor outcome prior to analysis. Cross-validation methods for evaluating the accuracy of predictive modeling of survival data are available in the BRB-ArrayTools software [6] available at: http://brb.nci.nih.gov without charge for non-commercial use. Information about BRB-ArrayTools is provided in the Appendix 1.

SURVIVAL RISK CLASSIFICATION

Regression models are commonly used either for inference or for prediction. Inferential applications focus on which variables are important and how that importance depends on which other variables are in the model. Such inferential objectives can often be achieved only to a limited extent in the p > n setting. In p > n problems it may be possible to develop models that are useful for prediction, but there will often be many models that predict about equally well. The models are generally unstable to small changes in the data and the number of events is often not nearly sufficient to distinguish among the accurately predicting models to determine which are the ‘best’ variables. Survival risk models can be developed in some p > n settings to provide accurate and useful predictions, however.

Several methods based on Cox’s proportional hazard model have been developed for survival risk modeling in the p > n setting. For these models, the log hazard function at time t for an individual with covariate vector x = (x₁, … , x_p) is of the form log[h(t)] + b × f(x) where h(t) is the baseline hazard function, b is a vector of regression coefficients and f(x) is a vector of projections of the full covariate vector x. Often, the projections are a selected set of the original individual variables. Proportional hazards models are popular because the effect of the predictors (b) can be estimated independently of assumptions about the form of the dependence of the log hazard on time. With the method of supervised principal components, the first q principal components of the variables with the strongest univariate correlation with survival are used as the predictors in the proportional hazards model [7]. Several alternative approaches have been proposed. For example f(x) may be taken as the full set of variables and b × f(x) is estimated by maximizing the L1 or L2 penalized log partial likelihood [8, 9]. Several authors have used partial least squares types of components of the projections f(x) [10–12] and others have adapted the classification tree methodology for use with survival data [13, 14]. For L1 penalized proportional hazards models the predictive index is b × f(x) = b1 × x₍₁₎ + ··· + bm × x_(m) where the variables x₍₁₎, … , x_(m) represent a subset of the full set of p variables that are selected as having non-zero coefficients by the penalized regression algorithm. These and other approaches have been reviewed and compared by Bovelstad et al. [15] and by van Wieringen et al. [16]. In this article, the BRB-ArrayTools package for survival risk modeling using supervised principal components proportional hazards modeling will be used to illustrate the cross-validation based approach.

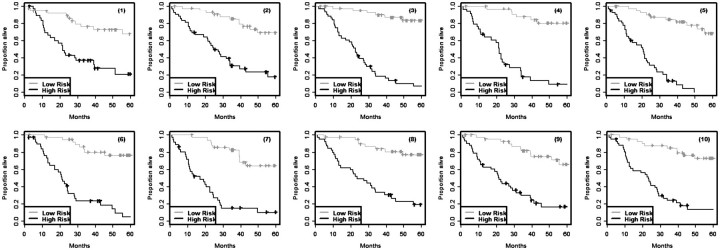
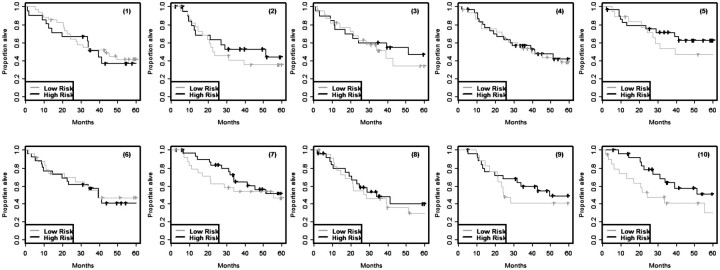
Survival modeling is usually performed to classify patients into two or more risk groups, not to predict exact survival time. The survival outcome for a group of patients is usually summarized by computing the Kaplan–Meier estimate of the survival function for that group. The Kaplan–Meier estimates for the risk groups computed on the same set of data used to develop the survival model are, however, very biased. Figure 1 shows results from a simulation performed by Subramanian and Simon [5] for high-dimensional survival modeling. There were 129 cases whose survival times and censoring indicators were known. Five thousand random variables were simulated from the standard normal distribution independently of the survival data. The 129 cases were randomly divided into training and test sets. A survival risk model involving feature selection and proportional hazards modeling was developed on the training set and the same training set patients were then classified into high- and low-risk based upon whether their predictive index was above or below the median. The entire simulation was repeated 10 times using different random divisions of the data into training and test sets. Kaplan–Meier survival estimates for the training set risk groups are shown in Figure 1. In this case, the survival distribution for patients classified as high risk should be the same as for those classified as low risk since the data was generated with no variables prognostic for survival. However, the wide separation of the Kaplan–Meier curves for high- and low-risk sets in this figure indicates the enormous bias of using the same data to develop a survival risk model and applying that model to the same patients without using any form of cross-validation. Figure 2 shows the Kaplan–Meier curves, computed by applying the same risk classifiers developed on the training sets shown in Figure 1 to cases in the corresponding independent test sets. The lack of separation between Kaplan–Meier curve for high- and low-risk patients for these independent test sets indicates that the classifiers developed in the training sets have no predictive value. This is as it should be based on the way that the data sets were generated.

Figure 1:

Re-substitution Kaplan–Meier survival estimates for cases in the training set classified as high- or low-risk based on survival risk models developed in the same training set. The training set data were simulated from a model in which none of the variables used for modeling were actually prognostic for survival. Each simulation is numbered.

Figure 2:

Kaplan–Meier survival estimates for cases in independent test sets classified as high- or low-risk using the same models developed in the corresponding training sets shown in Figure 1. Data for the independent test sets was simulated from the same model used for simulating data for the training sets; none of the variables used for modeling was prognostic for survival.

CROSS-VALIDATED KAPLAN–MEIER CURVES

We will present here a cross-validation based method for estimating the survival distribution of two or more survival risk groups for use when the number of cases is too small for effective sample splitting. To develop a cross-validated estimate of the survival distributions of the risk groups, the full data set D is partitioned into K approximately equal parts D₁, … , D_K. One then starts with forming a training set T₁ = D − D₁ by omitting the first subset of cases D₁. A survival risk model M₁ is developed using only the data in T₁ for variable selection, regression coefficient fitting and tuning parameter optimization. If a tuning parameter such as a penalty value for fitting an L1 or L2 penalized proportional hazards model is to be optimized by cross-validation, that cross-validation for model selection should be performed strictly within the training set T₁ [17]. One can then classify each of the cases in the test set D₁ into a survival risk group. One specifies in advance how many risk groups are of interest and how patients will be classified based on the models developed. For example, one might classify patients as low risk if their predicted probability of surviving 5-years is at least 0.75, high risk if their predicted probability is less than 0.5 and intermediate risk otherwise. For proportional hazards models, however, a method of assigning patients to risk groups will be described below that does not require the estimation of the baseline hazard function in the training set T₁. At the second step another survival risk model is developed from scratch using training set T₂ = D − D₂. Variable selection, tuning parameter optimization and model calibration are all re-performed using only data in T₂. The patients in the omitted set D₂ are then classified into risk groups based on this new model.

This process is repeated for each of the K loops of the cross-validation. After the cross-validation is complete, each case has been classified into one of the risk groups. Each case was classified using a model developed on a training set that they were not part of. A Kaplan–Meier curve estimate can be computed for each of the risk groups. Kaplan–Meier curves are not computed for each loop of the cross-validation. All the patients classified as low-risk in any of the loops of the cross-validation are grouped together and a single Kaplan–Meier curve is computed for that low-risk group. The Kaplan–Meier curves for the other risk groups are computed similarly. Since the classification process was cross-validated, we refer to the Kaplan–Meier curves as cross-validated.

Censoring of survival times is accommodated in two aspects of this process. First, within each loop of the cross-validation, the censored data is modeled to develop the survival risk model. In classifying the patients in some D_k based on the model developed in T_k = D − D_k, it does not matter whether the patients in D_k are censored because they are classified based only on their covariates and the model. After all the loops of the cross-validation are completed and the high and low (and any other) risk groups are fully defined, the Kaplan–Meier curves are computed in the usual way that takes censoring into account.

For proportional hazards models, risk group prediction can be performed without estimating the baseline hazard function. For example, consider a model in which the log hazard is log[h(t) + b × x], where h(t) is the baseline hazard function, b denotes the vector of regression coefficients and x denotes the vector of expression measurements for all genes. In this notation, b_j = 0 if gene j is not included in the model. Let b^(k) denote the estimated vector of regression coefficients determined based on training set T_k = D − D_k. If two approximately equal sized risk groups are desired, a case i in partition D_k can be assigned to the higher risk group if its cross-validated predictive index b^(k) x_i is above the median of 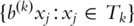, the full set of predictive indices for all cases in T_k. This is provided in BRB-ArrayTools software and permits survival risk classification of individual future cases.

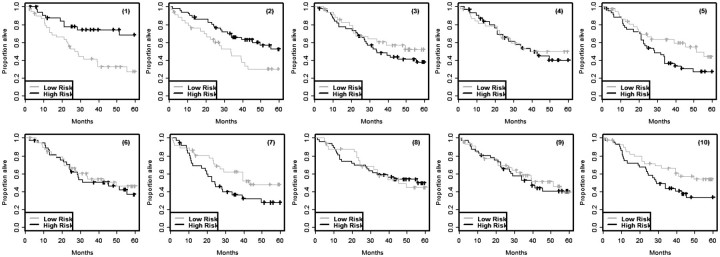
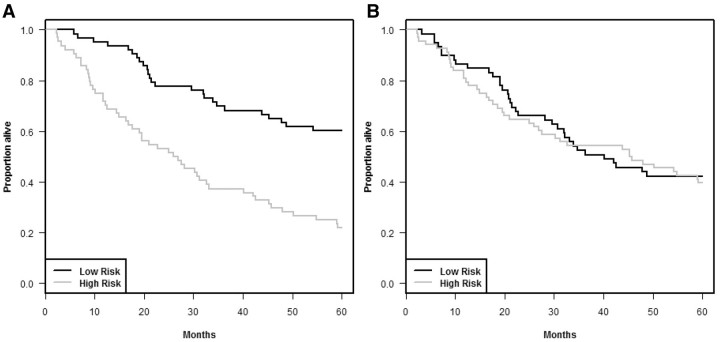
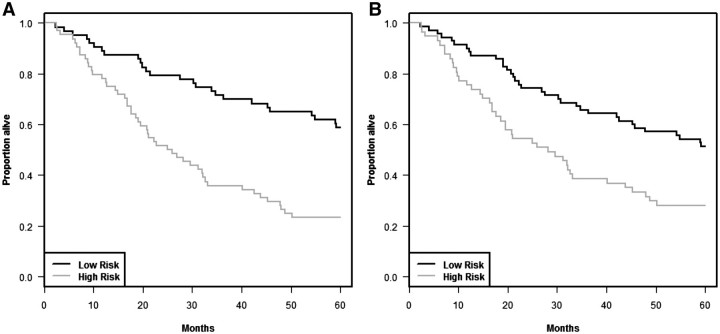
Cross-validated Kaplan–Meier curves are illustrated in Figure 3 using the null data described for the 129 cases in Figures 1 and 2 with K = 10. Figure 4A shows the re-substitution estimate of Kaplan–Meier curves for the training set data reported by Shedden et al. [18] for patients with non-small cell lung cancer. Figure 4B shows the cross-validated Kaplan–Meier curves for that same data. See the Appendix 1 for details on our analysis of the Shedden et al. [18] data.

Figure 3:

Cross-validated Kaplan–Meier survival estimates for the training sets shown in Figure 1.

Figure 4:

Kaplan–Meier survival curves for the data from Shedden et al. [18]. (A) Re-substitution estimates and (B) cross-validated estimates.

Although the log-rank statistic is a convenient measure of spread among the cross-validated survival curves, the log-rank test is not valid because the curves are cross-validated survival curves and hence the observations are not independent. In order to evaluate the statistical significance of the log-rank statistic, we obtain the permutation distribution of the cross-validated log-rank statistic. That is, we randomly permute the correspondence of survival times and censoring indicators to different gene expression profiles and repeat the entire K-fold cross-validation process. Then we compute the cross-validated survival curves and the cross-validated log-rank statistic for that random permutation. We repeat that entire process for many random permutations and generate the null distribution of the cross-validated log-rank statistic. The proportion of replicates with log-rank statistic greater than or equal to the value of the statistic for the un-permuted data is the statistical significance level for the test that survival is independent of all covariates. For the cross-validated Kaplan–Meier curves shown in Figure 4B, the log-rank statistic is 0.12 and the statistical significance level is 0.85 based on 500 random permutations.

TIME-DEPENDENT ROC CURVES

For binary disease classification problems (i.e. disease versus no disease), the commonly used measures of predictive accuracy are sensitivity, specificity, positive predictive value, negative predictive value and ROC curve [19]. Suppose we have a quantitative test result M and that values greater than a threshold c are considered positive and predictive of disease presence (D = 1). The sensitivity and specificity of the test are defined as Pr[M ≥ c | D = 1] and Pr[M < c | D = 0]. An ideal test has sensitivity and specificity of 1. A plot of sensitivity (y) versus 1-specificity (x) as the threshold c varies is called the ROC curve. If the test is un-informative, the plot will be the diagonal line y = x and the area under the curve will be 0.5. The area under the ROC curve is frequently taken as a measure of predictive accuracy of the test. The positive and negative predictive values are defined as Pr[D = 1 | M ≥ c] and Pr[D = 0 | M < c], respectively. They are important in practice, but are less frequently used for evaluation of tests in developmental studies because they depend on the prevalence of the disease Pr[D = 1] which may vary among contexts of use of the test.

Heagerty et al. [20] defined measures of sensitivity, specificity and ROC curve for use with survival data. These are based on a defined landmark time t. The sensitivity and specificity are defined as Pr[M ≥ c | T ≤ t] and Pr[M < c | T > t], respectively, where T is the random variable denoting survival time, M is the test value and c the threshold of positivity. For applications with proportional hazards survival risk models, the test value M for a patient is taken as the cross-validated predictive index for that patient. Using Bayes’ theorem, sensitivity and specificity can be estimated as:

(1)

and

(2)

Uno et al. [21] modeled Pr[T ≤ t | M] directly for a fixed landmark t, but for the general kinds of survival models considered here, Kaplan–Meier estimators of the terms Pr[T ≤ t | M ≥ c] and Pr[T > t | M < c] can be computed for subsets of patients with M ≥ c and M < c, respectively. The denominators can be estimated by Kaplan–Meier estimators for the entire set of cases. The term Pr[M ≥ c] is just the proportion of cases with cross-validated predictive index greater than or equal to the threshold c. Heagerty et al. [20] also provide ‘nearest neighbor’ estimators of the sensitivity and specificity as functions of the threshold c that ensure monotonicity as a function of the threshold. A plot of the sensitivity versus one minus the specificity is called the ‘time-dependent ROC curve’. It can be estimated for various values of the landmark time t. The area under the time-dependent ROC curve can be used as a measure of predictive accuracy for the survival risk group model. If the cross-validated predictive indices are used for the test values, then the time-dependent ROC curve is cross-validated.

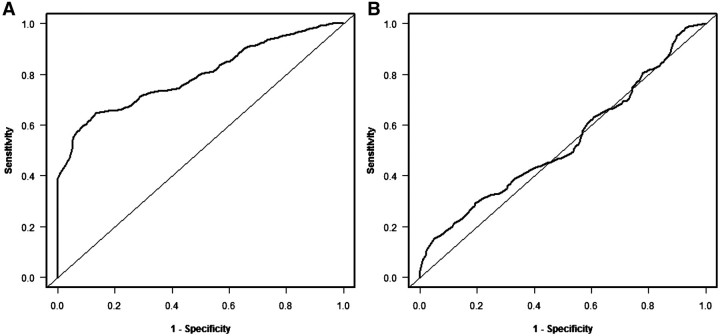
One can determine the null distribution of the area under the cross-validated time-dependent ROC curve by permuting the survival times (and censoring indicators), repeating the cross-validation procedure to create the cross-validated predictive indices for the permuted data, and re-computing the cross-validated time-dependent ROC curve and the area under the curve. This can be repeated for multiple permutations to generate the null distribution. Figure 5(B) shows the cross-validated time-dependent ROC curve for the Shedden et al. [18] data in Figure 4. The area under this curve is 0.53 and the statistical significance level of the test that this AUC = 0.5 is 0.25 based on 500 random permutations. The ROC curves in Figure 5 are based on a landmark time t = 180 months. In some cases it may be useful to compute cross-validated time dependent ROC curves using several clinically relevant time points, although issues of multiple statistical significance testing would then have to be considered. The R package survivalROC (version 1.0.0) was used for plotting the time dependent ROC curves and to compute the area under the time dependent ROC curve using the nearest neighbor option. We provided cross-validated predictive indices as input to the package. The survivalROC package can be downloaded from the Comprehensive R Archive Network (http://cran.r-project.org) and run within R. The calculation of cross-validated time-dependent ROC curves and use of AUC values in permutational testing will be included in the next release of BRB-ArrayTools.

Figure 5:

Time dependent ROC curves for the data from Shedden et al. [18]. (A) Re-substitution estimates and (B) cross-validated estimates. The resubstitution area under the curve (AUC) is 0.79 and the cross-validated AUC is 0.53.

COMPARISON TO MODEL CONTAINING STANDARD COVARIATES

Many disease areas utilize standard staging systems or other prognostic variables for evaluating patient prognosis. A new survival risk classifier is only likely to have medical utility if it provides classifications that are more refined than those provided using the accepted standard measurements. The methods described above can also be used to evaluate whether genomic variables add survival risk discrimination to a model based on standard covariates.

Several approaches to developing combined survival risk models are possible [22]. The BRB-ArrayTools software uses a method based on the supervised principal component approach of Bair and Tibshirani [7]. For each training set, genes are selected for the combined model by fitting p proportional hazards regressions each containing a single gene and all of the clinical covariates. Genes are selected if their expression adds significantly to the clinical covariates at a pre-specified nominal significance level. The first few (q) principal components of those selected genes are computed for the training set and a proportional hazards model is fit to the training set using those q principal components and the clinical covariates. That model is used to compute the predictive index for the test cases and the test set cases are assigned to risk groups. When all K loops of the cross-validation are completed, the cross-validated Kaplan–Meier curves for the combined model are computed for these predicted risk groups.

Other methods of building combined models are also possible. For example one can use L1 penalized proportional hazards regression in which the penalty applies only to the gene expression variables and the clinical covariates are automatically included in the model [23]. The boosting approach of CoxBoost of Binder and Schumacher [24] also allows for the inclusion of mandatory clinical covariates. Boulesteix and Hothorn [25] have developed a two-stage boosting approach for penalized logistic regression which is also applicable to proportional hazards modeling with mandatory clinical covariates. Bovelstad et al. [22] also describe other approaches. Whatever method is used for building combined models containing the standard covariates and the gene expression measurements, one uses the approach described above to obtain cross-validated predictive indices for the combined model. One can compute cross-validated Kaplan–Meier curves for the combined model based on grouping cases into risk groups based on these cross-validated predictive indices. One can similarly obtain cross-validated predictive indices for the standard covariate only model. It is best to cross-validate the standard covariate only model also because over-fitting can become a problem even for models when the number of variables is much less than the number of cases or events.

We can compare the combined survival risk model to the model based only on standard covariates using as a test statistic the difference between the cross-validated log-rank statistic for the combined model minus the log-rank statistic for cross-validated Kaplan–Meier curves for the standard covariate model. The difference in areas under the cross-validated time-dependent ROC curves can be used as an alternative test statistic. The null distribution of the test statistic is generated based on permuting the gene expression vectors among cases. In these permutations, the correspondence between survival times, censoring indicators and standard covariates are not disrupted. The null hypothesis tested is that the gene expression data are independent of survival and standard covariates. It is not possible in this way to test the hypothesis that gene expression is conditionally independent of survival given the vector of standard covariates. This permutation approach has also been used by Boulesteix and Hothorn [25].

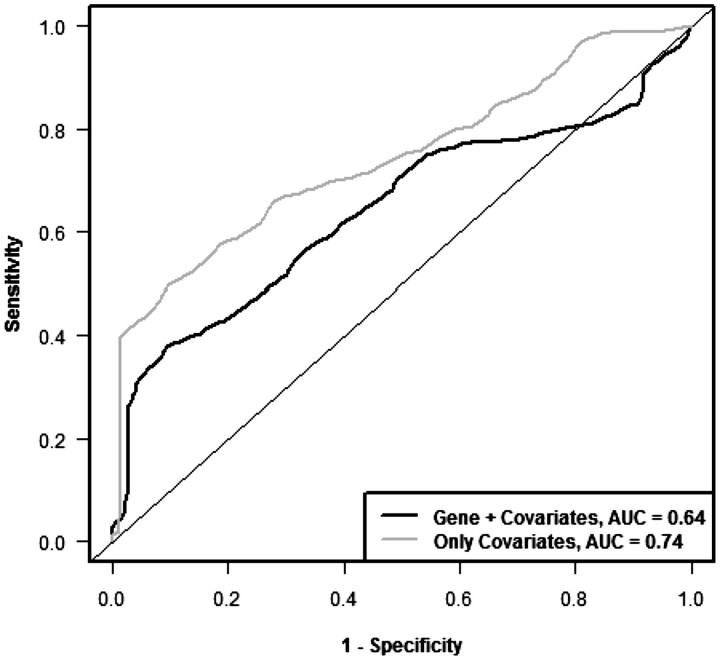
Figures 6 and 7 show the cross-validated Kaplan–Meier curves and cross-validated time dependent ROC curves, respectively, for the standard covariates in the Shedden data sets. Figure 6A shows the Kaplan–Meier curve for the standard covariate only model and Figure 6B shows Kaplan–Meier curves for the model containing both standard covariates and gene expression variables. It is clear from the curves that the gene expression variables do not provide additional survival risk discrimination to that already provided by the standard covariates (P = 0.62 for log-rank statistic, P = 0.72 for AUC of ROC curve based on 500 permutations).

Figure 6:

Cross-validated Kaplan–Meier curves to compare the prognostic model containing only standard covariates with the model containing both standard covariates and gene expression variables in the data set from Shedden et al. [18]. (A) Only standard covariates and (B) standard covariates and gene expression variables.

Figure 7:

Cross-validated time dependent ROC curves to compare the prognostic model containing only standard covariates with the model containing both standard covariates and gene expression variables in the data set from Shedden et al. [18].

DISCUSSION

Developments in whole genome biotechnology have stimulated statistical focus on development of methodology for predictive medicine in settings where the number of candidate variables is large relative to the number of cases. For applications in oncology, there is often interest in classifying patients into survival risk groups. Measures of discrimination for survival risk models include separation of survival curves, time-dependent ROC curves and Harrell’s concordance index [26]. For high-dimensional data applications, however, computing these measures as re-substitution statistics on the same data used for model development results in highly biased estimates. Most developments in methodology for survival risk modeling with high-dimensional data have utilized separate test data sets for model evaluation. For example, Li and Gui [10] utilized the time-dependent ROC curve for survival modeling in the context of a separate test set. Cross-validation has sometimes been used for optimization of tuning parameters but rarely for the evaluation of survival risk models. An exception is the study by van Houwelingen et al. [9] that used cross-validation to evaluate L2 penalized proportional hazards survival risk models. In many applications, however, the data available is too limited for effective division into training and test sets and consequently authors have often either reported re-substitution statistics or analyzed their data using binary classification methods in order to utilize familiar cross-validation. In this article we have tried to indicate how to utilize cross-validation for the evaluation of survival risk models; specifically how to compute cross-validated estimates of survival distributions for predicted risk groups and how to compute cross-validated time-dependent ROC curves. We have also discussed evaluation of the statistical significance of a survival risk model and evaluation of whether high-dimensional genomic data adds to the predictiveness of a model based on standard covariates.

In this article we have emphasized proper evaluation of models for classifying patients based on survival risk. Using cross-validated time dependent ROC curves, these methods can be evaluated without grouping patients into fixed risk groups. Schumacher et al. [27] have developed methods for the evaluation of models for prediction of survival functions of individual patients. For each time t, the Brier score for patient i is [Y_i(t) − r(t, x_i)]², where 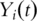is an indicator function whether patient i survives beyond time t and 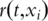denotes the predicted probability of surviving beyond time t for a patient with covariate vector x_i. Schumacher et al. show how to adapt the Brier score to censored data and utilize an out-of-box 0.632 bootstrap cross-validation estimate of the Brier score as a function of t for a given data set. Binder and Schumacher [24] have used the Brier score to evaluate high-dimensional survival risk models built with mandatory covariates and the permutation tests described here could be applied to the Brier score either at a fixed landmark time t or averaged over times.

There are some advantages to partitioning a data set into separate training and test sets when the numbers of patients and events are large. Such partitioning enables model development to be non-algorithmic, taking into account biological considerations in selecting genes for inclusion. It also enables multiple analysts to develop models on a common training set in a manner completely blinded to the test set. Some commentators recommend the use of a separate test set because cross-validation is so often used improperly without re-selecting genes to be included in the model within each loop of the procedure [1, 28]. In many cases, however, proper cross-validation provides a more efficient use of the data than does sample splitting. If the training set is too small, then the model developed on the training set may be substantially poorer than the one developed on the full data set and hence the accuracy measured on the test set will provide a biased estimate of the prediction accuracy for the model based on the full data set [3].

Proper complete cross-validation avoids optimistic bias in estimation of survival risk discrimination for the survival risk model developed on the full data set. Cross-validated estimates of survival risk discrimination can be pessimistically biased if the number of folds K is too small for the number of events, and the variance of the cross-validated risk group survival curves or time-dependent ROC curves will be large, particularly when K is large and the number of events is small. For example, for the null simulations of Figure 3, there are several cases in which the cross-validated Kaplan–Meier curve for the low-risk group is below that for the high-risk group. This is due to the large variance of the estimates. This can also be seen in Figure 6 where the separation in the estimated survival curves for the combined model is less than that for the model containing only clinical covariates. This large variance is properly accounted for, however, in the permutation tests for evaluating whether the separation between cross-validated survival curves is statistically significant and whether the separation for the combined model is better than for the clinical covariate only model. Molinaro et al. [3] have studied the bias-variance tradeoff for estimating classification error for a variety of complete re-sampling methods including leave-one-out cross-validation, K-fold cross-validation, replicated K-fold cross-validation, sample splitting and the 0.632 bootstrap. The relative merits of the different methods depended on sample size, separation of the classes and type of classifier used. For small sample sizes of fewer than 50 cases, they recommended use of leave-one-out cross-validation to minimize mean squared error of the estimate of prediction error in use of the classifier developed in the full sample for future observations. Subramanian and Simon [29] have extended this evaluation to survival risk models using area under the time-dependent ROC curve as the measure of prediction accuracy. With survival modeling the relative merits of the various re-sampling strategies depended on number of events in the data set, the prediction strength of the variables for the true model and the modeling strategy. They recommended use of 5- or 10-fold cross-validation for a wide range of conditions. They indicated that although the leave-one-out cross-validation was nearly unbiased, its large variance too often led to misleadingly optimistic estimates of prediction accuracy. Replicated K-fold cross-validation was found by Molinaro et al. [3] to provide small reductions in the variance of prediction error estimates somewhat for binary classification problems. It increases the complexity of identifying risk groups in survival modeling, however. Although it is offered in the BRB-ArrayTools for the validation of class prediction, it is not offered for validation of survival risk prediction.

In summary, we believe that cross-validation methodology, if employed correctly, can be useful for the evaluation of survival risk modeling and should be utilized more widely. It can provide a more efficient use of data for model development and validation than does fixed sample splitting. In data sets with few events, however, the survival risk models developed may be much poorer than could be developed with more data and the cross-validated Kaplan–Meier curves of risk groups and time dependent ROC curves will be imprecise [2]. Although the cross-validation approaches described here are broadly useful, they are not a good substitute for having a substantially larger sample size when that is possible. Often, however, larger studies come later when initial results are felt promising. The ‘promise’ of initial results should be evaluated unbiasedly, however and this is often not the case. It should also be recognized that both cross-validation and sample splitting represent internal validation and do not reflect many of the sources of variability present in applying a predictive classifier in broad clinical practice outside of research conditions in which assaying of samples are performed in a single laboratory. Nevertheless, the development of effective diagnostics is a multi-stage process, starting with developmental studies in which efficient methods of internal validation play an important role.

Key Points.

• Survival risk groups should generally be developed directly using the survival data without reducing survival times to binary categories.

• Cross-validation methods are available for computing cross-validated survival curves and cross-validated ROC curves. These methods, if used properly, are more efficient than splitting a small data set into training and testing subsets.

• To use cross-validation properly, complete re-development of the survival risk model from scratch is required for each loop of the cross-validation process. This means that any variable selection or tuning parameter optimization should be repeated within each loop of the cross-validation.

• The cross-validated estimate of survival discrimination is an almost unbiased estimate of the survival risk group discrimination expected from classifying similar future patients using the risk groups obtained from applying the survival risk group development algorithm to the full data set.

• A permutation based significance test of the null hypothesis that survival risk discrimination is null can be computed based on the cross-validated log-rank statistic or the area under the cross-validated ROC curve. Similarly, one may test whether high-dimensional genomic variables add survival discrimination to standard clinical and histopathologic variables.

• Many of the tools for developing survival risk models and for evaluating such models using cross-validation are available in the BRB-ArrayTools software package.

Biographies

Dr Richard M. Simon is Chief of the Biometric Research Branch at the US National Cancer Institute. He holds a doctor of science degree in Applied Mathematics and Computer Science and is Chief Statistician for the NCI Division of Cancer Treatment and Diagnosis.

Dr Jyothi Subramanian obtained her doctoral degree in Statistics from the Indian Institute of Technology, Bombay, India. Dr Subramanian was a Visiting Fellow with the Biometric Research Branch of the National Cancer Institute.

Dr Ming-Chung Li received his PhD degree from the University of Iowa, Department of Statistics and Actuarial Science. He currently works as a Statistician for the EMMES Corporation.

Ms Supriya Menezes received her Masters degree in Applied Statistics from Oakland University. She also has a Masters degree in Computer Science and Management from University of Pune, India. She currently works as a Statistician for the EMMES Corporation.

APPENDIX 1

ANALYSIS OF THE DATA FROM SHEDDEN ET AL.

The data used in our study to illustrate cross-validated Kaplan–Meier and time dependent ROC curves was obtained from the study of Shedden et al. [18] for patients with non-small cell lung cancer. Only samples from the University of Michigan Cancer Center (UM) that were also included in the Shedden et al. [18] analysis were used in our study. All patients with survival times censored prior to 60 months were also excluded. These resulted in 127 samples of which there were 75 events. The clinical covariates considered were age, pathologic nodal stage (N0, N1 or N2), pathologic tumor stage (T1, T2, T3 or T4) and differentiation (poorly, moderately or well differentiated). Data for these covariates were available for all the 127 samples.

Gene normalization and filtering was carried out using BRB-Array tools (developed by Dr Richard Simon and the BRB-ArrayTools Development Team, http://linus.nci.nih.gov/BRB-ArrayTools.html). In short, the expression data was log-transformed to the base-2 scale after assigning a value of 1 to expression values <1. Each array was then normalized using the median array and normalized expression values greater than 10 000 were truncated to 10 000. Following this, a filter based on variance was applied and 75% of the genes having the lowest variance were excluded. There were 5552 genes which passed the filtering criteria and these genes were used for the development of prognostic models.

Prognostic models using gene expression alone was developed using the first 3 principal components of the 10 most significant genes resulting from univariate Cox regression models. In the case of prognostic models that used clinical covariates and gene expression, 10 most significant genes were first selected by fitting proportional hazards regression each containing a single gene and all of the clinical covariates. The first three principal components of those selected genes were computed and proportional hazards model was fit using those three principal components and the clinical covariates. For prognostic models using clinical covariates alone, no further variable selection was done and all the clinical covariates were used as such in a proportional hazards model. For making the cross-validated predictions, gene selection and the computation of principal components were done inside the cross-validation loop. In the case of modeling with clinical covariates alone too, cross-validated predictions were obtained. A 10-fold cross-validation was employed in all cases.

The package survivalROC (version 1.0.0) was used for plotting the time dependent ROC curves and to compute the area under the time dependent ROC curve.

BRB-ARRAYTOOLS

BRB-ArrayTools is menu driven software that provides numerous state-of-the-art statistical analysis tools for microarray gene expression and copy-number data. It is designed to be used by non-statisticians as well as statisticians. It attempts to educate users to select the analysis tool appropriate for their biological or clinical objective and to avoid improper cross-validation and misleading analyses. It imports data from all arraying platforms and is not tied to any database system. BRB-ArrayTools is highly computationally efficient; accommodating individual projects of over 1000 arrays of more than 50 000 probes or probe sets. Analysis tools included in BRB-ArrayTools are selected by R. Simon and include methods developed by many statisticians. In some cases the original author’s R package is used, but more frequently the algorithms are re-programmed in a compiled language such as C or Fortran for computational speed. The compiled code runs invisibly to the user; users interact with BRB-ArrayTools through menus and dialog boxes programmed within Excel. Excel is used only for the user interface; the data is stored in binary files in order to avoid the restrictions of Excel and none of the analysis facilities of Excel are employed.

BRB-ArrayTools includes an extensive suite of analysis tools. For example, for class prediction the following tools are included: diagonal linear discriminant analysis, nearest neighbor and nearest centroid classification, support vector machine with recursive feature elimination, shrunken centroid classification, random forest, compound covariate classification, Bayesian compound covariate probabilistic prediction, top scoring pairs classification and L1 penalized logistic regression with clinical and genomic covariates. Internal validation options include leave-one-out cross-validation, K-fold cross-validation, repeated K-fold cross-validation, 0.632 bootstrap re-sampling and split sample validation.

BRB-ArrayTools incorporates extensive biological annotations and analysis tools such as gene set analysis that incorporates those annotations. It also incorporates powerful tools for 2D and 3D graphical exploratory analysis of high-dimensional data. It includes a plug-in facility that enables users to run their R functions on data stored in BRB-ArrayTools.

There are over 13 000 registered users of BRB-ArrayTools internationally and it has been cited in over 1300 publications.