Abstract
Data-driven statistical approaches, such as cluster analysis or independent component analysis, applied to in vivo functional neuroimaging data help to identify neural processing networks that exhibit similar task-related or restingstate patterns of activity. Ideally, the measured brain activity for voxels within such networks should exhibit high autocorrelation. An important limitation is that the algorithms do not typically quantify or statistically test the strength or nature of the within-network relatedness between voxels. To extend the results given by such data-driven analyses, we propose the use of Moran’s I statistic to measure the degree of functional autocorrelation within identified neural processing networks and to evaluate the statistical significance of the observed associations. We adapt the conventional definition of Moran’s I, for applicability to neuroimaging analyses, by defining the global autocorrelation index using network-based neighborhoods. Also, we compute network-specific contributions to the overall autocorrelation. We present results from a bootstrap analysis that provide empirical support for the use of our hypothesis testing framework. We illustrate our methodology using positron emission tomography (PET) data from a study that examines the neural representation of working memory among individuals with schizophrenia and functional magnetic resonance imaging (fMRI) data from a study of depression.
Keywords: Spatial autocorrelation; Moran’s I; neuroimaging; fMRI, ICA, cluster analysis
1. INTRODUCTION
Much of the recent work regarding the analysis of brain imaging data has focused on examining functional connectivity of the human brain. For example, independent component analysis (ICA) and cluster analysis attempt to divide the brain into different networks involved in performing certain tasks or characterizing a “default mode” of the restingstate brain.
Clustering
Cluster analysis uses positron emission tomography (PET) or functional magnetic resonance imaging (fMRI) data to help identify dissociable networks or clusters, each consisting of voxels that show relatively homogeneous patterns of measured brain function. These clustering solutions do not define the underlying neuroanatomical connections, but instead focus on functional associations between voxels. Ideally, within-cluster voxels should exhibit high functional (or spatial) autocorrelation, validating that the neural responses within clusters are functionally related.
Numerous investigators have proposed the use of clustering methods for neuroimaging data including Balslev et al. (2002); Baumgartner et al. (2000); Bowman and Patel (2004); Cordes et al. (2002); Fadili et al. (2000, 2001); Filzmoser et al. (1999); Goutte et al. (1999, 2001); Poline (1994); Simon et al. (2004); Sommer and Wichert (2003); Stanberry et al. (2003). Clustering algorithms generally fall into one of two categories, namely hierarchical clustering algorithms or partitioning algorithms. Hierarchical clustering performs a series of nested merges or divisions, ranging from a solution with one large cluster containing all voxels to a solution in which every voxel represents a separate cluster. Among the available hierarchical clustering procedures are Ward’s, beta-flexible, centroid linkage, variable linkage, median linkage, single linkage, and complete linkage algorithms (Bowman and Patel, 2004). Partitioning algorithms, such as K-means and fuzzy K-means, specify the number of clusters at the outset and sequentially reallocate voxels to clusters until obtaining a final clustering solution (Fadili et al., 2001).
Independent Component Analysis (ICA)
Among the data-driven techniques, ICA has become a very popular method, successfully employed to decompose fMRI time-series into sets of spatial maps and associated time-courses. ICA is an application of blind source separation, which attempts to decompose the data set into components that are as statistically independent from each other as possible (Common, 1994; Herault and Jutten, 1986; Jutten and Herault, 1991). One can pursue either temporal (Biswal and Ulmer, 1999) or spatial (McKeown et al., 1998) independence of the target components. One method of performing ICA minimizes the mutual information between components (Bell and Sejnowski, 1995; McKeown et al., 1997, 1998; Calhoun and Pekar, 2000). The fixed-point algorithm (Hyvärinen, 1999) pursues the same goal of minimizing the mutual information, but uses the concept of normalized differential entropy or negentropy (Common, 1994). One interpretation of negentropy is as a measure of non-normality, so maximizing the negentropy finds directions of maximal non-normality in the data. Beckmann and Smith (2004) propose a probabilistic ICA (PICA) model aimed at solving the problem of overfitting in classical ICA applied to fMRI data, by including a Gaussian noise term in the classical ICA decomposition. Several methods for extending the single-session probabilistic ICA model to higher dimensions and making group inferences from fMRI data have been proposed (Calhoun et al., 2001; Beckmann and Smith, 2005). In our analysis, we consider the group ICA approach proposed by Beckmann and Smith (2005) to our experimental fMRI data.
The two methods described above help provide important insights into functional integration (association between different brain regions). The major drawback is that there has been limited research in terms of formally validating the results of these methods through statistical hypothesis testing.
Despite the successful application of clustering methods to neuroimaging data, statistical procedures for testing the validity of the resulting cluster structure are still lacking. Although a clustering solution suggests the existence of networks of functionally related voxels, the clusters exhibit unknown levels of autocorrelation, which is a desirable characteristic of behaviorally relevant neural circuits. Typical cluster analyses neither quantify the strength or nature of the relatedness between within-cluster voxels using an easily interpretable measure nor apply formal tests of hypotheses to evaluate the statistical significance of the level of autocorrelation. These limitations are particularly noteworthy since clustering procedures always produce a solution, even in the absence of true functional connections in the data. Therefore, a valuable addition to cluster analyses applied in functional neuroimaging studies is to measure the degree of functional autocorrelation within a clustering solution and to evaluate the statistical significance of the observed associations.
Similarly, even though ICA has proved promising, there is a need to study the properties of ICA as applied to fMRI data. One major issue in application of ICA is that the reliability of the estimated independent components (ICs) is unknown. The results from ICA may vary considerably with different algorithm starting points, sampling of subjects, preprocessing steps or type of decomposition algorithm (Calhoun et al., 2003). Therefore, validation of estimated ICs has become important for correct interpretation of ICA results. There has been previous work related to evaluating the results of ICA by testing mutual independence between the extracted source signals (Murata, 2001; Shimizu and Kano, 2001; Chiu et al., 2003; Stogbauer et al., 2004; Wu et al., 2009). There have also been several measures proposed to evaluate the fit of the estimated ICs to the data (McKeown et al., 1998; Esposito et al., 2002; Himberg et al., 2004) and some attempts to investigate the reliability of the ICA estimates (Himberg and Hyvärinen, 2003; Himberg et al., 2004). Still, it may remain unclear how much autocorrelation is present in the identified components.
In this paper, we introduce a global index to evaluate the validity of neural processing networks identified by functional clustering or by ICA. Specifically, we propose the use of Moran’s I statistic (Cliff and Ord, 1973) to quantify and test the autocorrelation present within computed functional networks. We tailor our definition of the global index to neuroimaging applications through the use of network-based neighborhoods, and we compute network-specific contributions to the overall autocorrelation. Consequently, our methods target autocorrelation exhibited by voxels within defined neural processing networks, rather than between voxels globally throughout the entire brain. Thus, we make no assumptions (or statements) about statistical dependence between voxels on a global level. Hypothesis testing results from our framework augment the descriptive findings of data-driven analysis by determining the presence, direction, and statistical significance of functional autocorrelation within neural processing networks. For applications of the proposed methods to resting-state fMRI data, we present an explicit temporal component. We illustrate the use of our methodology with data from two studies: a PET study of regional cerebral blood flow (rCBF) correlates of parametrically manipulated working memory among individuals with schizophrenia and an fMRI resting-state study of depression. Moreover, we provide empirical support for the use of the proposed methods using a bootstrap analysis and a simulation study.
2. EXPERIMENTAL DATA
PET Data on Working Memory in Schizophrenia Patients
We illustrate cluster analysis using PET data from a study of schizophrenia, but the cluster analysis is also applicable to fMRI data. Our data are from a parametric study of working memory in an executive function task in individuals with schizophrenia. We use data from N=16 subjects, each having a total of 8 PET scans obtained using the blood flow tracer [15O]H2. After aligning and re-slicing the PET images for each subject (Woods et al., 1998a), we spatially normalize each subject’s scans to a population-representative PET atlas (Woods et al., 1998b) centered in Talairach stereotaxic coordinates (Talairach and Tournoux, 1988). We refrain from spatial smoothing of the PET data during preprocessing to avoid artificially inducing correlations between nearby voxels. We analyze data from 9,919 voxels, consisting primarily of gray-matter voxels that exhibit at least a 1.6% change throughout the study. The study design encompasses 2 replicate sessions of 4 scans, where the scans in each session represent four experimental conditions that parametrically vary working memory load-the ability to manipulate information in short–term memory. Specifically, the conditions are defined as digit shadowing (minimal working memory load) and low, moderate, and high working memory loads in the form of serial addition tasks. In the digit shadowing condition, the subjects simply repeat a number that they receive by an auditory presentation, which imposes a negligible load on working memory. In the other three experimental conditions, the subjects receive auditory presentations of a series of positive integers and are instructed to provide the sum of the current number and the preceding number, which requires that they store the previous number in short-term memory and mentally suppress the previous sum. The range of the integers in the working memory load presentations distinguishes the conditions. Both numbers in the low load condition fall between 1 and 3, both numbers in the moderate load condition are between 1 and 5, and the high load condition includes integers between 1 and 9. On average, the sums for the three active load conditions during our experiment are 4.23 (low), 7.22 (moderate), and 10.09 (high).
FMRI Data from a Study on Depression
We use data from a second study intended to characterize the impact of childhood abuse/early trauma, and its developmental course, on brain structure and connectivity. For our purpose, we analyze fMRI resting-state scans of seven women with a history of major depression. While in the scanner, subjects had their eyes open and were looking at a visual fixation cross. Functional data were acquired on a Siemens 3T whole body scanner (Trio). During a 7.5 min acquisition, a series of 210 scans were acquired with TR=2sec, 20 axial slices, 3.4 × 3.4 × 4 mm3 resolution. The functional runs were collected with a Z-saga sequence to avoid orbitofrontal signal ablation. A group ICA was applied to investigate the resting-state functional connectivity of the depressed patients. There is substantial interest in determining associations between the brain activity characteristics of different regions while subjects are in a resting state. For example, a set of regions has been consistently identified in these investigations and has been labeled as the default mode network (DMN).
The first step in the analysis (preprocessing and the group ICA) of the fMRI data was done in FSL (FMRIB’s Software Library, www.fmrib.ox.ac.uk/fsl) software package. The preprocessing and the first level, individual subject analysis of the PET data was done in SPM (Statistical Parametric Mapping, Welcome Department of Cognitive Neurology, London, UK, www.fil.ion.ucl.ac.uk/spm/). The rest of the analyses were carried out in Matlab.
3. METHODS
Notation and terminology
The framework we present allows estimation (and testing) for the presence of autocorrelation separately for each experimental condition p (p = 1, …,P) or scan s (s= 1,…,S). Data from a single scan are represented as a 3-D rectangular lattice, comprised of a large number of voxels, indexed by a mapping of coordinates (x, y, z) to υ = 1,…, V. Each voxel contains intensity information corresponding to measures of localized brain activity for fMRI data, or rCBF in case of PET data.
3.1 Clustering
Summary statistics, such as means or regression coefficients, are often inputs for clustering procedures applied to task-related fMRI or PET data (Simon et al., 2004). We develop notation for this case, but the methodology extends to settings that cluster the original response data directly, e.g. in resting-state fMRI studies. We denote rCBF, as a proxy for brain activity, by Yk (υ) = (Yk1(υ),…,YkS (υ))′, representing localized blood flow measurements from all S scans for subject k, k= 1,…,K(at voxel υ). For clustering, we typically consider statistics T(υ) = (T1(υ),…,TP(υ))′ = f(Y1(υ),…, YK(υ)), P≤S,that summarize data from all individuals, e.g. where Tp(υ) is the mean or estimated effect associated with experimental condition p.By selecting the pth element of the summary vector from every voxel, we also define the vector Tp= (Tp(1),…, Tp(V))′, which will facilitate our upcoming discussion of functional autocorrelation.
Clustering procedures classify the V voxels in an image into G groups, with each cluster consisting of Vg voxels, where g = 1,…,G and . Most methods classify voxels by measuring the distance (dissimilarity) between the activity time courses for every pair of voxels and combining voxels with small distances. For example, one popular measure of distance between the activity in voxels i and j is the Euclidean distance given by
| (1) |
Descriptions of particular clustering algorithms are available in Rencher (2002), and Bowman et al. (2004) highlight several of these algorithms for neuroimaging applications.
Some clustering criteria and stopping rules for hierarchical clustering methods quantify measures based on within-cluster similarity, e.g. proportional to the change in within-cluster variation, relative to between-cluster variation. However, these quantities are limited because they are relative measures, e.g comparing two consecutive levels of a clustering hierarchy. Also, these measures often lack easy interpretability and are not amenable to formal hypothesis testing. The probability distributions of clustering criteria are difficult to derive theoretically (Hartigan, 1977, 1978) and thus do not provide a basis for formal hypothesis testing using a conventional Neyman-Pearson framework. Furthermore, even if one successfully derives the distribution of a particular clustering criterion, the result may be somewhat limited in practice in cases where an alternative clustering algorithm provides better performance. We evaluate statistical significance of the functional autocorrelation present in the final clustering solution, regardless of the clustering algorithm employed to obtain the solution and without relying on specific distributional assumptions of the data.
3.2 ICA
Classical ICA
Let Y denote an S×V matrix of the observed voxel time courses, where S is the total number of scans, and V is the number of voxels included in the analysis; C is an N×V random matrix whose rows Ci are to be filled with the unknown realizations of the N spatial components (images, reshaped in 1-D vectors), and A is an S×N mixing matrix, whose columns contain the associated time-courses of the N components. The spatial ICA problem for fMRI time series can be formulated as an estimation of the following model:
| (2) |
There are no assumptions about the mixing matrix A, while the constraint on the spatial processes Ci is that they are (ideally) mutually statistically independent. The amount of statistical dependence within a fixed number of spatial components can be quantified by means of their mutual information, an important function in information theory (Common, 1994). Thus, the ICA decomposition of Y can be defined (up to a multiplicative constant and to the sign) as an invertible transformation: C = UY, where the matrix U (so-called unmixing matrix) is determined such that the mutual information of the target components Ci is minimized (i.e., such that Ci’s are “as independent as possible”). The matrix A is the (pseudo)inverse of U. In McKeown et al. (1998), the sources are estimated by iteratively optimizing the unmixing matrix U so that C = UY contains mutually independent rows, using the ‘infomax’ algorithm.
Probabilistic ICA (PICA)
The model of equation (2) does not include random noise. The PICA model, which extends model (2), is formulated as a generative linear latent variables model. The model “is characterized by assuming that the S-variate vector of observations is generated from a set of q statistically independent non-Gaussian sources via a linear instantaneous mixing process corrupted by additive noise η(t)” (Beckmann and Smith, 2004):
where yυ denotes the S-dimensional column vector of individual measurements at voxel location υ, cυ denotes the q-dimensional column vector of non-Gaussian source signals contained in the data and ηυ denotes Gaussian noise ηυ~ N(0,σ2Συ). The number of source processes is assumed to be smaller than the number of observations in time (q < S). The model is closely related to factor analysis. The individual component maps are obtained using a modified fixed-point iteration scheme to optimize for non-Gaussian source estimates via maximizing the negentropy. The maps are then separately transformed to spatial Z-scores. These Z-score maps depend on the amount of variability explained by the entire decomposition at each voxel location relative to the residual noise. Next, Gaussian/Gamma mixture models are fitted to the individual Z-maps in order to infer voxel locations that are significantly modulated by the associated time-course. For more details on PICA, we refer the reader to Beckmann and Smith (2004).
Group ICA
In Beckmann and Smith (2005), the singlesession PICA has been extended to higher dimensions allowing for a model-free analysis of multi-subject or multi-session fMRI data. For group ICA, either tensorial ICA (where the data is decomposed into spatial maps, time courses and subject/session modes), or a simpler temporal concatenation approach (a single 2D ICA is run on the concatenated data matrix obtained by stacking all 2D data matrices of every single data set on top of each other) are possible. The latter approach is recommended to use when the interest is in finding a common spatial pattern, but we cannot assume that the associated temporal response is consistent between subjects, such as in the analysis of data acquired without stimulation (e.g. resting-state data). We hence apply this approach for IC analysis of our fMRI data set. The technique is derived from parallel factor analysis (Harshman, 1970; Harshman and Lundy, 1994). 1
We define Y(υ) = (Y1(υ)′,…,YK (υ)′)′, representing concatenated measures of localized brain activity at voxel υ, across all subjects. In our upcoming fMRI example, Y(υ) is a (210*7) × 1 vector. We also define the mean vector of brain activity, across all voxels in all ICs as .
3.3 Functional Autocorrelation Statistic
Functional autocorrelation measures the extent to which voxels within neural processing networks exhibit similar patterns of brain activity. For any selected element of the summary vector (indexed by p), we measure the functional autocorrelation of a clustering, or ICA solution using Moran’s I (Moran, 1950), defined as
| (3) |
In the case of clustering, Zp = [Tp− (T̅p1V)], with 1V denoting a (V ×1) vector of ones and T̅p denoting the mean summary element across all voxels (i.e., and W is the symmetric spatial connectivity matrix representing the clustering solution. The matrix W defines all pairs of voxels that are in the same cluster, i.e. that exhibit functional connectivity, by including a nonzero value in the appropriate off-diagonal element. Specifically, we define W such that the diagonal elements are Wυυ = 0, and the (u,υ)th off-diagonal element is either Wυu = 1, if voxels u and υ are in the same cluster, or Wυu = 0, otherwise.
When applied to group ICA results, we define Z = [(Y(1)′,…,Y(V)′)′ − (1V ⊗ T̅)], where ⊗ denotes the Kronecker product, or the direct product operator. Here we drop the index p for convenience, since in our fMRI data example there is only one experimental condition. W is now a block matrix: W = W1 ⊗ I(K*S)×(K*S), where W1 is a V × V connectivity matrix (i.e. and , if voxels u and υ are in the same IC and 0 otherwise). V and S0 are the same as defined above. Connectivity matrices in other areas of statistical application, e.g. geostatistics, typically specify connections between locations that are physically adjacent, e.g. neighboring cities. We adapt Moran’s I by tailoring our definition of adjacency to reflect the distributed neural processing networks, which typically contain voxels that are not all spatially contiguous. Since our application defines the proximity of voxels based on measures of brain function, rather than physical or spatial distance, we refer to Moran’s I as a functional autocorrelation index. However, the phrase spatial autocorrelation is also appropriate since we view functional networks as spatially dissociable regions on a brain map.
The massive amount of data collected in functional neuroimaging studies yields high dimensional spatial connectivity matrices, which may lead to computational difficulties. In the case of clustering (and similarly for ICA), we can re-express Ip, using the following, perhaps more computationally convenient, expression
| (4) |
A similar formula can be obtained when (3) is applied to an ICA solution from fMRI data. In (4), the numerator of Moran’s I calculates the products of the mean-centered summary statistics for within-cluster voxel pairs and computes the sum of all such products. The denominator gives a measure of variation about the overall mean. These interpretations reveal the conceptual similarity of Moran’s I to the Pearson correlation coefficient, with Moran’s I representing a spatially weighted version of Pearson’s measure. Moran’s I generally ranges between −1 and 1. A large positive value of Ip indicates the presence of functional clusters in which there is high within-cluster similarity and a negative value indicates clusters exhibiting dissimilarity between voxels. Randomly assigning voxels to clusters typically results in uncorrelated rCBF between the voxels within each group.
3.4 Hypothesis Testing
The randomization scheme, characterized by the random allocation of voxels to neural processing networks, serves as the basis for establishing the null hypothesis and related distributional properties for evaluating the statistical significance of any observed value of Moran’s I. To conduct a test to determine if statistically significant functional autocorrelation is present in a clustering solution, compute the test statistic
| (5) |
where E(Ip)and V(Ip)represent the theoretical mean and variance of Moran’s I under randomization, respectively (we provide expressions below). Next, calculate Pr(|Zp| > zα/2), the probability that the magnitude of the observed statistic Zp exceeds the critical value from a standard normal distribution corresponding to type-I error at level α. The test rejects the null hypothesis of uncorrelated networks, e.g. no true cluster structure, when the absolute value of Zp is sufficiently large. Therefore, a statistically significant test result indicates that the observed functional autocorrelation exhibited by a clustering or ICA solution is large relative to the expected value of the autocorrelation under randomization (Goodchild, 1986).
Calculating the test statistic Zp requires expressions for the expected value and the variance of Moran’s I under the random assignment of voxels to functional networks. The mean and the variance of Moran’s I under randomization are given by following formulas (Moran, 1948, 1950; Cliff and Ord, 1973, 1981):
| (6) |
| (7) |
where , and
| (8) |
Using Monte Carlo simulations based on our PET data, we empirically validate the theoretical properties of Moran’s I under randomization to protect against potential bias, e.g. caused by intrinsic spatial autocorrelation in PET data (see the Results section, Bootstrap analysis). Substituting the computed quantities (6)–(8) into equation (5) gives the observed value of the test statistic upon which to base hypothesis testing and statistical inferences regarding functional autocorrelation.
4. RESULTS
Working Memory Data
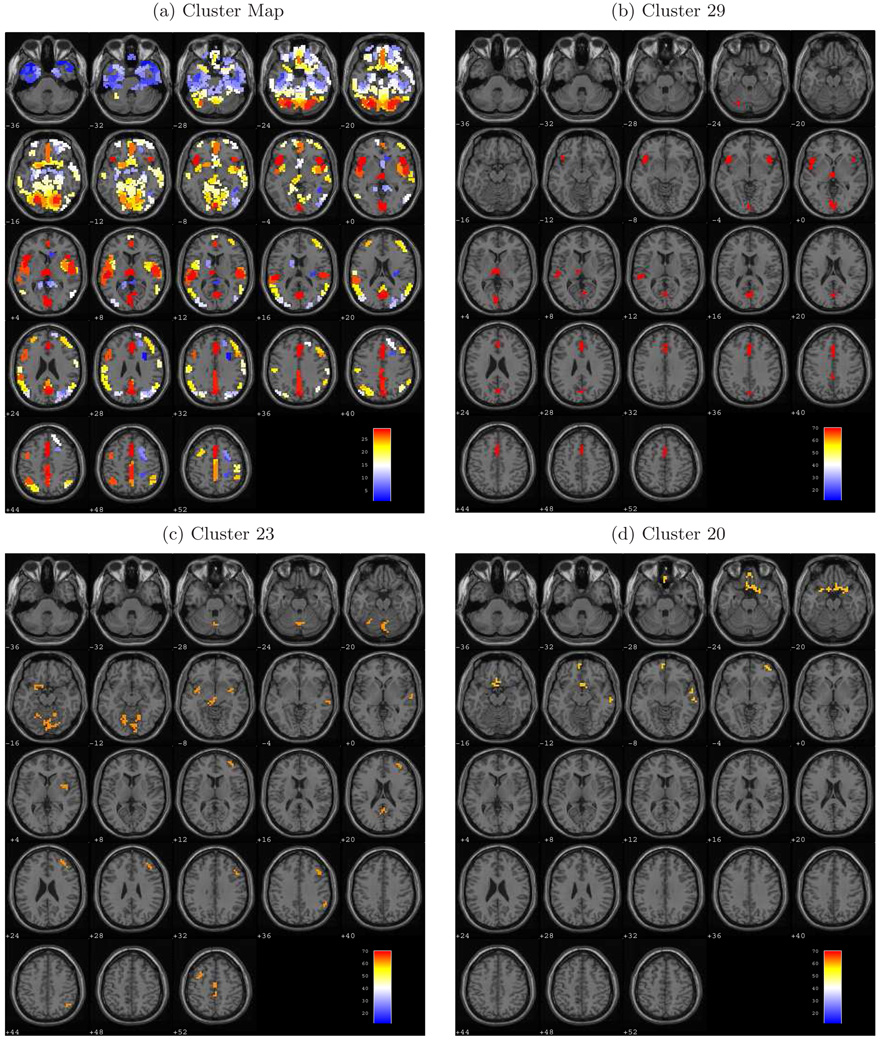
We begin by fitting the working memory data using a general linear model with expected value parameters representing the four experimental conditions (digit shadowing and low, moderate, and high working memory loads) and a covariate adjustment for global cerebral blood flow (gCBF). We obtain ordinary least-squares estimates of the regression parameters and perform clustering using the vector of summary statistics T(υ) = β̂(υ) for each voxel. We perform hierarchical clustering using Ward’s method (Rencher, 2002) and determine the number of clusters using the cubic clustering criterion (CCC) (Sarle, 1983). Generally, CCC compares the square of the observed correlation coefficient (R2) and an approximation of its expected value under specified regularity conditions. A plot of CCC ranging from 1 to 40 clusters (not shown here) clearly identified G = 29 as the number of clusters present in the data. Therefore, the final clustering solution contains 29 clusters, and we depict the cluster map in Figure 1.
Figure 1.
Cluster maps from Ward’s method displayed on axial brain slices ranging from −36mm to +52mm relative to the anterior/posterior commissure plane (z). (a) View of the 29 clusters, with each cluster containing voxels that exhibit similar responses across varying loads on working memory. (b) Cluster 29 includes voxels in the inferior frontal gyrus (BA 47), thalamus, anterior and posterior cingulate (BA 30;32), and the lingual gyrus (BA 17;18). (c) Cluster 23 consists of voxels in the precentral and middle frontal gyri (BA 9), in the middle, medial, and superior frontal gyri (BA 6), and along the supramarginal gyrus (BA 40). (d) Cluster 20 spans portions of the right middle frontal gyrus (BA 10), the left medial frontal gyrus (BA 11), and the anterior cingulate (BA 25).
The cluster sizes range widely with the smallest cluster (1) containing only 8 voxels and the largest cluster (17) containing 773 voxels. The average number of voxels in a cluster is 342 with a standard deviation of 165 voxels. We calculated the mean normalized rCBF values for all voxels within a cluster (averaged across levels of working memory load), and arranged them in increasing order. Cluster 1 contains voxels with outlying observations and has a mean of only 14.0. The most active cluster (29) has a mean value of 69.8. Ten of the clusters identified by Ward’s method exhibit brain activity that is lower than the global average of 50, while the other clusters show increased activity relative to the global average value.
Typical cluster analyses cease after establishing a cluster solution and perhaps quantifying associated descriptive statistics. While the descriptive cluster map provides some insights on functional associations in the brain, it does not quantify the similarity of voxels within the 29 clusters. Our methodology allows us to compute a global measure of the functional autocorrelation using Moran’s I statistic and to evaluate the validity of the clustering solution by examining the statistical significance of the autocorrelation. Overall, the clusters exhibit very strong positive functional autocorrelation for the digit shadowing condition (0.80), the low working memory load condition (0.81), the moderate load condition (0.81), and the high load condition (0.81). The large positive values of the functional autocorrelation index suggest that there is generally strong coherence between the voxel profiles within the defined neural processing clusters. Furthermore, these functional autocorrelations are highly statistically significant with p-values all less than 0.0001, confirming the validity of the clustering solution relative to the expected associations under spatial randomness.
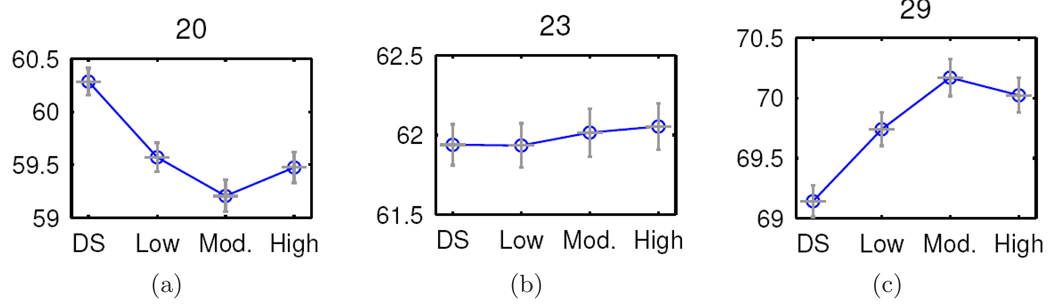
Our analysis identifies clusters containing voxels that, on average, reveal activity profiles resembling particular polynomial curves as a function of varying working memory load levels. The representative mean profiles for three clusters appear in Figure 2; we display the associated standard errors using vertical bars. The plots reveal potentially important functional characteristics of the relationship of cluster-level activity to working memory. The nonlinear trends apparent in the plots provide insights on the nature of the stimulus-response relationship in the cluster and may assist in guiding subsequent statistical modeling, particularly in studies of parametrically varying experimental conditions.
Figure 2.
Mean rCBF profiles, along with standard errors, for 3 representative clusters across levels of working memory load ranging from digit shadowing (DS) to the high load. Many clusters (not all shown here) exhibit nonlinear trends over the parametrically varied memory loads.
Cluster 29 is the most active cluster, i.e. has the highest normalized rCBF, associated with the neural processing underlying working memory. The voxels within this cluster reveal a roughly quadratic trend in rCBF, exhibiting an increase in measured brain activity from digit shadowing through the moderate working memory load, followed by slight attenuation in the activity at the high load (see Figure 2(c)). Axial slices of the cluster map in Figure 1(b) show that this neural processing cluster consists of voxels localized bilaterally in the inferior frontal gyrus (Brodmann area (BA) 47) (Brodmann, 1909), extending into the left superior temporal gyrus (BA 22); thalamus; anterior (BA 32) and posterior (BA 30 and 31) cingulate cortex; and the lingual gyrus (BA 17 and 18). The quadratic trend that these voxels display suggests that, in individuals with schizophrenia, the activity in this cluster increases to accommodate more substantial memory loads, but then diminishes when the working memory load exceeds capacity. There was not a precipitous fall in the performance of the serial addition task imposing a high working memory load, rather a near linear decrease in accuracy from the digit shadowing to high load conditions. Performance at high load levels may be subsumed by other clusters (e.g. cluster 20).
Cluster 20 defines a network of functionally related voxels spanning portions of the prefrontal cortex including the right middle frontal gyrus (BA 10), left ventromedial frontal gyrus (BA 11), and the subcallosal cortex (BA 25), all visible in axial slices z = −12 mm through −4 mm of Figure 1(d). As indicated by Figure 2(a), these voxels exhibit an approximate quadratic pattern of task-related activity with declining activity from digit shadowing to moderate working memory load and a slight increase at the high load level.
The full set of individual cluster maps identify functional associations related to the neural activity involved in performing parametrically varying working memory tasks. Here, our detailed inspection of two clusters reveals distinct profiles of task-related brain activity and reveals associations between brain regions that have been previously linked to working memory tasks. Numerous studies have detected the involvement of both dorsal lateral and ventral lateral regions of the prefrontal cortex in working memory functions (D’Esposito, 2001). In addition, several studies have implicated distributed activations in the posterior parietal cortex (BA 40/7), anterior cingulate cortex (BA 32), and the thalamus, as well as premotor areas (BA 6 and 8) (D’Esposito et al., 1998; Perlstein et al., 2003; Picard and Strick, 1996).
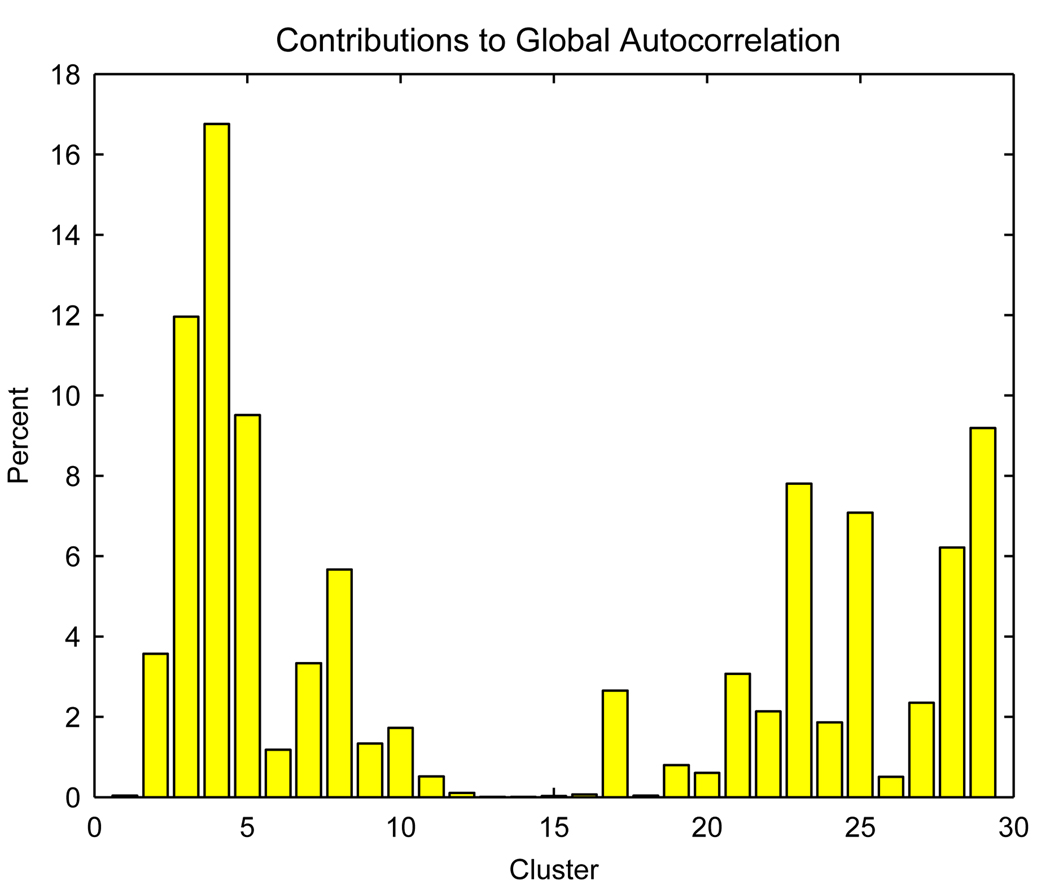
The global autocorrelation measures augment the descriptive findings of classification procedures by evaluating the strength and direction of the associations within the defined neural processing clusters. Local measures of autocorrelation do not extend readily to neuroimaging classification applications because they would require definitions of within-cluster adjacency or functional connections. To provide a crude measure of the contribution that each cluster has on the overall Moran’s I autocorrelation statistic, we compute the percent contribution of each cluster. Figure 3 displays the results of this local measure. The plot reveals that several clusters with large or small mean rCBF values contribute more heavily to the global autocorrelation measure. Generally, a cluster’s contribution to the overall level of global autocorrelation gives an indication of the degree of similarity of rCBF profiles from voxels within the cluster and of the spatial extent of the cluster. Both a high degree of within-cluster homogeneity in working memory-related rCBF values and a large cluster size lead to greater influence on the overall level of functional autocorrelation. Clusters 3, 4, 5, 23, and 29 have the largest impact on the overall functional coherence, attesting to the high degree of functional autocorrelation in these clusters.
Figure 3.
The cluster-specific contributions to the overall autocorrelation index.
Depression Data
We first perform a group ICA analysis of the fMRI data using PICA (Beckmann and Smith, 2004) as implemented in the FSL tool MELODIC (Multivariate Exploratory Linear Decomposition into Independent Components) Version 3.09. The following data preprocessing was applied to the input data: masking of non-brain voxels; voxel-wise de-meaning of the data; normalisation of the voxel-wise variance. Pre-processed data were whitened and projected into a 33-dimensional subspace using Principal Component Analysis. The whitened observations were decomposed into sets of vectors which describe signal variation across the temporal domain (time-courses), the session/subject domain and across the spatial domain (maps) by optimizing for non-Gaussian spatial source distributions using a fixed-point iteration technique (Hyvärinen, 1999). Estimated component maps were divided by the standard deviation of the residual noise and thresholded by fitting a mixture model to the histogram of intensity values (Beckmann and Smith, 2004). The optimal number of components determined by the PICA algorithm (Beckmann and Smith, 2004) is 33. Many brain voxels were allocated to more than one IC, and some voxels were not assigned to any of the ICs. Out of a total of 19,257 intracranial voxels, 17,197 were assigned to at least one of the ICs. We assign each of the latter voxels to a single IC, based on the largest (in magnitude) Z-score.
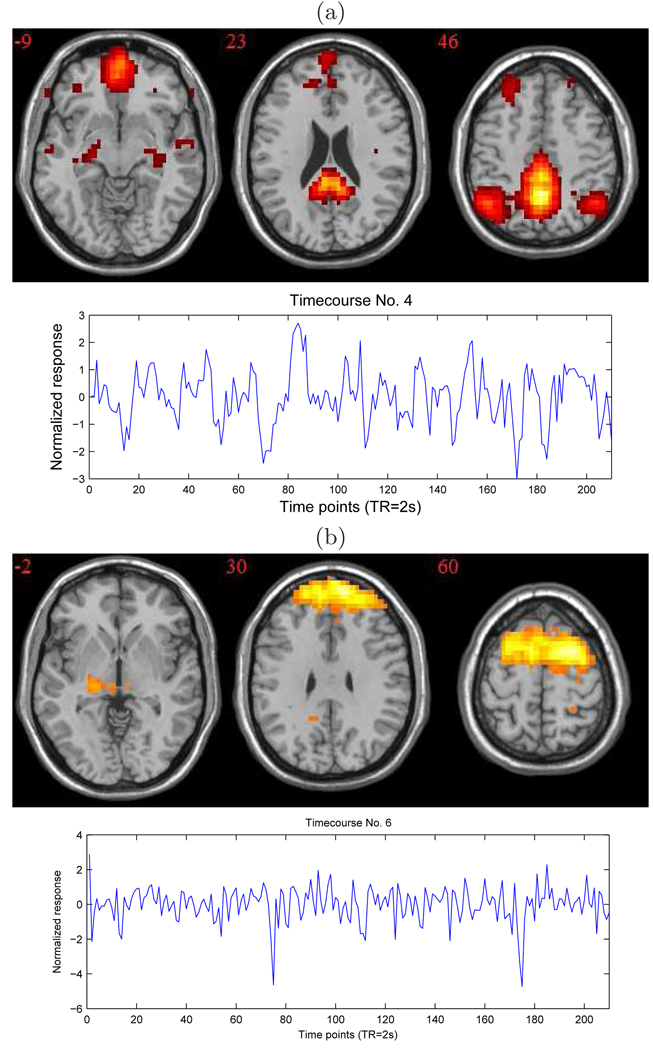
For this data set, the functional autocorrelation index is 0.17. Even though it is modest compared to the one for PET data, it is statistically significant with a p-value less than 0.0001. There are only 4 ICs for which the crude estimates of local autocorrelation are > 0.01, and Figure 4 shows two of them. IC 4 represents the DMN, and IC 6 contains voxels in several brain areas (e.g. dorsolateral prefrontal cortex (BA 9), anterior prefrontal cortex (BA 10), and left thalamus) relevant in depression (Mayberg, 1997; Goldapple et al., 2004)). Table 1 lists the IC-specific contribution to the global autocorrelation index, number of voxels and Brodmann regions in which the IC’s voxels lie for several ICs.
Figure 4.
ICA results with optimal number of components (33); (a) IC 4 (with the corresponding time course): the DMN; (b) IC 6.
Table 1.
Network-specific contributions to the overall autocorrelation index of selected ICs (as identified by ICA) of the fMRI data from the study on depression.(l and r denote the ‘left’ and ‘right’ hemisphere).
| IC | % of global autocorrelation |
# voxels | BA’s |
|---|---|---|---|
| 4 | 12.41 | 843 | 7, 9, 10, 11, 23, 30, 39, 40 |
| 5 | 6.88 | 1032 | putamen, 3, 4, 6, 48 |
| 6 | 7.24 | 968 | thalamus(1), 6, 9, 10, 46 |
| 17 | 10.65 | 1464 | 6, 9, 24, 32, 46 |
| 27 | 0 | 45 | 21(r), 22(r), thalamus (r) |
| 29 | 4.24 | 827 | 40(r), 44(r), 45(r), 47 |
Since for this data set, we calculate the global Moran’s I statistic based on the voxels’ time courses (not the summary statistic vectors), the statistic I is small, mainly due to the fact that the denominator in (3) increases very fast since the number of time points is large (210). For this reason, we apply another approach to evaluate the global autocorrelation. We calculate the global Moran’s I separately for each time point, this way obtaining a (210 * 7 × 1) vector of global indices of autocorrelation, for our ICA solution. The obtained values are of a larger scale. They range from 0.03 to 0.53, with the peak values within subjects reaching at least 0.3. The corresponding IC-specific contributions to the overall autocorrelation index agree with the previous results reported in Table 1. Namely, the ICs with the largest range of ‘local’ Moran’s I statistics are still IC 4 (range of I’s [0, 0.19]), IC 5 (range of I’s [0, 0.14]), IC 6 (range of I’s: [0, 0.15]), and IC 17 (range of I’s [0, 0.26]). Therefore, both approaches bring us to similar conclusions about which of the 33 ICs are most functionally and spatially coherent neural networks. There are several possible reasons why, for this data set, the estimated global autocorrelation index is relatively small. First, the sample size is small for a group analysis (only 7 subjects). This is resting-state data, so the signal to noise ratio is likely to be lower than for task data (such as our PET data set). Also, even though the ICA analysis should ideally result in functionally correlated ICs, the approach is based on conceptually different criteria which results in ICs that are as statistically independent as possible.
Bootstrap Analysis
We do not perform spatial smoothing of the PET data prior to conducting the cluster analysis to avoid artificially inflating the correlations between the rCBF measurements in nearby voxels. A related issue is whether the intrinsic spatial correlations in PET data, e.g. stemming from the acquisition and reconstruction processes, may bias Moran’s I toward higher values. If true, then the upward bias of Moran’s I would call for modifications to the hypothesis testing framework outlined previously. We conduct a Monte Carlo simulation study to evaluate the expected value and the variability of Moran’s I under the null hypothesis of random cluster assignments.
We conduct a bootstrap analysis that includes 500 samples drawn, with replacement, from the working memory data. For each sample, we compute summary statistics representing the four working memory load conditions, adjusted for gCBF. To establish the null distribution of Moran’s I, we randomly allocate voxels to clusters in each bootstrap sample, with the cluster sizes matching those obtained in our original analysis, and then we calculate Moran’s I for the resulting randomized clustering solutions. The 500 computed statistics represent the empirical distribution of Moran’s I under the null hypothesis. The bootstrap distribution allows a comparison of empirical and theortical properties of Moran’s I including both its mean and variance.
Table 2 summarizes the results of the bootstrap analysis. Theoretically, the mean of Moran’s I is equal to −0.000101. The similarity of the theoretical and empirical mean values provides strong evidence of negligible bias in Moran’s I for our PET application. We find the empirical distributions of the bootstrap biases, reflecting estimates of Moran’s I obtained from the boostrap samples (under randomization) minus the theoretical value of the mean. Averaging over all the bootstrap samples gives the bootstrap estimate of bias, for each condition. Although slightly negative, the biases are all extremely small. Similarly, the bootstrap variance estimates exhibit close correspondence to the theoretical values. The magnitudes of all differences between the empirical and theoretical variances are less than 0.4224 × 10−6. The accuracy of the theoretical mean and variance expressions relative to their empirical counterparts obtained from the bootstrap estimates supports the use of the hypothesis testing procedure outlined in the Methods section.
Table 2.
Summary of the Bootstrap analysis designed to evaluate a potential bias of Moran’s I (e.g. caused by intrinsic spatial autocorrelation) in PET data.
| Mean Moran’s I |
Working memory load | |||
|---|---|---|---|---|
| digit shadowing (DS) | low | moderate | high | |
| Theoretical | −0.000101 | −0.000101 | −0.000101 | −0.000101 |
| Bootstrap | −0.00033 | −0.00025 | − 0.00029 | −0.00030 |
| Bias | −2.29 × 10−4 | −1.49 × 10−4 | −1.89 × 10−4 | −1.99 × 10−4 |
| Variability | 0.62 × 10−3 | 0.62 × 10−3 | 0.63 × 10−3 | 0.63 × 10−3 |
Simulated Data Example
We analyze simulated data based on the working memory PET study to illustrate further the utility of Moran’s I for detecting the presence of functional autocorrelation in clustering solutions. We simulate data using a mixture model that takes a weighted average of the global mean and the mean of the voxel-specific summary values within the same neural processing cluster, with weights defined by a spatial dependence (correlation) parameter ρ. Specifically, we generate data for a particular voxel within cluster g using
| (9) |
where , µ is the overall mean, e.g. 50; and T̅Nυ is the mean of the summary statistics from the Vg − 1 voxels in the same cluster as voxel υ, i.e. from the functional neighborhood of υ, denoted by Nυ. We consider six simulated data sets with the correlation parameter varying across the set of values ρ ∈ {0, 0.2, 0.4, 0.6, 0.8, 1}. We use the 29 clusters computed from the working memory data to define the cluster structure and the corresponding cluster sizes Vg. We utilize estimates of the variance parameters and the summary statistic vector from the working memory data.
The error terms from different voxels in model (9) are independent. However, the model yields simulated values that depend on the activity levels from other voxels within the same neural processing cluster, when ρ > 0. The activity in a given voxel is uncorrelated with the activity of the other voxels within the same cluster when ρ = 0.
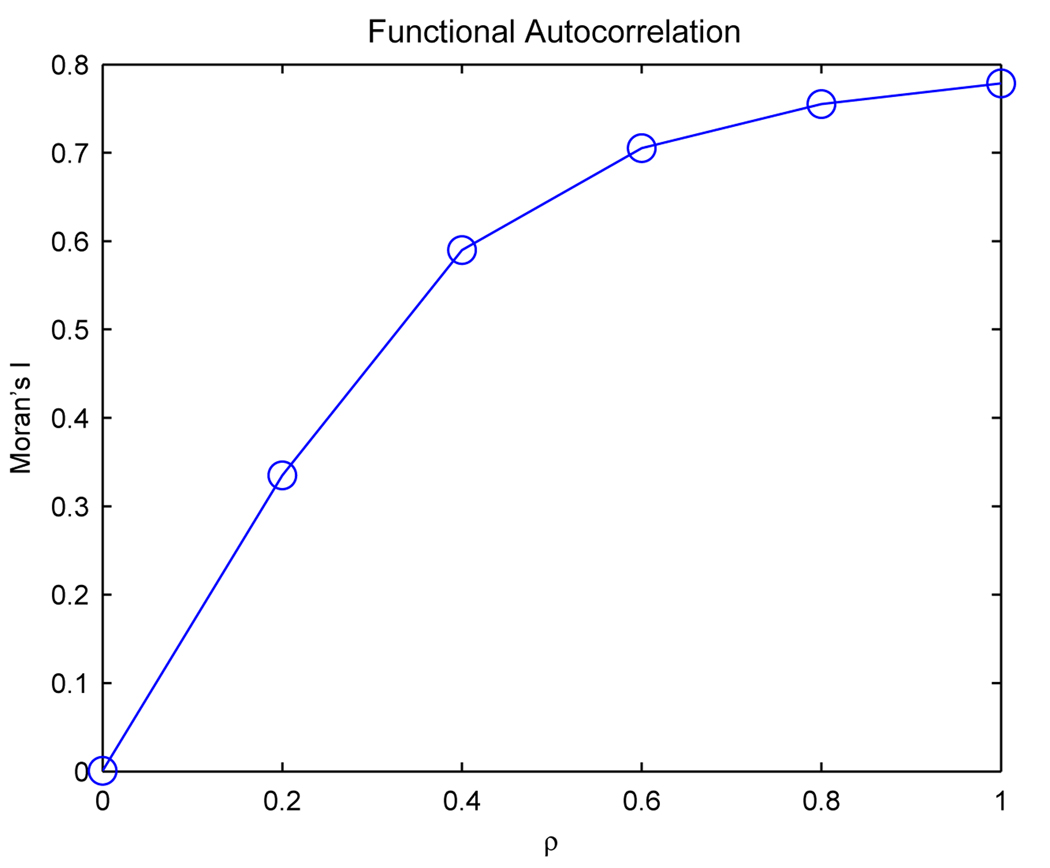
We compute Moran’s I for the clustering solution corresponding to each simulated data set, and Figure 5 displays the relationship between Moran’s I and the correlation parameter for the simulated data. The plot illustrates that Moran’s I is effective for detecting and quantifying functional autocorrelation in clustered data. The value of Moran’s I is zero in the absence of functional autocorrelation. In practice, the importance of revealing the absence of functional autocorrelations lies in the fact that a simple cluster analysis would yield misleading results by providing a clustering solution when no true underlying structure is present in the data. Moran’s I increases as a function of ρ, reinforcing that the global index captures the functional autocorrelation inherent within the computed clusters. The simulated data do not achieve perfect correlation, even when ρ = 1, primarily due to the addition of random noise specified by our simulation model. Consequently, Moran’s I is approximately equal to 0.8 when the correlation parameter for the simulated data equals 1.
Figure 5.
Plot of Moran’s I versus the correlation parameter ρ for the simulated data. Data with increased functional autocorrelation yield larger values of Moran’s I.
5. DISCUSSION
Data-driven approaches, such as cluster analysis and ICA, are extremely useful tools for describing the functional structure and patterns present in neuroimaging data. Cluster analyses help dissociate groups of voxels that exhibit similar patterns of brain activity over time or across experimental conditions. ICA is very useful for detecting resting-state neural networks. In this paper, we extend the interpretations given by those two methods by introducing Moran’s I for statistical estimation and hypothesis testing of the functional autocorrelation present in neural processing networks as identified by clustering or ICA. Applying these procedures helps to evaluate the validity of the typological descriptions given by a clustering or an ICA solution. Computing Moran’s I is fast and easy to program using standard statistical software such as R or SAS. We use MATLAB to calculate the functional autocorrelation of neural processing networks of (functional clusters or ICA components) from PET working memory data, fMRI depression data, and simulated data.
We propose a definition of Moran’s I that estimates the functional autocorrelation separately for each element of the summary statistic vector, e.g. pertaining to a specified experimental condition such as high working memory load. For studies that cluster time courses measured under numerous experimental stimuli, it is perhaps more beneficial to aggregate the spatial index across the components of the summary statistic vector. One can easily modify Moran’s I to define a more crude measure that “averages” across all elements of the summary vector. When computing the functional network-specific contributions to the global autocorrelation index, the network sizes impact the corresponding contributions. The data must provide extremely strong evidence that a small neural processing network (e.g. a small cluster) contributes substantially to the global autocorrelation for the network to weigh heavily in the global calculation. The number of networks may also affect estimates of the functional autocorrelation. Assigning voxels into a large number of groups will allow the solution to reflect strong resemblances among within-cluster voxels, whereas designating fewer groups will often lead to less coherence within clusters.
We demonstrate the use of Moran’s I using PET neuroimaging data analyzed using cluster analysis and fMRI resting-state data analyzed using ICA. In addition, Moran’s I may combine with results from related descriptive procedures such as principal component analysis (Friston et al., 1993). Structural equation modeling is a useful approach to examine the direct and indirect effects that one brain region has on another (McIntosh and Gonzalez-Lima, 1994), but it requires the specification of anatomical models and substantially simplifies spatial representations from a large number of voxels to a small number of regions. Both cluster analyses and ICA generally serve as exploratory tools, but often the ultimate objectives of neuroimaging studies require the use of inferential or confirmatory statistical procedures. In this light, conducting such analyses, followed by an assessment of the functional autocorrelation, helps provide insights about characteristics of neuroimaging data that may prove valuable for subsequent modeling, estimation, and hypothesis testing.
Footnotes
This research was supported by NIH grants R01-MH079251 (Bow-man) and NIH predoctoral training grant T32 GM074909-01 (Derado).
The research by Beckmann and Smith described above has been implemented as MELODIC (Multivariate Exploratory Linear Optimized Decomposition into Independent Components - a stand alone C++ program). It is freely available as part of FSL (FMRIB’s Software Library).
Contributor Information
Gordana Derado, Department of Biostatistics and Bioinformatics, The Rollins School of Public Health, Emory University, gderado@emory.edu.
F. Dubois Bowman, Department of Biostatistics and Bioinformatics, The Rollins School of Public Health, Emory University, dbowma3@sph.emory.edu.
Timothy D. Ely, Department of Psychiatry and Behavioral Sciences, School of Medicine, Emory University, tely01@emory.edu
Clinton D. Kilts, Department of Psychiatry and Behavioral Sciences, School of Medicine, Emory University, sdpcdk@emory.edu
REFERENCES
- Balslev D, Nielsen F, Frutiger S, Sidtis J, Christiansen T, Svarer C, Strother S, Rottenberg D, Hansen L, Paulson O, Law I. Cluster analysis of activity-time series in motor learning. Human Brain Mapping. 2002;15:135–145. doi: 10.1002/hbm.10015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumgartner R, Ryner L, Richter W, Summers R, Jarmasz M, Somorjai R. Comparison of two exploratory data analysis methods for fMRI: fuzzy clustering vs. principal component analysis. Magnetic Resonance Imaging. 2000;18:89–94. doi: 10.1016/s0730-725x(99)00102-2. [DOI] [PubMed] [Google Scholar]
- Beckmann C, Smith S. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Transactions on Medical Imaging. 2004;23(2):137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Beckmann C, Smith S. Tensorial extensions of independent component analysis for multisubject FMRI analysis. NeuroImage. 2005;25(1):294–311. doi: 10.1016/j.neuroimage.2004.10.043. [DOI] [PubMed] [Google Scholar]
- Bell A, Sejnowski T. An information maximisation approach to blind separation and blind deconvolution. Neural Computation. 1995;(6):1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Biswal B, Ulmer J. Blind source separation of multiple signal sources of fMRI data sets using independent component analysis. Journal of Computer Assisted Tomography. 1999;23(2):265–271. doi: 10.1097/00004728-199903000-00016. [DOI] [PubMed] [Google Scholar]
- Bowman F, Patel R. Identifying spatial relationships in neural processing using a multiple classification approach. NeuroImage. 2004;23:260–268. doi: 10.1016/j.neuroimage.2004.04.022. [DOI] [PubMed] [Google Scholar]
- Bowman F, Patel R, Lu C. Methods for detecting functional classifications in neuroimaging data. Human Brain Mapping. 2004;23:109–119. doi: 10.1002/hbm.20050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodmann K. “Vergleichende Lokalisationlehre der Grosshirnrinde in ihren Prinzipien Dargestellt auf Grund des Zellenbaues,” translated by Garey, L.J. as Brodmann’s ‘Localisation in the Cerebral Cortex’. London: Smith-Gordon; 1994 [original publication date 1909]. [Google Scholar]
- Calhoun V, Adali T, Hansen LK, Larsen J, Pekar J. ICA of functional MRI data: an overview. Fourth International Symposium on Independent Component Analysis and Blind Source Separation, Nara, Japan; 2003. pp. 281–288. [Google Scholar]
- Calhoun V, Adali T, Pearlson G, Pekar J. Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms. Human Brain Mapping. 2001;13:43–53. doi: 10.1002/hbm.1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun V, Pekar J. When and where are components independent? On the applicability of spatial- and temporal- ICA to functional MRI data. Sixth International Conference on Functional Mapping of the Human Brain., NeuroImage; Academic Press; 2000. [Google Scholar]
- Chiu K-C, Liu Z-Y, Xu L.A statistical approach to testing mutual independence of ica recovered sources 2003Proceedings of 4th International Symposium on Independent Component Analysis and Blind Signal Separation (ICA2003) Japan [Google Scholar]
- Cliff A, Ord J. Spatial Autocorrelation. London: Pion Limited; 1973. [Google Scholar]
- Cliff A, Ord J. Models and Applications. London: Pion; 1981. Spatial Processes. [Google Scholar]
- Common P. Independent component analysis, a new concept? Signal Processing. 1994;36:287–314. [Google Scholar]
- Cordes D, Haughton V, Carew J, Arfanakis K, Maravilla K. Hierarchical clustering to measure connectivity in fMRI resting-state data. Magnetic Resonance Imaging. 2002;20:305–317. doi: 10.1016/s0730-725x(02)00503-9. [DOI] [PubMed] [Google Scholar]
- D’Esposito M. Handbook of Functional Neuroimaging of Cognition, chapter Functional Neuroimaging of Working Memory, pages 293–327. Cambridge, MA: The MIT Press; 2001. [Google Scholar]
- D’Esposito M, Aguirre G, Zarahn E, Ballard D. Functional MRI studies of spatial and non-spatial working memory. Cognitive Brain Research. 1998;7:1–13. doi: 10.1016/s0926-6410(98)00004-4. [DOI] [PubMed] [Google Scholar]
- Esposito F, Formisano E, Seifritz E, Goebel R, Morrone R, Tedeschi G, Salle F. Spatial independent component analysis of functional MRI time-series: to what extent do results depend on the algorithm used? Human Brain Mapping. 2002;16:146–157. doi: 10.1002/hbm.10034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fadili M, Ruan S, Bloyet D, Mazoyer B. A multistep unsupervised fuzzy clustering analysis of fMRI time series. Human Brain Mapping. 2000;10:160–178. doi: 10.1002/1097-0193(200008)10:4<160::AID-HBM20>3.0.CO;2-U. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fadili M, Ruan S, Bloyet D, Mazoyer B. On the number of clusters and the fuzziness index for unsupervised FCA application to BOLD fMRI time series. Medical Image Analysis. 2001;5(55–67) doi: 10.1016/s1361-8415(00)00035-9. [DOI] [PubMed] [Google Scholar]
- Filzmoser P, Baumgartner R, Moser E. A hierarchical clustering method for analyzing functional MR images. Magnetic Resonance Imaging. 1999;17:817–826. doi: 10.1016/s0730-725x(99)00014-4. [DOI] [PubMed] [Google Scholar]
- Friston K, Frith C, Liddle P, Frackowiak R. Functional connectivity: the principal component analysis of large data sets. Journal of Cerebral Blood Flow & Metabolism. 1993;13:5–14. doi: 10.1038/jcbfm.1993.4. [DOI] [PubMed] [Google Scholar]
- Goldapple K, Segal Z, Garson C, Lau M, Bieling P, Kennedy S, Mayberg H. Modulation of cortical-limbic pathways in major depression: treatment specific effects of cbt. Archives of General Psychiatry. 2004;61:34–41. doi: 10.1001/archpsyc.61.1.34. [DOI] [PubMed] [Google Scholar]
- Goodchild M. Spatial Autocorrelation. CATMOG; 1986. [Google Scholar]
- Goutte C, Nielsen F, Liptrot M, Hansen L. Featurespace clustering for fMRI meta-analysis. Human Brain Mapping. 2001;13:165–183. doi: 10.1002/hbm.1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutte C, T P, Rostrup E, Nielsen F, Hansen L. On clustering fMRI time series. Neuro Image. 1999;9:298–310. doi: 10.1006/nimg.1998.0391. [DOI] [PubMed] [Google Scholar]
- Harshman R. Foundations of the PARAFAC procedure: models and conditions for an “exploratory” multimodal factor analysis. UCLA Working Papers in Phonetics. 1970;16:1–84. [Google Scholar]
- Harshman R, Lundy M. Parafac: parallel factor analysis. Computational Statistics & Data Analysis. 1994;18:39–72. [Google Scholar]
- Hartigan J. Classification and Clustering, chapter Distribution Problems in Clustering. New York: Academic Press, Inc; 1977. [Google Scholar]
- Hartigan J. Asymptotic distributions for clustering criteria. Annals of Statistic. 1978;6:117–131. [Google Scholar]
- Herault J, Jutten C. Space or time adaptive signal processing by neural network model. In: Denker JS, editor. Neural Networks for Computing. Proceedings of AIP Conference; New York: American Institute of Physics; 1986. pp. 206–211. [Google Scholar]
- Himberg J, Hyvärinen A. Icasso: software for investigating the reliability of ICA estimates by clustering and visualization. IEEE Workshop on Neural Networks for Signal Processing (NNSP2003), Toulouse, France; 2003. pp. 259–268. [Google Scholar]
- Himberg J, Hyvärinen A, Esposito F. Validating the independent components of neuroimaging time series via clustering and visualization. NeuroImage. 2004;22(3):1214–1222. doi: 10.1016/j.neuroimage.2004.03.027. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Transactions on Neural Networks. 1999;10(3):626–634. doi: 10.1109/72.761722. [DOI] [PubMed] [Google Scholar]
- Jutten C, Herault J. Blind separation of sources, part I: An adaptive algorithm based on neuromimetic architecture. Signal Processing. 1991;24(1):1–10. [Google Scholar]
- Mayberg H. Limbic-cortical dysregulation: A proposed model of depression. Journal of Neuropsychiatry and Clinical Neurosciences. 1997;9:471–481. doi: 10.1176/jnp.9.3.471. [DOI] [PubMed] [Google Scholar]
- McIntosh A, Gonzalez-Lima F. Structural equation modeling and its application to network analysis in functional brain imaging. Human Brain Mapping. 1994;2:2–22. [Google Scholar]
- McKeown M, Makeig S, Brown G, Jung T, Kindermann S, Bell A, Sejnowski T. Analysis of fMRI data by decomposition into independent components. Neurology. 1997;48:6056. [Google Scholar]
- McKeown M, Makeig S, Brown G, Jung T, Kindermann S, Bell A, Sejnowski T. Analysis of fMRI data by blind separation into independent spatial components. Human Brain Mapping. 1998;6(3):160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran P. Some theorems on time series. II. The Significance of the serial correlation coefficient. Journal of the Royal Statistical Society, Series B. 1948;35:255–260. [Google Scholar]
- Moran P. Notes on continuous stochastic phenomena. Biometrika. 1950;37:17–23. [PubMed] [Google Scholar]
- Murata N. Properties of the empirical characteristic function and its application to testing for independence. Proceedings of Third International Conference on Independent Component Analysis and Blind Signal Separation; 2001. pp. 19–24. [Google Scholar]
- Perlstein W, Dixit N, Carter C, Noll D, Cohen J. Prefrontal cortex dysfunction mediates deficits in working memory and prepotent responding in schizophrenia. Biological Psychiatry. 2003;53(25–38) doi: 10.1016/s0006-3223(02)01675-x. [DOI] [PubMed] [Google Scholar]
- Picard N, Strick P. Motor areas of the medial wall: A review of their location and functional activation. Cerebral Cortex. 1996;6:342–335. doi: 10.1093/cercor/6.3.342. [DOI] [PubMed] [Google Scholar]
- Poline JB, M B. Cluster analysis in individual functional brain images: Some new techniques to enhance the sensitivity of activation detection methods. Human Brain Mapping. 1994;2:103–111. [Google Scholar]
- Rencher A. Methods of Multivariate Analysis. 2nd ed. New York: John Wiley & Sons, Inc.; 2002. 2 edition. [Google Scholar]
- Sarle W. Cubic Clustering Criterion, SAS Technical Report A-108. 1983 Technical report, , SAS Technical Report A-108. [Google Scholar]
- Shimizu S, Kano Y. Examination of independence in independent component analysis. Proceedings of 2001 International Meeting of the Psychometric Society.2001. [Google Scholar]
- Simon O, Kherif F, Flandin G, Poline J-B, Rivière D, MJ-FLBDDS Automatized clustering and functional geometry of human parietofrontal networks for language, space, and number. NeuroImage. 2004;23(3):1192–1202. doi: 10.1016/j.neuroimage.2004.09.023. [DOI] [PubMed] [Google Scholar]
- Sommer F, Wichert A. Exploratory analysis and data modeling in functional neuroimaging. Cambridge, MA: The MIT Press; 2003. pp. 17–42. [Google Scholar]
- Stanberry L, Nandy R, Cordes D. Cluster analysis of fMRI data using dendrogram sharpening. Human Brain Mapping. 2003;20:201–219. doi: 10.1002/hbm.10143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stogbauer H, Andrzejak R, Kraskov A, Grassberger P. Lecture Notes in Computer Science: Independent Component Analysis and Blind Signal Separation. volume 3195. 2004. Reliability of ICA estimates with mutual information; pp. 209–216. [Google Scholar]
- Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain. New York: Thieme Medical Publishers, Inc.; 1988. [Google Scholar]
- Woods R, Grafton S, Holmes C, Cherry S, Mazziotta J. Automated image registration: I. general methods and in-trasubject, intramodality validation. Journal of Computer Assisted Tomography. 1998a;22:139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]
- Woods R, Grafton S, Watson J, NL S, JC M. Automated image registration: II. Intersubject validation of linear and nonlinear models. Journal of Computer Assisted Tomography. 1998b;22:153–165. doi: 10.1097/00004728-199801000-00028. [DOI] [PubMed] [Google Scholar]
- Wu E, Yu P, Li W. A smoothed bootstrap test for independence based on mutual information source. Computational Statistics & Data Analysis archive. 2009;53(7):2524–2253. [Google Scholar]