TreeKO: a duplication-aware algorithm for the comparison of phylogenetic trees

Abstract

Comparisons of tree topologies provide relevant information in evolutionary studies. Most existing methods share the drawback of requiring a complete and exact mapping of terminal nodes between the compared trees. This severely limits the scope of genome-wide analyses, since trees containing duplications are pruned arbitrarily or discarded. To overcome this, we have developed treeKO, an algorithm that enables the comparison of tree topologies, even in the presence of duplication and loss events. To do so treeKO recursively splits gene trees into pruned trees containing only orthologs to subsequently compute a distance based on the combined analyses of all pruned tree comparisons. In addition treeKO, implements the possibility of computing phylome support values, and reconciliation-based measures such as the number of inferred duplication and loss events.

INTRODUCTION

Phylogenetic trees represent evolutionary relationships among groups of species or biological sequences. The growing availability of sequence data from whole genomes, as well as the development of faster computers and more efficient phylogenetic programs, has facilitated the reconstruction of large collections of phylogenetic trees. In parallel, this has brought about the necessity of scaling up the analysis of phylogenetic trees to genomic scales (1). A recurrent analysis in phylogenetic studies is the comparison of the topologies of two or more phylogenetic trees. This is routinely used, for instance, to measure the support of tree partitions in a bootstrapping analysis or to compare alternative phylogenetic hypotheses (2). Additional applications include, but are not limited to, the reconstruction of a single species tree from a number of individual gene trees (3), the evaluation of orthology inference (4), the detection of horizontal gene transfer events (5) or the detection of host-pathogen co-evolution (6).

Two main types of algorithms are available that compute topological distances between phylogenetic trees. A first class of algorithms uses the information directly from the topological arrangement of terminal nodes (i.e. leaves) in the trees. For instance, the popular Robinson-Foulds (RF) distance counts how many leaf splits are implied by only one of the compared trees (7). Similarly, the quartet distance is defined as the number of subsets of four leaves that are implied by only one of the compared trees (8). Finally, the so-called maximum agreement subtree is a similarity measure based on the largest subtree present in the two compared trees (6). A second group of algorithms measures the minimal number of topological re-arrangements necessary to transform one topology into the other one. This is the rationale behind the transposition distance (9,10), the prune and regraft distance (11,12) and the tree edit distance (13). Despite their extensively proven usefulness, all these algorithms share one limitation, namely the requirement that the mapping of leaves between the trees is complete and univocal (i.e. every leaf in one tree corresponds to only one leaf in the other tree). Thus, when applied to the comparison of gene family trees, these algorithms are unable to deal with trees that contain duplications (i.e. there is more than one gene per species) or losses (i.e. not all species are represented in both trees). As a result, only a reduced fraction of gene trees in a given phylogenomic study may be subject to analysis. For instance, Rasmussen and Kellis (14) found that for 9 fungal and 12 drosophila species, only 739 and 5154 protein families, respectively, contained no duplications. Thus gene trees suitable for comparison with the above mentioned methods will account for only 11 and 37% of their respective genomes. The fraction of tractable gene trees will decrease as the number of species in the set and their evolutionary distance increase (see comparative analysis below).

Some algorithms have been designed to tackle this problem. For instance, PhyloPattern (15) can search for trees containing a specific topological pattern, which may present duplications. However this only serves to search for identical subtrees and does not provide a distance measure. Another alternative consists of reconciling the gene trees to a particular species tree and then measure their distances in terms of the number of inferred deep coalescence or duplication and loss events to the reference tree. This is indeed used by a number of species tree reconstruction algorithms that search for the topology that implies the least number of such events in a set of gene trees (16–18). These methods have recently been effectively applied at genome-wide scales (19,20). Current implementations of these methods, focused on the reconstruction of super-trees, do not allow for computing such distances between any given pair of trees. To enable their use for comparison of any set or type of trees, we have implemented these distances in treeKO. However, although the use of reconciliation-based approaches may be preferred in some applications, there is still a need to extend the use of topological distances such as the popular Robinson and Foulds to trees that include duplications. A clear advantage of such a measure is that it does not need any prior assumption of a species tree topology or on the expected level of duplications and losses.

A solution to extend RF-type measures to gene trees including duplications, was implemented by Puigbò et al. in the TOPD/FMTS program (21), which is able to compare any pair of trees regardless of the number of duplications contained. While TOPD/FMTS does indeed provide an estimate of the distance, it has several drawbacks. First, whenever a species is represented by multiple sequences, TOPD/FMTS randomly prunes all but one to produce a single pruned gene tree without duplicated sequences. While this should ideally be done for each possible combination of duplicated genes, this becomes unfeasible for relatively small number of duplications. In such cases, TOPD/FMTS produces only a set of randomly chosen trees, which would provide an approximate, non-reproducible, distance measure. Besides this, the main limitation of TOPD/FMTS is that the inter-species orthology and paralogy relationships are not considered during the pruning process, resulting in pruned trees that contain a mixture of orthologous and paralogous sequences. These drawbacks hamper the interpretation of the distances provided by TOPD/FMTS. For instance, the comparison of identical trees containing some duplications will often provide distances >0 (see comparative analysis below).

In order to address this important issue so that genome-wide collections of gene trees can be effectively compared using a topological approach, we have developed treeKO. TreeKO is a novel, duplication-aware algorithm that is able to compare two tree topologies regardless of the number of duplications and, at the same time, provide a RF-based distance measure that is evolutionarily meaningful and that does not require any prior evolutionary assumption. In addition treeKO, implements the possibility of computing so-called phylome support values (22), and reconciliation-based measures such as the number of inferred duplications and losses events.

METHODS

Overview

The treeKO algorithm has three main components: (i) tree decomposition into a set of pruned trees, (ii) pruned trees pairing and (iii) distance calculation. The three components are described in more detail below and in the on-line documentation (http://treeko.cgenomics.org). In brief, given two input rooted trees in which duplication and speciation nodes are labelled, the decomposition phase is applied to both trees to generate a set of pruned trees. Pruning is performed at each duplication node so that the resulting pruned trees contain no duplication and thus all sequences contained in a pruned tree are orthologous to each other. Subsequently, a pruned tree pairing step finds optimal matches between sets of pruned trees from the two input trees. Different pairing procedures are applied depending on the desired distance measure (see below). Finally, a distance based on RF is computed by weighting the distances between all paired pruned trees.

Tree decomposition

The tree decomposition algorithm implemented in treeKO, proceeds as follows (Figure 1): given an input rooted tree with n labelled duplication nodes, the tree is traversed from the root to the most external nodes. At each duplication node, two daughter trees are produced by alternatively pruning each of the two post-duplication branches. Note that these trees are partially overlapping, since all pre-duplication nodes are retained in both pruned trees. This algorithm is applied recursively on each produced pruned tree that still contains duplications, until no duplication nodes are contained in the resulting set of pruned trees.

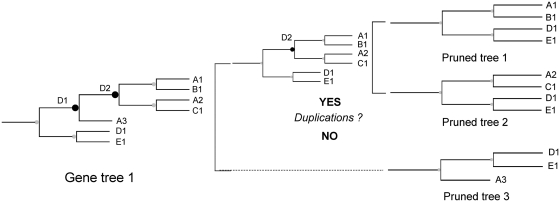
Figure 1.

Example of how treeKO derives pruned trees from a tree containing duplications. The initial tree (tree on the left) contains two duplication nodes (in black) marked as node 1 and node 2. treeKO splits the tree by node 1 and generate two different trees, each one of them containing one of the daughter partitions of node 1. This results in pruned tree 1 and an intermediate pruned tree that still contains duplication (node 2). treeKO will then scan these pruned trees for more duplications. In this case one of the pruned trees has a second duplication and the subtree will be once again split and reconstructed, resulting in pruned trees 2 and 3. treeKO will repeat this process until no resulting subtree contains further duplication nodes.

Tree pairing

Once both initial trees have been decomposed into their corresponding sets of pruned trees, all possible pairings of pruned trees between the two sets are compared and a distance measure is assigned to each pair (see below). The specific distance measures and weighting of the different pairs of pruned trees varies for the different distance metrics as explained below.

Strict distance

In order to assess the similarity between pruned trees obtained by the decomposition algorithm, both trees are pruned so that they contain the same species and then the RF distance is calculated for a pair of pruned trees (d), as indicated by the formula [1]:

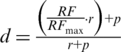(1)

where RF and RF_max represent the RF distance between the two trees and the maximum possible RF distance, respectively; r is the number of remaining leaves in the two pruned trees after the pruning phase and p the total number of leaves that were pruned. When comparing the two sets of pruned trees from the original trees A and B, each pruned tree from tree A will be matched to the most similar pruned tree from tree B (i.e. minimal strict distance). Each pruned tree can only be matched once. If two pairs have the same distance, then other factors such as lower RF/RFmax ratio or a larger pruned tree size, in this order, are used to decide between pairs. If all these factors are equal, then one of the pairs is chosen randomly, as the choice will not influence the final result. Rejected pruned trees have to be matched to a worse option or remain unpaired. Note that theoretically, this greedy pairing algorithm does not guarantee to find always the optimal solution, and may render near-optimal solutions under some circumstances. Finally, the combined weighted distance between trees A and B (D_a,b) is composed by two terms, one representing each initial tree (a and b), and is computed as explained in formula [2].

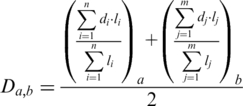(2)

where n and m, represent the total number of pruned trees for tree A and B, respectively, resulting from the decomposition algorithm. d_i represents the distance between the i^th pruned tree of A to its best match in the set of pruned trees of B and l_i the number of leaves in the i^th pruned tree of A. d_j and l_j are defined identically as d_i and l_i but with respect to tree B. The unpaired pruned trees are added to their corresponding term by assuming that d = 1. A minimal distance of 0 will only be obtained when the two trees are identical in terms of topology, including the inferred duplication and loss events.

Speciation distance

In this case all pruned trees from both tree A and B are matched to their best pruned trees from the other tree, regardless of whether the best matched pruned tree has been previously matched. The pruned tree distance is calculated as explained above, but the normalized RF distance is not corrected by the number of pruned leaves (term p above), resulting in a simple normalized RF distance [3]

(3)

The weighted final distance between the two trees (D_a,b) is computed as explained above.

Reconciliation-based distances

In addition of the above mentioned RF-distances, treeKO implements two other distances based on the number of inferred duplication (duplication distance) or duplication and loss events (reconciliation cost distance) after reconciling with a species tree, as earlier described. In this case one of the two compared trees should be a species tree to which the gene tree will be reconciled using a strict reconciliation algorithm (16) as implemented in ETE (23).

treeKO implementation

treeKO has been implemented using the python programming language and the ETE programming toolkit (23). The input of treeKO are two bifurcated phylogenetic trees in which the species source for the different sequences is indicated (by default a three letters pre-fix is expected). The entry trees should be rooted or a rooting strategy indicated (midpoint rooting is used by default if an un-rooted tree is provided; an option to minimize the total number of inferred duplication is also implemented). Moreover, the duplication nodes should be marked in the tree or a duplication-detection strategy indicated. By default treeKO will use the species-overlap algorithm implemented in ETE. In brief, this algorithm traverses the tree from every leaf in direction to the root. For every node, the species content of the two daughter branches are compared, nodes are considered speciation events if no species is shared or duplication events otherwise. A strict reconciliation algorithm, as implemented in ETE can be used if indicated by the user. Alternatively the user can specify duplications (inferred by any method) directly in the extended newick format (see details in http://treeko.cgenomics.org). An additional configuration file can be included in the treeKO command line in order to adapt some parameters to the users’ trees. For more details see http://treeko.cgenomics.org.

Fungal species trees

The T12a and T60 fungal species trees described in (22) contain 12 and 60 species, respectively, and were used as the reference tree topologies in the comparative analyses we present below. ETE was used to generate additional species tree topologies by swapping consecutive pairs of branches of the post-WGD (post-Whole Genome Duplication) species included in the tree (Saccharomyces cerevisiae, Saccharomyces paradoxus, Saccharomyces mikatae, S. kudriavzevii, S. bayanus, Candida glabrata, Saccharomyces castellii and Kluyveromyces polysporus). A total of six alternative topologies were considered in each case (see Supplementary Figure S1).

Phylome to species trees comparison

A phylome is defined as the complete collection of phylogenetic trees for each gene encoded in a given genome (24). The speciation distance implemented in treeKO was used to compare each tree in the P12a and P60 phylomes [see (22)] to each different species tree. The resulting distance distributions were compared with a t-test as implemented in the R package (http://www.r-project.org).

Comparison with alternative methods

The phylomes described above, plus P12b and P21, based on different sets of species (22) were also used to evaluate the number of trees that could be used by each tree comparison program. For the comparison between TOPD/FMTS and treeKO three sets of 100 trees were selected. Each tree was compared to itself. TOPD/FMTS was run on default mode, calculating the split distance (equivalent to the RF distance) and generating a maximum of 100 pruned trees, no random analysis was included.

RESULTS AND DISCUSSION

Decomposing a tree into all possible pruned trees by recursively splitting duplication nodes

The main rationale behind treeKO is the decomposition of gene-family trees to be compared into a set of pruned trees so that every pruned tree is formed by the maximum number of sequences that are orthologous to each other, without including any paralogous sequence. This can be achieved by recursively splitting the gene family tree at each duplication node. Subsequently all pruned trees produced by the two trees can be compared so that a weighted distance measure is produced (see below). We have implemented this algorithm in treeKO, which is freely available here: http://treeko.cgenomics.org. The algorithm of tree decomposition is briefly described below (Figure 1), additional details can be found in the ‘Methods’ section and the on-line documentation of treeKO.

The input of the treeKO tree decomposition algorithm is a rooted tree in which duplications nodes are indicated (if necessary, treeKO can automatically root and annotate duplications, see ‘Methods’ section). treeKO splits the original tree into single gene pruned trees that contain only one of the paralogous partitions resulting from each duplication. To do so, treeKO traverses the tree and, for each duplication node, two pruned trees are produced, each of which contains only one of the paralogous partitions that derive from the duplication. TreeKO will continue recursively on each resulting tree until all possible pruned trees are generated from the combination of the different single gene partitions. Finally, the sets of pruned trees produced by each input tree are compared to obtain a final topological distance. The set of pruned trees produced by the treeKO decomposition algorithm has some special properties that make it useful to derive evolutionarily sound distance measures. First, the pruned trees will contain only speciation nodes and thus all sequences in a given tree will be orthologous to each other. Moreover, considering that pre-duplication nodes are included in the two resulting pruned trees, each speciation node will be represented in the total set of pruned trees proportionally to the number of descendant sequences (i.e. sequences whose path to the root will traverse that node in the original tree). Finally, the total number of pruned trees produced by the decomposition process depends on the specific topological arrangement of the duplication nodes, but it is always equal or smaller than those implied by alternative decomposition algorithms such as the one implemented in TOPD (see Supplementary Figure S2). More specifically, if all duplications are nested, that is all of them occur in the same path from the root to a terminal node, the total number of pruned trees produced for an original gene tree containing n duplication is n+1. Instead, If all duplications are parallel to each other and occur in specific lineages, i.e. they are not nested, then the total number of pruned trees produced is 2ⁿ. If a combination of nested and parallel duplications occurs, then the final number of total trees is in the range of (n+1) to 2ⁿ trees. For the case of the yeast phylome (P12a), used in this study, the effective number of pruned trees is close to n+1 although it deviates significantly in some families (see Supplementary Figure S3).

Evolutionarily-sound topological distances

Distances calculated by treeKO are based on the RF distance or on reconciliation-based distances. The latter have been implemented as defined elsewhere (25,26), and basically compute the number of gene duplication and/or loss events that need to be implied when reconciling the gene tree to a given species tree.

The two RF-based distance measures, ‘strict distance’ and ‘speciation distance’, are new and we define them here (see ‘Methods’ section). The ‘strict distance’ is basically a weighted RF that, in addition, penalizes differences in evolutionarily relevant events such as gene duplications and gene losses. In contrast, the ‘speciation distance’ does not compute differences that can be attributed to duplication and loss events, so that two trees with a speciation distance of 0 are not necessarily identical, but the inferred history of speciation events of the shared species will be the same (i.e. they are fully congruent in terms of the inferred species tree).

These two RF-based distances have been implemented keeping in mind the different applications of tree comparison. The strict distance, which penalizes differential gene loss and duplication patterns, would be more appropriate when searching for protein families with a similar history of duplication, loss and speciation events. Such searches are common in studies of co-evolution and inference of protein function. For instance, correlated gene loss has been used to predict functional interactions between mitochondrial proteins (27). In contrast, the speciation distance would fit better in studies where the main focus is the underlying species phylogeny (28). There are many possible applications in which the availability to compare gene trees using an RF-based approach in the presence of duplications will present an advantage, although, certainly, other more specific methods may be better suited for some particular applications. In the present study we put the focus on the issue of evaluating alternative species tree topologies and present one such case in which the genome-wide support to alternative species phylogenies is explored by measuring the distance of each alternative species topology to the complete collection of phylogenies for all genes encoded in a given genome.

A practical use of treeKO: assessing the genome-wide support of two alternative species tree topologies

The evolution of twelve completely sequenced yeast species, encompassing the Saccharomyces and the Kluyveromyces clades, is mostly well resolved (22). Only the relative order of divergence of Candida glabrata and Saccharomyces castellii species remains unresolved. Most phylogenomic studies support an earlier splitting of C. glabrata (22,29,30). In contrast, analysis of chromosomal gene order has shown that the number of inversions that occurred during the evolution of these species is minimized in a scenario in which S. castellii diverges before C. glabrata (31).

Most species trees reconstructed from phylogenomic methods are evaluated with bootstrapping techniques that assess how stable a given topology is to random re-samplings of the input alignment. Since the input alignment generally comprises a small fraction of the genes present in a genome, gene sampling effects may result in highly supported topologies which are not representative of the evolution of a given genome. An alternative strategy to study the evolution of a genome is to analyze the complete collection of phylogenetic trees of all its genes (i.e. the phylome). Evaluating a given species topology over such genome-wide set of gene-trees would provide a more accurate measure on whether it is fairly representative at a genome-wide scale.

Although phylomes have successfully been used to determine which nodes in the fungal species tree are most congruent at genomic-scales (22), there is as yet no RF-based measure of the levels of similarity between a given species tree and a complete phylome. Here, we address the question of whether the distributions of speciation distances to a given phylome can be used to decide among alternative evolutionary scenarios. For this we used treeKO to compute the speciation distances of the yeast phylome [P12a dataset described in (22) and available at PhylomeDB (32)] against different alternative species trees. Gene trees were rooted with midpoint so that no assumptions on the species tree topology were made a priori. Alternative topologies were derived from a reference species tree by swapping pairs of neighboring branches (i.e. interchanging the positions of Saccharomyces paradoxus and Saccharomyces mikatae or the positions of C. glabrata and S. castellii as shown in Figure 2 and Supplementary Figure S1). Resulting distance distributions were compared with a t-test.

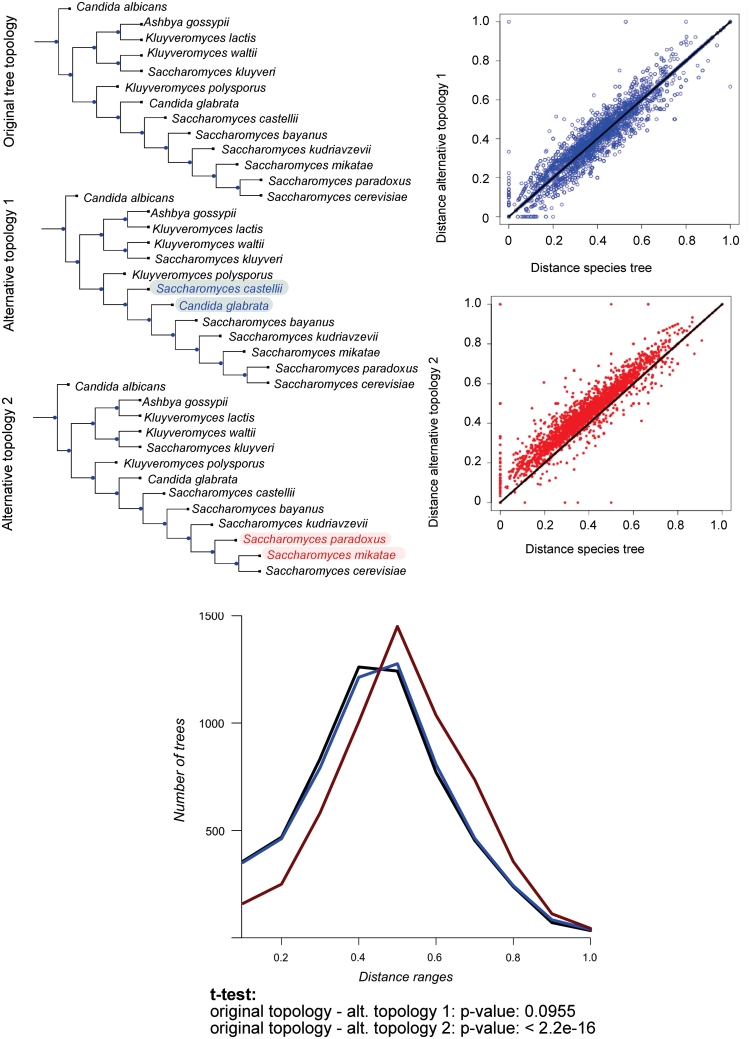
Figure 2.

Distribution of distances between trees in P12a phylome and three alternative species trees. The upper left part of the figure shows the three topologies used. The first one is the T12a tree while the other two represent changes in this topology. Alternative topology 1 represents a change in a poorly supported node while Alternative topology 2 represents a well supported node. The two upper right graphs plot each distribution of distances of the alternative topologies against the reference T12a topology. The lower panel represents the frequency graph for the three distance distributions.

As seen in Figure 2, the swapping of the well-supported S. paradoxus and S. mikatae branches (alternative topology 2) resulted in significantly larger distances (P-value < 2 × 10⁻¹⁶), whereas inter-changing the controversial positions of C. glabrata and S. castellii (alternative topology 1) presented distances that were not significantly different (P-value = 0.0955). We extended the analysis to all the topologies created by swapping consecutive pairs of post-whole genome duplication (post-WGD) species. In all cases, the distances obtained were significantly larger to those found in comparisons to the reference species tree. Similar results were obtained when the phylome and the species trees considered were based on a broader taxonomic range of 60 fungal species (see ‘Methods’ section). Similar results were obtained when we repeated the analysis by using alternative rooting methods or by collapsing poorly-supported branches in the tree (see Supplementary Table S1).

Thus, this test would discard all alternative topologies examined with the exception of a swap of C. glabrata and S. castellii positions. These results are congruent with earlier findings, in which C. glabrata/S. castellii was reported to be the only post-WGD node displaying a low phylome support (22). There are many possible causes for the observed high topological variability among gene trees, including incomplete lineage sorting, genetic introgression or systematic phylogenetic artifacts [see (33) and (22) for a discussion]. Considering this, it is presumable that results from previous phylogenomic studies might have been affected by sampling effects, and it would be therefore useful to consider alternative information such as gene order conservation to resolve that node (31). In contrast to the speciation distance, reconciliation-based distances, such as total number of gene duplication or loss events implied, were unable to distinguish among many of the alternative topologies. This suggest that RF-based distances such as the speciation distance proposed here is more sensitive to topological variations and thus more appropriate to evaluate alternative hypotheses (see Supplementary Table S1).

To test the performance of treeKO under controlled conditions, we performed a series of sequence evolution simulations with varying levels of sequence divergence and duplication and loss rates. In all circumstances tested, all types of distance metrics effectively identified the true species tree, although tests based on speciation distances tended to be more statistically significant (see Supplementary Data and Table 1). We believe that this type of comparisons provides an alternative way to evaluate, in a statistically sound manner, the genome-wide support for alternative phylogenetic hypotheses.

Table 1.

Percentage of tractable trees by comparison algorithm

Phylome	TreeKO (%)	TOPD/ FMTS (%)	RF (%)	RF + pruning (%)
P60	100	100	0	22
P21	100	100	0	36
P12a	100	100	14	38
P12b	100	100	2	27

Percentage of gene trees in a given phylome that is suitable for comparison by any given method. Columns represent the four compared programs: treeKO, TOPD/FMTS, RF and RF with an initial pruning step. Rows represent each of the fours yeast phylomes with different taxonomic coverage that can be found in phylomeDB (32).

Comparative analysis

To show that these type of analyses, ensuring a genome-wide coverage, are difficult with existing methods, we compared the performance of treeKO to that of (i) a standard RF measure, (ii) a RF measure after a pruning phase to remove species not present in the two trees and (iii) a distance measure provided by TOPD/FMTS. In all cases we evaluated the number of trees suitable to analysis in several yeast phylomes of varying taxonomic scopes (Table 1), and, whenever possible, we also evaluated the distance obtained when comparing two identical trees, and the average computing time (Table 2). An ideal method to perform genome-wide analyses would be fast, able to compare all gene trees and would produce a distance measure that is easy to interpret (e.g. identical trees would provide a distance of 0).

Table 2.

Comparative performance of tree-comparison algorithms

	TreeKO			TOPD/FMTS			RF
	Set1	Set2	Set3	Set1	Set2	Set3	Set1	Set2	Set3
Percentage of trees compared (%)	100	100	100	100	100	100	34	43	41
Average time consumption per tree (s)	1.31	1.65	1.95	10.38	8.84	9.57	–	–	–
Average time consumption per single-gene tree (s)	1.09	1.09	1.15	2.12	2.26	2.07	0.06	0.07	0.05
Average time consumption per multi-gene tree (s)	2.62	3.22	3.42	22.00	21.05	22.11	–	–	–
Average distance	0	0	0	0.45	0.36	0.43	–	–	–
Average distance single gene trees	0	0	0	0	0	0	0	0	0
Average distance multiple gene trees	0	0	0	0.70	0.61	0.69	–	–	–

Comparison between three tree comparison programs (treeKO, TOPD/FMTS and RF). Three sets containing 100 randomly chosen trees of the P12a phylome were used for comparison. Columns represent one of the sets of trees and a program. Rows contain data regarding the percentage of trees that were compared, the time consumption (expressed in seconds) and the average distance between pairs of identical trees. Data on separated by single-gene and multi-gene trees is also provided.

The main disadvantage of RF distances as implemented in standard programs such as Ktreedist (34) or PHYLIP (35), is that only a minor fraction (0–14%) of gene trees are suitable for comparisons. This is ameliorated by the inclusion of a pruning step (22–38%). As expected, treeKO and TOPD/FMTS yield 100% coverage. To compare the performance of treeKO, TOPD/FMTS and RF, as implemented in Ktreedist, we randomly selected three sets of 100 trees from the phylome. The programs were compared in terms of time consumption and average distance between two identical trees. While distances calculated by treeKO and RF are null for identical trees, TOPD/FMTS reports an average split distance of 0,41. These non-zero distances result from the sub-set of multi-gene tree comparisons (average distance of 0,67). Finally, as seen in Table 2, RF is by far the fastest method. treeKO and TOPD/FMTS have similar computing times for trees without duplications, but for multi-gene trees treeKO is approximately seven times faster. This could be attributed to the fact that the number of pruned trees generated by treeKO is much lower than in TOPD/FMTS (see Supplementary Figure S2), even when this program only takes 100 random pruned trees into account. This is the result of considering duplication nodes as the splitting point for the pruned trees generation instead of considering each species independently.

CONCLUSION

We have developed treeKO, a tree comparison tool that is able to compare trees in the presence of duplication and loss events. By addressing the main limitations of previous approaches, treeKO enables the comparison of genome-wide phylogenetic datasets. Besides implementing earlier reconciliation-based metrics (25,26), treeKO provides two new alternative RF-based distance metrics that are biologically sound and specifically adapted to applications such as the search for co-evolving protein families or the assessment of topological congruence in the inferred order of speciation events. Additionally, we have implemented in treeKO the possibility of comparing only specific nodes in the tree, which can be used to compute measures of congruence of specific topologies with large collections of phylogenetic trees, such as the phylome support value described earlier (22). It is important to note that the existence of horizontal gene transfer (HGT) events in the considered trees may result in the presence of apparent duplication and speciation events. This will affect any distance measure, by treeKO or any other method that does not account for HGT. To properly deal with the presence of HGT, we have implemented a protocol that treats nodes resulting only from a transference event as special case, thus allowing the computation of distances only based on true speciation and duplication nodes (see treeKO manual for details). In the future we plan to include additional distance measures. The use of treeKO opens the door to novel phylogenomic analyses such as the one presented here that evaluates whether differences in genome-wide support to two alternative topologies are statistically significant. Another potential use of the decomposition algorithm implemented in treeKO is that, combined with the use of reconstruction programs such as CLANN (36), it enables truly genome-wide coverage in popular super-tree approaches that minimize the topological distance of a species tree to a collection of gene trees.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Spanish Ministry of Science and Innovation (GEN2006-27784E, BFU2009-09168).

Conflict of interest statement. None declared.