Explaining the varied glycosidic conformational, G-tract length and sequence preferences for anti-parallel G-quadruplexes

Abstract

Guanine-rich DNA sequences tend to form four-stranded G-quadruplex structures. Characteristic glycosidic conformational patterns along the G-strands, such as the 5′-syn-anti-syn-anti pattern observed with the Oxytricha nova telomeric G-quadruplexes, have been well documented. However, an explanation for these featured glycosidic patterns has not emerged. This work presents MD simulation and free energetic analyses for simplified two-quartet [d(GG)]₄ models and suggests that the four base pair step patterns show quite different relative stabilities: syn-anti > anti-anti > anti-syn > syn-syn. This suggests the following rule: when folding, anti-parallel G-quadruplexes tend to maximize the number of syn-anti steps and avoid the unfavorable anti-syn and syn-syn steps. This rule is consistent with most of the anti-parallel G-quadruplex structures in the Protein Databank (PDB). Structural polymorphisms of G-quadruplexes relate to these glycosidic conformational patterns and the lengths of the G-tracts. The folding topologies of G2- and G4-tracts are not very polymorphic because each strand tends to populate the stable syn-anti repeat. G3-tracts, on the other hand, cannot present this repeating pattern on each G-tract. This leads to smaller energy differences between different geometries and helps explain the extreme structural polymorphism of the human telomeric G-quadruplexes.

INTRODUCTION

Guanine-rich oligonucleotides have the potential to self-assemble into right-handed four-stranded helical structures called G-quadruplexes (sometimes also termed G-DNA or G4-DNA). Helical aggregates of guanosine 5′-monophosphate were first observed almost six decades ago (1), and in the late 1980s based on gel-mobility shift assays, a parallel four-stranded structure was hypothesized (2). Since then, many parallel and anti-parallel G-quadruplex structures have been solved and hypothesized to have in vivo roles in meiosis, telomere maintenance and gene regulation (3–5). G-quadruplex structures have also drawn increasing interest as potential anti-cancer therapeutic targets (6–12).

The basic structural unit of the G-quadruplex is the G-quartet (or G-tetramer or G-tetrad) that is a co-planar structure formed by four hydrogen-bonded guanines (2). In the G-quartet, the four electronegative carbonyl oxygen atoms of the guanines are directed toward the center of the G-quartet, and metal ions (monovalent cations) coordinate between the G-quartet planes to stabilize the structures. This enables several G-quartets to stack on each other to form the G-quadruplex. G-quadruplex structures are in some cases highly polymorphic due to the variability in the number of stacked G-quartets, the G-strand (G-tract) orientations, the orientation patterns of glycosidic bonds of the guanines along a G-tract and the various different loop types that can connect the G-strands (3). Parallel G-quadruplexes are structurally consistent and do not display significant structural polymorphisms. This occurs because all the guanine residues adopt anti conformations for the glycosidic bond orientation and all the four strands have the same orientation (3). In contrast, anti-parallel G-quadruplexes display both anti and syn guanines and at least one of the four strands must be oriented anti-parallel to the others (3). There are three types of anti-parallel G-strand topologies or scaffolds that have been observed: abab, where each strand has two adjacent neighbors in the opposite direction (with orientation denoted by a or b); aabb, where each strand has one adjacent neighbor in the same direction and the other in the opposite direction and the ‘3 + 1’ scaffold, in which three strands are in one direction and a fourth one is in the opposite direction. The ‘3 + 1’ scaffold is sometimes referred to as the hybrid (parallel and anti-parallel) topology; however, in this work we classify this scaffold within the anti-parallel class. In addition to strand orientation and glycosidic bond orientation pattern, generally three types of loops are observed to connect the strands in G-quadruplexes: lateral, diagonal and double-chain reversal (propeller) loops (3). Lateral loops connect two adjacent anti-parallel G-strands, diagonal loops join the opposite across the quartet anti-parallel G-strands and the double-chain reversal loops connect two adjacent parallel G-strands.

Besides such factors as the ion identity, loop length and sequence, and 5′, 3′-flanking sequences, the G-tract length also has a great influence on the stability and folding topologies of G-quadruplexes. Lee et al. (13) showed that anti-parallel G-quadruplexes with four quartets are significantly more stable than quadruplexes with three quartets, and further that single-base mutations in one of the G-tracts dramatically influences the conformational dynamics of the human telomeric G-quadruplex (14). Abu-Ghazalah and Macgregor (15) reported that modifying the G-tract length of the Oxytricha nova telomeric sequence d(T₄G₄)₄ has profound effects on the folding topology and leads to polymorphic behavior. Thermal melting, CD and gel electrophoresis experiments also suggest varied topologies and stabilities for sequences of different G-tract lengths intervened by the short T and T₂ sequences (16). Human telomeric G-quadruplexes d(TTAGGG)₄ that contain three quartets show remarkable structural polymorphism and dynamic equilibrium, and this is suggested to be intrinsic to its highly conserved sequence (17), a feature that is quite distinct from the Oxytricha nova telomeric quadruplex. In general, it is well established that more quartets lead to more stability (18–20). However, the rules regarding how the G-tract length affects the folding topology and polymorphism of G-quadruplexes have not been fully elucidated. This is further complicated by the presence of loops, the loop length and sequence which can subtly shift this balance.

In anti-parallel G-quadruplexes, different glycosidic bond (χ) orientation patterns have been observed around the G-quartets, specifically: syn•anti•syn•anti, syn•syn•anti•anti, syn•anti•anti•anti and syn•syn•syn•anti. These χ angle orientation patterns are directly related to the relative G-strand orientations. For example, with the abab strand orientation pattern, each G-quartet displays the syn•anti•syn•anti (or anti•syn•anti•syn) glycosidic bond orientation pattern; with the aabb strand orientation pattern, each G-quartet displays the syn•syn•anti•anti (or anti•anti•syn•syn) pattern; in the ‘3 + 1’ scaffold, both syn•syn•syn•anti and anti•anti•anti•syn quartets have been observed. There is a simple rule to describe the relationship between the glycosidic conformation and the strand orientation, specifically: same strand direction, same glycosidic conformation. In other words, for a given G-quartet, if any two guanines belong to the two strands oriented in the same direction, the two guanines display identical glycosidic conformation. If their strand orientations are opposite, they show opposite glycosidic conformations.

Beyond the glycosidic bond orientations around the G-quartets, the characteristic glycosidic conformations along the G-tracts have also been well documented. The alternating syn-anti conformation for each adjacent pair of guanines along the strand was reported two decades ago in the G-quadruplexes formed by d(G₂T₅G₂) or d(G₂T₄CG₂) sequences (21,22). The thrombin-binding aptamer (TBA; d(GGTTGGTGTGGTTGG)) forms an anti-parallel G-quadruplex structure composed of two G-quartets and three lateral loops, and these structures always adopt 5′-syn-anti glycosidic bond orientation patterns in each of the G-tracts (23–26). This 5′-syn-anti conformation allows the TBA to form a well-defined G-quadruplex structure, whereas changing the glycosidic bond orientation pattern would perturb the formation, stability or folding topology of the G-quadruplex (27). The G-quadruplex formed by the Oxytricha nova telomere sequence d(G₄T₄G₄)₂ or d(G₄T₄G₄T₄G₄) inevitably features a 5′-syn-anti-syn-anti pattern along each G₄-tract, regardless of the monovalent ion type (Na⁺ or K⁺). Even though G-quadruplexes formed by the human telomere sequences d(TTAGGG)₄ are highly polymorphic (17), the predominant conformation observed in K⁺ solution is the ‘3 + 1’ scaffold: three tracts with a 5′-syn-anti-anti pattern in one direction and one 5′-syn-syn-anti pattern pointing in the opposite direction. The above sequences consistently show the syn conformation at 5′-end and the anti conformation at 3′-end of each G-tract, and the observations suggest that the glycosidic bond orientation pattern is related to the length of the G-tract involved. However, little is known about why these molecules display such variable glycosidic conformations along the G-tracts, although it is likely that this is also influenced by the loop connectivity, length, sequence and choice of monovalent salt.

The G-tract glycosidic bond orientation patterns can be regarded as different combinations of the four possible glycosidic base pair step patterns, specifically: the 5′-anti-anti step, the 5′-syn-anti step, the 5′-anti-syn step and the 5′-syn-syn step (Figure 1). Analysis of the known structures suggests that in standard anti-parallel G-quadruplexes, a quadruplex core contains only syn-anti steps, contains a combination of syn-anti steps with anti-syn steps or the core contains syn-anti steps together with anti-anti and syn-syn steps. In those few interlocked or V-shaped G-quadruplexes (28–31), syn-anti steps are observed only with anti-anti steps.

Figure 1.

Four types of glycosidic steps in G-quadruplexes: (a) syn-anti step, (b) anti-anti step, (c) anti-syn step and (d) syn-syn step. The residue shown in black is at the 5′-side.

The definitive glycosidic bond conformational patterns observed along G-tracts led to our hypothesis that different glycosidic steps have different relative stabilities, and these differences in stability lead to the different glycosidic bond orientation patterns observed in anti-parallel G-quadruplexes. To test this hypothesis, we built up six two-quartet models (Figure 2) and performed explicit solvent molecular dynamics (MD) simulations with modern force field and simulation protocols. The simulation results provide an understanding of the relative free energies of different G-DNA syn/anti patterns and explain the structural polymorphism of particular G-quadruplex sequences.

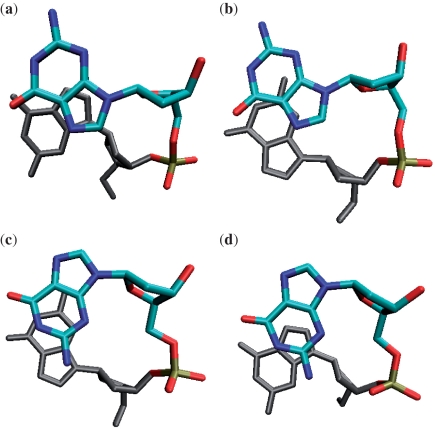
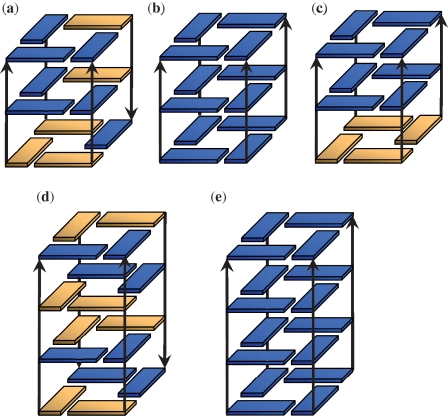
Figure 2.

Six two-quartet models were investigated in this work: (a) SA-aabb, (b) SA-abab, (c) SA-aaab, (d) AA, (e) AS and (f) 3AA + 1SS. The notation ‘a’ and ‘b’ refers to the relative strand orientations. Yellow is for syn and blue is for anti glycosidic bond orientations. The channel cation (K⁺) is not shown.

METHODS

Building the two-quartet models

Six two-quartet models were investigated in this work (Figure 2). The starting structures were generated from experimental structures found in the Protein Databank (PDB) (32). Three syn-anti (SA) models (SA-aabb, SA-abab and SA-aaab) were built. They all have four (SA) steps but with different strand orientations (‘a’ and ‘b’ denote the strand directions around the G-quartet). The coordinates of the first and the second quartets with sandwiched K⁺ ions were obtained from the crystal structure of the diagonal anti-parallel G-quadruplex [d(G₄T₄G₄)]₂ [(33); PDB: 1JPQ] and were used as the initial structure for the SA-aabb model. The SA-abab structure was built from the NMR solution structure of the thrombin-binding DNA aptamer d(GGTTGGTGTGGTTGG) [(23); PDB: 148D, the first frame]. The SA-aaab was built from the first two quartets of the NMR solution structure of the human telomere G-quadruplex d(T₂G₃TTAG₃TTAG₃TTAG₃A) [(34); PDB: 2GKU, first frame]. In the AA model, all the guanines have anti glycosidic bond orientations, and the structures have four parallel anti-anti steps. The respective coordinates were taken from the first and the second G-quartets of the parallel quadruplex d(TTGGGGT)₄ NMR solution structure [(35); PDB: 139D; the first model was used]. The AS model was built from the second and the third quartets of 1JPQ (33); this model has four anti-syn steps arranged in the ‘aabb’ scaffold. In the ‘3AA+1SS’ model, there are three anti-anti steps and one syn-syn step, and the initial coordinates were obtained from the second and third quartets of 2GKU (34). The 2GKU experimental structure is characterized by 12 representative solution structure models. Among these models, the syn-syn steps show two types of non-canonical backbone geometries with either g⁻/g⁻ or g⁺/g⁻ α/γ dihedral combinations. Thus, we built two initial structures (‘3AA + 1SS-I’ and ‘3AA + 1SS-II’) from the first model (α/γ g⁻/g⁻) and the 10th model (α/γ g⁺/g⁻) structures, respectively. Note that the canonical α/γ values are g⁻/g⁺. For all the models built from solution structures, a K⁺ ion was added manually into the channel between the two quartets in each structure. The TIP3P-specific potassium parameters (atomic radius 1.705 Å and well depth 0.1936829 kcal/mol) of Joung and Cheatham (36) were used.

MD simulations

MD simulations in explicit solvent and free energy analysis were carried out with AMBER 10 (37). The calculations were initially done using the parmbsc0 modifications to the ff99 force field (38,39). After initial peer review of the article, and in order to better ascertain the statistical significance of the observed results, the two-quartet models were further re-investigated in five independent sets of simulations for each model both with the parmbsc0 modifications to the ff99 force field and also a newer ff99-bsc0 force field modification, OL, that improves the description of the glycosidic torsions and is most appropriate for RNA (40). Each solute was solvated in an octahedral box of TIP3P (41) water with an extension of at least 10 Å from each side of the solute, and additional K⁺ were added to net-neutralize the system. Periodic boundary conditions were applied, and the particle mesh Ewald method (42) was used to calculate the long-range electrostatics with a charge grid spacing of ∼1 Å and a DSUM_TOL value of 10⁻⁵ Å. SHAKE (43) was used to constrain covalent bonds involving hydrogen with a tolerance of 0.00001 Å and the integration time step was set to 2 fs. Langevin dynamics (44) was applied for temperature control with a collision frequency of 1ps⁻¹. The non-bonded list built to 10 Å was updated whenever any atom moved >0.5 Å since the last list update, and a cutoff of 9 Å was applied to the Lennard-Jones and direct space electrostatic interactions. The solvated system was first minimized (500 steepest descent cycles followed by 500 conjugate gradient cycles) with a restraint of 100 kcal/(mol•Å²) on the solute (including the channel K⁺ ion). This was followed by a 25 ps MD simulation with 100 kcal/(mol • Ų) positional restraints applied on the solute atoms, and the temperature was slowly increased from 0 to 300 K with a collision frequency of 0.2 ps⁻¹. This was followed by another cycle of the above minimization and dynamics steps with a decreased restraint force constant of 25 kcal/(mol • Ų). Equilibration continued with five rounds of 1000 step minimizations with a solute restraint force constants of 20, 15, 10, 5 and 0 kcal/(mol • Ų), respectively. The equilibration was followed by a 250 ps unrestrained MD simulation during which the temperature was increased from 0 to 300 K with a collision frequency of 0.2 ps⁻¹. The above equilibration steps were carried out at constant volume. Finally, a 250 ps unrestrained MD simulation at 300 K with 1-atm constant pressure (45) was carried out to equilibrate the density, and this was followed by production MD simulations under equivalent conditions without restraints.

Free energy calculations

The approximate free energies for each of the two-quartet models were calculated over the MD trajectories taking snapshots at 200 ps intervals (unless specified otherwise) using the MM-PBSA script distributed with AMBER-9.0 (46). The channel bound K⁺ ion was included explicitly in the free energy calculations, which is essential to obtain consistent results of quadruplex stems, as is explained in detail elsewhere (47). The size of the K⁺ ion was modified to 1.705 Å in the MM-PBSA script to obtain consistent solvation energies (47). Note that solute rotational, translational and vibrational entropies were not included in the MM-PBSA estimates reported in the main text. As all the models are of similar size, small and have similar degrees of freedom and flexibility, the differences in the solute entropy among the models are very small and similar trends are observed (see the later discussion and information provided in the supporting information that supports this claim).

RESULTS

Free energy calculations

Although some of the two-quartet stems are unstable on longer simulation time scales with the ff99-bsc0 force field, as will be shown below, we were able to calculate approximate free energies from the stable portions of the respective MD trajectories. Our aim was to understand the relative free energy order of the four glycosidic steps. Table 1 shows the estimated free energies calculated with MM-PBSA. The three SA models show very similar free energies. The implication is that in anti-parallel G-quadruplexes, the strand orientations alone do not significantly alter the stem stability assuming the 5′-syn arrangement. The influence of strand orientation on stability is therefore likely only dependent on the types of loops necessary to connect the strands. This result is consistent with the previous conclusion that the syn•anti•syn•anti and syn•syn•anti•anti G-quartets are equally stable (48).

Table 1.

MM-PBSA results (kcal/mol) of the two-quartet stem models

Model	Regions used for calculation	MM_ele	MM_vdw	MM_int	PB_sur	PB_cal	G	ΔG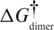
SA-aabb	30–40 ns	−1362.1	−41.7	340.4	11.3	−486.6	−1538.7	−32.2	−3.6 (–5.1)
SA-abab	15–25 ns	−1362.9	−40.4	342.8	11.2	−489.2	−1538.5	−32.0	−3.6 (–5.0)
SA-aaab	15–25 ns	−1366.7	−39.4	342.4	11.3	−485.1	−1537.5	−31.0	−3.3 (–4.8)
SA-aabb-r	23–33 ns	−1333.5	−43.6	353.4	11.7	−509.0	−1521.0	−14.5	−3.6 (–3.6)
AA	30–40 ns	−1348.2	−39.9	368.7	11.9	−499.0	−1506.5	0	0
AS	15–25 ns	−1303.5	−41.0	358.2	11.8	−527.4	−1501.9	4.6	1.2 (1.2)
AS	0–300 ps	−1309.4	−43.0	367.3	11.5	−518.8	−1492.4	14.1	3.5 (3.5)
AS-r	0–1 ns	−1332.0	−42.0	374.5	11.4	−502.9	−1491.0	15.5	3.9 (3.9)
AS-r	4–11 ns	−1337.8	−39.8	372.7	11.4	−499.7	−1493.2	13.3	3.3 (3.3)
3AA + 1SS_I (α/γ: g−/g−)	5–7 ns	−1348.5	−37.8	362.0	11.6	−493.6	−1506.3	0.2	4.6 (3.2)
3AA + 1SS_I (α/γ: g−/ g+)	10–12 ns	−1341.1	−41.1	359.2	11.6	−501.7	−1513.1	−6.6	−2.2 (–3.6)
3AA + 1SS_II (α/γ: g−/ g+)	5–7 ns	−1345.4	−41.2	363.1	11.6	−499.4	−1511.3	−4.8	−0.4 (–1.8)
3AA + 1SS_II-r (α/γ: g+/g−)	5–7 ns	−1336.9	−42.1	362.7	11.6	−501.4	−1506.1	0.4	4.8 (3.4)

The MM_ele, MM_vdw and MM_int represent the electrostatic, van der Waals and the internal (bond, angle, dihedral angle) potential energies (in kcal/mol), respectively. PB_sur stands for the non-electrostatic solvation energy, and PB_cal is the electrostatic solvation energy. G is the estimated absolute free energy of each model, which is the sum of the above five energy components and includes the channel bound ion. The ΔG^†_dimer values show the energy per dimer excluding contributions from the H-bonds formed at 5′ syn-dG which amount to −4.4 kcal/mol (or in parenthesis a more conservative value of −3.0 kcal/mol) for each H-bond. Note: As discussed in the main text, the solute entropic contributions were not included. As reported in the supporting information, similar trends are observed when solute entropic contributions are included. In SA-aabb-r, AS-r and 3AA + 1SS_II-r, the ‘r’ represents restrained simulations.

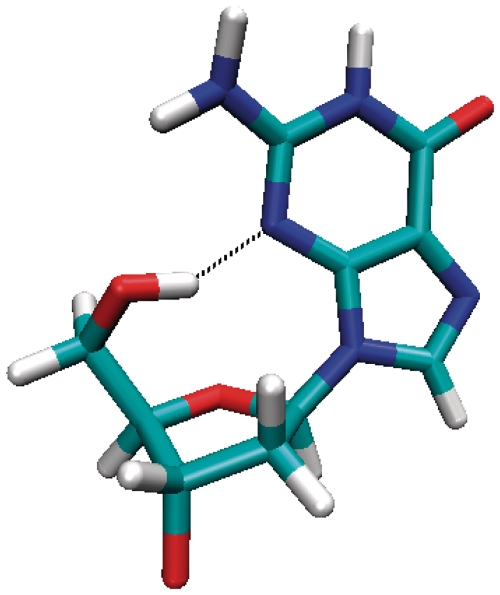
As anti-anti steps are dominant in the DNA double helix, the AA model was used as a reference to calculate the relative free energy of each model. Surprisingly, the free energy results suggest that the SA models are significantly more stable than the AA model. The differences in estimated free energies are large (−32 kcal/mol) and dominated by the internal (bond, angle and dihedral) and electrostatic free energy contributions. Much of this overstabilization is due to hydrogen bonds at the 5′ syn-dG due to the dangling ends (see the ΔG^† values in Table 1). When the 5′-terminal guanine has a syn glycosidic bond orientation, a hydrogen bond between O5′-H···N3 will form with a high occupancy during the MD simulations (Figure 3); this is not observed when the 5′-terminal guanine has an anti glycosidic bond orientation. Similar hydrogen bonding is also observed in experimental structures with at most one 5′-dG syn O5′-H···N3 hydrogen bond in monomeric anti-parallel quadruplexes and two in the dimeric anti-parallel quadruplexes. The simple two-quartet models studied here introduce more 5′-ends because of the absence of connecting loops. The SA models have four O5′-H5T···N3 hydrogen bonds that bring extra stability to the system; however, this is not representative of the native folded quadruplex structures generated from a single contiguous sequence. To exclude these contributions, we ran an additional simulation on the SA-aabb model with a restraint to prevent the formation of the O5′-H···N3 hydrogen bonds (referred to as SA-aabb-r). A lower bound restraint distance of 3.5 Å with a force constant of 5 kcal/(mol • Ų) was applied to the H5T and N3 atoms at each of the four 5′-ends. A stable MD trajectory over 33 ns was observed, and the last 10 ns was used to estimate MM-PBSA energetics calculated at 200-ps intervals. The restrained SA-aabb-r model is now −14.5 kcal/mol (−3.6 kcal/mol per strand) more stable than the AA model. Additionally, we recalculated the energetics omitting these hydrogen bonds with the three unrestrained SA trajectories and similar results are obtained. The free energetic results suggest that the four 5′-end hydrogen bonds in total contribute −17.7 kcal/mol to the free energy of the SA-aabb model, i.e. −4.4 kcal/mol for each hydrogen bond. When these dangling end hydrogen bonds are omitted, a more reasonable ∼4 kcal/mol per strand difference is obtained. The large values are in part due to the approximate nature of the MM-PBSA method, and it is common with MM-PBSA to reproduce the correct free energy trends yet tend to overestimate the absolute values of free energy differences (49).

Figure 3.

Molecular graphics highlighting the hydrogen bond formed with a high occupancy within the 5′-terminal syn guanosine during the MD simulation.

As the AS model quickly underwent structural change (at ∼300 ps; see the following discussion), we estimated the free energy for the initial 300 ps (with a 6-ps interval between frames in the MM-PBSA) and also for the models over 15–25 ns (with a 200 ps interval). The results show that before the structural change, the AS model is ∼14 kcal/mol less stable than the AA model, while after the change the system gained ∼9 kcal/mol in stability compared with the first 300 ps. The AS model with restraints on the α/γ angles (AS-r) maintained the quadruplex structure for 19 ns; however, other dihedral angles such as χ, ε and ζ were not properly maintained. Calculations on the initial parts of the trajectories where the original geometries were still maintained (0–1 ns) or where the sampled structures were close to the original geometries (4–11 ns) suggest that the restrained model has a similar stability to the initial AS model even though the component energies show differences.

For the ‘3AA+1SS’ models, the structure with canonical α/γ (g⁻/g⁺) angles for the syn-syn step is more stable than the AA model by −5 to −7 kcal/mol, while both α/γ (g⁻/g⁻) (3AA+1SS_I, 5-7 ns) and α/γ (g⁺/g⁻) (3AA+1SS_II-r, 5-7 ns) initial geometries show similar free energies to the AA model. When the contributions of the dangling-end hydrogen bonds are omitted, the ‘3AA + 1SS’ models in their original geometries are less stable than the AA model by ∼5 kcal/mol.

Relative stabilities of different glycosidic steps and G-quadruplex folding rules

The free energies in Table 1 show that the SA model is ∼14.5 kcal/mol more stable than the AA model; the AS model is ∼15.5 kcal/mol less stable than the AA model and the 3AA-1SS models are ∼5 kcal/mol less stable than the AA model. To facilitate comparison per quadruplex strand, the relative free energies of the SA, AA and AS models were divided by four to get the relative free energies of each of the syn-anti, anti-anti and anti-syn steps. The 3AA + 1SS model can be regarded as the combination of three anti-anti steps and one syn-syn steps, therefore the instability of ∼5 kcal/mol of each of the 3AA + 1SS models relative to the AA model comes entirely from the relative instability of the syn-syn step to the anti-anti step. Considering the results together, the free energetic results suggest that the approximate relative stabilities of the four types of step are: syn-anti (−4 kcal/mol) > anti-anti (0 kcal/mol) > anti-syn (4 kcal/mol) > syn-syn (5 kcal/mol). Based on the significant differences in the relative stabilities of the four glycosidic steps, representing approximately 2–3 orders of magnitude shifts to lower populations between syn-anti to anti-anti and anti-anti to anti-syn and syn-syn, we propose the following rules: (i) Anti-parallel quadruplexes have a strong propensity to form as many syn-anti steps as possible and (ii) once the maximum numbers of syn-anti steps are obtained, avoid the anti-syn and syn-syn steps as much as possible. Based on these rules, we infer that the glycosidic bond orientation patterns are predetermined by the length of the G-tract, and the most favorable glycosidic conformation along the G2, G3 and G4 tracts in anti-parallel G-quadruplexes are syn-anti, syn-anti-anti and syn-anti-syn-anti, respectively. Additional simulations with the newer ff99-bsc0-OL force field variant (Supplementary Data) show similar trends to the results discussed, with a slight destabilization of the syn-anti relative to the anti-anti conformations [i.e. syn-anti (approximately −1 to −3 kcal/mol) > anti-anti (0 kcal/mol)] that is more consistent with experimental observations of all anti conformations in some parallel G-quadruplexes. Note that with the ff99-bsc0-OL force field variant the two-quartet structures were more stable in MD simulation as exemplified by maintaining the folded structure for longer periods.

Entropy calculations

As entropy calculations are less reliable and harder to converge compared with the other energy components within the MM-PBSA approximations, we did not include entropy contributions in the free energy calculations shown. However, free energies with entropy contributions are provided separately in the Supplementary Table S1, and the results suggest that the inclusion of entropy does not change the relative stability ranking of the four glycosidic steps.

MD of the two-quartet models

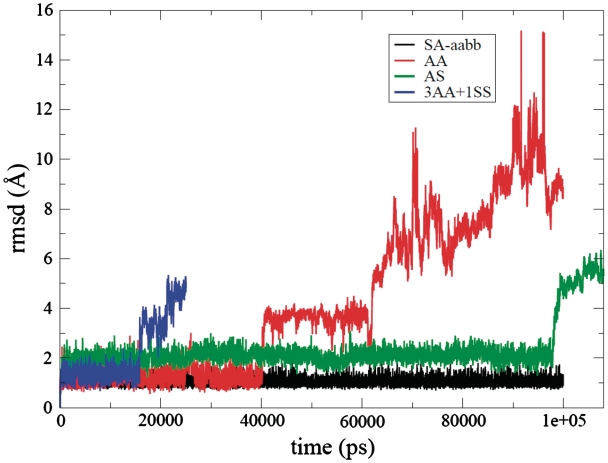
The all-atom RMSD values for the four two-quartet models over the MD trajectories are shown in Figure 4. The SA-aabb model remained close to the initial structure indicative of a stable trajectory throughout the 100 ns of MD simulation. The other two SA models, SA-abab and SA-aaab, were also built to test the influence of the arrangement of the four strands, and they also both sampled very stable trajectories as suggested by low RMSD (an average all-atom RMSD of 0.8 Å for SA-abab and 0.9 Å for SA-aaab) throughout 25-ns-length simulations.

Figure 4.

RMSD curves (Å) versus time (ps) for the SA-aabb (black), AA (red), AS (green) and 3AA + 1SS (blue) model simulations.

The starting structure of the AA model was maintained for the first 40 ns. Then the molecule converted from a right-hand helical to a left-hand helical structure that was stable until 56 ns whereupon the quadruplex structure was lost entirely. The model structure then sampled several different geometries with the most typical exemplified by a structure with all eight bases stacked effectively into a single-stranded helix (Supplementary Figure S1). This structure was found to be considerably more stable by MM-PBSA free energy analysis than the two-quartet AA model. The free energy estimations suggest that this collapse process to the fully stacked structure is mainly driven by improvement of van der Waals interactions (Supplementary Figure S2) and also partly by reductions in the internal (bonds, angles and dihedrals) free energy. Note that the loss of quadruplex structure was not preceded by loss of channel bound ion. The instability of the AA model in our MD simulation is consistent with the observation that no experimental structure has been reported for the two-quartet parallel G-quadruplex except in the case where it forms multimers by stacking with other G-quadruplex molecules (50,51).

For the AS model, the quadruplex structure was maintained for 98 ns (Supplementary Figure S3); however, structural adjustments were observed at the very beginning of the simulation. In the initial structure of the AS model, the four anti-syn steps all show non-canonical dihedral angles: two strands have α/γ backbone angle (g⁻/g⁻) conformations and the other two strands have α/γ (g⁺/g⁻) conformations. The two α/γ (g⁻/g⁻) strands quickly changed to the canonical α/γ (g⁻/g⁺) conformation during the equilibration period, and this backbone conformational transition did not significantly alter the stacking or co-planarity of the quartets. At ∼300 ps post-equilibration, two of the four strands changed to γ (trans) conformation: one in α/γ (g⁺/t) conformation and one in α/γ (g⁻/t) conformation. Such a backbone geometry change led to less co-planarity of the quartets and an increased overlap between two sequential base groups. The other two strands changed to the α/γ (g⁺/t) conformation at 2 and 35 ns, respectively. Even though α/γ (g⁺/trans) is not the most favorable crankshaft conformation, particularly with the parmbsc0 force field modifications that strongly disfavor γ = trans (39), this likely represents a compromise between the dihedral angles and desire to keep the quadruplex structure. Supplementary Figure S3 shows the averaged structure of the AS model at 50 ns where three strands occupy α/γ (g⁺/t) conformations and one strand occupies α/γ (g⁻/t). The superimposed structures of the anti-syn steps in the original α/γ (g⁺/g⁻) and α/γ (g⁻/g⁻) conformations and in the simulated α/γ (g⁺/t) conformation are also shown in the Supplementary Figure S3. As the α/γ (g⁻/g⁻) and α/γ (g⁺/g⁻) conformations were not maintained with this force field, simulations with a restraint of 5 kcal/(mol • A²) on the α/γ angles (AS-r) were also performed to force the dihedral angles to the original conformations. With restraint applied on the α/γ angles, the quadruplex structure was maintained for 19 ns. However, other backbone angles such as χ, ε and ζ sampled other geometries during this period of time. Therefore, only trajectories keeping the original geometries (0–1 ns) or very close to the original geometries (4–11 ns) were used for the MM-PBSA calculations (Table 1).

Neither of the ‘3AA + 1SS’ models started from two different initial structures maintained the quadruplex structure in MD simulation: the ‘3AA + 1SS_I’ lost the quadruplex structure at ∼15 ns and ‘3AA + 1SS_II’ lost the structure at ∼10 ns. In the ‘3AA + 1SS_I’ model structure, the initial α/γ (g⁻/g⁻) conformation of the syn-syn step was maintained for 8 ns before moving directly to the canonical α/γ (g⁻/g⁺) value. In contrast, with the ‘3AA + 1SS_II’ model structure, the initial α/γ (g⁺/g⁻) changed rapidly to the α/γ (120°/trans) geometry during equilibration, and then moved to canonical α/γ (g⁻/g⁺) values at the beginning (800 ps) of the production MD simulation. As the syn-syn step in the 3AA + 1SS_II model changed its original α/γ (g⁺/g⁻) conformation so quickly, a 5 kcal/(mol•A²) restraint on the α/γ angles was applied in MD simulation (3AA + 1SS_II-r) for 33 ns; this model structure lost its quadruplex structure after ∼9 ns of MD. A clear correlation between the syn-syn backbone conformations and stacking of bases is not obvious from the MD simulations; moreover, experimental structures do not show unambiguous backbone topologies for syn-syn steps.

MM-PBSA calculations for the three-quartet and four-quartet stem models

The two-quartet models applied in this work are very simplified models for MD simulations; they were used to get reasonable and straightforward energetic estimates for the four glycosidic steps. To test whether the same trends are maintained in the stems of more quartet layers, similar work investigated various three-quartet and four-quartet stem models (Figure 5). The (3SAA + 1SSA) model was built from the human telomeric G-quadruplex 2GKU (34); AAA was built from the first three G-quartets of the NMR parallel structure 139D (35). A model with four parallel syn-ant-anti strands (SAA-parallel) was also built based on the previous NMR experiments indicating that [d(TG^MeGGT)]₄ form a parallel quadruplex possessing an all syn quartet (52). The (3SAA + 1SSA) model was used as the template to build the SAA-parallel model through UCSF Chimera (53). In this SAA-parallel model, only syn-anti and anti-anti steps exist, therefore comparison to the AAA model was straightforward. The four-quartet parallel and anti-parallel stem models were built from the G-quartets of the structures 139D and 1JPQ (33), respectively. Additional three-quartet stem models were investigated; however, the anti-syn and syn-syn steps in these models lost the original backbone α/γ geometry during the simulation equilibration steps, so these results are not shown here.

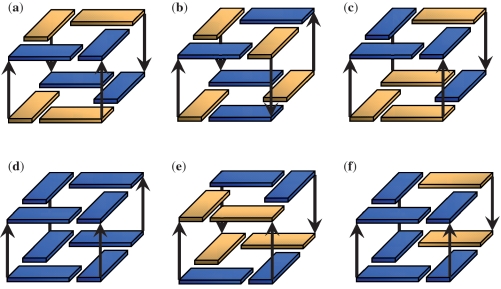
Figure 5.

Cartoons of the three-quartet and four-quartet stem models tested in this work are shown: (a) 3SAA + 1SSA, (b) AAA, (c) SAA-parallel, (d) ASA-parallel, (e) SASA and (f) AAAA. Yellow is for syn and blue is for anti glycosidic bond orientations. The channel cations (K⁺) present in the models and simulations are not shown. Note that because the original backbone geometry of the anti-syn steps in the SASA model were not maintained in the MD simulations, restraints were applied to the α/γ angles of the anti-syn steps in a manner similar to those applied with the two-quartet models. The MD simulations on these stem models all produced very stable trajectories. With the three-quartet models, the two channel-K⁺ maintained their positions throughout all the simulations. With the four-quartet models, the three channel-K⁺ are more mobile and two main channel cation arrangements were observed: either all three K⁺ within the channel, or two K⁺ in the channel and one K⁺ located at the channel entrance.

The MM-PBSA calculations showed trends consistent with the results from the two-quartet models: the anti-parallel stems that accommodate more favorable syn-anti steps are generally more stable than their parallel counterpart (Tables 2 and 3). The SAA-parallel model is much more stable than the AAA parallel model, which is consistent with the experimental results that [d(TG^MeGGT)]₄ shows a higher T_m of 66°C versus 45°C than [d(TGGGT)]₄ (52), and this result is also consistent with the calculations from the two-quartet model: the syn-anti step is more stable than the anti-anti step.

Table 2.

MM-PBSA results (kcal/mol) of the three-quartet stem models

Model	Regions used for calculation	MM_ele	MM_vdw	MM_int	PB_sur	PB_cal	G	ΔG	ΔG†
3SAA + 1SSA	0–100 ns	−1959.4	−97.0	536.0	14.5	−1092.4	−2598.3	−26.0a	−8.4
3SAA + 1SSA	0–5 ns	−1980.5	−99.7	542.7	14.2	−1065.0	−2588.3	−20.6b	−3.0
AAA	0–100 ns	−1968.9	−100.6	557.2	14.8	−1074.8	−2572.3	0	0
AAA	0–5 ns	−1965.4	−100.2	559.7	14.9	−1076.7	−2567.7	0	0
SAA-parallel	0–50 ns	−1995.9	−97.2	534.8	14.7	−1058.5	−2602.1	−29.8a	−12.2
SAA-parallel	0–5 ns	−1996.5	−99.0	539.1	14.6	−1055.8	−2597.6	−29.9b	−12.2

In the (3SAA + 1SSA) model, the original backbone geometries (α/γ = g⁻/g⁻) of the syn-syn step were kept for 5.4 ns. Free energies were estimated both for the whole trajectory and for the 0–5 ns region for each model.

^aRelative to the free energy of AAA (0–100 ns).

^bRelative to the free energy of AAA (0–5 ns).

Table 3.

MM-PBSA results (kcal/mol) of the four-quartet stem models

Model	Regions used for calculation	MM_ele	MM_vdw	MM_int	PB_sur	PB_cal	G	ΔG	ΔG†
SASA-ra	0–2 ns	−2372.7	−164.5	729.6	17.3	−1867.1	−3657.4	−28.0	−10.4
SASA-rb	10–15 ns	−2334.3	−164.4	730.4	17.4	−1905.6	−3656.5	−23.5	−5.9
AAAAa	8.3–10.4 ns	−2388.2	−164.6	750.0	17.7	−1844.3	−3629.4	0	0
AAAAb	10.5–20 ns	−2355.5	−163.3	746.5	17.9	−1878.6	−3633.0	0	0

In the anti-parallel SASA model, two of the anti-syn backbones lost the original α/γ (g⁻/g⁻) geometry during the equilibration, therefore restraints were put on the α and γ dihedral angles in each anti-syn step to force the backbone to the original geometries (SASA-r). With the four-quartet stem models the three channel K⁺ are more mobile and one of the terminal K⁺ frequently moved to the channel entrance position, so free energies were estimated for these two conformations—a: three K⁺ in the channel; b: two K⁺ in the channel and one K⁺ at the channel entrance position.

The computed results consistently suggest that the anti-parallel structures are more favorable than the parallel counterparts. However, it is widely assumed that the tetrameric quadruplex structures predominantly adopt parallel conformations with all residues showing anti glycosidic bond angles. This discrepancy may be caused by several factors. For example, there are experiments suggesting that rapid annealing produces parallel structures, whereas slow annealing produces anti-parallel structures (16). This would mean that anti-parallel structures are thermodynamically favored, whereas parallel structures are kinetically favored. Therefore, the tetrameric parallel structures could possibly be the kinetically favored products; once formed, disruption of the structure to convert to the more thermodynamically favored structures is too difficult. Monomeric all-parallel structures have also been reported for various promoter quadruplexes (54,55), and in these cases the parallel structures could be promoted by the extremely short loops. Human telomeric quadruplexes adopt a parallel stranded all-anti arrangement in the X-ray structure. However, in this particular case the balance may be affected by crystal packing, because the all-parallel structure with propeller loops allows stacking of guanine stems. Of course, it is also clear that the results may be influenced by approximations in the force field description and free energy computations. While we assume that the computed results are valid for rationalization of intrinsically preferred topologies of various anti-parallel stems, to fully capture the parallel to anti-parallel stem balance may be more challenging. In fact, the latest ff99-bsc0-OL force field designed for RNA simulations indicates that the DNA ff-bsc0 force field somewhat overestimates stability of the syn conformation. Furthermore, although the solute entropy computations are difficult to converge, they also suggest shift of the free energies in favor of the anti-anti steps. Considering both factors would bring the anti-anti step energies basically in par with the syn-anti steps; further analysis can be found at the end of the discussion section and in the supporting information.

DISCUSSION

Validation of the G-quadruplex folding rules with experimental structures

Based on the theoretical estimates on the relative stabilities of the four glycosidic steps, simple folding rules were proposed with an emphasis on the glycosidic conformations of G-quadruplexes. To validate these folding rules, most of the anti-parallel G-quadruplex structures available in the PDB were investigated. To reach the maximum number of syn-anti steps, each tract of the sequence composed of G2 repeats needs to adopt a syn-anti conformation. Therefore, all the G-quadruplexes formed from TBA sequences show the same glycosidic bond orientation pattern of 5′-syn-anti-loop-syn-anti-loop-syn-anti-loop-syn-anti (23–26,56,57). The quadruplex formed from d(GGTTTTGGCAGGGTTTTGGT) has a double-chain reversal loop and two diagonal loops, and each of the G2-tract adopts a syn-anti conformation (58). In the tetrameric quadruplexes formed from [d(TAGG)]₄, the G2-tract in each strand also adopts the syn-anti pattern (59). The same pattern is also observed exclusively in dimeric quadruplexes with two quartet layers (60,61).

For sequences composed of G4-tracts, each G4-tract can accommodate at most two syn-anti steps, in a pattern 5′-syn-anti-syn-anti. This explains why the dimeric or monomeric G-quadruplexes formed from the Oxytricha nova telomeric sequences all show the alternating 5′-syn-anti-syn-anti glycosidic bond orientation pattern along each G-tract, regardless of the nature of the coordinated cations (33,62–66).

As mentioned in the Introduction, if two guanines within the same G-quartet belong to two strands oriented in parallel, the two residues in each strand show the same glycosidic bond angle conformation, whereas if the two guanines belong to two anti-parallel strands, inverted or opposite glycosidic bond orientations are observed. In G2 and G4 tracts, the glycosidic bond orientation patterns (5′-syn-anti and 5′-syn-anti-syn-anti) are self-symmetric, that is the inverted glycosidic patterns are the same regardless of strand orientation. Therefore, in anti-parallel G-quadruplexes formed from G2, G4 or other even-numbered G-tracts, each of the four G-tracts will adopt the syn-anti alternating conformation to maximize the number of syn-anti steps.

G3-tracts are quite different from G2- and G4-tracts: the glycosidic conformations must be different for two G3-tracts to align in opposite directions. There are four glycosidic bond orientation patterns that will accommodate the maximum of one syn-anti step: 5′-syn-anti-anti, 5′-syn-anti-syn, 5′-anti-syn-anti and 5′-syn-syn-anti. According to the relative stability of the four steps, 5′-syn-anti-anti is the most favorable geometry, and this is likely the reason why most of the monomeric anti-parallel quadruplexes from human telomeric sequences share the same characteristic: i.e. three strands with the 5′-syn-anti-anti conformation with a less favorable 5′-syn-syn-anti strand accommodated to finish the anti-parallel folding (67–69). The data suggest that other anti-parallel G-quadruplexes composed of G-tracts of odd-numbered guanines will also show this characteristic: i.e. at least one tract will not present the most stable glycosidic bond orientation pattern.

Dihedral angles in anti-syn and syn-syn steps

As shown, the non-canonical α/γ dihedral angle geometries of the anti-syn and syn-syn steps from the experimental structures were not maintained in the MD simulations. This suggests that the parmbsc0 force field modifications to AMBER ff99 may overdestabilize the correct, yet non-canonical, dihedral angles of the anti-syn and syn-syn steps. Moreover, the energy barrier may be underestimated thereby facilitating the conformational changes. Similar results were shown recently for the first loop nucleotide in parallel stranded X-ray structure of the human telomeric quadruplex (70). This nucleotide has γ-trans in the experiment while it is shifted to the canonical conformation in parmbsc0 simulations. Similarly, in A-RNA double helices, parmbsc0 appears to overcorrect γ-trans substates (71). However, the balance in the force field is complex and unresolved, and therefore we should not prematurely conclude that parmbsc0 universally overpenalizes γ-trans conformations. The torsional profiles of simple pairwise additive force fields represent only very approximate and rather unphysical models of electronic structures of the real molecules. Thus, we should not expect ideal balance simply through small modifications to the torsional profile. The suppression of the γ-trans conformations by the parmbsc0 force field has been shown to be an absolutely crucial force field refinement to achieve global stability of B-DNA simulations (72–74). In contrast to the above-mentioned cases, for B-DNA on A-tracts, it appears that γ-trans substates remain slightly overpopulated albeit they no longer preferentially occupy the incorrect global minimum (75). The inability of the current force field to fully populate the expected geometries for the anti-syn and syn-syn steps could lead to errors in the free energy calculations. More accurate assessment on the four glycosidic steps may depend on the refinement of current nucleic acid force fields or more accurate methods such as quantum mechanical calculations. Despite this, the energetic trends observed are consistent with experimental G-quadruplex structure.

Comparison to earlier results

Earlier molecular mechanics calculations of base stacking suggested that the sequential syn-syn, anti-anti and syn-anti quartet stacks are almost equal in energy, and the anti-syn stack is less favorable by 4 kcal/mol (76). These results are inconsistent with the current data. However, this is not surprising because the earlier analysis is based on crude in vacuo computations of energy contributions based on short 150 ps MD simulations. Moreover, the relative stabilities of different steps were derived solely from calculated base stacking energies, neglecting important contributions from the DNA backbone and the bound channel cations. Such calculations are not sufficient to derive relative stabilities of different nucleic acid conformations that exhibit a very complex balance between the molecular forces. It is well established that the intrinsic (gas phase) stacking trends are often completely lost or even inverted (77,78). In contrast, the current sets of MD simulations with explicit water were performed for much longer time scale (up to 100 ns) with current state-of-the-art force fields and simulation protocols for DNA while including full balance of all energy contributions. As our results show that the stability differences of the four steps comes primarily from the dihedral potentials and electrostatics (Table 1, MM_int and MM_elec) rather than from the stacking interactions, this reasonably explains the differences between the MD and QM studies.

Non-canonical G-quadruplexes

Sequences with unequal number of guanines in each G-tract may form V-shaped or interlocked G-quadruplexes (28–31). Although the rules and influences are likely more complex in those cases, we note that in these structures only syn-anti and anti-anti steps have been experimentally observed. In some of the structures (30,79), where the glycosidic bond orientation angles in the range of approximately −35° to −50° are reported as syn rather than anti, these structures adopt ‘3 + 1’-like glycosidic pattern where three strands in syn-anti-anti conformation are populated with one additional strand populating a syn-anti conformation to avoid the unfavorable syn-syn step. Therefore, the interlocked or V-shaped scaffolds could possibly be strategies for G-quadruplexes to avoid the unfavorable anti-syn and syn-syn steps. For some other non-canonical G-quadruplexes, the current analysis may also help explain the observed folding topologies. One interesting example is the bimolecular quadruplex formed with [d(G₄T₄G₃)]₂, where the two G4 repeats display the expected 5′-syn-anti-syn-anti pattern to maximize the number of syn-anti steps, and the two G3 repeats display 5′-syn-anti-syn and 5′-anti-syn-anti patterns, respectively, to finish the self-folding (80). In the modified TBA sequence containing a 5′–3′ inversion of polarity, the first two guanines reversed their glycosidic bond orientation patterns to maintain the syn-anti conformation along the 5′→3′ direction (81). This example suggests that what matters most are the glycosidic bond orientation patterns along the G-tract, rather than the local glycosidic bond orientation pattern around the G-quartet. As our models only considered the guanine residues, it is not clear if the rules proposed will generalize to non-canonical G-quadruplexes with dC or dA residues in the stem or d(GCGC) quartets (82,83).

G-quadruplexes with modified residues

Based on the significant energetic differences for the four glycosidic steps discussed, the most stable glycosidic conformation for a certain length of G-tract appears to be well defined. Knowing what leads to instability may suggest modifications that could stabilize the less favorable glycosidic bond orientation patterns to increase the stability of the G-quadruplex. For example, bulky bromide or methyl groups may be introduced at C8 position to shift guanine to favor the syn conformation, while rG or LNA modifications with 3′-endo sugar conformations have a greater propensity to form anti glycosidic bond orientation patterns. Previous experiments have shown clear relationships among the glycosidic conformations, stabilities and folding topologies (14,27,67,84,85), and the current results provide a simple means to understand these observations based on energetics. For example, in the work by Tang, they observed that when rG was introduced at the second position of each G2-tract of TBA, the molecule kept the anti-parallel structure; while if rG was introduced at the first position of each G2-tract, the molecule changed to a parallel structure (27). According to our results and conclusions, when rG is introduced at the second position of each G2-tract of TBA, it stabilizes the syn-anti conformation of each tract and therefore increases the stability of the molecule; while if rG is introduced at the first position of each G2-tract, it is difficult to form stable syn-anti steps, and therefore the most stable step that the G2-tract can form with the first position in an anti conformation is the anti-anti step, and this forces the molecule to fold into a parallel form. Our simulation results on the two-quartet AA model and also the absence of the two-quartet parallel G-quadruplexes in the PDB indicate that a TBA sequence cannot form a stable parallel quadruplex structure by itself. Electrophoresis and thermal denaturation studies have shown that the molecule solves this problem by forming multi-stranded structures (27).

G-quadruplex of G2 and G4-tracts: more definite folding topologies

The results suggest that the G-tract lengths determine the glycosidic conformations in anti-parallel G-quadruplexes and that G-tracts of different lengths show quite different behaviors. For the G-quadruplexes formed from sequences of G2 or G4-tracts, each strand adopts the same syn-anti or syn-anti-syn-anti pattern and the quadruplex core with this conformation is more stable than that with any other pattern. Similar stabilities of the SA-aabb, SA-aaab and SA-abab models (Table 1) suggest that different strand orientations do not significantly affect the quadruplex core stability as long as the compositions of the glycosidic steps are the same. This implies that loops play an extremely important role in determining the folding topologies of the G-quadruplexes of G2- and G4-tracts and explain why the folding topologies of these molecules are more definite and less polymorphic.

G-quadruplex of G3-tracts: the extreme polymorphism

The most stable geometry of the G-quadruplex core in quadruplexes with G3 repeats is the ‘3 + 1’ scaffold. This occurs because two G-tracts with the same glycosidic bond orientation pattern cannot be aligned in opposite directions. Thus, three strands are in the most stable syn-anti-anti conformation in the same direction, and the fourth strand in the less stable syn-syn-anti conformation in the opposite direction. This geometry is the major form observed for the monomeric human telomeric G-quadruplexes in K⁺ solution (34,67,69). The asymmetric dimeric G-quadruplex formed from one and three human telomeric repeats d(TAGGG), d(GGGTTAGGGTTAGGGT) also form ‘3 + 1’ scaffolds (86). In addition to the ‘3 + 1’ geometry, other geometries have also been observed for the human telomeric sequences. The monomeric basket-type structure is reported in Na⁺ solution, and this has two strands with the 5′-syn-anti-syn pattern and the other two strands with the 5′-anti-syn-anti pattern (87). Recently a two-quartet structure in K⁺ solution was reported (88). Even though only two quartets are formed in this structure, the unfavorable syn-syn steps are avoided, and moreover, the guanines not involved in the quartets still form extensive base pairing and stacking, which contribute to the overall stability of this folding geometry. Between the two quartets are the four stable syn-anti steps, which is consistent with our previous conclusions. More recently, another two-quartet structure was reported with the human telomeric sequences and this structure also maintains four 5′-syn-anti steps between the quartets (89). Monomeric or dimeric parallel structures have also been reported for the human telomeric sequences (90,91), but the equilibrium between the anti-parallel structure and intramolecular parallel structure might involve more complex kinetics and multimer association issues and will not be covered here. Moreover, the simulations in this work were carried with K⁺, so the rules may not be completely applicable to the Na⁺-favored structures. In Na⁺ solutions a basket-type structure was reported with two strands in syn-anti-syn conformation and the other two strands in anti-syn-anti conformations (87).

In the ‘3 + 1’ geometry, the unfavorable syn-syn step effectively lowers the energy differences between different conformations, thus contributing to the greater structural polymorphism for the human telomeric G-quadruplexes. The extent of structural polymorphism lies in the length of G-tract and sequences of G3-tracts (or G-tracts of odd-numbered guanines) show more structural polymorphism than sequences carrying G-tracts with an even number of guanines. The human telomeric sequence d(TTAGGG)_n is strongly conserved among the vertebrates (92) and the majority of guanine-rich sequences found in eukaryotic promoter regions also form G-quadruplexes with three quartets (93). The structural polymorphism, folding kinetics and the relative stability of G-quadruplexes may be very important for their biological function.

In summary, MD simulation and free energy analysis of two-quartet stem models suggests that the four types of glycosidic steps in G-quadruplexes have different stabilities, specifically with a favoring order of syn-anti > anti-anti > anti-syn > syn-syn. This energetic order is consistent with the glycosidic conformations experimentally observed for G-quadruplexes. When folding, quadruplex molecules are prone to create more syn-anti steps and avoid the unfavorable anti-syn and syn-syn steps. The energetic analysis brings us a step closer to understanding the effect of G-tract lengths on quadruplex folding and polymorphism. To further elucidate the folding rules underlying G-quadruplexes more work is needed to investigate the effect of the intervened loop sequence; and this work is currently in progress in our labs. Additional lessons learned relate to the inability of the current AMBER nucleic acid force fields to describe the non-canonical backbone geometries in the anti-syn and syn-syn steps which could lead to errors regarding the magnitude of the stability differences between four glycosidic steps. However, considering the consistency of the calculation results with experimental observations, the deficiencies are unlikely to affect the relative stability order.

Tetrameric parallel G-quadruplexes with all anti glycosidic conformations

Present calculation results have reasonably explained the glycosidic conformations of the anti-parallel G-quadruplexes. However, tetrameric parallel G-quadruplexes adopt anti conformation for each stem residues, and this suggests the most stability of the anti-anti step among the four glycosidic steps. This discrepancy may come from several factors such as the free-energy calculation method and potential deficiencies in the glycosidic torsional potential. When solute entropy estimates are considered during MM-PBSA calculation, the syn-anti and anti-anti steps become closer in stabilities: syn-anti (−2 kcal/mol) > anti-anti (0 kcal/mol) (Supplementary Table S1). Simulations on the 2-quatet stems with the newer ff99-bsc0-OL force field variant (40) that improves the description of the glycosidic torsions also show a slight destabilization of the syn-anti relative to the anti-anti conformations (i.e. syn-anti [approximately −1 to −3 kcal/mol) > anti-anti (0 kcal/mol)] (Supplementary Table S2). These results both show the shift in favor of anti and are more consistent with experimental observations of the all anti tetrameric parallel G-quadruplexes. However, based on the facts that the current OL modification has only been recommended for RNA (40) and entropy calculations are less reliable compared with the other energy components within the MM-PBSA method, we decided to present the respective results primarily in the Supplementary Data. Note that these computations do not alter our suggestions regarding the rules for anti-parallel stems. Moreover, the complex folding behavior and possible involvement of the multimers make the issue of parallel versus anti-parallel structure balance even more complicated. Further investigations are necessary to solve the apparent discrepancy and to confidently extend the theory to include also the all-parallel structures.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

U.S. National Institutes of Health (TEC3; grant no. R01-GM59306890); Ministry of Education of the Czech Republic (grant nos AVOZ50040507, AVOZ50040702 and LC06030 to J.Š.); Grant Agency of the Academy of Sciences of the Czech Republic (grant no. IAA400040802 to J.Š.); Grant Agency of the Czech Republic (grant no 203/09/1476 to J.Š.); Center for High Performance Computing at the University of Utah, Computer time; U.S. National Science Foundation supported TeraGrid allocation (TEC3; grant no. MCA01S027). Funding for open access charge: National Institutes of Health grant (R01-GM59306890).

Conflict of interest statement. None declared.