Lens intracellular hydrostatic pressure is generated by the circulation of sodium and modulated by gap junction coupling

Abstract

We recently modeled fluid flow through gap junction channels coupling the pigmented and nonpigmented layers of the ciliary body. The model suggested the channels could transport the secretion of aqueous humor, but flow would be driven by hydrostatic pressure rather than osmosis. The pressure required to drive fluid through a single layer of gap junctions might be just a few mmHg and difficult to measure. In the lens, however, there is a circulation of Na⁺ that may be coupled to intracellular fluid flow. Based on this hypothesis, the fluid would cross hundreds of layers of gap junctions, and this might require a large hydrostatic gradient. Therefore, we measured hydrostatic pressure as a function of distance from the center of the lens using an intracellular microelectrode-based pressure-sensing system. In wild-type mouse lenses, intracellular pressure varied from ∼330 mmHg at the center to zero at the surface. We have several knockout/knock-in mouse models with differing levels of expression of gap junction channels coupling lens fiber cells. Intracellular hydrostatic pressure in lenses from these mouse models varied inversely with the number of channels. When the lens’ circulation of Na⁺ was either blocked or reduced, intracellular hydrostatic pressure in central fiber cells was either eliminated or reduced proportionally. These data are consistent with our hypotheses: fluid circulates through the lens; the intracellular leg of fluid circulation is through gap junction channels and is driven by hydrostatic pressure; and the fluid flow is generated by membrane transport of sodium.

INTRODUCTION

Our bodies contain many stratified epithelia. In the eye alone, there are the ciliary body, corneal epithelium, conjunctiva, and lens. Such epithelia consist of two or more layers of cells with adjacent layers coupled by gap junctions. Most stratified epithelia transport fluid, but detailed mechanistic descriptions of their transport properties are largely absent. For example, a fundamental question is: do the gap junctions connecting adjacent strata carry the fluid that is transported? We were unable to find data that directly address this question one way or the other.

Gap junction channels are aqueous pores that form electrical and diffusional connections between the cytoplasm of neighboring cells (Harris, 2001). A hemichannel in one cell is formed from the oligomerization of six subunit proteins called connexins. The alignment and covalent binding of two hemichannels in adjacent cells result in a cell-to-cell channel that excludes the extracellular environment. The channels thus formed are relatively nonselective for small cytoplasmic solutes, but they have a size cutoff of ∼2-nm minor diameter. Because the interior of the channel allows entry of small charged and uncharged hydrophilic solutes (Harris, 2001), there is little doubt that water can get through the channels. For a stratified epithelium like that in the ciliary body, however, the fluid secreted (the aqueous humor) is essentially isotonic with the extracellular solution of the body (Hayward et al., 1976; Gaasterland et al., 1979). A near isotonic solution of 0.3 M solute and 55 M water implies that for every solute molecule secreted, ∼180 water molecules follow. It is not known whether gap junction channels can accommodate such a relatively large fluid flow.

Mathias et al. (2008) reviewed the gap junction channels of the ciliary epithelium. As mentioned above, we could find no direct evidence that gap junction channels, in any stratified epithelium, conduct the transported fluid, so we addressed this issue by modeling. We asked the question: what junctional properties would be needed for the channels to conduct the secretion of aqueous humor? If gap junction channels conduct the secreted fluid, solute and fluid share the same path, so there would not be local osmosis. As stated in the Theory section below, this conclusion is equivalent to assuming the reflection coefficient (Kedem and Katchalsky, 1958) is essentially zero, so significant fluid flow requires a transjunctional hydrostatic pressure difference. For a single layer of gap junction channels between the pigmented and nonpigmented epithelia, the pressure difference was predicted to be just a few mmHg, and a difference that small would be difficult to measure. However, there are data suggesting that the lens has an internal circulation of fluid, which crosses hundreds of layers of gap junctions, so a significant hydrostatic pressure might be present.

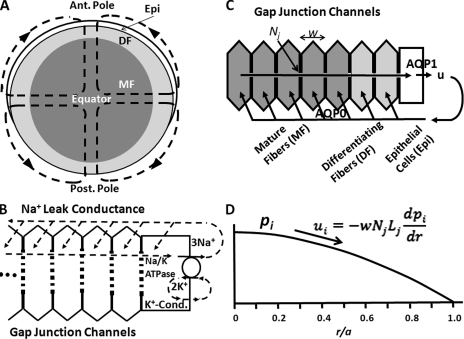
The lens has an internal circulation of Na⁺ that enters at both poles and exits at the equator (see Fig. 1 A). This circulation was recently reviewed (Mathias et al., 2007), so only a brief overview will be presented. Fig. 1 B shows a more detailed view of the entry of Na⁺ into the extracellular spaces between lens cells where it flows toward the lens center. There is a large fiber cell transmembrane electrochemical gradient for sodium, causing it to move from the extracellular spaces into the intracellular compartment, where it reverses direction and is driven by an intracellular electrochemical gradient to flow through gap junction channels back to the surface. It is directed to flow in the interesting circulating pattern shown in Fig. 1 A because gap junction coupling conductance in the equatorial region of differentiating fibers (DFs; the outer shell of fiber cells that retain their organelles) is very high (Baldo and Mathias, 1992). Hence, once a sodium ion enters the intracellular compartment, DF gap junctions facilitate flow to the equator. Moreover, equatorial epithelial cells have a relatively high expression of Na/K ATPase protein (Gao et al., 2000), and almost all of the Na/K ATPase activity in the lens occurs at the equatorial surface where sodium is transported out of the lens (Candia and Zamudio, 2002). Lens K⁺ channels colocalize with the Na/K ATPase in lens epithelial cells (Mathias et al., 1997). Thus, K⁺ efflux colocalizes with K⁺ influx, and there is little net circulation of K⁺, as shown in Fig. 1 B. Fiber cells have Cl⁻ channels as well as Na⁺ leak channels (Webb and Donaldson, 2008), but Cl⁻ is close to electrochemical equilibrium, so the flux is small relative to the Na⁺ flux and has only small modulatory effects on the overall circulation. To summarize, the circulation of Na⁺ ultimately exists because of energy supplied by the Na/K ATPase, but it is directly generated by the fiber cell transmembrane electrochemical gradient for Na⁺. The circulating pattern of Na⁺ current is a result of the concentration of gap junction coupling conductance in the equatorial DF and the relatively high Na/K ATPase activity in the equatorial epithelium.

Figure 1.

A sketch of the hypotheses being tested in this study. (A) The net flux of Na⁺, followed by fluid, enters the lens at both poles and exits at the equator. The interesting pattern of circulation ensures maximum stirring of the fluid, which is hypothesized to act as a micro circulatory system for the avascular lens (Mathias et al., 2007). (B) A more detailed view of Na⁺ and K⁺ fluxes. Na⁺ flows into the lens along the extracellular spaces between cells, moves down its electrochemical gradient to enter fiber cells, reverses its direction, and flows back to the lens surface, where the Na/K ATPase transports it out of the lens to complete the circulation. The circulating pattern of flow shown in A occurs because gap junctions coupling DF cells direct the intracellular leg of the circulation to the equator. (C) Our first hypothesis is that water circulates through the lens as shown in this panel. Our second hypothesis is that the water circulation follows and is driven by the Na⁺ flux. Water enters each fiber cell through AQP0 resulting from local osmotic gradients created by the transmembrane Na⁺ flux, and leaves the lens through AQP1 resulting from local osmotic gradients generated by the Na/K ATPase. For the intracellular water to flow back to the surface of the lens, we hypothesize that a hydrostatic pressure (p_i mmHg) develops that drives the water from cell to cell through gap junctions. (D) The predicted hydrostatic pressure gradient. The intracellular hydrostatic pressure is graphed as a function of normalized distance (r/a) from the lens center, where a (cm) is the lens radius, and r (cm) is the distance from the lens center. The equation relates intracellular water flow (u_i cm/s) to the hydrostatic pressure gradient (dp_i/dr mmHg/cm), the hydraulic conductivity of a single gap junction channel (L_j (cm³/s)/(mmHg)), the number of gap junction channels per area of cell-to-cell contact (N_j cm⁻²), and the fiber cell width (w cm).

We (Mathias, 1985; Mathias et al., 1997) have hypothesized that the circulating Na⁺ current represents a circulation of solute that drives fluid by local osmosis to flow in the same pattern. Local osmotic gradients across fiber cell membranes are proposed to bring fluid into the intracellular compartment through the fiber cell membrane water channel AQP0 (Fig. 1 C). The fluid moves to the lens surface where, again, local osmotic gradients cause it to exit the lens through the epithelial membrane water channel AQP1 (Fig. 1 C).

Several investigators have experimentally measured lens-associated water flow. Fischbarg et al. (1999) reported that cultured lens epithelial cells, from bovine or mouse, vigorously transported fluid in the basolateral to apical direction. If this can be extrapolated to an intact lens, fluid would be transported from the aqueous humor into the extracellular spaces at the anterior of the lens, consistent with our hypothesis. Fowlks (1973) and Fischbarg et al. (1999) placed intact rabbit lenses in Ussing chambers that isolated the anterior surface from the posterior surface by occluding the equatorial surface. They each found fluid transport, but in opposite directions. Based on our hypothesis, the normal route of fluid exit from the lens is the equator, so depending on how the lenses were mounted, the equatorial fluid could be forced into either the anterior or posterior Ussing chamber. Candia and Alvarez (2006) reviewed their studies of intact bovine lenses in a chamber that isolated the anterior, equatorial, and posterior surfaces, and measured water flow into or out of each. They found the dominant path of fluid circulation was into the anterior surface and out at the equator. They did not measure the pattern of circulating currents. The sketch in Fig. 1 A shows the circulation as symmetric about the equator, but that is an idealism that simplifies analysis, whereas in reality, the circulation is never symmetric and the asymmetry depends on species. Small rodent and frog lenses have a much more symmetric circulation than the larger rabbit lens, which has more of an anterior to equator circulation. The bovine lens may be more similar to rabbit than small rodents. Despite the lack of a complete characterization of salt and water transport in a lens from one species, all of these studies are consistent with the hypothesis that the lens generates fluid transport.

If the intracellular water flow from the lens center to surface is through fiber cell gap junctions, then there should be an intracellular hydrostatic pressure gradient, as derived in the Theory section and illustrated in Fig. 1 D. Because the fluid must transverse hundreds of layers of gap junction channels, the hydrostatic pressure might be sufficiently large to be measured.

The purpose of this study was to test the following hypotheses: the lens has an internal circulation of fluid; the circulation of fluid is generated by and follows the circulation of Na⁺; and the intracellular leg of the fluid circulation is driven by hydrostatic pressure to go through fiber cell gap junction channels. Our data are consistent with these hypotheses, so other fluid transporting stratified epithelia may use the same mechanism: hydrostatic pressure drives transported fluid through layers of gap junction channels connecting the strata. Thus, the implications of this study may be widespread.

Theory

A comprehensive model of lens transport, including osmotic and hydrostatic pressure gradients in both the intracellular and extracellular compartments of the lens, is beyond the scope of this paper. The purpose here is to generate a structurally based, physically reasonable description of intracellular pressure, so our pressure data can be curve fit and quantified. The model therefore focuses on the intracellular leg of fluid flow, using experimentally measured values of transport and structural parameters, but also using several simplifying assumptions.

We assume gap junction channels are right circular cylinders with radius a_j = 1 nm and length ℓ = 14 nm (Mathias et al., 2008). Within the channel we assume laminar fluid flow, so the single-channel hydraulic conductivity is determined by standard physics:

$$L_j=\frac{\pi a_j^4}{8\eta \ell }\approx 4\times {10}^{-18}\frac{c{m}^3/3}{mmHg},$$ (1)

where the viscosity of water is η = 7 × 10⁻⁶ mmHg-s. If there are N_j channels per cm² of cell-to-cell contact (N_j ∼10¹⁰/cm²), the gap-junctional hydraulic conductivity will be N_jL_j ((cm/s)/mmHg)). Kedem and Katchalsky (1958) (reviewed in Schultz, 1980) used thermodynamics to derive equations describing neutral solute and water fluxes through a barrier permeable to both. Their equation for water flow was u = L(Δp − σRTΔc), where σ is the reflection coefficient. If σ = 1, no solute can enter the water channels, whereas if σ = 0, all solutes can enter the channels. Gap junction channels exclude cytoplasmic proteins, but the osmolarity of these is small; therefore, for simplicity, we make the approximation σ ≈ 0, so junctional water flow u_j (cm/s) depends only on the transjunctional pressure drop Δp_j (mmHg). Namely,

$$u_j=-N_j{L}_j\Delta p_j.$$ (2)

In the lens, there are hundreds of layers of cells between the center and surface. Each cell layer has a width w (∼3 × 10⁻⁴ cm), hence gap junctions are separated by the distance w (see Fig. 1 C). The pressure drop between the lens center and surface will mostly occur at discrete locations across gap junctions, but because junctions are closely spaced relative to the distance over which pressure changes, we treat intracellular pressure p_i (mmHg) as a continuous function of radial position r (cm). Intracellular radial water flow u_i (cm/s) is therefore related to p_i by:

$$u_i=-{\Lambda }_i\frac{d{p}_i}{dr},$$ (3)

where the effective intracellular hydraulic conductivity is given by

$${\Lambda }_i=w{N}_j{L}_j\sim 0.0012\left(\frac{\mu m^2/s}{mmHg}\right).$$ (4)

An estimate of u_i can be made based on membrane water flow entering a fiber cell, u_m (cm/s):

$$\frac{1}{r^2}\frac{d}{dr}\left(r^2{u}_i\right)=\frac{S_m}{V_T}{u}_m,$$ (5)

where S_m/V_T (∼6,000 cm⁻¹) is the surface area of fiber cell membrane per unit volume of tissue (Mathias et al., 1997). Lastly, membrane water flow can be related to membrane solute flux, which has been experimentally measured (Mathias et al., 1997). Our hypothesis is that fluid flow is primarily generated by fiber cell transmembrane Na⁺ transport (j_Na, ∼0.5 pmol/cm²/s). The theoretical maximum fluid flow velocity is “isotonic transport” (Mathias and Wang, 2005), which would be j_Na/c_o, where c_o (300 μmoles/cm³) is the concentration of extracellular solute. However, this would require membrane water permeability to be infinite, which is not possible, so fluid flow will always be less than isotonic. We therefore assume that u_m = Kj_Na/c_o, where 0 < K < 1. Water flow and Na⁺ flux have not been measured in a lens from the same species, so K is an unknown fraction. Assuming j_Na is approximately a constant (i.e., independent of r),

$$u_i\left(r\right)=\frac{S_m}{V_T}K\frac{j_{Na}}{c_o}\frac{r}{3}.$$ (6)

Intracellular water flow from lens center (r = 0) to surface (r = a) is therefore approximately a linear function of distance from the center, going from zero at the center to its maximum value at the surface. Inserting Eq. 6 into Eq. 3 and integrating implies p_i will vary as r², with the maximum p_i at the center and p_i = 0 at the surface (see Fig. 1 D).

A caveat to this relatively simple analysis is that gap junction coupling conductance and the connexin composition of channels changes at the differentiating to mature fiber (DF to MF) transition (defined as r = b, where b ≈ 0.85a; see Fig. 1), with DF coupling conductance generally being higher than that in MF (Mathias et al., 2010). For gap junction–mediated water flow, the slope of pressure versus radial location curve should change at r = b. To account for this change in coupling, when Eq. 6 is inserted into Eq. 3, we assume Λ_i = Λ_DF in the zone of DFs, whereas Λ_i = Λ_MF in the zone of MFs (see Fig. 1 A), and then the integration is done in two steps, giving:

$$\begin{array}{ll}\frac{S_m}{V_T}K\frac{j_{Na}}{c_o}\frac{a^2-r^2}{6{\Lambda }_{DF}}& b\le r\le a\\ p_i=\\ \frac{S_m}{V_T}K\frac{j_{Na}}{c_o}\left[\frac{a^2-b^2}{6{\Lambda }_{DF}}+\frac{b^2-r^2}{6{\Lambda }_{MF}}\right]& 0\le r\le b.\end{array}$$ (7)

Eq. 7 was curve fit to the data in Results.

The value p_i(0) provides a simple measure of the effect of the number of gap junction channels on hydrostatic pressure. Inserting b = 0.85a into Eq. 7 and evaluating it at r = 0 yields:

$$p_i\left(0\right)=\frac{S_m}{V_T}K\frac{j_{Na}}{c_o}\frac{a^2}{6}\left[\frac{0.28}{{\Lambda }_{DF}}+\frac{0.72}{{\Lambda }_{MF}}\right].$$ (8)

All of the different types of lenses studied had a similar radius of a ≈ 0.1 cm, all appeared healthy and were expected to have similar values of intracellular water flow, u_i (Eq. 6), so differences in p_i(0) in the different types of lenses depend on Λ_DF and Λ_MF, but primarily on Λ_MF, which depends on the number of gap junction channels coupling MF cells. Thus, p_i(0) was used to assess the effect on pressure ofsecb altering the number of MF gap junction channels.

MATERIALS AND METHODS

Isolation of lenses

Wild-type (WT), heterozygous connexon 46 knockout (KO; Cx46(+/−)) and connexon 46 for connexon 50 knock-in (KI; Cx50(46/46)) mice used in this study were in a C57 genetic background, whereas the glutathione peroxidase 1 (GPX) KO (GPX(−/−)) mice were in a C57/J129 mixed genetic background. All mice were euthanized, and then the eyes were removed and placed in a Sylgard-lined Petri dish filled with normal Tyrode’s solution containing (in mM): 137.7 NaCl, 2.3 NaOH, 5.4 KCl, 2 CaCl₂, 1 MgCl₂, 5 HEPES, and 10 glucose, pH 7.4. To isolate and mount lenses, the cornea and iris were removed and the optic nerve was cut. The sclera was cut into four flaps from the posterior surface. Then, the lens was transferred and pinned to the bottom of a chamber with a Sylgard base. The chamber was mounted on the stage of a microscope and perfused with normal Tyrode’s solution.

Measurements of intracellular pressure within lenses

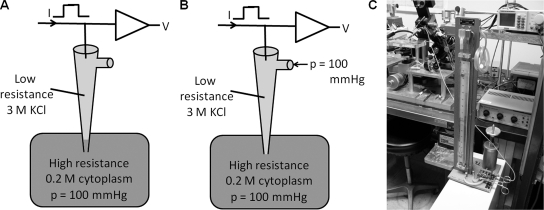
A pulse generator (model 182A; Wavetec) and a digital real-time oscilloscope (TDS 210; Tektronix) interfaced with a self-built amplifier were used to measure microelectrode resistances. The resistance of the voltage electrode was 1.5–2.0 MΩ when filled with 3 M KCl, and that of the reference electrode was 0.2 MΩ when filled with agar (dissolved in 3 M KCl) to prevent the Cl⁻-induced liquid junction potential. About 30% of the experiments were terminated because the electrode clogged or occasionally the tip broke. We use low resistance microelectrodes for intracellular recordings in the lens because sharper, higher resistance microelectrodes usually break before they penetrate the lens capsule, and the higher the resistance the more prone the electrode is to irreversible clogging. Serial current pulses with amplitudes of 100 nA and durations of 15 ms were applied during the measurements of intracellular pressure within lenses. The amplitude of voltage steps responding to current pulses indicated the resistance of the tip of the electrode. First, the resistance of the voltage electrode was recorded when the voltage electrode was immersed in the bath (normal Tyrode’s solution). Then, the electrode was inserted into the lens. Pressure within the lens was higher than that in the tip of the electrode, so the higher pressure pushed intracellular cytoplasm into the tip of the electrode (Fig. 2 A). Because cytoplasm has relatively high resistance, the amplitude of the electrode resistance increased. The port of the tightly sealed electrode holder was connected to a mercury manometer by plastic tubing, which allowed us to adjust the pressure within the electrode. The manometer can record a pressure of about ±400 mmHg. The pressure is generated by turning the crank shown in Fig. 2 C. We increased pressure within the electrode to push cytoplasm back into the intracellular space. When pressure within the electrode is equal to intracellular pressure, cytoplasm should be completely pushed out of the electrode, and the amplitude of the electrode resistance should return to its original level measured in the bathing solution (Fig. 2 B). Thus, the reading from the manometer when the applied pressure caused the resistance to return to its original value represented the intracellular pressure within the lens. However, if the applied pressure exceeded that within the lens cell, the electrode resistance should remain the same as recorded in the bath. The pressure generated by the manometer was therefore backed off until the resistance just began to increase. This was the value recorded for the intracellular pressure.

Figure 2.

The intracellular pressure measuring system. (A) A sketch of the effect of intracellular pressure on the electrode–intracellular solution interface. An elevated intracellular pressure (e.g., 100 mmHg) over that in the bathing solution causes the interface to move up the shank of the electrode, thus filling the narrow tip with relatively high resistance cytoplasm. (B) When the same 100-mmHg pressure is applied to the port of the microelectrode, the interface moves back to the tip as shown, and the electrode resistance is restored to its relatively lower value recorded in the bathing solution. (C) The manometer used to adjust the hydrostatic pressure at the electrode port. The crank drives a piston to create the pressure, which is connected to the electrode port through the plastic tubing. When the electrode resistance is restored to its value in the bathing solution, such that an increase in applied pressure has no effect on resistance, whereas a small reduction in pressure causes a small increase in resistance, we assume the applied pressure equals the intracellular pressure. The value of applied pressure is then read from the column of mercury.

We inserted the voltage electrodes into different depths within the lenses. Intracellular pressures and locations of the electrode tips were measured to establish the relationship between pressure and location within the lenses. After pressure measurements were completed, we routinely pulled out the electrode and checked its resistance in the bathing solution to make sure that changes in resistance during measurements within lenses were not because of clogging or breakage of the electrode tip.

RESULTS

The lens generates an intracellular pressure gradient

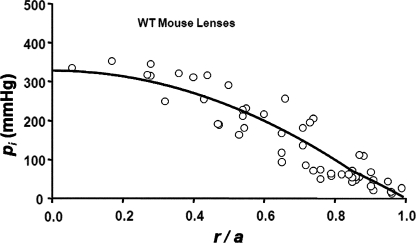
Fig. 3 illustrates the hydrostatic pressure gradient measured in WT mouse lenses. The data were recorded in 14 lenses taken from seven mice. The pressures at two to six locations in each lens were recorded, and then the data from all 14 lenses were pooled and graphed as a function of normalized distance from the lens center. The smooth curve is the best fit of Eq. 7 to the pooled data. Table I includes average parameter values for this group of lenses. The best-fit value for the average pressure at the lens center was 328 mmHg. For a lens whose radius is a = 1 mm and fiber cell width is w = 3 µm, there are 333 shells of gap junctions; hence, the average pressure drop across each shell of gap junctions is ∼1 mmHg. The presence of the measured standing hydrostatic pressure gradient shown in Fig. 3 suggests the existence of intracellular fluid flow from the lens center to surface. It also suggests that the fluid flow might be through lens gap junction channels, because a large pressure gradient was predicted in the Theory section for water flow through gap junction channels. Nevertheless, one could think of other possibilities, so we sought more direct evidence on whether gap junction channels were mediating water flow.

Figure 3.

The standing hydrostatic pressure gradient in lenses from WT mice, which were ∼2 mo old. The hydrostatic pressure (p_i mmHg) is graphed as a function of normalized distance (r/a) from the lens center, where a (cm) is the lens radius, and r (cm) is the distance from the lens center. The data are from 14 lenses from seven mice. The pressures at two to six radial locations were recorded from each lens. The smooth curve is the best fit of Eq. 7 to the data.

Table I.

Parameter values from the various different types of lenses

Type of mouse	a (cm)	$\frac{{\Lambda }_{DF}}{K}\left(\frac{\mu m^2/s}{mmHg}\right)$	$\frac{{\Lambda }_{MF}}{K}\left(\frac{\mu m^2/s}{mmHg}\right)$	pi(0) (mmHg)
WT	0.11 ± 0.005	0.0080	0.0056	328
Cx50(46/46)	0.10 ± 0.004	0.0135	0.0078	188
GPX(−/−)	0.10 ± 0.004	0.0040	0.0031	496
Cx46(+/−)	0.11 ± 0.003	0.0083	0.0025	632

Intracellular pressure varies inversely with the number of gap junction channels

We have genetically engineered mouse models that have different levels of fiber cell gap junction coupling conductance (see Table II). Based on Western blotting, these differences arise because of differences in the number of gap junction channels, so coupling conductance and water permeability should be correlated. The mouse models we have chosen all appear to have healthy, transparent lenses, so the water flow should be similar in each type of lens, but when the number of gap junction channels is altered, the pressure needed to drive the water flow should change. Indeed, p_i(0) should vary inversely with the number of channels, where the number of channels coupling the MF is of primary importance (Eq. 8). Thus, if the number of channels coupling MF is doubled, we expect the value of p_i(0) to be about half normal, whereas if the number of channels coupling MF is halved, we expect the value of p_i(0) to be approximately twice normal.

Table II.

A comparison of pressures at r = 0 and MF coupling conductances

X =	Cx50(46/46)	GPX(−/−)	Cx46(+/−)
$\frac{G_{MF}\left(X\right)}{G_{MF}\left(WT\right)}$	2.04	0.59	0.50
$\frac{p_i\left(0\right)\left(WT\right)}{p_i\left(0\right)\left(X\right)}$	1.74	0.66	0.52

G_MF values in Cx50(46/46) and Cx46(−/−) lenses were taken from Mathias et al. (2010), and those in GPX(−/−) lenses were from Wang et al. (2009).

Lens fiber cells express two connexins, Cx46 and Cx50. In WT lenses, gap junction channels made from Cx46 and Cx50 contribute about equally to the coupling conductance between DF (G_DF ≈ 1 S/cm² of cell-to-cell contact), whereas channels made from Cx46 provide the coupling conductance between MF (G_MF ≈ 0.5 S/cm² of cell-to-cell contact; Mathias et al., 2010). The change in coupling conductance at the DF to MF transition appears to be a result of truncation-mediated loss of functional Cx50 channels in the MF (DeRosa et al., 2006). Pressure gradients in the lens are dominated by the extensive volume of MF, so we looked at mouse models that express different levels of Cx46 and would therefore have significantly different levels of coupling between MF.

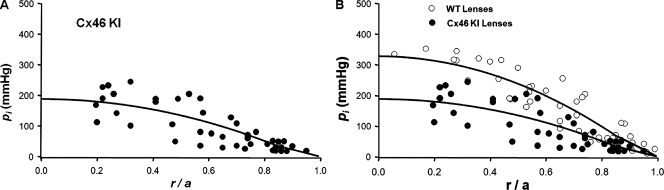
When Cx46 was knocked into the Cx50 gene locus (Cx50(46/46)), G_MF essentially doubled (Martinez-Wittinghan et al., 2004), and the number of Cx46 channels appeared to double (White, 2002). Thus, we expected that the pressure gradient should be about half that in WT lenses. Pooled pressure measurements from 12 Cx46 KI lenses are graphed as a function of distance from the lens center in Fig. 4 A. Fig. 4 B shows an over-plot of the KI and WT pressure data. As can be seen, the pressure is significantly lower at all radial locations in the KI lenses. Based on the best fit of Eq. 7 to the data, the value of p_i(0) was 188 mmHg (see Table I), or a little greater than half that in WT lenses (see Table II). These data are consistent with water flow through an increased number of lens gap junction channels.

Figure 4.

The effect on intracellular hydrostatic pressure of increasing the number of gap junction channels coupling the MFs. (A) The standing hydrostatic pressure gradient in lenses from Cx46 KI mice, which were ∼2 mo old. The hydrostatic pressure (p_i mmHg) is graphed as a function of normalized distance (r/a) from the lens center, where a (cm) is the lens radius, and r (cm) is the distance from the lens center. The data are from 12 lenses from six mice. The pressures at two to six radial locations were recorded from each lens. The smooth curve is the best fit of Eq. 7 to the data. Based on previous studies, the MF coupling conductance in the Cx46 KI lenses is approximately double that in WT lenses (Mathias et al., 2010). Based on the derivation of Eq. 7, if fluid flow in WT and KI lenses is the same, the pressure gradient in the KI lenses should be approximately half that in WT lenses. The best fits of the model to the data give the ratio of p_i(0) in Cx46 KI/WT lenses as 0.57. (B) An over-plot of the Cx46 KI and WT data.

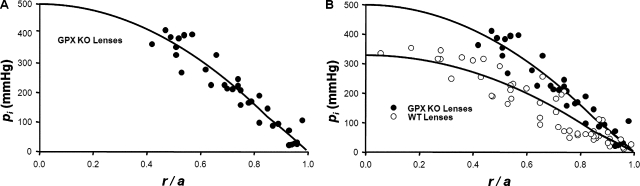
GPX is a cytoplasmic enzyme that protects the lens against oxidative damage by H₂O₂ (Reddy, 1990). KO of GPX results in age-onset nuclear cataracts (Reddy et al., 2001); however, in KO mice at 2 mo of age, the lenses are transparent and have normal transport properties except for reductions in gap junction coupling conductance. Western blots suggest that these reductions are a result of loss of both Cx46 and Cx50 (Wang et al., 2009). Based on curve fits of series resistance data from 2-mo-old WT and GPX KO lenses, G_MF was reduced to ∼59% normal (Wang et al., 2009). Pooled pressure measurements from 10 lenses from GPX KO mice are graphed as a function of radial location in Fig. 5 A. At ∼60% of the radial distance into the lenses (r/a = 0.4), the pressures significantly exceeded 400 mmHg, which is the maximum pressure the manometer can measure. Hence, we do not have data on the central pressures, other than that they exceeded 400 mmHg. However, by curve fitting Eq. 7 to the peripheral data, we can project the average central pressure. Based on the curve fit, the average value of p_i(0) was ∼496 mmHg, or ∼1.5 times that in WT lenses, consistent with water flow through a reduced number of gap junction channels. Fig. 5 B is an over-plot of the GPX KO and WT pressure data. In the range of radial locations where pressure in both types of lenses could be measured, the pressures in the KO lenses are consistently higher than those in WT lenses.

Figure 5.

The effect on intracellular hydrostatic pressure of reducing the number of gap junction channels coupling the differentiating and MFs. (A) The standing hydrostatic pressure gradient in lenses from GPX-1 KO mice, which were ∼2 mo old. The hydrostatic pressure (p_i mmHg) is graphed as a function of normalized distance (r/a) from the lens center, where a (cm) is the lens radius, and r (cm) is the distance from the lens center. The data are from 10 lenses from five mice. The pressures at two to six radial locations were recorded from each lens. The smooth curve is the best fit of Eq. 7 to the data. Because the manometer can only measure ∼400 mmHg, the pressures at locations closer to the lens center than ∼0.4a could not be determined, other than that they exceeded 400 mmHg. The MF coupling conductance in the GPX-1 KO lenses was ∼60% of that in WT lenses (Wang et al., 2009). Based on the derivation of Eq. 7, the pressure gradient should be approximately inversely proportional to the MF coupling conductance, or ∼1.67 times greater than in WT. The best fits of the model to the data give the ratio of p_i(0) in GPX-1 KO/WT lenses as 1.52. (B) An over-plot of the GPX-1 KO and WT data.

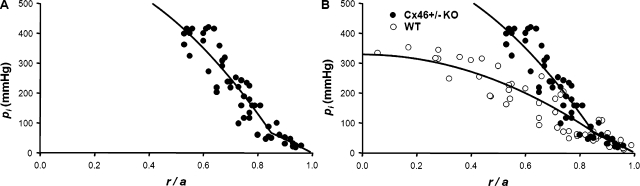
Homozygous KO of Cx46 (Cx46−/−) caused complete loss of gap junction coupling between MFs, leading to loss of calcium homeostasis in MFs and a dense central cataract (Gao et al., 2004). However, heterozygous KO of Cx46 (Cx46+/−) yielded healthy lenses that were transparent, but G_DF went from ∼1 S/cm² in WT to 0.75 S/cm² in Cx46+/− lenses, and G_MF went from 0.5 S/cm² to 0.25 S/cm², because of about a 50% reduction in the amount of Cx46 protein (Mathias et al., 2010). Pooled pressure measurements from 12 Cx46+/− lenses are graphed as a function of normalized radial location in Fig. 6 A. At ∼45% of the distance into the lenses (r/a = 0.55), the pressures consistently exceeded 400 mmHg and could not be determined using the manometer. So again, as in Fig. 5, the average central pressure was estimated from curve fitting Eq. 7 to the peripheral pressure data. Based on the curve fit, the average value of p_i(0) was 632 mmHg, or ∼1.9 times that in WT lenses, so halving the number of MF gap junction channels almost doubled the pressure gradient, as expected for water flow through fiber cell gap junction channels. Moreover, in these lenses, the change in slope of the pressure versus radial location at r = b is quite noticeable, even in the raw data. This is also consistent with the water flowing through fiber cell gap junction channels, because gap junction coupling conductance abruptly decreases by about a factor of 3 at the DF to MF transition in Cx46+/− lenses. However, as described below, parallels between DF/MF coupling conductance and hydraulic conductivity are not perfect. In particular, the value of G_DF in Cx46+/− lenses was ∼25% lower than in WT lenses, whereas there is no noticeable difference in the best-fit values Λ_DF between these two types of lenses. This may simply be because of variability in the pressure data, as discussed in the next paragraph. Fig. 6 B provides an over-plot of pressure data from Cx46(+/−) and WT lenses. In the range of radial locations where Cx46+/− pressures in the MF could be measured, the pressure data are consistently higher than those measured in WT lenses, and the slope of the MF pressure gradient in Cx46+/− lenses is clearly much steeper than that in WT lenses. These data are consistent with water flow through lens fiber cell gap junctions.

Figure 6.

The effect on intracellular hydrostatic pressure of approximately halving the number of gap junction channels coupling the MFs. (A) The standing hydrostatic pressure gradient in lenses from Cx46+/− KO mice, which were ∼2 mo old. The hydrostatic pressure (p_i mmHg) is graphed as a function of normalized distance (r/a) from the lens center, where a (cm) is the lens radius, and r (cm) is the distance from the lens center. The data are from 12 lenses from six mice. The pressures at two to six radial locations were recorded from each lens. The smooth curve is the best fit of Eq. 7 to the data. Because the manometer can only measure ∼400 mmHg, the pressures at locations closer to the lens center than ∼0.55a could not be determined, other than that they exceeded 400 mmHg. The MF coupling conductance in Cx46+/− KO lenses was ∼50% of that in WT lenses (Mathias et al., 2010). Based on the derivation of Eq. 7, the pressure gradient should be approximately inversely proportional to the MF coupling conductance, or approximately two times greater in the KO than WT lenses. The best fits of the model to the data give the ratio of p_i(0) in Cx46+/− KO/WT lenses as 1.92. (B) An over-plot of the Cx46+/− and WT data.

The parameter values in Eq. 7 for the fits to the data in Figs. 3–6 are summarized in Table I. The hydraulic conductivities (Λ_DF and Λ_MF) and the degree to which intracellular water flow approaches isotonic (K) are all unknowns. However, one can see in the model (Eqs. 7 and 8) that the pressure is determined by the ratio of Λ/K, so they cannot be individually determined by the data. We therefore curve fit to the ratios Λ_DF/K and Λ_MF/K. If one assumes the calculated hydraulic conductivities are accurate, fiber cell transmembrane water flow is ∼20% of its isotonic limit, which is given by j_Na/c_o. This implies that intracellular water flow varies from 0 nm/s at the lens center to a maximum value of 0.7 nm/s at the lens surface. However, our model of the relationship between hydrostatic pressure and water flow through lens gap junction channels is at a preliminary stage and has not been subjected to experimental tests. In the Discussion, we point out several factors that are not included in the present model, and describe how these factors might significantly reduce the pressure needed per volume of water flow.

The relative value of Λ_DF to Λ_MF is of interest because Λ_MF represents channels formed from Cx46, whereas Λ_DF, in all models except the Cx50(46/46) lenses, represents channels made from both Cx46 and Cx50. It would be interesting to know the relative water permeability of channels made from these different connexins. However, the best-fit values did not tell a consistent story. Therefore, we examined the sensitivity of the curve fits to the relative values of Λ_DF and Λ_MF. To study the sensitivity of the fits, Λ_DF was manually set, and then the value of Λ_MF was curve fit to the data. We found that there is a trade-off, such that the fits appear equally good if Λ_DF is decreased somewhat and Λ_MF increased, or vice versa, so a quantitative comparison of Λ_DF with Λ_MF is beyond the accuracy of the data. We noticed, however, that the calculated value of p_i(0) did not significantly change with this procedure. The conclusion was that both Cx46 and Cx50 contribute significantly to WT Λ_DF, but the relative contributions are uncertain. Assuming Λ_MF is representative of the contribution of Cx46 channels to Λ_DF, reasonable fits were obtained with Λ_MF/Λ_DF ranging from 0.7 to 0.5, so Cx46 channels could contribute anywhere from 50 to 70% of the water permeability of DF, whereas they contribute ∼50% of the ion permeability. Despite this uncertainty, Eq. 7 provides a way to quantitatively specify the average pressure gradient in a particular type of lens, and allows estimation of the values of p_i(0) in the different types of lenses.

Table II summarizes the experimental relationship between p_i(0) and MF coupling conductance. Based on the derivation of Eq. 8 in the Theory section, if water flow is through gap junction channels coupling the MF, there should be an approximate reciprocal relationship between p_i(0) and G_MF, insofar as G_MF is proportional to the number of gap junction channels per area of cell-to-cell contact (N_j). This relationship is not only qualitatively present in the data summarized in Table II, but it is quantitatively reasonably accurate, particularly because the experiments were done at different times, in different groups of each type of lens, and using very different techniques. This correlation is consistent with water flow through lens gap junction channels.

Lens pressure gradient is proportional to the circulation of sodium

To test this hypothesis, we reduced the circulation of sodium and measured the effects on the pressure gradient. We do not have a means to increase the Na⁺ circulation, but we can either block it, by eliminating the transmembrane electrochemical gradient for Na⁺, or reduce its short-time amplitude by inhibiting the Na/K ATPase.

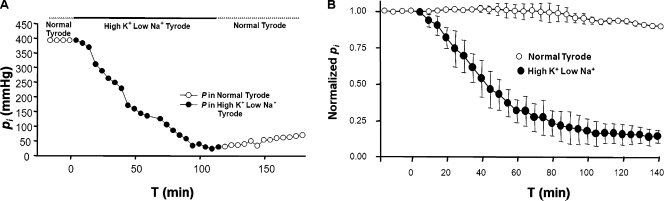
Parmelee (1986) used the vibrating probe technique to measure currents at the surface of isolated frog lenses. She determined that replacing external Na⁺ with K⁺, such that [Na⁺]_o = [K⁺]_o, significantly reduced the currents, whereas complete replacement of external Na⁺ by K⁺ reversed the direction of current flow. Mathias et al. (1997) successfully predicted these experimental outcomes using the Na⁺ circulation model described in the Introduction. The model suggested that the fiber cell transmembrane electrochemical gradient for Na⁺ was reduced or reversed, causing the observed changes in circulating current. By extrapolation, we could cause the circulation of Na⁺ to approach zero by immersing the lens in a modified Tyrode’s solution that contained 140 mM [K⁺]_o and 5 mM [Na⁺]_o. The high [K⁺]_o causes the fiber cell membrane voltage to approach zero, whereas the low [Na⁺]_o causes the Nernst potential for Na⁺ to approach zero; thus, the transmembrane electrochemical gradient for Na⁺ should approximately be eliminated. The elimination will not be immediate, however, because the new bathing solution needs to diffuse along extracellular spaces all the way to the lens center to completely stop transmembrane Na⁺ influx. The effect was evaluated by recording intracellular hydrostatic pressure in a central fiber cell. But the reduction in hydrostatic pressure will lag the reduction in Na⁺ influx, because once Na⁺ has ceased entering the lens and thus fluid entry has stopped, sufficient fluid must be transported out of the lens to allow the pressure to fall to zero. Based on previous studies of diffusion of extracellular solutions into lenses (Mathias et al., 1985), we estimated that the solution exchange should require ∼1 h, and then another hour for the pressure to drop, so the overall process should require ∼2 h, as was observed.

Fig. 7 A shows the effect of the low Na⁺/high K⁺ external solution on pressure in a central fiber cell in a typical lens. The pressure declined to near zero in a period of ∼2 h, after which restoring normal external Tyrode’s solution caused the beginning of recovery of pressure. We never waited for total recovery, which we considered unlikely to occur given the severity of this treatment and its effects on Na⁺-dependent transport systems. Fig. 7 B shows the averaged normalized pressure in central fiber cells from seven lenses graphed as a function of time in low Na⁺/high K⁺ solution (filled circles). The pressure consistently fell to near zero in a time period of ∼2 h. The average normalized pressure in five control lenses in normal Tyrode’s solution for the same period of time (Fig. 7 B, open circles) remained relatively constant; the pressure at the end of 2 h was ∼85% of the initial value.

Figure 7.

The effect of approximately eliminating the transmembrane electrochemical gradient for Na⁺ on central hydrostatic pressure in WT mouse lenses. The high K⁺/low Na⁺ external solution contained 140 mM K⁺ and 5 mM Na⁺. (A) Typical data from one lens showing the time course of the reduction in central hydrostatic pressure associated with elimination of the electrochemical gradient for Na⁺. After ∼120 min in 5 mM of extracellular Na⁺, the pressure near the center of the lens dropped to near zero. Upon restoration of normal extracellular Na⁺, the pressure began to recover, but we did not wait for full recovery, which was unlikely because the long exposure to low extracellular Na⁺ affected many transport systems and was probably not completely reversible. (B) The average hydrostatic pressure in lenses immersed in high K⁺/low Na⁺ solution (seven lenses from seven mice) compared with the pressure in normal Tyrode’s solution (five lenses from five mice). The central pressure in lenses immersed in high K⁺/low Na⁺ solution consistently fell to near zero in a time period of ∼2 h. In control lenses, the hydrostatic pressure remained relatively constant over a period of more than 2 h. After a period of 140 min, the average pressure was 85% of its initial value.

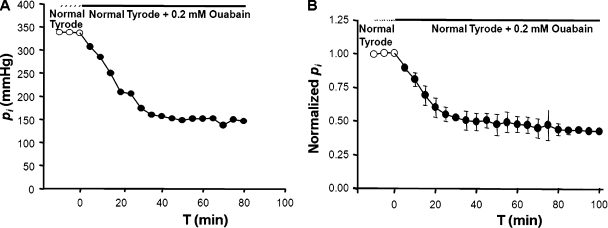
Parmelee (1986) also used the vibrating probe to measure the effect of Na/K ATPase inhibition on the circulating currents. She blocked pump activity with a saturating concentration of ouabain. She found that ouabain caused the outward equatorial current to fall to 50% of its original value in a period of ∼15 min. The initial wash-in of the extracellular ouabain and inhibition of the Na/K ATPase activity should occur in less than 5 min because the pumps are in surface epithelial cells. This should reduce the lens circulation by approximately one third because outward current would go from 3 Na⁺ to 2 K⁺ when the ATPase activity was blocked (Fig. 1 B). In WT lenses there is a radial gradient in Na⁺ concentration, with [Na⁺]_i going from ∼17 mM at the lens center to 5 mM at the surface (Wang et al., 2009). Model calculations suggest that there is a similar but opposite gradient in [K⁺]_i (Mathias, 1985). When Na/K ATPase activity ceases, both gradients will dissipate as Na⁺ accumulates in surface cells and K⁺ is depleted, further reducing the outward K⁺ current. These events probably account for the time course and amplitude of ouabain-induced inhibition of circulating current measured by Parmelee (1986).

Fig. 8 A shows the effect of a saturating concentration of ouabain on the central hydrostatic pressure in a typical lens. Fig. 8 B shows the averaged normalized central pressure from six lenses after immersion in normal Tyrode’s solution containing a saturating concentration of ouabain. The pressure declined to 50% of its initial value in a period of ∼30 min. Thus, as expected, the effect of ouabain is more rapid but not as complete as that of high K⁺/low Na⁺ solution. We assume that solute circulation declined to 50% normal in the first 15 min (Parmelee, 1986), and then it required another 15 min for sufficient water to be transported out of the lens for the central pressure to drop to 50% normal. Once the intracellular concentration gradient for Na⁺ has been dissipated, there will be slow accumulation of global Na⁺ as it enters fiber cells but is not transported out of the epithelial cells. Similarly, K⁺ will deplete to maintain electroneutrality as it moves out of epithelial cells and is replaced by Na⁺ (see Fig. 1 B). As a result, the fiber cell transmembrane electrochemical gradient for Na⁺ slowly moves toward equilibrium (0 mV). We observed intracellular pressures for a total of 100 min. In the last 70 min, one can see the slow linear decline in pressure that probably reflects this slow equilibration.

Figure 8.

The effect of Na/K ATPase inhibition with a saturating concentration of ouabain on central intracellular pressure in WT lenses. (A) Typical data from one lens showing the time course of the reduction in central hydrostatic pressure after blockade of the Na/K ATPase. After ∼30 min in ouabain, pressure near the center of the lens dropped to about half its original value. (B) The average time course of reduction in hydrostatic pressure in six lenses from six mice. The time course represents several events with different time scales, as described in Results.

Figs. 7 and 8 show that the pressure gradient changes in direct proportion to changes in the circulating currents. There is a plethora of data (Mathias et al., 2007) supporting the hypothesis that the circulating current is primarily carried by Na⁺; hence, these figures are consistent with our hypothesis: “Lens water flow is generated by and follows the circulation of sodium.”

DISCUSSION

The experiments described here were designed to test three hypotheses: fluid circulates through the lens; the intracellular leg of fluid circulation is through gap junction channels and is driven by hydrostatic pressure; and the fluid flow is generated by membrane transport of sodium. The data are obviously consistent with these hypotheses, but that does not necessarily mean our hypotheses are unique. An alternative explanation of our data is that water is in equilibrium; hydrostatic pressures are balanced by osmotic pressures, and there is no water movement. As described in the next section, this model can explain the data provided in this paper, but it becomes less plausible when other data are considered.

Equilibrium model

Assume there is no water flow, but there is a net flux of intracellular solute, flowing from the lens center to surface, and an equal but opposite flux of extracellular solute, flowing from the lens surface to center. There will be concentration gradients to drive these fluxes. The overall concentrations of solute have not been measured, but based on what we know about the lens, we can make reasonable estimates. The effective extracellular diffusion coefficient is significantly smaller than that for the intracellular compartment; therefore, we expect extracellular concentration gradients to be larger than those in the intracellular compartment. In a shell of fiber cells at radial distance r cm from the lens center (about halfway between the lens surface and center), we estimate the intracellular solute concentration c_i(r) = 302 mM, and the extracellular solute concentration c_e(r) = 292 mM, where the concentration in the bath c_o = 300 mM. The hypothesized osmotic gradient across the membranes of fiber cells in this shell is 10 mM, so if there were an intracellular pressure p_i(r) = 200 mmHg, then water is in equilibrium, p_i(r) = RT(c_i(r) − c_e(r)), and there would be no transmembrane water movement. Note that hydrostatic pressure in the extracellular spaces has to be zero because these are simple aqueous channels, and hydrostatic pressure would cause water to flow, contrary to our initial postulate. This value of p_i(r) is consistent with our data on hydrostatic pressure.

For the adjacent layer of fiber cells at a distance r+Δr cm from the lens center, solute concentrations will be slightly smaller and closer to c_o. In the previous paragraph, we assumed the extracellular diffusion gradient was four times greater than the intracellular gradient, so to be consistent, we assume here that the change in extracellular concentration will be four times greater than that in intracellular concentration. Thus, we assume c_i(r+Δr) = 301.99 mM and c_e(r+Δr) = 292.04 mM, so the transjunctional difference in solute concentration Δc_i = 0.01 mM, and the transmembrane osmotic gradient is 9.95 mM. Transmembrane equilibrium for water implies p_i(r+Δr) = 199 mmHg. Based on the data reported here, on average, intracellular hydrostatic pressure drops by ∼1 mmHg across a layer of lens gap junction channels; thus, all of these values are consistent with our pressure measurements.

There is no driving force for transmembrane water flow in either cell layer, the pressures are about what were reported here, and the assumed osmotic gradients are reasonable based on transport data, so the initial assumption of no water flow seems feasible. Moreover, osmotic gradients would be expected to decrease with decreased Na⁺ transport; hence, pressure gradients in this model would also be expected to decrease, as shown by our data. Lastly, diffusion gradients are expected to vary reciprocally with gap junction coupling; therefore, pressure gradients in this model would also be expected to vary reciprocally with the number of gap junction channels, as shown by our data. However, there is a pressure drop of 1 mmHg across the gap junction channels connecting these two layers of fiber cells. If water is in the channels (L_j ≠ 0), water will move, thus violating our initial assumption.

Inconsistencies of the equilibrium model

Studies of invertebrate gap junction channels formed from innexins showed that they contain both salt and water (Brink, 1983; Verselis and Brink, 1986; Bennett and Verselis, 1992). Similar studies of gap junction channels formed from connexins have not been done; however, all small hydrophilic solutes studied permeate the channels (Harris, 2007), and H₂O is a very small and very hydrophilic molecule. Moreover, there is no suggestion in the literature that water cannot enter the channels. Lastly, as described in the Introduction, water flow has been measured in lenses, so water does not appear to be in equilibrium. We therefore favor the dynamic model, which fits with many other observations on lens transport (Donaldson et al., 2010) and is consistent with the data presented in this paper.

Water flow through gap junction channels

Based on the dynamic model, local osmosis resulting from membrane Na⁺ flux causes water to move from the extracellular spaces within the lens to enter the intracellular compartment. When it enters the intracellular compartment, it creates a hydrostatic pressure that drives intracellular water flow from the lens center to surface. The center to surface pressure difference varied inversely with the number of fiber cell gap junction channels, consistent with the idea that gap junctions mediate the water flow. The pressure difference varied directly with the circulation of Na⁺, consistent with the idea that water flow is generated by local osmosis and follows the lens circulation of Na⁺. The hypotheses we set out to test at the outset are, therefore, consistent with the results presented here. These hypotheses are not new (Mathias, 1985), and they have been tested in a variety of experiments (Donaldson et al., 2010). Although there seems to be general agreement on the circulation of Na⁺, the circulation of fluid is not universally accepted (Beebe and Truscott, 2010). However, the hydrostatic pressure gradients, and our ability to predictably modulate them, are consistent with experimentally measured fluid flow (Candia and Alvarez, 2006).

New questions

The experimentally determined values of Λ/K were generally about fivefold larger than predicted for Λ in the Theory section (see Eq. 4 and Table I). The most direct interpretation is that K ≈ 0.2, or fiber cell transmembrane water flow is just 20% of its maximum isotonic limit. However, this conclusion presumes that the value of Λ and the pressure–water flow relationship derived in the Theory section are accurate. Pressure-driven water flow through gap junction channels is a relatively new idea and has not been subjected to experimental evaluation, other than the data presented here. We could think of three questions, whose answers might alter our expectation for the effective intracellular hydraulic conductivity and thus the lens pressure gradient.

(1) What is the optimal geometry of a channel that carries fluid?

The predicted single-channel hydraulic conductivity (see Eq. 1) is based on laminar flow through a right circular cylinder. We considered the possibility that pore geometry might significantly affect hydraulic conductivity. The pore length of 14–16 nm is well supported by diffraction studies of the channel structure for several connexins (Unger et al., 1997; Maeda et al., 2009), but the internal geometry of the pore is not generally known. Maeda et al. (2009), with a resolution of 3.5 Å, described the pore of Cx26 channels as a series of concatenated cylinders and funnel-like domains, but similar data are not available for channels made from Cx46. However, an experimentally well-defined parameter for Cx46 is the single-channel electrical conductance. A cylindrical aqueous pore of the dimensions assumed here should have a single-channel conductance of ∼150 pS, which is in accord with electrical experiments on Cx46 channels (Hopperstad et al., 2000). When we considered pores formed from concatenated cylinders and funnel domains, the geometric changes were constrained to give the same single-channel conductance. With this constraint, a right circular cylinder always gave the highest value of hydraulic conductivity (i.e., the lowest pressure per unit of flow). However, it is possible, or perhaps likely, that the single-channel conductance is not significantly affected by pore geometry (Veenstra et al., 1995; Veenstra, 1996). For example, the conductance could be primarily determined by charged binding sites, so a relatively wide channel with a very short charged constriction, which sets single-channel conductance, size cutoff diameter for solutes, and selectivity for second messengers, could have a much larger hydraulic conductivity than we have estimated. To test this kind of speculation, the single-channel hydraulic conductivity needs to be experimentally measured and contrasted with high resolution structural data for gap junction channels formed from lens connexins.

(2) Does the plasma membrane contribute to cell-to-cell movement of water?

The plasma membrane represents a parallel path to gap junctions. However, if it was a dominant parallel path, the measured pressures should not have varied with the number of gap junction channels. Moreover, we can make an upper limit estimate of the cell-to-cell membrane hydraulic conductivity based on experimental measurements of fiber cell membrane water permeability, which is <80 µm/s (Varadaraj et al., 2005), the value determined in high intracellular calcium. If we ignore the thin layer of extracellular solution between the broad surfaces of adjacent fiber cells, the cell-to-cell water permeability of two fiber cell membranes in series is 40 µm/s. Transforming this number into the effective hydraulic conductivity gives a value of 0.0002 (µm²/s)/mmHg, or about an order of magnitude smaller than the predicted values of Λ (Eq. 4). Thus, the most likely answer to this question is “no.”

(3) Does electro-osmosis drive water through lens gap junction channels?

Electro-osmosis is the movement of fluid in the presence of a voltage gradient. The circulation of Na⁺ in the normal mouse lens requires about a −10-mV intracellular gradient between the center and surface, with the central voltage being about −60 mV and the surface voltage about −70 mV (Gong et al., 1998). Given that there are ∼330 layers of cells, gap junction plaques connecting adjacent layers of cells experience an average voltage drop of about −30 µV. If the interior wall of each gap junction channel bears a fixed negative charge, there will be an excess of mobile positive ions within each channel. The −30-µV voltage drop (an electric field of −2.1 V/cm) exerts a force on the mobile positive charges causing them to move and, through viscous drag, move fluid with them. This form of electro-kinetic phenomenon has been known for many years (Overbeek and Wiersema, 1967), and a theoretical description can be found in most textbooks in this area.

Based on model calculations, McLaughlin and Mathias (1985) concluded that electro-osmosis could drive significant water flow along lateral intercellular spaces of fluid-transporting epithelia. However, the effect of electro-osmosis was not to generate water flow but to reduce the hydrostatic pressure needed to drive lateral water flow, which was generated through osmosis at the plasma membrane. Thus, lens gap junction channels bearing a net negative charge might require less hydrostatic pressure to drive the intracellular fluid flow u_i, and a model that neglected electro-osmosis would predict a higher transjunctional pressure drop than was needed to drive the flow. The problems are: (a) we do not know the amount of fixed charge on the internal wall of any lens gap junction channel; and (b) theoretical treatments assume that the charges are randomly placed and can be considered to be uniformly smeared over the wall, whereas in a protein that always expresses the same sequence and folds in the same way, the charges are deterministically placed in certain domains (Maeda et al., 2009). This lack of both experimental knowledge and an appropriate theoretical framework makes it difficult to conclusively answer this question at this time.

The above questions relate to possible physical reasons that could have caused us to overestimate the effective intracellular hydraulic conductivity in the lens and thus underestimate fluid flow (i.e., underestimate K). More direct experiments on the pressure–flow relationship for lens gap junction channels are needed to resolve these issues.

Implications for other stratified epithelia

Our data suggest that lens fiber cell gap junction channels carry cell-to-cell water flow, which is driven by hydrostatic pressure, so other fluid transporting stratified epithelia may use the same mechanism. Thus, the lens has provided the first direct data on a hypothesis that has been discussed for many years, but one which has never before been directly tested.

In the lens, fiber cell gap junction channels are formed from Cx46 and Cx50, but in the ciliary body, the channels connecting the pigmented and nonpigmented layers are formed from Cx40 and Cx43. Connexins are a diverse family of proteins, and some of that diversity may make channels formed from certain connexins better water channels. An interesting area of investigation will be to compare the water permeability of channels formed from different connexins. Thus, the answer to one old question has opened up a plethora of new questions.