Mutant cycles at CFTR’s non-canonical ATP-binding site support little interface separation during gating

Abstract

Cystic fibrosis transmembrane conductance regulator (CFTR) is a chloride channel belonging to the adenosine triphosphate (ATP)-binding cassette (ABC) superfamily. ABC proteins share a common molecular mechanism that couples ATP binding and hydrolysis at two nucleotide-binding domains (NBDs) to diverse functions. This involves formation of NBD dimers, with ATP bound at two composite interfacial sites. In CFTR, intramolecular NBD dimerization is coupled to channel opening. Channel closing is triggered by hydrolysis of the ATP molecule bound at composite site 2. Site 1, which is non-canonical, binds nucleotide tightly but is not hydrolytic. Recently, based on kinetic arguments, it was suggested that this site remains closed for several gating cycles. To investigate movements at site 1 by an independent technique, we studied changes in thermodynamic coupling between pairs of residues on opposite sides of this site. The chosen targets are likely to interact based on both phylogenetic analysis and closeness on structural models. First, we mutated T460 in NBD1 and L1353 in NBD2 (the corresponding site-2 residues become energetically coupled as channels open). Mutation T460S accelerated closure in hydrolytic conditions and in the nonhydrolytic K1250R background; mutation L1353M did not affect these rates. Analysis of the double mutant showed additive effects of mutations, suggesting that energetic coupling between the two residues remains unchanged during the gating cycle. We next investigated pairs 460–1348 and 460–1375. Although both mutations H1348A and H1375A produced dramatic changes in hydrolytic and nonhydrolytic channel closing rates, in the corresponding double mutants these changes proved mostly additive with those caused by mutation T460S, suggesting little change in energetic coupling between either positions 460–1348 or positions 460–1375 during gating. These results provide independent support for a gating model in which ATP-bound composite site 1 remains closed throughout the gating cycle.

INTRODUCTION

CFTR, whose failure causes cystic fibrosis (Riordan et al., 1989), belongs to the ATP-binding cassette (ABC) transporter superfamily. Although most ABC transporters use the energy derived from ATP binding and hydrolysis for active transport across membranes, in CFTR, the binding and hydrolysis of ATP drive channel gating (Muallem and Vergani, 2009). Like other ABC transporters, CFTR consists of two homologous halves, each containing a cytosolic ABC, otherwise known as a nucleotide-binding domain (NBD) and a transmembrane-spanning domain (Locher, 2009). NBDs are highly conserved among all ABC proteins, containing several conserved motifs, including the Walker A and B motifs (Walker et al., 1982) in a RecA-like subdomain (“head”) and the signature sequence (LSGGQXXR) in a helical subdomain (“tail”; e.g., Hung et al., 1998; Karpowich et al., 2001). High resolution crystal structures of ABC transporters and isolated NBD dimers reveal that in ATP-bound crystals, NBDs can form tight “head-to-tail” dimers (e.g., Hopfner et al., 2000; Smith et al., 2002; Chen et al., 2003; Zaitseva et al., 2005), with two ATP molecules sandwiched at the interface in composite binding sites, each comprising the Walker A and B motifs from the head of one NBD and the signature sequence from the tail of the other.

CFTR belongs to a subgroup of “asymmetric” ABC transporters in which the functional unit comprises two divergent NBDs (27% identity between NBD1 and NBD2 of human CFTR). In the asymmetric ABC proteins, only one of the interfacial sites presents conserved consensus residues in all the motifs involved in ATP binding and hydrolysis. In contrast, on both faces of the other site there are nonconservative substitutions at key residues (Basso et al., 2003). Biochemical evidence suggests reduced (or absent) catalytic activity in the non-canonical site of CFTR (Aleksandrov et al., 2002; Basso et al., 2003; Cui et al., 2006) and other asymmetric ABC proteins (Gao et al., 2000; Hou et al., 2000; Matsuo et al., 2000; Procko et al., 2006). Here, we refer to the non-canonical composite site formed by the head of the N-terminal NBD1 and the tail of the C-terminal NBD2 as site 1, and the conserved composite site formed by the head of NBD2 and the tail of NBD1 as site 2.

In CFTR, channel opening is thought to be driven by ATP binding (Gunderson and Kopito, 1994; Venglarik et al., 1994; Winter et al., 1994) and subsequent formation of the intramolecular NBD dimer (Vergani et al., 2005). Because in biochemical experiments ATP stays bound at site 1 for periods that are much longer than a channel gating cycle (Basso et al., 2003), the binding of ATP to site 2 is thought to be the trigger for channel opening. Hydrolysis at site 2 is thought to be the rate-limiting step in channel closure, as inhibiting hydrolysis at site 2 causes prolonged open-channel bursts (Gunderson and Kopito, 1994, 1995; Hwang et al., 1994; Zeltwanger et al., 1999; Vergani et al., 2003, 2005). Thus, ATP binding and hydrolysis at site 2 are clearly critical for channel gating.

On the other hand, the role of site 1 is less clear. Mutations around site 1 have varying effects on channel function. Introducing a bulky phenylalanine side chain in the Walker A motif of NBD1 strongly slowed channel opening, likely by interfering with ATP binding at site 1 (Berger et al., 2005). A mutation in the conserved Walker A lysine of NBD1, K464A, reduced channel opening rate at low [ATP] (Vergani et al., 2003), suggesting that ATP binding at site 1 can be made rate limiting for channel opening. However, this remains controversial. In other studies, neither the K464A mutation (Powe et al., 2002) nor mutation of an aromatic residue (W401), which is seen to stack against the adenine moiety of ATP in some crystals of CFTR NBD1 (Lewis et al., 2005, but cf. Lewis et al., 2004; Thibodeau et al., 2005), affected the [ATP] dependence of opening rate (Zhou et al., 2006). Several mutations around site 1 reduced the duration of prolonged bursts obtained by inhibiting hydrolysis at NBD2 (Powe et al., 2002; Vergani et al., 2003; Bompadre et al., 2005; Zhou et al., 2006), leading to the suggestion that the precise conformation around site 1 affects the stability of the NBD dimer (Zhou et al., 2006). In a recent study (Tsai et al., 2010) using a ligand exchange protocol, the effects on CFTR opening and closing rate of the high affinity ATP analogue N⁶-(2-phenylethyl)-ATP could be separately ascribed to the N⁶-(2-phenylethyl)-ATP molecule bound at site 2 and site 1, respectively. The delayed onset of the site-1 effect provided a measure for the rate of exchange of nucleotide bound at site 1, suggesting a mean residence time of 30–50 s for ATP in site 1 of wild-type (WT) CFTR during normal gating (which is characterized by a cycle time of ∼1 s). Further, it was shown that nucleotide exchange at site 1 takes place only in closed channels. Finally, because mutations at either side of site 1 dramatically shortened the residence time of ATP bound here, it was suggested that the NBD dimer interface remains formed around composite site 1 throughout several gating cycles.

To validate a mechanistic model in which only small conformational changes occur around site 1 during a normal gating cycle, we used an independent approach, applying mutant cycle analysis (Serrano et al., 1990; Fersht, 1999). We identified three positions located on the NBD2 side of site 1, each close enough on homology structural models to contact T460 in NBD1, a structurally conserved Walker A residue interacting directly with the γ phosphate of bound ATP. In addition, statistical analysis of amino acid distributions in multiple sequence alignments yielded high correlation scores when pairing each of the NBD2 positions with T460, suggesting coevolution and functional interaction. We found that, although individual mutations on both sides of site 1 could produce clear-cut functional phenotypes, for none of the three pairs did energetic coupling between the two target positions change during gating. This is consistent with the hypothesis that the protein structure around site 1 does not undergo large conformational changes during CFTR’s gating cycle.

MATERIALS AND METHODS

Molecular biology

pGEMHE-WT (Chan et al., 2000), carrying the coding sequence of human WT CFTR, was used as a template for mutants T460S, L1353M, H1348A, H1375A, T460S/L1353M, T460S/H1348A, and T460S/H1375A. pGEMHE-K1250R (Vergani et al., 2005) was used as a template for the corresponding nonhydrolytic mutants. Mutations were introduced using the QuikChange mutagenesis protocol (Agilent Technologies). For each construct, the entire CFTR coding sequence was verified by automated sequencing.

Xenopus laevis oocyte expression

Xenopus females were killed by non-recovery anesthesia in accordance with the Animals (Scientific Procedures) Act of 1986. Oocytes were extracted and collagenase-treated in OR2, which contained (in mM) 82 NaCl, 2 KCl, 1 MgCl₂, and 5 HEPES, pH 7.5 with NaOH, and prepared as described previously (Chan et al., 2000). 0.1–10 ng of WT or mutant CFTR cRNA was injected per oocyte to give expression levels appropriate for single-channel or macroscopic recordings. Postinjection oocytes were incubated at 17°C for 1–5 d in OR2 with the addition of 1.8 mM CaCl₂ and 50 µg/ml gentamycin.

Electrophysiology

Patch clamp recording in the excised inside-out configuration was performed using an Axopatch 200B amplifier (Molecular Devices) with 3–10-MΩ resistance, fire-polished borosilicate glass pipettes. All experiments were performed at room temperature (23–25°C). Pipette solution contained (in mM): 136 NMDG-Cl, 2 MgCl₂, and 5 HEPES, pH 7.4 with NMDG. Oocytes were kept in bath solution, which contained (in mM): 134 NMDG-Cl, 2 MgCl₂, 5 HEPES, and 0.5 EGTA, pH 7.1 with NMDG. Bath solution was applied to the cytoplasmic side of excised patches. 2 mM MgATP (Sigma-Aldrich) was added from 200–400 mM of aqueous stock solution (pH 7.1 with NMDG). 2 mM Na₂H₂P₂O₇ (pyrophosphate; Sigma-Aldrich) was added from a 200-mM stock solution (pH 7.1 with NMDG) and supplemented with 2 mM MgCl₂. Three alternative sources of the catalytic subunit of cAMP-dependent protein kinase (PKA), extracted from bovine heart, were used to pre-phosphorylate CFTR: (1) 300 nM PKA (provided by A. Nairn, Yale University, New Haven, CT); (2) 130 U/ml PKA (Promega); and (3) ∼130 U/ml PKA (Sigma-Aldrich). The amounts listed above all gave similar saturating levels of CFTR activity. Recordings were made after PKA removal by applying ATP in the absence of PKA. Most recordings were performed within 5 min of PKA removal. We did not observe significant rundown within this period.

Unitary inward currents were recorded at a membrane potential of −80 mV (pipette potential, +80 mV). Macroscopic currents were recorded at a membrane potential of −20 to −80 mV (CFTR gating is largely voltage independent; Cai et al., 2003). Current data were digitized at 1 or 5 kHz.

Kinetic analysis of multichannel patches

Multichannel records from patches containing 1–10 channels, in which individual channel-gating events could clearly be identified, were analyzed to obtain mean burst durations using a custom written set of programs (Csanády, 2000). Current traces were Gaussian filtered offline at 50 Hz (pCLAMP 10.2; Molecular Devices), baseline corrected, and idealized. Channel gating was described with a simple C↔O↔C_F model, where C is the long-lived closed state, O is the open state, and C_F is a closed state that accounts for short flickery closures. The corresponding rate constants (r_CO, r_OC, r_OF, and r_FO) were estimated by a simultaneous maximum likelihood fit to the dwell-time histograms for all conductance levels, with a correction for a fixed dead time of 4.5 ms. Burst duration was calculated as τ_b = (1/r_OC)(1 + r_OF/r_FO). The parameter r_CO, and consequently the estimates of interburst duration (τ_ib = 1/r_CO) and open probability (P_o), is sensitive to correct estimation of the number of channels in the patch. Because this is frequently not possible, in particular with patches containing more than one channel, we estimated P_o from steady-state noise analysis (see below), and then recalculated τ_ib using the relationship τ_ib ≈ τ_b(1−P_o)/P_o. “Opening rate” and “closing rate” are defined here as the inverses of the mean interburst and burst durations, respectively.

Fitting of macroscopic current relaxations

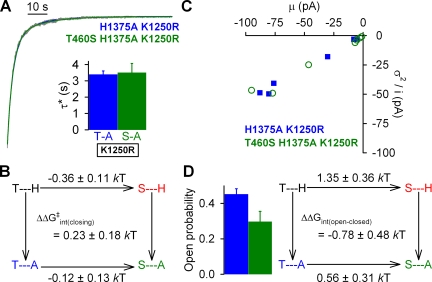
Macroscopic current decay time courses were fit with single- or bi-exponential equations (pCLAMP 10.2; Molecular Devices). Fitting the relaxation time course after ATP removal for the nonhydrolytic H1375A/K1250R and T460S/H1375A/K1250R constructs consistently required a double exponential with two slow time constants (each in the seconds range), suggesting two populations of open-channel bursts (see Fig. 9 A). For these two constructs, average steady-state burst duration (τ*) was estimated from the two fitted time constants (τ₁ and τ₂) and their fractional amplitudes (A₁ and A₂) as τ* = (A₁+A₂)τ₁τ₂/(A₁τ₂+A₂τ₁), and average closing rate for the mutant cycle in Fig. 9 B was defined as 1/τ*.

Figure 9.

Effects of mutations at positions 460 and 1375 on nonhydrolytic gating in the K1250R background. (A) Representative normalized decay time courses of macroscopic currents for H1375A/K1250R and T460S/H1375A/K1250R CFTR after the removal of 2 mM ATP. Solid blue and green lines are fitted bi-exponentials. Fitted parameters were τ₁ = 2.8 s, τ₂ = 11 s, A₁ = 0.77, and A₂ = 0.23 for the H1375A/K1250R trace, and τ₁ = 2.8 s, τ₂ = 15 s, A₁ = 0.82, and A₂ = 0.18 for the T460S/H1375A/K1250R trace. Average steady-state burst durations (τ*; inset) were estimated from the two fitted time constants (τ₁ and τ₂) and their fractional amplitudes (A₁ and A₂) as τ* = (A₁+A₂)τ₁τ₂/(A₁τ₂+A₂τ₁). (B) Thermodynamic mutant cycle for target pair T460-H1375 built on average nonhydrolytic closing rates (1/τ*). The top two corners of the mutant cycle were taken from Fig. 5 B. (C) Noise analysis for estimation of P_o for H1375A (blue symbols) and T460S/H1375A (green symbols); each symbol represents one patch. (D; left) Mean ± SEM P_o for H1375A (blue bar) and T460S/H1375A (green bar). (Right) Thermodynamic mutant cycle for target pair T460-H1375 built on K_eq = P_o/(1−P_o) values under nonhydrolytic conditions. The top two corners of the mutant cycle were taken from Fig. 5 D.

Noise analysis

Steady-state noise analysis was performed as described previously (Szollosi et al., 2010), by exploiting the relationship between the variance (σ²) and the mean (μ) of a steady macroscopic current. Estimates for σ² and μ were obtained directly from current records using pCLAMP 10.2 (Molecular Devices) and corrected for background noise using segments of records in which all channels were closed. A graph of σ²/i (i; unitary current amplitude) as a function of μ produces a straight line, with slope (1−P_o) (Gray, 1994). However, to give equal weight to each record, we calculated P_o separately for each recording, reporting here mean ± SEM, rather than use linear regression analysis to estimate the slope.

Mutant cycle analysis

Mutant cycle analysis (Serrano et al., 1990; Fersht, 1999) was used to give a measure of the energetic coupling between residues (ΔΔG_int) at various stages of the gating cycle, as described previously (Vergani et al., 2005; Szollosi et al., 2010). In brief, mutation-induced changes in activation free energy barriers (ΔΔG^‡) for opening and closing were calculated from the changes in opening and closing rates, respectively. Mutation-induced changes in free energy differences between the open and closed state (ΔΔG_open-closed) for each nonhydrolytic construct could be calculated from the equilibrium constant estimate P_o/(1−P_o). Mutation-induced changes in free energy differences between ATP-bound and ATP-free (at site-2) closed states were calculated based on the equilibrium constant estimate K_rCO (see Results). ΔΔG_int was defined as the difference between ΔΔG values along parallel sides of the mutant cycle. All ΔGs are given as mean ± SEM. Because the numbers of observations, N, for each corner of the cycle are similar, SEMs were calculated using the mean value for N.

Statistics

Data are described as mean ± SEM. To compare data, unpaired Student’s t tests were performed; differences are reported as significant for P < 0.05.

Online supplemental material

Supplemental text and Table S1 detail the results of statistical coupling analysis relevant to the positions targeted in this paper. Table S2 gives pairs of correlated positions within the NBDs identified by CorrMut, showing distances between the α carbons for each pair, measured on a crystal structure. “AsymmetricABC.txt” is an alignment including full-length sequences (trimmed at the N and C termini) of 182 asymmetric ABC proteins, human CFTR’s closest relatives. Fig. S1 shows amino acid frequency distributions at the positions studied in this paper, in symmetric and asymmetric transporters. Fig. S2 illustrates experiments to assay the rate of unlocking from the pyrophosphate-induced locked-open state for WT, T460S, L1353M, and T460S/L1353M channels. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201110608/DC1.

RESULTS

Selection of three pairs of positions on opposite sides of composite site 1

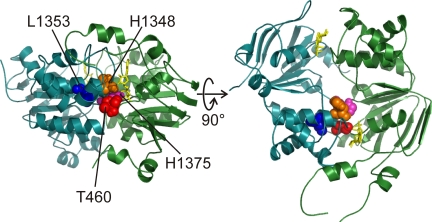
Two positions, T460 in NBD1 (in Walker A sequence; Fig. 1, red) and L1353 in NBD2 (just downstream of the signature sequence; Fig. 1, blue), were identified by phylogenetic statistical coupling analysis (Lockless and Ranganathan, 1999), using sequence alignments of thousands of NBD sequences, which suggested that the two (the equivalent T460 and L1353 in site 1, and T1246 and R555 in site 2 of CFTR) had been conserved as a pair during evolution (Vergani et al., 2005). In homology models of the CFTR NBD1/NBD2 heterodimer (Mense et al., 2006; Mornon et al., 2008; Serohijos et al., 2008), the two α carbons are separated by <10 Å (Fig. 1). Indeed, energetic coupling between R555 and T1246 in site 2 was shown to be state dependent (Vergani et al., 2005). Unlike R555 and T1246, T460 and L1353 in site 1 cannot form a hydrogen bond, consistent with a distinct fine structure and functional role of the degenerate site. However, within an alignment of 182 full-length sequences of “asymmetric” transporters in which sequence abnormalities suggest a functionally degenerate site 1 (including most sequences of the organic anion conjugates, anions, and drugs group of the ABCISSE database; see Dassa and Bouige, 2001, and supplemental AsymmetricABCs.txt), the residues at these positions are well conserved (>94% of sequences have a Valine-Leucine or a Threonine-Leucine pair). It is therefore likely that some interaction between them is maintained.

Figure 1.

Spatial arrangement of target residues on opposite sides of CFTR’s composite site 1 in homology models. In a homology model of CFTR’s NBD dimer (Mornon et al., 2008), T460 (red) in the Walker A motif of NBD1 is close to NBD2 residues H1348 (gold; in the signature sequence), L1353 (blue; at the end of the signature sequence), and H1375 (magenta; in the D-loop).

Statistical coupling analysis also identified position H1348 (in NBD2 signature sequence; Fig. 1, gold) and H1375 (in NBD2 D-loop; Zaitseva et al., 2005; Fig. 1, magenta) as possibly coevolving with position T460, although the statistical coupling was somewhat lower (see supplemental text). However, because statistical coupling analysis assumes independence of all sequences in the multiple sequence alignment—an unrealistic assumption given the branched nature of phylogenetic trees—it can yield false positive correlations. To address this problem, the CorrMut algorithm reconstructs the phylogenetic tree and only considers substitutions that arise on the same branches. Further statistical robustness is gained by a bootstrapping analysis, which provides confidence intervals for the correlation values (Fleishman et al., 2004). We therefore ran CorrMut to identify coevolving positions on opposite sides of composite site 1, using as an input the alignment of asymmetric transporters, particularly suited for the analysis of non-canonical site 1. This algorithm also highlighted position H1375 as highly correlated with position T460. The 460–1375 pairwise correlation is the highest correlation at the NBD1/NBD2 interface (Pearson’s correlation coefficient, r = 0.43, and a 95% confidence interval spanning 0.16 < r < 0.67). Importantly, in homology models (Mense et al., 2006; Mornon et al., 2008; Serohijos et al., 2008; Fig. 1) the 460–1348 and 460–1375 α-carbon distances are both <8.4 Å.

The positions studied here are all within motifs (Walker A for T460, and signature or D-loop for the NBD2 sites) well conserved among all NBDs. However, at the specific target sites, amino acid distributions within the alignment of asymmetric transporters are quite distinct from those in the alignment of thousands of NBDs (Fig. S1), possibly reflecting non-canonical NBD–NBD interactions, typical for the asymmetric subgroup.

Thus, based on coevolution and spatial proximity in homology models, the three pairs, 460–1353, 460–1348, and 460–1375, are likely to interact. We therefore studied possible relative movements between these three residue pairs during channel gating by building thermodynamic mutant cycles.

Effects of mutations at positions 460 and 1353 on ATP-dependent (hydrolytic) gating

We first tested changes in energetic coupling between positions 460 and 1353 by perturbing these positions using mutations T460S and L1353M. WT and mutant CFTR channels in excised inside-out patches were activated by phosphorylation with PKA and 2 mM ATP. Once steady state was reached, the PKA was washed off, and all subsequent measurements were made by applying ATP in the absence of PKA.

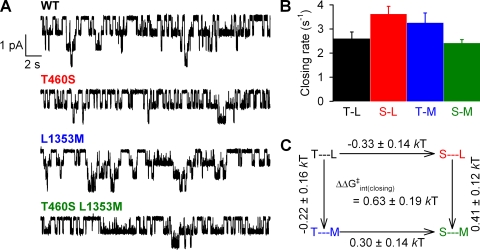
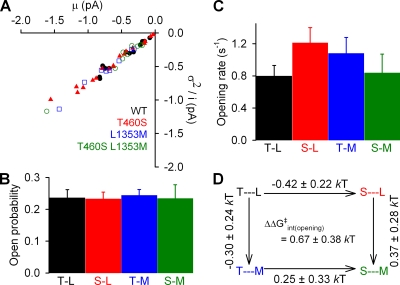
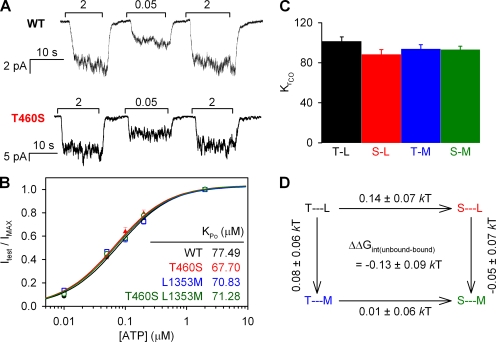
To determine if the mutations T460S and L1353M, individually or together, had any effect on channel gating in saturating 2 mM ATP, burst durations were determined from patches containing 1–10 channels (Fig. 2 A). There was a small increase in closing rate (defined as inverse of the mean burst duration; Fig. 2 B) for T460S (3.6 ± 0.3 s⁻¹; n = 20; Fig. 2 B, red bar) and L1353M (3.3 ± 0.4 s⁻¹; n = 8; Fig. 2 B, blue bar) compared with WT (2.6 ± 0.3 s⁻¹; n = 13; Fig. 2 B, black bar), whereas there was no significant change for T460S/L1353M (n = 9; Fig. 2 B, green bar). Accordingly, a thermodynamic mutant cycle built on closing rates (Fig. 2 C) yielded an interaction free energy (ΔΔG_int(closing)), which was significantly different from zero (P = 0.007) but rather small (0.63 ± 0.19 kT). To obtain correct estimates of opening rates, we first determined P_o using noise analysis (Fig. 3 A; see Materials and methods). There was no significant difference between P_o in WT and mutants (Fig. 3 B), with values ranging between 0.23 and 0.25. Accordingly, the calculated (see Materials and methods) opening rates (Fig. 3 C) were slightly increased for the single mutants, but for this parameter the resulting mutant cycle (Fig. 3 D) yielded a ΔΔG_int not significantly different from zero (P = 0.1).

Figure 2.

Effect of mutations at positions 460 and 1353 on channel closing rates. (A) Representative traces of multichannel recordings of prephosphorylated WT and mutant CFTR channels, used to determine burst duration. Downward deflection indicates inward current. (B) Closing rates of WT and mutant CFTR channels, defined as the inverse of the mean burst duration (see Materials and methods). (C) Thermodynamic mutant cycle for target pair T460-L1353 built on the closing rates from B; each corner is represented by the side chains at positions 460 and 1353, respectively. ΔΔG⁰ values (mean ± SEM) on arrows show mutation-induced changes in the stability of the transition state for closure with respect to the open ground state and were used to calculate (see Materials and methods) the coupling energy for the 460–1353 interaction (ΔΔG^‡_{int (closing)}).

Figure 3.

Effect of mutations at positions 460 and 1353 on channel opening rates. (A) The same records used for determining burst duration (see Fig. 2) were used for noise analysis. Each data point represents one recording. (B) Mean ± SEM of P_o values estimated for each patch from the corresponding data point in A (see Materials and methods). (C) Mean ± SEM of opening rates calculated for each patch using the estimate for P_o (see B) and the closing rate (see Fig. 2 B). (D) Thermodynamic mutant cycle for target pair T460-L1353 built on opening rates (from C); notation as in Fig. 2 C.

To test for possible effects on ATP binding, a dose–response for ATP (Fig. 4 B) was obtained by measuring relative current in macro-patches containing >40 channels. All exposures to test [ATP] were bracketed with periods of exposure to 2 mM (approximately saturating) ATP used for normalizing (Fig. 4 A). There was no significant difference in relative current at any [ATP] between WT and mutants. The apparent affinities, K_Po, determined from fitting the Michaelis-Menten equation to the dose–response of the normalized current were between 68 and 77 µM. For WT, the decrease in steady-state current at low [ATP] is a result of a reduced opening rate without any change in closing rate (Gunderson and Kopito, 1994; Venglarik et al., 1994; Winter et al., 1994). We confirmed this was also the case for T460S and L1353M using multichannel analysis on patches containing <10 channels (not depicted), which showed that when [ATP] was reduced from 2 mM to 50 µM, burst duration was not significantly affected, and the fractional P_o supported by 50 µM ATP (0.39 ± 0.07 and n = 6 for T460S, and 0.51 ± 0.08 and n = 5 for L1353M) could be accounted for by the fractional opening rate observed under the same conditions (0.39 ± 0.06 and n = 6 for T460S, and 0.46 ± 0.07 and n = 5 for L1353M). Thus, we could estimate for each construct the apparent affinity of ATP for affecting channel opening rate (K_rCO; Fig. 4 C) using the relationship K_rCO = K_Po/(1−P_o,max) (Csanády et al., 2000; P_o,max values were taken from Fig. 3 B). Because ATP binding to the NBD2 site is likely a rapid equilibrium process relative to the slow (∼1-s⁻¹) channel opening step (Zeltwanger et al., 1999), K_rCO approximates the K_d of ATP from the NBD2 head of closed channels and therefore reflects ΔG between closed states with or without ATP bound to NBD2 (compare Szollosi et al., 2010). However, because none of our mutations affected K_rCO (Fig. 4 C), a mutant cycle built on this parameter (Fig. 4 D) yielded a ΔΔG_int ≈ 0.

Figure 4.

Mutations at positions 460 and 1353 do not affect apparent affinity for ATP. (A) Representative traces showing macroscopic current response for WT and T460S to a test [ATP] of 50 µM, bracketed with applications of 2 mM ATP. Different [ATP] were tested several times within one recording. (B) [ATP] dose–response relationships for WT and mutant CFTR channels; currents in test [ATP] were normalized to the average of the currents observed in bracketing segments in the presence of 2 mM ATP. Solid lines show fits of the Michaelis-Menten equation; K_Po values are plotted in the panel. Between 5 and 14 measurements were made for each concentration tested. (C) Estimates of K_rCO for each construct, calculated (see Results) using K_Po from B and P_o;max from Fig. 3 B. (D) Thermodynamic mutant cycle for target pair T460-L1353 built on K_rCO values.

Thus, in contrast to mutations at R555 and T1246 in composite site 2 (Vergani et al., 2005), mutations at T460 and L1353 in composite site 1 exert only small effects on normal channel gating.

Effect of mutations at positions 460 and 1353 on nonhydrolytic gating

WT channels, under normal hydrolytic conditions, are thought to close only rarely through the much slower nonhydrolytic pathway, reversing the opening transition (Csanády et al., 2010). However, we might expect the nonhydrolytic closing rate to increase if stabilizing interactions at the dimer interface are disrupted. To determine if the mutations had any effect on nonhydrolytic closure, we looked at mutant channel gating behavior when hydrolytic closure was inhibited.

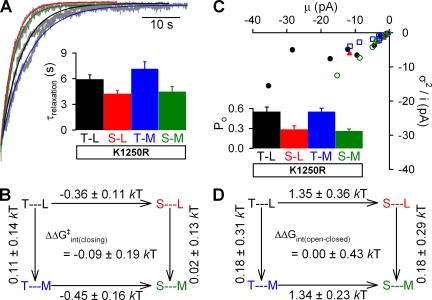
Hydrolysis can be inhibited by mutating key catalytic residues at composite site 2. In other ABC transporters, mutating the Walker A lysine to arginine greatly reduced or abolished hydrolysis (e.g., Urbatsch et al., 1998; Lerner-Marmarosh et al., 1999). In CFTR, the equivalent mutation, K1250R, caused an increase in open burst duration (Vergani et al., 2005; Csanády et al., 2006), consistent with blocking of the fast hydrolytic closure pathway. To determine if the mutations T460S, L1353M, and T460S/L1353M increased the rate of nonhydrolytic closure from an open state with ATP bound at both composite sites, we introduced the above site-1 mutations in a K1250R background. Closing rates were determined from the rates of macroscopic current decay upon ATP removal, which followed single-exponential time courses (Fig. 5 A; colored lines are fitted exponentials). The fitted time constant for current decay, τ_relaxation (Fig. 5 A, inset), provided an estimate for the average lifetime of the open state, which was 5.9 ± 0.5 s (n = 13) for K1250R (black bar) and unchanged in L1353M/K1250R (7.2 ± 0.8 s; n = 10; P = 0.11; blue bar), but significantly reduced in T460S/K1250R (4.2 ± 0.3 s; n = 13; P < 0.01; red bar). Because τ_relaxation was additively affected in T460S/L1353M/K1250R (4.5 ± 0.6 s; n = 10; P < 0.05; green bar), ΔΔG^‡_int(closing) was not significantly different from zero (Fig. 5 B), indicating that the coupling between the two residues on opposite sides of composite site 1 was not changed along the nonhydrolytic closure pathway between the ATP-bound open state and the transition state.

Figure 5.

The T460S mutation destabilizes the open state of CFTR in the nonhydrolytic K1250R background. (A) Representative normalized decay time courses of WT and mutant CFTR macroscopic currents after the removal of 2 mM ATP (gray). Solid colored lines are fitted exponentials; mean ± SEM relaxation time constants (τ_relaxation) are shown in the inset. (B) Thermodynamic mutant cycle for target pair T460-L1353 built on nonhydrolytic closing rates (1/τ_relaxation). (C) Noise analysis was performed on 2–3-min records from patches containing <100 channels. Each point represents one patch. P_o was calculated for each patch; mean ± SEM P_o values are shown in the inset. (D) Thermodynamic mutant cycle for target pair T460-L1353 built on K_eq = P_o/(1−P_o) values under nonhydrolytic conditions.

Inorganic pyrophosphate (PP_i) can cause prolonged burst durations when applied in the presence of ATP (Gunderson and Kopito, 1994; Carson et al., 1995; Tsai et al., 2009), likely by inhibiting hydrolytic closure (Scott-Ward et al., 2007; Tsai et al., 2009). Therefore, as an alternative means to study nonhydrolytic channel closing rates, we also determined the effect of mutations T460S, L1353M, and T460S/L1353M on the closing of channels locked open by ATP plus PP_i (Fig. S2). Although both single mutations drastically shortened the lifetime of the PP_i locked-open state, these effects were again additive in the double mutant, yielding a ΔΔG_int ≈ 0 for closure from the PP_i locked-open state.

When channels can close through the irreversible hydrolytic pathway, the observable gating process is not at thermodynamic equilibrium (Csanády et al., 2010). Therefore, P_o cannot be used to estimate the difference in free energy between the open and closed ground states (ΔG_open-closed), especially because ΔG_open-closed is not readily defined (Csanády et al., 2006). However, in constructs carrying the K1250R mutation, the hydrolytic pathway is effectively blocked, and the gating cycle, in saturating [ATP], is reduced to a simple equilibrium between the open and closed states. Thus, we can use P_o in the K1250R background to determine the free energy difference between the open and closed states for each of the constructs (ΔG_open-closed) and analyze the results using mutant cycle formalism. We measured P_o using noise analysis on current records containing <100 channels (Fig. 5 C). Consistent with changes in closing rate, P_o was significantly reduced for T460S/K1250R (0.28 ± 0.06; n = 6; P < 0.01; Fig. 5 C, red bar) and T460S/L1353M/K1250R (0.26 ± 0.03; n = 8; P < 0.01; green bar) compared with K1250R (0.55 ± 0.07; n = 9; black bar), but not for L1353M/K1250R (0.55 ± 0.05; n = 8; blue bar). Here too, the coupling energy, ΔΔG_{int(open-closed)}, was not significantly different from zero (Fig. 5 D), indicating that there was no change in energetic coupling between the two residues between the open and closed ground states, again in contrast to what is seen for site 2 (Vergani et al., 2005).

Energetic coupling between positions 460 and 1348 is little changed during gating

Following a similar methodology, we proceeded to study changes in coupling between positions 460 and 1348 during gating, using perturbations T460S and H1348A. In these mutant cycles, two of the corners (WT and single-mutant T460S) are identical to the corresponding corners of the respective T460-L1353 mutant cycle. To rigorously compare the effects of the H1348A mutation onto the T460S versus WT backgrounds, the gating parameters for the latter two constructs should have been repeatedly measured in experiments side by side with those conducted on H1348A and T460S/H1348A. However, because ΔΔG_int can be calculated using any two parallel sides of a mutant cycle, we did not repeat experiments for WT and T460S; instead, we calculated ΔΔG_int using the two horizontal sides of each cycle, i.e., by comparing the effects of the T460S mutation onto the H1348A versus WT backgrounds. For this reason, we refrain from providing absolute ΔG values for the vertical sides of the T460-H1348 mutant cycles (Figs. 6, B and D, and 7, B and D); and the same applies for the T460-H1375 mutant cycles (see below; Figs. 8, B and D, and 9, B and D).

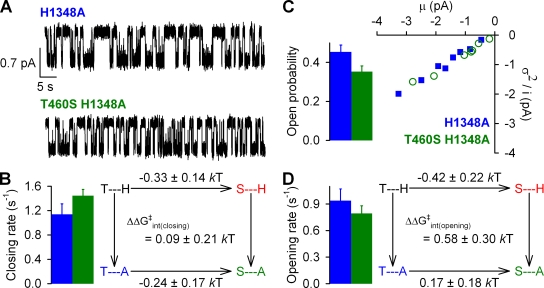
Figure 6.

Effects of mutations at positions 460 and 1348 on normal hydrolytic channel gating. (A) Representative single-channel current traces from prephosphorylated H1348A and T460S/H1348A CFTR channels gating in 2 mM ATP. Downward deflection indicates inward current. (B; left) Closing rates of H1348A (blue bar) and T460S/H1348A (green bar), defined as the inverse of the mean burst duration (see Materials and methods). (Right) Thermodynamic mutant cycle for target pair T460-H1348 built on closing rates. The top two corners of the mutant cycle (representing WT and T460S) were taken from Fig. 2 C. Because the bottom two corners (representing H1348A and T460S/H1348A) were evaluated in separate sets of experiments, the absolute ΔΔG values are not printed for the vertical sides of the cycle. (C) Noise analysis was used to estimate P_o for H1348A (blue bar) and T460S/H1348A (green bar). (D; left) Opening rates of H1348A (blue bar) and T460S/H1348A (green bar), obtained using the estimate for P_o (see C) and the closing rate (see B). (Right) Thermodynamic mutant cycle for target pair T460-H1348 built on opening rates. The top two corners of the mutant cycle were taken from Fig. 3 D.

Figure 7.

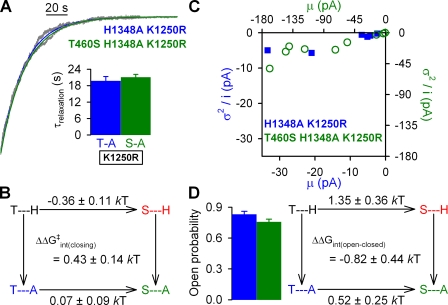
The H1348A mutation stabilizes the open state of CFTR in the nonhydrolytic K1250R background. (A) Representative normalized decay time courses of macroscopic currents for H1348A/K1250R and T460S/H1348A/K1250R CFTR after the removal of 2 mM ATP (gray). Solid blue and green lines are fitted exponentials; mean ± SEM relaxation time constants (τ_relaxation) are shown in the inset. (B) Thermodynamic mutant cycle for target pair T460-H1348 built on nonhydrolytic closing rates (1/τ_relaxation). The top two corners of the mutant cycle were taken from Fig. 5 B. (C) Noise analysis for estimation of P_o for H1348A (blue symbols) and T460S/H1348A (green symbols); each symbol represents one patch. (D; left) Mean ± SEM P_o for H1348A (blue bar) and T460S/H1348A (green bar). (Right) Thermodynamic mutant cycle for target pair T460-H1348 built on K_eq = P_o/(1−P_o) values under nonhydrolytic conditions. The top two corners of the mutant cycle were taken from Fig. 5 D.

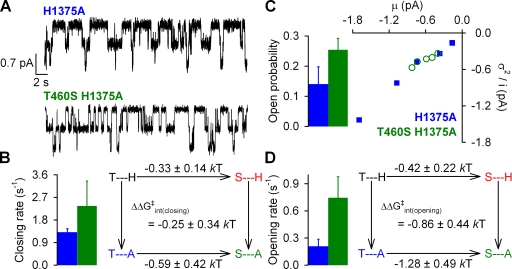
Figure 8.

Effects of mutations at positions 460 and 1375 on normal hydrolytic channel gating. (A) Representative single-channel current traces from prephosphorylated H1375A and T460S/H1375A CFTR channels gating in 2 mM ATP. Downward deflection indicates inward current. (B; left) Closing rates of H1375A (blue bar) and T460S/H1375A (green bar), defined as the inverse of the mean burst duration (see Materials and methods). (Right) Thermodynamic mutant cycle for target pair T460-H1375 built on closing rates. The top two corners of the mutant cycle (representing WT and T460S) were taken from Fig. 2 C. (C) Noise analysis was used to estimate P_o for H1375A (blue bar) and T460S/H1375A (green bar). (D; left) Opening rates of H1375A (blue bar) and T460S/H1348A (green bar), obtained using the estimate for P_o (see C) and closing rate (see B). (Right) Thermodynamic mutant cycle for target pair T460-H1375 built on opening rates. The top two corners of the mutant cycle were taken from Fig. 3 D.

We first studied the single-channel gating pattern of H1348A and T460S/H1348A under normal hydrolytic conditions (Fig. 6 A) and extracted single-channel closing rates (Fig. 6 B, left). Although the H1348A mutation dramatically slowed closure (to 1.1 ± 0.2 s⁻¹; n = 8), the closing rate for T460S/H1348A was slightly accelerated relative to that of H1348A (compare green and blue bar in Fig. 6 B, left), just as that of T460S relative to WT (compare red and black bar in Fig. 2 B). Thus, ΔΔG_int for the mutant cycle built on closing rates (Fig. 6 B, right) was not significantly different from zero. The slight difference in closing rates between T460S/H1348A and H1348A was mirrored by the slightly lower P_o value of the double mutant (Fig. 6 C; compare green and blue bar). Consequently, for the calculated opening rates (Fig. 6 D, left), we did not detect the slight acceleration by the T460S mutation, which was observed when this mutation was introduced into a WT background (compare red and black bars in Fig. 3 C). Nonetheless, the resulting mutant cycle did not yield a ΔΔG_int significantly different from zero (Fig. 6 D, right; P = 0.08).

To look for changes in interactions between positions 460 and 1348 during nonhydrolytic closure, we created nonhydrolytic H1348A/K1250R and T460S/H1348A/K1250R channels and compared their closing rates by studying macroscopic current relaxations after ATP removal (Fig. 7 A). Interestingly, mutation H1348A prolonged the time constant of the current relaxation (to 20 ± 2 s; n = 8; Fig. 7 A, blue bar) to a similar extent as it did normal burst durations; and noise analysis (Fig. 7 C) attested to the fact that the prolonged open time of H1348A/K1250R is associated with an unusually high open probability (P_o = 0.83 ± 0.03 s; n = 6; Fig. 7 D, left, blue bar). Although neither the slight shortening of nonhydrolytic τ_relaxation nor the reduction in nonhydrolytic P_o by the T460S mutation (compare red vs. black bars in Fig. 5, A and C) was apparent when this mutation was introduced into an H1348A/K1250R background (compare green vs. blue bars in Fig. 7, A and D, left), these deviations from additivity resulted in a small change in T460-H1348 interaction energy only between the transition state for nonhydrolytic closure and the open ground state (ΔΔG_int(closing) = 0.43 ± 0.14 kT; P = 0.01; Fig. 7 B), but not between open and closed ground states (Fig. 7 D, right; P = 0.1).

Energetic coupling between positions 460 and 1375 is little changed during gating

To study interactions between positions 460 and 1375, we compared the effects of mutation T460S in H1375A and WT backgrounds. For single channels gating under normal hydrolytic conditions (Fig. 8 A, top), mutation H1375A also slowed closure (to 1.3 ± 0.1 s⁻¹; n = 6; Fig. 8 B, left, blue bar), similarly to what was observed for H1348A (see Fig. 6 B, left, blue bar). A slight tendency of mutation T460S to accelerate channel closure was also observed in this background (see Fig. 8 B, left, green bar), such that a mutant cycle built on closing rates (Fig. 8 B, right) did not reveal significant non-additivity (ΔΔG_int ≈ 0). The increased open probability of T460S/H1375A relative to that of H1375A (Fig. 8 C, green vs. blue bar) attested to an increased opening rate in the double mutant (Fig. 8 D, left, green vs. blue bar). However, because a similar tendency (although to a lesser extent) was also apparent in the WT background (see Fig. 3 C, red vs. black bar), the mutant cycle built on opening rates (Fig. 8 D, right) again yielded no significant change in interaction energy (P = 0.08).

We next studied the effect of the mutations at our target pair T460-H1375 on nonhydrolytic closing rate, in a K1250R background. Because for both H1375A/K1250R and T460S/H1375A/K1250R adequate fitting of the relaxation time course after ATP removal consistently required a double exponential with two slow time constants (each in the seconds range; Fig. 9 A), average steady-state closing rate was estimated from a double-exponential fit as described in Materials and methods. Unexpectedly, when the H1375A mutation was introduced into the K1250R background, average nonhydrolytic closing rate was not slowed, but rather slightly accelerated (Fig. 9 A, blue bar). Although in this double-mutant background the T460S mutation did not noticeably affect the rate of nonhydrolytic closure (Fig. 9 A, green bar; compare with Fig. 5 A, red vs. black bar), this small deviation from additivity did not result in any significant coupling energy (Fig. 9 B; P = 0.2). Finally, by noise analysis (Fig. 9 C), mutation T460S reduced P_o in the H1375A/K1250R background (compare green vs. blue bars in Fig. 9 D, left) to a similar extent as it did in the single-mutant K1250R background (compare red vs. black bars in Fig. 5 C), yielding a ΔΔG_{int(open-closed)} not significantly different from zero (Fig. 9 D; P = 0.15).

DISCUSSION

In a subgroup of ABC proteins including CFTR, one of the two composite ATP-binding sites is not catalytically active, and the role of this degenerate composite site 1 is still unclear. Based on kinetic arguments it was recently suggested that in CFTR, the NBD1–NBD2 interface does not separate around composite site 1, even when the pore closes, remaining intact for several gating cycles (Tsai et al., 2010). To validate this proposal using an independent approach, we resorted to thermodynamic measurements that quantify changes in interaction energy between select pairs of positions.

The results of a mutant cycle study can be interpreted at two different levels. First, the functional phenotypes of individual mutants might provide some mechanistic insight. However, this level of interpretation is often problematic because a mutation typically perturbs several structural interactions, and the observed functional effect is a combined consequence of these perturbations. A second level of interpretation is provided by the ΔΔG_int value obtained from the entire mutant cycle. Because the energetic effects on parallel sides are subtracted, ΔΔG_int provides a specific and quantitative measure for the change in the interaction energy between the two target side chains while the protein transits from one conformational state to another (Fersht, 1999). Below, we discuss our results at these two different levels.

Site-1 mutations affect channel closing, likely by affecting the relative stability of open states

In contrast to composite site-2 mutations R555K and T1246N (Vergani et al., 2005, but compare Teem et al., 1996), in positions equivalent to T460 and L1353, all site-1 mutations studied here had relatively small effects on channel gating, consistent with the notion that the gating cycle is driven by the catalytic cycle at composite site 2. The most significant phenotypes were observed for T460S and H1348A, which, respectively, increased and decreased not only normal hydrolytic channel closing rate (Figs. 2 B and 6 B) but also the rate of nonhydrolytic closure (Figs. 5 A and 7 A; compare Fig. S2 B), suggesting that these mutations simultaneously affect the energy barriers for both closing pathways. An alteration in both energy barriers for closing could result from either a simultaneous perturbation of both transition states or, more simply, from a perturbation of the open ground state. Our results on T460S/K1250R and H1348A/K1250R indeed show a respective decrease and increase in P_o (Figs. 5 C and 7 D), confirming that the open ground state is destabilized in T460S/K1250R, but stabilized in H1348A/K1250R, with respect to the closed ground state. The simplest interpretation is that the T460S and H1348A mutations specifically affect the stability of the open state. Given the likely positions of these residues in the composite site, this suggests that the mutations may affect interactions at the NBD dimer interface (either protein–protein or protein–ATP interactions), thus altering dimer stability.

In contrast to the simple interpretation of the effects of the above two mutations, the functional consequences of the H1375A mutation are more complex. This mutation affected the rates of hydrolytic (Fig. 8 B) and nonhydrolytic (Fig. 9 A) closure in opposite ways, and in the K1250R background, the double-exponential relaxation after ATP removal suggested a mixture of two types of nonhydrolytic bursts. H1375 is part of the “D-loop” seen to interact with the conserved switch histidine of the opposite NBD, thus mediating NBD–NBD interactions in ATP-bound dimeric crystals (Zaitseva et al., 2005). Possibly, the presence of a distinct second nonhydrolytic burst might be related to alternative conformations of this crucial loop, kinetically unavailable in the faster hydrolytic gating cycle.

Although the H1375A phenotypes are not easily interpretable, altogether our findings are generally consistent with evidence from other studies of mutations in site 1, which suggest that protein–nucleotide and protein–protein interactions at composite site 1 contribute to the stability of the open-state dimer (Vergani et al., 2003; Bompadre et al., 2005; Cai et al., 2006; Zhou et al., 2006; Tsai et al., 2009).

No large changes in energetic coupling between residues at the site-1 interface during channel gating

Despite robust changes in several of the gating parameters in our single mutants, these changes proved mostly additive in the double mutants. Thus, the changes in coupling energy between open and closed ground states and transition states, for all three target pairs we have studied, were either not significantly different from zero (for the mutant cycles in Figs. 5 D, 6, B and D, 7 D, 8, B and D, 9, B and D, and S1 C) or very small (∼0.6 kT for the cycle in Fig. 2 C; ∼0.4 kT for that in Fig. 7 B)—far smaller than the energy of a single van der Waals interaction (∼0.2 kT per atom involved; Alberts et al., 2002). Although the latter findings could leave room for small movements occurring during the closing transition, they are inconsistent with formation/disruption of side chain interactions, as would be expected for a separation of the NBD1 and NBD2 surfaces around composite site 1.

There are two possible interpretations for little or no change in energetic coupling during gating: either there is no interaction between the pairs of target residues (neither in the ground states nor in the transition states), or the two residues do interact, but the magnitude of the coupling energy is similar in open, transition, and closed states. Because no structure of a degenerate site in an asymmetric NBD dimer has yet been solved, it is not known whether our three chosen pairs of target residues in CFTR’s site 1 do interact; a completely novel interdomain arrangement at site 1 might prove the opposite. However, such a scenario is rather unlikely. First, monomeric structures of both NBD1 (Lewis et al., 2004) and NBD2 (Atwell et al., 2010; Protein Data Bank accession no. 3GD7) of CFTR have been solved, and the overall fold of both of these structures is closely similar to that of all other solved ABC NBDs. Second, the recently solved structure of a CFTR NBD1 head-to-tail homodimer (Atwell et al., 2010) shows an NBD interaction surface typical to all solved ABC NBD dimer structures (e.g., Smith et al., 2002; Zaitseva et al., 2005). Third, the sequences surrounding both T460 in NBD1 and our three target residues on the NBD2 side are well conserved (apart from the four to five non-canonical substitutions present in degenerate sites; Basso et al., 2003; Procko et al., 2006). Fourth, we obtain high correlation scores for pairs of residues that are close on homology models. Most correlation analysis algorithms, statistical coupling included, have very limited predictive value with respect to structure (Fodor and Aldrich, 2004). A somewhat higher accuracy might be achieved for the highest correlations (including the 460–1375 pair; r = 0.43) obtained from the CorrMut analysis, which attempts to eliminate false positives (Fleishman et al., 2004; see Table S2). Collectively, these facts suggest that homology models of the CFTR NBD dimer (Mense et al., 2006; Mornon et al., 2008; Serohijos et al., 2008) give a reasonable prediction of the heterodimer structure around our target residues. In these, the residues face each other and are close (Fig. 1). We therefore consider it unlikely that none of our three target residue pairs forms a molecular contact. In this case, our results would suggest that close contact around site 1, present in the open state, is also present in the transition state for closing and the closed ground state.

These findings provide independent support for the model recently proposed by Tsai et al. (2009, 2010), who hypothesized that the NBD dimer only partially separates after ATP hydrolysis. Preliminary ATP binding at NBD1 triggers formation of a tight dimer interface around the inactive composite site 1, which is then maintained during several channel gating cycles (but compare Poletto Chaves and Gadsby, 2011). This proposal is consistent with, and refines, earlier models (Basso et al., 2003; Vergani et al., 2003) in which the conformational changes at the NBDs associated with channel gating occur mainly around site 2. Channel opening is driven by ATP binding at NBD2 to trigger complete dimer formation (dehydration of dimer interface around site 2; Vergani et al., 2005; Csanády et al., 2006), whereas closure follows ATP hydrolysis (Csanády et al., 2010) and rehydration of the dimer interface around site 2.

In symmetric ABC proteins, although both sites are catalytically functional, it has been suggested that one site is temporarily catalytically inactive while hydrolysis occurs at the other (Tombline et al., 2005; Siarheyeva et al., 2010). Also, molecular dynamics simulation of a symmetric NBD dimer led to the proposal of a comparable “constant contact” model, in which the contact at one site is maintained while the ATP at the other site is hydrolyzed (Jones and George, 2009). In a separate study, also on a bacterial NBD homodimer, simulations show that replacing the ATP at one of the two sites by ADP plus Pi is enough to allow the dimer interface to open around this “post-hydrolysis” site while the other composite site remains tightly closed (Wen and Tajkhorshid, 2008). Thus, the molecular mechanisms underlying the function of asymmetric and symmetric ABC proteins might be even closer than previously believed.