Reconstruction Using Witness Complexes

Abstract

We present a novel reconstruction algorithm that, given an input point set sampled from an object S, builds a one-parameter family of complexes that approximate S at different scales. At a high level, our method is very similar in spirit to Chew’s surface meshing algorithm, with one notable difference though: the restricted Delaunay triangulation is replaced by the witness complex, which makes our algorithm applicable in any metric space. To prove its correctness on curves and surfaces, we highlight the relationship between the witness complex and the restricted Delaunay triangulation in 2d and in 3d. Specifically, we prove that both complexes are equal in 2d and closely related in 3d, under some mild sampling assumptions.

1 Introduction

The problem of reconstructing a curve or a surface from scattered data points has received a lot of attention in the past. Although it is ill-posed by nature, since infinitely many shapes with different topological types can interpolate a given point cloud, a number of provably good methods have been proposed. The common denominator of these methods is the assumption that the input point set is densely sampled from a sufficiently regular shape: this assumption makes the reconstruction problem well posed, since all sufficiently regular shapes interpolating the point set have the same topological type and are close to one another geometrically. It suffices then to approximate any of these shapes to get the right answer. The notion of ε-sample, introduced by Amenta and Bern [1], provides a sound mathematical framework for this kind of approach, the corresponding set of reconstructible shapes being the class of manifolds with positive reach [26]. A number of provably-good algorithms are based on the ε-sampling theory—see [9] for a survey, and several extensions have been proposed to reconstruct manifolds in higher-dimensional spaces [15] or from noisy point cloud data [24]. The theory itself has been recently extended to a larger class of shapes, known as the class of Lipschitz manifolds [8]. In all these methods, the Delaunay triangulation of the input point set plays a prominent role since the final reconstruction is extracted from it.

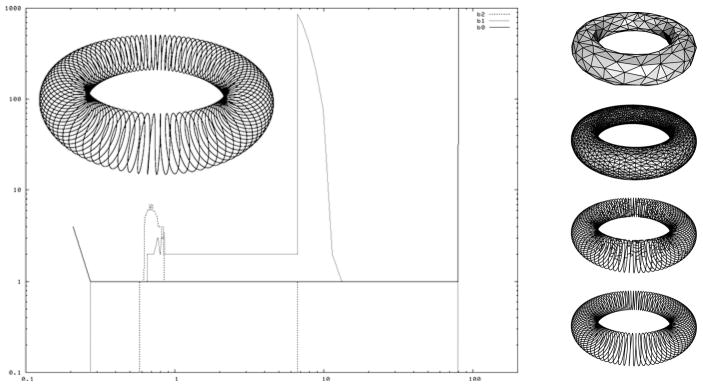
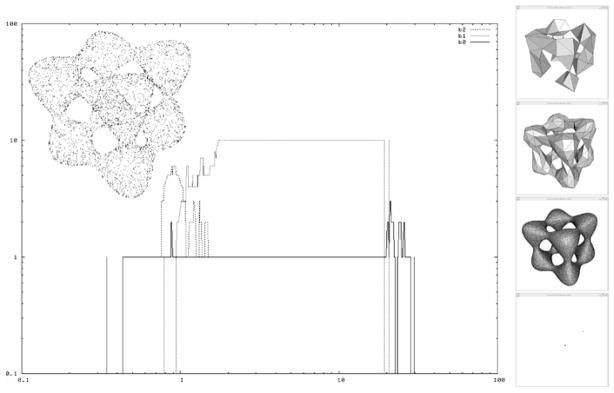
This approach to surface reconstruction is limited because it assumes implicitly that a point cloud should always represent a single class of shapes. Consider the example of a closed helical curve rolled around a torus in ℝ³—see Fig. 1. Take a very dense uniform point sample of the curve: what does this point set represent, the curve or the torus? Although both objects are well sampled according to Amenta and Bern’s sampling theory, classical reconstruction methods always choose a single class of shapes, here the curve or the torus, by restricting themselves either to a certain dimension or to a certain scale: for instance, the reconstruction method of [15] or the dimension detection algorithm of [23] will detect the curve but not the torus, since the point set is a sparse sample of the curve but not of the torus. Now, we claim that the result of the reconstruction should not be either the curve or the torus, but both of them. More generally, the result of the reconstruction should be a one-parameter family of complexes, whose elements approximate the original shape at different scales, as illustrated in Fig. 1. This point of view, inspired from recent results by Chazal et al. [10], stands in sharp contrast with previous work in the area and is echoed in the literature on nonlinear dimensionality reduction [34, 36] and topological persistence [19, 25, 37].

Fig. 1.

Helical curve drawn on a torus (left). From a uniform sampling of the curve, our algorithm builds a one-parameter family of complexes (right) and maintains their Betti numbers (left)

This paper presents a novel reconstruction algorithm that, given an input point set W sampled from an object S, builds a one-parameter family of complexes that approximate S at different scales. At a high level, the method is very similar to Chew’s surface meshing algorithm [7, 17]: it constructs a subset L of W iteratively, while maintaining a subcomplex of the Delaunay triangulation of L. The one-parameter family of complexes obtained from this iterative process is the result of the algorithm. The difference with Chew’s approach is that, instead of maintaining the restricted Delaunay triangulation of L, we maintain its witness complex (L) relative to W. The main advantages are that the underlying object S does not have to be known, and that the full-dimensional Delaunay triangulation (L) does not have to be computed. Moreover, the algorithm can be used in any metric space, ultimately enabling new applications of the Delaunay-based reconstruction ideas.

The witness complex can be viewed as a weak version of the Delaunay triangulation, well defined and computable in any metric space—see Sect. 2 below. As such, it has played an important role in the context of topological data analysis [22]. It was first introduced by de Silva [20], who proved that (L) is a subcomplex of (L) whenever the points of L lie in general position in a Euclidean space. Moreover, if the set W of witnesses spans the whole ambient space, then (L) is equal to 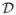(L). Now the question is whether this property holds when the points of W are sampled from a subspace of the ambient space, such as for instance a submanifold: in [22], Carlsson and de Silva observed that (L) is then closely related to the restricted Delaunay triangulation (L), and they conjectured that both objects should coincide under some sampling assumptions on W and L. We prove that this conjecture is valid for a curve in the plane but not for a surface in 3d. In the latter case, we show how to relax the definition of the witness complex so that it contains (L), and then how to extract a subcomplex that approximates (L) (and hence S). This proves that our reconstruction algorithm is correct when applied to point samples of Lipschitz curves or surfaces. We are only aware of one related result: in [4], Attali et al. show that (L) and (L) coincide whenever the set W of witnesses spans an entire submanifold of ℝⁿ of dimension one or two. This result differs from ours in two ways: our set W can be finite, which makes our result more practical, yet in return our set L has to be sparse compared to W, for (L) to contain (L). This sparseness condition is not an issue in practice, since the set L is constructed by the algorithm. Other noticeable differences are that our manifolds can have singularities and that our point samples can be noisy. Our assumption on the input point set W is fairly mild, since it amounts to saying that the Hausdorff distance between W and S is sufficiently small. In particular, there is no sparseness condition on W, and the amplitude of the noise can be as large as the sampling density. This noise model, introduced in [12] and used in subsequent work on reconstruction [10, 13, 29, 30], is less restrictive than its predecessors [16, 24, 28], and it makes our algorithm more practical.

The paper is organized as follows. In Sect. 2, we recall several concepts that will be used later on. In Sect. 3, we present our structural results. Specifically, we prove that the restricted Delaunay triangulation and the witness complex are equal in 2d (Sect. 3.1) and closely related in 3d (Sect. 3.2), under some mild sampling assumptions. In Sect. 4, we introduce our reconstruction algorithm and present some experimental results.

2 Background and Definitions

Let S be a subset of ℝ² (resp. ℝ³), L a finite set of points in ℝ² (resp. ℝ³), and ε a positive number.

Definition 2.1

• L is an ε-noisy sample of S if no point of L is farther than ε from S.

• L is an ε-sample of S if no point of S is farther from L than ε.

• L is ε-sparse if the pairwise distances between the points of L are at least ε.

A 0-noisy sample is called a noise-free sample. When the first two conditions of the definition apply simultaneously, for a same ε, the Hausdorff distance between L and S is bounded by ε. We denote by 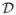(L) the Delaunay triangulation of L.

Definition 2.2

The Delaunay triangulation of L restricted to S, or (L) for short, is the subcomplex of 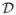(L) made of the Delaunay faces whose dual Voronoi faces intersect S.

Let W be another set of points in ℝ² (resp. ℝ³), finite or infinite.

Definition 2.3

• Given a point w ∈ W and a simplex σ = [p₀, …, p_l] with vertices in L, w witnesses σ if p₀, …, p_l belong to the l + 1 nearest neighbors of w, that is,

  $$\forall i\in \{0,\dots ,l\},\forall q\in L\backslash \{p_0,\dots ,p_l\},\text{d}(w,p_i)\le \text{d}(w,q).$$

• The witness complex of L relative to W, or (L) for short, is the maximum abstract simplicial complex with vertices in L, whose faces are witnessed by points of W.

The fact that (L) is an abstract simplicial complex means that a simplex belongs to the complex only if all its faces do. By the so-called Weak Witness Theorem [20], we have (L) ⊆ (L), which implies that (L) is an embedded simplicial complex. In the sequel, L will be referred to as the set of landmarks, and W as the set of witnesses.

Lipschitz curves and surfaces

Boissonnat and Oudot [8] introduced a new framework for the analysis of Delaunay-based sampling algorithms. This framework relies on a quantity, called the Lipschitz radius, which plays a role equivalent to the local feature size of Amenta and Bern [1], on a much larger class of shapes—the class of Lipschitz curves and surfaces.

Definition 2.4

Let S be the boundary of a bounded open subset of ℝ² (resp. ℝ³). Given a point p ∈ S, the k-Lipschitz radius of S at p, or lr_k(p) for short, is the maximum radius r such that ∩ B(p, r) is the intersection of B(p, r) with the hypograph of some k-Lipschitz univariate (resp. bivariate) function. We call lr_k(S) the infimum of lr_k over S.

Recall that the hypograph of a real-valued bivariate function f is the set of points (x, y, z) ∈ ℝ³ such that z < f(x, y). The function f is k-Lipschitz if: ∀p, q ∈ ℝ², $\frac{\mid f(p)-f(q)\mid }{\left|\right|p-q\left|\right|}\le k$. It is proved in [8] that lr_k(S) > 0 whenever S is a k-Lipschitz curve in ℝ² or surface in ℝ³. In such a case, one can attach to each point p ∈ S a so-called k-Lipschitz normal n_k(p) and a so-called k-Lipschitz support plane T_k(p), which play a role similar to the usual normal vector and tangent plane in the Lipschitz setting:

Definition 2.5

Given p ∈ S, the k-Lipschitz normal of S at p, noted n_k(p), is the z vector of an oriented orthonormal frame (x, y, z) in which ∩ B(p, lr_k(p)) is the intersection of B(p, lr_k(p)) with the hypograph of a k-Lipschitz function f(x, y). The k-Lipschitz support plane at p, noted T_k(p), is the plane orthogonal to n_k(p) that passes through p.

The main result of [8] is the following:

Theorem 2.6

Let S be a k-Lipschitz surface in ℝ³ and L ⊂ S a finite point set such that:

• H1L is an ε-sample of S with $\epsilon <\frac{1}{7}{\text{lr}}_k(S)$,
• H2the triangles of (L) have radius-edge ratios of at most ϱ with $\varrho <\frac{cos2\theta }{2sin\theta }$ and θ = arctan k.

Then, (L) is a 2-manifold isotopic to S, at Hausdorff distance at most ε from S, and whose oriented normals approximate the k-Lipschitz normals of S within an angle of arcsin(2ϱ sin θ).

Another useful result, proved in [31], is an equivalent of Proposition 13 of [5] for Lipschitz surfaces:

Lemma 2.7

Let S be a k-Lipschitz surface in ℝ³ with k < 1. Then, ∀p ∈ S, ∀r ≤ lr_k(p), S ∩ B(p, r) is a topological disk.

Similar results can be proved in the planar case (we recall their proofs for completeness):

Lemma 2.8

Let S be a k-Lipschitz curve in ℝ² with k < 1. Then, ∀p ∈ S, ∀r ≤ lr_k(p), S ∩ B(p, r) is a topological arc. Moreover, the orthogonal projection of S ∩ B(p, r) onto T_k(p) is a segment whose vertices are the orthogonal projections of the two endpoints of S ∩ B(p, r).

Proof

Since S is an embedded curve without boundary, S ∩ B(p, r) is a collection of pairwise-disjoint simple arcs, whose endpoints lie on the circle ∂B(p, r). Proving that S ∩ B(p, r) is a topological arc reduces then to showing that |S ∩ ∂B(p, r)| ≤ 2.

Since r ≤ lr_k(p), S ∩ B(p, r) is the graph of some k-Lipschitz univariate function f defined over T_k(p) with k < 1. This implies that S ∩ B(p, r) lies in the double wedge K of apex p, of axis T_k(p), and of half-angle θ. Now, at every point of K ∩ ∂B(p, r), the line tangent to ∂B(p, r) makes an angle of at least $\frac{\pi }{2}-\theta$ with T_k(c). Thus, for any two points u, v of ∂B(p, r) lying in the same wedge of K, the line (u, v) makes an angle of at least $\frac{\pi }{2}-\theta >\theta$ with T_k(c). It follows that S ∩ ∂B(p, r) cannot have more than one point per wedge of K, since otherwise the fact that S ∩ B(p, r) coincides with the graph of f would be contradicted. As a result, S ∩ B(p, r) is a topological arc, whose endpoints are precisely the two points u, v of S ∩ ∂B(p, r).

Since S ∩ B(p, r) coincides with the graph of f, the orthogonal projection of S ∩ B(p, r) is one-to-one, and thus it maps the arc S ∩ B(p, r) to a segment whose vertices are the orthogonal projections of the endpoints of S ∩ B(p, r).

Theorem 2.9

If S is a k-Lipschitz curve in the plane with k < 1, and if L is an ε-sample of S with ε < lr_k(S), then (L) is a polygonal curve homeomorphic to S and at Hausdorff distance at most ε from S.

Proof

Since L is an ε-sample of S, no point of S is farther than ε from L ⊆ (L). Conversely, every point of (L) belongs to some Delaunay edge circumscribed by a Delaunay ball centered on S. This ball has a radius of at most ε, since L is an ε-sample of S. Thus, no point of (L) is farther than ε from S. This proves that (S, (L)) ≤ ε.

Let us now show that S and (L) are homeomorphic. Let [u, v] be an edge of (L). Let B(c, r) be a Delaunay ball centered on S that circumscribes [u, v]. Since L is an ε-sample of S, we have r ≤ ε < lr_k(S). Therefore, S ∩ B(c, r) is a topological arc whose endpoints are u and v, by Lemma 2.8. Moreover, S intersects ∂B(c, r) only in u and v. Thus, u and v are consecutive points of L on S.

Assume conversely that u and v are two points of L consecutive on S. Let γ be the elementary¹ arc of S that joins u and v. Let l be the bisector line of [u, v]. Since l divides ℝ² into two regions, one of which contains u while the other contains v, γ intersects l. Let c be a point of intersection, and let r = d(c, L). If the circle ∂B(c, r) passes through u and v, then B(c, r) is a Delaunay ball and hence [u, v] belongs to (L). Otherwise, ∂B(c, r) passes through some other point t ∈ L. Since u and v are consecutive along S, t does not belong to γ. Hence, S ∩ B(c, r) contains a piece of γ (since c ∈ γ) and also a piece of S\γ, and these pieces are disjoint, since B(c, r) does not contain u nor v. As a result, S ∩ B(c, r) is disconnected, which implies that r > lr_k(S), by Lemma 2.8. Now, since L is an ε-sample of S, we have r ≤ ε < lr_k(S), which contradicts the above statement. Therefore, [u, v] belongs to (L).

It follows from the last two paragraphs that there is a bijection between the elementary arcs of S and the edges of (L). For any edge e = [u, v] of (L), let h_e be a homeomorphism from e to the elementary arc of S joining u and v, such that h_e(u) = u and h_e(v) = v. Let h be the map defined by: ∀p ∈ (L), h(p) = h_e(p), where e is any edge of (L) containing p. Since the edges of (L) have pairwise-disjoint relative interiors, and since the h_e coincide at vertices (they leave the vertices unchanged), h(p) does not depend on the choice of the edge e of (L) that contains p. It follows that h is a well-defined and continuous function from (L) to S. Moreover, since the h_e are bijective, and since there is a bijection between the edges of (L) and the elementary arcs of S, h is bijective. In addition, the inverse of h is continuous, since (L) is compact. It follows that h is a homeomorphism from(L) to S.

3 Structural Results

In this section, we highlight the relationship between the witness complex and the restricted Delaunay triangulation in 2d and in 3d. Let S be a k-Lipschitz manifold, i.e., either a k-Lipschitz curve in the plane (Sect. 3.1) or a k-Lipschitz surface in 3d (Sect. 3.2), for some constant k ≥ 0. For convenience, we define θ = arctan k ∈ [0, π/2[. Let W be a δ-noisy δ-sample of S and L ⊂ W an ε-sparse ε-sample of W. The constants δ and ε will be explicited later on. Clearly, L is a (δ + ε)-sample of S.

For the sake of simplicity, we assume for now that the points of L belong to S, i.e., that L is a noise-free sample of S. We will see in Sect. 3.3 that this condition can actually be removed, since whenever L is a δ-noisy ε-sparse ε-sample of a k-Lipschitz surface S, there exists some nearby and isotopic k′-Lipschitz surface S′ with k′ = O(k) and lr_k′(S′) = Ω(lr_k(S)) such that the points of L lie on S′ (Theorem 3.16).

Our assumption that L is a sparse point set may look a bit restrictive at first sight. However, in our application the set of landmarks will not be given as input and will be made sparse by construction—see Sect. 4.

3.1 The Planar Case

Theorem 3.1

Assume that $\theta <arcsin\frac{1}{8}\approx 7.2deg$ and that $\delta <min\{\frac{1-8sin\theta }{12},\frac{3cos\theta -2}{4(9cos\theta +6)}\}{\text{lr}}_k(S)$. If ε satisfies $max\{\frac{12sin\theta }{1-8sin\theta },\frac{6}{3cos\theta -2}\}\delta <\epsilon <\frac{1}{8}{\text{lr}}_k(S)-\frac{3}{2}\delta$, then (L) coincides with (L).

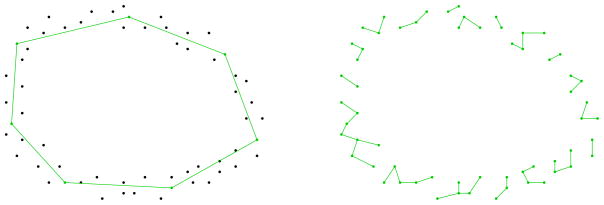
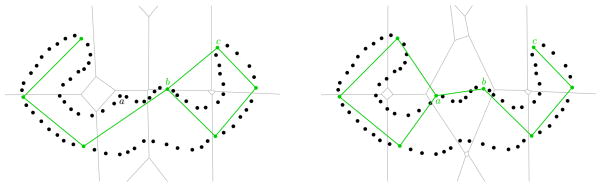
The lower bound on ε means that the set W of witnesses must be sufficiently dense² compared to the set L of landmarks, for the simplices of (L) to be witnessed. An illustration is given in Fig. 2, which shows that (L) contains (L) when L is sparse (left picture), whereas when L = W (ε = 0), (L) coincides with the nearest neighbor graph of L, which has nothing to do with (L) (right picture). The upper bound on ε ensures that the set L of landmarks is sufficiently dense, so that the nice properties of (L) stated in Sect. 2 hold and that classical local arguments can be applied to show that (L) is included in (L).

Fig. 2.

(Color online) A set of witnesses sampling a smooth closed curve with noise, and two different subsets of landmarks (in green) together with their witness complexes

To prove the theorem, we will need the following technical result:

Lemma 3.2

Assume that $\theta <\frac{\pi }{6}$. Then, every Voronoi vertex lies at least $min\{\frac{1}{2}{\text{lr}}_k(S),\frac{\epsilon }{2sin\theta }\}$ away from L.

Proof

Let c be a Voronoi vertex, and let (u, v, w) be its dual Delaunay triangle. Since L ⊂ S, the points u, v, w belong to S. Let r = d(c, u). Assume for a contradiction that $r<min\{\frac{1}{2}{\text{lr}}_k(S),\frac{\epsilon }{2sin\theta }\}$. Then, (u, v, w) is included in the ball B(u, 2r) ⊆ B(u, lr_k(S)), and thus lines (u, v), (u, w), and (v, w) form angles of at most θ with T_k(u). It follows that each inner angle of triangle (u, v, w) is smaller than 2θ or larger than π − 2θ. Since $\theta <\frac{\pi }{6}$, the larger inner angle of the triangle is at least π − 2θ, hence the radius-edge ratio of (u, v, w) is at least $\frac{1}{2sin\theta }$. As a consequence, we have $r\ge \frac{\epsilon }{2sin\theta }$, since the lengths of the edges of (u, v, w) are at least ε (recall that L is ε-sparse). This contradicts the assumption that $r<min\{\frac{1}{2}{\text{lr}}_k(S),\frac{\epsilon }{2sin\theta }\}$ and thereby concludes the proof of the lemma.

We will now prove Theorem 3.1 in two steps: first, we will show that (L) is included in (L) (Lemma 3.3), then we will show that (L) is included in (L) (Lemma 3.4).

Lemma 3.3

Assume that $\theta <\frac{\pi }{6}$ and that $\delta <min\{\frac{1-2sin\theta }{2},\frac{3cos\theta -2}{2(3cos\theta +4)}\}{\text{lr}}_k(S)$. If ε satisfies $max\{\frac{2sin\theta }{1-2sin\theta },\frac{6}{3cos\theta -2}\}\delta <\epsilon <\frac{1}{2}{\text{lr}}_k(S)-\delta$, then (L) is included in (L) and has no simplex of dimension two or more.

Proof

Let e = [u, v] be an edge of (L). By the definition of (L), the dual Voronoi edge of e intersects S at some point c. Let r = d(c, u) = d(c, v) = d(c, L), which is at most ε + δ, since L is a (δ + ε)-sample of S. Since W is a δ-sample of S, there is some w ∈ W at distance at most δ from c. Then, u and v are both included in B(w, ε + 2δ).

Let p be any point of L\{u, v}. We will prove that p ∉ B(w, ε + 2δ), which means that w witnesses e. Consider the portion of S that lies in B(c, r). Since r ≤ ε + δ < lr_k(S), we know from Lemma 2.8 that S ∩ B(c, r) is a topological arc whose endpoints are u, v and whose orthogonal projection onto T_k(c) is the line segment [ū, v̄], where ū, v̄ are the orthogonal projections of u, v. If p does not belong to B(c, lr_k(S)), then it does not belong to B(w, ε + 2δ) either, since B(w, ε + 2δ) ⊂ B(c, ε + 3δ), which by hypothesis is included in B(c, lr_k(S)). Otherwise, since p ∈ L\{u, v}, S ∩ B(c, r) contains c but not p. Therefore, p̄ (the orthogonal projection of p onto T_k(c)) does not belong to [ū, v̄], because the projection from S ∩ B(c, lr_k(S)) to T_k(c) is one-to-one. As a consequence, d(c, p) is at least d(c, p̄) ≥ d(c, {ū, v̄}) + d(p̄, {ū, v̄}). Since L is ε-sparse, we have d(p, u) ≥ ε, d(p, v) ≥ ε, and $\text{d}(c,u)=\text{d}(c,v)\ge \frac{\text{d}(u,v)}{2}\ge \frac{\epsilon }{2}$. Moreover, since S ∩ B(c, lr_k(S)) is the graph of a k-Lipschitz univariate function defined over T_k(c), we have d(p̄, ū) ≥ d(p, u) cos θ, d(p̄, v̄) ≥ d(p, v) cos θ, d(c, ū) ≥ d(c, u) cos θ, and d(c, v̄) ≥ d(c, v) cos θ. As a result,

$$\text{d}(c,p)\ge \text{d}(c,\overline{p})\ge \text{d}(c,\{\overline{u},\overline{v}\})+\text{d}(\overline{p},\{\overline{u},\overline{v}\})\le \frac{\epsilon }{2}cos\theta +\epsilon cos\theta =\frac{3}{2}\epsilon cos\theta .$$

This expression is greater than ε + 3δ, since $\epsilon >\frac{6\delta }{3cos\theta -2}$, by hypothesis. It follows that p is farther than ε + 3δ from c and hence farther than ε + 2δ from w. Thus, w witnesses [u, v]. Similarly, every other edge of (L) is witnessed by some point of W. Since L ⊆ W, the vertices of (L) witness themselves, hence the 1-skeleton of (L) is included in (L).

Let us now focus on higher-dimensional simplices. Since L is a (δ + ε)-sample of S with $\delta +\epsilon <min\{\frac{1}{2}{\text{lr}}_k(S),\frac{\epsilon }{2sin\theta }\}$ by hypothesis, all the points of S lie within distance $min\{\frac{1}{2}{\text{lr}}_k(S),\frac{\epsilon }{2sin\theta }\}$ of L. Therefore, S cannot contain any Voronoi vertex, by Lemma 3.2. This means that (L) has no triangle. As a consequence, (L) has no simplex of dimension two or more, and therefore it is equal to its 1-skeleton, which is included in (L).

Lemma 3.4

Assume that $\theta <arcsin\frac{1}{8}$ and that $\delta <\frac{1-8sin\theta }{12}{\text{lr}}_k(S)$. If ε satisfies $\frac{12sin\theta }{1-8sin\theta }\delta <\epsilon <\frac{1}{8}{\text{lr}}_k(S)-\frac{3}{2}\delta$, then (L) is included in (L) and has no simplex of dimension two or more.

Proof

Let v be a vertex of (L). By assumption, we have v ∈ L ⊂ S, therefore the Voronoi cell of v intersects S, which implies that v is a vertex of (L). Let now [u, v] be an edge of (L), and let w ∈ W be a witness of [u, v]. We assume without loss of generality that d(w, u) ≤ d(w, v).

Claim 3.4.1

d(w, u) ≤ d(w, v) ≤ 2ε + 3δ.

Proof

Let w̄ be a point of S closest to w. Since W is a δ-noisy sample of S, we have d(w, w̄) ≤ δ. It follows that d(w̄, u) ≤ δ + ε < lr_k(S). Since S ∩ B(w̄, lr_k(S)) is the graph of a k-Lipschitz univariate function defined over T_k(w̄), u belongs to the double wedge K of apex w̄, of axis T_k(w̄), and of half-angle θ. Let K_u be the wedge of K that contains u (if u = w̄, then take either wedge of K for K_u). Since $\theta <\frac{\pi }{4}$, for any point p ∈ K\K_u, the point of K_u closest to p is w̄. In particular, given any r ∈]δ + ε, lr_k(S)[, every point p of S ∩ ∂B(w̄, r)\K_u satisfies d(p, u) ≥ d(p, w̄) = r. If v does not belong to B(w̄, 2r), then d(p, L) ≥ r > δ + ε, which contradicts the fact that L is a (δ + ε)-sample of S. Since this is true for all r ∈ ]δ + ε, lr_k(S)[, v belongs to the ball B(w̄, 2(δ + ε)), which implies that d(w, v) ≤ 3δ + 2ε, since d(w, w̄) ≤ δ.

Consider the set of balls centered on the line segment [w, v] and whose bounding spheres pass through v. Since B(w, d(w, v)) contains u, one of these balls (called B) is such that ∂B contains both u and v. Clearly, B ⊆ B(w, d(w, v)). Since w witnesses [u, v], the interior of B(w, d(w, v)) cannot contain any point of L other than u, thus no point of L lies in the interior of B. Therefore, B is a Delaunay ball. Let c be its center. It lies on the Voronoi edge e dual to [u, v]. Moreover, its distance to L is at most d(w, v). By Claim 3.4.1, we have d(w, v) ≤ 2ε + 3δ, which, according to the hypothesis of the lemma, is less than $min\{\frac{1}{4}{\text{lr}}_k(S),\frac{\epsilon }{4sin\theta }\}$. Hence, $\text{d}(c,L)<min\{\frac{1}{4}{\text{lr}}_k(S),\frac{\epsilon }{4sin\theta }\}$.

Claim 3.4.2

If a Voronoi edge contains a point closer to L than $min\{\frac{1}{4}{\text{lr}}_k(S),\frac{\epsilon }{4sin\theta }\}$, then this edge intersects S.

Proof

Let e be a Voronoi edge containing a point c closer to L than $r=min\{\frac{1}{4}{\text{lr}}_k(S),\frac{\epsilon }{4sin\theta }\}$. Let [u, v] be the Delaunay edge dual to e. We have d(c, u) = d(c, v) = d(c, L) < r. It follows that d(u, v) ≤ 2r. Since 2r < lr_k(S), S ∩ B(u, 2r) is the graph of a k-Lipschitz univariate function defined over T_k(u). As a consequence, S ∩ B(u, 2r) lies outside the double wedge K(u) of apex u, of axis aligned with n_k(u), and of half-angle $\frac{\pi }{2}-\theta$. Moreover, by Lemma 2.8, S ∩ B(u, 2r) is a topological arc whose endpoints lie on the circle ∂B(u, 2r). Since c lies in B(u, r), it can be proved that S ∩ B(u, 2r) intersects any line³ included in the double wedge K(c) of apex c, of axis aligned with n_k(u), and of half-angle θ: a proof of this fact is given in Claim 6.6.3 of [8] for the 3d case, and it holds the same in 2d. Now, since v lies outside K(u), the angle between n_k(u) and the line l supporting e is at most θ, which means that l is included in K(c) and thus intersects S inside B(u, 2r). Finally, we assumed that e intersects B(u, 2r), while Lemma 3.2 states that the vertices of e lie outside of B(u, 2r). Hence, l ∩ B(u, 2r) = e ∩ B(u, 2r), and therefore e intersects S.

It follows from this claim that e intersects S. Therefore, [u, v] is an edge of (L). As a result, the 1-skeleton of (L) is included in (L). Let us now show that (L) has no simplex of dimension two or more. Recall that a simplex σ belongs to (L) only if all its faces belong to (L). Therefore, it suffices to prove that (L) has no triangle.

Claim 3.4.3

For any triangle t of (L), at least one edge of t does not belong to (L).

Proof

Let (u, v, w) be a triangle of (L). Assume for a contradiction that edges [u, v], [v, w], and [u, w] belong to (L). Since L is a (δ + ε)-sample of S, the three edges are circumscribed by Delaunay balls of radius at most δ + ε. It follows that the triangle (u, v, w) is included in B(v, 2(δ + ε)). Let c be the circumcenter of this triangle. Since c is a Voronoi vertex, Lemma 3.2 states that $\text{d}(c,L)\ge min\{\frac{1}{2}{\text{lr}}_k(S),\frac{\epsilon }{2sin\theta }\}$, which by assumption is greater than 2(ε + δ). Therefore, c does not belong to B(v, 2(ε + δ)), and hence it does not belong to triangle (u, v, w) either. This means that c is not a local maximum of the distance to L. As a consequence, there is a Voronoi edge e incident to c such that d(x, L) increases as point x moves away from c along e. Since the local maxima of the distance to L are Voronoi vertices, d(x, L) keeps increasing until x reaches the other vertex of e. Thus, every point of e is at least d(c, L) away from L with d(c, L) > 2(δ + ε). This implies that e cannot intersect S, because otherwise some point of e would be at most δ + ε away from L (recall that L is a (δ + ε)-sample of S). Now, the Delaunay edge dual to e is an edge of (u, v, w). Therefore, at least one edge of (u, v, w) does not belong to (L), which contradicts our assumption.

Since (L) is included in (L), and since its edges belong to (L), any triangle of (L) is a Delaunay triangle whose edges belong to (L). Hence, by Claim 3.4.3, (L) has no triangle, which concludes the proof of the lemma.

3.2 The 3d Case

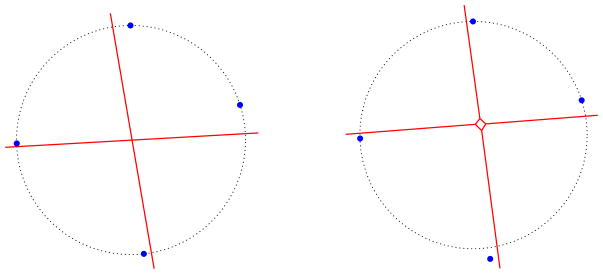
Unlike in the planar case, the witness complex and the restricted Delaunay triangulation of points sampled from a surface in 3d may not always coincide, even in situations where the sets of witnesses and landmarks satisfy strong sampling conditions. The reason is that, when a tetrahedron t of (L) has almost cocircular vertices, the chance for any of the diagonal edges of t to be witnessed by a point of W is small—such a tetrahedron is called a sliver in the literature [35]. In order to give an intuition of this fact, let us assume for simplicity that the surface is flat and that the vertices of t are cocircular, as in Fig. 3 (left). The order-two Voronoi diagram of the vertices is then degenerate, the Voronoi cells of the diagonal edges being reduced to a single point p that lies at the intersection of the edges of the diagram. Therefore, any diagonal edge can be witnessed only by p, which means that the probability for any triangle of the quadrangle to be witnessed when W is finite is zero. As a result, holes appear with probability one in the witness complex, as illustrated in Fig. 4 (left).

Fig. 3.

Order-two Voronoi diagrams of two sets of points in the plane

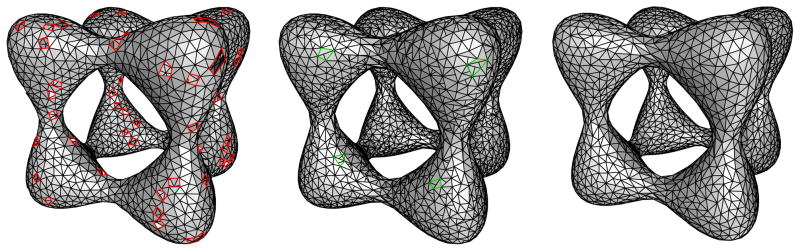
Fig. 4.

Witness complex, ν-witness complex, and extracted manifold

When the vertices of tetrahedron t are almost-cocircular, as in Fig. 3 (right), the order-two Voronoi cell of one diagonal edge is empty, while the cell of the other diagonal edge is arbitrarily small. Thus, the probability for any triangle of the quadrangle to be witnessed when W is finite is also arbitrarily small. Although it is always possible to perturbate the point set L so that the points are in general position, guaranteeing that the order-two Voronoi cells of the edges of (L) are sufficiently large requires large perturbations, which are not tractable in practice, since the underlying surface S is unknown.

3.2.1 The ν-witness Complex

Our approach for dealing with the above issue consists in relaxing the definition of the witness complex, so that the latter includes the restricted Delaunay triangulation. This requires to modify the concept of witness:

Definition 3.5

Given an integer m, a point w ∈ W, and a simplex σ = [p₀, …, p_l] with vertices in L, w m-witnesses σ if all the d(w, p_i) are among the m smallest values of the set {d(w, q), q ∈ L}.

Observe that, in the case where m ≤ l, some vertices of σ must be equidistant to w for w to m-witness σ. In particular, if m = 1, then all the points of σ must be equidistant to w, which means that w is a strong witness of σ, or equivalently, that σ is a Delaunay simplex. If m = 0, then no point w ∈ W can m-witness σ. In [22], the authors use m-witnesses only for edges. More generally, we use them for simplices of all dimensions:

Definition 3.6

Given a countable sequence ν of integers, the ν-witness complex of L, or ${\mathcal{C}}_{\nu }^W(L)$ for short, is the maximum abstract simplicial complex with vertices in L such that each i-face is ν_i-witnessed by some point of W.

Since the simplices of ${\mathcal{C}}_{\nu }^W(L)$ have their vertices in L, their dimension is at most |L| − 1. Hence, in the sequence of integers, only ν₀ through ν_|L|−1 are used. There is a strong relationship between (L) and ${\mathcal{C}}_{\nu }^W(L)$: if ν_i ≥ i + 1 ∀i, then ${\mathcal{C}}_{\nu }^W(L)$ contains (L); in contrast, if ν_i ≤ i + 1 ∀i, then ${\mathcal{C}}_{\nu }^W(L)$ is included in (L); thus, ${\mathcal{C}}^W(L)={\mathcal{C}}_{\nu }^W(L)$ whenever ν_i = i + 1 ∀i. In addition, if ν_i = 0 for some i, then the i-skeleton of ${\mathcal{C}}_{\nu }^W(L)$ is empty, since a simplex cannot be 0-witnessed, and the dimension of ${\mathcal{C}}_{\nu }^W(L)$ is then at most i − 1.

Theorem 3.7

Assume that $\theta <arccos(2sin\frac{\pi }{7})\approx 29.7deg$ and that $\delta <\frac{cos\theta -2sin\frac{\pi }{7}}{3cos\theta +2sin\frac{\pi }{7}}·{\text{lr}}_k(S)$. If ε satisfies $\frac{8sin\frac{\pi }{7}}{cos\theta -2sin\frac{\pi }{7}}\delta <\epsilon <{\text{lr}}_k(S)-3\delta$, then, for any sequence ν of integers such that ν₀ ≥ 1, ν₁ ≥ 6, and ν₂ ≥ 6, (L) is included in ${\mathcal{C}}_{\nu }^W(L)$.

Proof

Since the vertices of (L) belong to L, which is included in W, they witness themselves and thus belong to ${\mathcal{C}}_{\nu }^W(L)$. In addition, (L) contains no tetrahedron generically.

Let σ be a simplex (edge or triangle) of (L), and let B(c, r) be a Delaunay ball centered on S and circumscribing σ. Since W is a δ-sample of S, there is a point w ∈ W at distance at most δ from c. Then, σ lies in the ball B(w, r + δ), which is included in B(c, r + 2δ).

Claim 3.7.1

The ball B(c, r + 2δ) contains at most six points of L.

Proof

Since L is a (δ + ε)-sample of S, the radius r of the surface Delaunay ball is at most δ + ε. Therefore, r + 2δ ≤ ε + 3δ, which is less than lr_k(S) according to the hypothesis of Theorem 3.7. It follows that S ∩ B(c, r + 2δ) is the graph of a k-Lipschitz bivariate function defined over the plane T_k(c).

Let p₁, …, p_l be the points of L ∩ B(c, r + 2δ). We call p̄₁, …, p̄_l their orthogonal projections onto T_k(c). Since L is ε-sparse, the p_i are at least ε away from one another. And since they belong to S ∩ B(c, lr_k(S)), which is the graph of a k-Lipschitz bivariate function defined over the plane T_k(c), their projections p̄_i are at least ε cos θ away from one another. Moreover, since B(c, r) is a Delaunay ball, the p_i are at least r away from c, hence the p̄_i are at least r cos θ away from c.

The rest of the proof depends on whether r ≥ ε or r < ε. In fact, the overall ideas are the same, but some technical details differ.

• If r ≥ ε, then, inside T_k(c), c and the p̄_i are centers of pairwise-disjoint open disks of radius $\frac{\epsilon }{2}cos\theta$. Let D_c, D₁, …, D_l denote these disks. Since the p_i belong to B(c, r + 2δ), the p̄_i belong to the disk D(c, r + 2δ). Therefore, D_c, D₁, …, D_l form a congruent packing of the disk $D(c,r+2\delta +\frac{\epsilon }{2}cos\theta )$. Now, according to the hypotheses of the theorem, we have:

  $$r+2\delta +\frac{\epsilon }{2}cos\theta \le \epsilon +3\delta +\frac{\epsilon }{2}cos\theta <\frac{\epsilon }{2}cos\theta \left(\frac{1}{sin\frac{\pi }{7}}+1\right).$$

  Hence, by a classical result on congruent packings of disks [27, 33], there are at most seven disks of radius $\frac{\epsilon }{2}cos\theta$ packed in $D(c,r+2\delta +\frac{\epsilon }{2}cos\theta )$. The fact that D_c is one of them implies that l ≤ 6, which proves the claim in the case where r ≥ ε.

• If r < ε, then c and the p̄_i are centers of pairwise-disjoint open disks of radius $\frac{r}{2}cos\theta$. Let D_c, D₁, …, D_l denote these disks. Since the belong to B(c, r + 2δ), D_c, D₁, …, D_l are included in $D(c,r+2\delta +\frac{r}{2}cos\theta )$. Now, B(c, r) is a Delaunay ball, hence its bounding sphere contains at least two points of L, which implies that $r\ge \frac{\epsilon }{2}$. Moreover, the hypotheses of the theorem state that $\delta <\frac{\epsilon }{4}(\frac{cos\theta }{2sin\frac{\pi }{7}}-1)$, which is at most $\frac{r}{2}(\frac{cos\theta }{2sin\frac{\pi }{7}}-1)$. Therefore, D_c, D₁, …, D_l form a congruent packing of a disk of radius

  $$r+2\delta +\frac{r}{2}cos\theta <r+r\left(\frac{cos\theta }{2sin\frac{\pi }{7}}-1\right)+\frac{r}{2}cos\theta =\frac{r}{2}cos\theta \left(\frac{1}{sin\frac{\pi }{7}}+1\right).$$

  It follows, by the same result as above on congruent packings of disks, that l ≤ 6, which proves the claim in the case where r < ε.

The claim implies that the vertices of σ are among the six nearest neighbors of w. Since this is true for any edge or triangle of (L), and since the vertices of (L) belong to ${\mathcal{C}}_{\nu }^W(L),{\mathcal{C}}_{\nu }^W(L)$ contains all the edges and triangles of (L). This ends the proof of the theorem.

The next theorem guarantees that the simplices of ${\mathcal{C}}_{\nu }^W(L)$ are not too large as far as the ν_i remain bounded. It follows that the size of ${\mathcal{C}}_{\nu }^W(L)$ is linear in |L|, since L is sparse. This property can be generalized to higher dimensions, at the price of an exponential growth of the constant factor. This motivates the use of the witness complex instead of the Delaunay triangulation.

Theorem 3.8

Assume that δ, ε satisfy $\delta +\epsilon <\frac{cos\theta }{\sqrt{6}}{\text{lr}}_k(S)$. Then, for any point w ∈ W, the distance between w and its sixth nearest neighbor among the points of L is at most $\delta +(\frac{\sqrt{6}}{cos\theta }+\text{1)(}\delta +\epsilon )$. As a consequence, for any sequence ν of integers such that ν₁ ≤ 6, the total number of simplices of ${\mathcal{C}}_{\nu }^W(L)$ is at most $2^{O({(\frac{\delta +\epsilon }{\epsilon cos\theta })}^3)}\mid L\mid$, which is linear with respect to |L| as far as θ is fixed and δ is within a constant factor of ε.

Proof

Let w ∈ W, and let w̄ be a point of S closest to w. Since W is a δ-noisy sample of S, we have d(w, w̄) ≤ δ. We call p₁, …, p_l the points of L that lie in $B(\overline{w},(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))$, and p̄₁, …, p̄_l their orthogonal projections onto the plane T_k(w̄). We will prove that l ≥ 6.

Since L is a (δ + ε)-sample of S, the balls B_i = B(p_i, δ + ε) cover $S\cap B(\overline{w},\frac{(\delta +\epsilon )\sqrt{6}}{cos\theta })$ (observe that, among the balls of radius δ + ε centered at the points of L, only the B_i intersect $B(\overline{w},\frac{(\delta +\epsilon )\sqrt{6}}{cos\theta })$). It follows that, inside T_k(w̄), the disks D_i = D(p̄_i, δ + ε) cover the orthogonal projection of $S\cap B(\overline{w},\frac{(\delta +\epsilon )\sqrt{6}}{cos\theta })$. Now, according to the hypothesis of the lemma, we have $\frac{(\delta +\epsilon )\sqrt{6}}{cos\theta }<{\text{lr}}_k(S)$. Thus, by Lemma 2.7, $S\cap B(\overline{w},\frac{(\delta +\epsilon )\sqrt{6}}{cos\theta })$ is a topological disk whose orthogonal projection onto T_k(w̄) contains the projection D of the intersection of $B(\overline{w},\frac{(\delta +\epsilon )\sqrt{6}}{cos\theta })$ with the cone of apex w̄, of axis aligned with n_k(w̄), and of half-angle $\frac{\pi }{2}-\theta$. Therefore, the D_i cover D, which is a disk of center w̄ and radius $(\delta +\epsilon )\sqrt{6}$. Thus, the number of disks D_i is at least

$$\frac{\text{Area}(D)}{\text{Area}(D_i)}=\frac{6\pi {(\delta +\epsilon )}^2}{\pi {(\delta +\epsilon )}^2}=6.$$

It follows that the number of points of L that lie in $B(\overline{w},(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))$ is at least 6. As a result, the distance from w to its sixth nearest landmark is at most $\text{d}(w,\overline{w})+(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon )\le \delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon )$.

Let us now bound the size of ${\mathcal{C}}_{\nu }^W(L)$. Let p be a point of L. From the above paragraph we deduce that the edges of ${\mathcal{C}}_{\nu }^W(L)$ incident to p are included in balls of radii at most $\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon )$. Hence, all edges belong to a common ball of center p and radius $r\le 2\delta +2(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon )$, which is equal to $2\epsilon (1+\frac{\sqrt{6}}{cos\theta }+(\frac{\sqrt{6}}{cos\theta }+2)\frac{\delta }{\epsilon })$. The neighboring vertices q₁, …, q_l of p in ${\mathcal{C}}_{\nu }^W(L)$ belong to B(p, r) as well. Now, since the points of L are farther than ε from one another, the q_i are centers of pairwise-disjoint balls of radius $\frac{\epsilon }{2}$, hence their number l is at most $\frac{\text{Vol}(B(p,r))}{\text{Vol}(B(p,\frac{\epsilon }{2}))}\le 64{(1+\frac{\sqrt{6}}{cos\theta }+(\frac{\sqrt{6}}{cos\theta }+2)\frac{\delta }{\epsilon })}^3=O(\frac{1}{{cos}^3\theta }{(1+\frac{\delta }{\epsilon })}^3)$. Since every simplex of ${\mathcal{C}}_{\nu }^W(L)$ incident to p is uniquely defined as a subset of {q₁, …, q_l}, the number of simplices of ${\mathcal{C}}_{\nu }^W(L)$ incident to p is at most 2^l, which gives the result.

3.2.2 Manifold Extraction

It follows from Theorem 3.7 that ${\mathcal{C}}_{\nu }^W(L)$ contains (L), but Fig. 4 (center)⁴ shows that ${\mathcal{C}}_{\nu }^W(L)$ is not restricted to (L) and contains additional simplices that are small enough to be ν-witnessed. Nevertheless, it is possible to extract from ${\mathcal{C}}_{\nu }^W(L)$ a simplicial surface Ŝ isotopic to S and at Hausdorff distance O(ε + δ) of S. The extraction procedure takes a number ϱ as parameter and proceeds as follows:

1. Since the goal is to extract a 2-manifold, only the 2-skeleton of ${\mathcal{C}}_{\nu }^W(L)$ is considered. Since it may not be an embedded complex, we intersect it with (L). The result is a pure 2-dimensional subcomplex of (L).

   To guarantee that the output simplicial surface has no skinny triangle, we delete from all the triangles whose radius-edge ratios are greater than ϱ.

2. We greedily remove from all the triangles incident to sharp edges. An edge is sharp if all its incident triangles in lie in a small wedge of angle at most $\frac{\pi }{2}$. This definition applies in particular to edges that are incident to one single triangle.

   By a depth-first walk in the dual graph of the remaining part of , we extract the outer boundary of .

Observe that steps 3 and 4 correspond to the manifold extraction procedure of [1–3]. As argued in these papers, the outcome is a simplicial complex Ŝ whose dihedral angles are greater than $\frac{\pi }{2}$. Moreover, thanks to step 2, the radius-edge ratios of the facets of Ŝ are at most ϱ. However, two issues arise: first, by greedily removing non-Delaunay triangles or triangles with sharp edges or large radius-edge ratios from ${\mathcal{C}}_{\nu }^W(L)$, steps 1 through 3 might end up with an empty complex . As a result, Ŝ may be empty. Second, the outer boundary of might not be an embedded surface, since it may contain multiple vertices or edges. By proceeding with a depth-first search on the dual graph of , step 4 duplicates multiple vertices and edges, so that the resulting complex Ŝ is a simplicial surface whose immersion in ℝ³ coincides with the outer boundary of .

Theorem 3.9

Let $\varrho =1+\frac{1-2sin\frac{\pi }{7}}{8sin\frac{\pi }{7}}\approx 1.038$. Assume that $\theta <arctan\frac{\sqrt{3}}{1+4\varrho }\approx 18.6deg$ and that $\delta <\frac{{cos}^4\theta (cos\theta -2sin\frac{\pi }{7})}{(2{cos}^2\theta +\sqrt{6}cos\theta +4cos\theta sin\frac{\pi }{7}-2\sqrt{6}sin\frac{\pi }{7})(cos\theta +\sqrt{6})(4+3{cos}^2\theta )\varrho \sqrt{3}}{\text{lr}}_k(S)$. If ε satisfies $\frac{8sin\frac{\pi }{7}}{cos\theta -2sin\frac{\pi }{7}}\delta <\epsilon <\frac{{cos}^3\theta }{(cos\theta +\sqrt{6})(4+3{cos}^2\theta )\varrho \sqrt{3}}{\text{lr}}_k(S)-\frac{2cos\theta +\sqrt{6}}{cos\theta }\delta$, then, for any sequence ν of integers such that ν₀ ≥ 1 and ν₁ = ν₂ = 6, the simplicial complex Ŝ extracted from ${\mathcal{C}}_{\nu }^W(L)$ with parameter ϱ is an embedded surface isotopic to S and at Hausdorff distance at most $(\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))\frac{\varrho \sqrt{3}}{{cos}^2\theta }$ from S.

The proof of the theorem follows roughly the same scheme as in [8] and it uses material that comes mainly from that paper. Here is a short overview:

• First, we show that the triangles of (L) are not skinny and make large dihedral angles. This fact, combined with Theorem 3.7, implies that complex contains (L) after step 3 above. We deduce that Ŝ is not empty, since (L) is a manifold without boundary, by Theorem 2.6.

• Second, we use Theorem 3.3(ii) of [8] to show that Ŝ is a Lipschitz surface, which implies in particular that it is an embedded surface.

• Third, we use Proposition 6.4 of [8] to bound the Hausdorff distance 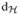(Ŝ, S) between Ŝ and S. We show that 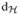(Ŝ, S) is small compared to the Lipschitz radii of Ŝ and S.

• Finally, we apply Theorem 6.2 of [11] to show that Ŝ and S are isotopic.

The rest of Sect. 3.2 is devoted to the details of the proof of Theorem 3.9 and it can therefore be skipped in a first reading. The following results from [8] will be useful:

Lemma 3.10 (Triangle Normal)

Let S be a k-Lipschitz surface, and θ = arctan k. For any p ∈ S and for any triangle f = (u, v, w) such that u, v, w ∈ S ∩ B(p, lr_k (S)) and that the radius-edge ratio of f is at most ϱ, the angle between n_k (p) and the line orthogonal to the plane aff(u, v, w) is at most arcsin(2ϱ sin θ).

Lemma 3.11 (Normal Variation)

Let S be a k-Lipschitz surface, and θ = arctan k. ∀p, q ∈ S s.t. d(p, q) < lr_k (p), (n_k (p), n_k (q)) ≤ 2 θ.

Moreover, the hypotheses of Theorem 3.9 imply that the following conditions are satisfied:

$$\begin{array}{l}\text{C}1\delta <\frac{cos\theta -2sin\frac{\pi }{7}}{8sin\frac{\pi }{7}}\epsilon .\\ \text{C}2\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon )<\frac{{cos}^2\theta }{(4+3{cos}^2\theta )\varrho \sqrt{3}}{\text{lr}}_k(S).\end{array}$$

Ŝ is not Empty

Lemma 3.12

(L) is a 2-manifold with obtuse dihedral angles, isotopic to S, at Hausdorff distance δ + ε from S, and whose triangles have radius-edge ratios of at most ϱ.

Proof

Recall that L is a (δ + ε)-sample of S with $\delta +\epsilon <\frac{1}{7}{\text{lr}}_k(S)$, by C2. Therefore, hypothesis H1 of Theorem 2.6 is satisfied with ε replaced by δ + ε. Let now f be a triangle of (L), and let B(c, r) be a surface Delaunay ball that circumscribes f. Since L is a (δ + ε)-sample of S, we have r ≤ δ + ε, which implies that the circumradius of f is bounded by δ + ε. Moreover, since L is ε-sparse, the length of the shortest edge of f is at least ε. Therefore, the radius-edge ratio of f is at most $1+\frac{\delta }{\epsilon }$, which by C1 is less than $1+\frac{cos\theta -2sin\frac{\pi }{7}}{8sin\frac{\pi }{7}}\le \varrho$. This property holds for every triangle f of (L). Since in addition we assumed that $\theta <arctan\frac{\sqrt{3}}{1+4\varrho }$, we have $2\varrho sin\theta <cos(\theta +\frac{\pi }{6})<cos(2\theta )$, and thus hypothesis H2 of Theorem 2.6 is satisfied as well. It follows then from Theorem 2.6 that (L) is a 2-manifold isotopic to S and at Hausdorff distance δ + ε of S. Moreover, the oriented normals of (L) approximate the k-Lipschitz normals of S within an angle of arcsin(2ϱ sin θ). This means that, for any triangles f₁ and f₂ of (L) that share an edge, for any common vertex v, the normals n(f₁) and n(f₂) make angles of at most arcsin(2ϱ sin θ) with the k-Lipschitz normal n_k (v). Since $\theta <arctan\frac{\sqrt{3}}{1+4\varrho }$, arcsin(2ϱ sin θ) is less than $\frac{\pi }{4}$, hence the dihedral angle between f₁ and f₂ is greater than $\frac{\pi }{2}$.

Let us now prove that the closed 2-manifold (L) is included in complex upon termination of step 3 of the extraction process. This will imply that Ŝ is not empty, since it coincides with the outer boundary of , which encloses (L). According to Theorem 3.7, (L) is included in ${\mathcal{C}}_{\nu }^W(L)$ initially. By definition, (L) is a subcomplex of (L), and by Lemma 3.12 it is a 2-manifold (and thus a pure 2-dimensional complex). Thus, (L) is included in upon termination of step 1 of the extraction process. Still by Lemma 3.12, the radius-edge ratios of the triangles of (L) are at most ϱ, and (L) has obtuse dihedral angles. As a consequence, (L) remains in throughout steps 2 and 3.

Ŝ is a Lipschitz Surface

As argued in Sect. 3.2.2, the subcomplex Ŝ extracted from ${\mathcal{C}}_{\nu }^W(L)$ is a combinatorial surface, but its immersion in ℝ³ may not be an embedding. However, it coincides with the outer boundary of complex , thus, by moving the vertices of Ŝ slightly in ℝ³, one can easily turn the immersion into an embedding. Therefore, up to an infinitesimal perturbation of the vertices of Ŝ, we consider from now on that Ŝ is an embedded surface. This is needed for the sake of our proofs, but we will see after Lemma 3.15 that actually no perturbation is needed to embed Ŝ.

C2 and Theorem 3.8 imply that any triangle f of ${\mathcal{C}}_{\nu }^W(L)$ is included in a ball of radius $\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon )$. Since the radius-edge ratio of f is at most ϱ, a quick computation shows that the circumradius of f is at most $(\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))\varrho \sqrt{3}$, which by C2 is less than $\frac{{cos}^2\theta }{4+3{cos}^2\theta }{\text{lr}}_k(S)<\frac{1}{7}{\text{lr}}_k(S)$.

Orientation Convention 3.13

We orient every triangle f of Ŝ such that n(f) · n_k (v) ≥ 0 for each vertex v of f.

The existence of such an orientation follows from C2 and Lemmas 3.10 and 3.11. We will now prove that this convention induces a valid orientation of Ŝ.

Lemma 3.14

The Orientation Convention 3.13 induces a valid orientation of Ŝ.

Proof

It suffices to prove that the orientation of the triangles of Ŝ is consistent across the edges of Ŝ, i.e., that the orientations of any two adjacent triangles of Ŝ induce opposite orientations of their common edge. Let f and f′ be two triangles of Ŝ with a common edge e. Let v be a vertex of e. We call f_v and $f_v^{\prime }$ the respective orthogonal projections of f and f′ onto the plane T_k (v). Inside T_k (v), we endow triangles f_v and $f_v^{\prime }$ with the same orientations as f and f′ respectively. The Orientation Convention 3.13 states that n(f ) · n_k (v) and n(f′) · n_k (v) are both positive, hence so are n(f_v ) · n_k (v) and $\mathbf{n}(f_v^{\prime })·{\mathbf{n}}_k(v)$. Now, by the triangle normal Lemma 3.10, the planes aff(f ) and aff(f′) make angles of at most $arcsin(2\varrho sin\theta )<\frac{\pi }{4}$ with T_k (v). Since the dihedral angle between f and f′ is at least $\frac{\pi }{2}$, f_v and $f_v^{\prime }$ lie on either sides of the projection of e onto T_k (v). It follows that the orientations of f_v and $f_v^{\prime }$ induce opposite orientations of their common edge. Similarly, the orientations of f and f′ induce opposite orientations of e. Since this is true for any two triangles of Ŝ with a common edge, Ŝ is consistently oriented by the orientation convention.

Lemma 3.15

Ŝ is a k′-Lipschitz surface with ${\text{lr}}_{k^{\prime }}(\widehat{S})\ge {\text{lr}}_k(S)-3\varrho \sqrt{3}(\delta +(\frac{\sqrt{6}}{cos\theta }+1)\times (\delta +\epsilon ))$.

Proof

Let $d=(\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))\varrho \sqrt{3}$. For any point p ∈ Ŝ and any triangle f of Ŝ intersecting B(p, lr_k (S) − 3d), the circumradius of f is at most d, hence f is included in B(p, lr_k (S) − d). Let f_p be a triangle of Ŝ containing p, and let v be a vertex of f_p closest to p. We have d(p, v) ≤ d, hence f is included in B(v, lr_k (S)). Since the radius-edge ratio of f is at most ϱ, the triangle normal Lemma 3.10 states that (n(f ), n_k (v)) ≤ arcsin(2ϱ sin θ). Since this is true for any point p ∈ Ŝ and any triangle f ∈ Ŝ intersecting B(p, lr_k (S) − 3d), Theorem 3.3(ii) of [8] states that Ŝ is a k′-Lipschitz surface with k′ = tan(arcsin(2ϱ sin θ)) and lr_k′(Ŝ) ≥ lr_k (S) − 3d.

The fact that Ŝ is a Lipschitz surface implies that any infinitesimal perturbation of its vertices yields another Lipschitz (and thus embedded) surface. As a consequence, no perturbation of the vertices of Ŝ is in fact needed to embed Ŝ.

Hausdorff Distance (Ŝ, S)

Let $d=(\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))\varrho \sqrt{3}$. To apply Proposition 6.4 of [8] and bound (Ŝ, S), we need to check that the following conditions are satisfied:

• The vertices of Ŝ lie on S: this is true, since Ŝ is a subcomplex of ${\mathcal{C}}_{\nu }^W(L)$ and since L ⊂ S, by assumption.

• The circumradii of the triangles of Ŝ are at most d with $d<\frac{1}{7}{\text{lr}}_k(S)$: this is ensured by C2 and Theorem 3.8.

• For any triangle f of Ŝ and any vertex v of f, the angle between n(f ) and n_k (v) is less than $\frac{\pi }{3}-\theta$: this is ensured by the triangle normal Lemma 3.10 and by the fact that $\theta <arctan\frac{\sqrt{3}}{1+4\varrho }$.

• Ŝ has vertices on all the connected components of S: this is true because Ŝ encloses complex , which contains the closed surface (L) that has vertices on all the connected components of S (by Lemma 3.12), and because the triangles of are too small to connect distinct connected components of S.

It follows then from Proposition 6.4 of [8] that

$${\text{d}}_{\mathcal{H}}(S,\widehat{S})\le \frac{d}{{cos}^2\theta }=\left(\delta +\left(\frac{\sqrt{6}}{cos\theta }+1\right)(\delta +\epsilon )\right)\frac{\varrho \sqrt{3}}{{cos}^2\theta }.$$ (1)

Ŝ is isotopic to S

By (1), we have $d_{\mathcal{H}}(\widehat{S},S)\le \frac{d}{{cos}^2\theta }$, where $d=(\delta +(\frac{\sqrt{6}}{cos\theta }+1)(\delta +\epsilon ))\varrho \sqrt{3}$. By C2, this quantity is less than $\frac{1}{4}({\text{lr}}_k(S)-3d)$, which, by Lemma 3.15, is at most $\frac{1}{4}min\{{\text{lr}}_k(S),{\text{lr}}_{k^{\prime }}(\widehat{S})\}$. As a consequence, (Ŝ, S) is less than half the so-called weak feature sizes of ℝ³\Ŝ and of ℝ³\S, by Theorem 3.8 of [8]. This implies that Ŝ and S are isotopic, by Theorem 6.2 of [11].

3.3 Dealing with Noisy Data

Our previous results hold as far as the set L of landmarks lies on the surface S. This property can be ensured by assuming that the set W of witnesses, which contains L, is noise-free. However, Theorem 3.16 below shows that the property can still be ensured when W, L are noisy samples of S. In the sequel, λ₀ ≈ 0.078 denotes the smallest positive root of the polynomial 64λ⁶ + 832λ⁵ + 1008λ⁴ − 160λ³ − 4λ² − 12λ + 1. Moreover, given any $\theta \in [0,\frac{\pi }{2}]$, λ (θ) denotes the smallest positive root of 16 (4 sin² θ − 1)λ⁶ + 32λ⁵ − 12(2 + 3 sin² θ)λ⁴ + 8λ³ + (4 sin² θ + 63)λ² + 64λ − 16.

Theorem 3.16

Let S be a k-Lipschitz surface and L a δ-noisy ε-sparse (δ + ε)-sample of S. Assume that δ, ε satisfy the following conditions, where θ = arctan k:

$$\begin{array}{l}\text{N}1\delta <min\{\frac{1}{4},\frac{\sqrt{2}-4sin\theta }{2(\sqrt{2}+4sin\theta )},\frac{cos(2\theta )-2sin\theta }{2(cos(2\theta )+2sin\theta )},{\lambda }_0,\lambda (\theta )\}\epsilon .\\ \text{N}2\delta <min\{\frac{1}{14}{\text{lr}}_k(S)-\frac{1}{2}\epsilon ,\frac{1}{6}{\text{lr}}_k(S)-\frac{7}{12}\epsilon \}.\end{array}$$

Then, there exists a k′-Lipschitz surface S′, passing through the points of L, isotopic to S, and at Hausdorff distance of S at most ε + 3δ, such that:

$$\{\begin{array}{l}{k}^{\prime }=tan(arcsin(\frac{4((1+2sin\theta )\frac{\delta }{\epsilon }+sin\theta )}{2sin(arcsin\frac{1-2\frac{\delta }{\epsilon }}{2(1+2\frac{\delta }{\epsilon })}-2arcsin\frac{2\frac{\delta }{\epsilon }}{1-2\frac{\delta }{\epsilon }})}))=O(k+\frac{\delta }{\epsilon }),\hfill \\ {\text{lr}}_{k^{\prime }}(S^{\prime })\ge {\text{lr}}_k(S)-(2\epsilon +7\delta )>\frac{1}{2}{\text{lr}}_k(S).\hfill \end{array}$$

If the set W of witnesses is a δ-noisy δ-sample of a k-Lipschitz surface S for some sufficiently small δ (as compared to lr_k (S)), then Theorem 3.16 ensures that there exists an interval of values of ε such that any ε-sparse ε-sample L of W lies on a k′-Lipschitz surface S′ with $k^{\prime }=O(k+\frac{\delta }{\epsilon })$ and lr_k (S′) = Ω(lr_k (S)). Theorem 3.9 can then be applied to S′, W, L, provided that k, ε, and $\frac{\delta }{\epsilon }$ are small enough to meet its hypothesis. Then, because S′ is isotopic to S and close to it for the Hausdorff distance, the conclusion of Theorem 3.9 holds for S, W, L as well, with a slightly worse bound on the Hausdorff distance. There also exists a version of Theorem 3.16 for Lipschitz curves, which can be combined with the structural results of Sect. 3.1. The proof is roughly the same.

The rest of Sect. 3.3 is devoted to the proof of Theorem 3.16, which builds an isotopy φ: [0, 1] × S → ℝ³ such that S′ = φ(1, S) is a k′-Lipschitz surface passing through the points of L with $k^{\prime }=O(k+\frac{\delta }{\epsilon })$ and lr_k′(S′) = Ω(lr_k (S)). Intuitively, since the points of L lie ε away from one another, with ε large compared to the amplitude δ of the noise, the surface S can be snapped onto the points of L without changing its normals too much. This can be easily seen on simple examples, such as for instance when S is the x-axis in ℝ² (in this case, the snapped curve is the polygonal chain connecting the points of L in the order of their abscissae).

To build the isotopy φ, we first map the points of L to their nearest neighbors on S. If some point p ∈ L has two or more nearest neighbors on S, then we choose either of them. We get a new point set L̃ ⊂ S, together with a surjective map μ: L → L̃. The restricted Delaunay triangulation of L̃, (L̃), will play a prominent role in our construction.

Lemma 3.17

Under the hypotheses of Theorem 3.16, for any distinct points p, q of L, d(μ(p), μ(q)) ≥ ε − 2δ > 0.

Proof

Since L is δ-noisy, we have d(p, μ(p)) = d(p, S) ≤ δ and d(q, μ(q)) = d(q, S) ≤ δ. Moreover, since L is ε-sparse, we have d(p, q) ≥ ε. It follows by the triangle inequality that d(μ(p), μ(q)) ≥ ε − 2δ, which is positive, by N1.

It follows from this lemma that μ is one-to-one and hence bijective. Therefore, we can define a function φ̃: [0, 1] × L̃ → ℝ³ as follows:

$$\forall t\in [0,1],\forall p\in \stackrel{\sim }{L},\stackrel{\sim }{\phi }(t,p)=(1-t)p+t{\mu }^{-1}(p).$$

We can then extend φ̃ to [0, 1] × (L̃) by linearity:

$$\forall t\in [0,1],\forall p\in {\mathcal{D}}^S(\stackrel{\sim }{L}),\stackrel{\sim }{\phi }(t,p)={\lambda }_u\stackrel{\sim }{\phi }(t,u)+{\lambda }_v\stackrel{\sim }{\phi }(t,v)+{\lambda }_w\stackrel{\sim }{\phi }(t,w),$$

where λ_u, λ_v, λ_w are the barycentric coordinates of p in any triangle (u, v, w) of (L̃) containing p. If p belongs to several triangles, then φ̃(t, p) does not depend on the choice of the triangle, since (L̃) is an embedded simplicial complex. Moreover, φ̃ is a continuous function in variables (t, p).

Since L is a δ-noisy (ε + δ)-sample of S, L̃ is a noise-free (ε + 2δ)-sample of S with $\epsilon +2\delta <\frac{1}{7}{\text{lr}}_k(S)$, by N2. Therefore, hypothesis H1 of Theorem 2.6 is satisfied. Moreover, by Lemma 3.17, L̃ is (ε − 2δ)-sparse, hence the radius-edge ratios of the triangles of (L̃) are at most $\stackrel{\sim }{\varrho }=\frac{\epsilon +2\delta }{\epsilon -2\delta }$, which by N1 is less than $\frac{cos(2\theta )}{2sin\theta }$. It follows that hypothesis H2 is also satisfied, which implies that (L̃) is isotopic to S, by Theorem 2.6. This means that there is an isotopy I: [0, 1] × S → ℝ³ such that I (1, S) = (L̃). We define φ by applying I and φ̃ successively, at double speed:

$$\{\begin{array}{ll}\forall t\in [0,\frac{1}{2}],\forall p\in S,\hfill & \phi (t,p)=I(2t,p),\hfill \\ \forall t\in [\frac{1}{2},1],\forall p\in S,\hfill & \phi (t,p)=\stackrel{\sim }{\phi }(2t-1,I(1-p)).\hfill \end{array}$$

This is the standard way of composing isotopies. In particular, φ is well defined, since I (1, p) ∈ (L̃) for all p ∈ S. To prove that φ is an isotopy, it suffices to show that φ̃ itself is an isotopy, which boils down to showing that φ̃(t, .) is one-to-one as a function of p for all t ∈ [0, 1], since we already know that φ̃ is continuous and since (L̃) is compact. We will use an intermediate result:

Lemma 3.18

Under the hypotheses of Theorem 3.16, the following assertions hold:

1. For any two vertices u, v of (L̃), d(u, v) ≥ ε − 2δ.

2. For any vertex v and any non-incident simplex (edge or triangle) σ of (L̃), the distance between v and σ is at least $\epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}$.

3. For any two disjoint edges e, e′ of (L̃), the distance between e and e′ is bounded from below by $\epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}\sqrt{1-4\frac{{(1+2\frac{\delta }{\epsilon })}^2}{2{(1-2\frac{\delta }{\epsilon })}^2}{sin}^2\theta }$.

Proof

(i) is a direct consequence of the fact that L̃ is (ε − 2δ)-sparse.

Concerning (ii), it is proved in [8, Lemma 5.8] that, since assumptions H1–H2 of Theorem 2.6 are satisfied, (L̃) is a k̃-Lipschitz surface with k̃ = tan(arcsin(2ϱ̃ sin θ)) and lr_k̃ ((L̃)) ≥ lr_k (S) − 3(ε + 2δ). Let v be a vertex of (L̃), and σ a simplex (edge or triangle) of (L̃) that is not incident to v. If σ does not intersect B(v, lr_k̃((L̃))), then its distance to v is at least lr_k̃ ((L̃)) ≥ lr_k (S) − 3(ε + 2δ), which by N2 is greater than $\frac{\epsilon }{2}\ge \epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}$. Otherwise, the point p ∈ σ closest to v lies inside the ball B(v, lr_k̃ ((L̃))). Since (L̃) ∩ B(v, lr_k̃ ((L̃))) coincides with the graph of a bivariate function defined over the k̃-Lipschitz support plane of (L̃) at v (called T_k̃(v), for short), the orthogonal projection p̄ of p onto T_k̃(v) lies outside Ū(v), the orthogonal projection of the umbrella U(v) of triangles of (L̃) incident to v. Since v lies in the interior of Ū(v), the line segment [v, p̄] intersects the boundary of Ū(v). Let q̄ be a point of intersection, and q the point of the boundary of U (v) that projects onto q̄. Inside the plane that contains v, p and p̄ (and hence also q and q̄), (L̃) ∩ B(v, lr_k̃((L̃))) coincides with the graph of a k̃-Lipschitz univariate function defined over the line (v, p̄). Since⁵ k̃ < 1, the fact that q̄ ∈ [v, p̄] implies that d(v, q) ≤ d(v, p). Hence, d(v, p) is at least the distance between v and the boundary of U(v), which we must now bound from below. For any triangle (u, v, w) of (L̃) incident to v, the distance h from v to line (u, w), also known as the height of triangle (u, v, w), is given by $\text{d}(v,u)sin\widehat{\mathit{vuw}}$, and it is a lower bound on the distance between v and edge [u, w]. According to (i), we have d(v, u) ≥ ε − 2δ. Moreover, since the radius-edge ratios of the triangles are at most $\stackrel{\sim }{\varrho }=\frac{\epsilon +2\delta }{\epsilon -2\delta }$, every inner angle of (u, v, w) is at least $arcsin\frac{\epsilon -2\delta }{2(\epsilon +2\delta )}$. Therefore, we have $\widehat{\mathit{vuw}}\ge arcsin\frac{\epsilon -2\delta }{2(\epsilon +2\delta )}$ and $h\ge \frac{{(\epsilon -2\delta )}^2}{2(\epsilon +2\delta )}=\epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}$. Since this is true for any triangle of (L̃) incident to v, the distance between v and the boundary of U(v) is at least $\epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}$, which proves (ii).

By the same argument, for any disjoint edges e, e′ of (L), and for any point p ∈ e, the distance from p to e′ is at least the distance from p to the boundary of U(e) = U(u) ∪ U(v), where u, v are the vertices of e. Therefore, the proof of (iii) reduces to finding a lower bound on the distance between e and the points of ∂U (e). Let q be the point of ∂U (e) whose orthogonal projection q̄ onto the k̃-Lipschitz support plane T_k̃(v) minimizes the distance to the orthogonal projection ē = [ū, v] of e. The distance from any point p ∈ ∂U (e) to e is at least the distance from its orthogonal projection p̄ to ē, which is bounded from below by d(q̄, ē). Moreover, we have d(q̄, ē) ≥ d(q, e) cos(arctan k̃), since U (e) ⊂ (L̃) ∩ B(v, lr_k̃((L̃))), which coincides with the graph of a k̃-Lipschitz bivariate function defined over T_k̃(v). Therefore, the distance of any point of ∂U (e) to e is at least $\text{d}(q,e)cos(arctan\stackrel{\sim }{k})=\text{d}(q,e)\sqrt{1-4\frac{{(1+2\frac{\delta }{\epsilon })}^2}{{(1-2\frac{\delta }{\epsilon })}^2}{sin}^2\theta }$. We must find a lower bound on d(q, e). Let Σ ⊂ T_k̃(v) be the strip whose boundaries are the lines orthogonal to ē passing through ū and v. For any point p̄ ∉ Σ, the nearest neighbor of p̄ on ē is either ū or v. Hence, if q̄ ∉ Σ, then $\text{d}(q,e)\ge \epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}$, by (ii). For any point p̄ ∈ Σ, the nearest neighbor of p̄ on ē is also its nearest neighbor on the line aff(ē). Hence, if q̄ ∈ Σ, then q̄ is either a vertex of ∂Ū (e) (meaning that q is a vertex of ∂U (e)) or a point of ∂Σ (meaning that the nearest neighbor of q̄ on ē is either ū or v). In both cases, we have $\text{d}(q,e)\ge \epsilon \frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}$, by (ii). This proves (iii).

Let t ∈ [0, 1]. Observe that, since L is a δ-noisy sample of S, φ̃(t, .) moves the points of L̃ by at most δ. It follows, by convexity,⁶ that every point of (L̃) is moved by at most δ. Using Lemma 3.18, we can prove that φ̃(t, .) is one-to-one:

• For any simplex (vertex, edge, or triangle) σ of (L̃), the restriction of φ̃(t, .) to σ is one-to-one. Indeed, since φ̃(t, .) is linear on σ, its restriction to σ is one-to-one, provided that φ̃(t, σ ) has the same dimension as σ. This is clearly the case if σ is a vertex. If σ is an edge [u, v], then, since by N1 we have 2δ < ε − 2δ, φ̃(t, u) and φ̃(t, v) are distinct, by Lemma 3.18(i). If σ is a triangle (u, v, w), then we must show that φ̃(t, u), φ̃(t, v), and φ̃(t, w) are not collinear. Since every vertex of the triangle moves by at most δ, vertices u and v move by at most 2δ relative to w. Thus, each of them reduces the angle $\widehat{\mathit{uwv}}$ by at most $arcsin\frac{2\delta }{\epsilon -2\delta }$, since the vertices are at least ε − 2δ away from one another initially. Recall that the radius-edge ratio of (u, v, w) is at most $\stackrel{\sim }{\varrho }=\frac{2+2\delta }{\epsilon -2\delta }$, hence angle $\widehat{\mathit{uwv}}$ is at least $arcsin\frac{1}{2\stackrel{\sim }{\varrho }}=arcsin\frac{\epsilon -2\delta }{2(\epsilon +2\delta )}$ initially. It follows that $\widehat{\mathit{uwv}}$ does not vanish as u, v, w are moved by φ̃, since by N1⁷ we have $2arcsin\frac{2\delta }{\epsilon -2\delta }<arcsin\frac{\epsilon -2\delta }{2(\epsilon +2\delta )}$. Since this is true for any inner angle of (u, v, w), φ̃(t, (u, v, w)) is a nondegenerate triangle.

• Since the restriction of φ̃(t, .) to any simplex of (L̃) is one-to-one, φ̃(t, .) itself is one-to-one provided that the images of any two disjoint simplices of (L̃) (which are simplices of same dimensions) are disjoint, and that the images of any two non-disjoint simplices of (L̃) have disjoint relative interiors. Assume for a contradiction that two disjoint (resp. non-disjoint) simplices σ₁, σ₂ of (L̃) have non-disjoint images (resp. images with non-disjoint relative interiors) through φ̃(t, .). Since σ₁ ∩ σ₂ = ∅ (resp. int(σ₁) ∩ int(σ₂) = ∅), and since φ̃ moves the points of (L̃) continuously at some time t′ ∈ [0, t], either φ̃(t′, v₁) ∈ φ̃(t′, σ₂) for some vertex v₁ of σ₁ non-incident to σ₂, or φ̃(t′, v₂) ∈ φ̃(t′, σ₁) for some vertex v₂ of σ₂ non-incident to σ₁, or φ̃(t′, e₁) ∩ φ̃(t′, e₂) ≠ ∅ for two disjoint edges e₁ ∈ σ₁ and e₂ ∈ σ₂. In all three cases, the two simplices involved (namely, v₁ and σ₂, or v₂ and σ₁, or e₁ and e₂) lie at most 2δ away from each other in (L̃), since φ̃(t, .) does not move the points of (L̃) by more than δ. This contradicts Lemma 3.18, since by N1⁸ we have $\delta <\frac{\epsilon }{2}\frac{{(1-2\frac{\delta }{\epsilon })}^2}{2(1+2\frac{\delta }{\epsilon })}\sqrt{1-4\frac{{(1-2\frac{\delta }{\epsilon })}^2}{{(1-2\frac{\delta }{\epsilon })}^2}{sin}^2\theta }$. Therefore, disjoint simplices of (L̃) have disjoint images through φ̃(t, .), and non-disjoint simplices of (L̃) have images through φ̃(t, .) with disjoint relative interiors, which implies that φ̃(t, .) is one-to-one.

It follows that φ̃ is an isotopy from (L̃) to S′ = φ̃(1, (L̃)). As a consequence, φ is an isotopy from S to S′. In addition, since L̃ is a noise-free (ε + 2δ)-sample of S, we have (S, (L̃)) ≤ ε + 2δ, by Theorem 5.4 of [8]. Moreover, since φ̃(1, .) moves the points of (L̃) by at most δ, we have ((L̃), S′) ≤ δ. As a result, the Hausdorff distance between S and S′ is at most ε + 3δ. For each oriented simplex σ = [v₀, …, v_l ] of (L̃), we set the orientation of simplex φ̃(1, σ ) to [φ̃(1, v₀), …, φ̃(1, v_l)]. Since (L̃) is an oriented surface and φ̃ is an isotopy from (L̃) to S′, we get a valid orientation of S′. We conclude the proof of Theorem 3.16 with the following lemma:

Lemma 3.19

Under the hypotheses of Theorem 3.16, S′ is a k′-Lipschitz surface, with $k^{\prime }=tan(arcsin(\frac{4((1+2sin\theta )\frac{\delta }{\epsilon }+sin\theta )}{2sin(\text{arcsin}\frac{1-2\frac{\delta }{\epsilon }}{2(1+2\frac{\delta }{\epsilon })}-2\text{arcsin}\frac{2\frac{\delta }{\epsilon }}{1-2\frac{\delta }{\epsilon }})}))$ and lr_k′(S′) ≥ lr_k (S) − (2ε + 7δ).

Proof

The proof is roughly the same as for Lemma 5.8 of [8]. Let f′ be a triangle of S′, and f̃ the triangle of (L̃) such that f′ = φ̃(1, f̃). Since L̃ is an (ε + 2δ)-sample of S, f̃ is circumscribed by a ball of radius at most ε + 2δ. And since φ̃(1, .) does not move the vertices of f by more than δ, f′ is included in a ball of radius at most ε + 3δ, although its circumradius might be much larger. Moreover, as shown above in the proof of isotopy, the radius-edge ratio of f′ is at most ${\varrho }^{\prime }=\frac{1}{2sin(arcsin\frac{\epsilon -2\delta }{2(\epsilon +2\delta )})-2arcsin\frac{2\delta }{\epsilon -2\delta })}$.

Let p′ be a point of S′, and p a point of S closest to p′. Since (S, (L̃)) ≤ ε + 2δ and ((L̃), S′) ≤ δ, we have d(p, p′) ≤ ε + 3δ. Let r = lr_k (S) − (2ε + 7δ). For any triangle f′ = (u′, v′, w′) of S′ that intersects B(p′, r), f′ intersects B(p, r + ε + 3δ) and is therefore included in B(p, r + 2ε + 6δ). Let f̃ = (ũ, ṽ, w̃) be the triangle of (L̃) such that f′ = φ̃(1, f̃). Since φ̃(1, .) does not move the vertices of f̃ by more than δ, f̃ is included in B(p, r + 2ε + 7δ) = B(p, lr_k (S)). Therefore, lines (ũ, ṽ), (ṽ, w̃), and (w̃, ũ) make angles of at least $\frac{\pi }{2}-\theta$ with the k-Lipschitz normal n_k (p) of S at p. As a consequence,

$$\begin{array}{l}\mid ({\mathbf{w}}^{\prime }-{\mathbf{v}}^{\prime })·{\mathbf{n}}_k(p)\mid \le \mid ({\mathbf{w}}^{\prime }-\stackrel{\sim }{\mathbf{w}})·{\mathbf{n}}_k(p)\mid +\mid (\stackrel{\sim }{\mathbf{w}}-\stackrel{\sim }{\mathbf{v}})·{\mathbf{n}}_k(p)\mid +\mid (\stackrel{\sim }{\mathbf{v}}-{\mathbf{v}}^{\prime })·{\mathbf{n}}_k(p)\mid \\ \le \delta +\left|\right|\stackrel{\sim }{\mathbf{w}}-\stackrel{\sim }{\mathbf{v}}\left|\right|sin\theta +\delta .\end{array}$$

Since L̃ is an (ε + 2δ)-sample of S, we have ||w̃ − ṽ|| ≤ 2ε + 4δ. Moreover, since L is ε-sparse, we have ||w′ − v′|| ≥ ε. It follows that the angle between n_k (p) and line (v′, w′) is:

$$\begin{array}{l}arccos\frac{\mid ({\mathbf{w}}^{\prime }-{\mathbf{v}}^{\prime })·{\mathbf{n}}_k(p)\mid }{\left|\right|{\mathbf{w}}^{\prime }-{\mathbf{v}}^{\prime }\left|\right|}\ge arccos\frac{2\delta +(2\epsilon +4\delta )sin\theta }{\epsilon }\\ =\frac{\pi }{2}-arcsin\left(2(1+2sin\theta )\frac{\delta }{\epsilon }+2sin\theta \right).\end{array}$$

The same relation holds for lines (u′, v′) and (u′, w′) as well. Since the radius-edge ratio of f′ is at most ϱ′, the triangle normal Lemma 3.10 states that the angle between n_k (p) and the oriented normal n(f′) of f′ is at most $arcsin(4{\varrho }^{\prime }((1+2sin\theta )\frac{\delta }{\epsilon }+sin\theta ))$. Since this is true for any triangle of S′ that intersects B(p, r), Theorem 3.3(ii) of [8] states that S′ is a k′-Lipschitz surface with $k^{\prime }=tan(arcsin(4{\varrho }^{\prime }((1+2sin\theta )\frac{\delta }{\epsilon }+sin\theta )))$ and lr_k′(S′) ≥ r = lr_k (S) − (2ε + 7δ).

4 Application to Reconstruction from Point Samples

4.1 Algorithm

The algorithm works in any metric space. It takes as input a finite point set W, identified as the set of witnesses, and an optional countable sequence ν of integers, whose default value is ν_i = i + 1 ∀i (which corresponds to ${\mathcal{C}}_{\nu }^W={\mathcal{C}}^W$). The algorithm constructs a set L ⊆ W of landmarks iteratively, starting with L = ∅, and in the mean-time it maintains ${\mathcal{C}}_{\nu }^W(L)$. At each iteration, the witness lying furthest away from L is inserted in L, and ${\mathcal{C}}_{\nu }^W(L)$ is updated as described below. The process stops when L = W. The output of the algorithm is either the one-parameter family of complexes ${\mathcal{C}}_{\nu }^W(L)$ built throughout the process, or simply the diagram of their Betti numbers computed on the fly using the persistence algorithm⁹ of [37]. With this diagram at hand, the user can determine the scale at which to process the data: it is then easy to generate the corresponding subset of landmarks (the points of W have been sorted according to their order of insertion in L) and to rebuild its witness complex.

4.2 Update of ${\mathcal{C}}_{\nu }^W(L)$

Our strategy to update ${\mathcal{C}}_{\nu }^W(L)$ relies on the following observation: when a witness p is inserted in L, every simplex that appears in ${\mathcal{C}}_{\nu }^W(L)$ is incident to p, whereas every simplex that disappears from ${\mathcal{C}}_{\nu }^W(L)$ has a face that is no longer ν-witnessed because of the insertion of p in the set of landmarks. It follows that the ν-witnesses of all these simplices belong to the reverse κ-nearest witnesses¹⁰ of p, where κ = min{|L|, max_i ν_i }. Hence, ${\mathcal{C}}_{\nu }^W(L)$ can be updated, first by searching for the reverse κ-nearest witnesses of p, and then, for each witness w in the outcome, by searching for the κ nearest landmarks of w, to determine which simplices to insert or delete from ${\mathcal{C}}_{\nu }^W(L)$. A number of dynamic data structures exist that can perform these queries efficiently—see [18] for a survey. Note however that κ can be as large as |W|, a case in which the above queries take linear time. Moreover, when ν_i ≥ |L| ∀i, ${\mathcal{C}}_{\nu }^W(L)$ coincides with the complete hypergraph of L and hence has an exponential size. Nevertheless, in Euclidean space ℝⁿ, κ is more likely to be a constant depending (exponentially) on n, which reduces the size of ${\mathcal{C}}_{\nu }^W(L)$ to O(|L|), by Theorem 3.8. The total time spent by the algorithm to maintain ${\mathcal{C}}_{\nu }^W(L)$ is then O(|W|²), since any newly-created landmark has Θ(|W|) reverse κ-nearest witnesses (these can be detected naively by an exhaustive search on the set W), each of which witnesses a constant number of simplices (these can be found by maintaining the list of κ nearest landmarks of each witness). We conjecture that it should be possible to reduce the time complexity to O(|W| log |W|), under some sparseness condition on W.

4.3 2d and 3d Cases

We take ν = (1, 2, 3) in 2d and ν = (1, 6, 6, 4) in 3d, as prescribed by the theory. Moreover, we replace ${\mathcal{C}}_{\nu }^W(L)$ by its intersection with (L), noted $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L)$. This makes sense because, (L) being a subset of (L), Theorems 3.1 and 3.9 hold the same if ${\mathcal{C}}_{\nu }^W(L)$ is replaced by $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L)$. The advantage is that $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L)$ can be stored as a subcomplex of (L), which allows to speed-up the (reverse) nearest neighbors queries in practice. Another thing in 3d is that we also maintain the subcomplex Ŝ extracted from $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L)$ by the procedure of Sect. 3.2.2.

4.4 Theoretical Guarantees

Let L(i) denote the set L at the end of the ith iteration of the algorithm. We call ε(i) the minimum number such that L(i) is an ε(i)-sample of W. Since L(i) grows with i, ε(i) is a decreasing function of i. Moreover, we have the following:

Lemma 4.1

At any iteration i, L(i) is an ε(i)-sparse ε(i)-sample of W.

Proof

At each iteration j ≤ i of the algorithm, the witness p(j ) farthest from L(j − 1) is inserted in L(j − 1). Right before this insertion, L(j − 1) is an ε(j − 1)-sample of W. This means that the distance from p(j ) to L(j − 1) is ε(j − 1). Since L keeps growing during the process, we have ε(j ) ≥ ε(j + 1) ∀ j ≤ i. Therefore, every point inserted in L before or at iteration i is at least ε(i) away from L at the time of its insertion. This implies that L(i) is an ε(i)-sparse point sample.

Combining this lemma with the structural results of Sects. 2 and 3, we obtain a guarantee on the stability of the topological type of the witness complex during the course of the algorithm:

Theorem 4.2

Assume that the input W is a δ-noisy δ-sample of some k-Lipschitz curve (resp. surface) S in ℝ² (resp. ℝ³). Then, $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L(i))$ (resp. Ŝ(i)) is isotopic to S and close to S for the Hausdorff distance whenever L(i) satisfies the hypotheses of Theorems 2.9, 3.1, and 3.16 (resp. 3.9 and 3.16), which eventually happens if δ and k are small enough.

Under mild assumptions on the input, the theorem guarantees that the topological type of $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L(i))$ (resp. Ŝ(i)) stabilizes for some time during the course of the algorithm and therefore that a plateau appears in the diagram of the Betti numbers of $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L(i))$ (resp. Ŝ(i)), showing the correct values. In practice, the user does not know exactly where the plateau should be located in the diagram, because δ, k, and lr_k (S) are unknown. Nevertheless, our structural results give a lower bound on the length of the plateau, which is of order of (alr_k (S) − bδ), where a, b are two constants. As a consequence, for sufficiently small δ, the plateau is long enough to be detected by the user or any statistical analysis performed in a post-processing step. In the case where W samples several manifolds (such as in the example of Fig. 1), Theorem 4.2 guarantees¹¹ that several plateaus appear in the diagram of Betti numbers, each one showing a plausible reconstruction, depending on the scale at which the input data set W is processed. Once again, these guarantees hold as long as the input point set W is sufficiently dense compared to lr_k (S). In particular, no sparseness condition on W is required, although S can be non-smooth and W can be noisy. This makes our reconstruction method more practical than previous work in this context [8, 24].

4.5 Experimental Results and Discussion

Figures 5 and 6 show the evolution of the Betti numbers of Ŝ(i) throughout the course of the algorithm on two different input point sets. The abscissa represents $\frac{1}{\epsilon (i)}$, which is an increasing function of i and gives an idea of the scale at which the input data is being processed. The first point set was generated using Chew’s algorithm on an algebraic surface commonly known as the tanglecube. The second point set is courtesy of the Stanford shape repository and was obtained from a 3d scanner.

Fig. 5.

Diagram of Betti numbers of Ŝ for the Tanglecube point set

Fig. 6.

Diagram of Betti numbers of Ŝ for the Happy Buddha point set

Figure 5 shows three phases in the evolution of the Betti numbers. At first, their behavior is erratic, which means that the topology of Ŝ(i) keeps changing because ε(i) is not yet small enough compared to lr_k (S). The top picture in the right column shows Ŝ(i) at some point during this phase. Then, ε(i) satisfies the hypothesis of Theorem 3.9 for a while, which implies that the Betti numbers stabilize to the right value and a plateau appears in the diagram—here, the surface is connected, of genus five, and without boundary, hence β₀ = β₂ = 1 and β₁ = 10. The size of the plateau depends on the value of δ compared to lr_k (S). The two middle pictures in the right column show Ŝ(i) at two different times during this phase. Finally, ε(i) becomes too small, and $({\mathcal{C}}_{\nu }^W\cap \mathcal{D})(L(i))$ does not contain (L(i)) any longer. As a result, some holes appear in the complex, and Ŝ(i) is simply the boundary of a myriad of randomly agglomerated tetrahedra. An example is shown in the bottom-right corner of the image.

The same kind of phenomenon occurs in Fig. 6, where the plateau is smaller due to the fairly high value of δ. The top-right picture shows Ŝ(i) at some point on the plateau. Interestingly enough, the value of β₁ on the plateau (β₁ = 12) means that the genus of Ŝ(i) is six, which coincides with the genus of the scanned physical model but not with that of the mesh provided by the repository, which contains extra handles such as the one shown at the center of Fig. 6. The reason is that, due to the presence of noise and holes in the input point cloud, standard reconstruction algorithms fail at retrieving the topology of the original object because they consider the data at full scale only. In contrast, our algorithm performs reconstructions at various scales and generates plateaus whenever the topological type of the reconstruction is stable, which corresponds to plausible topological types of the original object. As an illustration, observe that a new plateau starts on the right-hand side of the main plateau, right before the data structure becomes unstable. This new plateau shows β₁ = 14, which indicates that a new handle has been detected, as illustrated in the bottom-right corner of Fig. 6. Another example is shown in Fig. 1, where the diagram has two well-separated plateaus corresponding to two plausible reconstructions: a torus, and a simple closed curve drawn on that torus. To handle the change in dimension (shown on the right-hand side of the figure), we maintained ${\mathcal{C}}_{\nu }^W(L(i))$ for both ν = (1, 2, 3, 4) and ν = (1, 6, 6, 4) simultaneously and determined at each step the complex to keep according to their Betti number β₂.

The definitive choice of the scale(s) at which to deal with the data is highly dependent on the application, and therefore it should be made by the user. We expect that statistical analysis on our diagrams would allow our algorithm to detect the plateaus and to suggest reasonable choices. Note however that not all the plateaus are guaranteed to be meaningful. Indeed, the fact that the homotopy type of the complex remains stable over a period of time does not imply that the complex itself is stable combinatorially. In the example of Fig. 7 for instance, the insertion of a new landmark creates a loop but at the same time destroys another loop in the complex, thereby keeping its Betti numbers unchanged, whereas the sets of generators of the homology groups of the complex do differ. Such events leading to fake plateaus in the diagram are likely to be rare and short, since they correspond to highly unstable phases of the course of the algorithm, where the sampling conditions are not satisfied. Nevertheless, according to the example of Fig. 7, they can occur, and the question of whether they can be detected and discarded automatically is still open.

Fig. 7.

(Color online) A set W of witnesses (in black) sampling a smooth curve in the plane, and a sparse subset L of landmarks. The witness complex of L relative to W is shown in green, while the edges of the order-two Voronoi diagram of L are shown in grey. Note how the insertion of a ∈ W in L creates a new loop but at the same time removes edge [b, c] from the complex, thereby destroying the former loop. The homotopy type of the complex remains unchanged

5 Conclusion

We have introduced a new reconstruction method based on the use of the witness complex. This method uses inter-sample distances alone and can therefore be used in any metric space. Moreover, it stands in sharp contrast with previous work in the area, since it is multiscale and gives some insights on the various plausible topological types of the original object. We believe that this approach to manifold reconstruction is highly practical and has a number of potential applications, such as for instance topological noise removal or mesh compression. As a side product, in order to prove our algorithm correct on Lipschitz curves and surfaces, we have worked out interesting relationships between the witness complex and the restricted Delaunay triangulation in 2d and 3d. Our structural results assume that the set L of landmarks is an ε-sparse ε-sample of the set W of witnesses. This hypothesis is stringent but not unrealistic in practice, since L is generated by the algorithm. In contrast, our assumption on the input W is fairly mild.

Let us mention that our structural results still hold in the somewhat more general setting where W is an adaptive δ-sample of S in the sense of [1] and where L is an (ε, κ)-sample of W in the sense of [24]. The proofs are roughly the same, with an additional twist which slightly degrades the constants.

A number of theoretical questions are left open by this work, including:

• Is it possible to devise automatic procedures for discriminating the fake plateaus from the meaningful plateaus in the diagram of Betti numbers? One possible approach, suggested by the example of Fig. 7, would be to keep track of the generators of the homology groups of the complex throughout the course of the algorithm, similarly to what is done in persistent homology [37]. The difficulty here is that our family of complexes is not a filtration, the complex at iteration i being neither a subset nor a superset of the complex at iteration i + 1.

• Can the time complexity of the algorithm be reduced to O(|W| log |W|)? Reverse nearest neighbors queries can take linear time in the worst case, because a landmark can be among the nearest landmarks of a linear number of witnesses. As a consequence, reducing the time complexity requires to control the sizes of the lists of reverse nearest witnesses, which can probably be done under some sparseness condition on W. However, can it be done under weaker conditions?

• The behavior of our reconstruction algorithm depends highly on the order in which the witnesses are inserted in L—in some sense, the algorithm is parameterized by this order. In the present paper, we use one possible ordering of the witnesses, prescribed by the furthest-point criterion. However, many other orderings could be considered, some of which might be relevant in different contexts. One appealing example is the problem of reconstructing curves and surfaces in the presence of background noise, where the furthest-witness strategy applied in this paper fails for obvious reasons.

• Can our structural results be extended to manifolds of higher dimensions? Since the publication of the conference version of this paper, significant steps have been made in this direction: de Silva has extended the Weak Witness Theorem to the case of point clouds lying on Riemannian manifolds of constant sectional curvature [21]. Unfortunately, focusing on the Euclidean case, we have seen that the Weak Witness Theorem does not hold for general smooth submanifolds of ℝⁿ [32]. Nevertheless, Cheng, Dey, and Ramos had proved that restricted Delaunay triangulations of dense point samples enjoy similar properties in higher dimensions as they do in ℝ³, provided that the standard Delaunay test is replaced by a weighted Delaunay test [15]. Building on their work, we have extended the results of this paper to the general case of smooth submanifolds of ℝⁿ, with the Euclidean metric replaced by a weighted metric [6]. Combined with recent advances on the front of topological persistence, these results have led to a new class of reconstruction algorithms, inspired from this work and based on the use of the witness complex, whose space and time complexities scale up with the intrinsic dimension of the point cloud data, as opposed to the dimension of the ambient space [14].