Variance computations for functional of absolute risk estimates

Abstract

We present a simple influence function based approach to compute the variances of estimates of absolute risk and functions of absolute risk. We apply this approach to criteria that assess the impact of changes in the risk factor distribution on absolute risk for an individual and at the population level. As an illustration we use an absolute risk prediction model for breast cancer that includes modifiable risk factors in addition to standard breast cancer risk factors. Influence function based variance estimates for absolute risk and the criteria are compared to bootstrap variance estimates.

1 Background

Computing variances of complex statistics can be challenging, especially for designs other than simple random sampling. We show how influence function linearization techniques can be used to obtain variances for estimates of absolute risk of disease and functional of absolute risk. We apply the approach to functions recently proposed by Petracci et al. (submitted) to assess the impact of changes in the risk factor distribution on absolute risk for an individual and at the population level. These variance estimates are easy to implement and can accommodate various sampling designs. We also discuss alternatives to the influence function approach to variance computation. As an example, we use an absolute risk prediction model for breast cancer that includes modifiable risk factors in addition to standard breast cancer risk factors.

2 Absolute Risk

The cause specific formulation of absolute risk of an event, for example breast cancer, is as follows. Let 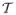denote the time to event of cause one. The absolute risk in the age interval (a, a + τ] for a person who has survived event free to age a is defined as

$$r(a,\tau ,\mathbf{x})=P(\mathcal{T}\le a+\tau ,\mathit{cause}=1\mid \mathcal{T}>a)=\frac{{\int }_a^{a+\tau }{h}_1(t,\mathbf{x})exp\{-{\int }_0^t{h}_1(u,\mathbf{x})+h_2(u,\mathbf{x})du\}dt}{exp\{-{\int }_0^a{h}_1(u,\mathbf{x})+h_2(u,\mathbf{x})du\}}={\int }_a^{a+\tau }{h}_1(t,\mathbf{x})exp\{-{\int }_a^t{h}_1(u,\mathbf{x})+h_2(u,\mathbf{x})du\}dt,$$ (1)

where x denotes individual risk or protective factors, h₁(t, x) is the cause specific hazard for cause 1, and h₂(t, x) denotes the competing mortality hazard. While one could model h₂ as a function of x given appropriate data, we assume that it depends only on age, i.e. h₂(t, x) = h₂(t).

The cause-specific hazard can be modeled as h₁(a, x) = h₁₀(a)rr(a, x), the product of the age-specific baseline hazard rate, h₁₀(a), and a relative risk model, rr(a, x) that includes covariates and may depend on age. Both, rr(a, x) and h₁₀(a) can be estimated directly from cohort data, nested case-control data (Langholz and Borgan, 1997) or case-cohort data (Self and Prentice, 1988). However, while relative risks may be estimated reliably from such data, absolute risks may not be representative for the target population of interest and data on competing causes of death may be imprecise. An alternative approach is to combine relative risk estimates rr(a, x) and age-specific attributable risk estimates, AR(a), obtained from cohort data, nested case-control data, case-cohort or case-control data with age-specific incidence rates $h_1^{\ast }(a)$ from registries to obtain the age-specific baseline hazard rates from $h_{10}(a)=\{1-AR(a)\}{h}_1^{\ast }(a)$, see e.g. Gail et al. (1989).

In what follows we approximate formula (1) by assuming a piecewise exponential model, where h₁₀(a) = h_1j and h₂(a) = h_2j are constant over single year age intervals [a_j–1, a_j), j = 1, …, J, leading to

$$r(a,\tau ,\mathbf{x})=\sum _{j=a}^{a+\tau -1}\frac{h_{1j}{rr}_j(\mathbf{x})}{h_{1j}{rr}_j(\mathbf{x})+h_{2j}}[1-exp\{-(h_{1j}{rr}_j(\mathbf{x})+h_{2j})\}]exp\{-\sum _{l=a}^{j-1}(h_{1l}{rr}_l(\mathbf{x})+h_{2l})\}.$$ (2)

3 Criteria to assess the effects of changes in risk factors on risk for individuals and for a population

Sometimes factors X in (1) include non-modifiable factors, denoted by X₁, and modifiable risk factors, X₂. In our motivating breast cancer model an example of a non-modifiable risk factor is age at menarche, and a modifiable risk factor is alcohol consumption. We now review novel criteria we proposed earlier (Petracci et al, submitted) to quantify the impact of changes in the risk factor distribution on absolute risk for an individual and at the population level.

To assess the impact of changing X₂ to their lowest levels, X₂₀, we defined the risk reduction as d(X₁, X₂) = {r(X₁, X₂) – r(X₁, X₂₀)}, where r denotes the absolute risk estimate (1). The corresponding fractional risk reduction is fd(X₁, X₂) = {d(X₁, X₂)/r(X₁, X₂)}. To evaluate the effects of risk modification at the population level for a given population, d and fd are averaged over the entire population or within subgroups. Subgroups can be defined by particular risk factor combinations or by using the Lorenz curve to identify risk factor combinations that account for a given percentage of total population risk. The mean risk reduction for a specific subset S is calculated from the formula:

$${\overline{d}}^S({\mathbf{X}}_1,{\mathbf{X}}_2)=E(d({\mathbf{X}}_1,{\mathbf{X}}_2)\mid ({\mathbf{X}}_1,{\mathbf{X}}_2)\in S)=\frac{{\int }_{X_1,X_2}\{r({\mathbf{X}}_1,{\mathbf{X}}_2)-r({\mathbf{X}}_1,{\mathbf{X}}_{20})\}I\{({\mathbf{X}}_1,{\mathbf{X}}_2)\in S\}dF({\mathbf{X}}_1,{\mathbf{X}}_2)}{{\int }_{{\mathbf{X}}_1,{\mathbf{X}}_2}I\{({\mathbf{X}}_1,{\mathbf{X}}_2)\in S\}dF({\mathbf{X}}_1,{\mathbf{X}}_2)},$$ (3)

where I{(X₁, X₂) ε S} = 1 if (X₁, X₂) ε S and 0 otherwise. When S corresponds to the whole population, then (3) reduces to

$$\overline{d}({\mathbf{X}}_1,{\mathbf{X}}_2)=E\{d({\mathbf{X}}_1,{\mathbf{X}}_2)\}={\int }_{{\mathbf{X}}_1,{\mathbf{X}}_2}\{r({\mathbf{X}}_1,{\mathbf{X}}_2)-r({\mathbf{X}}_1,{\mathbf{X}}_{20})\}dF({\mathbf{X}}_1,{\mathbf{X}}_2).$$ (4)

Similarly, the mean fractional risk reduction is f̄d(X₁, X₂) = E{fd(X₁, X₂)}, which is different from Petracci et al., who computed the percent reduction in mean risk.

4 Variance estimation

4.1 Approaches to variance estimation

A general analytic approach to computing the variance of a complex statistic, T, is linearization, by which T is approximated by a linear function of random variable(s), whose variances can often be easily obtained. A well known linearization is the parametric delta method, for which T(θ̂) ≈ T(θ)+T′(θ)(θ̂–θ). This approach requires that θ be finite dimensional. Benichou and Gail (1995) used this approach for the variance computation of absolute risk with discrete covariates, which lead to very complicated expressions that are difficult to program. Because we wished to develop a method that applies to continuous covariates (such as body mass index) and makes no parametric assumptions on them, we used the influence function linearization approach proposed by Deville (1999) and used by Graubard and Fears (2005) to obtain Taylor deviates for the computation of the variance of the attributable risk, to find the variances of estimates of absolute risk and the criteria in Section 3. A great advantage of this approach is that is simple, easy to implement, and can easily be extended to accommodate complex sampling designs. Results are also available for linearization methods for estimates defined as the solution of estimating equations (Binder, 1983). However, in our setting estimating equations are not readily formulated.

Alternatively one could use resampling approaches, such as the jackknife and bootstrap, to estimate the variance of complex statistics. The jackknife is based on repeated computation of the statistic for a dataset that omits one of the observations at a time, which can make it computationally intensive. Jackknife and linearization methods are similar in the sense that analytical derivatives in the linearization are replaced by numerical approximation in the jackknife (Davison and Hinkley, page 50, 1997). The bootstrap recomputes the statistic based samples drawn with replacement from the original dataset, which requires considerable computation and makes bootstrap estimates of variances random. In our example we compare the influence function based variance estimates to those obtained from a bootstrap.

4.2 Variance computation using influence functions

We assume relative risk parameters are estimated from population based case-control data and combined with age-specific disease incidence and mortality rates from registries. As registries have large samples and are typically independent from the case-control data, the incidence and mortality rates can be treated as fixed, and the variability of the absolute risk estimates arises solely from the estimation of the relative risk parameters.

We assume that age is a categorical variable, indexed by j ε {1, …, J}. Let y_ij be one if individual i is a case of age j and zero otherwise and let x_ij denote a 1 × p vector containing the covariate information for the i-th individual that may also include interaction terms with age. We obtain relative risk estimates from the case-control data assuming that the probability of disease is given by

$$ln\frac{P(Y_{ij}=1\mid {\mathbf{x}}_{ij})}{1-P(Y_{ij}=1\mid {\mathbf{x}}_{ij})}=ln\frac{p({\mathbf{x}}_{ij},\mu ,\mathit{\beta })}{1-p({\mathbf{x}}_{ij},\mu ,\mathit{\beta })}=\mu +{\mathit{\beta }}^{\prime }{\mathbf{x}}_{ij},$$ (5)

where β is a vector of regression parameters and all risk factors x are coded such that the components of β are positive, β_k > 0.

The adjusted age-specific AR_j for rare diseases can be computed from the distribution of risk in the cases using a formula by Bruzzi et al. (1985),

$${\widehat{AR}}_j=1-\frac{{\sum }_{i=1}^{N}exp(-{\widehat{\mathit{\beta }}}^{\prime }{\mathbf{x}}_{ij})y_{ij}}{{\sum }_{i=1}^N{y}_{ij}},$$ (6)

where N = N₀ + N₁ is the total sample size and N₀ and N₁ are the number of controls and cases respectively. The relative risk associated with x is exp(β′x). While N₁ and N₀ are fixed by design, the number of cases in a specific age category is typically a random quantity.

If cases and controls are sampled based on complex designs, for example from surveys, then each y_ij would be multiplied by a sampling weight w_ij, the inverse of the probability of being included in the sample. While all our computations generalize to unequal weights, we omit the weights for ease of notation and because our example was based on a simple random sample of cases and controls.

4.2.1 Influence function based variance of the absolute risk estimate

We base our variance derivation on a linearization approach, that allows one to obtain variance estimates of a statistic T̂ through a first order approximation of T̂, such that

$$\text{Var}(\widehat{T})\approx \text{Var}\{\sum _1^n{\mathrm{\Delta }}_i(\widehat{T})\},$$ (7)

where Δi(T̂) denotes the influence function operator that captures the influence of observation i on T̂. Graubard and Fears (2005) summarize the properties of Δi(.), and further details can be found in Deville (1999).

We first derive the influence Δi(r̂) of the i-th individual in the case-control study on the absolute risk estimate r̂ from (2),

$${\mathrm{\Delta }}_i(\widehat{r})={\mathrm{\Delta }}_{i}r(a,\tau ,\mathbf{x},\widehat{\mathit{\beta }})=\sum _{j=a}^{a+\tau -1}{\mathrm{\Delta }}_i\left(\frac{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})}{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})+h_{2j}}[1-exp\{-(h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})+h_{2j})\}]exp\{-\sum _{l=a}^{j-1}(h_{1l}{rr}_l(\mathbf{x},\widehat{\mathit{\beta }})+h_{2l})\}\right).$$ (8)

Applying chain rule, we can express Δi(r̂) in terms of Δ_i{h_1jrr_j(x), β̂}, that we compute from

$$h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})=h_{1j}^{\ast }(1-A{R}_j){rr}_j(\mathbf{x},\widehat{\mathit{\beta }})=\frac{h_{1j}^{\ast }{\sum }_{k=1}^N{y}_{kj}exp\{-{\widehat{\mathit{\beta }}}^{\prime }({\mathbf{x}}_{kj}-\mathbf{x})\}}{{\sum }_{k=1}^N{y}_{kj}}=\frac{P_{1j}}{P_{2j}}.$$ (9)

Thus

$${\mathrm{\Delta }}_i\{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})\}=[\frac{\partial \{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})\}}{\partial P_{1j}}{\mathrm{\Delta }}_i(P_{1j})+\frac{\partial \{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})\}}{\partial P_{2j}}{\mathrm{\Delta }}_i(P_{2j})]$$ (10)

Straightforward differentiation yields

$$\frac{\partial \{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})\}}{\partial P_{1j}}=\frac{1}{{\sum }_{k=1}^N{y}_{kj}}\text{and}\frac{\partial \{h_{1j}{rr}_j(\mathbf{x},\widehat{\mathit{\beta }})\}}{\partial P_{2j}}=-\frac{{\sum }_{k=1}^N{h}_{1j}^{\ast }{y}_{kj}exp[-{\widehat{\beta }}^{\prime }({\mathbf{x}}_{kj}-\mathbf{x})]}{{({\sum }_{k=1}^N{y}_{kj})}^2}.$$ (11)

The corresponding influences are

$$\begin{array}{l}{\mathrm{\Delta }}_i(P_{1j})=h_{1j}^{\ast }{y}_{ij}exp\{-{\widehat{\mathit{\beta }}}^{\prime }({\mathbf{x}}_{ij}-\mathbf{x})\}+{(\frac{\partial P_{1j}}{\partial \widehat{\mathit{\beta }}})}^{\prime }{\mathrm{\Delta }}_i(\widehat{\mathit{\beta }})=\\ =h_{1j}^{\ast }{y}_{ij}exp\{-{\widehat{\mathit{\beta }}}^{\prime }({\mathbf{x}}_{ij}-\mathbf{x})\}-\sum _{k=1}^N{h}_{1j}^{\ast }{y}_{kj}{[({\mathbf{x}}_{kj}-\mathbf{x})exp\{-{\widehat{\mathit{\beta }}}^{\prime }({\mathbf{x}}_{kj}-\mathbf{x})\}]}^{\prime }{\mathrm{\Delta }}_i(\widehat{\mathit{\beta }})\end{array}$$ (12)

and Δ_i(P_2j) = y_ij. The influence Δ_i(β̂) is obtained from the estimating equation for the logistic regression model by solving $0={\mathrm{\Delta }}_i[{\sum }_{k=1}^N{\mathbf{x}}_{kj}\{y_{kj}-p({\mathbf{x}}_{kj},\widehat{\mu },\widehat{\mathit{\beta }})\}]$, where p stands for the logistic probability given in (5), to yield

$${\mathrm{\Delta }}_i(\widehat{\mathit{\beta }})=\frac{{\mathbf{x}}_{ij}\{y_{ij}-p({\mathbf{x}}_{ij},\widehat{\mu },\widehat{\mathit{\beta }})\}}{{\sum }_{k=1}^N{\mathbf{x}}_{kj}{\mathbf{x}}_{kj}^{\prime }p({\mathbf{x}}_{kj},\widehat{\mu },\widehat{\mathit{\beta }})\{1-p(x_{kj},\widehat{\mathit{\beta }})\}}.$$ (13)

Let y_i = 1 if a person in the study is a case and 0 otherwise. To accommodate the case-control design, the variance of r̂ is computed by treating cases and controls as separate strata and combining their empirical variance estimates,

$$\widehat{\text{Var}}(\widehat{r})=\frac{N_0}{N_0-1}\sum _{i=1}^N(1-y_i){\{{\mathrm{\Delta }}_i(r)-{\overline{\mathrm{\Delta }}}_{i0}(r)\}}^2+\frac{N_1}{N_1-1}\sum _{i=1}^N{y}_i{\{{\mathrm{\Delta }}_i(r)-{\overline{\mathrm{\Delta }}}_{i1}(r)\}}^2=N_0{S}_0\{\mathrm{\Delta }(\widehat{r})\}+N_1{S}_1\{\mathrm{\Delta }(\widehat{r})\},$$ (14)

where Δ̄_i0(r) and Δ̄_i1(r) denote the empirical means over the influences Δ_i(r) and S₀ and S₁ the sample variances of Δ in controls and cases, respectively.

4.2.2 Variance of the criteria of the impact of risk factor modifications

We now use the influences Δ_i(r̂) to compute the variance estimates of the criteria presented in Section 3. For ease of exposition we let r̂₁₂ = r̂ (a, τ, X₁, X₂) and r̂₁₀ = r̂ (a,τ,X₁,X₂₀). For the variance of the risk difference d(X₁, X₂) we compute the two influences, Δ_i(r̂₁₂) and Δ_i(r̂₁₀) and then find

$$\widehat{\text{Var}}\{d({\mathbf{X}}_1,{\mathbf{X}}_2)\}=N_0{S}_0\{\mathrm{\Delta }({\widehat{r}}_{12})-\mathrm{\Delta }({\widehat{r}}_{10})\}+N_1{S}_1\{\mathrm{\Delta }({\widehat{r}}_{12})-\mathrm{\Delta }({\widehat{r}}_{10})\}.$$ (15)

To find the variance of the corresponding fractional risk reduction, we first linearize $\widehat{fd}({\mathbf{X}}_1,{\mathbf{X}}_2)$,

$$\widehat{fd}({\mathbf{X}}_1,{\mathbf{X}}_2)-(r_{12}-r_{10})/r_{12}=({\widehat{r}}_{12}-{\widehat{r}}_{10})/{\widehat{r}}_{12}=1-{\widehat{r}}_{10}/{\widehat{r}}_{12}\approx {\widehat{r}}_{12}\frac{r_{10}}{r_{12}^2}-{\widehat{r}}_{10}\frac{1}{r_{12}}.$$

Hence

$$\widehat{\text{Var}}fd({\mathbf{X}}_1,{\mathbf{X}}_2)=\frac{N_0}{{\widehat{r}}_{12}^2}{S}_0\{\frac{{\widehat{r}}_{10}}{{\widehat{r}}_{12}}\mathrm{\Delta }({\widehat{r}}_{12})-\mathrm{\Delta }({\widehat{r}}_{10})\}+\frac{N_1}{{\widehat{r}}_{12}^2}{S}_1\{\frac{{\widehat{r}}_{10}}{{\widehat{r}}_{12}}\mathrm{\Delta }({\widehat{r}}_{12})-\mathrm{\Delta }({\widehat{r}}_{10})\}.$$

The variance of the population average difference in risk, (4), is computed similarly to $\widehat{\text{Var}}\{d({\mathbf{X}}_1,{\mathbf{X}}_2)\}$. We let r̂_k2, k = 1,…, K denote the absolute risk estimates for all K risk factor combinations (X_1k,X_2k) in a given population, with r̂₂ = (r₁₂,…, r_K2)′, and we let r̂_k0, k = 1,…K denote the absolute risk estimates for all K risk factor combinations with X₂ set to the lowest levels, X₂₀. We also set r₀ = (r₁₀,…,r_K0)′. The known probabilities of risk factor combinations (X_1k, X_2k) are p_k = P(X_k1, X_2k), with p = (p₁,…,p_K)′. The mean risk in the whole population is then given by p′ r̂₂, and the mean risk difference by d̄(X₁, X₂) = p′(r̂₂ − r̂₀).

For the ith individual in the case-control study, the influences for the K original risk factor combinations are Δ_i(r̂₂) = (Δ_i(r̂₁₂), Δ_i(r̂₂₂), ···, Δ_i(r̂_K2))′, and the corresponding influences of the risk factor combinations with X₂ at its lowest level are Δ_i(r̂₀) = (Δ_i(r̂₁₀), Δ_i(r̂₂₀), ···, Δ_i(r̂_K0))′. Then

$$\widehat{\text{Var}}\{\overline{d}({\mathbf{X}}_1,{\mathbf{X}}_2)\}=\widehat{\text{Var}}\{{\mathbf{p}}^{\prime }({\widehat{\mathbf{r}}}_2-{\widehat{\mathbf{r}}}_0)\}=N_0{\mathbf{p}}^{\prime }{\mathbf{S}}_0\{\mathbf{\Delta }({\widehat{r}}_2)-\mathbf{\Delta }({\widehat{r}}_0)\}\mathbf{p}+N_1{\mathbf{p}}^{\prime }{\mathbf{S}}_1\{\mathbf{\Delta }({\widehat{r}}_2)-\mathbf{\Delta }({\widehat{r}}_0)\}\mathbf{p},$$ (16)

where S_i, i = 0,1 is the K × K sample covariance matrix of the K differences in influences in controls and cases respectively.

To compute the variance of the difference in risk in a subset S of the population, we multiply each element p_k of p by the indicator I{(X_1k, X_2k) ∈ S} and divide by the sum of the non-zero elements to obtain the distribution of risk factors in S, p_S. The mean risk in S is then computed as ${\mathbf{p}}_s^{\prime }\mathbf{r}$, the mean risk difference in S is ${\overline{d}}^S({\mathbf{X}}_1,{\mathbf{X}}_2)={\mathbf{p}}_s^{\prime }({\widehat{\mathbf{r}}}_2-{\widehat{\mathbf{r}}}_0)$, and the variance of d̄^S(X₁,X₂) is obtained by replacing p by p_S in (16).

The mean fractional risk reduction is $\overline{f}d({\mathbf{X}}_1,{\mathbf{X}}_2)={\mathbf{p}}^{\prime }(\mathbf{1}-{\widehat{\mathbf{r}}}_0^{\prime }{(\mathbf{I}{\widehat{\mathbf{r}}}_2)}^{-1})$ where I denotes the K × K identity matrix, and 1 = (1,…, 1) is a vector of K ones. defining two vectors ${\mathbf{c}}_1=({\widehat{r}}_{01}/{\widehat{r}}_{21}^2,\dots ,{\widehat{r}}_{0K}/{\widehat{r}}_{2K}^2)$ and c₂ = (1/r̂₂₁,…, 1/r̂_2K), $\widehat{\text{Var}}\{\overline{f}d({\mathbf{X}}_1,{\mathbf{X}}_2)\}=N_0{\mathbf{p}}^{\prime }{\mathbf{S}}_0\{\mathbf{\Delta }{({\widehat{r}}_2)}^{\prime }\mathbf{I}{\mathbf{c}}_1-\mathbf{\Delta }{({\widehat{r}}_0)}^{\prime }\mathbf{I}{\mathbf{c}}_2\}\mathbf{p}+N_1{\mathbf{p}}^{\prime }{\mathbf{S}}_1\{\mathbf{\Delta }{({\widehat{r}}_2)}^{\prime }\mathbf{I}{\mathbf{c}}_1-\mathbf{\Delta }{({\widehat{r}}_0)}^{\prime }\mathbf{I}{\mathbf{c}}_2)\}\mathbf{p}$.

5 Application: effects of risk factor modifications on projections of absolute risk of breast cancer

Recently Petracci et al. (submitted) developed a model to predict the absolute risk of invasive breast cancer for Italian women, that includes modifiable and non-modifiable risk factors. Relative risks were estimated by logistic regression using an Italian case-control study comprised of 2,569 cases and 2,588 controls both aged 23–74 years. The non-modifiable risk factors in the model were age at menarche, number of previous breast biopsies, number of first-degree female relatives with breast cancer, age at first live birth, educational level, occupational physical activity at ages 30 – 39 years. Three potentially modifiable factors were body mass index (BMI), leisure-time physical activity at age 30 – 39 years and alcohol consumption (never, current, and former drinkers). Because BMI reduced breast cancer risk in women age < 50 and increased risk in older women, it was included only through the products BMI · AgeLT50 and BMI · (1 − AgeLT50), where AgeLT50 = 1 if a woman’s age is < 50 years and 0 otherwise.

Five-year age-specific incidence rates for invasive breast cancer and estimated age-specific hazard rates from competing mortality from causes other than breast cancer were obtained from the Florence Cancer Registry. The age-specific ARs were obtained from the distribution of risk factors in cases, separately for women aged < 50 years and for women aged ≥ 50. For women aged ≥ 50 we assumed that AR(a) is the same for all ages in that range, and the same assumption was made for the AR for women aged < 50 years.

Table 1 shows the influence function based standard errors and bootstrap standard errors used by Petracci et al. for comparison for individual absolute risk estimates. Each bootstrap sample was drawn with replacement from the cases and separately from the controls in the case-control study, with the original number of cases and controls in each replication. For each bootstrap replication, we estimated new relative risks and attributable risks. By saving 1000 such sets of these quantities, we could compute 1000 estimates of absolute risk and obtain bootstrap standard errors. Bootstrap standard errors for other quantities, such as absolute risk reductions, were likewise based on the stored sets of relative and attributable risks. The bootstrap standard errors for the individual risk predictions agree well with standard errors estimated from influence functions.

Table 1.

Examples of 10-year non-modified and modified absolute risk estimates of breast cancer for 65 year old women with different ages and risk factors profiles

AgeMen (yrs)	NumRel	NBiops	Age1st (yrs)	OccAct	Educat (yrs)	BMI (kg/m2)	CurrDrnk	LeiAct (hrs/w)	10-yrs Risk	IF SE	Bootstrap SE
7 – 11	≥ 1	≥ 1	≥ 30	Low	≥12	≥30	Yes	<2	22.9	0.0580	0.0600
7 – 11	≥ 1	≥ 1	≥ 30	Low	≥12	< 25	No	<2	17.8	0.0494	0.0403
7 – 11	≥ 1	≥ 1	≥ 30	Low	≥12	≥30	No	≥2	17.3	0.0460	0.0475
7 – 11	≥ 1	≥ 1	≥ 30	Low	≥12	< 25	No	≥2	13.8	0.0363	0.0377

AgeMen= age at menarche; NumRel= number of first-degree relatives; NBiops= number of biopsies; Age1st= age at first live birth; OccAct= occupational physical activity; Educat= education; BMI= body mass index; CurrnDrnk= current drinkers; LeiAct= leisure-time physical activity; IF SE is the estimated standard error from the influence function

Table 2 gives the mean risk, the mean risk difference and the mean fractional difference for a ten year absolute risk prediction from age 65 to 74 computed using the risk factor distribution of the 8426 women participating in the Florence-European Prospective Investigation into Cancer and Nutrition (EPIC) cohort study. The mean difference between non-modified absolute risk and risk was obtained by assuming that current drinkers became former drinkers, women who exercised less than two hours/week began exercising at least 2 hours/week and women aged ≥ 50 years maintained BMI < 25kg/m². Again, influence function based standard errors and bootstrap standard errors are presented and agree well for all criteria.

Table 2.

Estimated 10-year non-modified mean risk, mean risk reductions and mean fractional risk reductions based on the risk factor distribution in the European Prospective Investigation into Cancer and Nutrition (EPIC) population and in subgroups with a positive (FH+) and negative (FH−) family history.

	Non-modified mean risk	Mean risk reduction‡	Mean fractional reduction in risk
Age 65–74	0.03627	0.00412	0.11070
Bootstrap SE	0.00192	0.00356	0.09429
IF SE	0.00174	0.00341	0.10972
Age 65–74 and FH+	0.07826	0.00872	0.10873
Bootstrap SE	0.01013	0.00804	0.91945
IF SE	0.00895	0.00726	0.10993
Age 65–74 and FH−	0.03280	0.00374	0.11078
Bootstrap SE	0.00170	0.00331	0.09448
IF SE	0.00157	0.00310	0.09954

SE= standard error, IF= influence function

^‡Mean difference between non-modified absolute risk and risk obtained by assuming that all current drinkers became former drinkers, all women who exercised less than two hours/week began exercising at least 2 hours/week, and all women aged 50 years or more maintained BMI < 25kg/m²

6 Discussion

We present an influence function based approach for the computation of variances of estimates of absolute risk and functionals of absolute risk. This approach is simple, easily implemented and can be used for estimators that are defined explicitly or implicitly. Another advantage is that correlations among different pieces of a statistic, which often makes the parametrical version of the delta method challenging, are accounted for automatically in the final computational step for the variances. We illustrate this approach absolute risk estimates from a breast cancer risk prediction model and criteria to assess the impact of risk factor modification, and compared the influence function variances to those obtained using a bootstrap. While the bootstrap and influence function standard errors were very similar, the influence function method is deterministic, whereas the bootstrap estimate is random and requires significantly more computing time. For example, for the first risk profile in Table 1, the influence standard error estimate was 0.058, and the bootstrap standard error of the absolute risk estimate was 0.060, and this estimate had a standard error of 0.0016.

In addition, the influence function approach can easily be extended to accommodate complex sampling designs in the data that gave rise to the relative risk parameters (Graubard and Fears, 2005) and leads to proofs of asymptotic normality for functions of the influences. The application of resampling to complex designs needs to account for the underlying design, which can make it more difficult to implement.