Abstract
Networks are widely used in biology to represent the relationships between genes and gene functions. In Boolean biological models, it is mainly assumed that there are two states to represent a gene: on-state and off-state. It is typically assumed that the relationship between two genes can be characterized by two kinds of pairwise relationships: similarity and prerequisite. Many approaches have been proposed in the literature to reconstruct biological relationships. In this article, we propose a two-step method to reconstruct the biological pathway when the binary array data have measurement error. For a pair of genes in a sample, the first step of this approach is to assign counting numbers for every relationship and select the relationship with counting number greater than a threshold. The second step is to calculate the asymptotic p-values for hypotheses of possible relationships and select relationships with a large p-value. This new method has the advantages of easy calculation for the counting numbers and simple closed forms for the p-value. The simulation study and real data example show that the two-step counting method can accurately reconstruct the biological pathway and outperform the existing methods. Compared with the other existing methods, this two-step method can provide a more accurate and efficient alternative approach for reconstructing the biological network.
Introduction
One great challenge of postgenomic research is to explore complex biological pathways from genomic data such as DNA sequences, protein sequences, and gene expression profiles. The network building method is widely used throughout biology to reconstruct complex biological pathways.
We take MAPK pathway as an example. The MAPK/ERK pathway is a signal transduction pathway that couples intracellular responses to the binding of growth factors to cell surface receptors. Robert et al. [1] and related studies [2]–[5] based on biology experiments provide the MAPK pathway (Figure 1).
Figure 1. The PKC pathway in yeast.
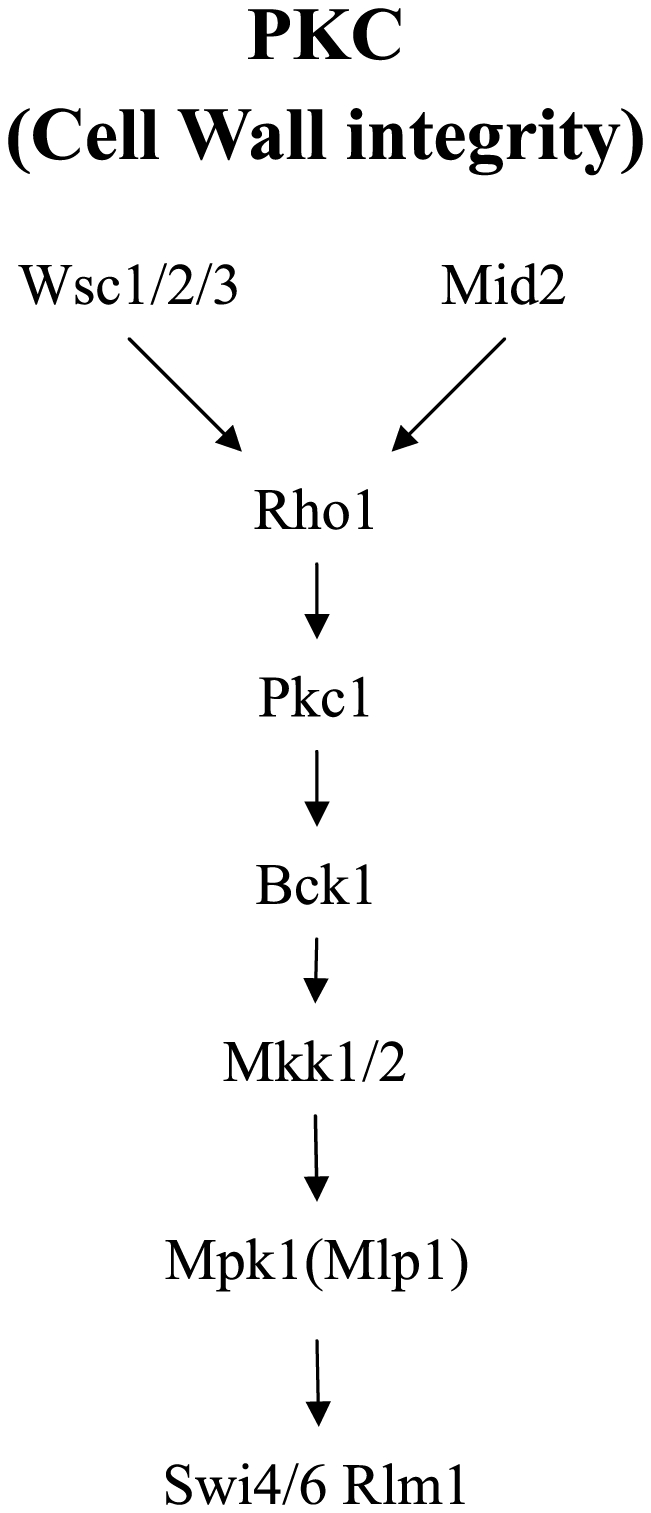
It would be interesting if Figure 1 can be reconstructed in terms of their expression profile of Wsc1/2/3, Mid2,…, etc. To reduce the cost of experiments, one possibility is to predict the activation status of these genes through their microarray expression data for inferring the pathway.
There have been methods proposed in literature for reconstructing genetic regulatory networks in terms of microarray data. For instance, the Bayesian network model is an important technique that has been studied in the last two decades [6]–[8]. In addition, Wei and Li [9] proposed a hidden spatial-temporal Markov random field model to identify genes that are related to biological pathway. Allocco et al. [10] provided a variety of methods to find the gene-pairs with similarity relationship. Moreover, other algorithms using linear models [11], [12], differential equation [11], [13], neural network [14] and structural equation modeling [15] have been proposed to explore gene regulatory networks based on genomewide data. However, most of these methods have limitations in dealing with large-scale gene regulatory network because of their complex model structures. Also, careful discretization can be used to denoise high-throughput data. One such example can be found in Xing and Karp [16].
To overcome the disadvantage of the mentioned methods, we consider a simple model based on the Boolean network to reconstruct a large scale gene network in this study. Boolean networks have been proposed and investigated for a long time in literature. Kauffman [17], [18] considered a dynamic version of Boolean networks. Liang et al. [19] proposed the algorithm REVEAL to infer gene regulatory network by calculating the Shannon entropy. Akutsu and Miyano [20] proposed an identification algorithm to reconstruct the Boolean network by comparing the collected data with all possible Boolean functions and input datasets. In order to make Boolean network more comprehensive, Shmulevich et al. [21] proposed the model of probability Boolean network (PBN). Moreover, for large-scale gene regulatory networks, Kim et al. [22] have used Boolean network with chi-square test on the yeast cell cycle microarray gene expression datasets. Markowetz et al. [23] proposed the nested effects model to infer the genetic network. Li et al. [24] made a comparison between the approaches of probabilistic Boolean network and dynamic Bayesian network. More recent developments are referred to Ay, Xu and Kahveci [25] and Davidich and Bornholdt [26].
In this article, we consider the directed acyclic Boolean (DAB) network as a tool for exploring biological pathways. Our goal is to construct a DAB network from the noisy array data. Since it involves noisy data, the reconstruction of the pathways cannot employ a deterministic inference. Instead, we need to establish a statistical model to capture its random characteristics. A DAB network is characterized by two kinds of pairwise relationships: similarity and prerequisite. The former represents a pair of elements with coherent on-off states. The latter is a partial order relationship, namely, the on-status of one element is a prerequisite for the on-status of another element. More specifically, if one element is a prerequisite to another element, the off-status of one element will restrict another element's off-status. A DAB network is uniquely determined by its state space: all possible on-off states subjected to the pairwise relationships.
Recently, a Boolean implication network is proposed with similar aspect as the DAB network, which investigates all Boolean implications between pairs of genes for large-scale genome microarray datasets [27]. For any pair of elements, they use two statistics to test whether there is any specific relationship between the pair of elements. However, the methods are more applicable for dealing with mass information of datasets.
The approach of building a DAB network based on the expectation-maximization (EM) algorithm to derive the maximum likelihood estimator [28] for a statistical model is established in Li and Lu [29]. Their strategy is to build up a statistical model with measurement error and assign scores for the possible relationships between two genes, and then use the scores to select the true relationship. This method involves more computation and cannot provide a simple closed-form statistic to recover the true relationships between genes.
In this study, we propose a simple method to estimate pairwise relationships between elements from noisy array data. The approach is based on two steps: the first one is to count the numbers of different pairwise relationships in a sample, and the second one is to test the relationship hypotheses according to their asymptotic p-values. Compared with the Li and Lu [29] method, this new approach has a simple closed form and it is not time-consuming. In addition, the proposed counting approach shows substantial improvement compared to the Sahoo et al. [27] method. We conduct a simulation study to an example used in Li and Lu [29]. It is shown that the proposed method can recover all of the true relationships. A simulation study for a larger scale network is given in the supplementary material. In addition, the proposed method is implemented on the MAPK pathway example. It can recover 6 true relationships among seven relationships, however, Li and Lu's method only recovers one true relationship in this example. In this real data example, the new method shows a significant improvement in adopting a DAB network for exploring the pathway.
Methods
To describe the model and notations, we adopted a simple example used in Li and Lu
[29] to illustrate
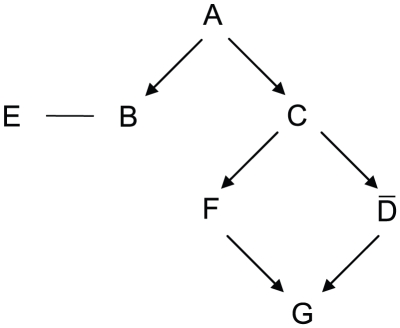
the model assumption. Figure 2
shows the relationships of the seven elements in this example derived from the 13
states of Table 1. In the
diagram, the notation 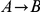 denotes that A is a
prerequisite of B and the notation
denotes that A is a
prerequisite of B and the notation  denotes that B and E
are similar. Note that
denotes that B and E
are similar. Note that 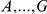 in Figure 2 are called elements. The
definitions of prerequisite and similar relationships for any two elements
in Figure 2 are called elements. The
definitions of prerequisite and similar relationships for any two elements
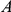 and
and 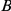 are defined as
follows.
are defined as
follows.
Figure 2. Diagram of a directed acyclic Boolean network with seven elements and twelve pair relationships.
Only arrows between covering pairs are shown.
Table 1. The table of states for directed acyclic Boolean network shown in Figure 2.
| case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| A | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| B | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| E | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Assume that an element only has two levels, on or off. We use “0” and
“1” to represent “off” and “on” states
respectively. For two elements 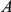 and
and
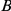 ,
, 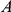 is a prerequisite for
is a prerequisite for
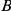 if the on-state of
if the on-state of 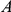 is necessary for the
on-state of
is necessary for the
on-state of 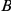 , and we denote it by
, and we denote it by 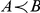 . When
. When
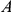 and
and 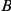 are on and off
simultaneously, the relationship between
are on and off
simultaneously, the relationship between 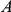 and
and
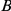 is called similar and is denoted by
is called similar and is denoted by
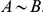 We define
We define  to be the dual state
of
to be the dual state
of 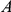 . It means that
. It means that 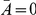 when
when
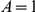 .
.
There are 4 possible situations for the prerequisite relationship, and 2 possible
situations for the similar relationship, see Table 2. Totally, there are 6 possible
relationships for any two genes. The prerequisite relationship is a partial order.
It is transitive on the ground-set, namely, 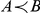 and
and
 implies
implies 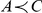 . The notations
“
. The notations
“ ” and “
” and “ ” in Table 2 denote the possible
states of
” in Table 2 denote the possible
states of 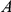 and
and 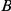 and the impossible
states of
and the impossible
states of 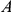 and
and 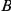 under the
relationship, respectively.
under the
relationship, respectively.
Table 2. Patterns for the six pairwise relationships assuming exhaustive sampling and no measurement error.
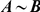
|
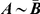
|
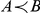 , ,
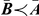
|
||||||
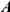 / /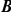
|
0 | 1 |
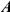 / /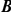
|
0 | 1 |
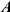 / /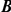
|
0 | 1 |
| 0 | + | − | 0 | − | + | 0 | + | − |
| 1 | − | + | 1 | + | − | 1 | + | + |
Let 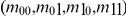 and
and 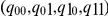 denote the counts and
probabilities corresponding to states
denote the counts and
probabilities corresponding to states 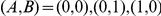 and
and
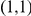 without measurement error. From the possible relationships
shown in Table 2, we can
propose a hypothesis corresponding to each relationship. For example, the first
similar relationship in Table
2 is
without measurement error. From the possible relationships
shown in Table 2, we can
propose a hypothesis corresponding to each relationship. For example, the first
similar relationship in Table
2 is 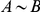 , which means that the two situations
, which means that the two situations
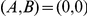 and
and 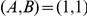 hold. In this case,
the probability of the two situations,
hold. In this case,
the probability of the two situations, 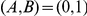 and
and
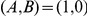 , should be zero. Thus, its corresponding hypothesis is
, should be zero. Thus, its corresponding hypothesis is
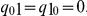 Other situations follow a similar argument. The hypotheses
for the 6 relationships are presented in Table 3. Under the measurement error model
assumption, let
Other situations follow a similar argument. The hypotheses
for the 6 relationships are presented in Table 3. Under the measurement error model
assumption, let 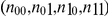 and
and 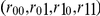 denote the counts and
probabilities corresponding to states
denote the counts and
probabilities corresponding to states 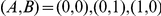 and
and
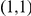 with misclassification probability
with misclassification probability
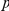 .
.
Table 3. The six pairwise between the two elements 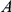 and
and
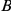 .
.
| Relationship | Hypothesis | |
| diagonal |
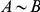
|
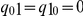
|
| similarity |
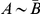
|
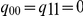
|
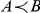
|
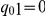
|
|
| triangular |
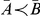
|
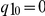
|
| prerequisite |
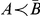
|
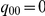
|
|
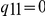
|
Because of the misclassification error, 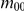 may be split up into
four categories. We use the notations
may be split up into
four categories. We use the notations 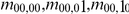 and
and
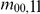 to represent the counts of four cells split from
to represent the counts of four cells split from
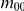 . Analogous notations are defined for
. Analogous notations are defined for
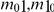 and
and 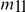 . Consequently, their
generating probabilities are calculated as follows:
. Consequently, their
generating probabilities are calculated as follows: 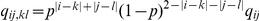 . Here, we adopt the
notation
. Here, we adopt the
notation 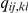 analogous to
analogous to 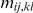 . The splitting counts
and probabilities implied by misclassification error are given in Tables 4 and 5.
. The splitting counts
and probabilities implied by misclassification error are given in Tables 4 and 5.
Table 4. Splitting counts caused by misclassification error.
| A/B | 0 | 1 | ||
| 0 |
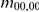
|
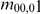
|
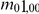
|
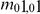
|
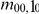
|
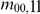
|
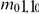
|
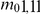
|
|
| 1 |
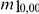
|
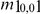
|
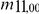
|
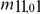
|
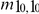
|
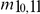
|
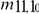
|
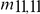
|
|
Table 5. Splitting probabilities caused by misclassification error.
| A/B | 0 | 1 | ||
| 0 |
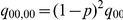
|
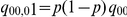
|
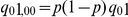
|
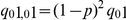
|
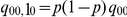
|
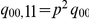
|
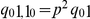
|
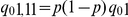
|
|
| 1 |
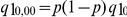
|
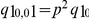
|
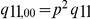
|
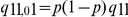
|
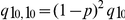
|
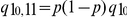
|
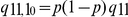
|
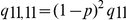
|
|
Now we go back to the example of Figure
2 which includes 7 elements. There are a total of
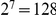 states for a seven-element network. Only thirteen of these
states in Table 1 are
compatible with the twelve pairwise relationships in the above example. From Figure 2, there are 12 true
relationships between the elements, which are
states for a seven-element network. Only thirteen of these
states in Table 1 are
compatible with the twelve pairwise relationships in the above example. From Figure 2, there are 12 true
relationships between the elements, which are
| (1) |
Under the measurement error model assumption, we do not directly observe the 13 states but observe states with measure error. We aim to reconstruct the true pathway. A proposed method is given in the following.
The two-step counting method
Suppose we have a sample 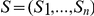 of size
of size
 for
for  genes where
genes where
 or 1. For example, in Table 1, there is a sample of size 13 for
seven genes. We propose a two-step approach to recover their relationships.
or 1. For example, in Table 1, there is a sample of size 13 for
seven genes. We propose a two-step approach to recover their relationships.
The first step: counting
For a pair of genes, say 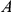 and
and
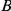 , we can count the numbers for 6 relationships in Table 2 for the
, we can count the numbers for 6 relationships in Table 2 for the
 states. The relationships with a counting number greater
than a given threshold are regarded as potential relationships.
states. The relationships with a counting number greater
than a given threshold are regarded as potential relationships.
If there are no measurement errors, it is reasonable to expect that the counting
number of two elements, say 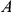 and
and
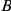 , satisfying the true relationship is exactly equal to
, satisfying the true relationship is exactly equal to
 . However, since it involves measurement errors, the
counting number with respect to the true relationship may not be exactly equal
to
. However, since it involves measurement errors, the
counting number with respect to the true relationship may not be exactly equal
to  . For each pair of elements, we count the numbers
satisfying the 6 relationships respectively, say
. For each pair of elements, we count the numbers
satisfying the 6 relationships respectively, say  . Since we expect
that the misclassification probability is low, the counting
number(
. Since we expect
that the misclassification probability is low, the counting
number(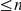 ) corresponding to
the true relationship should be close to
) corresponding to
the true relationship should be close to  . Thus, we can
select the relationships with a counting number greater than a threshold. The
threshold selection is suggested as follows.
. Thus, we can
select the relationships with a counting number greater than a threshold. The
threshold selection is suggested as follows.
Threshold Selection
The suggested thresholds for the similar and prerequisite relationships are
and
| (2) |
respectively, where
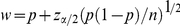 . Here, the misclassification error probability
. Here, the misclassification error probability
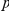 can be assumed to be known from empirical
experiences. If
can be assumed to be known from empirical
experiences. If 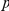 is unknown,
the maximum likelihood approach for estimating
is unknown,
the maximum likelihood approach for estimating
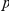 is given in Appendix D in the materials section.
is given in Appendix D in the materials section.
The argument for the threshold selection is given in Appendix A in the
materials section. It is based on a confidence bound approach associated
with the counting number formulas. The approach is to derive the formulas
for the two kinds of relationships, and then uses a confidence interval
approach to obtain a lower bound for the counting number formulas. The forms
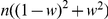 and
and 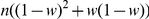 are inferred
by the counting number formulas with misclassification probability
are inferred
by the counting number formulas with misclassification probability
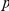 , where
, where 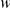 value is
derived by a confidence bound approach.
value is
derived by a confidence bound approach.
The second step: asymptotic p-value
Besides directly counting the relationships' numbers, the second step is to test the relationships in Table 3 using an asymptotic p-value. Then we combine both steps to estimate the true relationship between two elements.
The following simulation study shows that the two steps are both essential for selecting the true relationship. If any one of the steps is used solely in selecting the true relationship, the simulation shows that it cannot select the true relationships very accurately.
The p-values derived for the 6 hypotheses with misclassification probability
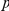 corresponding to the 6 relationships are listed as
follows. The derivations are given in Appendix B in the materials section.
corresponding to the 6 relationships are listed as
follows. The derivations are given in Appendix B in the materials section.
For testing 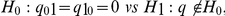 the asymptotic p-value for large sample size
the asymptotic p-value for large sample size
 is
is
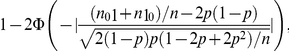 |
where
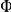 is the cumulative distribution of the standard normal
random distribution. The asymptotic p-value for testing
is the cumulative distribution of the standard normal
random distribution. The asymptotic p-value for testing
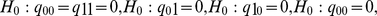 or
or 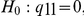 are the forms of
(10), (13),(14), (15) and (16), respectively, which are given in Appendix B in
the materials section.
are the forms of
(10), (13),(14), (15) and (16), respectively, which are given in Appendix B in
the materials section.
The extremeness of the observed value for the test statistic under the null hypothesis leads to a small p-value, which would imply rejection of the null hypothesis. Thus, if the null hypothesis is the true relationship, we expect to obtain a higher p-value. In the second step, we also set a threshold for the asymptotic p-value such that the relationships with asymptotic p-value greater than or equal to the threshold are selected.
A large p-value indicates a larger possibility that the null hypothesis holds. Note that the p-value is less than or equal to 1. In this study, we use the threshold 1 for the p-value criterion in the examples because the largest p-value for each relationship is one. From the simulation study and the real data example discussed in this study, setting 1 to be a threshold for p-value criterion can lead to very accurate results. Note that for other examples, it is possible that the largest p-value is not 1. In this case, we need to observe the p-values to select a suitable threshold.
It is worth noting that the hypothesis testing procedure corresponds to a confidence interval approach [30]. From the confidence interval viewpoint, when the p-value is large enough (close to 1) or small enough (close to 0), we have confidence to accept or reject the null hypothesis. Therefore, in this study, when p-value is 1, we have confidence to accept the null hypothesis.
The two-step method is described as follows.
Procedure for selecting the true relationship of
 elements
elements
Step 1
For a sample of size  for
for
 elements, calculate the counting numbers for the 6
relationships of each pair of the elements. Set a threshold for the counting
numbers. Select the relationships with a counting number greater than the
threshold.
elements, calculate the counting numbers for the 6
relationships of each pair of the elements. Set a threshold for the counting
numbers. Select the relationships with a counting number greater than the
threshold.
Step 2
For each pair of elements, derive the asymptotic p-values for each relationship and set a threshold for the p-value. Select the relationships with a asymptotic p-value greater than or equal to the threshold.
Step 3
For each pair of elements, select the relationships satisfying both criteria of Step 1 and Step 2. This relationship is the estimated relationship for the two elements.
Note that it is possible to have more than one relationship satisfying both criteria for two elements. But from a simulation result and a real data application, it shows that in most situation, there is only one relationship satisfying both criteria.
The asymptotic p-value has a closed form which can be easily calculated and the counting number can also be easily calculated. This shows that this method can provide a convenient way to recover the biological pathway.
An Example
We revisit the example of Figure
2 to illustrate the counting step. Assume that we only have a sample
of the states for the 7 elements and we want to recover the 12 true
relationships. Note that there are totally 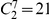 pairs of the 7
elements and there are only 12 pairs with relationships in this example. When
considering the case without measurement error, we can reconstruct the pathway
from a sample using the counting number method if the sample size is large
enough. We can construct the Boolean network for the example by identifying
prerequisite or similar relationships. From Table 1, we list the relationship
corresponding to the highest counting number for each pair as
follows:
pairs of the 7
elements and there are only 12 pairs with relationships in this example. When
considering the case without measurement error, we can reconstruct the pathway
from a sample using the counting number method if the sample size is large
enough. We can construct the Boolean network for the example by identifying
prerequisite or similar relationships. From Table 1, we list the relationship
corresponding to the highest counting number for each pair as
follows:
where 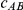 denotes the
counting number corresponding to the indicating relationship
denotes the
counting number corresponding to the indicating relationship
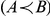 .
.
If there is only one relationship corresponding to the highest counting number,
we list that one, such as 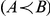 ; if there are more
than one relationship corresponding to the highest counting number, we list all
of the relationships, such as
; if there are more
than one relationship corresponding to the highest counting number, we list all
of the relationships, such as 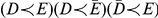 . In the 21 pairs,
the relationships corresponding to the highest counting number 13 is the 12 true
relationships, and the relationships with the counting number less than 13 are
not the true relationships.
. In the 21 pairs,
the relationships corresponding to the highest counting number 13 is the 12 true
relationships, and the relationships with the counting number less than 13 are
not the true relationships.
Comparison
We consider two existing methods for detecting the pairwise relationships between any two elements. A simulation study is conducted to compare the proposed method with the existing methods for the measurement error case.
Existing methods
Li and Lu [29]
proposed the directed acyclic Boolean network to recover the genetic network.
For any pair of element, they use the EM algorithm to calculate the maximum
likelihood estimator of misclassification rate 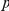 under the
multinomial distribution model structure and adopt a criterion that requires a
true relationship to correspond to a small estimator of
under the
multinomial distribution model structure and adopt a criterion that requires a
true relationship to correspond to a small estimator of
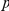 in order to select a relationship. Besides the
disadvantage that the EM algorithm is time-consuming, this method is also shown
to be less accurate than the counting method from a simulation study.
in order to select a relationship. Besides the
disadvantage that the EM algorithm is time-consuming, this method is also shown
to be less accurate than the counting method from a simulation study.
Another method for inferring the relationship of any two elements is proposed by
Sahoo et al.
[27]. For any
two genes 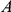 and
and 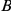 , let
, let
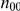 ,
, 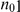 ,
,
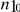 and
and 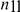 denote the numbers
of the four states
denote the numbers
of the four states 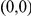 ,
,
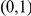 ,
, 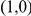 and
and
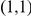 of
of 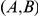 , respectively from
a sample. For example, to infer whether the relationship
, respectively from
a sample. For example, to infer whether the relationship
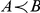 is true, they use the following two statistics to test
if the relation
is true, they use the following two statistics to test
if the relation 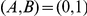 is
true:
is
true:
where “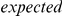 ” and
“
” and
“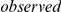 ” denote the
values of
” denote the
values of 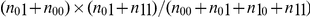 and
and 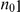 , respectively.
, respectively.
The relationship 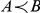 in Sahoo
et al. method is regarded as true when the
“
in Sahoo
et al. method is regarded as true when the
“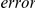
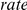 ” value is less than 0.1 and
“
” value is less than 0.1 and
“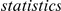 ” value is
greater than 3 [27]. However, from our calculation, the method may lead
to inaccurate results when the sample size is not large. For instance, suppose
the number of experiments we observed is 91 and the numbers of states
corresponding to (0,1), (0,0), (1,0) and (1,1) are 1, 30, 30 and 30
respectively, resulting in a small “
” value is
greater than 3 [27]. However, from our calculation, the method may lead
to inaccurate results when the sample size is not large. For instance, suppose
the number of experiments we observed is 91 and the numbers of states
corresponding to (0,1), (0,0), (1,0) and (1,1) are 1, 30, 30 and 30
respectively, resulting in a small “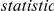 ” value of
2.94. Note that the state
” value of
2.94. Note that the state 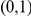 indicates that the
relationship
indicates that the
relationship 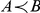 does not hold. However, since the state
does not hold. However, since the state
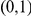 only occurs once, it may be due to a measurement error.
In this case, the method does not select the relationship
only occurs once, it may be due to a measurement error.
In this case, the method does not select the relationship
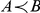 . This shows that the criterion is too conservative to
select a potential relationship when the sample size is not large enough.
. This shows that the criterion is too conservative to
select a potential relationship when the sample size is not large enough.
Simulation
We conduct a simulation study using the example of Figure 2 with 13 compatible states (Table 1) in order to compare
the proposed method with the two existing methods. With a misclassification
probability 0.05, we generate 100 states for the simulation comparison. Tables 6 and 7 show the counting numbers
and p-values for different relationships with a sample size of 100,
respectively. Note that the notations 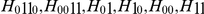 in Tables 6 and 7 denote the relationships
in order in Table 3.
in Tables 6 and 7 denote the relationships
in order in Table 3.
Table 6. The counting numbers for the 21 pairs in the 100 states under each relationship.
| hypothesis |
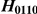
|
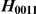
|
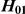
|
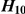
|
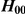
|
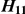
|
| (A, B) | 55 | 45 | 98 | 57 | 90 | 55 |
| (A, C) | 72 | 28 | 95 | 77 | 93 | 35 |
| (A, D) | 51 | 49 | 93 | 58 | 95 | 54 |
| (A, E) | 56 | 44 | 98 | 58 | 90 | 54 |
| (A, F) | 54 | 46 | 98 | 56 | 90 | 56 |
| (A, G) | 26 | 74 | 99 | 27 | 89 | 85 |
| (B, C) | 51 | 49 | 64 | 87 | 83 | 66 |
| (B, D) | 46 | 54 | 70 | 76 | 77 | 77 |
| (B, E) | 91 | 9 | 95 | 96 | 52 | 57 |
| (B, F) | 51 | 49 | 76 | 75 | 71 | 78 |
| (B, G) | 53 | 47 | 92 | 61 | 55 | 92 |
| (C, D) | 35 | 65 | 76 | 59 | 94 | 71 |
| (C, E) | 50 | 50 | 86 | 64 | 84 | 66 |
| (C, F) | 72 | 28 | 98 | 74 | 72 | 56 |
| (C, G) | 42 | 58 | 98 | 44 | 72 | 86 |
| (D, E) | 43 | 57 | 74 | 69 | 79 | 78 |
| (D, F) | 37 | 63 | 72 | 65 | 81 | 82 |
| (D, G) | 37 | 63 | 87 | 50 | 66 | 97 |
| (E, F) | 50 | 50 | 76 | 74 | 72 | 78 |
| (E, G) | 52 | 48 | 92 | 60 | 56 | 92 |
| (F, G) | 66 | 34 | 98 | 68 | 48 | 86 |
Table 7. The p-values for the 21 pairs in the 100 states under each relationship.
| hypothesis |
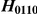
|
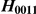
|
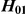
|
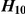
|
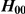
|
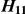
|
| (A, B) | 0.8207 | 0.0065 | 1 | 0 | 0.1358 | 0 |
| (A, C) | 1 | 0 | 1 | 0.0095 | 0.0680 | 0 |
| (A, D) | 0.1330 | 0.1511 | 0.7931 | 0 | 1 | 0 |
| (A, E) | 0.9228 | 0.0046 | 1 | 0 | 0.1201 | 0 |
| (A, F) | 0.7200 | 0.0092 | 1 | 0 | 0.1527 | 0 |
| (A, G) | 0 | 0.6534 | 1 | 1 | 0.7599 | 0.3630 |
| (B, C) | 0.9149 | 0.4654 | 0.0060 | 1 | 0.7636 | 0.0152 |
| (B, D) | 0.4237 | 1 | 0.6569 | 0.6504 | 0.9855 | 0.9855 |
| (B, E) | 1 | 0 | 0.8094 | 1 | 0 | 0 |
| (B, F) | 0.9994 | 0.8352 | 0.9990 | 0.9065 | 0.9118 | 0.9189 |
| (B, G) | 0.4376 | 0.1168 | 1 | 0 | 0 | 0.8556 |
| (C, D) | 0.0004 | 1 | 0.0268 | 0 | 1 | 0.0025 |
| (C, E) | 0.7452 | 0.6280 | 1 | 0.0058 | 0.9122 | 0.0165 |
| (C, F) | 1 | 0 | 1 | 0.0005 | 0.0014 | 0 |
| (C, G) | 0.0724 | 0.1689 | 1 | 0 | 0.0070 | 0.3746 |
| (D, E) | 0.1613 | 1 | 0.4171 | 0.4297 | 1 | 0.9031 |
| (D, F) | 0.0093 | 1 | 0.1226 | 0.1554 | 0.8975 | 1 |
| (D, G) | 0.0003 | 1 | 0.0377 | 0 | 0.0001 | 1 |
| (E, F) | 0.9367 | 0.9716 | 0.9702 | 0.7834 | 0.9965 | 0.9993 |
| (E, G) | 0.3662 | 0.1523 | 1 | 0 | 0 | 0.9043 |
| (F, G) | 1 | 0 | 1 | 0.0001 | 0 | 0.0110 |
In this case, the maximum value for the counting number is 100 because the sample size is 100. As discussed in above, we can set a threshold (2) for the counting number. In this case, the thresholds for the similar and prerequisite relationships are 86 and 93. And we set the threshold for the p-value to be 1 because the highest p-value for each pair is 1 in this case. The relationships corresponding to the hypotheses with a p-value 1 are the candidates for the true relationship.
For any pair of the 7 elements, there are 6 possible relationships of each pair.
Since there are 21 pairs for the 7 elements, there are totally 126 possible
relationships. Using the two thresholds set above, there are only 12
relationships satisfying the conditions, which are exactly the true
relationships (1). There are many relationships among the 126 relationships
satisfying only one condition, but not both. For example, the relationships
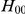 in
in 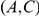 and
and
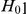 in
in 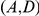 satisfy the
counting number condition, but not the p-value condition; the relationships
satisfy the
counting number condition, but not the p-value condition; the relationships
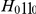 and
and 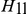 in
in
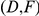 satisfy the p-value condition, but not the counting
number condition. It shows that any one of the two steps is an important
condition for identifying the true relationships. In this case, we can recover
all true relationships using the proposed method.
satisfy the p-value condition, but not the counting
number condition. It shows that any one of the two steps is an important
condition for identifying the true relationships. In this case, we can recover
all true relationships using the proposed method.
Next, we implement the algorithm of Li and Lu [29] in the simulated data. Since
this algorithm does not provide a specific threshold selection method, we adopt
different thresholds and find that the best situation is to recover 11
relationships . In this case, one relationship 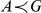 is misjudged to be
is misjudged to be
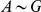 .
.
In order to compare the counting method with Sahoo et al.
[27], we
implement their method in this simulated data. There are only two relationships
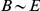 and
and  recovered from
their method with “
recovered from
their method with “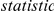 ” values 4.05
and 3.18, respectively. The “
” values 4.05
and 3.18, respectively. The “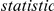 ” values for
relationships of other pair elements are smaller than 3, resulting in inaccuracy
of identifying the other true relationships. It shows that the method of [27] is less
efficient and accurate in recovering the true relationships than the counting
method from the simulation study for the case with measurement error.
” values for
relationships of other pair elements are smaller than 3, resulting in inaccuracy
of identifying the other true relationships. It shows that the method of [27] is less
efficient and accurate in recovering the true relationships than the counting
method from the simulation study for the case with measurement error.
Beside the example with 7 elements, a more comprehensive example with a larger network (Figure S1) that shows the superiority of the proposed method is given in the supplementary material.
Yeast expression data
We revisit the MAPK pathway example from the Introduction. The datasets used in analyzing the MAPK pathway include 81 experimental data excluding two data with missing values, 57 from Spellman et al. [31] and 26 from Zhu et al. [32] . The datasets from Spellman et al. [31] include 18 data from the alpha factor experiments, 14 data set from the Elutrtation experiments and 24 data sets from cdc15 experiments. The datasets from Zhu et al. [32] include 25 data from Forkhead experiments. The raw data can be download from the Stanford Microarray Database [33]. We adopt values corresponding to the Log(base2) column in the raw dataset to reconstruct the MAPK pathway, which are log ratio values of red to green signal.
A gene state is regarded as on state or off state when the log ratio value of red to green signal is greater than or less than 0, respectively. The gene expression data for the 81 experimental data (Table S1) are given in the supplementary material.
In this study, we apply the two-step approach to explore the expression profiles, and show exploratory results on the pathway. The results are also compared with the Li and Lu's method [29] and Shaoo et al. method [27].
We implement the proposed method to the yeast cell cycle data [31], [32]. In our
analysis, we assume that the level 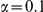 . According to the
threshold selection formulas (2), the thresholds for the similar and
prerequisite relationships are 61 and 69, respectively. And the threshold for
the asymptotical p-value we selected is 1.
. According to the
threshold selection formulas (2), the thresholds for the similar and
prerequisite relationships are 61 and 69, respectively. And the threshold for
the asymptotical p-value we selected is 1.
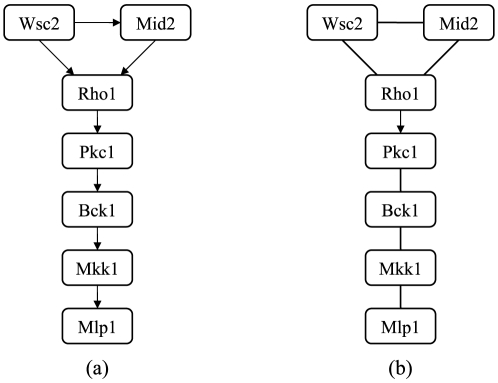
According to the network structure reconstructed using our proposed approach, we can see that Wsc2p and Mid2p activate Rho1p, Pkc1p and Bck1p which results in activation of the downstream of MAPK cascade, Mkk1p and Mlp1p. Activated Wsc2p also interacts with Mid2p. The functions of genes Swi4p, Swi6p and Rlm1p in the downstream of the network are not significant in our approach.
The reconstruction results of the DAB network using the two-step approach and the
method of Li and Lu [29] are illustrated in Figure 3(a) and Figure 3(b), respectively. In addition, we
also implemented the method of Shaoo et al.
[27] in this
real yeast data. The results show that there are no pair relationships detected
by the method of Shaoo et al.
[27], because
all “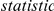 ” values are smaller than 3 for any two elements.
Therefore, compared with the methods in Li and Lu [29] and Shaoo et
al.
[27], our
proposed method is more useful for finding the cascade relationship.
” values are smaller than 3 for any two elements.
Therefore, compared with the methods in Li and Lu [29] and Shaoo et
al.
[27], our
proposed method is more useful for finding the cascade relationship.
Figure 3. Some pairwise relationships identified by the two-steps counting approach (a), and the Li and Lu method (b) using the expression data of yeast Saccharomyces cerevisiae.
Discussion
For the implementation of the network reconstruction algorithm, the greatest
complexity lies in the computation of p-value for every two elements. The number of
all pair is 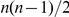 where
where  is the number of
elements. Therefore, the time complexity for the proposed approach is
is the number of
elements. Therefore, the time complexity for the proposed approach is
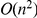 showing that the proposed method is capable of handling
thousands of genes simultaneously.
showing that the proposed method is capable of handling
thousands of genes simultaneously.
This study mainly focuses on reconstructing pathway by gene expression. Although pathway reconstruction methods based on gene expression have been widely discussed in the literature, there is a limitation on the gene expression methods. A biological pathway comprises more than genetic interactions alone. Long chains of vents may happen on the protein level (e.g. (de)activation by phosphorylation) which does not necessarily have to be regulated via gene expression. Therefore, these gene expression methods can be expected to reconstruct pathways that are regulated via gene expression, but not other biological interactions.
In summary, we propose a two-step approach to test the biological pathways from noisy array data. This new method has the advantages of easy calculation for the counting numbers and simple closed forms of the p-value. From the simulation results, we can see that this method can precisely estimate the true relationships for most of the situations. Compared with the other existing methods, it can provide a more accurate and efficient alternative approach for reconstructing the biological network.
Materials and Methods
Appendix A: Threshold Selection
(i) Suppose the misclassification probability is 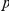 . For a similar
relationship such as the case
. For a similar
relationship such as the case 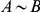 , in this case, we
have
, in this case, we
have
| (3) |
With misclassification error, the counting number corresponding to the relationship is
By (3), the last equation is equal to 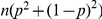 , which is the mean
of the counting number if this similar relationship holds. Since we cannot
expect that the counting number is always equal to the mean, we look for a lower
bound of the counting number as a threshold. From the viewpoint of constructing
confidence interval, if
, which is the mean
of the counting number if this similar relationship holds. Since we cannot
expect that the counting number is always equal to the mean, we look for a lower
bound of the counting number as a threshold. From the viewpoint of constructing
confidence interval, if 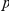 is unknown, a
is unknown, a
 upper bound of
upper bound of 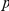 is
is
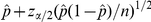 , where
, where 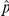 is an estimator of
is an estimator of
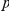 and
and 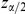 is the upper
is the upper
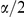 quantile of the standard normal distribution. The bound
quantile of the standard normal distribution. The bound
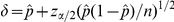 is an upper bound of
is an upper bound of 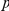 . Then
. Then
 is a lower bound of
is a lower bound of 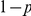 . Here we replace
. Here we replace
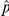 by
by 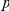 in the upper bound
and suggest
in the upper bound
and suggest 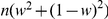 , where
, where 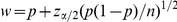 as a threshold. We
expect that the counting number is greater than the threshold if the similar
relationship holds. Beside using the conventional confidence interval, we can
also consider some improved intervals discussed in literature [34]–[37].
as a threshold. We
expect that the counting number is greater than the threshold if the similar
relationship holds. Beside using the conventional confidence interval, we can
also consider some improved intervals discussed in literature [34]–[37].
(ii) Assume for two elements 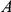 and
and
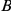 , a prerequisite relationship holds. In this case, we
have
, a prerequisite relationship holds. In this case, we
have
| (4) |
With misclassification errors, the counting number corresponding to the relationship is
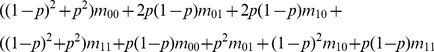 |
(5) |
By (4), (5) is equal to
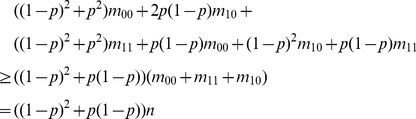 |
(6) |
By a similar argument as in (i), we suggest 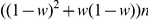 as a threshold for
the prerequisite relationship.
as a threshold for
the prerequisite relationship.
Appendix B: Computational details
The methods for testing the 6 hypotheses in Table 3 are listed as following.
(i) For deriving the p-value of the test:
(ii)
we
can consider the following two different situations. Note that the condition
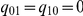 in hypothesis
in hypothesis 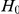 is equivalent to
is equivalent to
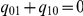 because
because 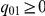 and
and
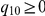 .
.
(I) The misclassification probability 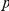 is zero.
is zero.
The statistics
| (7) |
has an asymptotic standard normal
distribution under the null hypothesis 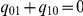 .
.
(II) The misclassification probability 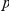 is greater than
zero.
is greater than
zero.
In this case, the mean and the variance of the random variable are
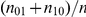 is
is
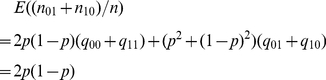 |
(8) |
and
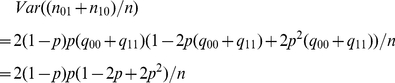 |
(9) |
under the null hypothesis.
Consequently, the asymptotic p-value is
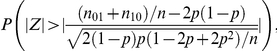 |
which can be rewritten as (3).
(iii) For deriving the p-value of the test:
(iv)
by
an argument similar to (i), for 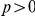 , the asymptotic
p-value is
, the asymptotic
p-value is
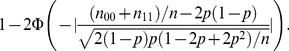 |
(10) |
(iii) For deriving the p-value of the test:
consider the case of
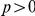 .
.
Under the null hypoyhesis, the mean and variance of the statistics
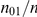 are
are
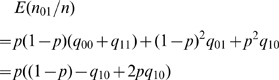 |
(11) |
and
| (12) |
under the null hypothesis.
The asymptotic p-value is
| (13) |
(iv) For deriving the p-value of the test:
by an argument similar to (iii), the asymptotic p-value is
| (14) |
(v) For deriving the p-value of the test:
by an argument similar to (iii), the asymptotic p-value is
| (15) |
(vi) For deriving the p-value of the test:
by an argument similar to (iii), the asymptotic p-value is
| (16) |
The estimators 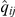 of
of 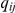 in the above
formulas of asymptotic p-values are given in Appendix C.
in the above
formulas of asymptotic p-values are given in Appendix C.
Appendix C: Frequency estimation
If the misclassification probability 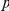 is known, the
methods for estimating the probability
is known, the
methods for estimating the probability 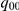 ,
,
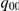 ,
, 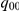 and
and
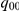 are listed as follows.
are listed as follows.
According to Table 5, we have
Note that 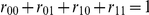 and
and 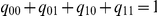 . By solving the
above equations, we have
. By solving the
above equations, we have
The derived values are used as estimators for 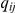 .
.
Appendix D: Misclassification probability estimation
If 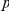 is unknown, we can apply the maximum likelihood approach
to estimate
is unknown, we can apply the maximum likelihood approach
to estimate 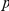 . By Table
5, we can rewrite the multinomial model for the observations
. By Table
5, we can rewrite the multinomial model for the observations
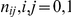 in terms of
in terms of 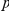 and other
parameters. The maximum likelihood approach for deriving the maximum likelihood
estimator of
and other
parameters. The maximum likelihood approach for deriving the maximum likelihood
estimator of 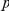 is based on the likelihood
function
is based on the likelihood
function
| (17) |
where
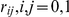 . This involve
. This involve 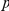 and other
parameters,
and other
parameters, 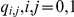 , given in Appendix C. The maximum likelihood approach is
to find the maximum likelihood estimators of
, given in Appendix C. The maximum likelihood approach is
to find the maximum likelihood estimators of 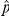 and
and
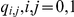 such that the estimators can maximize the likelihood
function (17) [29].
such that the estimators can maximize the likelihood
function (17) [29].
Supporting Information
An example of Boolean network with 10 elements.
(DOCX)
The 81 experimental yeast expression data.
(DOCX)
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: National Science Council (NSC 99-2118-M-009-001-MY2, NSC 98-2118-M-009-004-MY3), National Center for Theoretical Sciences, and Center of Mathematical Modeling and Scientific Computing. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Roberts CJ, Nelson B, Marton MJ, Stoughton R, Meyer MR, et al. Signaling and circuitry of multiple MAPK pathways revealed by a matrix of global gene expression profiles. Science. 2000;287:873–880. doi: 10.1126/science.287.5454.873. [DOI] [PubMed] [Google Scholar]
- 2.Buehrer BM, Errede B. Coordination of the mating and cell integrity mitogen-activated protein kinase pathways in Saccharomyces cerevisiae. Molecular and Cellular Biology. 1997;17:6517–6525. doi: 10.1128/mcb.17.11.6517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.O'Rourke SM, Herskowitz I. The hog1 MAPK prevents cross talk between the hog and pheromone response MAPK pathways in Saccharomyces cerevisiae. Genes & Development. 1998;12:2874–2886. doi: 10.1101/gad.12.18.2874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Madhani HD, Fink GR. Combinatorial control required for the specificity of yeast MAPK signaling. Science. 1997;275:1314–1317. doi: 10.1126/science.275.5304.1314. [DOI] [PubMed] [Google Scholar]
- 5.Posas F, Saito H. Osmotic activation of the HOG MAPK pathway via ste11p MAPKKK: scaffold role of pbs2p MAPKK. Science. 1997;276:1702–1705. doi: 10.1126/science.276.5319.1702. [DOI] [PubMed] [Google Scholar]
- 6.Jensen FV. New York: Springer; 2001. Bayesian Networks and Decision Graphs. [Google Scholar]
- 7.Jensen ST, Chen G, Stoeckert CJ., Jr Bayesian variable selection and data integration for biological regulatory networks. Annals of Applied Statistics. 2007;1:612–633. [Google Scholar]
- 8.Pearl J. San Mateo: Morgan Kaufmann; 1988. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. [Google Scholar]
- 9.Wei Z, Li H. A hidden spatial-temporal markov random field model for network-based analysis of time course gene expression data. Annals of Applied Statistics. 2008;2:408–429. [Google Scholar]
- 10.Allocco DJ, Kohane IS, Butte AJ. Quantifying the relationship between co-expression, coregulation and gene function. BMC Bioinformatics. 2004;5:18. doi: 10.1186/1471-2105-5-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.D'haeseleer P, Wen X, Fuhrman S, Somogyi R. Linear modeling of mRNA expression levels during CNS development and injury. Pacific Symposium on Biocomputing. 1999;4:41–52. doi: 10.1142/9789814447300_0005. [DOI] [PubMed] [Google Scholar]
- 12.van Someren EP, Wessels LFA, Reinders MJT. Linear modeling of genetic networks from experimental data. In: Proceedings 8th International Conference on Intelligent Systems for Molecular Biology. volume 8, 2000;355–366 [PubMed] [Google Scholar]
- 13.Chen T, He HL, Church GM. Modeling gene expression with di®erential equations. Pacific Symposium on Biocomputing. 1999;4:29–40. [PubMed] [Google Scholar]
- 14.Weaver DC, Workman CT, Stormo GD. Modeling regulatory networks with weight matrices. Pacific Symposium on Biocomputing. 1999;4:112–123. doi: 10.1142/9789814447300_0011. [DOI] [PubMed] [Google Scholar]
- 15.Liu B, De La Fuente A, Hoeschele I. Gene network inference via structural equation modeling in genetical genomics experiments. Genetics. 2008;178:1763–1776. doi: 10.1534/genetics.107.080069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xing EP, Karp RM. CLIFF: Clustering of high-dimensional microarray data via iterative feature filtering using normalized cuts. Bioinformatics. 2001;17:306–315. doi: 10.1093/bioinformatics/17.suppl_1.s306. [DOI] [PubMed] [Google Scholar]
- 17.Kauffman SA. Gene regulation networks: A theory for their global structure and behaviors. Current Topics in Developmental Biology. 1977;6:145–182. doi: 10.1016/s0070-2153(08)60640-7. [DOI] [PubMed] [Google Scholar]
- 18.Kauffman SA. Assessing the probable regulatory structures and dynamics of the metazoan genome. In: Thomas R, editor. Kinetic Logic: A Boolean Approach to the Analysis of Complex Regulatory Systems. Vol. 29. Berlin: Lecture Notes in Biomathematics. Springer-Verlag; 1979. pp. 30–60. [Google Scholar]
- 19.Liang S, Fuhrman S, Somogyi R. REVEAL, a general reverse engineering algorithm for inference of genetic network architectures. Pacific Symposium on Biocomputing. 1998;3:18–29. [PubMed] [Google Scholar]
- 20.Akutsu T, Miyano S. Pacific Symposium on Biocomputing; 1999. Identification of genetic networks from a small number of gene expression patterns under the boolean network model. pp. 17–28. [DOI] [PubMed] [Google Scholar]
- 21.Shmulevich I, Dougherty ER, Kim S, Zhang W. Probabilistic boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics. 2002;18:261–274. doi: 10.1093/bioinformatics/18.2.261. [DOI] [PubMed] [Google Scholar]
- 22.Kim H, Lee JK, Park T. Boolean networks using the chi-square test for inferring large-scale gene regulatory networks. BMC Bioinformatics. 2007;8:37. doi: 10.1186/1471-2105-8-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Markowetz F, Kostka D, Troyanskaya OG, Spang R. Nested effects models for high-dimensional phenotyping screens. Bioinformatics. 2007;23:i305–i312. doi: 10.1093/bioinformatics/btm178. [DOI] [PubMed] [Google Scholar]
- 24.Li P, Zhang C, Perkins E, Gong P, Deng Y. Comparison of probabilistic Boolean network and dynamic Bayesian network approaches for inferring gene regulatory networks. BMC Bioinformatics. 2007;8:S13. doi: 10.1186/1471-2105-8-S7-S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ay F, Xu F, Kahveci T. Scalable steady state analysis of Boolean biological regulatory networks. PLOS One. 2009;4:e7992. doi: 10.1371/journal.pone.0007992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Davidich MI, Bornholdt S. Boolean network model predicts cell cycle sequence of fission yeast. PLOS One. 2008;3:1672. doi: 10.1371/journal.pone.0001672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sahoo D, Dill D, Gentles A, Tibshirani R, Plevritis S. Boolean implication networks derived from large scale, whole genome microarray datasets. Genome Biology. 2008;9:R157. doi: 10.1186/gb-2008-9-10-r157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B (Methodological) 1977;39:1–38. [Google Scholar]
- 29.Li LM, Lu HH-S. Explore biological pathways from noisy array data by directed acyclic boolean networks. Journal of Computational Biology. 2005;12:170–185. doi: 10.1089/cmb.2005.12.170. [DOI] [PubMed] [Google Scholar]
- 30.Bickel PJ, Doksum KA. Mathematical statistics: basic ideas and selected topics. Prentice Hall. 2000;1 [Google Scholar]
- 31.Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, et al. Comprehensive identification of cell cycle-regulated genes of the yeast saccharomyces cerevisiae by microarray hybridization. Molecular Biology of Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhu G, Spellman PT, Volpe T, Brown PO, Botstein D, et al. Two yeast forkhead genes regulate the cell cycle and pseudohyphal growth. Nature. 2000;406:90–94. doi: 10.1038/35017581. [DOI] [PubMed] [Google Scholar]
- 33.Hubble J, Demeter J, Jin H, Mao M, Nitzberg M, et al. Implementation of GenePattern within the Stanford Microarray Database. 2009. [ http://smd.stanford.edu/] [DOI] [PMC free article] [PubMed]
- 34.Agresti A, Coull BA. Approximate is better than ‘exact’ for interval estimation of binomial proportions. The American Statistician. 1998;52:119–126. [Google Scholar]
- 35.Wang H. Exact confidence coe±cients of confidence intervals for a binomial proportion. Statistica Sinica. 2007;17:361–368. [Google Scholar]
- 36.Wang H. Exact confidence coeffcients of simultaneous confidence intervals for multinomial proportions. Journal of Multivariate Analysis. 2008;99:896–911. [Google Scholar]
- 37.Wang H. Exact average coverage probabilities and confidence coeffcients of confidence intervals for discrete distributions. Statistics and Computing. 2009;19:139–148. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
An example of Boolean network with 10 elements.
(DOCX)
The 81 experimental yeast expression data.
(DOCX)