Localization Accuracy of the Clinical Target Volume during Image-Guided Radiotherapy of Lung Cancer

Abstract

Purpose

To evaluate the position and shape of the originally-defined clinical target volume (CTV) over the treatment course, and assess the impact of gross tumor volume (GTV)-based online CT guidance on CTV localization accuracy.

Methods and Materials

Weekly breath hold CT scans were acquired in 17 patients undergoing radiotherapy. Deformable registration was used to propagate the GTV and CTV from the first weekly CT to all other weekly CT images. The on-treatment CT scans were registered rigidly to the planning CT scan based on the GTV location to simulate online guidance, and residual error in the CTV centroids and borders was calculated.

Results

The mean GTV volume after five weeks relative to volume at the beginning of treatment was 77% +/− 20%, while for the prescribed CTV it was 92% +/− 10%. The mean absolute residual error magnitude in the CTV centroid position after a GTV-based localization was 2.9 mm +/− 3.0 mm, and varied from 0.3 mm to 20.0 mm over all patients. Residual error of the CTV centroid was associated with GTV volume regression and anisotropy of regression during treatment (p=0.02 and 0.03, Spearman rank correlation). 77% of patients and 50% of fractions had a residual error in CTV border position greater than 2 mm. Of these fractions, residual error of the CTV borders was 3.5 +/− 1.6 mm (LR), 3.1 +/− 0.9 mm (AP), and 6.4 +/− 7.5 mm (SI).

Conclusions

Online guidance based on the visible GTV produces substantial error in CTV localization, particularly for highly-regressing tumors. The results of this study will be useful in designing margins for CTV localization or for developing new online CTV localization strategies.

INTRODUCTION

Geometric uncertainty remains a barrier to local control in locally-advanced lung cancer. The large safety margins necessary to ensure adequate target coverage with the prescription dose prohibit dose escalation at the expense of normal tissue toxicity. Sources of this geometric uncertainty certainly include target delineation error, setup error, and respiration-induced tissue motion (1). However, it has become apparent in the past several years that daily changes in the tumor position (2–5), respiratory pattern (6, 7), and gross tumor volume and shape (8–14) also contribute substantially to geometric uncertainty. Image-guided online correction to manage daily lung tumor position changes has been reported for hypofractionated therapy delivered in accelerated schedules (2, 3, 15–17). The model for online image-guided localization proposes that the target can be shifted as a rigid object in an invariant dose cloud (18, 19), preserving dose to the target structures. For such hypofractionated schedules, shape and volume change of the gross tumor volume (GTV) during the brief treatment calendar is generally small, and this model is likely valid.

However, lung tumors treated with conventional fractionation demonstrate substantial but variable change in volume during therapy (7–13, 20–22), which often presents in a time-trending regression in tumor volume. Average volume regression of approximately 30% to 40% after 50 Gy has generally been observed, although the range within each study population was also quite variable, with many patients having no measureable regression and some having more than 80% volume regression. Volume change and other deformations of the high-contrast GTV leads to error in the rigid correction model, as the high-contrast GTV is generally the structure used to guide online image-guided correction. This error may be somewhat mitigated as the regressing GTV is smaller than the planned GTV, and therefore it is likely that dose coverage of the GTV will not be compromised (23).

However, regression-induced deformations may impact dosimetric coverage to the clinical target volume. The clinical target volume (CTV), as it is generally defined as a rind around the GTV, may also exhibit deformation and shape change due to the influence of the regressing GTV on adjacent tissue. As the CTV is macroscopically composed of lung tissue rather than dense tumor, the mechanics of GTV regression may not directly translate to similar shape or volume change of the CTV. Possible shape and volume change of the tissue composing the CTV and the implications of such change on image-guided localization of the CTV have not been explored to date. The purpose of this study is to evaluate the position and shape of the initially-defined CTV over the course of therapy, and to assess the impact of conventional GTV-based online image-guided correction on CTV localization accuracy.

METHODS AND MATERIALS

The general method of this study was to use deformable image registration to propagate the GTV and originally-defined CTV (GTV plus isotropic margin) from a planning image to images acquired during treatment, and to evaluate changes in GTV and CTV geometric coverage after GTV-based localization simulating online image-guided localization.

Patient data

Seventeen patients being treated for non-small cell lung cancer and one patient with parenchymal small cell lung cancer provided informed consent and were enrolled on an Institutional Review Board approved imaging study. Each subject underwent weekly helical CT imaging under active breathing control (ABC) using a commercial device (Elekta Active Breathing Coordinator, Crawley, UK), as described previously (9). The ABC device was used to maintain a breath hold of at least eight seconds per scan at end of normal inspiration. The same physician delineated the primary tumor as GTV on each weekly CT image. The CTV was formed by isotropic expansion of the GTV on the first weekly image only, and manually edited on the first weekly image so that it did not cross the lung/chest wall interface or into large airways, unless infiltrated by the GTV. As the extent of microscopic disease may vary with tumor grade and among patients, two GTV to CTV margin expansions were evaluated: a 5 mm expansion (CTV_5mm) and an 8 mm expansion (CTV_8mm).

Deformable image registration

Both the GTV and CTVs were propagated to the weekly CT images from the first weekly CT image using displacement vector fields (DVF) derived from deformable image registration. Although the manually-delineated GTVs were available, we chose to use the propagated GTVs to make the comparison between propagated GTV and CTV position fairer. The first weekly image served as the reference image for the study, and the GTV and CTV on the reference image the reference GTV and reference CTV, respectively. For each subject, all other weekly images were registered to the subject’s reference image using a small deformation, inverse consistent, linear elastic (SICLE) algorithm (24). The reference GTV and reference CTV were converted to triangulated surface meshes using a research version of a commercial treatment planning system (Philips Pinnacle 8.1×, Philips Medical Systems, Fitchburg, WI). The DVF was used to propagate the reference GTV and CTV mesh points from the reference image to the weekly image from which the registration was performed, for each weekly image for each subject. The end result was a set of GTV and CTV structures on each weekly image for each subject.

The accuracy of the deformable registration process will impact the results of the study as designed. Therefore, knowledge of the error in the DVF near the GTV and CTV borders is necessary. The location of the manually delineated GTV mesh point positions were visually compared to the propagated GTV mesh point positions to assess GTV registration quality. As there is no anatomy directly defining the CTV, vessel bifurcations near the border of the reference CTV were used to assess error in the propagated CTV. Six to seven vessel bifurcation positions were marked on each weekly CT, distributed around the border of the CTV_5mm and CTV_8mm. The DVF was used to propagate the same vessel bifurcation positions from the reference image to all weekly images. The difference between the propagated bifurcation point position and the manually-marked position was calculated as the error in CTV propagation, in a subset of four randomly-chosen subjects.

Simulated image guidance and residual error calculation

Online image-guided correction for target position error was simulated by rigidly translating the weekly CT image to match the reference image, approximating the standard clinical techniques used with cone beam CT-guided radiotherapy. Each weekly image was translated such that the centroids of the GTV on the weekly image and the reference image were aligned. After GTV-based localization was performed, the error in localizing the CTV was measured by calculating the displacement of the CTV centroid relative to the reference position, and was separated into systematic and random components. First, the mean and standard deviation of the residual error was calculated for each patient. Then, these mean and standard deviations were grouped into a four-parameter population model following the method of Yan (25).

The effect of shape change on CTV localization was measured by calculating the difference between the weekly and reference CTV border position, after simulated online correction, for the left, right, anterior, posterior, superior, and inferior borders of the CTV. When considering the effect of border shifts on coverage or margin requirements, the direction of the shift is important to consider. If shifts only moved the border closer to the center of the structure, then it is likely that coverage would be maintained and no additional margin would be required. Therefore, only border variation that moved the weekly CTV border away from the centroid (relative to the reference CTV border) was scored (Figure 1). Additionally, volume change in the GTV and CTV relative to the volume on the reference image was quantified.

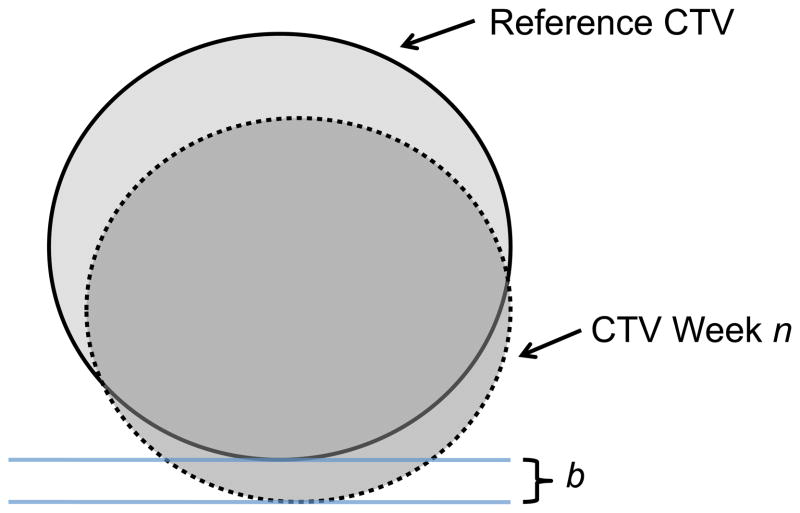
Figure 1.

Illustration of the border variation calculation for week n. The CTV week n (dotted line) is overlaid on the reference CTV (solid line) using the simulated image guidance procedure (matching the GTV week n and reference GTV centroids). For each cardinal border (left, right, anterior, posterior, superior, inferior), the distance from the reference CTV to week n CTV is calculated (b in the figure), radially from the reference CTV centroid. Finally, only positive border variation is scored; negative values imply the week n CTV remains inside the original reference CTV.

Anisotropy measurement

GTV regression may influence the adjacent normal tissue anisotropically, causing the distance from CTV to GTV border to change anisotropically over time. To quantify this effect, an anisotropy ratio is proposed. The distance, d, is measured from the CTV border position to the GTV border position radially towards the centroid, and measures the margin from GTV to CTV. For CTV larger than the GTV, d is always greater than zero. The anisotropy ratio, α, is calculated as:

$$\alpha =\frac{\mid d_A-d_B\mid }{d_A+d_B}$$ (1)

Where d_A and d_B are the CTV to GTV distances on opposite sides of the GTV (for example, either left/right, anterior/posterior, or superior/inferior). If α equals zero, the distance d is the same on both sides of the GTV. If α equals one, the GTV and CTV borders are at the same location on one side of the GTV, implying maximum anisotropy in the CTV margin. The value of α was calculated for each weekly image and for the reference image. The anisotropy ratio relative to the value in the reference image, which we term the relative anisotropy ratio, was calculated for each weekly image by subtracting the reference image α from the weekly image α. This process calibrated for reference images where α was not zero in the reference image (for example, when the CTV margin was shaved against the lung/chest wall interface). Relative anisotropy ratio was calculated independently along the left/right, anterior/posterior, and superior/inferior axes of the structure. Finally, the maximum relative anisotropy ratio in any one direction was selected for each patient.

Statistical analysis

Error in the CTV centroid was tested for association with the change in GTV volume over treatment, initial GTV volume, and with the relative anisotropy ratio. For volume change, the error in the CTV centroid for each weekly image was tested for association with the weekly change in GTV volume in relation to the first week volume using Spearman rank correlation. Initial GTV volume was tested for association with mean CTV centroid error using Spearman rank correlation. For the relative anisotropy ratio, the mean CTV centroid error for each patient was tested for association with the maximum relative anisotropy ratio measured on the last week of treatment, also with Spearman rank correlation.

RESULTS

Patient population

Seventeen patients were enrolled on the study. For two subjects, only one imaging session was acquired due to issues unrelated to the study, so both subjects were excluded from analysis due to lack of sufficient data. Two subjects developed, respectively, a sizeable pleural effusion and a collapsed lung during treatment that limited the ability of deformable image registration to generate accurate DVFs. Both subjects were also excluded from analysis. Table 1 lists the characteristics of the thirteen remaining subjects included in the analysis.

Table 1.

Patient subject characteristics

Subject	Stage	Histology	Tumor location	GTV volume (cc)
1	IIIA (T2N2M0)	S	LUL	23.8
2	IIIB (T4N2M0)	S	Bilat+mediastinum	100.3
3	IIB (T2N1M0)	A	LLL	65.0
4	IIIB (T1N3M0)	A	RUL/Supraclavicular	0.6
5	IIIA (T2N2M0)	NOS	RLL	241.9
6	IIB (T2N1M0)	S	RUL	11.3
7	IIIA (T2N2M0)	S	RUL	40.1
8	IIIB (T4N1M0)	S	Bilat	80.2
9	IIIA (T2N2M0)	A	RML	37.4
10	IIIA (T3N2M0)	S	LUL	376.4
11	IIA (T1N1M0)	A	LUL	74.0
12	IIIA (T3N1M0)	SCC	RUL	216.2
13	IIIB (T3N3M0)	S	RUL	58.3

Abbreviations: LUL, left upper lobe; RLL, right lower lobe; LLL, left lower lobe; RUL, right upper lobe; Bilat, bilateral; S, squamous cell carcinoma; A, adenocarcinoma; NOS, not otherwise specified; SCC, small cell carcinoma; GTV, gross tumor volume.

Registration accuracy

The mean registration error assessed near the CTV_5mm and CTV_8mm borders by vascular or bronchial bifurcation landmarks was 1.8 mm +/− 1.1 mm (left/right), 1.7 mm +/− 1.2 mm (anterior/posterior), and 1.8 mm +/− 1.0 mm (superior/inferior). The visual comparison of manual and propagated GTV contours found structure correspondence to be acceptable.

Volume Regression

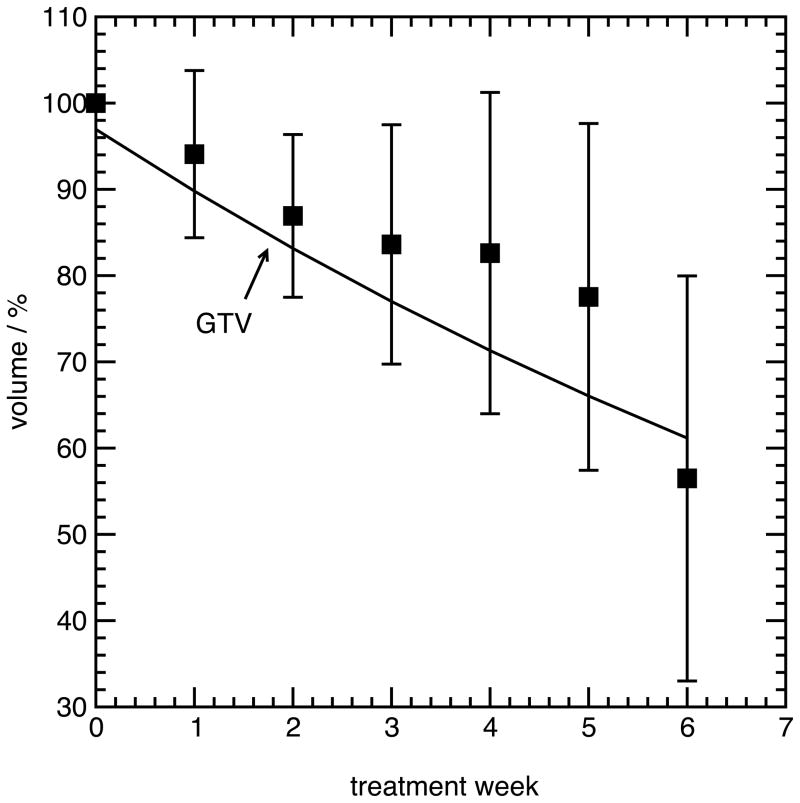
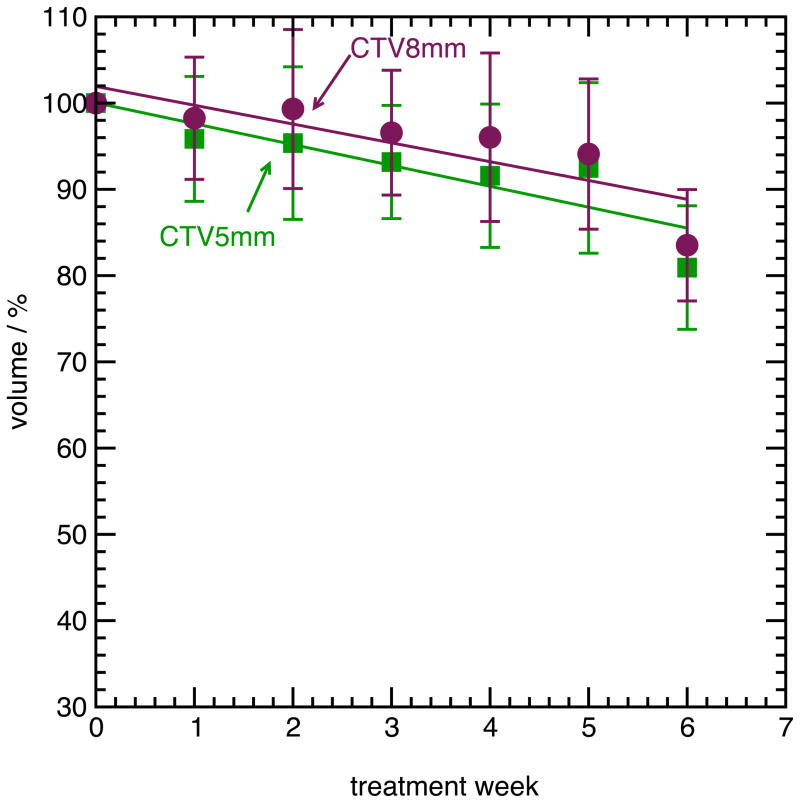
Figure 2 shows the mean relative GTV, CTV_5mm and CTV_8mm volume over all patients, for all weeks of treatment. An exponential fit is shown for the GTV volume, while the CTV volumes were fit to a linear function. Twelve of thirteen subjects demonstrated regression of the GTV, and to a lesser extent, the CTV. One subject (Subject 13) had a marked increase in both GTV and CTV volume. The mean volume of the GTV during the fifth week of treatment, relative to the volume during the first week of treatment, was 77% +/− 20% over all patients, with a range from 37% to 106%. The relative CTV_5mm volume during the fifth week of treatment was 92% +/− 10%, with a range from 83% to 109%, while the relative CTV_8mm volume was 94% +/− 9%, ranging from 83% to 100%.

Figure 2.

(A), mean volume of the GTV during radiotherapy, relative to the volume during the first week (error bars are one standard deviation among all subjects). (B), mean volume of the CTV_5mm and CTV_8mm during radiotherapy, relative to the volume during the first week.

As the CTV is always larger than the GTV, the same percentage change in volume will translate to a larger radial change for the CTV. To account for this effect, the change in effective radius between the first and last week was calculated, where the effective radius is the radius of a sphere with the same volume as the structure. Table 2 shows this change in effective radius for the GTV and CTVs, between the fifth and first week of treatment. A positive change in effective radius means the structure shrunk in effective radius from first to fifth week. The change in effective radius for the CTV_5mm was significantly larger than for the CTV_8mm (p=0.04, paired t test).

Table 2.

Change in effective radius (mm), first week of treatment to fifth week

Subject	GTV	CTV5mm	CTV8mm
1	1.4	1.7	1.8
2	1.2	1.3	−0.9
3	7.0	1.5	1.3
4	0.0	0.0	0.0
5	3.7	2.8	2.3
6	0.9	0.2	0.1
7	1.3	0.8	−1.2
8	1.7	0.9	0.7
9	1.2	1.0	0.7
10	2.0	2.6	2.6
11	0.5	0.0	0.0
12	4.1	1.9	2.0
13	−1.2	−0.9	−1.0
Mean	1.8	1.1	0.6
Standard Deviation	2.1	1.1	1.3

CTV centroid variation

The mean absolute residual error in the CTV centroid position after a GTV-based localization was 2.9 mm +/− 3.0 mm over all patient all weeks, and ranged from 0.3 mm to 20.0 mm for the CTV_5mm. For the CTV_8mm, the mean absolute residual error was 2.8 +/− 2.9 mm. Substantial heterogeneity in residual CTV centroid error was observed between subjects. Five subjects had greater than 2 mm of CTV_5mm centroid error in all fractions, six subjects had less than 2 mm error for all fractions, and two subjects had errors that varied widely between fractions (identical values were observed for the CTV_8mm). Evaluating error by individual weeks, residual error of the CTV centroid was associated with GTV volume change during treatment (p=0.02 for CTV_5mm and p=0.01 for CTV_8mm, Spearman rank correlation). Mean CTV centroid error was weakly associated with initial GTV volume for CTV_5mm (p=0.09 for CTV_5mm and p=0.17 for CTV_8mm, Spearman rank correlation). Table 3 shows the four-parameter population model of the residual error in CTV_5mm and CTV_8mm centroid position after GTV-based localization.

Table 3.

Four-parameter model of systematic and random residual error (mm) in CTV centroid position after GTV-based localization

	CTV5mm			CTV8mm
	LR (mm)	AP (mm)	SI (mm)	LR (mm)	AP (mm)	SI (mm)
M	0.2	−0.1	0.2	−0.1	−0.1	0.2
Σ	0.9	1.5	1.8	1.0	1.4	1.5
σ	0.6	0.8	0.5	0.6	0.9	1.6
Σ(σ)	0.8	1.3	0.7	0.9	1.0	2.6

Abbreviations: M: Group mean error; Σ: systematic error; σ: random error; Σ(σ): standard deviation of individual patient deviations; LR: left/right; AP: anterior/posterior; SI: superior/inferior.

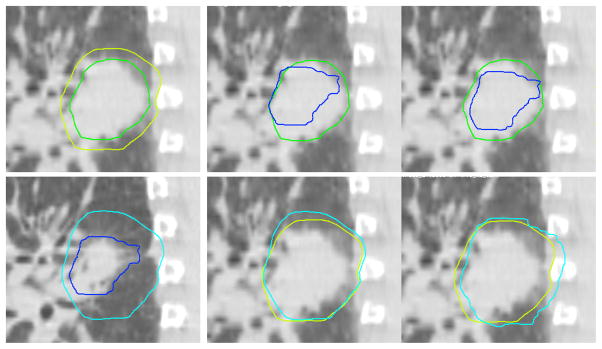
Figure 3 shows the GTV and CTV_5mm for an example subject (Subject 7) on week 1 and week 6. The GTV regressed to 83% of the week 1 volume and the CTV_5mm to 92%. However, the GTV also regressed more at the posterior aspect than the anterior aspect, leading to asymmetry between the GTV and CTV_5mm in week 6. By performing an online correction that localized the week 6 GTV to the center of the reference (week 1) GTV, this asymmetry introduced localization error to the CTV_5mm.

Figure 3.

GTV and CTV localization for Subject 7. Upper left, GTV (dark green) and CTV_5mm (light green) during week 1. Lower left, GTV (dark blue) and CTV_5mm (light blue) during week 6. Upper middle, week 6 GTV contour superimposed on Week 1 GTV, prior to online correction. Lower middle, week 6 CTV_5mm contour superimposed on Week 1 CTV_5mm, prior to online correction. Upper right, week 6 GTV contour superimposed on Week 1 GTV, after online correction to center the GTV. Lower right, week 6 CTV_5mm contour superimposed on Week 1 CTV_5mm, after online correction to center the GTV.

CTV border variation

77% of patients and 50% of weekly measurements had residual error in CTV_5mm border position greater than 2 mm (where only errors that moved the CTV outside the week 1 CTV border positions are scored), with similar results for CTV_8mm. Of these errors greater than 2 mm, residual error of the CTV_5mm borders was 3.5 +/− 1.6 mm (LR), 3.1 +/− 0.9 mm (AP), and 6.4 +/− 7.5 mm (SI); and 3.2 +/− 1.8 mm (LR), 3.6 +/− 1.4 mm (AP), and 7.3 +/− 7.6 mm (SI) for the CTV_8mm. Table 4 shows the mean (over all borders) and standard deviation of the change in border position from the first week to fifth week. It is evident that the change in the border position varied between patients, and between border locations in the same GTV. Mean border change was less for the CTV_5mm than the GTV in eleven of thirteen patients. Variation over all borders for the same patient was less for the CTV_5mm than the GTV in ten of thirteen patients.

Table 4.

Mean (over all borders) and standard deviation (in parentheses) of the change in border position, first week to fifth week, for all subjects, for GTV, CTV_5mm and CTV_8mm (mm). A positive mean denotes that the border position moved towards the centroid on the fifth week, relative to the first week

Subject	GTV	CTV5mm	CTV8mm
1	1.2 (1.8)	2.0 (1.1)	1.2 (1.8)
2	0.0 (2.7)	0.0 (2.1)	0.0 (3.5)
3	7.1 (5.3)	1.1 (4.1)	0.6 (4.5)
4	0.0 (0.9)	0.0 (1.1)	0.0 (1.2)
5	1.6 (2.4)	1.6 (2.6)	1.1 (3.2)
6	0.8 (0.9)	0.0 (0.7)	−0.4 (1.0)
7	1.0 (2.9)	0.9 (1.0)	−1.6 (1.6)
8	2.4 (1.9)	0.6 (2.9)	−0.3 (3.1)
9	1.8 (2.7)	1.1 (2.0)	0.4 (1.6)
10	2.3 (3.1)	1.2 (2.0)	1.1 (2.8)
11	0.8 (2.5)	0.0 (2.0)	0.0 (2.0)
12	2.2 (1.7)	0.9 (1.3)	0.9 (1.8)
13	−1.0 (2.5)	−1.4 (2.4)	−1.9 (3.1)

Table 5 shows the relative anisotropy ratio in GTV to CTV margin on the last week of treatment. A value of zero suggests the GTV to CTV margin is isotropic, in relation to the first week, after GTV regression. A value of one suggests maximum relative anisotropy in the margin after GTV regression. Residual error of the CTV centroid was significantly associated with relative anisotropy (p=0.03 for CTV_5mm and p=0.0002 for CTV_8mm, Spearman rank correlation). Subjects with more anisotropy in GTV regression relative to the CTV had larger errors in the CTV centroid after GTV-based localization.

Table 5.

Relative anisotropy ratio (α) on the last week of treatment. α measures the anisotropy in the GTV to CTV margin, relative to the value of α from the reference image

	α, last week
Subject	CTV5mm	CTV8mm
1	0.3	0.1
2	0.1	0.1
3	0.8	0.8
4	0.0	0.0
5	0.3	0.3
6	0.1	0.0
7	0.7	0.6
8	0.6	0.3
9	0.3	0.1
10	0.0	0.0
11	0.3	0.2
12	1.0	0.5
13	0.2	0.1

DISCUSSION

Although the CTV for lung cancer is not defined by an anatomical border, lung vasculature and bronchial vessels provide sufficient tissue features to enable tracking the location of the originally-defined CTV during a treatment course. As the GTV regresses during treatment, it changes shape and volume. In turn, the change in gross tumor mass apparently influences the location of adjacent lung tissue, which impacts the location of the originally-defined CTV border. The results of this study demonstrate that the originally-defined CTV undergoes substantial change in volume, shape, and position during a course of radiotherapy. Localizing the GTV using online image-guided correction may introduce error in CTV localization, as the GTV and CTV do not necessarily change shape, volume and position in a correlated manner.

Residual error in the CTV centroid and borders for 5mm and 8mm CTV expansions were similar, although the CTV_8mm had significantly less volume regression and slightly more volume variation between subjects than the CTV_5mm. This result is likely due to the local effect of GTV regression on surrounding tissue that diminishes with distance from the GTV. A second possible explanation is that the normal tissue itself (and any microscopic extension embedded in it) may be impacted by the delivered dose. As the edge of the CTV_8mm is close to the edge of the clinical PTV, it may have received less dose than the CTV_5mm, affecting the normal tissue position during treatment.

The difference in these changes between the GTV and CTV are likely a complex function of the mass effect of the GTV on the surrounding tissue, tissue composition of the GTV and CTV, and other biological factors which are yet unknown. The results of this study imply that additional margin is required for the CTV if GTV-based online correction is used. Table 3 suggests that a margin of approximately 3 to 5 mm on the CTV may be necessary, although other factors such as deformable registration error, delineation uncertainty, and precision of the image guidance system must also be considered.

The differential in the radial change of the GTV and CTV during treatment implies that there is some mass effect of the GTV on the surrounding tissue, and that this mass effect is variable between patients. Essentially, the radial change describes whether the adjacent lung tissue is ‘decompressing’ as the GTV regresses, or whether the GTV is ‘dissolving’ away from the lung tissue leaving the surrounding tissue relatively intact. For patients where the GTV and CTV regress by the same radial factor, the mass effect is large and as the tumor mass regresses, the surrounding normal tissue follows to fill in the empty space. For patients where the GTV radial change is larger than the CTV radial change, the GTV is ‘dissolving’ faster than the adjacent normal tissue is moving. This result implies a model where the tumor is more diffusely distributed in a fixed stratum of lung tissue, and regresses while leaving the lung tissue in place. An interesting follow up study would be to evaluate the potential association of mass effect and tumor grade due to the role grade plays in defining this type of microscopic tissue structure (26). The anisotropy ratio is a useful tool, augmenting the radial change, to further elucidate the mechanics of GTV regression relative to the CTV. In particular, this ratio describes whether this mass effect is isotropic or anisotropic between the opposite sides of the GTV. We found that anisotropy also varied widely between patients, although the study population was not large enough to evaluate possible predictors for anisotropy such as GTV size, location, histology, or tumor grade.

In this study, we tracked the originally-defined CTV and not a replanned CTV (e.g., expanding the new smaller GTV by a fixed margin of 0.5 cm). The study was designed in this manner due to a lack of knowledge of the mechanics of dose response of the presumed microscopic disease during treatment. Lacking such information, a conservative approach is to presume that the tissue encompassed by the originally-defined CTV must receive the originally-prescribed dose. It is likely that as microscopic disease becomes sterilized in the tissue far from the GTV, the CTV could be ‘shrunk’, reducing the necessity of additional margin on the CTV, although such an approach must be informed by appropriate preclinical studies.

The overall reduction in volume of the originally-defined CTV in some patients may counteract the margin requirement. However, we did not explore predictive models of GTV or CTV regression that would enable such a determination to be made during planning. Adaptive approaches that would enable patient-specific prediction of regression either anatomically (27) or biologically (28) may also be a solution. The overall reduction in CTV also has implications for anatomical adaptive replanning. Adaptation to the originally-defined CTV as it changes over treatment may enable reduced normal tissue dose, without requiring knowledge of the dose response of the microscopic extension. Exploring the possible benefit of such adaptation is a potential next step for this project.

Several issues may potentially impact the results. Helical CT, rather than cone beam CT (CBCT) was used to simulate image guidance. Helical CT was chosen to maximize the accuracy of the deformable image registration necessary to track the CTV. Breath hold images acquired with ABC were used, rather than free-breathing 4D imaging. However, we find no reason to believe regression mechanics would differ between the two types of respiration management, so the results are likely applicable to free-breathing patients. Furthermore, breath hold is a simple, effective technique to minimize respiration artifact in images, which enhances the quality of imaging and therefore deformable image registration for this type of study.

CONCLUSION

Regression of lung tumors during radiotherapy introduces geometrical changes in the normal tissue, which affects the CTV shape, volume, and position. The isotropy and differential in radial regression between the GTV and CTV varies widely between patients. Due to these effects, online image-guided correction for target localization based on aligning the visible GTV introduces error in localizing the CTV. The CTV localization error was found to be significantly associated with the amount of GTV volume regression and the anisotropy of the regression during therapy. This additional error source should be considered when designing CTV safety margins for image guided radiotherapy for lung cancer.