An optimal peak alignment for comprehensive two-dimensional gas chromatography mass spectrometry using mixture similarity measure

Abstract

Motivation: Comprehensive two-dimensional gas chromatography mass spectrometry (GC × GC–MS) brings much increased separation capacity, chemical selectivity and sensitivity for metabolomics and provides more accurate information about metabolite retention times and mass spectra. However, there is always a shift of retention times in the two columns that makes it difficult to compare metabolic profiles obtained from multiple samples exposed to different experimental conditions.

Results: The existing peak alignment algorithms for GC × GC–MS data use the peak distance and the spectra similarity sequentially and require predefined either distance-based window and/or spectral similarity-based window. To overcome the limitations of the current alignment methods, we developed an optimal peak alignment using a novel mixture similarity by employing the peak distance and the spectral similarity measures simultaneously without any variation windows. In addition, we examined the effect of the four different distance measures such as Euclidean, Maximum, Manhattan and Canberra distances on the peak alignment. The performance of our proposed peak alignment algorithm was compared with the existing alignment methods on the two sets of GC × GC–MS data. Our analysis showed that Canberra distance performed better than other distances and the proposed mixture similarity peak alignment algorithm prevailed against all literature reported methods.

Availability: The data and software mSPA are available at http://stage.louisville.edu/faculty/x0zhan17/software/software-development.

Contact: s0kim023@louisville.edu; xiang.zhang@louisville.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

An emerging technology, comprehensive 2D gas chromatography mass spectrometry (GC×GC–MS) brings much increased separation capacity, chemical selectivity and sensitivity for metabolomics analysis although there are several issues [Mondello et al. (2008); Ramos (2009)]. This approach usually uses a short column after the main analytical column. Typically, the second column is operated at a higher temperature than the first column with different stationary phase. The compounds co-eluted from the first column are further separated in the second column because of the difference of column temperature and the chromatography matrix. The further separated compounds are directed to a high capacity time-of-flight mass spectrometry system for detection. The GC × GC–MS platform offers significant advantages for analysis of complex samples including: an order-of-magnitude increase in separation capacity, significant increase in signal-to-noise ratio and dynamic range and improvement of mass spectral deconvolution and similarity matches Dettmer et al. (2007), Li et al. (2009). Since the GC × GC–MS system can provide more accurate information about compound retention times and mass spectrum, it represents a powerful tool for the analysis of compounds in complex biological systems. However, while gathering GC × GC–MS data, there is always a shift of retention times in the two columns. Retention time shifts make it difficult to compare metabolic profiles obtained from multiple samples.

In order to correct the retention time shifts in the GC × GC system, two alignment approaches have been developed: profile alignment and peak alignment. The profile alignment directly uses the entire chromatographic data, i.e. the raw instrument data, as the input data. In the peak alignment approach, the raw instrument data are first deconvoluted to peak list, and the peak lists of multiple samples are then employed as the input data to correct retention time shifts. The selection of the two approaches for retention time correction depends on the methods of downstream statistical analysis.

Currently, four profile alignment methods have been reported. Fraga et al. (2001) introduced an algorithm based on the generalized rank annihilation method. Mispelaar et al. (2003) developed a correlation-optimized shifting method. These two methods were designed to align small or local regions of interest in GC × GC data. In order to correct the entire chromatogram in both dimensions, Pierce et al. (2005) proposed an indexing scheme together with a piecewise retention time alignment algorithm. Zhang et al. (2008) developed a 2D correlation optimized warping (2-D COW) method for warping the GC × GC data. However, all the profile alignment methods align the GC × GC–MS data based on 2D retention times alone, although the signature feature of a compound, i.e. mass spectrum of fragment ions, is readily available in the raw instrument data. Aligning compound peaks solely based on the 2D retention times may introduce a high rate of false-positive alignment because some compounds with similar chemical functional groups have similar retention times in the two columns.

For this reason, two peak alignment methods, MSort (Oh et al., 2008) and DISCO (Wang et al., 2010), were developed. In these methods, the raw instrument data of each sample were first reduced to a compound peak list, where each compound was characterized by its two dimension retention times, mass spectrum and other features. The two dimension retention times and the mass spectrum of compound fragment ions were then used for compound alignment. These two methods greatly reduced the rate of false-positive alignment compared with the profile alignment methods. MSort was developed to align only for homogeneous data while DISCO can be applied to both homogeneous and heterogeneous data. The homogeneous data mean that all samples were analyzed under the identical GC × GC–MS experiment conditions while the heterogeneous data refer that experiment data were acquired under different GC × GC–MS conditions. In terms of analytical methods, there are two main differences between MSort and DISCO approaches. First, they employ the different peak distance measures, Maximum distance and Euclidean distance for MSort and DISCO, respectively. However, the effect of different peak distance measures was not examined. In this study, we examined the effect of the different peak distances on the peak alignment using four distance measures: Euclidean, Maximum, Manhattan and Canberra. Second, the different variation windows are used in both approaches. MSort requires a distance-based window and a spectral similarity-based window is required in DISCO. However, it is usually difficult for users to set an optimal value for each of the variation windows. To avoid this difficulty, we proposed a novel similarity measure, a mixture of the peak distance and the spectra similarity, and developed peak alignment algorithms in a software package named mSPA, using the proposed similarity measure in which any variation window is unnecessary. We evaluated the performance of the different peak alignment methods along with the different peak distance measures using two sets of GC × GC–MS data.

The remaining part of this article is organized as follows. The four different distance measures and spectral similarity measures are introduced along with two sets of real GC × GC–MS data in Section 2. In Section 3, the four peak alignment algorithms are described and followed by the introduction of the algorithms of the proposed mixture similarity peak alignment. All the peak alignment algorithms are then compared using the two sets of GC × GC–MS data in Section 4. Discussion and conclusion are given in Section 5. We will use the following notations throughout the article. Let T = {t₁, … , t_n} be a peak list of the target GC × GC–MS data and R = {r₁, … , r_m} the peak list of the reference GC × GC–MS data, where r_i and t_j (i = 1, … , m, j = 1, … , n) are composed of its first and second retention times (r_{(i, 1)}, r_{(i, 2})) and (t_{(j, 1)}, t_{(j, 2})), respectively. Note that the distance and the similarity always refer to the retention times and the mass spectra information, respectively. All the statistical analysis and simulations are performed using a statistical package R (www.r-project.org).

2 METHODS

2.1 Distance measure

The four different distance measures are employed in this study: Euclidean distance, Maximum (aka Chebyshev) distance, Manhattan distance and Canberra distance. Each distance measure between two peaks t_j and r_i is as follows:

(1)

(2)

(3)

(4)

where t_{(j, 1)} and r_{(i, 1)} are the first dimension retention time of the peaks t_j and r_i, and t_{(j, 2)} and r_{(i, 2)} are the second dimension retention time of the peaks t_j and r_i. To help understand the variation among the distance measures, the four distance measures are delineated in Figure S1 of the Supplementary Data II.

2.2 Similarity measure

We use the dot product Stein and Scott (1994), which is the most popular approach, for spectrum similarity measure between two mass spectra, I_tj and I_ri, of two peaks, t_j and r_i, as follows:

where < I_tj, I_ri> is an inner product between the two mass spectra, I_tj and I_ri, of two peaks t_j and r_i, and 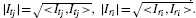. We also use the Pearson's correlation coefficient, corr(I_tj, I_ri), as an alternative method for the spectrum similarity calculation and it showed the same conclusions as the dot product (see Supplementary Data I). The difference between two similarity measures is centering of the variables and normalizing by the variance of each variable. In fact, Liu et al. (2007) compared the different measures of spectral similarity and concluded that the Pearson's correlation coefficient is robust but the difference between the dot product and the Pearson's correlation coefficient is subtle. We included the Pearson's correlation coefficient in our mSPA software as an option for users to select.

2.3 GC × GC–MS data

In this study, two sets of GC × GC–MS data were used. One is a mixture of 106 compound standards and the other is metabolite extract from rat plasma with spiked-in six compound standards. In the first dataset (Dataset I), the GC × GC–MS analysis were repeated 10 times under 5°C/min temperature gradient, resulting in a total of 10 datasets (S1–S10 in Table 1). As for the spiked-in sample (Dataset II), the compounds were analyzed five times on GC × GC–MS (D1–D5 in Table 1). The detailed procedure for generating these two datasets is described in the Supplementary Data II. The LECO ChromaTOF software version 3.4 was used for instrument control, spectrum deconvolution and compound identification. The peak list of each GC × GC–MS data was then manually examined. In case that there are multiple peaks identified as the same compound in an experiment, only the peak with the largest peak areas was selected.

Table 1.

The summary of two GC × GC–MS data: a mixture of compound standards (S1–S10) and a spiked-in sample (D1–D5)

RUN ID	S1	S2	S3	S4	S5	S6	S7
The number of	78	76	76	75	74	73	74
compounds	(180)a	(186)	(161)	(151)	(151)	(145)	(172)
S8	S9	S10	D1	D2	D3	D4	D5
76	77	75	466	456	436	452	418
(163)	(168)	(174)	(759)	(733)	(694)	(727)	(661)

^aThe number of peaks found by ChromaTOF before correcting multiple peaks.

3 ALGORITHM

3.1 Four peak alignment algorithms

Four algorithms are considered here to compare the performance of the peak alignment for the homogeneous GC × GC–MS data. For each peak alignment algorithm, we employ the four different distance measures.

3.1.1 Peak alignment without window

In this case, there are two methods. One is a peak alignment procedure using solely the peak distance without window (PAD) and the other peak alignment algorithm is rendered only based on the spectral similarity between two peaks without window (PAS). In detail, for each peak t_j ∈ T in the target chromatogram, the peak distances and spectral similarities between the current target peak and all the peaks r_h(∈ R), h = 1, … , m, in the reference sample are calculated for PAD and PAS, respectively. Then the best matched peak r_i (∈ R) of t_j is decided by:

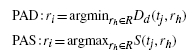where |R| = m and D_d is a distance measure (d = 1, … , 4).

3.1.2 Peak alignment with window

The previous methods find a best match by searching the peak with the minimum distance or the maximum spectral similarity. Therefore, there might be a false positive alignment if the experimental variations are bigger than the information of the peak distance or the spectral similarity. This can be resolved if both measures are used on the peak alignment at the same time. To this end, MSort (Oh et al., 2008) uses the distance-based window while the spectral similarity-based window is used by DISCO (Wang et al., 2010). In other words, MSort and DISCO require users to provide predefined variation windows for the distance and the spectral similarity among the different experiments. The detailed description of MSort and DISCO can be found in the Supplementary Data II.

We here introduce two algorithms which can be considered as generalized versions of MSort and DISCO, respectively. The first method is called the peak alignment with the distance-based window (DW-PAS) and the second method the peak alignment with the similarity-based window (SW-PAD). In case of DW-PAS, for each peak t_j ∈ T, the distances between the current target peak t_j and all the peaks r_i ∈ R in the reference chromatogram are calculated by the chosen distance measure and some of the reference peaks are selected for the peak alignment by the distance-based window,

(5)

where δ_(k) is the k-th closest peak's distance to the current peak t_j obtained by using the chosen distance measure D_d, d = 1, … , 4. Once the several reference peaks are selected by the distance-based window, the best matching reference peak r_i of the current target peak t_j is inferred using the following expression:

where |R_S| ≤ |R| = m. Note that MSort employs the Maximum distance D₂ to build the window and considers the Pearson's correlation as spectral similarity measure. The difference between DW-PAS and SW-PAD is the way to construct the variation window. In case of SW-PAD, the window is constructed by the spectral similarity measure, dot product in this work. Once some of the reference peaks are selected by the window constructed, the reference peak with the minimum distance is chosen as the best match of the current target peak. The entire procedure of SW-PAD for finding the best matching reference peak r_i ∈ R of the current target peak t_i ∈ T can be summarized by

where R_S = {r_h |S(t_j, r_h)≥ ρ, r_h ∈ R} and |R_S| ≤ |R| = m and ρ is the user-defined threshold for the spectra similarity by the dot product. SW-PAD becomes DISCO when the Pearson's correlation as a similarity measure is used to extract the subset R_S of R instead of the dot product accompanied by the Euclidean distance D₁.

3.2 Mixture similarity

We further developed a novel similarity measure which uses both the peak distance and the spectral similarity measures simultaneously. We call the proposed measure the mixture similarity, and the mixture similarity to r_i (∈ R) given t_j can be defined:

(6)

where w is the weight for the mixture similarity measure and 0 ≤ w ≤ 1. Note that the distance part in the right-hand side of Equation (6) is normalized so that the range becomes between 0 and 1. Certainly, when w = 1, the mixture similarity use the peak distance only and it is only based on the spectral similarity measure when w = 0. That is, M_d (t_j, r_i | w = 1) = 1/(1 + D_d (t_j, r_i)) and M_d (t_j, r_i | w = 0) = S(t_j, r_i). As the mixture similarity between r_i and t_j becomes large, the possibility of t_j matching to r_i increases. Using the mixture similarity measure, the peak alignment can be rendered as follows. For each peak t_j ∈ T, the mixture similarities between the current target peak and all the peaks r_h (∈ R), h = 1, … , m, in the reference sample are calculated. Then the best matching peak r_i (∈ R) of t_j is decided by

where |R| = m. We call this method the peak alignment using the mixture similarity without window (PAM). One of the main benefits of the proposed PAM method is the ability to use both the peak distance and the spectral similarity simultaneously without constructing the variation window differing from DW-PAS and SW-PAD in which both the distance and spectral similarity measures are used sequentially through a constructed window.

4 IMPLEMENTATIONS

In the previous section, the five methods are introduced for the peak alignment, which are PAD, PAS, DW-PAS, SW-PAD and PAM. For each method, we apply the four different distance measures, Euclidean, Maximum, Manhattan and Canberra distances, along with the spectral similarity measure to GC × GC–MS data. We first describe the comparison criteria to evaluate the performance of each method. Then we consider two cutoff values (k and ρ) which need to be predefined for the variation window-based peak alignment methods, DW-PAS and SW-PAD, as well as the weight w for the mixture similarity measure, PAM. Then the performances of each method are considered for each dataset and followed by the description of the method of finding the optimal distance measures and w value.

4.1 The comparison criteria

The performances of all five methods are compared by calculating the true positive rate (TPR), positive predictive value (PPV) and F1 score of the peak alignment. Suppose there are n target peaks T = { t₁, … , t_u, t_{u + 1}, … , t_n } and m reference peaks R = {r₁, r₂, … , r_u, r_{u + 1}, … , r_m } with u positive peak pairs {(t₁, r₁), (t₂, r₂), … , (t_u, r_u) }, where u ≤ min(n, m). Note that if two peaks are generated by the same compound, it is called a positive peak pair. If a certain peak alignment method is applied to the two datasets, T and R, and v matched peak pairs are found, then the values of TPR and PPV of the peak alignment between two datasets are estimated by the following equations:

where TP is the number of positive peak pairs that were aligned as positive (true positive) and is less than or equal to min(u, v), FP is the number of negative peak pairs that were aligned as positive (false positive) and is v-TP, FN is the number of positive peak pairs that were not aligned (false negative) and is u-TP and TN is the number of negative peaks that were not aligned (true negative) and is mn − u-FP. Note that the total number of peak pairs is mn. TPR is called recall and PPV precision and their harmonic mean (=2 × TPRċ PPV/(TPR + PPV)) is used as an accuracy which is called F1 score. Thus, we use F1 score as an accuracy of the peak alignment. Once all the implementations were finished, the means and standard errors (SE) of TPR, PPV and F1 score for all the cases of each peak alignment method were estimated for the purpose of comparing their performance. The results of this estimation are given in the Supplementary Data I.

4.2 The cutoff values and the weight w

DW-PAS method requires to construct the distance-based window for peak alignment. To do this, k, which is described in expression (5), should be set up prior to the peak alignment. It means that the window is constructed by the reference peaks which have less than or equal to the distance of the k-th closest reference peaks to the current target peak. In our studies, the five values, (3, 5, 10, 15, 20) were used to see the effect of the k value on the performance of the peak alignment. On the other hand, the cutoff value for the spectral similarity, ρ, is necessary for SW-PAD method and the 13 values (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.93, 0.95, 0.97, 0.99) were considered to investigate how the performance of the peak alignment was affected. The performance of PAM depends on the weight w of the mixture similarity. If w goes to one, then the peak distance will play an important role in the peak alignment and the contribution of the spectral similarity measure will increase as w goes down to zero. In this study, we examined the performance of PAM according to the 13 different w values, (0.01, 0.05, 0.1, 0.2 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 0.99).

4.3 Performance analysis of pair-wise peak alignment

All the pairs among the data are constructed, considering that one is a reference chromatogram and the other is a target chromatogram. As a result, there are a total of 45 homogeneous chromatogram pairs for Dataset I and 10 for Dataset II used for the comparison analysis of the peak alignment methods. For each peak pair, the five different peak alignment methods were implemented along with four different distance methods as well as the different cutoff and weight values.

4.3.1 Dataset I: a mixture of compound standards

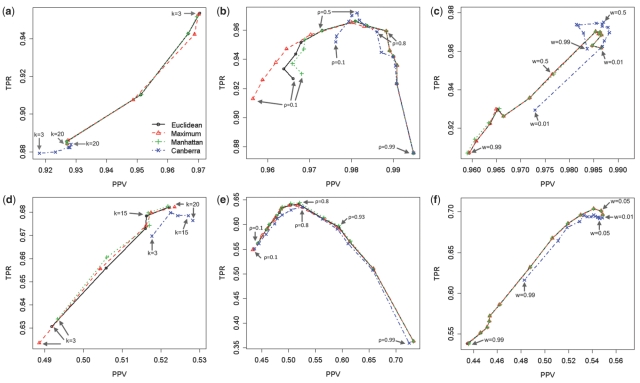
When PAD was used for Dataset I, Canberra distance measure significantly outperformed other distance measures in terms of F1 score. Their mean and SE of F1 scores are as follows: Euclidean = 0.9253 ± 0.0052; Maximum = 0.9035 ± 0.0072; Manhattan = 0.9276 ± 0.0049; Canberra = 0.9652 ± 0.0026 (see Supplementary Data I). The effect of the cutoff value, k, for the peak alignment method DW-PAS was first examined as depicted in Figure 1(a).

Fig. 1.

The effects of k, ρ, w on the peak alignment methods for Dataset I (a–c) and Dataset II (d–f). The scatter plots of the TPR versus the PPV are depicted for Datasets I and II. The Euclidean, Maximum, Manhattan and Canberra distances are depicted as black circles, red triangles, green pluses (+) and blue crosses (×), respectively. (a and d) The performance of the DW-PAS method is examined using different k values. (b and e) The performance of the SW-PAD method is examined using different ρ values. (c and f) The performance of the PAM method is examined using different w values.

Note that k is the rank of the distance in ascending order, meaning that if k is close to one, the distance goes to zero. Euclidean distance with PAD performs the best when k = 3, but its F1 score is overlapped with those of Maximum and Manhattan distances when k = 3 (F1: Euclidean = 0.9618 ± 0.0037; Maximum = 0.9614 ± 0.0037; Manhattan = 0.9604 ± 0.0039). Interestingly, the superiority of Canberra distance with PAD is disappeared in case of DW-PAS (F1 = 0.8981 ± 0.0069).

We examined the performance of the SW-PAD method according to its different cutoff value, ρ, which is used to construct the similarity-based window. Figure 1(b) displays that the optimal ρ may be around 0.5 for Dataset I. As ρ goes to near zero, both TPR and PPV tend to be decreased. If ρ goes to near one, the PPVs are increased but the TPRs are sharply decreased. When the cutoff value, ρ, is small, Canberra distance shows much better performances than other distance measures. However, no significant difference is observed among the different distance measures in case that the cutoff value is large. The ρ = 0.5 version for SW-PAD with Canberra distance performs the best (F1 = 0.9766 ± 0.0026).

Figure 1(c) shows the performance of the PAM method using the mixture similarity measure. The performances were examined according to the different weight values (w) between 0 and 1. Clearly, Canberra distance behaves differently from other distance measures. Namely, as w increases, the performance of the peak alignment of Euclidean, Maximum and Manhattan distances with PAM drop down sharply, while the performance of Canberra distance tends to increase up to some point as w goes to one. As a result, Canberra distance performs the best when w is greater than or equal to 0.5 and other distances have the best performance when w is smaller than 0.5. That is, while the spectral similarity plays an important role in the version of PAM with other distance measures, the peak distance and the spectral similarity are equally contributed to the case of PAM with Canberra distance. The w = 0.5 version of PAM with Canberra distance outperforms others (F1 = 0.9810 ± 0.0020).

When Dataset I was used for each peak alignment method, PAS (M2) shows the worst performance (F1 = 0.9023 ± 0.0069) as can be seen in Table 2 and Table S2 and Figure S3(a) of the Supplementary Data II. Apparently, PAM (M5) shows a promising performance, especially coupled with Canberra distance (D4) as depicted in Figure S3(a). Collectively, in case of Dataset I, the ρ = 0.5 version of SW-PAD with Canberra distance and the w = 0.5 version of PAM with Canberra distance have the better performances significantly different from other methods as shown in Table 2.

Table 2.

The maximum F1 scores of each peak alignment method for Dataset I and II

Dataset	Method	k	ρ (w)	Distance	F1	95% CI of F1
I	PAD			Canberra	0.9652	(0.9600–0.9704)
	PAS				0.9023	(0.8888–0.9157)
	DW-PAS	3		Euclidean	0.9618	(0.9546–0.9690)
	SW-PAD		0.5	Canberra	0.9766	(0.9716–0.9817)
	PAM		0.5	Canberra	0.9810	(0.9771–0.9849)
II	PAD			Manhattan	0.4729	(0.4382–0.5076)
	PAS				0.6109	(0.5908–0.6310)
	DW-PAS	15		Canberra	0.5932	(0.5716–0.6149)
	SW-PAD		0.93	Manhattan	0.5954	(0.5687–0.6221)
	PAM		0.05	Manhattana	0.6148	(0.5945–0.6351)

^aEuclidean and Maximum have the same F1 value as that of Manhattan.

4.3.2 Dataset II: a spiked-in sample

The performance of the five different peak alignment algorithms was examined with Dataset II and we observed several different trends from Dataset I. There was no clear distinction among the four different distance measures when PAD was employed in terms of F1 scores (F1: Euclidean = 0.4728 ± 0.0178; Maximum = 0.4677 ± 0.0179; Manhattan = 0.4729 ± 0.0177; Canberra = 0.4694 ± 0.0273).

PAS outperforms against PAD (F1: PAS = 0.6109 ± 0.0102; PAD with Manhattan = 0.4729 ± 0.0177), while PAD performed better than PAS significantly in case of Dataset I as shown in Table 2. This means that the variation in peak distance might be larger in Dataset II than that in Dataset I compared with the variation in spectral similarity, which is true because the sample complexity is significantly increased in the Dataset II. As a result, the contribution of the spectral similarity to the peak alignment will be larger than that of the peak distance in Dataset II.

When DW-PAS was applied to Dataset II, the Canberra version performed better than other distances as clearly shown in Figure 1(d). When k is three, the difference between Canberra and other distances becomes much bigger than when k is larger than 15. The k = 15 version of DW-PAS with Canberra distance shows the best performance (F1 = 0.5932 ± 0.0110) as can be seen in Tables 2 and S2.

It seems that the optimal cutoff value, ρ, for Dataset II is different from the value for Dataset I. As shown in Figure 1(e), the highest TPR is occurred when ρ = 0.8 which is consistent with the result of DISCO (Wang et al., 2010). However, if TPR and PPV are considered through F1 score which is the harmonic mean between TPR and PPV, then the best performance is occurred when ρ = 0.93. On the other hand, Dataset I gives us 0.5 as an optimal ρ as displayed in Figure 1(b).

All the distance measures have the similar trends according to w when PAM was applied to Dataset II as depicted in Figure 1(f). Namely, as w goes to one, the performance decreases, while the performance increases if w decreases to zero. Interestingly, when w = 0.99, the version of Canberra distance outperforms against other version of distance measures (F1: Euclidean = 0.4811 ± 0.0169; Maximum = 0.4814 ± 0.0168; Manhattan = 0.4815 ± 0.0169; Canberra = 0.5414 ± 0.0148 as shown in the Supplementary Data I), while no significant difference was observed when PAD was applied to the same dataset. This means that although the amount of the contribution of the spectral similarity is relatively small (1 − w = 0.01), the number of false positives can be reduced significantly by aid of the spectral similarity measure. Similar to the conclusion in Dataset I, PAM shows the best performance in peak alignment as shown in Table 2 and Figure S3(b).

4.4 Peak alignment of all peak lists

In the previous section, we considered the performance of the peak alignment of each method based on the pairwise peak alignment. However, the peak table that all peak lists were aligned together is absolutely necessary for further analysis. For this reason, we aligned all peak lists using the cases which have the maximum F1 score for each peak alignment method as summarized in Table 2 in order to examine the performance of the peak alignment of each method when all peak lists were aligned. As for Dataset I, we aligned 10 peak lists with 9 pairs of the pairwise alignment, (S1,S2), (S2,S3), (S4,S5), (S6,S7), (S7,S8), (S8,S9) and (S9,S10), by choosing the best cases of each pair for each method which has the maximum F1 score except for OP-PAM which is described in the next section. In case of OP-PAM, it was done by optimization. Similarly, Dastset II was aligned with four pairs of the pairwise alignment, (D1,D2), (D2,D3), (D3,D4) and (D4,D5). Once the peak table of all peak lists was constructed, the peaks that had at least one missing were deleted. Using the scheme described above, the peak alignment of the entire peak list was done with the best cases for each peak alignment as depicted in Figure S6 in the Supplementary Data II.

To examine the performance of the peak alignment for each algorithm, we calculated TPR, PPV and F1 score based on the true peak alignments for Datasets I and II as shown in Figure S5 in the Supplementary Data II. The true number of peaks matched throughout all the homogeneous chromatograms was 66 and 146 for Datasets I and II, respectively. The results were consistent with the previous validation studies in Section 4.3. Indeed, PAM outperforms others in terms of F1 scores. In case of Dataset I, SW-PAD and PAM show the largest F1 scores (F1: PAD = 0.9365; PAS = 0.8333; DW-PAS = 0.9219; SW-PAD = 0.9618; PAM = 0.9618) as can be seen in Figure S6(a). Figure S6(b) also shows that PAM performs the best out of the five peak alignment algorithms using Dataset II (F1: PAD = 0.3275; PAS = 0.5048; DW-PAS = 0.4940; SW-PAD = 0.5091; PAM = 0.5363).

4.5 Finding the optimal value of w for PAM method

For the PAM method, it is indispensable to find the optimal value of w and distance measure for the best performance of the peak alignment. Therefore, we developed an optimal version of PAM which is called OP-PAM. In case of OP-PAM, the optimal value of w and optimal distance measure will be estimated iteratively based on a certain likelihood function differently from fixing their values for PAM by users in advance. To do this, the following likelihood function L(Y, X|θ) was considered to evaluate the potential performance of the peak alignment:

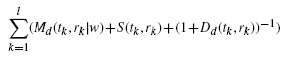(7)

where θ = (w, d), d is the index of the four different distance measure (1 = Euclidean; 2 = Maximum; 3 = Manhattan; 4 = Canberra), l is the number of all the matched peaks between T and R, |T| = n, |R| = m, and l ≤ min(n, m). Therefore, the optimal weight and distance measure, 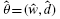are estimated given T and R by the following maximization:

The estimated optimal weight and distance measure, 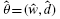, can be found in Table S3 in the Supplementary Data II. The initial value was 0.5 for all the cases and the maximization was done using the R package nlminb which is unconstrained and constrained optimization using PORT routines. In case of Dataset I, the estimates of w are consistent with the best case of PAM. That is, the best case of PAM was Canberra distance with w = 0.5 as shown in Table S2 and, in case of OP-PAM, Canberra distance was estimated as the best for all the peak pairs with the mean 0.6939 and SD 0.2558 of the estimates of w as can be seen in Table S3. As for Dataset II, the estimates of OP-PAM are different from the best case of PAM. Namely, the best case of PAM was Euclidean, Maximum and Manhattan distances with w = 0.05 in Table S2, while Canberra distance was selected having the maximum likelihood with the mean 0.6187 and 0.0786 of the estimates of w in Table S3.

The peak alignment of all peak lists was then done using OP-PAM for Datasets I and II as depicted in Figure S6. Interestingly, the performance of the peak alignment using OP-PAM is the same as that using PAM for Dataset I and outperforms others in case of Dataset II (F1 = 0.9618 for Dataset I and F1 = 0.5370 for Dataset II) as shown in Figure S6. Their detailed results such as aligned retention time, area and compound name tables can be seen in the Supplementary Data III.

5 DISCUSSION AND CONCLUSION

Homogeneous peak alignment using either the distance of peaks and/or the similarity of mass spectra was considered with four different distance measures and the mixture similarity measure by combining the peak distance and the spectral similarity. Then the performances of the five different alignment methods were compared. In addition, the optimal version of PAM, OP-PAM, was further implemented into a software package mSPA for automatic peak alignment.

Compound retention index (I), normalized retention time, can be employed for peak alignment. As for GC-MS data, Shimadzu (www.shimadzu.com) developed a retention time correction algorithm, which is called Automatic Adjustment of Retention Time (AART), inside their GCMS solution 2.5 software using I features and showed the promising performance. Similarly, I features can be used for GC × GC–MS data to correct the retention times of both dimensions. However, mSPA is designed for the alignment of homogeneous data, where the compound retention time shifts are not large and therefore, the advantage of converting retention time to I and then use I for alignment may not be significant.

Throughout the comparison, Canberra distance shows better performances than other distance measures. This may be because Canberra distance normalizes the variations of retention time by taking the weight, resulting in reducing the effect of the variation of each retention time.

The variation in peak distance of Dataset I is larger than that of Dataset II as seen in Figure S2 and Table S1. Consequently, PAD performed worst in Dataset II in terms of F1 score, while it showed better performance marginally in Dataset I in Table 2. However, although PAS showed the smallest F1 score in Dataset I in Table S2, PAS is less sensitive to the quality of data than PAD. It means that the measurement error of mass spectra is stable so that PAS may be robust to variation in peak distance.

In order to utilize the peak distance and the spectral similarity together, a novel similarity measure, the mixture similarity, was proposed. This is a mixture of the peak distance and spectral similarity information in that the contribution of each measure is controlled by the weight w. Therefore, if the peak distance plays an important role in peak alignment, w will be large and the weight w will be small if the spectral similarity plays a primary role in peak alignment as described in Equation (6). Indeed, when PAM with the mixture similarity measure was implemented, the smaller w values were observed when the variation in peak distance is larger (Dataset II) than when the variation is smaller (Dataset I) as shown in Table S2 and in the last column of Figure S4. In particular, it can be seen that PAM prevailed against other four methods in peak alignment.

As we stated above, the cutoff values are not consistent with the different dataset so that an optimal cutoff value should be found according to the quality of the dataset before the peak alignment. For this reason, OP-PAM, the optimal version of PAM, was developed to find the optimal value of w automatically to avoid this issue. The main advantages of OP-PAM to peak alignment are (i) it uses both peak distance and spectral similarity, (ii) it does not need to construct the window so that the cutoff values are not necessary, and (iii) it can find the optimal distance and weight w based on the likelihood function statistically as described in Equation (7). In our comparison analysis, it is demonstrated that OP-PAM outperformed all the literature reported peak alignment methods and other methods investigated in this work for the peak alignment of the entire peak lists as shown in Supplementary Figure S6. Especially, OP-PAM method can be an optimal approach for the peak alignment because it performed the best for both datasets. In other words, it provides high-quality peak alignment regardless of the quality of the GC × GC–MS data.