Subjective Probabilities in Household Surveys

Abstract

Subjective probabilities are now collected on a number of large household surveys with the objective of providing data to better understand inter-temporal decision making. Comparison of subjective probabilities with actual outcomes shows that the probabilities have considerable predictive power in situations where individuals have considerable private information such as survival and retirement. In contrast the subjective probability of a stock market gain varies greatly across individuals even though no one has private information and the outcome is the same for everyone. An explanation is that there is considerable variation in accessing and processing information. Further, the subjective probability of a stock market gain is considerably lower than historical averages, providing an explanation for the relatively low frequency of stock holding. An important research objective will be to understand how individuals form their subjective probabilities.

1. Introduction

It would seem obvious that any intertemporal decision would require the decision-maker to have some beliefs about the probabilities of future events that are pertinent to the decision, and that this statement would be true even when decision-making is suboptimal. In some situations these beliefs could be consistent with the actual probabilities of those events, but in other situations they need not be. I will call the beliefs the decision-maker uses in making intertemporal decisions his or her subjective probability distributions about those future events.

For many years the main model of intertemporal economic decision-making by individuals (or households) has been based on the maximization of expected utility. In this setup an individual makes a choice at time t , but the consequences of that choice will not be known immediately, and those consequences will depend on stochastic events that are not under the control of the individual. For example, in choosing how much to spend an individual should take into account that his or her health may deteriorate, in which case more resources will be required for health care spending. In that health change has a large stochastic component, the decision-maker must choose spending only knowing the probability of a health decline, not whether it actually will decline. To maximize expected utility the decision-maker will consider utility in each of the possible future health states, and choose current spending (and hence carry-forward wealth) that will maximize the weighted average of utility in the various health states, where the weights are estimates of the probabilities of the different health outcomes.

In this setup, the intertemporal choice will depend on preferences, the constraints in the environment such as economic resources, and the subjective probability distributions of pertinent events. The objective of a theoretical or empirical investigation into intertemporal choice aims to estimate preferences, and typically the constraints can be observed. However such an investigation requires information about the probability distribution that the decision-maker used in coming to his or her choices because choice outcomes can be explained either by preferences or by subjective probability distributions (Manski, 2004). For example, under uncertainty about future health, the choice to consume initially at a low level could be due to high risk aversion or to a subjective probability distribution on health outcomes that puts considerable probability on a transition to bad health.

The standard practice has been to assume that decision-makers have rational expectations; that is, their subjective probability distributions coincide with the true probability distributions. For example, in the case of returns in the stock market, the subjective probability distribution of returns held by individuals is the same as the actual probability distribution. For empirical study of decision-making there remains the problem of finding out what that true distribution is. In some situations, such as the stock market, historical data can be used to estimate the distribution of returns and the stability of the distribution of returns. If the stock market is roughly a random walk with drift, it may be reasonable to assume the true probability distribution of future returns can be estimated from historical data, and, indeed specialists have done that. In the study of portfolios, application of the rational expectations hypotheses means that individuals will use that same estimated historical distribution.¹ This type of reasoning and empirical work have led to the so-called equity holding puzzle and its close cousin the equity premium puzzle: based on historical rates of return (both mean and variance) low rates of stock market participation can only be explained by very high levels of risk aversion (Haliassos & Bertaut, 1995). However, many would say that these levels are unreasonable and that it is indeed a puzzle (Kocherlakota, 1996).

The reasonableness of the assumption of rational expectations depends on the situation. An argument, which may well apply to a number of business situations, is that individuals or firms that do not have rational expectations will be driven out of business, so that the remaining players will have rational expectations. This argument, however, is not relevant for many studies of interest. Individual decision-makers can have persistently incorrect expectations about pertinent events in their own lives and still live on to make further mistakes. Again a good example is the stock market. Professional traders most likely understand the main empirical regularities in historical rates of return and are familiar with the main lines of research. Yet, ordinary persons may have little knowledge of rates of return or stock market behavior. Their lack of participation may be the result of lack of information rather than risk aversion, and there is nothing in the environment to compel them to acquire that information. To separate lack of knowledge from risk aversion we need additional data on beliefs.

Even if each individual has rational expectations, in many situations circumstances vary from person to person and individuals have information about the likelihood of their own outcomes; that is, individuals often have information about the probability distributions they actually face, which vary from person to person. For example, a population life table shows survival conditional on sex and age, whereas an individual is likely to condition on many other additional variables such as own health, the longevity of parents, and health behaviors. Furthermore, some of these processes are stochastic processes in which the individual has varying degrees of control. Survival is a stochastic process in which individuals have rather limited control via their health behaviors, but they have considerable personal information. Thus self-rated health has strong predictive power for survival beyond what is contained in a life table. Retirement has a stochastic component, but it is under considerable control of the worker. For example, a 61 year-old worker may be quite confident that she will retire at 62, and, while health may intervene to force an earlier retirement, the probability of such an event is rather low. In these examples, even if each individual has rational expectations, using population probabilities rather than individual probabilities to explain individual choice amounts to model misspecification.

Recognizing the importance of having measures of subjective probabilities on household surveys, some designers of household surveys began in the early 1990s to include questions about subjective probabilities. For example, in 1993 the Survey of Economic Expectations fielded subjective probabilities about future economic status (Dominitz, 1998; Dominitz and Manski, 1997a, 1997b), and the Health and Retirement Study (HRS) put a large number of them into its baseline wave in 1992.² The HRS has been most influential because of its large sample size, its extensive number of subjective probabilities and because it is a long-running panel survey. Therefore, a focus of this paper will be the empirical properties of some of the subjective probabilities measured in the HRS.

2. The measurement of subjective probabilities in the Health and Retirement Study

The first wave of the HRS was a population-representative survey of individuals from the birth cohorts of 1931-1941 and their spouses (Juster & Suzman, 1995). Thus the individuals in the probability sample were approximately ages 51-61. In 1993 individuals from the birth cohorts of 1923 or earlier and their spouses were added, and in 1998 individuals from the birth cohorts of 1924-1930 and 1942-1947 and their spouses were added, so that in 1998 the HRS represented the population approximately aged 51 or over. In 2004 individuals from the birth cohorts of 1948-1953 and their spouses were added, again making the HRS representative of individuals approximately 51 or over. Because of the new cohorts the sample size of the HRS is about 20,000.

In the 1992 baseline wave subjective probability distributions were elicited about these domains: survival, retirement, inflation, health care expenditures, unemployment, giving financial help, housing prices, Social Security benefits, economic depression and health limitations. This was an important development because of the large sample size of the HRS (about 12,000 in the initial wave), the large number of domains of actual outcomes including labor market participation, health, economic status, family linkages and program participation, and because of the longitudinal nature of the HRS. These features attracted many users to the HRS, and many took an interest in subjective probabilities. The HRS is a biennial longitudinal survey, and the subjective probability measures were repeated in subsequent waves.³ The long-running nature of the HRS has meant that we can now see a number of the individual outcomes for which subjective probabilities were reported in early waves, and we have a large number of transitions providing data with which to study how subjective probabilities are updated when there is new information.

The first uses of the HRS data on subjective probabilities were cross-section studies that aimed to establish validity. In particular what was data quality in terms of the rate of item non-response and “outlier” type response; were average probabilities somewhat close to average actual outcomes; and did the probabilities vary across individuals in the same manner as the actual variation in outcomes? A main focus of research has been on subjective survival probabilities. The 1992 HRS asked about subjective survival to age 75. The rate of item nonresponse was just 2%, which is considerable lower than the rates for economic variables such as the components of income or wealth (Hurd & McGarry, 1995). Average subjective survival probabilities were compared with life tables based on the following reasoning: Suppose that each individual knew and accurately reported his or her true probability of survival to 75 (which would vary from person to person). Because the expected value of actual survival equals the probability of survival, the average of the subjective probabilities will be close to the average actual survival rate of those individuals, and in large samples the two will be the same. In 1992 HRS the average subjective survival probability was 0.65 and the life table survival rate (1990 period life table) was 0.68 (Hurd & McGarry, 1995). To the extent that the 1990 period life table accurately predicts actual survival, at the population level the subjective survival probabilities will accurately predict average population survival. This does not mean that individuals will necessarily have rational expectations: for example average subjective survival probabilities in subpopulations could differ from survival outcomes in those subpopulations even though the population predicts accurately its survival. But had the average survival probabilities been wildly off, it would be difficult to maintain that they are used by individuals in their decision-making.⁴

In the initial wave of HRS average subjective survival probabilities varied across subpopulations in the same qualitative manner as actual survival. For example smokers reported lower survival probabilities than nonsmokers, and those with worse self-rated health reported lower survival probabilities. Thus it was established even in cross-section that the subjective survival probabilities would have predictive power for actual mortality outcomes, although not whether they would have predictive power conditional on observables such as smoking and self-rated health.

With the second wave of HRS in 1994 two important facts were established: individuals who reported elevated subjective survival probabilities in 1992 tended to have lower actual mortality between 1992 and 1994; individuals who had new health events known to increase mortality risk such as a heart attack or the onset of cancer tended to reduce their subjective survival probabilities (Hurd & McGarry, 2002).

The initial favorable experience with subjective probabilities in the HRS combined with an increasing awareness of their potential value led to their use in a number of new surveys of the older population. They were put on the English Longitudinal Study of Ageing (ELSA), the Survey of Health Ageing and Retirement in Europe (SHARE), and the Korean Longitudinal Study of Aging, and on a number of well-known ongoing longitudinal surveys such as the Panel Study of Income Dynamics and the National Longitudinal Survey of Youth, 1997 Cohort.

Because of the large body of empirical results based on the HRS I will mainly illustrate the current state of research on subjective probabilities with result from the HRS. The format in the HRS for querying about subjective probabilities begins with an introduction about weather which is a topic often discussed probabilistically:

Next we would like to ask your opinion about how likely you think various events might be. When I ask a question I’d like for you to give me a number from 0 to 100, where “0” means that you think there is absolutely no chance, and “100” means that you think the event is absolutely sure to happen.

For example, no one can ever be sure about tomorrow’s weather, but if you think that rain is very unlikely tomorrow, you might say that there is a 10 percent chance of rain. If you think there is a very good chance that it will rain tomorrow, you might say that there is an 80 percent chance of rain.

Then the specific subjective probability is asked as follows:

What is the percent chance that you will live to be 75 or more?

In a face-to-face survey respondents may be given a physical representation of the scale, but because many surveys are by telephone most of the data are collected without the respondent using a visual scale.⁵

Although the original purpose of obtaining subjective probabilities in surveys about economic behavior was to help model and estimate intertemporal decision-making, subjective probabilities have been used for a number of other purposes. An important investigation has been whether they predict outcomes. If they do, they would be valuable because they provide a quantitative prediction that is hard to obtain by other methods. Furthermore, respondents are allowed to express uncertainty about their predictions of outcomes which can be use to establish confidence intervals about the predicted outcomes. The evaluation of the uncertainty about outcomes is important and cannot adequately be done using qualitative designations such as whether the outcome is “highly likely, likely, not likely” and so forth (Manski, 2004). In discussing the relationship between subjective probabilities and actual outcomes I will concentrate on the probabilities of survival, the probability of working at some future age, and the probability of stock market gains. These are useful benchmarks because they are important in models of economic behavior, they have been studied fairly extensively, and in the HRS panel we can observe in some cases the actual outcomes that correspond to the subjective probabilities.

3. Subjective Survival

In 1992, the HRS asked about survival until age 75. Age-eligible respondents were about 51-61, so that the event had a 20-year horizon on average. Table 1 has a comparison of average subjective survival probabilities with life table probabilities.⁶ Compared with a 1990 period life table the average P75 was remarkably close, 64% versus 68%. Men were optimistic relative to the life table and women pessimistic. The 1940 cohort life table is a more appropriate comparison because it reflects the actual mortality experience of the HRS cohort as well as incorporating projections of mortality improvements. It shows large improvements in survival for men relative to improvements for women so that men now appear to be slightly pessimistic and women quite pessimistic. According to the cohort life table, the HRS cohort will under-estimate survival by about eight percentage points.

Table 1.

Average P75 and life table survival rates from age 55.5 to age 75 (%)

	N	P75	1990 period life table	1940 cohort life table
Male	4134	62.12	59.71	66.99
Female	4960	66.36	74.94	76.55
All	9094	64.40	67.60	71.96

Sources: P75: Author’s calculations based on HRS. Life table: and Bell and Miller (2005)

By 2006 the HRS cohort was 65-75, so that we have not yet observed actual survival to age 75 for the entire cohort or even for a substantial fraction.⁷ But we have observed 14-year mortality so that we can examine the relationship between subjective survival probabilities and mortality over a long time period. Table 2 shows relative 14-year survival rates and relative subjective survival rates to age 75. For example, the 14-year survival rate of men was about 90% of the 14-year survival rate of women; yet, the ratio of average P75 of men to average P75 of women was 0.94. Thus men were optimistic relative to women. As reference to Table 1 suggests both men and women may turn out to be pessimistic but women more pessimistic.

Table 2.

Relative subjective survival to age 75 and relative actual survival 1992 to 2006

Personal or household characteristic		P75	Actual survival
Sex	Male	0.947	0.902
	Female	1.000	1.000
Education	Less than high-school	0.810	0.847
	High school graduate	0.916	0.943
	Some college	0.972	0.945
	College graduate	1.000	1.000
Wealth	Lowest quartile	0.836	0.792
	2	0.880	0.912
	3	0.970	0.951
	Highest quartile	1.000	1.000
Income	Lowest quartile	0.816	0.782
	2	0.908	0.909
	3	0.942	0.966
	Highest quartile	1.000	1.000
Current smoking	Yes	0.891	0.803
	No	1.000	1.000
Current drinking	Doesn’t drink	1.000	1.000
	less than 1 drink per day	1.123	1.065
	1-2 per day	1.112	1.037
	3-4 per day	0.996	0.933
	5+ per day	0.896	0.804

Source: Author’s calculations based on HRS

Note: Relative subjective survival is the ratio of average P75 of one group to average P75 of a reference group. Relative actual survival is a similar ratio based on actual survival from 1992 to 2006. The subjective survival and actual survival ratios are calculated over the same individuals.

The relative survival rates by education, wealth and income show well-known gradients: the less educated and poorer die sooner than the better educated and wealthier. For example, those lacking a high school education survived at a rate that was just 85% of the survival rate of those with a college education. The ratios of subjective survival probabilities exhibit the same pattern, and even the magnitudes are quite close. An implication is that even in the absence of mortality data, one could establish hypotheses about mortality risk factors from a study of subjective survival probabilities.

Survival as a function of smoking and drinking exhibits the expected pattern, which is mirrored in the ratios of P75. Quantitatively, however, smokers apparently are optimistic about their survival chances relative to observed mortality outcomes, as are heavy drinkers.⁸ Whether the relative optimism of smokers is a factor in their continuing to smoke is an open question.⁹

While the population-representative part of the HRS sample has not yet reached age 75, which is required to assess the accuracy of the level of P75 rather than just relative accuracy, part of the extended HRS sample has already reached age 75. They are older spouses of age-eligible HRS respondents: the HRS interviews spouses of respondents from the cohorts of 1931-1941 even though the spouses are not age-eligible. Of course, one would not want to compare the mortality experience of these spouses with life tables but a within group comparison is valid.

There are 656 HRS respondents from the 1992 wave which we can use to compare P75 with actual survival. Their initial ages were 61-64. The age range is limited in this manner because respondents age 65 or greater were not asked about survival to age 75, and younger respondents had not reached age 75 by the 2006 interview when their vital status was determined. About 73% of this group survived until age 75, yet their average subjective survival probability was 64%. Similar to Table 1 where the average of P75 is eight percentage points lower than survival according to the 1940 cohort life table, the difference for this group was nine percentage points. Thus I think it likely that the original HRS cohort from the birth years of 1931-1941 will have underestimated their survival, but we will not really know that for some years.

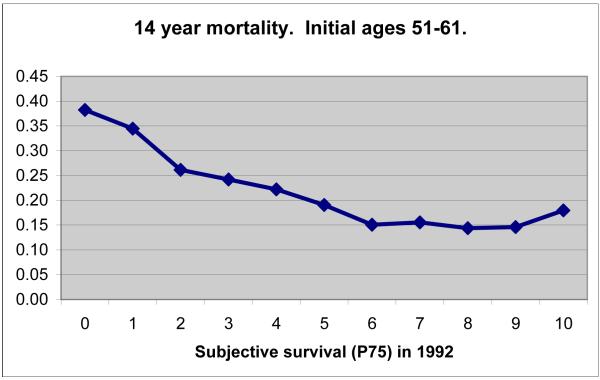
Figure 1 shows mortality as observed through year 2006 as a function of subjective survival which was stated by respondents in 1992 on a scale of zero to 10. The figure shows that P75 is very predictive of mortality for values below about 5, but has little discriminatory power at 6 or over. It remains to be seen whether future morality will reveal some discriminatory power at the upper end of P75. The other anomaly is the small but noticeable increase in mortality among respondents who reported P75 to be 10. This uptick is likely due to an interaction between question format, cognitive ability and underlying health. The question mentions a range of 0 to 10, with the “10” coming last. Most of HRS is administered by telephone, which increases a “recency effect,” the likelihood of respondents replying with the most recently mentioned acceptable response, which in this case is “10.” Those with low cognitive abilities are more likely to be influence by recency, and those with low cognition are more likely to be in worse health. Of course, only a fraction of those reporting “10” are such recency repliers: many are in excellent health. This illustrates the requirement that to understand and use subjective survival probabilities we need to account for heterogeneity in response behavior, a topic that I will return to later in this review.

Figure 1.

Source: Author’s calculations based on HRS

4. Subjective probability of working past age 62

In 1992 HRS asked all workers the following question abut work expectations:

Thinking about work generally and not just your present job, what do you think are the chances that you will be working full-time after you reach age 62?

There was a follow-up question with target age 65.¹⁰ I will call this the subjective probability of working past 62 (P62). Working past 62 is an example of a controlled stochastic process, where the degree of control varies considerable across individuals and where there is considerable private information.

Because the time horizon for working past age 62 is much shorter than for surviving to age 75, we can compare actual outcomes with predicted outcomes which are based on the subjective probabilities. An example of the method is to find workers in some particular age band, say 54-56, who reported a value for P62, and who reached age 62 or 63 by 2006 or earlier.¹¹ By using all waves we can achieve substantial sample size.

The comparison shows that the rate of actual full-time work at 62 or 63 is lower than the average of P62. For example, among workers age 52 or 53 the actual rate of full-time work when they were 62 or 63 was 32% yet the average P62 was 46%. Although the difference decreases with age, it remains substantial even among those close to age 62: among workers age 60-61 the discrepancy is seven percentage points. I do not want to make too much of these differences because of some ambiguity in the question about the precise target age, but they illustrate a general tendency, which I will discuss later, that when compared with actual outcomes, subjective probabilities tend to be biased toward 50%.

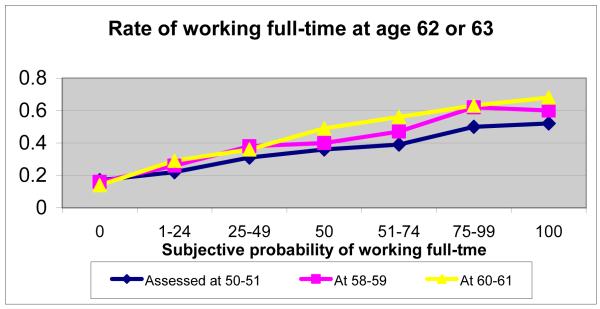
Figure 2 shows the predictive power of P62 for actual work according to the age at which P62 was assessed. Consider, for example, workers age 50-51, the bottom line in the graph. Among those who reported P62 of zero, the rate of full-time work at age 62 was 17%; among those who reported P62 of 100% the rate of full-time work was 52%. A notable feature, which verifies the discussion of the preceding paragraph, is that the rate of actual work is always less than the predicted average. A second notable feature is that the slope is considerably less than 1.0 which suggests measurement error on P62. The other lines in Figure 2 show the rates of work among workers age 58-59 and age 60-61 at assessment of P62. As the age of assessment nears 62 the slopes of the lines increase, showing greater explanatory power of P62 as workers near the target age. This increased explanatory power is, of course, to be expected because at ages just short of the target age a good deal of the uncertainty present at younger ages has been resolved.

Figure 2.

Source: Author’s calculations based on HRS

While the aim of the question about P62 was to inform research into retirement and saving behavior, it has received a particularly interesting application about the trend in labor force participation. Beginning in the late 1980s the retirement age of men, which had been declining through the late 1960s, 1970s and early 1980s, began to increase. This can be seen directly in CPS data on labor force participation: among men 60-64 the rate increased from 55.5% in 1990 to 58.6% in 2006 and among men 65-69 the rate increased from 26.0% to 34.4%, even as the participation rate of younger men decreased. There are a number of explanations for the increase, but what is interesting for this paper is that the cohorts predicted at least some of the increased work effort when they reported P62 in the HRS. Male workers age 51-56 reported average P62 of 51.0% in 1992; in 1998 male workers age 51-56 reported average P62 of 53.8%. Thus the change in P62 between 1992 and 1998 was 2.8 percentage points. These cohorts were 59-64 in 2000 and 2006 respectively. According to the CPS the actual change in labor force participation of 60-64 year-old men between 2000 and 2006 was 3.7 percentage points. While the comparison is not exact, it is clear that the change in P62 forecast at least qualitatively the change in labor force participation.

According to this comparison and subsequent measurements of P62, the participation rate of men (and of women) will continue to increase. The basis of that prediction is Figure 3. The figure shows the average of P62 among men 51-56 in 1992 and 1998 which was discussed above. It shows the average in 2004 as well as the average of P65 and the averages for women. The trends in P62 and in P65 suggest increasing work effort, and in the case of P65, the forecast is considerably into the future, 10 years from the present in the case of a 51 year-old.

Figure 3.

Source: Author’s calculations based on HRS

Using data on P62 to study retirement behavior rather than data on actual retirement has the advantage of making it easier to control for fixed effects. In models of retirement, as in many models of individual behavior, it is desirable to account for unobserved personal characteristics. When the model is linear with a continuous left-hand variable, first differences or fixed effects based on panel data are standard estimation methods, and they have the desirable features of imposing few restrictions and of being quite transparent. Retirement is mainly a binary event: most individuals retire once and remain retired so that in panel data the retirement outcomes are a string of “not retired” followed by a string of “retired.” An appropriate statistical model is a model for binary outcomes with fixed effects such as Chamberlain (1982) and Manski (1987). These models impose distributional assumptions on the unobserved error. Further, the estimation only uses transition waves: in the case of retirement, the wave preceding retirement and the wave just after retirement. In a long panel the reduction in data is substantial: to just two waves among those observed to retire and to no data among those not observed to retire. However, in estimation based on P62, the binary retirement variable is replaced by a (almost) continuous variable allowing for a simple and transparent first-difference estimator where the fixed effect is differenced out.¹² All waves are used whether or not an individual retires.

A good example is the effect of health on retirement. Because health may be correlated with additional unobserved causal factors, estimations that do not account for fixed effects may be misleading. But, if health influences the probability of retiring, P62 should respond to changes in health, and, indeed, that is what is found in HRS data (McGarry, 2004). Any unchanging personal characteristics are held constant in this comparison which is, in essence, a fixed effect estimator.

Although economic theory predicts that wealth will lead to early retirement, research on retirement typically finds very small wealth effects (Gustman & Steinmeier, 1986; Samwick, 1998). This may be due to the difficulty of modeling and estimating the response of wealth accumulation to planned retirement: those who are especially concerned about a financially secure retirement will retire later and accumulate more wealth than those who are less concerned. However, an unexpected change in wealth should induce earlier-than-planned retirement, which can be detected by changes in P62 in panel data. Thus Hurd, Reti and Rohwedder (forthcoming) studied the effect of the boom in the stock market in the late 1990s and the bust in the stock market in the early 2000s on retirement by the change in P62 and by the relationship between actual retirement and P62. They found that the boom had no noticeable effect on retirement whereas the bust reduced the rate of retirement. Their statistical method was essentially linear fixed-effect estimation.

5. Subjective probability of a Stock Market gain

Although leading models of saving behavior predict that (almost) everyone will own stocks, the rate of stock ownership is far from complete: according to the 2004 Survey of Consumer Finances some 49% of families held stocks directly or indirectly, with a large fraction holding them through tax-advantaged accounts such as a 401k (Bucks et al., 2006). The explanation for such low rates of stock holding has been high risk aversion because it was assumed that individuals had the same beliefs about stock returns as researchers who based their estimates on historical returns. However, there are at least two stages necessary to understand the relative lack of stock holding. The first is to understand the expectations individuals have about rates of return, and the second is to understand their purchasing conditional on their expectations. Only recently has research begun to gather data on their expectations via subjective probabilities.

From the point of view of understanding expectation formation, the stock market is particularly interesting because it is an uncontrolled stochastic process and because there is no private information. Therefore, differences in opinion must arise from differences in how individuals access and process information.

In 2002 the HRS added a question about stock market expectations in the form of a subjective probability as follows:

By next year at this time, what is the percent chance that mutual fund shares invested in blue chip stocks like those in the Dow Jones Industrial Average will be worth more than they are today?

Unless the respondent stated zero percent chance he or she was asked the follow-up

By next year at this time, what is the chance they will have grown by 10 percent or more?

These responses give two points on the subjective probability distribution of stock market outcomes. Under the assumption that each individual has a two-parameter distribution of one-year stock market gains such as a normal distribution, the two observations can be used to estimated the probability distribution of gains for each individual, and, in particular, the mean and variance of each distribution (Dominitz & Manski, 2007).¹³

According to the HRS data, individuals have substantially lower expectations of stock market gains than historical averages. In 2002 data, the average subjective probability of a stock market gain was just 49% whereas the historical probability was 73% (Kezdi & Willis, 2008). The average probability of a 10% gain was 30% compared to a historical probability of 47%. In the 2004 data the average subjective probability of a gain was just 52%.¹⁴

In monthly surveys of about 500 respondents per month aged 18 or over, the Survey of Consumer Confidence fielded by the University of Michigan asked about the subjective probability of a stock market gain during the period June 2002-Auguest 2004. The average was 46.4% (Dominitz & Manski, 2005). Thus pessimistic subjective probabilities about the stock market are not confined to the older population.

These very low probabilities of a stock gain are also found in data from the DNB Household Survey, an ongoing panel survey of Dutch households which is run by CentERdata at the University of Tilburg. In April, 2004 respondents were asked about their subjective probabilities of stock market gains with reference to mutual fund invested in “blue chip” stocks like those in the Amsterdam AEX stock market index or similar indices. Respondent were asked about the probability of any gain, of a gain of 10% or more, 20% or more, and 30% or more, and the probability of a loss, of a loss of 10% or more, 20% or more, and 30% or more (Hurd, van Rooij & Winter, 2008). Following Dominitz & Manski (1997), Hurd et al. fit individual normal distributions to the eight probability points reported by each person, producing a population distribution of the expected gain and of the variance of gain. The large number of points on the probability distribution should give more accurate estimates of the individual means and variances than in the case of HRS 2002 which had just two points.

The median expected rate of return in 2004 was just 0.3% and the median standard error was 10.6%. That is, the typical person believed that stock market barely had a positive rate of return, but that returns greater than 10.9% or less than −10.3% could be expected in about 32% of years. The historical median rate of return on the Amsterdam AEX from 1983-2006 was 14.0%. Thus the typical person in the population believed the one-year rate of return to be very much lower than the historical rate.

An obvious conclusion from the HRS, the Michigan survey and the DNB data is that on average households hold much more pessimistic expectations about stock market gains than the historical averages. Indeed in the DNB data the median person would view a savings account as dominating the stock market in that the stock market has a lower rate of return and a higher variance. In these data there is no equity holding puzzle and no evidence for high risk aversion, which is an inescapable implication of assuming rational expectations.

There is considerable heterogeneity in expectations about stock market gains, some of which is observation error, but some of which is systematic. For example, in the HRS, males, those with more education, those with higher cognitive scores and those with more wealth expect higher stock market returns (Kezdi & Willis, 2008). Based on Michigan Survey of Consumer Confidence, Dominitz & Manski (2005) also found more optimistic chances for a gain among males, the young and the more educated.

Beliefs about stock gains predict whether someone holds stocks. In the HRS 2004 data those who have higher expectations of a stock market gain are more likely to own stocks, and the rate of stock ownership increases fairly steadily in the probability of a gain (Dominitz & Manski, 2007). For example, among married males who reported the probability of a gain to be very low (1% to 10%), the rate of ownership was 27%; among those who reported the probability to be very high (90% to 99%) the rate was 43%. In the HRS 2002 data the average probability of a gain was 57% among those who hold stocks directly compared with just 41% among those who do not hold stocks (Kezdi & Willis, 2008). It seems likely that ownership was induced by expectations of stock market gains, but it certainly is possible that ownership induced curiosity about gains leading to higher expectations.

These results suggest that to understand stock holdings we should study the determinants of stock market expectations. A striking finding across several data sets is that expectations are substantially influenced by recent changes in stock prices. In 2004 HRS the average probability of a gain was 52%, three percentage points greater than the probability in 2002 (Kezdi & Willis, 2008). In the immediate year or so prior to 2002 the stock market had been in substantial decline, with the Dow Jones Industrial Average reaching a low in September 2002 which was 29% lower than two years earlier. By 2004 the stock market had substantially recovered. This suggests that in forming expectations about future stock market performance, individuals pay more attention to recent performance than to historical performance.

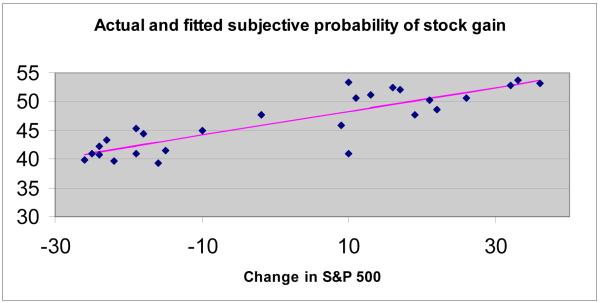
Dominitz & Manski (2005) analyzed monthly observations from June 2002 through August 2004 from the Michigan Survey of Consumer Confidence about the probability of a stock market gain. Because of the high frequency of observations during a time of volatile stock prices, they observed individuals at times of greatly differing stock market performance. Under the hypothesis that individuals pay more attention to recent stock performance than to historical data, we would expect a positive relationship between recent changes in stock prices and the subjective probability of a stock market gain. Figure 4, which I have constructed from data in their Table 1, shows a strong positive relationship between year-to-year changes in the S&P 500 and the probability of a stock market gain. The figure also shows a least squares fit to these points. It has a slope of 0.21 (0.02) and an R² of 0.75. The interpretation is an increase in the S&P 500 of 10 percentage points will result in an increase in the subjective probability of a stock gain of 2 percentage points. The standard error (0.02) is very small and the exogeneity of the right-hand variable is completely plausible: each month about 500 individuals are interviewed and their selection is at random. But each group would have observed different one-year gains in the stock market. Furthermore, any seasonality is taken care of by the 26 month observation period.

Figure 4.

Source: Author’s calculations based on Table 1 of Dominitz and Manski, 2005

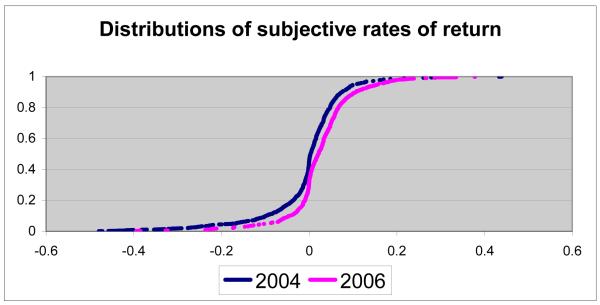
With respect to the DNB data, the Amsterdam AEX had been generally increasing before the April, 2004 baseline interview, but was declining in the weeks immediately preceding the interview week. In April of 2006 the DNB panel was re-interviewed about its stock market expectations using the same survey instrument with eight points on the probability distribution. At the second interview, the AEX had been steadily and strongly increasing for more than a year. Figure 5 shows the distributions of expected rates of return in 2004 and 2006. The distributions are similar but the 2006 distribution is shifted to the right: the median increased from 0.3% to 2.1%. The distributions of the variances of one-year rates of return are virtually identical (not shown), with the implication that stocks became a more attractive investment.

Figure 5.

Source: Hurd, van Rooij and Winter, 2008

6. Focal point responses

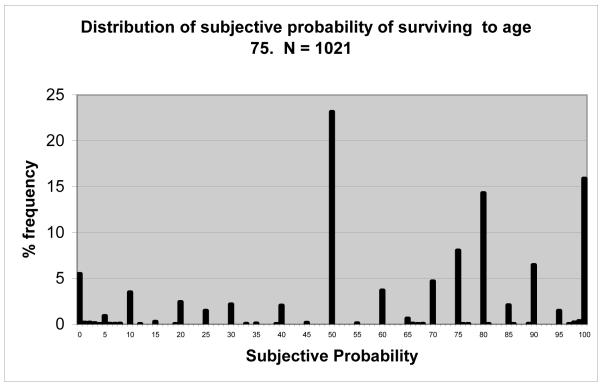
An important property of subjective probabilities as elicited in household surveys is the high frequency of focal point responses, responses of 0, 50 and 100. Depending on the topic, responses of 0 and 100 may represent (small) rounding, and responses of 50 are certainly reasonable in some cases. But in other cases the true probabilities are not zero or 100, and the number of 50s seems excessive. For example, Figure 6 shows the distribution of subjective survival probabilities to age 75 from HRS 2006. About 23% of the responses were 50, about 5% were zero and 15% were 100. Probabilities of zero and 100 cannot literally be true, but rounding from nearby values would make still these observations empirically useful. Indeed as shown in Figure 1, those extreme values have predictive power for actual mortality. More problematic is the large fraction of 50s. Of course, some may be due to rounding, and, indeed the small number of observations between 40 and 50 and between 50 and 60 supports this view. Some may be due to accurately formed beliefs that the chances are approximately 50%: according to a 2002 life table the probability that a 51 year-old man will survival to age 75 is about 0.61, so that the objective probability of someone in poor health could well be 0.50 or less. However, the spike in probability should not be greater at 50 than, say, at 60. The excess may due to so-called epistemic uncertainty, which is the lack of a well-formed probability distribution, or simply the tendency to choose toward the middle of a scale when the concept being queried is not understood (Fischhoff & Bruine de Bruin, 1999; Bruine de Bruin et al., 2000). Whatever the cause, the frequency of 50 percent reports is substantial across many domains.

Figure 6.

Source: Author’s calculations based on HRS

In 2006 HRS introduced some experimental questions designed to investigate the causes of the high prevelence of 50s.¹⁵ Respondents who answered 50% to the question about subjective survival were randomly assigned into a control group or into one of two experimental groups:

1. Do you think that it is about equally likely that you will die before 75 as it is that you will live to 75 or beyond, or are you just unsure about the chances?

or

2. Do you think that it is about equally likely that you will die before 75 as it is that you will live to 75 orbeyond, or are you just unsure about the chances, or do you think no one can know these things?

Similar assignment and questions were made and asked of those who gave a 50% response to the question about a one-year gain in the stock market. On analysis, the designers of the questions saw a flaw in question 2, so I will just report about the responses by those assigned to question 1.¹⁶

The rate of item nonresponse to the subjective survival question, P75, was just 4%. Among the responders, 23% reported a probability of 50%, and among those assigned question 1, just 37% said the chances of survival to age 75 were equally likely as the chances of dying before 75. Said differently, as classified by the responses to question 1, almost two-thirds of the 50% responses were uncertain about the true probability. Reference to Figure 6 shows that if the frequency of responses at 50% were reduced by two-thirds there would still be a focal point, but it would no longer be the largest focal point and could plausibly be due to rounding.

Item nonresponse to the question about a gain in the stock market was 24%, which already indicates that many people have little knowledge of the stock market. Among responders, about 30% gave a response of 50%, and among those answering question 1, 34% said a gain was about as equally likely as a loss. Thus 39% of the population indicated quite directly that it did not know a probability of a one-year gain in the stock market.

However, knowledge of the stock market is heterogeneous. Table 3 classifies individuals according to stock ownership and to whether they follow the stock market.¹⁷ Stock owners are much more likely to report a subjective probability of stock market gain, 11% “don’t know or refuse” (DK/RF) versus 29% among non-owners. About 62% of responses by owners were in the range 0-49% or 51-100% (and so did not responded with DK/RF or with 50%) compared with 50% among non-owners.

Table 3.

Subjective probability of stock market gain. Distribution of responses.

	N	0-49% or 51- 100%	50%	DK/RF	All
Owns stock
yes	4672	61.7	27.1	11.2	100.0
no	11738	49.5	21.6	28.9	100.0
Follows stock market
Very closely	1567	71.4	22.5	6.1	100.0
Somewhat	6131	62.3	27.0	10.7	100.0
Not at all	8105	43.3	20.9	35.8	100.0

Source: Hurd, Manski and Willis, 2007

While stock ownership does predict knowledge of the stock market, whether someone follows the stock market is a much more powerful predictor of knowledge:¹⁸ among those who follow the stock market closely (10% of the sample), the rate of DK/RF is just 6%. The high rate item nonresponse is concentrated in the part of the population that does not follow the stock market at all: it is 36% among that group.

Table 4 shows the distribution of the responses to the question that aims to uncover epistemic uncertainty. Compared with non-owners, stock owners more frequently say that a 50% response does, indeed, mean that the chances are equally likely that stocks will go up as will go down, but the difference is not large. As with item nonresponse, whether some follows the stock market is a much better predictor of epistemic uncertainty. About half of those who follow the stock market closely say that a 50% response means equally likely compared with just 27% among those who do not follow the stock market. Combining the item nonresponse data with the epistemic uncertainty data of Table 4 shows that some 82% of respondents who follow the stock market closely report usable probabilities of a stock market gain compared with just 49% among those who do not follow the stock market.¹⁹

Table 4.

Distribution of responses to epistemic uncertainty question Stock market gain. 50% responders only

	Equally likely	Unsure	DK/RF	Total
Owns stock
yes	37.6	62.1	0.4	100.0
no	33.0	65.6	1.4	100.0
Follows stock market
Very closely	47.5	52.5	0.0	100.0
Somewhat	39.2	59.7	1.1	100.0
Not at all	26.6	72.0	1.3	100.0

Do you think that it is about equally likely that these mutual fund shares will increase in worth as it is that they will decrease in worth by this time next year, or are you just unsure about the chances?Source: Hurd, Manski and Willis, 2007

7. Bias in subjective probabilities

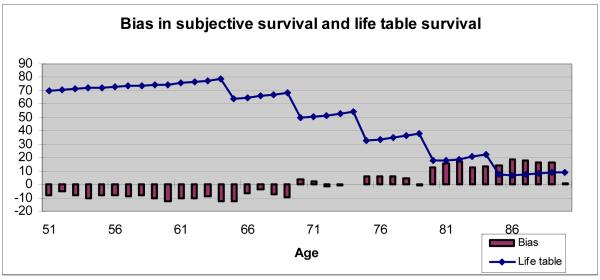
Compared with a cohort life table subjective survival has a negative bias (Table 1); compared with working past age 62, P62 has a positive bias; and compared with historical chances of a gain, stock market expectations have a negative bias. These examples suggest that when the true probability of an event is greater than 0.50, as is the case with P75 and with the stock market, the subjective probability will be understated (negative bias) and that when the true probability is less than 0.50, as is the case with P62, the subjective probability will be overstated. This is shown clearly in Figure 7 which has life table survival and the bias in subjective survival over the entire age range of HRS. The top line is life table survival. It has a step pattern because the target age changes with five-year age bands beginning at age 65. Thus the target age for those 65- 69 is 80, for those 70-74 it is 85 and so forth. The bars are the bias. The bias is negative until age 69, approximately zero from 70-74 and positive at 75 or over. Life table survival is greater than 0.50 until 70 when it is approximately 0.50 and less than 0.50 at 75 or over.²⁰

Figure 7.

Source: Author’s calculations based on HRS

This pattern of bias is to be expected from the excessive number of focal point answers at 50, but analysis shows that the bias cannot be completely be explained by the 50s. An additional explanation concerns the tendency of respondents to insufficiently adjust their answers away from 50% which is a natural starting point for assessing probabilities (Tversky & Kahneman, 1974).

8. Using subjective probabilities to explain behavior

Although the initial motivation for asking about subjective probabilities was to provide individual-level data about expectations that could be used in models of decision-making, by far most of their use has been in the types of applications which I have described above. There is a good reason for this emphasis: subjective probabilities are new measures and before they can be used in complex structural models their properties should be established. Furthermore, simple comparisons with outcomes that are not model dependent will best establish their credibility. However, there have some studies where subjective probabilities have been use to explain and understand choice. I will not review their findings in any detail because their come from a broad range of topics and will be of more interest to the specialist, nor will I attempt to list all of them. Rather I want to illustrate what can be done.

Finkelstein & McGarry (2006) studied whether the subjective probability of nursing home entry had explanatory power for actual entry and found that it did; but more importantly they found that the subjective probability influenced the holding of long-term care insurance. The approach allowed them to untangle risk aversion from adverse selection. Hurd, Smith & Zissimopoulos (2004) studied whether those who expect to be long lived delayed claiming Social Security benefits as would be predicted in a standard life-cycle model. They found that subjective survival only weakly predicted early claiming. Delavande, Perry & Willis (2006) addressed the same issue but used instrumental variables to control for observation error on subjective survival. They found much larger effects of subjective survival on early claiming. According to the life-cycle model an individual’s survival curve should influence her consumption and hence rate of wealth change, and the standard practice has been to assume life tables adequately describe an individuals survival expectations. Gan et al. (2004) constructed individualized survival curves from life tables, actual survival and subjective survival probabilities which they used to estimate a structure model of life-cycle consumption. They found that the model based on subjective survival probabilities had better fit than a model based on life table survival.²¹

The study of Kezdi & Willis (2008) on subjective stock market expectations illustrates their potential: “We estimated relevant heterogeneity [in stock market expectations] and related it to household investment behavior, with the help of a simple portfolio choice model. Our results confirm the validity of survey measures of expectations in predicting real behavior after measurement error is properly accounted for. A causal interpretation of the results suggest that heterogeneity in expectations leads to heterogeneity in stockholding, and low average expectations, high uncertainty, and large heterogeneity in expectations explain much of the stockholder puzzle” (p.23).

9. Conclusions

The Introduction states that to understand intertemporal decision-making we need some measure of the probabilities that individuals use when making their decisions. The measure must be properly scaled if it is to be used in models and must be comparable across individuals. These requirements rule out verbal descriptions such as “likely” or “unlikely,” which are not scaled and which have different meanings to different individuals. In situations where the true probability varies across individuals and where individuals have information about their personal probability, we should expect the measure to have predictive power for the actual outcome. Otherwise, it is unlikely that the measure will gain acceptance in the research or policy communities. This does not mean that the measure will have greater predictive power than any other predictor. A good example is survival where self-rated health is a more powerful predictor of survival than the subjective probability of survival: some individuals have little understanding of probabilities or their probabilities are not well formed whereas everyone has some understanding of their own health. The requirement that the measure has predictive power does not mean that it will be unbiased: individuals may be persistently misinformed about probabilities and base their decisions on incorrect probabilities. But we will not understand their decision-making unless we use those incorrect probabilities when studying their decisions.

The great majority of the research about subjective probabilities in economics has been concerned with their empirical properties: their predictive power, bias, scaling, focal point responses and so forth. Beyond increasing our understanding of the properties of subjective probabilities, some of this research has made important substantive findings about subjective beliefs in the population which explain behavior. The work on the subjective probabilities of stock market gain is an excellent example where direct measurement of the subjective probability of a gain resolves the stock-holding puzzle.

Despite the successes resulting from the measurement of subjective probabilities, in my view we still do not know whether the measures we use accurately correspond with the subjective probabilities that individuals use when making decisions. Partly this is a technical issue involved with survey methods. Recent experiments with focal point answers and rounding should lead to progress in the techniques used in surveys. But it also results from our not knowing how people make decisions conditional on their subjective probabilities. Of course, we have a theory that guides our thinking, but that theory may not be a good approximation at least for some individuals. It is also undoubtedly true that there is considerable heterogeneity in the population in the ability to form and report subjective probabilities. This is amply demonstrated in the recent experiments to explain the focal point responses of 50% about stock market gain.

Research should continue on the properties of the subjective probabilities. For example, the frequency of focal point answers varies from domain to domain suggesting that different mechanisms may be in operation or that the importance of the different mechanisms varies across domains. We need much more research on substantive economic issues that make use of subjective probabilities to explain behavior. And we need more research on the determinants of subjective probabilities. An obvious question about stock market expectations is why so many people are uninformed about the stock market when having better information would likely lead to better decisions and to better financial outcomes.

To use subjective probabilities effectively in models we need indicators of the quality of the reported probability by each individual: lacking such indicators, estimations may show only a weak relationship between subjective probabilities and behavior when, for a relevant part of the population, there is a strong relationship.