Dindel: Accurate indel calls from short-read data

Abstract

Small insertions and deletions (indels) are a common and functionally important type of sequence polymorphism. Most of the focus of studies of sequence variation is on single nucleotide variants (SNVs) and large structural variants. In principle, high-throughput sequencing studies should allow identification of indels just as SNVs. However, inference of indels from next-generation sequence data is challenging, and so far methods for identifying indels lag behind methods for calling SNVs in terms of sensitivity and specificity. We propose a Bayesian method to call indels from short-read sequence data in individuals and populations by realigning reads to candidate haplotypes that represent alternative sequence to the reference. The candidate haplotypes are formed by combining candidate indels and SNVs identified by the read mapper, while allowing for known sequence variants or candidates from other methods to be included. In our probabilistic realignment model we account for base-calling errors, mapping errors, and also, importantly, for increased sequencing error indel rates in long homopolymer runs. We show that our method is sensitive and achieves low false discovery rates on simulated and real data sets, although challenges remain. The algorithm is implemented in the program Dindel, which has been used in the 1000 Genomes Project call sets.

Small insertions and deletions (indels) are a common and functionally important type of sequence polymorphism. There have been surveys of genome-wide indel variation (Mills et al. 2006), but many studies focus on single nucleotide variants (SNVs) or large structural variants. The 1000 Genomes Project (The 1000 Genomes Project Consortium 2010; http://www.1000genomes.org) will allow a genome-wide and deep study of indel polymorphisms of frequency ≥1% in the population. This will provide an important resource for applications in medical resequencing, as indels have been implicated in a number of diseases (e.g., Miki et al. 1994; Draptchinskaia et al. 1999). Here, we present a Bayesian algorithm for calling indels from next-generation sequencing data in individuals and populations.

Small indels result in small structural differences between homologous chromosomes. Broadly speaking, there are two paradigms for identifying such variations. The first paradigm is to perform de novo assembly of short reads and detect indels by comparing contigs to a reference sequence. The second paradigm is to map each fragment directly and independently of other fragments to the reference sequence using a read mapper (e.g., Li et al. 2008; Langmead et al. 2009; Li and Durbin 2009). Here, a fragment may correspond to a single read in the case of single-end sequencing or a mated pair of reads in the case of paired-end sequencing. Sequence variation is then identified as a difference between the sequence of the reads mapped to a particular location, with the reference sequence at that location. The second paradigm is very powerful for detection of novel SNVs, but it is not suitable for detection of large insertions of sequence not present in the reference sequence. However, it is possible to detect large deletions through split-read approaches (Ye et al. 2009) or small insertions using paired-end sequencing and mapping. The approach that we propose starts from the second paradigm, thus requiring reads to be first mapped to a reference genome. However, it also incorporates elements of the first paradigm in considering alternative haplotype sequences to explain the data with a probabilistic model, thereby combining strengths of both.

Accurate inference of indels from short-read data is challenging for a number of reasons. First, compared with SNPs, indels occur at approximately eightfold lower rates (Lunter 2007; Cartwright 2009), which makes them more difficult to detect. Second, reads arising from indel sequence are generally more difficult to map to the correct location in the genome (Li et al. 2008). This holds true for long deletions, but it is especially the case for larger insertions. Third, since current read mappers align each fragment independently of other fragments to the reference sequence, reads supporting indel events may be aligned with multiple mismatches to the reference rather than with a gap. Finally, a complicating issue is that often small insertions and deletions cannot be uniquely positioned onto the reference. For example, in a repeat, a deletion that deletes any of the repeat units results in an equivalent alternative haplotype; for insertions, the same problem applies. Therefore, it is essential to consider haplotypes that include enough unique surrounding sequence to unambiguously evaluate evidence for the presence or absence of a deletion or insertion event with respect to the reference.

The rate of insertions and deletions due to sequencing errors tends to increase in those regions where the true indel polymorphism rate in the population is also increased, and this poses additional analytical challenges. Homopolymer runs are a prime example of this: The 454 Life Sciences (Roche) technology is particularly prone to sequencing error in this context; but we show here that Illumina GA(II) machines also show increased error rates in homopolymers. Both technological and biological artifacts, such as polymerase slippage during PCR amplification, contribute to increased sequencing error indel rates in homopolymer runs. As a result, the signal-to-noise ratio is decreased for this category of indels. Since dbSNP indels are overrepresented within long homopolymer runs as well, these difficult regions cannot simply be ignored, and a probabilistic approach is required to control power and false discovery rates in surveys of indel polymorphisms on a genome-wide scale.

Here, we propose Dindel (detection of indels), a Bayesian approach for calling small (<50 nucleotides) insertions and deletions from short read data. The basic idea is to realign all reads mapped to a genomic region to a number of candidate haplotypes. Each candidate haplotype is a sequence of at least 120 bp that represents an alternative to the reference sequence and corresponds to the hypothesis of an indel event and potentially other candidate sequence variants such as SNPs. By assigning prior probabilities to the candidate haplotypes, the posterior probability of a haplotype, and consequently an indel being present in the sample, can be straightforwardly estimated. Our Bayesian approach allows us to model different types and rates of error consistently in a single framework. The advantage of modeling hypotheses as candidate haplotypes is that all differences between the read and the candidate haplotype must be due to sequencing errors. In the realignment of a read to a candidate haplotype, we are able to naturally take into account the increased sequencing error indel rates in homopolymer runs, as well as the base-qualities, thus separating contributions of errors from statements about biological differences. The process of realigning reads to candidate haplotypes also cleanly resolves the issue of mismatches around indel events and corrects alignment artifacts introduced by the read mapper. Furthermore, we deal with mapping errors by interpreting mapping quality as the prior probability that a read should align to any of the candidate haplotypes (Li et al. 2008), which effectively reduces the weight of reads that cannot be confidently mapped to that location in the genome.

In our framework we make a crucial distinction between generating candidate indel variants and assessing the support in the reads for these candidate indel variants. We rely on other methods to provide a sensitive set of candidate indels; the goal of our method is to remove false-positives while maintaining as many true-positives as possible. Different methods can be used to provide candidate indels. Gaps in the alignments coming from the read mapper will be the primary source; other possible sources of candidate variants will be variants detected through assembly methods (Zerbino and Birney 2008; Simpson et al. 2009; Ye et al. 2009), or previous lists of indels such as those in dbSNP. Indeed, even if a read spanning an indel was not mapped, if its mate was mapped in the correct nearby location, we will also test it against candidate haplotypes, and thus can call an indel even if it was not picked up by the primary mapper. In this way our approach also allows accurate inference of longer indels from paired-end data sets.

Previously, a number of approaches have been proposed to infer indel events from short read data. Ye et al. (2009) proposed a split-read method to detect insertions and long deletions, but it is not designed for small indels (Ye et al. 2009). SAMtools (Li et al. 2009a) and VarScan (Koboldt et al. 2009) are similar in that they both call indels from the pileup (as created by SAMtools) of reads at every position along the reference sequence. The SAMtools indel caller allows specification of a constant sequencing error indel rate. Ng et al. (2010) remapped reads to a reference augmented with candidate indels, which is feasible for single high-coverage samples, but becomes impractical for large pooled data sets with many candidates such as the low-coverage pilot of the 1000 Genomes Project. Krawitz et al. (2010) explicitly addressed the issue that indels cannot always be assigned a unique position in the reference and propose to use the indel equivalent region to identify reads that span indel events; however, they do not provide a statistical framework to deal with context-dependent sequencing error indels and the problem of calling indel genotypes. Smith et al. (2008) and Qi et al. (2010) combined reference-based mapping with assembly methods to call indels, but these methods do not have a sequencing error indel model for Illumina reads and were not designed for analyzing pools of samples. To the best of our knowledge, our method is the first to address the realignment problem and various sources of errors explicitly in a single statistical framework, in particular the modeling of context-dependent sequencing error rates for Illumina reads, for both diploid samples and pools of samples.

We applied Dindel to simulated data sets, high-coverage data for a single individual, a targeted resequencing study, and the low-coverage data set from the 1000 Genomes Project. We assessed genotyping error rates and false discovery rates of calls made from short read data using traces from capillary sequencing.

Methods

Here, we provide an outline of the algorithm that we implemented in the Dindel program and refer to the Supplemental Methods for mathematical details.

Outline of Dindel

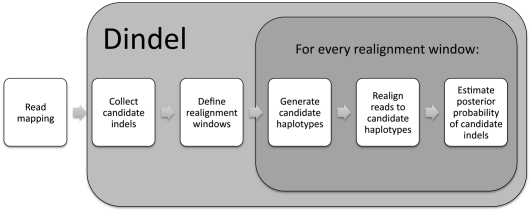
Figure 1 shows an outline of the Dindel algorithm. Dindel requires as input a file with mapped reads, a set of candidate indels, and the library insert size distributions. All of these can be inferred from the alignments produced by a read mapper, and Dindel has an option to extract candidate indels and the insert size distribution from the read-alignment file. For this, Dindel accepts files in the SAMtools BAM format (Li et al. 2009a). The user may choose to augment candidate indels from the read-alignment file with candidate indels or SNPs from alternative sources. For example, it is also possible to provide known SNPs and their population allele frequencies at this stage.

Figure 1.

Outline of the Dindel algorithm.

Dindel next performs two preprocessing steps on the input data. The first is to reposition each candidate variant to a canonical position. The purpose of repositioning is to ensure that different candidate variants that result in the same alternative haplotype sequence are not called twice as different indels. We choose to reposition the candidate variant to the leftmost position, which results in the same haplotype as the originally provided position and sequence. Note that this may result in a change of both the position and the actual sequence of the candidate variant. The second preprocessing step is to group all candidate SNPs and indels into realignment windows of at least 120 bp. For each window Dindel will generate candidate haplotypes, which, therefore, will also be at least 120-bp long. All candidate variants corresponding to a particular window will be considered against the same set of reads. This allows us to compare different hypotheses as formulated in terms of candidate haplotypes.

The core of the Dindel program is the realignment of reads to candidate haplotypes for each realignment window defined in the preprocessing step. We define R_i as the nucleotide sequence for read i, and H_j as the nucleotide sequence for candidate haplotype j. The main operations of the realignment algorithm for a particular window then are:

1. Identify the set of reads {R_i} to be realigned.

2. Generate the set of candidate haplotypes {H_j}.

3. Compute the maximum likelihood P_max(R_i | H_j) and maximum-likelihood alignment of each read R_i given each candidate haplotype H_j using the probabilistic realignment model.

4. Estimate haplotype frequencies from the read-haplotype likelihoods P_max(R_i | H_j) and the prior probability of each candidate haplotype.

5. Estimate quality scores for the candidate indels and other sequence variants.

The computation of the read-haplotype likelihood in step 3 is generally the most compute-intensive step. In the fourth step, different algorithms may be applied, depending on the setting. For diploid samples we explicitly evaluate posterior probabilities for every pair of haplotypes; for pooled reads or individuals we apply a Bayesian expectation-maximization (EM) algorithm to estimate haplotype frequencies. Below, we describe each of these steps in more detail.

Genotype likelihoods

As part of the output, Dindel also provides genotype likelihoods for each candidate indel. In the case of trios, the genotype likelihoods can be easily combined with a model for Mendelian segregation or a model that is specifically designed to detect de novo mutations. Another situation where a more complex prior is useful is in the analyses of a population of samples, especially when the samples are sequenced at low depth. In this case the Dindel pooled analysis is able to output a genotype likelihood for every sample and every candidate indel, which can then be used in imputation software that accepts likelihoods, e.g., Beagle (Browning and Browning 2007) or QCALL (Le and Durbin 2011), to obtain more accurate indel genotypes. This strategy was used for the low-coverage pilot of the 1000 Genomes Project to infer indel genotypes.

The realignment algorithm

Identification of reads for realignment

Dindel realigns mapped and unmapped reads to the candidate haplotypes. We assume that for the mapped reads the read mapper has found the correct region, and from the read-alignment file we include every read that has an overlap of at least 20 bp with the realignment window according to the read mapper. Importantly, Dindel also attempts to realign unmapped reads for which the mate is mapped in the region surrounding the window. We include every unmapped read for which the mate is mapped within a distance of the mean plus/minus four standard deviations of the library insert size distribution from the realignment window. This increases sensitivity for longer insertions and deletions, for which the read mapper may not have mapped all of the reads to the reference sequence.

Generation of candidate haplotypes

Dindel generates candidate haplotypes from the candidate variants provided by the user, but it also infers candidate variants from the read-alignment file itself. Candidate variants identified from the read-alignment file are mostly potential SNPs not specified by the user. Incorporating such a SNP may improve the alignment of reads to candidate haplotypes, and as a result improve the inference of the indel, since, in principle, each read should align to one of the two haplotypes (for a diploid individual) without mismatch in the absence of sequencing and mapping errors. The haplotypes are generated such that for every non-reference sequence variant, the reference variant is always present in one of the other candidate haplotypes so that genotype likelihoods can be calculated.

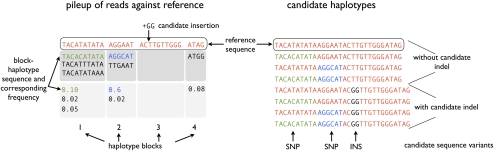
The generation of candidate haplotypes itself is a two-step process. Figure 2 illustrates the procedure with an example, and is described in more detail in the Supplemental material. First, candidate variants are inferred from the read-alignment file, creating a set of candidate haplotypes consisting of all combinations of these variants. Second, the candidate variants provided by the user are added to each of these candidate haplotypes, creating a set of candidate haplotypes where each input candidate variant is represented against a variety of additional local sequence variants. If, for a given position, a nucleotide or short sequence other than the reference has high empirical frequency, it will be considered as a local variant. To include a true SNP through this procedure, it is necessary that a large enough fraction of the reads with the non-reference allele are at least partially correctly aligned.

Figure 2.

Procedure for generation of candidate haplotypes. We first consider the empirical distribution of bases determined from the initial alignments of reads to the reference and infer a heuristic haplotype block model to preserve sequences that always occur together in one read. We then choose n block-haplotypes with the highest empirical frequency, and generate candidate haplotypes by considering all combinations of these n block-haplotypes. The number of candidate haplotypes obtained this way is thus 2ⁿ. It is possible that multiple subhaplotypes from the same block are chosen. In the second step, all candidate variants (most importantly, the candidate indels) are added to these n candidate haplotypes, resulting in a set of, at most,k · 2ⁿ candidate haplotypes, where k is the number of candidate variants tested.

By default, Dindel generates eight candidate haplotypes. Each candidate indel is applied to each of these eight candidate haplotypes, so that the number of candidate haplotypes is eight times the number of candidate indels considered in a given realignment window. In theory, one would like to use an unlimited number of candidate haplotypes; however, to maintain computational efficiency we restrict the number to eight, which yielded good results in practice.

Probabilistic realignment model

The goal of the probabilistic realignment model is to estimate the read-haplotype maximum likelihood P_max(R_i | H_j), the probability of observing the read R_i given that the true underlying haplotype sequence from which it was sequenced is given by H_j. This model includes the reliability of each base-call in the read (through base-qualities) and the probability that the read was not correctly mapped to the window by the read mapper (through mapping qualities). Furthermore, it includes a model of how likely it is to observe a sequencing error indel given a specific sequence context.

The probabilistic realignment model we use is similar to a profile hidden Markov model (HMM) (Durbin et al. 1998) and is described in detail in the Supplemental Methods. The model uses the mapping quality to specify the a priori probability that the read was generated by the candidate haplotype, and, therefore, should align to it. This prior probability also includes the insert size distribution and the mapping quality of the mate in case the read was mapped in pairs to the same chromosome by the read mapper. Thus, the mapping quality of a read effectively bounds the likelihood of observing a read given a candidate haplotype; consequently, a read that has low-sequence similarity, but also low-mapping quality, is not allowed to significantly influence the haplotype inference. We perform inference in this probabilistic model using the Viterbi algorithm, yielding a maximum-likelihood alignment of the read to the haplotype. This allows us to determine which parts of the candidate haplotype are covered by the read. The advantage of using the Viterbi algorithm is that it can be implemented more efficiently than full inference (i.e., summing over all configurations instead of maximization); the disadvantage is that it may underestimate the likelihood in case of uncertainty in the alignment of read to haplotype. In the Supplemental Methods we describe how we compensate for this for homopolymers.

Illumina sequencing error indel rates

The probabilistic realignment model we use allows specification of position-dependent rates of indel errors. We parameterize these rates by the length of the homopolymer run at each position. Error rates as a function of homopolymer run length were estimated using data from the low-coverage pilot of the 1000 Genomes Project (see below).

Haplotype inference in diploid samples

In diploid samples we call indels by comparing posterior probabilities of pairs of haplotypes with and without indels. We assume that each read is an independent observation of either the paternal haplotype or the maternal haplotype. Given the read-haplotype likelihoods P_max(R_i | H_j), the likelihood of a pair of candidate haplotypes (H_j, H_j′) given all reads is given by

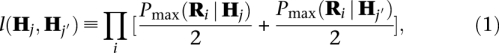where P_max(R_i | H_j) and P_max(R_i | H_j′) are the result of the realignment and are given by Equation 3 in the Supplemental material. The product runs over all reads i realigned in a given realignment window. The posterior probability P_post(H_j,, H_j′) for a pair of haplotypes (H_j, H_j′) is given by:

where P(H_j, H_j′) is the prior probability of a pair of candidate haplotypes and is determined by the candidate sequence variants present in the candidate haplotypes. Unless the user specifies otherwise, a 1/1000 prior probability for having a SNP site and a 1/10,000 prior probability for having an indel site is assumed.

Dindel assigns quality scores to the candidate indels as follows. First, the haplotype pair with the highest posterior probability containing at least one indel is identified:

Dindel assigns a single quality score to all candidate indels in this pair of haplotypes by comparing the posterior probability of this haplotype pair to the highest posterior probability of the haplotype pairs containing no indels. A phred-like quality score is obtained by normalization and converting to a logarithmic scale:

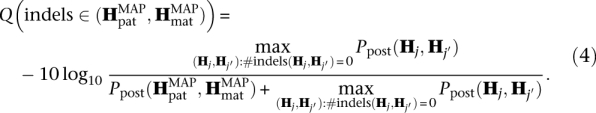A quality score of 10 (“q10”) corresponds to a confidence of 90%, and a quality score of 20 (“q20”) corresponds to a confidence of 99%. Quality scores for genotypes are computed separately for each candidate indel. The quality score Q(g_i) for genotype g_i corresponding to candidate indel i in the haplotype pair 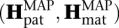is computed, comparing to the haplotype pair that has the highest posterior probability but a different genotype for indel i.

Our approach for assigning quality scores to candidate indels is an overestimate of the confidence in any one particular indel variant in situations where there is strong evidence for an indel, but where there is uncertainty in the precise sequence or location of the indel. The uncertainty will be reflected in the genotype quality scores. We have made this choice because it would be undesirable to not call an indel only because its exact sequence could not be inferred.

Since we consider combinations of sequence variants, it is, in principle, possible to infer phase between them from the posterior probabilities of the candidate haplotypes, although we have not evaluated the accuracy of the phasing.

Haplotype inference in pools of reads

We use a Bayesian EM algorithm to call sequence variants in pooled reads. The idea is to consider various subsets of candidate haplotypes, such that each subset of candidate haplotypes corresponds to a subset of candidate variants segregating in the population. We illustrate this with a simple example.

Suppose we have candidate haplotypes based on two candidate variants, a SNP and an indel, and we would like to infer whether (1) just the SNP is segregating, (2) just the indel is segregating, (3) both the SNP and indel are segregating, or (4) neither is segregating. In scenario 1, only the reference haplotype and the haplotype with the non-reference SNP allele segregate in the population. In scenario 2, only the reference haplotype and the haplotype with the non-reference indel allele segregate in the population. In scenario 3, four haplotypes may segregate: the reference haplotype, the SNP haplotype, the indel haplotype, and the haplotype with both the non-reference SNP allele and the non-reference indel allele. Finally, in scenario 4, only the reference haplotype segregates in the population. If a haplotype does not segregate, its population frequency must be zero. We then estimate for every subset of candidate haplotypes (in the example each of the four scenarios corresponds to a subset of haplotypes, therefore, k = 1,..., 4) the haplotype frequencies using a Bayesian EM algorithm. Given the estimated probability of the data 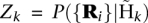for each subset of haplotypes 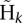, and the prior probability 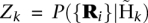for each scenario, we can calculate the posterior probability for each of the four sets of haplotypes. By summation over posterior probabilities of the subsets, we then calculate for each variant the posterior probability that it segregates in the population. We use a Bayesian EM algorithm that enforces sparsity of the haplotype frequencies within a subset of candidate haplotypes (Bishop 2007), because in a window of 120-bp sequence variants are generally assumed to be closely linked. It also has the effect of not letting one sequencing error drive a haplotype to high frequency. Similarly to the diploid case, the estimated haplotype frequencies could, in principle, be used to infer the degree of linkage between variants.

The subsets of haplotypes are defined by the candidate haplotypes. Each candidate haplotype contains a number of candidate sequence variants, and can be thought of as representing the hypothesis that all of those variants segregate in the population; one can then identify the subset of candidate haplotypes that are consistent with that hypothesis. Thus, the number of subsets for which the EM algorithm is run is equal to the number of candidate haplotypes. By default, we construct the subsets of candidate haplotypes such that only one non-reference variant per position is allowed to segregate. It is easy to use a different definition of the subsets 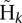to allow multiple different alleles to segregate at the same location. This option is implemented in Dindel; however, we have not used it to analyze the low-coverage data set of the 1000 Genomes Project because it appeared to be more difficult to control the false discovery rate.

Indel errors in Illumina reads

Illumina's GAII short-read sequencing technology offers a generally low indel error rate, promising high specificities for indel calls. To assess the overall rate, we used sequence data generated in the low-coverage pilot of the 1000 Genomes Project, in which 179 individuals were sequenced to 2–4× coverage.

We use three methods to bound indel error rates from above and from below. These bounds, stratified by homopolymer context, were used to derive an approximate homopolymer indel error model for Illumina data. In this section, we used indels called using a parsimony approach, rather than the probabilistic model used elsewhere in this study (see Supplemental material).

First, taking singleton indels as a proxy for indel sequencing errors, we estimate the background indel error rate per (nucleotide) site at 0.017 across all of the reads mapped with mapping quality >10 (or, after dividing by the modal coverage, 3.2 × 10⁻⁵ per site per read). True singleton indel mutations will contribute a negligible fraction to this rate; in fact, we only expect about θ_indel = 1.25 × 10⁻⁴ << 0.017 singleton indels per site across the population (see Supplemental material). Wrongly mapped reads will also contribute to indel errors to a degree that is probably low, but difficult to ascertain. The error rates we estimate here, therefore, relate to the pipeline of sequencing and mapping rather than to the sequencing platform alone.

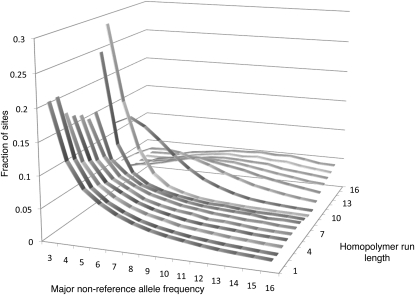
Analyzing the error rate in homopolymer runs is challenging, because although the error rate is expected to increase in this context, so is the true rate. However, it is likely that the allele frequency spectrum is quite distinct for errors and true variants. For true indels, population genetics predicts the allele count to follow a 1/f distribution.

In contrast, in a given homopolymer context we may expect indel errors to occur with approximately equal probability in any read, resulting in an approximately binomially distributed frequency spectrum.

Plotting the allele frequency spectrum separately for the various homopolymer contexts, we find for homopolymer runs up to 7 bp a spectrum that looks qualitatively as predicted by population genetics, while for longer homopolymers a characteristic binomial shape appears (Fig. 3). A simulation confirms that a standard population genetics model cannot explain this spectrum even at high mutation rates (see Supplemental material). This implies that indel errors dominate in these sequence contexts. For instance, in 10-bp homopolymer runs, the shape of the spectrum is consistent with a binomial of mean 5, corresponding to a rate of 0.5 indels per nucleotide across the data set, about 30-fold the background error rate. This is likely an underestimate, since not all errors will produce indels of the same length. It also shows that the singleton-based estimates significantly underestimate the indel rate in homopolymer contexts, because ambiguous placement and high rates cause errors to cluster.

Figure 3.

Indel allele frequency spectra by homopolymer context, with indel called directly from mapped reads using a parsimony approach. For short homopolymers the expected 1/f distribution appears. The distribution for long homopolymers is not predicted by population genetics, even for high mutation rates, but is consistent with a high error rate in this sequence context.

Finally, we obtained strict upper bounds, again stratified by homopolymer context, by assuming that all indels represent errors. Using the singleton-based estimates for complex sequence, and extrapolating from the allele-frequency-based lower bounds and the strict upper bound based on all indels, we arrive at an estimate of the overall indel error rate in homopolymer contexts, given in Supplemental Table S1. Full details are provided in the Supplemental material.

Data sets

Simulated data

To evaluate the performance of our method, we created two diploid single individual simulated data sets. The first data set was generated to evaluate performance of Dindel for constant sequencing error indel rates, i.e., without the context-dependent sequencing error indel model described above, and to estimate the power to detect indels of various sizes. In the second data set we simulated reads from indels called in the Yoruban individual NA19240 that was sequenced to ∼36× coverage as part of the high-coverage pilot project of the 1000 Genomes Project. Here, we used sequencing error indel rates estimated from the low-coverage pilot project of the 1000 Genomes Project, and evaluated the effect of this on the performance of Dindel.

For the first data set we simulated indels and SNPs at a 1:9 ratio in the 5-Mb region chr17:11,200,001–16,200,000. In total, there were 6237 indel sites and 55,897 SNP sites across the 10 individuals, and each site was assumed to be bi-allelic. These sites were then projected on the reference sequence for the region. The indel sequence of insertions was generated at random. The length of the indels varied from 1 to 10 bp, and the length distribution was such that the number of indels with length l was proportional to exp(−l), similar to what is observed in real data sets. Next, we generated 51-bp paired-end reads without sequencing error indels but with base-calling errors using MAQ (Li et al. 2008), with base-call error profiles estimated from real data. Sequencing indel errors were added using a 0.005% per-base error rate, where the maximum length of a sequencing error indel was 5, and the length distribution of sequencing error indels was the same as that of the simulated indel polymorphisms.

For the second data set we used 1419 indels called in NA19240 using Dindel for the region chr20:40,000,001–50,000,000. We simulated these indels and 12,479 randomly placed SNPs in 10 diploid individuals. As before, reads were again generated with the MAQ simulate tool using the same base-call error profiles. In contrast, with the first simulated data set we now added sequencing error indels to the reads according to the context-dependent error model as described above, such that sequencing error indel rates were increased in long homopolymer runs.

We also performed a simulation to evaluate the Bayesian EM algorithm of Dindel, which is designed for analyzing pools of samples. Here, we simulated data using the same approach as for the second data set, and simulated the indels called in NA19240 in 60 individuals using simulated 51-bp paired-end reads with increased sequencing error indel rates in homopolymers. For each individual we targeted an average coverage of 4× to emulate the settings of the low-coverage pilot 1 data of the 1000 Genomes Project. The aim of this simulation was to estimate sensitivity as a function of allele frequency; we choose the population allele count of each indel at random from 1, 3, 6, 12, and 24, corresponding to allele frequencies of, respectively, 0.8%, 2.5%, 5%, 10%, and 20%. All simulated data were mapped using BWA 0.5.7 (Li and Durbin 2009).

Real data sets

We used the whole-genome short-read data for NA18507 generated by Bentley et al. (2008) to call indels in regions that were also capillary sequenced by the ENCODE project (The ENCODE Project Consortium 2004, 2007). The short read data consists of 35- bp paired-end data sequenced with the Illumina GA platform, with an average depth of coverage of ∼30×.

We performed a segregation analysis using the data generated for the CEU trio as part of the 1000 Genomes Project for the chr20:40,000,001–50,000,000 region. The Illumina data is a mix of 35-bp, 50-bp, and 76-bp single-ended paired-end data. The average depth of coverage for the daughter and the two parents was, respectively, 33×, 32×, and 27×. In addition, 13.7 × 454 data was available for the daughter, which we used to validate the indel calls made from the Illumina data.

We also considered data from a high-depth-targeted resequencing study of a region on chromosome 11. On this data set we evaluated both the performance in terms of ability to detect polymorphic indel sites as well as genotyping performance. A 24-kb region was targeted using PCR in 96 individuals and then sequenced with 50-bp paired-end reads on the Illumina GAII platform. A 3.8-kb subregion of this gene had previously been comprehensively screened in all individuals for SNPs and indels using capillary sequencing, with all variants identified by visual inspection of trace files (MacArthur et al. 2007). The subregion contained two variable indel sites in this 3.8-kb region, of which one was a singleton.

We evaluated the false discovery rate of the Dindel pooling algorithm on a subset of the 1000 Genomes Project low-coverage pilot 1 data. For pilot 1, 179 individuals across three populations (CEU, YRI, JPT/CHB) were sequenced to 3.5× depth on average. We considered only the Illumina data from pilot 1, because the 454 Life Sciences (Roche) data has a different error profile, and Dindel currently cannot handle SOLiD color space data. The mean Illumina depth of coverage was 2.99×. In total, 45 individuals, 15 individuals of CEU, YRI, and JPT/CHB each, were also capillary sequenced in the ENCODE project. We pooled the short reads data for these 45 individuals and analyzed it using the Dindel Bayesian EM algorithm designed for analyzing pools of samples.

Results

We implemented Dindel as described above: a version specifically designed to analyze diploid samples, and a version to analyze pools of reads by estimating haplotype frequencies with a Bayesian EM algorithm. We compared Dindel with the consensus indel caller implemented in SAMtools (Li et al. 2009a) with the “varFilter” post-filter and VarScan (Koboldt et al. 2009).

Application to simulated data

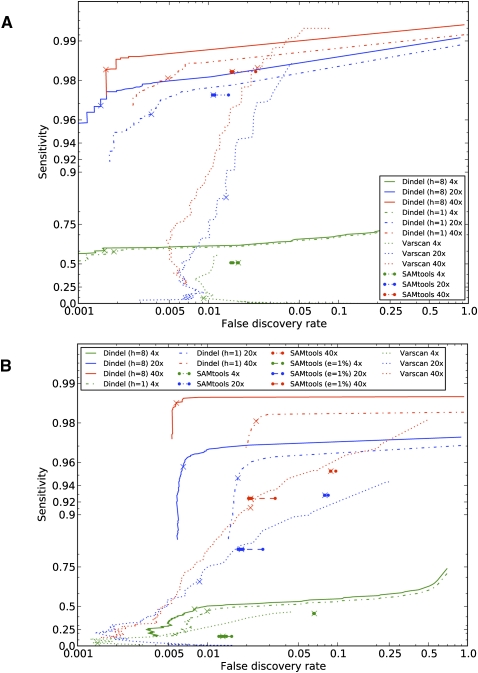
Dindel achieved high sensitivity and low false discovery rates for the various read-depths (Fig. 4A) on the simulated data with constant sequencing error indel rates. The false discovery rate was lower than 0.5% when only indels with quality scores of at least 20 (99% confidence) were called. SAMtools had a substantially higher false discovery rate at every read coverage. VarScan generally had lower sensitivity and higher false discovery rates than Dindel, except at 40×. The higher maximum sensitivity of VarScan in this case was primarily the result of VarScan also calling indels from reads with low mapping quality, whereas Dindel does not. At 4× coverage, the sensitivity to detect indel sites was still reasonable, and here Dindel was significantly more sensitive than SAMtools and VarScan. Dindel performed better with multiple candidate haplotypes: The analysis with eight candidate haplotypes had higher sensitivity and lower false discovery rates than the analysis with one candidate haplotype. We address this point further below. As previously demonstrated by Krawitz et al. (2010), sensitivity to detect longer indels was lower. At a read-depth of 4×, the power to detect indels decreased from 65% to 40% for, respectively, indels of 1 nt and 10 nt; at a read-depth of 40× the power decreased from 99% to 94%, although it should be noted that this depends on the length of the indel relative to the length of the reads (Krawitz et al. 2010).

Figure 4.

Accuracy of detection of indel sites of Dindel, SAMtools, and VarScan on simulated data. (A) Sensitivity and false discovery rates for reads simulated with a constant sequencing error indel rate of 0.005% per-base at coverages of 4×, 20×, and 40×. Dindel was run with one candidate haplotype (“h = 1”) and eight candidate haplotypes (“h = 8”). The crosses indicate performance at the 99% confidence level (quality score of 20) of a non-reference indel variant being present. True-positives here are defined as indel calls that result in the same alternative haplotype sequence as that of the simulated indel. (B) Performance on data simulated with indels that were called from high-coverage real data of HapMap individual NA19240 and a realistic sequencing error indel model. Under this model, reads were simulated with increased sequencing error indel rates in long homopolymers, with rates estimated from the low-coverage data set of the 1000 Genomes pilot project. SAMtools was run with a constant sequencing error indel rate of 0.01% and of 1% (“e = 1%”).

Dindel also performed well on simulated data with increased sequencing error indel rates in homopolymers (Fig. 4B), a phenomenon we observed in the low-coverage pilot data of the 1000 Genomes Project. This simulated data set contained 1419 polymorphic indel sites across the 10 individuals. Of those, 21% were homopolymers longer than 6 nt. Thus, despite the increased error rates and resulting lower signal-to-noise ratio, Dindel was still able to call insertions and deletions in the homopolymers. However, when Dindel analyzed the data with only one candidate haplotype, the false discovery rate was increased more than in the simulated data, with constant sequencing error indel rate (data shown in Fig. 4A). These false indel calls mostly occurred in homopolymers, where a SNP was simulated, and where, additionally, the reads mapped to that location contained sequencing error indels. In these situations, with only one candidate haplotype, Dindel could not accommodate the SNP in addition to the indel that was tested (in this case a sequencing error) and explained the mismatches due to the SNP away by calling an indel. This illustrates that it is important for Dindel to analyze the data with more than one candidate haplotype. Figure 4 demonstrates that the quality score reported by Dindel is well calibrated, as the 99% threshold (indicated by the crosses) strikes a good balance between true-positives and false-positives. SAMtools assumes an overall constant sequencing error indel rate that can be specified by the user. We found that SAMtools had lower sensitivity and higher false discovery rates than Dindel, both for error rate of 0.01% and 1% (Fig. 4B), illustrating that the false discovery rate of SAMtools could be reduced at the cost of lower sensitivity. The performance of VarScan was similar to that of SAMtools, although the calibration of the reported P-value varied with read-depth. Comparing the performance at 20× and 40× read-depth, Dindel's performance was less affected by the decrease in coverage than SAMtools and VarScan. We investigated the false indel calls that Dindel made for the read-depth of 20×. There were 89 false-positives at 24 unique sites across the 10 replicates. Of these 24, 16 were within 10 bp of a true simulated indel, four were in a dinucleotide repeat close to a simulated indel, and three were in a homopolymer run longer than 10 nt. This demonstrates that mapping errors remain a problem for precise detection of the indel event.

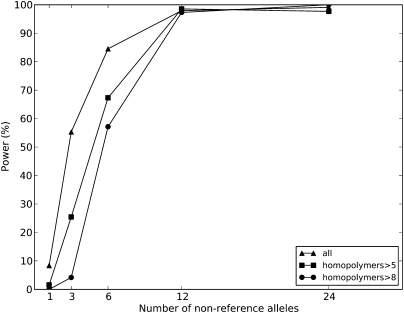
We also evaluated the performance of Dindel on pooled data with the Bayesian EM algorithm. The Bayesian EM algorithm was well powered to detect alleles present at more than six copies in 120 haplotypes, corresponding to, on average, 12 reads in a pool of, on average, 480 reads (Fig. 5). At three allele copies the sensitivity was ∼50%. Sensitivity was therefore lower than in the diploid single-individual setting. Here we used a posterior probability threshold of 99%, which yielded a false discovery rate of 1.4% (11/821). This is higher than the ∼0.4% in the diploid simulations at the same threshold (Fig. 4B). Of the 11 false-positives called, eight occurred in homopolymers longer than 10 bp. Excluding calls in homopolymers longer than 10 bp, the false discovery rate was 3/812 = 0.4%.

Figure 5.

Power as a function of non-reference allele frequency in a simulated pooled analysis. The Dindel Bayesian EM algorithm was used to detect indels in a pool of 60 individuals with simulated read-depth of 4×. Due to increased sequencing error indel rate in long homopolymers, power decreases as a function of homopolymer length. Calls were made using a 99% confidence threshold on the posterior probability of a non-reference indel variant being present.

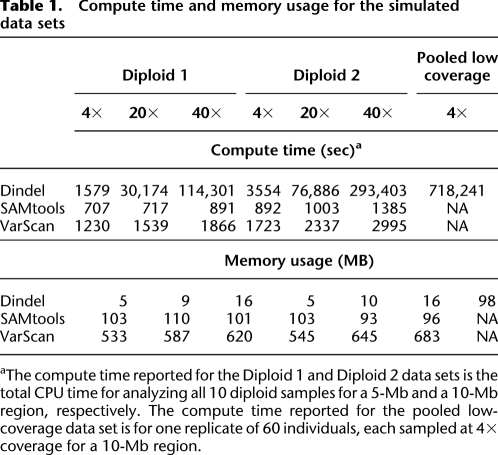
Table 1 shows the compute times and memory usage for the simulated data sets. On the 40× data, Dindel was two orders of magnitude slower than SAMtools and VarScan. This is because Dindel was used to test every indel identified by the read mapper, most of which will be sequencing errors. As the number of sequencing errors scales linearly with the number of reads, and the realignment procedure itself scales linearly with the number of reads, compute time increases quadratically with read-depth. The memory requirements of Dindel were lower than those of SAMtools and VarScan.

Table 1.

Compute time and memory usage for the simulated data sets

^aThe compute time reported for the Diploid 1 and Diploid 2 data sets is the total CPU time for analyzing all 10 diploid samples for a 5-Mb and a 10-Mb region, respectively. The compute time reported for the pooled low-coverage data set is for one replicate of 60 individuals, each sampled at 4× coverage for a 10-Mb region.

Application to real data

NA18507

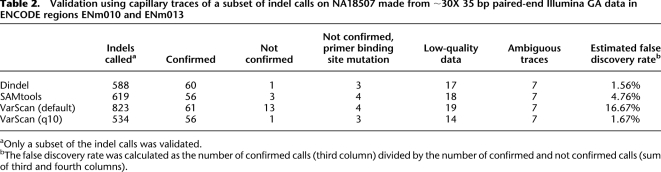
We applied Dindel, SAMtools, and VarScan to the short-read data for NA18507 of Bentley et al. (2008) to estimate false discovery rates in a high-depth diploid sample. We called indels in the ENCODE ENm010 and ENm013 regions and then visually inspected ∼100 capillary traces for each method for evidence of a subset of the indels called on the short-read data using Sequencher (Gene Codes Corporation) and Mutation Surveyor (Soft Genetics) software. We did not validate indels in homopolymer tracts longer than 10, as the capillary traces were often ambiguous and because VarScan and SAMtools do not have a homopolymer-dependent sequencing indel error model. We defined five categories of indels: (1) indels that were confirmed by a trace; (2) indels that were not confirmed by a trace; (3) indels that were not confirmed but had a SNP in the primer binding site (as determined from the short read data), potentially resulting in allele-specific PCR amplification; (4) indels for which the traces were of low quality; (5) indels for which the traces were ambiguous, in that there was some, but inconclusive evidence of an indel. We estimated the false discovery rate as the number of indels in the first category divided by the number of indels in the first and second categories.

Table 2 shows the results of the analysis as well as the total number of calls made in the two ENCODE regions, noting that only a subset was validated. Dindel achieved a low false discovery rate of 1.56%. SAMtools had a higher false discovery rate of 4.75% due to two additional false-positives. The default settings of VarScan yielded a very high false discovery rate of 16.7%. Changing the default settings and converting the P-value reported by VarScan to phred-like quality scores, we found that the false discovery rate of VarScan could be reduced to a value similar to that of Dindel using a threshold of q10 (confidence of 90%) at the cost of reducing the number of indel calls by 19% (second column in table). This suggests a significant loss of sensitivity for VarScan, which we confirmed in the segregation analysis below. Taking into account the higher estimated false discovery rate of SAMtools, the expected number of true calls made by Dindel and SAMtools was similar. The remaining false-positive called by VarScan was the same as the false-positive called by Dindel and occurred in a dinucleotide repeat close to an indel that was confirmed by a capillary trace. As the indel was also called by SAMtools, it is possible that this false-positive was due to mapping errors.

Table 2.

Validation using capillary traces of a subset of indel calls on NA18507 made from ∼30X 35 bp paired-end Illumina GA data in ENCODE regions ENm010 and ENm013

^aOnly a subset of the indel calls was validated.

^bThe false discovery rate was calculated as the number of confirmed calls (third column) divided by the number of confirmed and not confirmed calls (sum of third and fourth columns).

In addition to the ENCODE regions we compared the indel calls of Dindel, SAMtools, and VarScan (using a minimum quality score of 10) in autosomal protein-coding regions.

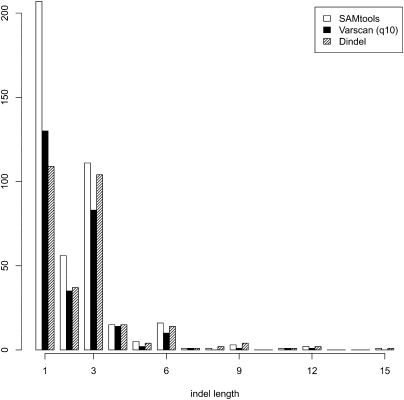
Figure 6 shows a histogram of the indel length for the three methods. The distribution of Dindel shows the strongest purification of frameshift (non-3n) indels: The fraction of indel calls resulting in a frameshift was 57% for Dindel, whereas it was 68% and 65%, respectively, for SAMtools and VarScan. SAMtools has a very high number of 1-bp indels, almost double the number of in-frame 3-bp indels, whereas for Dindel these numbers are almost the same. VarScan appears to lose sensitivity for longer indels, as evidenced by the lower number of 6-, 9-, 12-, and 15-bp indels.

Figure 6.

Distribution of indel lengths in autosomal protein-coding regions called from 30 × 35 bp paired-end Illumina GA reads for NA18507. The fraction of indel calls resulting in a frameshift was, respectively, 57%, 65%, and 68% for Dindel, VarScan, and SAMtools.

Segregation analysis

We performed a segregation analysis in the CEU trio sequenced to high depth as part of the 1000 Genomes Project. First, we called indels independently in the child and in the two parents, using only the Illumina data. Ignoring de novo mutations, which we expect to be extremely rare, each indel called in the child should be present in at least one of the parents. If a method calls an indel in the child, but not in the parents, this is either the result of a false-positive in the child or a false-negative in the parents. In order to distinguish false-positives in the child from false-negatives in the parents in the case of a nonsegregating indel, we visually verified whether there was at least one read in the 13.7× 454 data that contained the alternative haplotype sequence, as predicted from the indel called from the Illumina data. If there was evidence for the nonsegregating (i.e., called in the child but not in the parent) Illumina indel in the 454 data, the nonsegregating indel was called a false-negative in the parent, otherwise it was called a false-positive. We further assumed that segregating indels represent truly polymorphic sites. We excluded indels in homopolymer runs longer than 5 bp, since validation of these using the 454 data would be problematic due to increased sequencing error rates. We estimated the false discovery rate as the fraction of indels called in the child that were not called in the parent and also not confirmed by the 454 data. Combining the calls of all three methods, there were 729 indels that were found to be segregating (by any method) or confirmed by the 454 data. For each method we then estimated the false-negative rate in the daughter as the fraction of the indels in this union that were not called in the daughter. We removed 13 indel calls from the analysis where there was no 454 data covering the indel site. We considered different calling thresholds for VarScan, as the analysis for NA18507 indicated that this had a strong effect on the false discovery rate.

Table 3 shows that Dindel achieved a lower false-negative rate than SAMtools and VarScan. The false discovery rate of Dindel was lower than that of SAMtools and that of VarScan at its most sensitive settings. Using a more stringent quality threshold, it was possible to lower the false discovery rate of VarScan below that of Dindel; however, only at the expense of a significant increase of the false-negative rate.

Table 3.

Segregation analysis for 10-Mb region on chromosome 20 in the CEU trio of the 1000 Genomes Project

Indels were called in daughter and parents independently from Illumina data only. The indels that were called in the daughter but not in the parents (defined as the nonsegregating indels in the third and fourth columns) were validated using the 13.7X 454 data available for the daughter. We considered three different calling thresholds for VarScan, with q10 and q20 corresponding to 90% and 99% confidence thresholds, respectively.

Genotyping

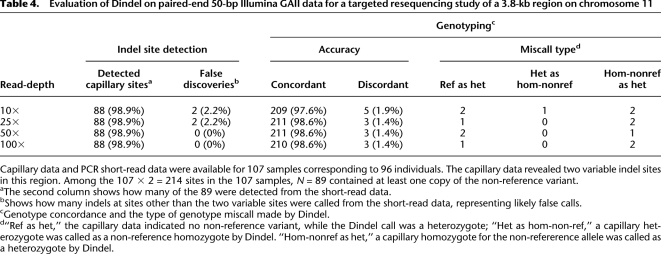
Next, we investigated the performance of Dindel on a targeted resequencing study of a 3.8-kb region on chromosome 11 (MacArthur et al. 2007). For 107 samples corresponding to 96 individuals, both capillary sequence and short read data was available. The capillary data revealed two variable indel sites in this region; among the 107 × 2 = 214 corresponding sites in the 107 samples, 89 contained at least one copy of the non-reference variant. We investigated the ability of Dindel to detect these (i.e., without giving the locations and indel sequence) at read-depths increasing from 10× to 100× obtained by down-sampling the mapped reads. At all coverages, Dindel detected 88 of 89 known variable sites (98.9%). The estimated false discovery rate was 2.2% at 10× and 20× coverage. At higher read-depths no indel sites other than the two sites with evidence from capillary data were detected, indicating a low false discovery rate. Genotyping was performed by explicitly testing the indel as a candidate in each sample and making calls as follows: If the quality score for the indel was higher than 20 (99% confidence level), the indel genotype with the highest posterior probability was chosen, and if the quality score for the indel was below 1.0, the genotype was set to homozygous for the reference allele. Genotypes for indels with intermediate quality scores were not called. The genotype concordance was also high (Table 4, five rightmost columns), with a small number of discrepancies between the genotype called from the short read data and the genotype called from the capillary data.

Table 4.

Evaluation of Dindel on paired-end 50-bp Illumina GAII data for a targeted resequencing study of a 3.8-kb region on chromosome 11

Capillary data and PCR short-read data were available for 107 samples corresponding to 96 individuals. The capillary data revealed two variable indel sites in this region. Among the 107 × 2 = 214 sites in the 107 samples, N = 89 contained at least one copy of the non-reference variant.

^aThe second column shows how many of the 89 were detected from the short-read data.

^bShows how many indels at sites other than the two variable sites were called from the short-read data, representing likely false calls.

^cGenotype concordance and the type of genotype miscall made by Dindel.

^d“Ref as het,” the capillary data indicated no non-reference variant, while the Dindel call was a heterozygote; “Het as hom-non-ref,” a capillary heterozygote was called as a non-reference homozygote by Dindel. “Hom-nonref as het,” a capillary homozygote for the non-refererence allele was called as a heterozygote by Dindel.

Low-coverage data

We evaluated the false discovery rate of the Dindel Bayesian EM pooling algorithm on 45 individuals from the pilot 1 of the 1000 Genomes Project in the ENCODE ENm010 region. We visually inspected the capillary traces of all individuals for 90 indels called by Dindel in this region. In 18 cases the capillary data was of a too low quality, did not map to the reference sequence, or was not available for the individuals with support for the indel event, and in four cases the traces were ambiguous. We found confirmation of 64 indels and no support for three, yielding an estimated false discovery rate of 3/67 = 4.5%.

SeattleSNP indels

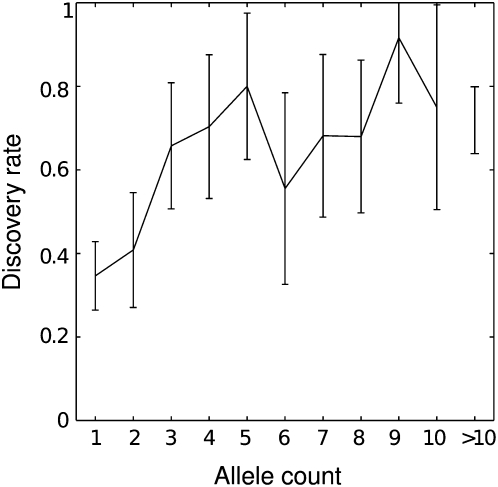
Lastly, we considered the sensitivity of the Dindel pooling algorithm on real data (Fig. 7). To assess this, we exploited the overlap of 32 individuals between the SeattleSNP project and the individuals sequenced in the 1000 Genomes pilot 1 project for which Illumina data was available (32 in total). For those, capillary sequencing data has been generated in the SeattleSNP project for 321 genes and their introns, covering 10.67 Mb in total. We compared the indel calls made from this data (890 in total) with those made by Dindel on all of the 1000 Genomes pilot 1 samples with Illumina data (170 individual sequenced at 2.99× on average). Dindel recovered 593 of the 890 indels, equivalent to a sensitivity of 67%. Many of the SeattleSNP indels existed at frequency 1 in the intersection (406/890 called once by SeattleSNP), although possibly some may have been undercalled. For indels at SeattleSNP frequency, at least three among the shared individuals, sensitivity was 78% (320/411). This relatively low sensitivity is possibly due to a fraction of missed candidates, caused by difficulties in mapping the relatively short and in some cases single-end reads in the presence of indels and the low-coverage design of the pilot 1 project.

Figure 7.

Discovery rate of SeattleSNP indels from the 1000 Genomes pilot 1 samples with Illumina data (170 individual sequenced at 2.99× on average). The horizontal axis represents the indel allele count in the SeattleSNP data set, the vertical axis the corresponding discovery rate in 1000 Genomes pilot 1 data.

Discussion

We have described a Bayesian approach for accurate calling of indel sites and indel genotypes by realigning reads to candidate haplotypes. This approach allowed us to explicitly account for increased sequencing errors in long homopolymer runs, which is important for accurate inference in genome-wide surveys of indel polymorphism. By formulating the problem in terms of haplotypes, we also provide a solution to the problem of ambiguous indel definition and deal with complexities introduced by tightly linked SNPs. The Dindel software is general in that it can test support in reads for candidate insertions and deletions identified by other programs or techniques.

Our method depends on other methods to provide a sensitive list of candidate indels. In our analyses we have considered indels detected by the BWA and MAQ read mappers. Sensitivity can be significantly increased by using read mappers that are optimized for indels. We provide an example of this in Supplemental Figure S1, where we used the Stampy read mapper (Lunter and Goodson 2011; http://www.well.ox.ac.uk/project-stampy) to map reads to the reference. Another promising approach to detect long candidate deletions is to use the assembly methods, such as Pindel (Ye et al. 2009) or whole-genome de novo assembly methods (Zerbino and Birney 2008; Simpson et al. 2009; Li et al. 2010). The program inGAP (Qi et al. 2010), which calls indels using local assembly with the multiple-sequence alignment program MUSCLE (Edgar 2004), takes such an approach, but had a false discovery rate of 4% and a sensitivity of 35% at read-depth of 20×. This illustrates that assembly methods by themselves are not necessarily accurate. However, we believe that a powerful strategy will be to combine the ability of assembly methods to detect (large) sequence variants with the ability of our Bayesian approach to take into account various types of error in order to reduce false discovery rates.

The accuracy of Dindel depends heavily on the accuracy of the alignments of the read mapper. Dindel explicitly uses mapping qualities estimated by the read mapper in the probabilistic model. In our experience the calibration of mapping quality can have a big effect on the false discovery rate. It is not sufficient for a read mapper to simply map as many reads as possible to the correct region, it is also of great importance that the read mapper correctly estimates the probability that the reported location is correct. In our experience, MAQ, BWA, and Stampy provide reasonably well-calibrated mapping qualities, but we have not explicitly evaluated other read mappers.

The method we have proposed is computationally intensive since it realigns every read to at least two candidate haplotypes. The complexity is dominated by the product of the total number of candidate variants, the number of candidate haplotypes per window, the number of reads to be realigned, the length of the reads, and the length of the candidate haplotypes. The total compute time for analyzing all 225,648 candidate indels identified by the BWA read mapper for 10 individuals at 40× read-depth in a 10-Mb region was 293,403 CPU sec, or equivalently ∼1 sec per candidate variant (at this read-depth). Although we cannot change the inherent complexity of our proposed approach, we believe that by improving and optimizing the implementation, the compute times of Dindel can be significantly reduced. Another promising direction will be to prefilter the set of candidate indels using a faster method that is sensitive but not highly specific.

On simulated data we have shown that Dindel achieved false discovery rates lower than 0.5%. However, on the real data sets our estimates of the false discovery rates through comparisons with capillary sequence data were consistently higher, of the order of 2% − 5%. Our genotype concordance was lower than results that have been reported for SNPs (e.g., Li et al. 2009b; Ng et al. 2010). Both in the whole-genome resequencing study and the targeted resequencing study, the main source of false-positives were cases where the short-read data did have a number of reads with high mapping quality supporting the indel event, but where the capillary data clearly showed no evidence. It is likely that at least some of these cases are errors in the capillary data, in particular for PCR-product resequencing, where allelic drop-out can result in an undercall. Errors in the short read data could be due to mapping errors: a pair of reads that has been mapped to wrong genomic region, or a pair of reads from novel sequence not present in the reference but similar to the region where the indel is called. These errors are very difficult to correct by realignment, as the assumption is that the reads have been mapped to at least approximately the correct region. Another possible explanation for increased false-positive rates is underestimation of sequencing error indel rates outside of homopolymer runs. This is a problem we aim to address in future research. Finally, for the targeted resequencing study we considered another source of potential errors is contamination in the multiplexed samples being sequenced, or in the multiplex tag decoding.

The segregation analysis of the 1000 Genomes trio data we performed has a number of caveats. First, the false-negative rate estimate is expected to be an underestimate as even the union of the indels confirmed by segregation or 454 data will not be complete. Second, mapping errors in the child and parents are not independent, as the reads are mapped to the same reference sequence. This means that indels that appear to be segregating could be false-positives in both the parents and the child. Sequencing errors also depend on sequence context, both for Illumina and 454, but to an extent we controlled for this by excluding indels in homopolymers longer than 5 nt. Third, while the depth of the 454 data is considerable, it is still possible that heterozygous indels in the child were missed due to lack of coverage. Finally, we did not take into account the effect of having a false-positive both in the child and the parent, or a true-positive in the child and a false-positive in one of the parents, as no 454 data for the parents was available. The consequences of mapping to a reference sequence can be seen from Table 3. Interestingly, increasing the quality threshold for VarScan from q10 to q20 did not strongly affect the fraction of indels found to be segregating (third column divided by the second column), while it did strongly affect the false-negative rate (respectively, ∼1% vs. ∼25%). We believe that this can be explained as follows. Since the quality scores of VarScan correspond strongly to the number of times the indel was identified by the read mapper, higher quality scores correspond to relatively more complex sequence contexts, where the read mapper already consistently identifies the correct indel event, despite the fact that the starting position of reads supporting the indel event will be different. These are precisely situations where our realignment approach does not add much. In more repetitive sequence contexts the read mapper may identify the indel event only in one read, and full support for the indel event is only uncovered upon realignment as Dindel does.

For analysis of samples from a population sequenced at low depth, we believe the best approach is to generate genotype likelihoods using the Bayesian EM algorithm of Dindel, and then impute genotypes using software such as Beagle (Browning and Browning 2007) and QCALL (Le and Durbin 2011), which support genotype likelihoods as input, IMPUTE (Howie et al. 2009), or MACH (Li and Abecasis 2006). We applied this strategy to the low-coverage data of the 1000 Genomes Project using QCALL, which uses local LD structure estimated from HapMap3 haplotypes to infer genotypes from the sequence data. We found that only a small number of sites (<0.2%) called by Dindel were not called by QCALL, consistent with the false discovery rate of <5% of Dindel. The Bayesian EM pooling algorithm in Dindel currently outputs genotype likelihoods per individual when the label for each read is known.

Filters can improve specificity on practical data sets of next-generation sequencing methods. A useful filter can be the requirement that the indel should be supported by reads on the forward and reverse strand to eliminate possible PCR artifacts. One filter we have also implemented in Dindel is the requirement that every indel candidate variant in a haplotype should be supported by at least one read, where the read should cover the range of positions so that the indel can be positioned without changing the resulting haplotype. This approach has been proposed by Krawitz et al. (2010). This filter will result in a loss of sensitivity in regions with low coverage, and it depends on the application whether sensitivity or specificity is prioritized, but it will provide a degree of protection against artifacts. One potential issue in this light is sensitivity to misspecification of the parameters of the probabilistic model. These filters were not applied to the simulated and real data presented here.

Misalignment of reads around indel events by the read mapper leads to false SNP calls. To avoid false SNP calls, an attractive solution is to call SNPs after realignment of reads by the Dindel indel calling. Dindel provides support for outputting realigned BAM files for each window in which reads have been realigned, from which SNPs can be called using dedicated software.

Many of the problems with detecting and correctly calling indels, including mapping errors, will be substantially reduced by increasing read lengths. However, as longer reads allow access to more repetitive regions, e.g., di- and trinucleotide repeats, the issues that are currently complicating indel calling will still apply, and a statistical approach such as Dindel will be beneficial.

Single-molecule “third-generation” sequencing platforms such as the newly launched Pacific Biosciences technology will offer longer read-lengths, but are likely to suffer from increased indel error rates compared with second-generation technologies such as Illumina. For these platforms, a careful probabilistic framework for alignment and indel calling as we described here will be even more important.