Maximum Shell Size, Growth Rate, and Maturation Age Correlate With Longevity in Bivalve Molluscs

Abstract

Bivalve molluscs are newly discovered models of successful aging, and this invertebrate group includes Arctica islandica, with the longest metazoan life span. Despite an increasing biogerontological focus on bivalves, their life history traits in relation to maximum age are not as comprehensively understood as those in vertebrate model aging organisms. We explore the allometric scaling of longevity and the relationship between development schedules (time to maturity and growth rate) and longevity in the Bivalvia. Using a traditional nonphylogenetic approach and the phylogenetically independent contrasts method, the relationship among these life history parameters is analyzed. It is demonstrated that in bivalves, maximum shell size, development, and growth rates all associate with longevity. Our findings support the observations of life history patterns in mammals and fish. This is the first investigation into the relationship among longevity, size, and development schedules throughout this group, and the results strengthened by the control for phylogenetic independence.

BIVALVE molluscs (clams, oysters, and mussels) are newly discovered models of natural aging (1), and the taxonomic class includes species with the longest metazoan life span— exceeding 400 years (2). The class Bivalvia also holds the record within the animal kingdom for the greatest number of species, which attain ages in excess of 150 years (1). For example, the Geoduck clam (Panopea abrupta), the freshwater pearl mussel (Margaritifera margaritifera), and the ocean quahog (Arctica islandica) are all exceptionally long lived attaining maximum ages of 163, 190, and 405 years, respectively (2–4).

In recognition of these animals attaining exceptional ages, there has been an increasing biogerontological focus on the group (3,5,6), and they have also been the subject of several aging reviews (1,7,8). In addition to its use in determining age, the hard calcareous shell of many bivalves also contains an ontogenetic record of growth in the form of annually resolved growth lines and increments (9). The advantage of this is that bivalves sampled from a range of environmental settings can provide reliable and accurate information on their individual ontogenetic life history, including their chronological age (10). Despite an increasing focus on bivalves from a biogerontological perspective, the relationship of their other life history traits to maximum age is not as comprehensively understood as those in vertebrate groups, such as mammals and birds. It would therefore be interesting to understand how life history traits and development schedules in bivalves are related to longevity and compare these with the relationships observed in humans and with traditional vertebrate model aging organisms.

Factors correlating with the maximum longevity in animal groups other than molluscs have received considerable attention, particularly with regard to life history theory (11,12). In mammals and birds, adult body size (most commonly represented as body mass) correlates positively with longevity, larger animals living, on average, longer than smaller ones (13–16). The most plausible explanation for the widely established relationship between body size and longevity appears to be the role of ecological factors. For example, larger animals are less prone to predation and thus have lower mortality rates, which in turn leads to a greater longevity and, according to evolutionary theory, the evolution of a slower aging process (17,18). Developmental schedules, such as time to maturity and postnatal growth rate, have also been associated with longevity in birds and mammals (16,19). Specifically, age at maturity is positively correlated with maximum species longevity (20) and negatively correlated with demographic aging rate (19), whereas postnatal growth rate are negatively correlated with maximum longevity in mammals (16) and with demographic aging rates in terrestrial vertebrates (19,21). The present study explores whether the same relationships hold within the Bivalvia. In the only study to investigate these life history traits in bivalves (22), concentrating on the freshwater mussels, concluded that overall, longevity was negatively related to the growth rate, which explained a high percentage of variation in longevity. By contrast, size and relative shell mass explained little variation in longevity.

Through the application of the phylogenetically independent contrast (PIC) method of Felsenstein (23), which statistically removes bias due to the effects of shared evolutionary history, de Magalhães and colleagues (16) demonstrated that time to maturity is associated with adult life span in mammals, with evidence suggesting an even stronger association than previously thought. The length of time a mammal will live after maturity, that is, its adult life span, is proportional to the amount of time it took to reach maturity. Ricklefs (19) noted the same relationship between time to maturity and actuarial aging more generally across all terrestrial vertebrates.

We investigate the allometric scaling of longevity and whether there is a relationship between development schedules and longevity in bivalves. Using a traditional nonphylogenetic approach (ie, simple regression of species values at the tip of the phylogeny), the relationship between maximum asymptotic size and maximum longevity was initially analyzed (see Table 1). Although traditional nonphylogenetic approaches have been historically used in comparative biology; it has been clearly demonstrated during the last 20 years that interspecific comparisons can be potentially compromised by statistical nonindependence of species values (23–26), leading to unacceptably high Type I error rates (incorrectly accepting alternate hypotheses) and inaccurate estimations of correlations or slopes (27–29), although under what circumstances such concerns are warranted is not clear (30).

Table 1.

Symbols and Abbreviations Used in This Study

Parameter	Definitions
K	Parameter of the von Bertalanffy growth function, of dimension per year, expressing the rate at which the asymptotic length is approached
L∞	Asymptotic length in millimeters; parameter of the VBGF expressing the mean length that the species would reach if indefinite growth
Tsex	Age at first maturity (years)
Tmax	Maximum age or life span reached in a population (years)
Tad	Age at first maturity substituted from the maximum age (Tmax − Tsex)
VBGF	von Bertalanffy growth function, used to describe the growth in length of fish and marine invertebrates

The overall aim of our study is to investigate whether bivalves demonstrate similar life history strategies to those of terrestrial vertebrates where body size and developmental schedules are associated with longevity and therefore possibly with aging rates. In addition, species that do not fit the allometry of life span may hold clues about the evolutionary forces shaping longevity and aging (16). In this article, we specifically investigate using previously published data three hypotheses related to bivalve longevity (a) that bivalve size correlates positively with maximum longevity, (b) that postmaturational longevity is proportional to time to maturation, and (c) that the earlier a bivalve attains its maximum asymptotic size, the shorter will be its life span.

MATERIALS AND METHODS

The symbols and abbreviations of the growth parameters and life history traits to be investigated in this study are listed and defined in Table 1.

Data collection: Allometric Scaling of Longevity

Initially, we set out to investigate the relationship between body mass and maximum life span (T_max) in bivalves in a similar manner to that which has been carried out by de Magalhães and colleagues (16) for a range of other animal groups. Unfortunately, body mass and maximum age data are unavailable for molluscs in sufficient quantities to allow meaningful analyses to be undertaken. However, data were available on maximum bivalve size, that is, the maximum asymptotic size (L_∞; shell length or shell height) derived from the Von Bertalanffy growth equation (31,32). We have therefore used this dimension rather than mass in our analyses.

The values for T_max that we have used refer to the published reported maximum life span of the oldest animal recorded in a population or the longevity estimate obtained from an age frequency analysis. Many species of bivalves contain a growth record in the form of annually deposited internal shell increments, and therefore, estimates of the age of individual bivalves are accurate and reliable (9). Using these two parameters (L_∞ and T_max), the allometric relationship between body size and longevity was investigated. To what extent T_max is an accurate estimation of the rate of aging depends critically on the number of individuals sampled in a population, and the rate of mortality increase with age, so its utility has been a source of debate (15,16). The consensus is that to the extent that it measures real differences in achieved longevity, differences in T_max are proportional to genetic limitations on longevity among species. Thus, it has been argued to be related to a species’ rate of physiological aging (33–35). There are additional estimates of aging rate, which could be used in place or alongside T_max, such as the mean adult longevity or adult mortality rate doubling time, which is a demographic measurement of aging. However, the greater availability of estimates of T_max in the literature governed our decision to use this parameter as the estimator of aging rate.

Data Collection: Developmental Schedules and Longevity

In the second part of our study, we investigated the relationship between developmental rate and longevity. Any estimate of species longevity incorporates developmental time, that is, time from birth to maturation, potentially adding bias to the analysis as discussed by de Magalhães and colleagues (16). Therefore, for this analysis, we have used the maximum adult life span (T_ad), which is defined as T_max minus age at sexual maturity (T_sex). Bivalves have varying reproductive strategies, including brooding, for example, some oyster species, although the majority employ external fertilization; therefore, T_sex can be defined simply as the age at which reproductive maturity is attained. Using these two parameters (T_ad and T_sex), the relationship between development rate and longevity was investigated.

For proxy measures of developmental schedules, T_sex was used as a measure of a bivalve’s growth rate. Previous investigations of terrestrial vertebrates have used postnatal growth rate as a measure of developmental schedule (16,19); however, such data are unavailable for bivalves. Instead, we used the van Bertalanffy growth coefficient K (per year), an appropriate alternative that is widely available in the literature. This parameter expresses the rate at which L_∞ is approached. T_sex is later demonstrated (see results later) to be directly proportional to adult life span. Therefore, the relationship between K and total longevity is investigated, not simply adult life span, due to the nature of available data.

We obtained from the literature growth and life history parameters for a total of 111 species and populations of bivalves from natural marine or estuarine or freshwater environments. The phylogenetic range of the bivalves included in each of the regression analyses and the PICs are presented in Table 2. In instances where the literature provided estimates for both sexes of a species, the arithmetic mean of the two was used. To exclude potentially problematic growth parameter estimates, data from species sampled from within heavily fished or other anthropogenically impacted areas were not included in our analyses. It is reasonably assumed that in such areas, estimates of T_max are not reliable or representative of the actual achievable longevity for that species.

Table 2.

The Phylogenetic Coverage of the Bivalves Included in the Regression Analyses and the Analyses of Phylogenetic Independent Contrasts

Parameters	N	No. of Species	No. of Families	No. of Orders	No. of Bivalve Subclasses	% Heterodonta
L∞ vs. Tmax	56	56	25	7	4	70
Tad vs. Tsex	50	50	20	6	3	70
Tmax vs. K	35	35	20	6	4	82
Contrasts
Contrasts of L∞ vs. Tmax	55	56	25	7	4	n/a
Contrasts of Tad vs. Tsex	49	49	20	6	3	n/a
Contrasts of Tmax vs. K	34	35	20	6	4	n/a

Statistical Analyses

A traditional nonphylogenetic approach (ie, simple regression of species values ignoring phylogeny) was initially used to compare the relationship between five different parameters (L_∞, T_max, T_ad, T_sex, and K). To meet the assumptions required for least squares linear regression, data were ln-transformed prior to statistical analysis. Although traditional nonphylogenetic approaches have been widely used in comparative biology, computer simulations (27,28) have demonstrated that such approaches can lead to unacceptably high Type I error rates (incorrectly accepting alternate hypotheses) and inaccurate estimations of correlations or slopes (29). To assess these potential problems, significant correlations from the traditional analyses were further investigated using the PIC method of Felsenstein (23).

Standardized independent contrasts were computed following the methods of Garland and Janis (29) and Garland and Adolph (36). To assure contrasts were appropriately standardized, the absolute values of the standardized contrasts were correlated with their standard deviations; if no correlation was apparent, the branch lengths adequately standardized the independent contrasts as described (37). The relationship between the standardized independent contrasts is investigated through ordinary least squares regression analysis, with regression lines constrained to pass through the origin (24,27,37–39). During the statistical analysis of PICs, associated p values can generally be determined by reference to conventional statistical tables (36). Therefore, the significance level was set at .05.

Phylogenetic Information

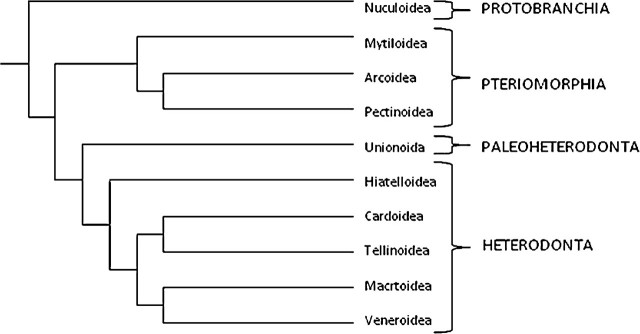
Although the precise topological structure of the bivalve phylogenetic tree is not completely resolved, the general relationships between the taxa are (for bivalve phylogenies, see (40–45)). This enabled a phylogenetic tree to be created (Figure 1), which contained accurate relationships of all the species used in the study. Where possible, the branch length data from Taylor and colleagues (45) were used; where no branch length data were available, an arbitrary branch length was used, this length was the mean of all branch lengths contained in the Taylor and colleagues (45) phylogeny, with branch lengths in the units substitutions per site. Although this latest molecular phylogeny was largely constructed to describe the phylogeny of the Heterodonta, Taylor and colleagues (45) utilized species from the order Palaeoheterodonta (Trigoniidae, Margaritiferidae, and Unionidae) as outgroups, so there is broad coverage of the class Bivalvia.

Figure 1.

Phylogenetic relationships of the class Bivalvia documenting the relationships between the four main subclasses and the main speciose orders and superfamilies (drawn from (45)).

Provided accurate phylogenetic topologies and branch lengths are used, the statistical power of independent contrasts is identical to that of traditional nonphylogenetic approaches (36). Although it is not ideal to utilize arbitrary branch lengths, computer simulations have demonstrated that independent contrasts are reasonably robust with respect to violation of assumptions (including errors in branch lengths: (28,46,47) providing arbitrary branch lengths are appropriately checked for statistical adequacy (37)).

RESULTS

Allometric Scaling of Longevity With Size

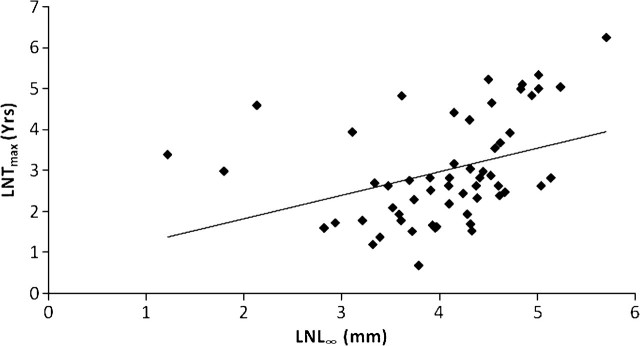
Data from 56 species of bivalves reveal a statistically significant positive impact of L_∞ on T_max (Figure 2, Table 2), although only 13.1% of the variation in maximum longevity is accounted for by asymptotic size. PIC analysis of the same 56 species confirmed this relation and even enhanced the statistical significance (Table 3). This result suggests that the evolution of body size in bivalves is associated with that of longevity.

Figure 2.

The relationship between the natural log of the asymptotic length (L_∞; centimeters), derived from the von Bertalanffy growth formula, and the natural log of the maximum age (T_max; years) attained by bivalve species. Nonphylogenetic regression analysis: n = 56, F = 8.72 and p = .004, r² = .137.

Table 3.

Results of the Regression Analysis for Each Set of ln-Transformed Data, Documenting the df, r² Value, F Statistic, and Associated p Value

Parameters	df	r2	F statistic	Associated p Value
L∞ vs. Tmax	56	.131	8.721	.004*
PIC L∞ vs. Tmax	55	.138	11.278	.001*
Tad vs. Tsex	50	.484	30.912	<.001*
PIC Tad vs. Tsex	49	.302	18.995	<.001*
Tmax vs. K	35	.643	86.343	<.001*
PIC Tmax vs. K	34	.619	80.718	<.001*

^*Indicates the result is statistically significant at the 95% level. PICs = phylogenetically independent contrasts.

Developmental Schedules and Longevity

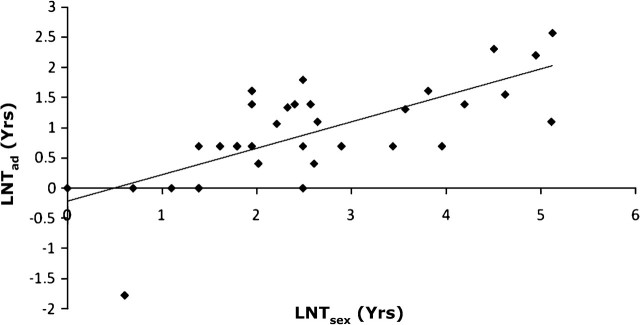
Data from 35 bivalve species were used to investigate the relationship between adult life span and age at maturity (in years; Table 2). In both traditional (Figure 3) and PIC analysis (Table 3), age at sexual maturity was significantly related to adult life span, explaining 48.4% and 30.2% of the variation, respectively. These results strongly suggest that development time, measured as time to maturity, not only influences adult life span but also may coevolve with adult life span. The amount of time a bivalve will live after maturity, that is, its adult life span, is proportional to the amount of time it took to attain maturity.

Figure 3.

The relationship between the natural log of the age at sexual maturity (T_sex) and the natural log of the adult life span (T_ad; years) attained by bivalve species. Nonphylogenetic regression analysis: n = 50, F = 30.912 and p ≤ .001, r² = .484.

Growth Rate and Longevity

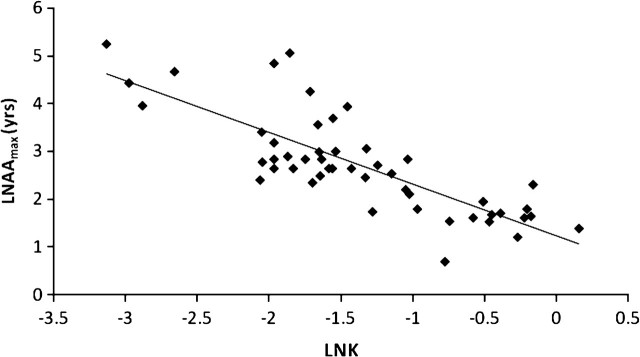
We then investigated the relationship between growth rate (K per year) and longevity (Figure 4). Analysis of 50 species demonstrated a robust significant negative relationship between K and T_max using either nonphylogenetic (Figure 4) or PIC analyses (Table 3), explaining 64.3% and 61.9% of the variance, respectively. These results indicate that the faster a bivalve grows, the shorter its life span.

Figure 4.

The relationship between the natural log of the maximum age (years) attained by bivalve species (T_max) and the natural log of the growth coefficient K as derived from the von Bertalanffy growth formula for bivalve species. Nonphylogenetic regression analysis: n = 35, F = 86.343 and p ≤ .001, r² = .643.

DISCUSSION

This study is the first to investigate in invertebrates the much documented relationships between longevity and size and development schedules that occur in terrestrial vertebrates (16,19). More importantly, it investigates these relationships in the exceptionally long-lived molluscan class Bivalvia.

Allometric Scaling of Body Size and Longevity

In multiple vertebrate taxa, there is a well-established relationship between body size and longevity (16,48), for which de Magalhães and colleagues (16) suggest that evolutionary ecological factors appear the most plausible explanation. Simply, larger species are believed to be less prone to predation and therefore experience lower mortality rates, as seen in fish by Pauly (49). Greater survivorship in turn leads to longer life spans and, according to evolutionary theory, the evolution of a slower aging process (17,18).

We have demonstrated that body size in bivalves significantly correlates with longevity, a relationship that has been observed in many other animal taxonomic groups, including mammals (16) and freshwater mussels (22). Although a significant relationship was observed, body size in bivalves explains far less of the variation in longevity than in other taxonomic groups, only 13% compared with 49% in birds (16) and 66% in mammals (16). The mammalian data are probably the least analogous comparison deriving from largely captive populations. This reduced relationship between longevity and size in bivalves may be due to confounding factors such as burrowing ability and shell thickness among the group, factors that strongly influence their vulnerability to predation. For example, Kirby (50) demonstrated that in two species of the oyster genus, Crassostrea, longevity is strongly influenced by shell thickness, suggesting that shell thickness may provide greater resistance to extrinsic hazards (eg, predation or fluctuations in temperature) leading to a longer life.

Recent analyses investigated the relationship between size and longevity in the fresh water mussels and obtained similar results, although a significant positive correlation between size and longevity, size, and relative shell mass explained little variation in longevity (22).

Developmental Schedules and Longevity

Evolutionary theories of aging propose that the rate of aging is caused by the force of natural selection acting to optimize fitness early in life (51). The antagonistic pleiotropy theory of aging suggests the existence of pleiotropic genes that endow benefits early in life at the cost of deleterious effects later to explain the evolution of senescence (52), therefore proposing a trade-off between reproduction and longevity. In a classic article, Williams (52) expounded that reproductive maturation is the most significant milestone in the evolution of senescence and that senescence may theoretically initiate immediately after this stage in development, that is, “the sooner this point is reached, the sooner senescence should begin and the sooner it should have demonstrable effects.” Therefore, according to the theory, the time a bivalve will live after maturity should be proportional to the amount of time it took to reach maturity.

Mammalian maximum adult life span correlates with age at maturity (16,20). In support of these findings, Ricklefs (19) demonstrated that age at maturity is negatively correlated with demographic aging rate in terrestrial vertebrates. Ricklefs (19) states that the rate of aging within a species is primarily related to that of extrinsic mortality, and those young individuals must wait longer to enter the breeding population in species with lower extrinsic mortality rates. We have shown that maximum adult life span in bivalves is also significantly and positively correlated with age at maturity, a correlation that is predicted by the antagonistic pleiotropy theory of aging.

It has been suggested that the optimization theories of aging, including the antagonistic pleiotropy and the disposable soma theories of aging, may not be relevant to animals that demonstrate neither a decrease in fecundity with age or an observable decline in their fitness (53). In longer lived bivalves, there is no evidence of reproductive senility and gonad production continues, regardless of age, and as there is indeterminate growth (although a minimal amount at advanced ages), gonad production is reported to actually increase with age (54,55). Although at the individual level this will be the case, it is almost inconceivable that the mortality rate (age dependant and age independent) would not result in the older cohort of clams leaving less gametes than the younger cohorts (increase in gamete production with age in the population would be offset by loss of individuals from the population), which, according to the two optimization theories of aging, would result in natural selection acting to optimize fitness early in life, that is, senescence will creep into a population, albeit at a slow rate. These longer lived bivalves have also been suggested to be good examples of a group of organisms displaying negligible senescence (56) or possibly negative senescence (57). Our findings here align with, and were predicted by, the antagonistic theory of aging. Regardless of the growth and reproductive characteristics of the taxonomic class, we suggest that antagonistic pleiotropy is still a relevant theory for explaining aging in bivalves because, at the population level, the rate of extrinsic mortality results in a decrease in gamete production per age cohort, despite gamete production increasing with age at the individual level (55) and hence a reduction in the strength of natural selection with age.

The final hypothesis investigated the relationship between shell growth rate, another proxy measure of the developmental schedule, and longevity. Longevity is significantly negatively correlated with growth rate, expressed as the von Bertalanffy growth coefficient (K). In mammalian species, de Magalhães and colleagues (16) demonstrated that a fast postnatal growth rate in mammals is associated with a shorter life span. Furthermore, Ricklefs and Scheuerlein (21) and Ricklefs (19) have demonstrated that postnatal growth rate is negatively correlated with demographic aging rates in terrestrial vertebrates. Although the von Bertalanffy growth coefficient (K) is not the precise equivalent of postnatal growth rate, it is the closest analogous parameter available for bivalves. In the freshwater mussels, Haag and Rypel (22) also demonstrated longevity related negatively to the growth rate, K, which explained more than 75% of variation in longevity. These patterns remained when data were corrected for phylogenetic relationships among species, and furthermore, path analysis supported the conclusion that K was the most important factor influencing longevity both directly and indirectly through its effect on shell mass (22).

The two most commonly accepted optimization theories of aging, the antagonistic pleiotropy and the disposable soma theories of aging, suggest that growth rate should be associated with the life span of a species. Kirkwood and Holliday (58), the proponents of the disposable soma theory of aging, argue that “it may be selectively advantageous for higher organisms to adopt an energy-saving strategy of reduced accuracy in somatic cells to accelerate development and reproduction, but the consequence will be eventual deterioration and death.” Therefore, longevity is determined through the trade-offs between resources spent on somatic maintenance and reproduction (59). Williams (52) similarly predicted a trade-off between reproduction (reproductive success, fitness, and vigor) and longevity as part of the antagonistic pleiotropy model stating that “rapid individual development should be correlated with rapid senescence.”

Growth rate had much greater explanatory power (in terms of the r² value) than either age at maturity or shell size. The explanatory power of growth rate on longevity observed in bivalves was very similar to that in other taxonomic groups, 0.67 in both mammals (not including cetaceans) and birds (16). Haag and Rypel (22) found similar, stating that 75% of the variation in the longevity of freshwater mussels was explained by the growth rate. It is probable that the reduced accuracy in somatic maintenance associated with the rapid growth rate has the most direct influence longevity, whereas the other parameters hold a more indirect complex relationship or there maybe confounding factors. As mentioned previously, the reduced relationship between longevity and size in bivalves may be due to confounding factors, which strongly influence their vulnerability to predation and other extrinsic factors (eg, burrowing and shell thickness).

Conclusions

This is the first demonstration of a relationship between longevity, size, and development schedules in bivalves, newly discovered models of natural aging (1), and the results are strengthened by the control for phylogenetic independence. From our results, it appears that in bivalves, maximum size, development, and growth are associated with longevity, and these findings are in accord with the two main evolutionary theories of aging and support the findings of other researchers working on mammals and fish. However, in comparison with the vertebrate studies to date, there is a reduced relationship between longevity and size in bivalves. These results therefore have implications in the design and interpretation of comparative studies of aging in bivalves. When investigating similar relationships in mammals, de Magalhães and colleagues (16) concluded that “developmental schedules such as the time to maturity and growth rates have a physiological basis that should be taken into consideration in the comparative biology of aging.” Ignoring this requirement may result in incorrectly assuming that the mechanisms involved in development are associated with aging rather than as a consequence of the correlation between developmental schedules and longevity (16,60). To further understand the actual biologic mechanisms that cause species to display different rates of aging, more detailed biochemical and molecular investigations are required (16).

FUNDING

This work was supported by a National Institute on Aging/Biotechnology and Biological Sciences Research Council Partnering Award to Support Collaborative Research on the Biology of Aging (R01).