Mining Boundary Effects in Areally Referenced Spatial Data Using the Bayesian Information Criterion

Abstract

Statistical models for areal data are primarily used for smoothing maps revealing spatial trends. Subsequent interest often resides in the formal identification of ‘boundaries’ on the map. Here boundaries refer to ‘difference boundaries’, representing significant differences between adjacent regions. Recently, Lu and Carlin (2004) discussed a Bayesian framework to carry out edge detection employing a spatial hierarchical model that is estimated using Markov chain Monte Carlo (MCMC) methods. Here we offer an alternative that avoids MCMC and is easier to implement. Our approach resembles a model comparison problem where the models correspond to different underlying edge configurations across which we wish to smooth (or not). We incorporate these edge configurations in spatially autoregressive models and demonstrate how the Bayesian Information Criteria (BIC) can be used to detect difference boundaries in the map. We illustrate our methods with a Minnesota Pneumonia amd Influenza Hospitalization dataset to elicit boundaries detected from the different models.

1 Introduction

The growing popularity of Geographical Information Systems (GIS) has generated much interest in analyzing and modelling geographically referenced data. Geographical referencing depends upon the resolution of the data: when data referencing is done with respect to the coordinates of the location (e.g. latitude and longitude), we call them point-referenced, as is common in environmental and ecological studies, while data aggregated over regions in a map (e.g. mortality rates by counties or zip-codes) are called areally-referenced or lattice. In the domain of public health, due to patient confidentialities, data are usually of the latter type and are usually available as case counts or rates referenced to areal regions, such as counties, census-tracts or ZIP codes, rather than the geographical location of the individual residences. These regions offer a convenient way of grouping the population and preserving confidentiality.

Statistical models for spatial data are primarily concerned with explaining variation, separating spatial signals from noise and improving estimation and prediction. These models capture associations or correlations across space depending upon the type of referencing in the data. For point-referenced datasets, models customarily employ spatial processes to capture spatial associations as a function of Euclidean geometric objects such as distance and direction. These models are popular in geostatistics (see, e.g., Cressie, 1993; Banerjee et al., 2004) and provide spatial interpolation or “kriging” accounting for uncertainty in estimation and prediction.

For areally-referenced data, the association structures are built upon adjacencies or neighborhood structures of the regions. Here the statistical models regard observations from a region to be more similar to those from its neighboring regions than those arising from regions farther away. These structures underpin spatially weighted regression models and spatial autoregressive models that have been widely employed for smoothing maps and evincing spatial trends and clusters. They have been applied extensively in econometrics (see, e.g. Anselin, 1988, 1990; Le Sage, 1997; Le Sage and Pace, 2009) and public health (see, e.g., Banerjee et al., 2004; Waller and Gotway, 2004).

Subsequent inferential interest often resides not in the statistically estimated maps themselves, but on the formal identification of “edges” or “boundaries” on the spatial surface or map. The ‘boundary’ here refers to those on the map that reflect sharp differences of the outcome variable between its two incident regions. Detecting such boundaries for contagious diseases such as influenza, can help surveillance systems control or at least slow down the spread of the infection and better manage local treatment response (e.g. targeting vaccine delivery).

In this article, we offer a BIC based spatial autoregressive model to Minnesota Pneumonia and Influenza Hospitalization data. We identify the boundaries that separate the more affected areas from the less affected areas. These boundaries could provide information to the government or other related departments to identify areas of the most rapid change in incidence and prevalence for adjusting local treatment response (e.g. targeting vaccine delivery).

2 “Wombling”: Detecting boundaries of abrupt change on maps

This boundary detection problem is often referred to as “wombling”, after a foundational article by Womble (1951), much like “kriging” obtained its name from the pioneering work of Krige. For point-referenced models, investigators often seek boundaries that reflect rapid change on the estimated spatial surface. Applications in the literature include detection of ecotones in forests (Fortin, 1994) and the edges of distinct soil zones. Fortin and Drapeau (1995) reported that this technique correctly detects boundaries in both simulated and real environmental data. For example, raster wombling, also known as lattice wombling, operates on numeric raster data – where the sampling locations are aligned in a rectangular grid, forming pixels. Barbujani et al. (1990, 1997) used raster wombling to identify genetic boundaries in Eurasian human populations. Bocquet-Appel and Bacro (1994) applied a multivariate approach to genetic, morphometric and physiologic characteristics, and found that it correctly detected the locations of simulated transition zones. Fortin (1997) delineated boundaries for tree and shrub density, percent coverage, and species presence-absence. Recently Banerjee and Gelfand (2006) developed a more formal statistical inferential framework for detecting curves representing rapid change on estimated spatial process surfaces.

While wombling methods have been applied extensively to point-referenced data, they are relatively less visible in areal contexts. Areal wombling, also known as polygonal wombling, has been addressed by Jacquez and Greiling (2003a, 2003b) to estimate boundaries of rapid change for colorectal, lung and breast cancer incidence in Nassau, Suffolk and Queens counties in New York. They proposed algorithms assigning boundary likelihood values (BLV’s) to each areal boundary using an Euclidean distance metric between neighboring observations. This Euclidean distance metric is looked upon as a “dissimilarity” value. Dissimilarity values are calculated for each pair of adjacent regions, adjacency being defined as sharing a border. Thus, if i and j are neighbors then the BLV associated with the edge (i, j) is ∥y_i − y_j ∥, where ∥ · ∥ is some appropriate metric (for instance Euclidean for continuous responses, Hamming for binary responses). Locations with higher BLV’s are more likely to be a part of a difference boundary, since the variable changes rapidly there.

While attractive in their simplicity and ease of use, the algorithmic approaches do not account for all sources of uncertainty and can lead to spurious statistical inference. For instance, public health data are often characterized by extremeness in counts and rates corresponding to certain thinly populated regions that arises due to random variation in the observed data rather than any systematic differences. Statistical models assist in capturing spatial variation and separating them from random noise. A more detailed review of the existing algorithmic approaches and their deficiencies can be found in Lu and Carlin (2005), who proposed a statistical modelling framework to carry out areal wombling. They considered disease count data (Y_i, E_i), where Y_i and E_i are the observed and internally standardized expected counts from the i^th county and employed a spatial hierarchical model that is estimated using Markov chain Monte Carlo (MCMC) methods. Statistical inference proceeds from the posterior distribution of the parameters. Lu and Carlin (2005), and Wheeler and Waller (2008) investigate different metrics Δ_ij for the BLV and identify boundaries using the posterior means of the BLV. The CAR model, however, smooths across all geographical neighbors, and can lead to over-smoothing and subsequent underestimation of several Δ_ij’s.

To remedy this problem, Lu et al. (2007) and Ma, Carlin and Banerjee (2008) investigated estimating the adjacency matrix within a hierarchical framework using priors on the adjacency relationships. However, these models often involve weakly identifiable parameters that are difficult to estimate from the data. Fairly informative prior knowledge is required that is usually unavailable. Furthermore, they employ computationally expensive MCMC algorithms that can be inexorably slow in converging to the desired posterior distributions.

The current article focuses primarily upon areally-referenced models and detecting “difference boundaries” on spatial maps. Our current work investigates a middle ground between the algorithmic approaches that ignore sources of variation and the fully Bayesian hierarchical modelling approaches that are computationally prohibitive. We treat the areal wombling problem as one of model comparison and seek to learn about difference boundaries from the data by considering the influence of each edge on these models. For this purpose, we employ the Bayesian Information Criteria (BIC) that has become a popular tool in statistical learning and data mining to approximate the marginal posterior probabilities of the different models and identify the influence of the edges. Exhausting all possible models will again become computationally prohibitive, hence we consider a “leave-one-out” algorithm that assesses the influence of each edge in the map, given all the other edges are present.

The remainder of the paper is organized as follows. Section 3 we review spatial autoregression models for areal data analysis. Section 5 discusses the Bayesian inferential paradigm and the Bayesian Information Criteria. Section 6 illustrates the BIC methodology for areal wombling using some simulated scenarios as well as an appication to a Pneumonia and Influenza (P& I) dataset from Minnesota. Finally, Section 7 concludes the paper with some discussion and indication towards future work.

3 Statistical models for areal data analysis

Areal data are referenced by regions in a geographical map, which can be represented as an n × n matrix W, whose (i, j)-th entry, w_ij, connects units in i and j spatially in some fashion. Customarily w_ii is set to 0. Possibilities include binary choices, i.e. w_ij = 1 if i and j share some common boundary, perhaps a vertex (as in a regular grid). Alternatively, w_ij could reflect “distance” between units, e.g., a decreasing function of inter-centroidal distances between the units (as in a county or other regional map). But distance can be returned to a binary determination. For example we could set w_ij = 1 for all i and j within a specified distance. Or, for a given i, we could get w_ij = 1 if j is one of the K nearest (in distance) neighbors of i. While W is often symmetric, it is not necessarily so; for instance, the K-nearest neighbors example provides a setting where symmetry may be violated. For the illustrations in this article we will consider a connected map (i.e. no islands) and a symmetric binary proximty matrix W.

As the notation suggests, the entries in W can be viewed as weights. More weight will be associated with j’s closer (in some sense) to i than those farther away from i. In this exploratory context W provides the mechanism for introducing spatial structure into statistical models. To see this consider the symmetric binary specification for W and let y = (y₁, … , y_n)′ be an n × 1 vector of outcomes where y_i has been observed in the i-th region. An intuitively appealing spatial smoother would smooth the obervation in each region by taking the mean of its neighbors. Thus, each y_i would be predicted by the average of its neighbors, say ${\widehat{y}}_i=\frac{1}{w_{i+}}{\sum }_{j~i}{y}_j$ with ~ denoting “is a neighbor of” and w_i+ being the number of neighbors of region i. A statistical model for this smoother would relate the i-th observation to the mean of its neighbors. Specifically, we write $y_i={\sum }_{j=1}^n\rho {\stackrel{\sim }{w}}_{\mathit{ij}}{y}_j+{\epsilon }_i$, where w̃_ij = w_ij/w_i+, ρ is a parameter representing the strength of the spatial association and ${\epsilon }_i\stackrel{\mathit{iid}}{\sim }\sim N(0,{\tau }^2)$ is a stochastic error or noise component for each observation. This error could be representative of variability from a number of sources including unobserved explanatory variables, sampling error and so on.

The key problem in statistical inference is to sensibly model spatial associations over the map while yielding a theoretically valid joint probability distributions. Letting W̃ be the row-normalized matrix with entries w̃_ij, we can write the above model as y = ρW̃ y + ε, whence y = (I − ρW̃)⁻¹ε. Provided that the inverse exists, we have the dispersion matrix of y as Σ(τ², ρ, W) = τ²[(I − ρW̃′) (I − ρW̃)]⁻¹. Using standard eigen-analysis (see, e.g., Banerjee et al., 2004; Anselin, 1988) it can be shown that (I − ρW̃)⁻¹ exists whenever ρ ∈ (1/λ₍₁₎, 1), where λ₍₁₎ is the smallest eigen-value of W̃. It is also true that λ₍₁₎ is real-valued and negative, but restricting ρ ∈ (0, 1) yields non-negative elements in (I − ρW̃)⁻¹. This seems to be more intuitive in spatial settings, where negative associations between proximate locations is difficult to envision. With this restriction on ρ, we obtain a valid joint multivariate Gaussian distribution y ~ MV N(0, Σ(τ², ρ, W)). This is called a Simultaneous Autoregression (SAR) model.

In public-health data analysis contexts, it is often desired to carry out spatial inference after adjusting for certain important covariates that explain the large-scale variation seen in the data. This leads to random effect or hierarchical linear models,

$$y_i={\mathbf{x}}_i^T\mathit{\beta }+{\varphi }_i,i=1,\dots ,n,$$ (1)

where y_i is the dependent variable, x_i a vector of areally-referenced regressors and ϕ_i are spatial random effects that model association between adjacent regions. Thus, we would now let ϕ = (ϕ₁, … , ϕ_n)′ follow a SAR model, i.e. ϕ ~ MV N(0, Σ(τ², ρ, W)). A very important point, at least in our current context, is to note that the SAR models are well-suited to maximum likelihood estimation but not at all for MCMC fitting of Bayesian models. In fact, the log likelihood associated with (1) is

$$\frac{1}{2}\log \mid {\tau }^{-1}\left(I-\rho \stackrel{\sim }{W}\right)\mid -\frac{1}{2{\tau }^2}{(\mathbf{y}-X\mathit{\beta })}^T\left(I-\rho \stackrel{\sim }{W}\right)\left(I-\rho {\stackrel{\sim }{W}}^{\prime }\right)(\mathbf{y}-X\mathit{\beta }).$$ (2)

Though ρW̃ will introduce a regression or autocorrelation parameter, the quadratic form is quick to evaluate (requiring no matrix inverse) and the determinant can usually be calculated rapidly using diagonally dominant, sparse matrix approximations. Thus maximization can be done iteratively but, in general, efficiently. On the other hand, we note that the absence of a hierarchical form with random effects implies complex Bayesian model fitting.

The SAR model, with the help of the proximity matrix, captures spatial associations by assuming that neighboring regions are likely to exhibit greater association than regions that are not neighbors. This degree of association is controlled by the so-called spatial autocorrelation parameter ρ. A consequence of this is that the SAR model smooths the outcome across neighboring regions to produce maps that better reveal regions where the response tends to cluster. However, smoothing across all geographical boundaries may lead to oversmoothing resulting in maps that would tend to conceal difference boundaries. Arriving at models that are formally selected using a statistical paradigm will deliver the optimal adjacency matrix W_k and, in the process, would have solved the “wombling” problem by identifying “true” edges that should not be smoothed across. Indeed these edges are the “complements” of W_k in being those entries that were 1 in W but are 0 in W_k, i.e., edges corresponding to the 1 entries in W − W_k.

Unlike SAR models, a Conditional Autoregression (CAR) specification would model each effect conditional upon the remaining effects. Such a model specifies conditional distributions

$${\varphi }_i\mid {\varphi }_j,j\ne i~N\left(\rho \sum _{j=1}^K\frac{w_{ij}}{w_{i+}}{\varphi }_j,\frac{{\tau }^2}{w_{i+}}\right).$$

Besag (1974) proved that these full conditional distributions specify a joint distribution for the phi_i’s such that ϕ ~ MV N (0, τ²[D − ρW]⁻¹). Now, one needs to make sure that D − ρW is positive definite, a sufficient condition for which (see, e.g., Banerjee et al., 2004) is to restrict ρ ∈ (1/λ₍₁₎, 1). Assuncao and Krainski (2009) also provide discussion of the ρ parameter and explanations that help the practitioner to view the covariance matrix of a CAR model in a natural way. The CAR model has been especially popular in Bayesian inference as its conditional specification is convenient for Gibbs sampling and MCMC schemes. The relationship between the CAR and SAR models in terms of resulting spatial correlations and their interpretations has been explored by Wall (2001).

4 Statistical detection of boundary effects

Returning to our primary problem of detecting difference boundaries, we formulate this problem as one of comparing between models that represent different boundary hypotheses. A boundary hypotheses corresponds to a particular underlying map specifying which edges should be smoothed over and which should not. A few issues, however, arise regarding the exact choice of the model. For instance, consider the hypothesis of no difference boundaries at all in the map. What model would correspond to this hypothesis?

If we believe there are no difference boundaries at all, should we consider the map as comprising a single region? This implies having no region-specific effects at all or, equivalently, W = 0 (the null matrix), thereby reducing (1) to a simple linear regression model with no random effects and ε ~ MV N(0, σ²I). Alternatively, we could still regard y_i as arising from n different regions but, given the absence of difference boundaries, we would retain independent regional effects instead of spatial structures in the model. This would amount to ρW = I so that Cov(ϕ, ε) = 0 and we obtain a linear random effects model with iid regional effects. The choice is not straightforward and may depend upon the objectives of the analysis.

Here we will adopt the second approach, where we always retain random effects and consider models varying in their specification of W that controls spatial smoothing. At the other extreme all the geographical edges may in fact be difference boundaries. Any intermediate model that lies between these extremes is completely specified by modifying the original map to delete some edges.

Ideally we would like to consider a class of models M = {M₁, … , M_K} representing all possible models or all possible maps derived from W by deleting combinations of geographical edges. In other words, let W = {w_ij} be the adjacency matrix of the map (i.e., w_ii = 0, and w_ij = 1 if i is adjacent to j and 0 otherwise). Model M_k will be a SAR model with the adjacency matrix W_k that has been derived by changing some of the 1’s to 0’s in W. This amounts to dropping some edges from the original map or, equivalently, combining two regions into one. However, now we encounter an explosion in the number of models. To be precise, if W is the original geographical map, we have 2^1′W1/2 models to compare. This is infeasible and will require sophisticated MCMC Model Composition or MC³ algorithms (see. e.g., Hoeting et al., 1999) for selecting models. These formal statistical methods will again become computationally intensive and inconducive for learning of edge effects in large maps. Therefore, we consider only models that arise by changing only one entry in the W matrix. This avoids MCMC and resorts to the simpler Bayesian Information Criteria that requires only the maximum likelihood estimates for the models.

5 The Bayesian information approach

By modelling both the observed data and any unknown parameter or other unobserved effects as random variables, the hierarchical Bayesian approach to statistical analysis provides a cohesive framework for combining complex data models and external knowledge or expert opinion (e.g., Berger, 1985; Carlin and Louis, 2000; Robert, 2001; Gelman et al., 2003; Lee, 2004). In this approach, in addition to specifying the distributional model f(y∣θ) for the observed data y = (y₁, … , y_n) given a vector of unknown parameters θ = (θ₁, … , θ_k), we suppose that θ is a random quantity sampled from a prior distribution p(θ ∣ γ), where γ is a vector of hyperparameters. Inference concerning θ is then based on its posterior distribution,

$$p(\mathit{\theta }\mid \mathbf{y},\mathit{\gamma })=\frac{p(\mathbf{y},\mathit{\theta }\mid \mathit{\gamma })}{p(\mathbf{y}\mid \mathit{\gamma })}=\frac{p(\mathbf{y},\mathit{\theta }\mid \mathit{\gamma })}{\mathit{\int }p(\mathbf{y},\mathit{\theta }\mid \mathit{\gamma })d\mathit{\theta }}=\frac{p(\mathbf{y}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\gamma })}{\mathit{\int }p(\mathbf{y}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\gamma })d\mathit{\theta }}.$$ (3)

Notice the contribution of both the data (in the form of the likelihood p(y ∣ θ)) and the external knowledge or opinion (in the form of the prior p(θ∣γ)) to the posterior. If γ is known, this posterior distribution is fully specified; if not, a second-stage prior distribution (called a hyper-prior) may be specified for it, leading to a fully Bayesian analysis. Alternatively, we might simply replace γ by an estimate γ̂ obtained as the value which maximizes the marginal distribution p(y ∣ γ) viewed as a function of γ. Inference proceeds based on the estimated posterior distribution p(θ ∣ y, γ̂), obtained by plugging γ̂ into equation (3). This is called an empirical Bayes analysis and is closer to maximum likelihood estimation techniques.

The Bayesian decision-making paradigm improves upon the classical approaches to statistical analysis in its more philosophically sound foundation, its unified approach to data analysis, and its ability to formally incorporate prior opinion or external empirical evidence into the results via the prior distribution. Statisticians, formerly reluctant to adopt the Bayesian approach due to general skepticism concerning its philosophy and a lack of necessary computational tools, are now turning to it with increasing regularity as classical methods emerge as both theoretically and practically inadequate. Modelling the θ_i’s as random (instead of fixed) effects allows us to induce specific (e.g. spatial, temporal or more general) correlation structures among them, hence among the observed data y_i as well. Hierarchical Bayesian methods now enjoy broad application in the analysis of complex systems, where it is natural to pool information across from different sources (e.g. Gelman et al., 2003). Modern Bayesian methods seek complete evaluation of the posterior distributions using simulation methods that draw samples from the posterior distribution. This sampling-based paradigm enables exact inference free of unverifiable asymptotic assumptions on sample sizes and other regularity conditions.

A computational challenge in applying Bayesian methods is that for many complex systems, inference under (3) generally involves distributions that are intractable in closed form, and thus one needs more sophisticated algorithms to sample from the posterior. Forms for the prior distributions (called conjugate forms) may often be found which enable at least partial analytic evaluation of these distributions, but in the presence of nuisance parameters (typically unknown variances), some intractable distributions remain. Here the emergence of inexpensive, high-speed computing equipment and software comes to the rescue, enabling the application of recently developed Markov chain Monte Carlo (MCMC) integration methods, such as the Metropolis-Hastings algorithm and the Gibbs sampler. See the books by Gelman et al. (2004), Carlin and Louis (2000) and Robert (2001) for details on Bayesian analysis and computing.

Bayesian inference proceeds by considering a set of models, say M = {M₁, … ,M_K}, each representing a hypothesis, and then selecting the best model(s) using some statistical metric. Assuming that model M_j has parameters, say θ_j, associated with it and we have specified priors p(θ_j∣M_j) for each j, we will seek posterior distributions of the model itself,

$$p(M_j\mid \mathbf{y})=\frac{p(M_j)p(\mathbf{y}\mid M_j)}{{\sum }_{k=1}^{K}p(M_k)p(\mathbf{y}\mid M_k)}=\frac{p(M_j)\times \mathit{\int }p({\mathit{\theta }}_j\mid M_j)p(\mathbf{y}\mid {\mathit{\theta }}_j,M_j)d{\mathit{\theta }}_j}{{\sum }_{k=1}^{K}p(M_k)\times \mathit{\int }p({\mathit{\theta }}_k\mid M_k)p(\mathbf{y}\mid {\mathit{\theta }}_k,M_k)d{\mathit{\theta }}_k}.$$ (4)

To compare two models, say M₁ and M₂, we form their posterior odds

$$\frac{p(M_1\mid \mathbf{y})}{p(M_2\mid \mathbf{y})}=\frac{p(M_1)}{p(M_2)}\times \frac{p(\mathbf{y}\mid M_1)}{p(\mathbf{y}\mid M_2)}.$$ (5)

If the odds are greater than one, we choose model M₁, otherwise we opt for M₂. The Bayes factor is defined as

$${\mathit{BF}}_{12}=\frac{p(\mathbf{y}\mid M_1)}{p(\mathbf{y}\mid M_2)}$$ (6)

and represents the contribution of the data towards the posterior odds. Often, we will have no prior reason to favor one model over another and the posterior odds will equal the Bayes Factor. Thus, one seeks to evaluate the marginal distribution of the data, given a model, as

$$p(\mathbf{y}\mid M_j)=\mathit{\int }p(\mathbf{y}\mid {\mathit{\theta }}_j)p({\mathit{\theta }}_j\mid M_j)d{\mathit{\theta }}_j.$$ (7)

Computation of the marginal distribution in (7) for general hierarchical models can be much more complicated and has occupied plenty of attention over the last several years. Many of these methods, while offering better evaluations and approximations, involve computationally intensive simulation algorithms, such as MCMC methods, that require much finessing and several thousands of iterations to yield accurate results.

LeSage and Parent (2007) provide a computationally simple and fast approach to evaluating the true log-marginal likelihood for the SAR model. However, their approach seems to be best suited to the Zellner g-prior on the regression coefficients and may not be directly applicable to more general priors. LeSage and Pace (2009; Ch.6) also discuss the issue of comparing SAR models based on different adjacency matrices W. They rely upon univariate numerical integration over the range of support for the parameter ρ in the SAR model, which involves calculating log (det(I_n − ρW)) for every value of the parameter ρ. Computationally fast methods to compute the log determinant terms are presented in Pace and Barry (1997) and Barry and Pace (1999) . Here we approximate the marginal distribution in (7) using the Laplace-approximation, which avoids the numerical integration over the parameter space.

In edge detection problems, as outlined earlier, we encounter a large number of models. Hence, a faster approach will be to employ an inexpensive approximation to (7). One such approximation is based upon a Laplace-approximation and some subsequent simplifications (see, e.g., Raftery, 1995):

$$\log p(\mathbf{y}\mid M_j)=\log p(\mathbf{y}\mid {\widehat{\mathit{\theta }}}_j)-\frac{\dim (M_j)}{2}\log n+O(1),$$ (8)

where dim(M_j) is the number of parameters that are being estimated in the model M_j. The Bayesian Information Criteria is derived from this approximation as

$${\mathit{BIC}}_j=-2\log p(\mathbf{y}\mid {\widehat{\mathit{\theta }}}_j)+\dim (M_j)\log n.$$ (9)

Therefore, choosing the model with the minimum BIC amounts to choosing the model with the maximum posterior probability. In fact, if we consider the models in M then we can estimate the posterior probability for each model as

$$p(M_j\mid \mathbf{y})\approx \frac{\exp (-\frac{1}{2}{\mathit{BIC}}_j)}{{\sum }_{k=1}^K\exp (-\frac{1}{2}{\mathit{BIC}}_k)}.$$ (10)

The advantages of computing the posterior model probabilities as (10) include computational simplicity and a direct connection with the thoroughly investigated BIC. While the justification of the approximation (10) is asymptotic in general, this can also be looked upon as an approximation for a noninformative prior even for moderate and small sample sizes.

6 Bayesian Information Criteria in SAR/CAR models to detect difference boundaries: Illustrations

6.1 Simulation Experiments

We illustrate our model comparison approach first with some simulation studies and then apply it to a real data analysis in Section 6.2. The simulation was set up under two scenarios: with and without explanatory variables. The spatial adjacency matrix was based on the Minnesota county map and in another scenario, the 8 × 8 rectangular grid. There are 87 counties and 211 boundaries between counties on the Minnesota map, thus there are 211 different boundary hypotheses in our analysis. We generated data {Y_i} from a Poisson distribution whose true parameter values are known.

Without the explanatory variables, we divided the Minnesota map into six regions, and let μ_i ∈ {0, 0.5, 1, 1.5, 2, 2.5} with the true difference boundaries mapped on Figure 1. Note that two of the clusters are shaded white. The one in the interior comprises a single county (Sherburne) and has mean 0, while the other has a mean of 0.5. This configuration creates a county with all its boundaries being true difference boundaries. Letting Y_i be the simulated number of cases in county i, we generate {Y_i} ~ Poisson(5 exp(μ_i)) for i = 1, 2, … , 87. Let $E_i=\frac{{\sum }_{k=1}^N{Y}_i}{{\sum }_{k=1}^N{O}_i}{O}_i$ be the expected number of cases, where O_i is the population of county i, and N is the total number of counties. Assuming equal population in all counties, we take the log standardized morbidity ratio, y_i = log(100 × Y_i/E_i), as our outcome variable. Note that this is essentially a relative rate expressed as a percentage and transformed to a logarithmic scale to strengthen its Gaussian behavior.

Figure 1.

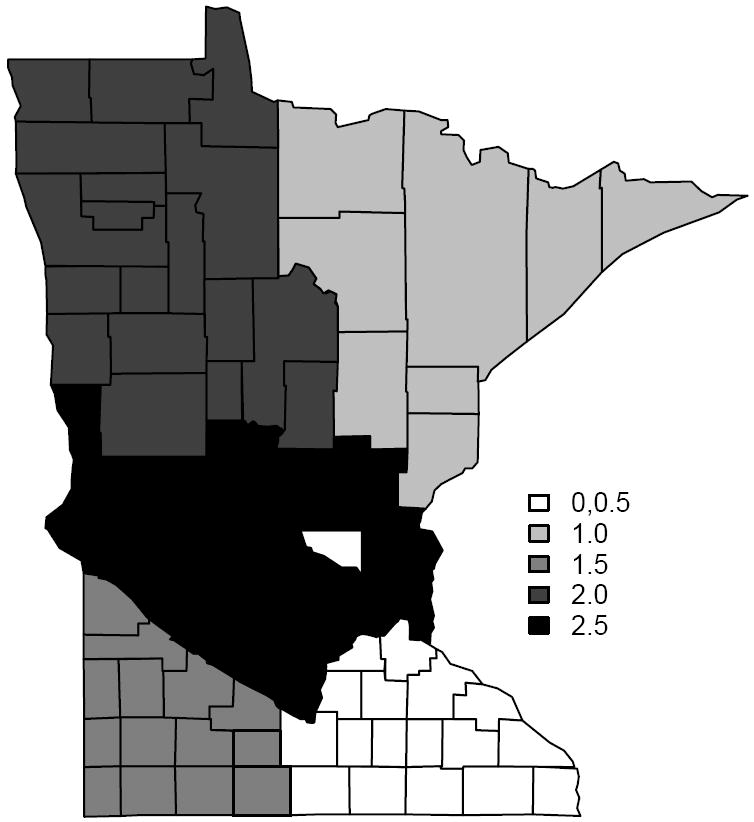
A map of the simulated data with the grey-scales showing the six different clusters, each having its own mean. Two of the clusters are shaded white with the one in the interior comprising a single county (Sherburne) and has mean 0, while the other has a mean of 0.5. There are 47 boundary segments that separate regions with different means (shades).

We next fit the model in (1) with y_i as the response, where the regression structure consists only of an intercept, i.e. ${\mathbf{x}}_i^{\prime }\mathit{\beta }={\beta }_0$, and {ϕ_i}’s follow a SAR and a CAR distribution (see Section 3). There are 211 different boundary hypothesis in our analysis, as there are 211 edges on the Minnesota County Map and each model arises from deleting (hence not smoothing across) exactly one geographical edge. We compute the BIC for all these models using (9), in which the log likelihood is computed by (2). Therefore, each model corresponds to one edge and the models with higher posterior probabilities provide evidence in favor of the corresponding edge being a difference boundary.

As we know the 47 true difference boundaries on the map, we are able to obtain the “true” detection rates (sensitivity) for the BIC approach by declaring the edges corresponding to the top 47 models as difference boundaries. We compare the results with the existing methods, e.g. Lu and Carlin (2005) (LC). The average detection rate of the 50 simulated datasets for the different methods are listed in Table 1. The sensitivity of the BIC based model comparison approach is competitive with the LC approach, especially when the SAR prior probability model is specified for the spatial effects. Indeed, Table 1 reveals that the detection rate for the BIC based approach using SAR spatial effects differs from the Lu and Carlin method by only 1.5%. With CAR spatial effects, this difference is slightly higher at 4.6%. Yet, the inferential procedure in LC employs MCMC algorithms that involve substantially greater computational demands. The BIC based model comparison approach that we proffer here provides much quicker inference via generalized least squares, while losing little sensitivity as compared to the LC method.

Table 1.

Average detection rate in the simulation study (50 datasets) by BIC-based model comparison approach with SAR and CAR spatial effects, the LC method as well as a simple ranking based upon absolute differences. The simulation study was based on MN county map and 8 × 8 rectangular grid respectively.

	MN county map	8 × 8 grid
BIC-SAR	77.2	73.3
BIC-CAR	74.1	64.6
LC	78.7	79.5
BLV’s	83.8	78.5

In another scenario, we conduct the simulation on an 8 × 8 rectangular grid. We partition the 64 rectangular units into 5 areal clusters, as depicted in Figure 2. We assign four grey-scale values to these five clusters, with the clusters in the lower left and the extreme right column having the highest true grey-scale value of 5.0. The region in the upper middle has the lowest true value of 2.0, the upper-left has a true value of 3.0, while the cluster in the lower middle has a true value of 4.0. Analogous to the previous scenario, we generate {Y_i} ~ Poisson(exp(μ_i)), and use y_i = log(100 × Y_i/E_i) as the response variable in the model. The average detection rate of the 50 simulated datasets for the different methods are listed in Table 1. The detection rate for the BIC based approach using SAR spatial effects differs from the Lu and Carlin method by 6.2%. With CAR spatial effects this difference is slightly higher at 14.9%.

Figure 2.

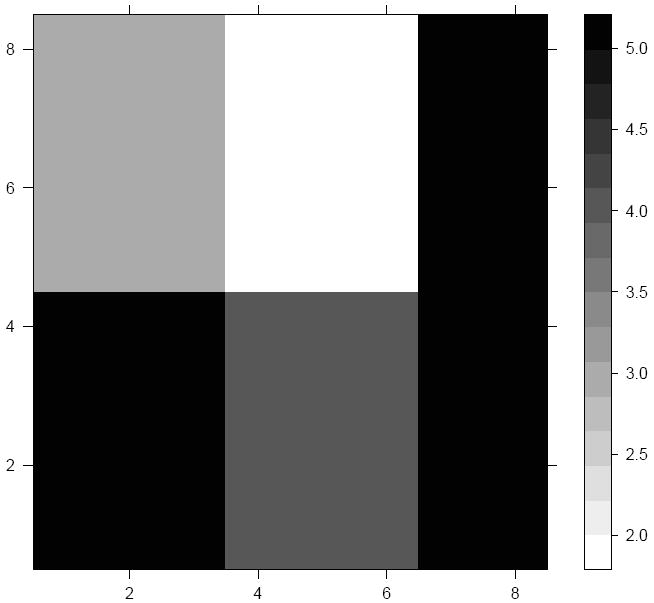
A 8 × 8 rectangular grid of the true values with the grey-scales showing the five different clusters. There are a total of 112 boundaries of which 22 are designated as true difference (“wombling”) boundaries.

We also computed the BLV’s associated with the edges (see Section 2). These are the absolute difference of the outcomes, i.e. Δ_ij = ∥y_i − y_j∥, computed for every pair of adjacent counties. We identified the 47 highest BLV’s as difference boundaries (see, e.g., Jacquez and Greiling, 2003a; 2003b). The last row of Table 1 presents the average detection rates from the 50 simulated datasets based upon the Δ_ij’s. These were 84.8% for the Minnesota county map and 78.5% for the 8 × 8 grid. While the Δ_ij’s seem to provide a simple and practical way of identifying boundaries for the outcome variable, this procedure is not model-based and will not apply to our next scenario.

In our final scenario, we assume that there is an explanatory variable associated with the outcome. In other words, we now set ${\mathbf{x}}_i^{\prime }=(1,x_i)$ in (1), where we generate each x_i from N(μ_i, σ) with μ_i taking values in 0, 0.2, 0.4, 0.6, 0.8, 1, depending upon where county i lies in the map in Figure 1, and σ = 0.5. We subsequently fix these generated x_i’s and draw the spatial random effects, i.e. the ϕ_i’s from a SAR model. Next, we simulate Y_i ~ Poisson(exp(θ₀ + θ₁x_i + ϕ_i)) with θ₀ = 0, θ₁ = 5. In fitting the model and carrying out subsequent boundary analysis, we again use y_i = log(100 × Y_i/E_i) as our outcome variable, where E_i is as defined in the preceding scenarios.

When the model accommodates an explanatory variable, as in our current scenario, the boundary effects of interest pertain not to the outcome, but the residuals after adjusting for the explanatory variable. Since the residuals are never observed, BLVs defined as Euclidean metrics between observations is no longer applicable for detecting the difference boundaries on the spatial residual map. Nevertheless, the BIC based approach and the LC method are both able to do so. True difference boundaries are unknown in this case. As such, we compute the rank of each of the 211 models based on BIC, and compare them with the difference between the spatial residuals produced by LC. Figure 3 plots the difference in spatial residuals from the LC approach against the rank of the model using BIC. A locally weighted scatter-plot smoother or “loess” (Cleveland and Devlin, 1988) is also fitted ot the plot. The figure reveals a very clear decreasing trend indicating that the model with a better fit (lower BIC) will tend to have larger differences in the spatial residuals from the LC method. This indicates consistency between the BIC-based methods and the LC method. Again, we note the computational efficiency of the BIC-based methods as compared to the LC method.

Figure 3.

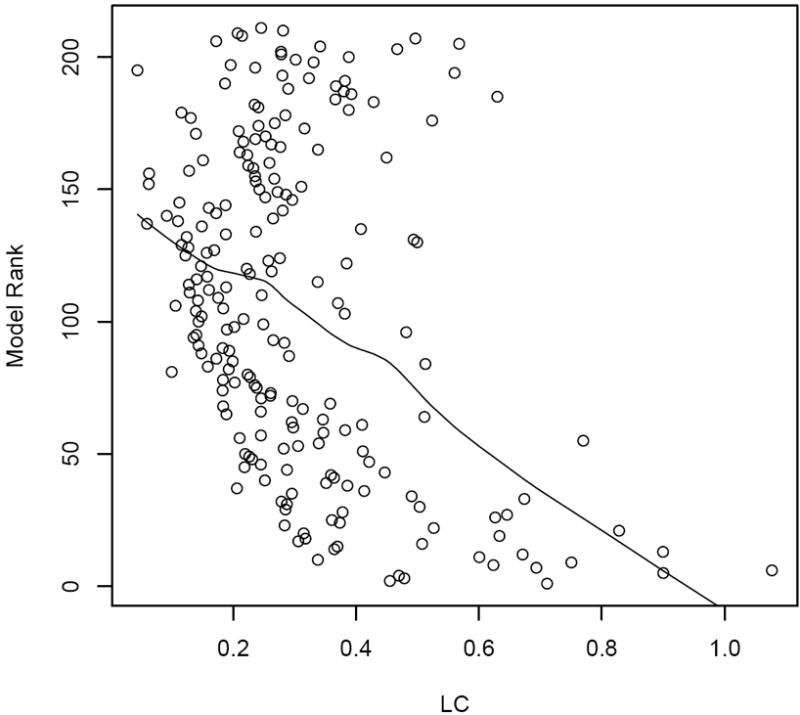
A simulation example with a single explanatory variable in the model. The x-axis is the expectation of the absolute difference between the spatial residuals of the adjacent counties by LC method. The y-axis marks the ranks produced by BIC for the 211 models using SAR spatial effects. A loess smoothed line is also shown on the plot.

6.2 Application to Minnesota P& I dataset

We apply our model comparison approach to a Pneumonia and Influenza diagnosis dataset from the state of Minnesota. Residents of Minnesota who were 65 years of age and older and who were enrolled in the Medicare fee-for-service program as of December 31, 2001, were included in our study. This population had been identified as part of a multi-year study regarding the impact of vaccination on elderly Minnesota residents. The Medicare Denominator file for 2001 was used to define the cohort. In addition to meeting the criteria for age and state of residence, to be eligible for inclusion in the study the person had to be enrolled in both Medicare Part A and Medicare Part B, not be enrolled in a Medicare Advantage health plan, and not have end-stage renal disease. The Denominator file also indicated the county of residence for each person. County-level average per capita income was obtained from the 2000 U.S. Census SF3 file.

Hospitalizations for pneumonia and influenza (P&I) were identified by the Medicare Provider Analysis and Review (MedPAR) short stay inpatient file for the above Minnesota residents. This annual file contains one record per hospitalization based on the date of discharge. Hospitalizations for P&I (Pneumonia and Influenza) were identified using ICD-9-CM codes 481-487. Rates of P&I hospitalization are traditional measures of the impact of influenza virus in the elderly population. Boundary analysis might help identify barriers separating counties that experience different impacts of the influenza virus. Here we studied the number of hospitalizations from P&I in both influenza and shoulder period among persons at risk in each county. We adjust for the average income per person in each county by incorporating it as an explanatory variable in our model. Therefore, the vector x in (1) has two columns, the other being an intercept. Let Y_i be the observed number of hospitalizations in county i, $E_i=\frac{{\sum }_{k=1}^N{Y}_i}{{\sum }_{k=1}^N{O}_i}{O}_i$ be the expected number of cases, where O_i is the population (age 65 and older) of county i, and N is the total number of counties. Similar to the simulation study, we take log transformation y_i = log(100 × Y_i/E_i) as our outcome variable under study.

The intercept from the SAR model was estimated to be 5.12 (mean) with a 95% credible interval (4.62, 5.63), while for the CAR model these were 5.13 and (4.63, 5.63) respectively. The regression coefficient for average income per person was estimated to be −0.017 with a 95% credible interval (−0.037, 0.003) from the SAR model, while they were −0.017 and (−0.037, 0.002) from the CAR model. The estimate of τ² from the SAR and CAR models were 0.097 and 0.095 respectively, while ρ was estimated to be 0.072 and 0.127 respectively. The parameter ρ has different interpretations for the SAR and CAR models and can be looked upon as a measure of spatial smoothing. It is, however, dangerous to interpret this as a spatial correlation in the strict statistical sense (Wall, 2004).

Tables 2 and 3 list the adjacent counties having the 50 largest boundary effects, ranked by their BIC scores from the SAR and CAR models respectively. Forty-six of the top fifty pairs are present in both tables (although they may not necessarily agree in rank), while four (in bold) boundaries are unique. The top seven county pairs also agree in their rankings. The fifty difference boundaries detected by the model comparison approach using SAR spatial effects are highlighted in Figure 4. Figure 5 reveals a similarly consistent performance between the SAR and CAR effects in detecting difference boundaries on this map. Models ranked higher (or that fit better) usually detect boundaries with a big difference in the raw data, which corroborates our approach. But some of the points with large differences in the raw data are ranked low in the plot. This could be attributed to the smoothing and borrowing of strength from neighboring regions that could diminish the strength of the neighboring regions and dilute the difference in some cases. Figure 6 is the choropleth map of the spatial residuals under the model which has a neighborhood structure with fifty detected boundaries (i.e. non-smoothing boundaries).

Table 2.

Names of adjacent counties that have significant boundary effects from the SAR model. The numbers in the first column are the ranks according to their BIC scores.

1	Cook, Lake
2	Itasca, Koochiching
3	Beltrami, Koochiching
4	Steele, Waseca
5	Pope, Stearns
6	Cass, Wadena
7	Todd, Wadena
8	Murray, Redwood
9	Traverse, Wilkin
10	Koochiching, Lake of the Woods
11	Freeborn, Steele
12	Isanti, Sherburne
13	Clearwater, Mahnomen
14	Renville, Yellow Medicine
15	Chippewa, Renville
16	Cottonwood, Murray
17	Isanti, Mille Lacs
18	Koochiching, St. Louis
19	Grant, Wilkin
20	Lyon, Redwood
21	Becker, Mahnomen
22	Cottonwood, Jackson
23	Lincoln, Pipestone
24	Goodhue, Olmsted
25	Cass, Morrison
26	Murray, Pipestone
27	Morrison, Todd
28	Redwood, Yellow Medicine
29	Jackson, Martin
30	Goodhue, Wabasha
31	Otter Tail, Todd
32	Douglas, Pope
33	Becker, Wadena
34	Brown, Renville
35	Kandiyohi, Pope
36	Benton, Morrison
37	Fillmore, Houston
38	Anoka, Isanti
39	Blue Earth, Brown
40	Hubbard, Wadena
41	Carver, McLeod
42	Clay, Otter Tail
43	Blue Earth, Watonwan
44	Mille Lacs, Morrison
45	Murray, Nobles
46	Dodge, Olmsted
47	Morrison, Stearns
48	Douglas, Grant
49	Dakota, Goodhue
50	Fillmore, Olmsted

Table 3.

Names of adjacent counties that have significant boundary effects from the CAR model. The numbers in the first column are the ranks according to their BIC scores.

1	Cook, Lake
2	Itasca, Koochiching
3	Beltrami, Koochiching
4	Pope, Stearns
5	Steele, Waseca
6	Cass, Wadena
7	Todd, Wadena
8	Renville, Yellow Medicine
9	Koochiching, St. Louis
10	Clearwater, Mahnomen
11	Isanti, Sherburne
12	Chippewa, Renville
13	Koochiching, Lake of the Woods
14	Freeborn, Steele
15	Murray, Redwood
16	Isanti, Mille Lacs
17	Traverse, Wilkin
18	Cottonwood, Murray
19	Grant, Wilkin
20	Becker, Mahnomen
21	Lyon, Redwood
22	Goodhue, Olmsted
23	Cottonwood, Jackson
24	Redwood, Yellow Medicine
25	Jackson, Martin
26	Goodhue, Wabasha
27	Otter Tail, Todd
28	Lincoln, Pipestone
29	Hubbard, Wadena
30	Carver, McLeod
31	Becker, Wadena
32	Douglas, Pope
33	Anoka, Isanti
34	Cass, Morrison
35	Kandiyohi, Pope
36	Murray, Pipestone
37	Morrison, Todd
38	Brown, Renville
39	Clay, Otter Tail
40	Blue Earth, Watonwan
41	Dodge, Olmsted
42	Blue Earth, Watonwan
43	Mahnomen, Norman
44	Le Sueur, Scott
45	Benton, Morrison
46	Aitkin, Kanabec
47	Dakota, Goodhue
48	Fillmore, Houston
49	Mille Lacs, Morrison
50	Dakota, Hennepin

Figure 4.

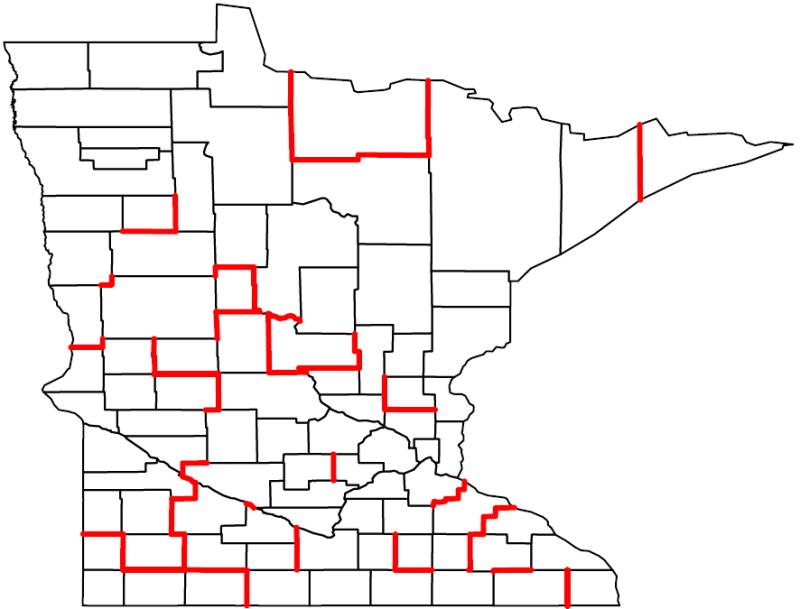
Difference Boundaries detected by the BIC based model comparison approach with SAR spatial effects. Top 50 boundaries corresponding to models with lowest BIC are highlighted. The map for the CAR spatial effects is very similar and not shown.

Figure 5.

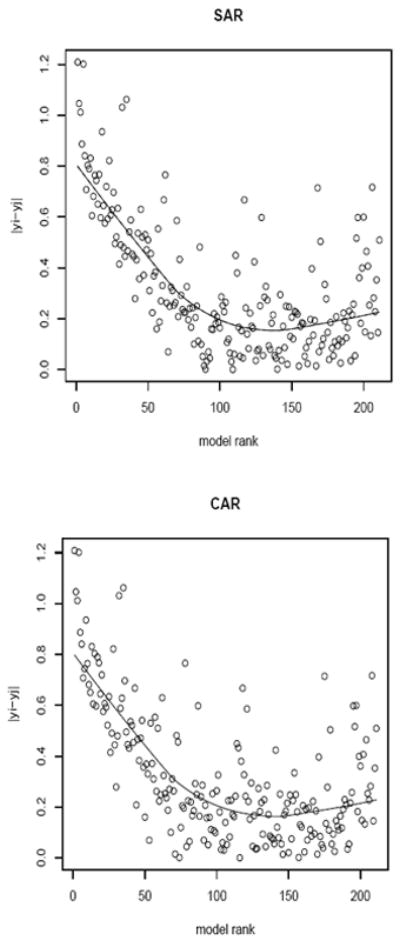
Plot of model rank (SAR: top panel; CAR: bottom panel) against the absolute difference of the observed log standardized morbidity ratio. The horizontal axis is the rank of the models in terms of increasing BIC. The vertical axis is the absolute difference of the observed log standardized morbidity ratio. A loess smoothed line is also shown on the plots.

Figure 6.

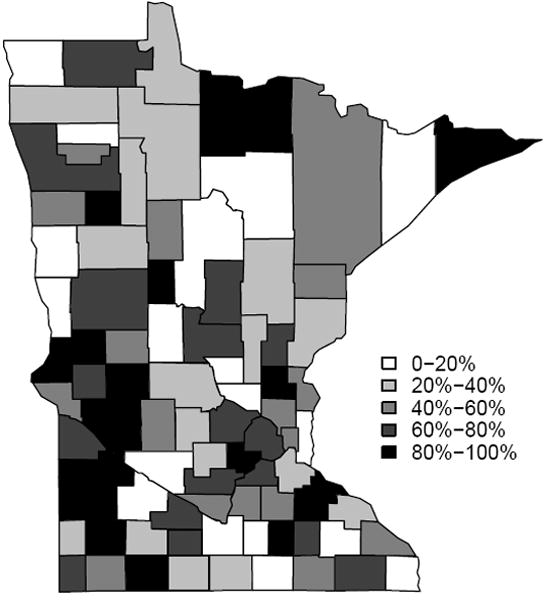
Choropleth map of residuals from the SAR model. The map from the CAR model is very similar. Darker colors represents higher value of the spatial residuals after adjusting for the covariate, which also implies the county is more affected by P&I.

7 Discussion and Future Directions

Clearly we have only skimmed the surface of the edge detection problem. In fact, here we have investigated the Bayesian Information Criteria and its utility in marginal probability approximations. Still, our approach of formulating the edge detection problem as a model comparison problem is relatively novel. We view our current work as a relatively simple data-mining tool that can suggest influential boundary effects in health maps. The use of the BIC is straightforward in our leave-one-out framework and can prove a useful tool for spatial analysts.

Our future methodolological investigations will focus upon three directions: (i) more sophisticated model search algorithms such as MC³ (Markov Chain Monte Carlo Model Composition) and Bayesian Model Averaging algorithms that exhaust the space of all models (see Hoeting et al., 1999); (ii) using Bayesian False Discovery Rates together with a formal Bayesian hypothesis testing framework to make decisions regarding wombling boundaries, and (iii) to develop alternative nonparametric Bayesian models for areal data that would facilitate boundary detection.

The third direction merits some further discussion. Instead of incorporating random “edge effects” (as done in Lu et al. 2007; Ma et al. 2008), one can explore an alternative stochastic mechanism that would let us detect wombling boundaries by considering probabilities such as P(ϕ_i = ϕ_j∣i ~ j). Clearly using direct CAR specifications will simply not work as it yields continuous measures for the ϕ_is, rendering P(ϕ_i = ϕ_j∣i ~ j) = 0. The challenge here is to model the spatial effects in an almost surely discrete fashion while at the same time accounting for the spatial dependence. A nonparametric Bayesian framework that models the spatial effects as almost sure discrete realizations of some distribution comes to mind – the Dirichlet process (Ferguson, 1973) has been employed extensively for modelling clustered data and presents itself as a natural choice, but how do we accommodate the spatial dependence? These and other issues will form a part of our future research plans.