Electronic Noise Modeling in Statistical Iterative Reconstruction

Abstract

We consider electronic noise modeling in tomographic image reconstruction when the measured signal is the sum of a Gaussian distributed electronic noise component and another random variable whose log-likelihood function satisfies a certain linearity condition. Examples of such likelihood functions include the Poisson distribution and an exponential dispersion (ED) model that can approximate the signal statistics in integration mode X-ray detectors. We formulate the image reconstruction problem as a maximum-likelihood estimation problem. Using an expectation-maximization approach, we demonstrate that a reconstruction algorithm can be obtained following a simple substitution rule from the one previously derived without electronic noise considerations. To illustrate the applicability of the substitution rule, we present examples of a fully iterative reconstruction algorithm and a sinogram smoothing algorithm both in transmission CT reconstruction when the measured signal contains additive electronic noise. Our simulation studies show the potential usefulness of accurate electronic noise modeling in low-dose CT applications.

I. Introduction

Accurate electronic noise modeling is important for low-dose X-ray CT applications where the number of detected photons are limited. For clinical X-ray CT systems utilizing energy-integrating detectors, it has been shown that the detected X-ray intensity follows a compound Poisson distribution, see, e.g., [1]–[3]. Because of its complicated expression, it is not yet clear how an iterative reconstruction algorithm can be derived based on the exact form of the likelihood function. Researchers have proposed various approximations, either in the sinogram domain (after the log-transform) using a mean-variance dependent Gaussian density [4], [5], or in the transmitted intensity using a (scaled) Poisson approximation [6], [7]. In the transmitted intensity domain when the Poisson approximation is used, the electronic noise compensation problem can be dealt with by a shifted Poisson approximation [6]. This approximation was proposed in [8] and [9] to compensate for readout noise in CCD cameras and was also used in PET reconstruction [10] to model randoms precorrected transmission data.

We have previously introduced a subclass of the exponential dispersion (ED) model to approximate the exact compound Poisson distribution of the signal statistics in integration mode X-ray detectors [11]. In this work, we further extend our model to include electronic noise when the X-ray detected signal is not necessarily Poisson distributed. Specific examples include the Poisson and the ED model. We formulate the image reconstruction problem as a maximum-likelihood (ML) estimation problem. However, the likelihood function of the sum of the ED model and a Gaussian distributed electronic noise is not analytically tractable. To circumvent this difficulty, we propose an expectation-maximization (EM) framework and combine it with the surrogate function approach and the optimization transfer principle [12]–[16] for electronic noise compensation. The result of this combination, a simple “substitution rule,” constitutes the central idea of this paper.

The organization of this paper is as follows. In Section II, we briefly summarize the properties of the compound Poisson distribution of the X-ray signal statistics as described in [1]–[3]. In Section III, we present the central idea of this paper, i.e., a simple “substitution rule,” which states that under certain linearity conditions, if μ = (y) is a reconstruction algorithm where y is the measured X-ray intensity signal without electronic noise contamination, then μ = 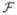(E(Y | Z = z)) is a reconstruction algorithm where the measured signal Z = Y + N is contaminated by electronic noise N. As we demonstrate in Section V, the word “reconstruction” should be understood in the general sense of parameter estimation. More specifically, in μ = 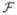(E(Y | Z = z)), μ is merely the unknown parameter in a maximum-likelihood estimation problem. We describe one method for calculating the conditional expectation E(Y | Z). This method can be regarded as a genalization of the shifted Poisson approximation in [8] and [9]. The substitution rule can be applied to a fully iterative reconstruction algorithm for X-ray CT or a statistical sinogram restoration algorithm. In Section V, we provide two examples of how to apply the substitution rule in these two settings. We present simulation studies in Section VI to demonstrate the effectiveness of accurate electronic noise modeling for transmission CT reconstruction. Section VII concludes this paper and outlines some possible future work. Throughout this paper, we use upper case letters, e.g., Y and Z to denote a random variable, and their lower case counterparts, e.g., y and z to denote a sample realization.

II. Background

In clinical X-ray CT systems, a simplified model of the detected signal can be described by the energy weighted photon counts [1]–[3], [6]. If we denote by Y_i the X-ray intensity measured at the ith detector bin, then Y_i can be modeled as the following:

$$\begin{array}{l}{Y}_i=\sum _k{E}_k{\lambda }_i(E_k)\\ =\sum _k{E}_k\text{Poisson}[{\overline{\lambda }}_i(E_k)]\end{array}$$ (1)

where

$${\overline{\lambda }}_i(E_k)=N_i(E_k)e^{-{\sum }_j{s}_{ij}{\mu }_j(E_k)}$$

and k is the energy-bin index, N_i(·) is the incident photon number spectrum (in units of # of photons per detector element), μ_j (E_k) is the energy-dependent linear attenuation coefficient at the pixel j, and s_ij is the intersection pathlength between the boundaries of jth pixel and the ray connecting the ith detector to the X-ray focal spot. The notation Poisson [·] represents a Poisson distributed random variable (r.v.) with its argument as the mean. If we consider the contribution to Y_i from each individual detected photon, denote which by X_i,1, X_i,2, etc., then each photon generates a signal E_k from a probability distribution that is proportional to the detected spectrum. Equivalently, the detected signal can be written as

$$Y_i=X_{i,1}+X_{i,2}+\cdots +X_{i,\mathrm{\Lambda }}$$ (2)

where Λ = Σ_k λ_i (E_k) is the (random) total number of detected photons regardless of their energies, and

$$X_{i,·}=E_k,\text{with}\text{the}\text{probability}\text{of}\frac{\overline{\lambda }(E_k)}{{\sum }_k\overline{\lambda }(E_k)}.$$ (3)

As is written in (2), the random variable Y_i follows a compound Poisson model [17, p.177], which by definition is the summation of a Poisson distributed, random number of independent and identically distributed (i.i.d.) r.v.’s X_i,·. For the particular compound Poisson distribution in energy-integrating X-ray detection (1), the Poisson variable Λ has a mean of Σ_k λ̄_i (E_k) [cf. (1)], and each component follows the probability distribution in (3). More rigorous derivations and discussions about the density function of Y_i can be found in [1]–[3]. Since the exact form of the likelihood function of Y is not amenable for algorithm derivation, researchers have often approximated the compound Poisson distribution by either the Poisson distribution [6] or the Gaussian distribution. We have previously proposed an exponential dispersion (ED) model to approximate the exact X-ray signal statistics, and derived a maximum-likelihood reconstruction algorithm based on the ED model [11]. The ED model is a class of probability density functions that includes a special compound Poisson distribution with i.i.d. Gamma distributed components. This work further extends our previous work by incorporating electronic noise modeling into the iterative reconstruction process.

III. Expectation-Maximization Formulation for Electronic Noise Modeling

Electronic noise can be adequately modeled as a Gaussian distributed random variable with a certain mean m and a variance σ². The offset mean m can be estimated accurately prior to each scan and subtracted from the measured intensity [18]. Without loss of generality, we assume the raw detected intensity Z is the summation of a random variable Y and a zero-mean Gaussian distributed r.v. N modeling electronic noise. We do not specify the distribution of Y yet, but our result requires a certain linearity condition on the log-likelihood function of Y which will become clear shortly.

We formulate the maximum-likelihood reconstruction problem in the expectation-maximization (EM) framework. The raw detected intensity Z is written as

$$Z=Y+N$$ (4)

where Y is the detected X-ray intensity whose distribution depends on the unknown parameter μ, N ~ 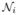(0, σ²) describes the Gaussian distributed electronic noise, and the random variables Y and N are independent. Here, we omit the detector index i for notational clarity, since it is not needed to distinguish between different detector elements at this point. Let S = (Y, N) be the complete data in the EM formulation, and Z be the incomplete data. The incomplete log-likelihood can be written as [12]

$$logP\{z;{\mu }^{\prime }\}=E_{S\mid Z;\mu }logP\{s;{\mu }^{\prime }\}-E_{S\mid Z;\mu }logP\{s\mid Z;{\mu }^{\prime }\}.$$ (5)

Note that log P{z;μ′} is the objective function in a maximum likelihood reconstruction algorithm. Here, μ′ denotes the parameter to be estimated, and μ denotes the parameter estimate at the current iteration. The notation E_{S | Y;μ} f (s; μ′) denotes the conditional expectation of f (s; μ′) given, represented symbolically as

$$E_{S\mid Y;\mu }f(s;{\mu }^{\prime })=\int f(s;{\mu }^{\prime })\text{d}(\text{probability}\text{measure}\text{of}S\mid Y_{\mu })$$

where the distribution of Y is parameterized by μ. The first term on the right hand side (RHS) of (5), in the langrange of optimization transfer [16], is a surrogate function for the incomplete log-likelihood log P {z; μ′}. Since Y and N are independent, the first term on the right-hand-side (RHS) of (5) splits into two terms, i.e.,

$$E_{S\mid Z;\mu }logP\{s;{\mu }^{\prime }\}=E_{Y\mid Z;\mu }logP\{y;{\mu }^{\prime }\}+E_{N\mid Z;\mu }logP\{n\}.$$ (6)

Note that in the second term of (6), we dropped the dependency of the electronic noise on the unknown parameter μ. The log-likelihood part of the first term in (6) log P {y; μ′} would be the objective function in an iterative reconstruction algorithm if electronic noise were not present, whose maximization is often accomplished, at least in transmission CT reconstruction, through maximizing a surrogate function Q (y, μ′; μ) at each iteration. Our first result is that maximizing the conditional expectation of this surrogate ensures a nondecreasing change in the incomplete log-likelihood log P {z; μ′}.

Theorem 1: Let Q (y, μ′; μ) be a surrogate function for log P {y; μ′} that satisfies the following conditions [15]¹:

$$logP\{y;{\mu }^{\prime }\}\ge Q(y,{\mu }^{\prime };\mu ),\text{and}logP\{y;\mu \}=Q(y,\mu ;\mu ).$$ (7)

Then if we choose μ′ such that

$$E_{Y\mid Z;\mu }Q(y,{\mu }^{\prime };\mu )\ge E_{Y\mid Z;\mu }Q(y,\mu ;\mu )$$ (8)

then

$$logP\{z;{\mu }^{\prime }\}\ge logP\{z;\mu \}.$$ (9)

Proof: We replace the log-likelihood log P {y; μ′} in (6) by its surrogate Q (y, μ′; μ) and combine with (5) to define the following:

$$\overline{Q}(z,{\mu }^{\prime };\mu )\triangleq E_{Y\mid Z;\mu }Q(y,{\mu }^{\prime };\mu )+E_{N\mid Z;\mu }logP\{n\}-E_{S\mid Z;\mu }logP\{s\mid Z;{\mu }^{\prime }\}.$$ (10)

Using (7), we see that

$$logP\{z;{\mu }^{\prime }\}\ge \overline{Q}(z,{\mu }^{\prime };\mu )$$ (11)

$$logP\{z;\mu \}=\overline{Q}(z,\mu ;\mu ).$$ (12)

Q̄ (z, μ′; μ) is a legitimate surrogate function for the incomplete log-likelihood that we want to maximize. Since the function E_{S | Z;μ} log P {s | Z;μ′} reaches a maximum at μ′ = μ, choosing μ′ to satisfy (8) will imply

$$\overline{Q}(z,{\mu }^{\prime };\mu )\ge \overline{Q}(z,\mu ;\mu )$$

which, in turn, forces an increase in log P {z; μ′}, i.e., (9).

Effectively, the EM formulation (5) provides a first surrogate (the first term on the RHS, subject to a constant difference), then the function Q̄ (z, μ′; μ) defined in (10) can be also understood as a second surrogate of this EM surrogate for maximizing the incomplete log-likelihood log P {z; μ′}. The idea of Theorem 1 is simple. If electronic noise were not considered, we would like to maximize log P {y; μ′}. Due to its complicated relationship with the unknown parameter μ′, we instead maximize a surrogate function Q (y, μ′; μ) iteratively. Theorem 1 says that if we consider electronic noise, we can keep the derived surrogate function Q (y, μ′; μ) and calculate its conditional expectation given the raw measurement Z. The resulting E_{Y | Z; μ} Q (y, μ′; μ) is a surrogate function for the incomplete log-likelihood log P {z; μ′}. We then maximize E_{Y | Z; μ} Q (y, μ′; μ) iteratively with respect to μ′. Theorem 1 holds regardless of the specific distribution function of Y as long as Y is independent of N, and the distribution of N does not depend on the unknowns μ.

One advantage of this EM formulation becomes obvious by examining the expression of Q (y, μ′; μ). As our example later shows, despite its complicated dependence on μ′ Q (y, μ′; μ) can be a simple (e.g., affine) function of y. Since the conditional expectation in E_{Y | Z; μ} Q (y, μ′; μ) = Q (E (Y | Z; μ), μ′;μ) is calculated at the old parameter μ Q (E (Y | Z; μ), μ′;μ) maintains exactly the same relationship with respect to μ′ as Q (y, μ′; μ). Hence, the first derivative, second derivative of E_{Y | Z; μ} Q (y, μ′; μ) with respect to μ′ can be written out from Q′ (*, μ′; μ) and Q″ (*, μ′; μ) directly, with * replaced by E(Y | Z; μ). These derivatives are needed in deriving an update equation for μ′ using, e.g., the Newton’s method. Suppose μⁿ⁺¹ = 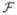(y, μⁿ) is a “reconstruction” algorithm given the measured intensity y without electronic noise contamination, then our result implies that to account for electronic noise, we can use the update equation μⁿ⁺¹ = 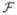(E(Y | Z = z), μⁿ); this we will refer to as the ‘substitution rule’ for electronic noise modeling in a maximum-likelihood iterative reconstruction algorithm.

Unlike Theorem 1, the substitution rule works only when Q (y, μ′;μ) is affine in the measurement Y = y. Examples of such surrogate functions are abundant in the literature. For instance, the convex surrogate Q (μ | μⁿ) for the monochromatic transmission model [14, (5)]; the Q₁ (x, x^k) function in emission tomography [12, (26)] (but not Q₂ (x, x^k) [12, (27)]) which is quadratic in the measurements); the quadratic surrogate function Q (μ; μⁿ) [15, (12)], using either the maximum curvature or the optimum curvature. In all these examples, follows the Poisson distribution. One example of a non-Poisson distributed can be found in [16].

IV. Calculating the Conditional Expectation

To model and compensate for electronic noise, when the surrogate function Q (y, μ′; μ) is affine in y, we only need to replace all occurrences y by E(Y | Z = z) in a previously derived algorithm totally ignoring electronic noise. The calculation of E(Y | Z) would depend on the distribution of Y. We have previously introduced an exponential dispersion (ED) model [19], [20] as an accurate approximation of the exact compound Poisson density function of in energy-integrating X-ray detectors. This ED model greatly facilitates the derivation of a maximum-likelihood iterative reconstruction algorithm for X-ray CT [11]. It is a special class of compound Poisson distributions with Gamma distributed components and its log-density function satisfies the following relationship [20]:

$$\frac{\partial logf}{\partial \overline{Y}}=\frac{y-\overline{Y}}{\phi {\overline{Y}}^p}$$ (13)

where Ȳ is the mean of the random variable Y, and φȲ^p is its variance, 1 < p < 2 and φ > 0 are the so-called power and dispersion parameters, respectively. For φ = 1 and p = 0, 1, 2, 3, (13) can be shown to reduce to the familiar Gaussian, Poisson, Gamma, and inverse Gaussian distribution [19], [20].

Next, we describe how to calculate the conditional expectation E(Y | Z) using (13) as the model of Y. Snyder et al.’s work [8], [9] on electronic readout noise compensation for CCD cameras considered calculating E(Y | Z) where Z is the summation of a Poisson distributed Y and a Gaussian noise N. They proposed two methods, one based on a shifted Poisson approximation, the other by saddlepoint approximation. The following discussion can be regarded as a generalization of the shifted Poisson approximation method; applying the saddlepoint approximation to the ED model can be found in [21].

It is well known that E(Y | Z) satisfies the following minimal error property:

$$E{[Y-E(Y\mid Z)]}^2\le E{[Y-u(Z)]}^2\text{for}\text{all}u(Z).$$

In other words, among all functions of Z, E(Y | Z) has the minimal estimation error. When Y has a distribution described by (13), E(Y | Z) is conceivably a very complicated function of Z. We can approximate E(Y | Z) by an affine function a₀ + a₁Z, and seek the coefficients a₀ and a₁ such that

$$E\{[Y-(a_0+a_{1}Z)]Z^i\}=0,\text{for}i=0,1.$$ (14)

The relationship in (14) is obtained from the normal equations for least square estimations. Solving (14) for a₀ and a₁, we obtain the best affine estimator for E(Y | Z) as the following:

$$\begin{array}{l}E(Y\mid Z)\approx \frac{\overline{Y}{\sigma }^2+Z\ast \text{Var}Y}{\text{Var}Y+{\sigma }^2}\\ =\frac{\overline{Y}{\sigma }^2+\phi {\overline{Y}}^{p}Z}{\phi {\overline{Y}}^p+{\sigma }^2}\triangleq E_{\text{aff}}(Y\mid Z).\end{array}$$ (15)

The best affine estimator E_aff(Y | Z) is a convex combination of Ȳ and Z with the relative variances σ² and φȲ^p as coefficients. Note that E_aff(Y | Z = Ȳ) = Ȳ. From (15), we see that if Y had followed a Poisson distribution, which is a special case of the ED model by setting p = φ = 1, the best affine estimator would be Ȳ (σ² + Z)/(Ȳ + σ²). This coincides with the shifted Poisson method [8], [9]. In the shifted Poisson approximation, we first augment the measurement Z by σ², and treat Z + σ² = Y + (N + σ²)as the summation of two independent Poisson distributions, one with mean Ȳ, the other with mean σ². The conditional expectation of Y given Z (or equivalently Z + σ²) is then just Ȳ (Z + σ²)/(Ȳ + σ²). Applying the substitution rule, we obtain. μⁿ⁺¹ = Q (E(Y | Z), μⁿ. If we take the expectation on both sides, Eμⁿ⁺¹ = E Q (E(Y | Z), μⁿ) = Q (E(E(Y | Z)), μⁿ) = Q (Ȳ, μⁿ), which means that the ensemble mean of noisy-reconstruction is equal to the noise-free reconstruction.

V. Application of the Substitution Rule in X-Ray CT Reconstruction

We present two examples of applying the substitution rule in X-ray CT reconstruction. The first example is based on the well-known convex algorithm [14] and demonstrates how a fully iterative reconstruction algorithm can be modified to account for additional electronic noise in the measurements. This example may have applications in X-ray CT systems using CCD cameras. The second example applies the substitution rule in a sinogram restoration problem. It is also more pertaining to clinical X-ray CT imaging as we use the ED model to approximate the compound Poisson distribution of energy-integrating X-ray detectors.

A. Convex Algorithm

The convex algorithm was proposed in [14] and has been studied and used in a wide variety of applications. Its derivation is based on the Poisson log-likelihood of the measured intensity Y and a surrogate function Q (μ | μⁿ) [14 (5)] that is affine in Y_i. To apply the subsitution rule, we write

$${\mu }_j^{n+1}={\mu }_j^n+\frac{{\mu }_j^n{\sum }_i{l}_{ij}[d_i{e}^{-\langle l_i,{\mu }^n\rangle }-E(Y_i\mid Z_i,{\mu }^n)]}{{\sum }_i{l}_{ij}\langle l_i,{\mu }^n\rangle d_i{e}^{-\langle l_i,{\mu }^n\rangle }}$$ (16)

$$\approx {\mu }_j^n+\frac{{\mu }_j^n{\sum }_i{l}_{ij}\left[d_i{e}^{-\langle l_i,{\mu }^n\rangle }-\frac{{\overline{Y}}_i^n}{{\overline{Y}}_i^n+{\sigma }_i^2}(z_i+{\sigma }_i^2)\right]}{{\sum }_i{l}_{ij}\langle l_i,{\mu }^n\rangle d_i{e}^{-\langle l_i,{\mu }^n\rangle }}$$ (17)

where ${\overline{Y}}_i^n=d_{i}exp\{-\langle l_i,{\mu }^n\rangle \}$. Equation (16) is obtained by substituting Y_i in [14, (7)] by its conditional expectation given the raw measurements E(Y_i | Z_i, μⁿ). From (16) to (17), we used the best affine approximation (or the shifted Poisson aproximation since Y is assumed Poisson) of E(Y_i | Z_i, μⁿ). Equation (17) gives the explicit update equation of the convex algorithm extended to account for electronic noise.

B. Sinogram Restoration for X-Ray CT

To further illustrate the applicability of the substitution rule, we derive a penalized-likelihood sinogram restoration algorithm based on the ED model in (13). The idea of sinogram restoration is to try to recover a set of ideal line integrals, free of off-focal radiation [6], beam hardening effects, etc., from the measured X-ray transmission data that are contaminated by these physical-degrading factors. The image reconstruction is performed by analytical methods such as the filtered backprojection (FBP) from the restored ‘ideal’ data.

We start by assuming electronic noise does not exist, i.e., the measurements y_i are the detected X-ray intensity signals following the ED model. Assume the different detector elements are independent, the penalized log-likelihood function can be written as the following:

$$\mathrm{\Psi }(\underset{\_}{l},\underset{\_}{y})\triangleq L(\underset{\_}{l},\underset{\_}{y})-\beta \sum _i{R}_i(\underset{\_}{l})$$ (18a)

$$=\sum _i\frac{1}{{\phi }_i}\left(y_i\frac{{\overline{Y}}_i^{1-p_i}}{1-p_i}-\frac{{\overline{Y}}_i^{2-p_i}}{2-p_i}\right)+\sum _{i}c(y_i,{\phi }_i,p_i)-\beta \sum _i{R}_i(\underset{\_}{l}).$$ (18b)

The log-likelihood function of the ED model L (l, y) is obtained by integrating both sides of (13), c(y_i, φi, p_i)is the integration constant independent of Ȳ_i. Here, Ȳ_i denotes the mean of the detected X-ray intensity signal at the detector bin i. In this example, we use the following simplified model for Ȳ_i:

$$\begin{array}{l}{\overline{Y}}_i=\int EN(E)e^{-{\sum }_j{s}_{ij}{m}_w(E){\rho }_j/m_w(E_0)}\text{d}E\\ \triangleq \int \stackrel{\sim }{N}(E)e^{-m_w(E)l_i/m_w(E_0)}\text{d}E\end{array}$$ (19)

where l_i ≜ Σ_js_ijρ_j. Comparing with (1), we use the model m_w(E)ρ_j/m_w(E₀) to approximate the energy-dependent attenuation coefficients of the object. Here, m_w (E) is the mass attenuation coefficient of water at the energy E, and E₀ is a predetermined reference energy; ρ_j is the water-equivalent attenuation at pixel j. This formulation approximates all materials in the scanned object as water with different densities. We use the notation Ñ (E) ≜ E N (E) to account for the incident X-ray spectrum, the detector gain and efficiency etc. The unknowns of the sinogram smoothing problem are the line integrals l_i of the water-equivalent attenuation at the reference energy E₀. In (18), the penalization weighting β ≥ 0 controls the strength of smoothing, R_i(·) penalizes abrupt changes in l_i, we use the following quadratic form in [6]:

$$R_i(\underset{\_}{l})=\sum _{j\in {\mathcal{N}}_i}\frac{{(l_i-l_j)}^2}{2}$$

where 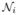_i consists of the neighborhood pixels of the pixel i. For a nonboundary pixel i, we penalize the horizontal (channel direction) and vertical (view direction) differences in the sinogram similar to [6], i.e., a neighborhood of 4 pixels with equal weights.

The objective function in (18b) is not a concave function of the unknowns. We apply the optimization transfer principle [12], [13], [15], [16] and derive in Appendix A the following separable quadratic surrogate for the log-likelihood part L (l, y) in (18a) (ignoring the penalty terms for now)

$$Q(\underset{\_}{l};{\underset{\_}{l}}^n)\triangleq \sum _i\frac{1}{{\phi }_i}\left[y_i\frac{{\overline{Y}}_{l_i^n}^{1-p_i}}{1-p_i}-\frac{{\overline{Y}}_{l_i^n}^{2-p_i}}{2-p_i}+(l_i-l_i^n)\left({\overline{Y}}_{l_i^n}^{1-p_i}-\frac{y_i}{{\overline{Y}}_{l_i^n}^{p_i}}\right)B(l_i^n)-\frac{{(l_i-l_i^n)}^2}{2}C(l_i^n)\right]$$ (20)

where

$$\begin{array}{l}{\overline{Y}}_{l_i}=\int \stackrel{\sim }{N}(E)e^{-m_w(E)l_i/m_w(E_0)}dE\\ B(l_i)=\int \stackrel{\sim }{N}(E)m_w(E)e^{-m_w(E)l_i/m_w(E_0)}/m_w(E_0)dE.\end{array}$$

The expression of C (l) is provided in Appendix A (32). A separable quadratic surrogate function for the penalization term in (18b) can be derived as in [13]. Combining the two parts, the update equation for lⁿ can be written as (21), shown at the bottom of the page. The constant β controls the strength of the overall smoothing, and l_j, j ∈ N_i, is the jth pixel in the neighborhood 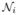_i of l_i, N is the total number of neighbors of pixel i; for a non-boundary pixel i, we have N = 4.

$$l_i^{n+1}=\frac{\left({\overline{Y}}_{l_i^n}^{1-p_i}-\frac{y_i}{{\overline{Y}}_{l_i^n}^{p_i}}\right)B(l_i^n)/{\phi }_i+l_i^{n}C(l_i^n)/{\phi }_i+{\beta }_i{\sum }_{j\in N_i}{l}_j^n}{C(l_i^n)/{\phi }_i+{\beta }_i\text{N}}$$ (21)

We have up to this point completely ignored the electronic noise contribution to the raw measurements. Equation (21) is a penalized sinogram restoration algorithm assuming the ED model for the detected intensity Y_i (no electronic noise contamination). For our purpose, it suffices to point out that the curvature function C(·) as derived in (32) is an affine function of the measurement y_i. Then despite its complicated expression, the quadratic surrogate function in (20) is an affine function of the measurements y_i. From the results in Section III, we can write out a sinogram restoration algorithm with electronic noise compensation from (21) directly by replacing all occurrences of y_i by its conditional expectation E(Y_i | Z_i = z_i). If we use the affine approximation in Section IV, then

$$\begin{array}{l}E(Y_i\mid Z_i=z_i)\approx {\widehat{E}}_{\text{aff}}(Y_i\mid Z_i=z_i)\\ =\frac{{\widehat{\overline{Y}}}_i{\sigma }^2+\phi {\widehat{\overline{Y}}}_i^p{z}_i}{\phi {\widehat{\overline{Y}}}_i^p+{\sigma }^2}\end{array}$$ (22)

where ${\widehat{\overline{Y}}}_i={\overline{Y}}_{l_i^n}$ is the estimated mean transmission at the current iteration.

As shown in Appendix A, the quadratic surrogate function (for the log-likelihood part) (20) is valid in the range [l_n − ε, l_n + ε] for a prespecified value ε > 0. This constraint must be enforced in the update values l_n+1 calculated by (21). In our algorithm implementation, we clip $l_i^{n+1}$ so that $l_i^{n+1}\ge 0$ and |l_n+1 − l_n| ≤ 0.2.

We show in Appendix B that the surrogate function (20) reduces to that in [6, (51)] for the special case where p_i = φ_i = 1 for all the detector bins. In Section IV, we have demonstrated that in this case the affine estimator coincides with the shifted-Poisson approximation. Combining these two points, it can be shown that the surrogate function in [6, (50)], and, hence, the sinogram smoothing algorithm derived using a shifted Poisson likelihood can be obtained by first ignoring the electronic noise, then applying the substitution rule using the affine estimator.

The point of the above argument is not that we may either apply the shifted Poisson approximation to the log-likelihood directly as done in [6] or use it at a later stage in calculating the conditional expectation as we do here. The power of the substitution rule becomes more apparent when the data is not Poisson distributed. In this case it would not be obvious how to apply an analogous “shift” and write out the approximate log-likelihood function of a non-Poisson random variable plus a Gaussian noise. However, all we need for applying the substitution rule and for compensating for the Gaussian noise is, essentially, the knowledge that the log-likelihood is affine in the measurement and a way to calculate the conditional expectation E(Y | Z).

There are other examples in the literature where a simple substitution worked. In Snyder et al. [8], considering the update equations for nonuniform flat-field, nonzero background, but with (18) and without readout noise (15), the only difference is that we replace r(j), with no readout noise, in (15) by its conditional expectation F[r(j), û_k, σ]. Even (15) can be regarded as the result of applying the substitution rule to a nonuniform flat-field, zero-background algorithm (without the μ₀(j)). However, this time the substitution rule can be applied exactly as the conditional expectation of a Poisson r.v. given the sum of i.i.d. Poisson r.v.’s has an analytical form. These examples are all based on Poisson distributions and a linear detection model. However, as we have demonstrated, this idea can be applied to non-Poisson distributed random variables and nonlinear detection models. No surrogate functions were mentioned in these examples since the algorithm derivations were based on the log-likelihood functions, which are certainly legitimate surrogates.

VI. Numerical Evaluations

We perform two simulation studies, corresponding to the sinogram restoration algorithm and the fully iterative reconstruction algorithm we discussed in Section V, to study the effectiveness of electronic noise modeling in low dose X-ray CT reconstruction.

A. Sinogram Restoration FBP Reconstruction

We simulated fan-beam projection data of polychromatic X-rays passing through a transaxial slice of a clock phantom with diameter 48 cm. The clock phantom consists of water cylinders of various densities and sizes. The uniform air scan intensity (i.e., no bowtie filter) was around 3 × 10⁷ in units of keV × # photons. Some other geometric simulation parameters are listed in Table I. The projection data were generated using the Siemens DRASIM© simulation package. The continuous X-ray incident spectrum was sampled at a 5-keV interval, and for each 5-keV energy bin, the mean attenuated photon number λ̄ (E_k) was replaced by a Poisson random variable with mean λ̄ (E_k). This noisy photon number was multiplied by the mean energy of each energy bin and the total detected signal was the sum from all the energy bins following the model in (1). We then added Gaussian noise to the transmission signal to simulate effects of electronic noise. Our incident polychromatic X-ray spectrum has an effective energy of around 55 keV; the additive Gaussian noise has a variance of 330², which corresponds to the counting statistics of about 36 X-ray photons.

TABLE I.

Parameters for Fan-Beam Simulation

# channels	# views/360°	Focus-ISO	ISO-detector
672	512	595.0 mm	490.6 mm
Fan angle	Detector size	Recon image size	Recon pixel size
52°	1.47 mm	512×512	0.96 mm

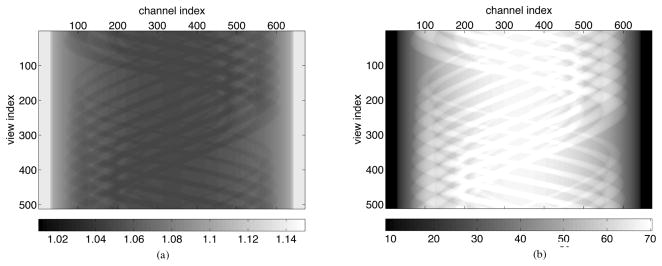
The ED model parameters p_i, φ_i are assumed known a prior. They are obtained by fitting the ED model to the compound Poisson density of energy-integrating detectors [22]. The model parameters p_i, φ_i have the same size as the projection data, and one such set that we used in the sinogram smoothing algorithm (21) is shown in Fig. 1. These parameters together with the transmission projection data are input to the ED-model based penalized maximum-likelihood sinogram restoration algorithm (21). Since our phantom only consists of water with different densities, we chose m_w(E) as the mass attenuation coefficient of water. The reference energy E₀ was the effective energy of the incident X-ray spectrum, 55 keV. We used the affine estimator to estimate E(Y | Z). The stopping criterion of the sinogram smoothing algorithm was that $\mid l_i^{n+1}-l_i^n\mid \le {10}^{-5}$ for all detector bins i at two consecutive iterations. Depending on the value of the smoothing strength β, this criterion required iteration numbers ranging from 10 (small β value) to less than 200 (large β value). The final reconstruction was done by the FBP algorithm. [23]

Fig. 1.

(a) Power parameter p_i and (b) the dispersion parameter φ_i in the ED-modeled based sinogram smoothing algorithm.

To visualize the effect of electronic noise, we simulated one set of noise-free transmission data but added the same amount σ² = 330² of electronic noise. The reconstructed images using the FBP algorithm, without preprocessing by sinogram domain smoothing, from these two sets of data are shown in Fig. 2. Beam-hardening artifacts are obvious in both reconstructions. In addition, the reconstructed image with the electronic noise appear grainier especially toward the central region. The noise texture from electronic noise do not seem to be distinguishable from those resulting from transmission noise only.

Fig. 2.

(a) Direct FBP reconstruction from noise-free data, and no electronic noise was added to projection data. (b) Direct FBP reconstruction with noise-free transmission data and electronic noise with variance σ² = 330². The display window for both images is [0.18, 0.25] cm⁻¹.

We simulated ten independent realizations of the noisy transmission projection, and applied sinogram smoothing using different strengths β of the quadratic penalization term to sweep out the tradeoff between noise and resolution. One sample reconstructed image is shown in Fig. 3(a). To test the effectiveness of electronic noise compensation alone, for each set of data we ran the sinogram smoothing algorithm twice assuming σ² = 0 and σ² = 330², respectively. We also looked at the absolute baseline where electronic noise was not present in the simulation data nor was it compensated for in the sinogram smoothing process. This baseline provides a loose upper bound of the performance of an ideal electronic noise compensation method.

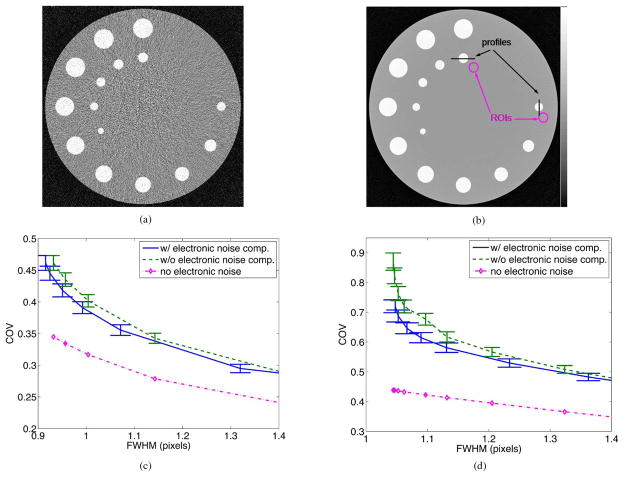
Fig. 3.

(a) FBP reconstruction from the smoothed sinogram data with electronic noise compensation. The display window is [0, 0.4] cm⁻¹. (b) The definition of ROIs and line profiles for measuring resolution. (c) Noise-resolution trade-off of different reconstruction procedures for the cylinder at 3 o’clock position and (d) for the smaller cylinder at 12 o’clock position.

We measured the tangential (vertical) profile of the cylinder insert at 3 o’clock position [Fig. 3(b)] and fit that by a Gaussian kernel edge-spread function [24]. The full-width-at-half-maximum (FWHM) of the fitted Gaussian kernel was used as a resolution measure at that point. We averaged this FWHM from ten independent realizations to reduce effects of noise. We also calculated the coefficient of variation (COV) in a small uniform ROI near the 3 o’clock cylinder to quantify noise. In Fig. 3(c), we plot the noise-resolution tradeoff from the three different sinogram processing methods, 1) no electronic noise simulated, 2) with electronic noise but no compensation, and 3) with electronic noise and with compensation. The curves were swept out by varying the quadratic smoothing strengths β from 0.1 to 200. Fig. 3(d) is the noise-resolution tradeoff for the inner cylinder at 12 o’clock position. In both cases, we can see that with electronic noise compensation we obtain a better noise-resolution tradeoff than without.

Because of the use of the quadratic smoothing priors, the sinogram smoothing algorithm in (21) may introduce bias in the final FBP-reconstructed images, especially at larger β values. We calculated the mean reconstructed images from the ten sets of noisy data, and compared the mean reconstruction near the background region [ROI-1, Fig. 3(b) 12 o’clock position] with water’s attenuation coefficient 0.22 cm⁻¹ at the effective energy of 55 keV. This comparison was repeated for the various smoothing strengh β that we used for sinogram smoothing. The normalized mean bias and its standard deviation are listed in Table II. As we can see, the normalized bias is around 1 HU for all the β values that we used in the sinogram smoothing step.

TABLE II.

Bias Calculation for Sinogram Smoothing FBP Recon

β	1.0	2.0	5.0	10.0	20.0	50.0
normalized bias (× 10−3)	1.291	1.292	1.295	1.297	1.290	1.242
stdv bias (× 10−3)	0.2933	0.283	0.2657	0.2483	0.2257	0.187

B. Fully Iterative Reconstruction

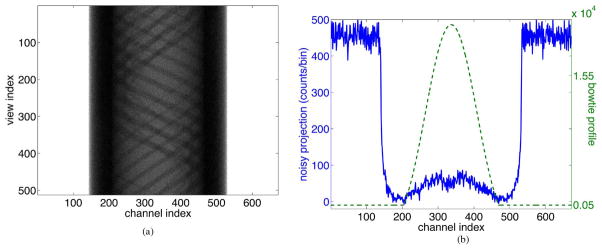
We performed a second simulation study to test the effectiveness of electronic noise modeling and compensation in the fully iterative reconstruction algorithm (17). As the convex algorithm is based on a monochromatic X-ray source spectrum with a photon counting X-ray detector, we used the DRASIM© simulation package to generate noise-free counting mode data using the same scanning geometry as in Section VI.A. The monochromatic X-ray source was set at 70 keV. The same phantom composition but scaled-down to 30-cm diameter was used. The DRASIM© package by default assumes a uniform air scan intensity. To emulate the effect of a bowtie filter, from the noise-free transmission data generated by DRASIM© we adjusted the detected intensity according to a bowtie filter profile that can normalize a 20-cm water cylinder [green dashed line Fig. 4(b)], after which Poisson distributed photon noise and electronic noise (σ² = 36) were added. One sample projection data and its profile at view index 255 are shown in Fig. 4.

Fig. 4.

(a) One sample of the noisy projection data used in the second simulation study. (b) The bowtie intensity profile (dashed line) and the projection profile at view index 255 (solid line). The units of both vertical axes are photon counts per bin.

We used the original convex algorithm and its extended version (17) with electronic noise modeling for reconstruction. Fig. 5 shows two example reconstructed images using the two methods at matched resolution for the cylindrical insert at 3 o’clock position. The qualitative difference between the two reconstruction methods is clearly visible. From Fig. 4, we see that the bowtie intensity profile is not wide enough for the 30-cm phantom. As a consequence, the peripheral region receives very little radiation, and electronic noise over these region plays a relatively more significant role than the interior region. With electronic noise compensation the algorithm (17) can achieve lower noise at matched resolution.

Fig. 5.

Reconstructed images at matched resolution without (a) and with electronic noise compensation (b). The display window for both images is [0, 0.4] cm⁻¹.

VII. Conclusions and Discussions

We previously proposed an exponential dispersion model (ED) for approximating the compound Poisson statistics of the energy-integrating X-ray detectors, and demonstrated how such a model can be utilized in deriving an iterative X-ray CT reconstruction algorithm [11]. In this work, we extended our model to include electronic noise. We presented an expectation-maximization formulation and explained how it can be combined with the surrogate function approach and the optimization transfer principle to account for electronic noise in an ML estimation problem. This formulation is applicable to a general class of distribution functions; the only requirement is that the electronic noise component is independent of the “useful” signal, and that the distribution of the electronic noise does not depend on the unknown parameters to be estimated. If in addition the log-likelihood of the ‘useful’ signal is affine in the data, then a reconstruction algorithm with electronic noise compensation can be obtained by a minimal modification to one previously derived for the electronic-noise-free case.

The algorithm implementation involves calculating the conditional mean E(Y | Z) of the nonelectronic-noise contaminated signal Y given the raw measurements Z = Y + N. When Y is modeled by the exponential dispersion model, we described an affine approximation for calculating E(Y | Z); a saddlepoint approximation method was proposed in [21]. These two methods can be regarded as generalization of similar methods in [8] and [9] from the Poisson to the ED model.

We used the convex algorithm as an example to demonstrate how the substitution rule can be applied. In addition, we also derived a sinogram smoothing algorithm with electronic noise modeling for low-dose CT applications where the X-ray intensity signal follows the ED model. For its simplicity, we only used the best affine estimator in combination with the sinogram smoothing algorithm and the fully iterative reconstruction algorithm. It was found in [9] that using a more accurate estimator (i.e., saddlepoint) introduced a negligible to modest improvement over a less accurate (Poisson) estimator for readout noise compensation in CCD cameras. Further studies may also investigate the same question when we have a nonlinear model such as in X-ray CT and a wider dynamic range of the signal statistics.

Biographies

Jingyan Xu (M′03) received the B.S. degree from Tsinghua University, China, and the M.S. and Ph.D. degrees from Stanford University, Stanford, CA, all in electrical engineering.

She was a part-time research engineer at SC Solutions, Inc., Sunnyvale, CA, during her Ph.D. study. She worked as a postdoctoral intern at Robert Bosch Corporation, Research and Technology Center, Palo Alto, CA, before joining the Division of Medical Imaging Physics, Department of Radiology, Johns Hopkins University, Baltimore, MD, in 2004, where she is currently a Research Associate. Her research interests include design, implementation, performance evaluation of image reconstruction algorithms, and the modeling and compensation for the image-degrading factors in SPECT and X-ray CT systems.

Benjamin M. W. Tsui (F′77) received the B.S. degree in physics from the Chinese University of Hong Kong in 1970, the M.A. degree in physics from Dartmouth College, Hanover, NH, in 1972, and the Ph.D. degree in medical physics from the University of Chicago, Chicago, IL, in 1977.

After graduation, he continued to work at the University of Chicago as a Postdoctoral Fellow and became an Assistant Professor of radiology in 1979. He joined the University of North Carolina, Chapel Hill, in 1982 as a Research Associate Professor of radiology and biomedical engineering (BME) and was promoted to tenured Professor and became the Director of the Medical Imaging Research Laboratory and the Associate Chair of the Department of BME in 1991. He joined the Johns Hopkins University, Baltimore, MD, in 2002, as a Professor of radiology, electrical and computer engineering, environmental health sciences, and biomedical engineering and as the Director of the Division of Medical Imaging Physics in the Department of Radiology. His research interests include imaging physics of SPECT, PET and CT, 4-D computer generated phantoms that realistically mimic human anatomy and physiology, computer simulation techniques including the use of Monte Carlo methods, statistical and quantitative image reconstruction methods, 4-D cardiac and respiratory motion compensation, and image quality evaluation using model and human observers, as well as preclinical small animal imaging instrumentation and techniques.

Appendix A Surrogate Function Derivation

We derive a quadratic surrogate function for the log-likelihood

$$\mathrm{\Phi }(l)=y\frac{{\overline{Y}}^{1-p}}{1-p}-\frac{{\overline{Y}}^{2-p}}{2-p},1<p<2.$$ (23)

where Ȳ is defined as in (19). Note that we omitted the detector index i since we can look at each i separately. The nonseparability of the objective function (18) is only involved in the penalization term. We look for a quadratic surrogate function S(l;l_n) satisfying the following conditions:

$$\begin{array}{l}\mathrm{\Phi }(l)\ge S(l;l_n)=\mathrm{\Phi }(l_n)+{\mathrm{\Phi }}^{\prime }(l_n)(l-l_n)-C(l_n)\frac{{(l-l_n)}^2}{2},C(·)>0\\ \mathrm{\Phi }(l_n)=S(l_n;l_n).\end{array}$$ (24)

As a preparation for finding C(l_n), we list some quantities that we will need shortly

$$\stackrel{.}{\mathrm{\Phi }}(l)=\left(\frac{y}{{\overline{Y}}^p}-\frac{\overline{Y}}{{\overline{Y}}^p}\right)\frac{\partial \overline{Y}}{\partial l}$$ (25)

$$\ddot{\mathrm{\Phi }}(l)=-\frac{y}{{\overline{Y}}^{p+1}}{\left(\frac{\partial \overline{Y}}{\partial l}\right)}^2+(p-1)\left(\frac{1}{{\overline{Y}}^p}-\frac{y}{{\overline{Y}}^{p+1}}\right){\left(\frac{\partial \overline{Y}}{\partial l}\right)}^2+\left(\frac{y}{{\overline{Y}}^p}-\frac{\overline{Y}}{{\overline{Y}}^p}\right)\frac{{\partial }^2\overline{Y}}{\partial l^2}$$ (26)

$$\frac{\partial \overline{Y}}{\partial l}=-\int \stackrel{\sim }{N}(E)m^{\prime }(E)e^{-m^{\prime }(E)l}dE$$ (27)

$$\frac{{\partial }^2\overline{Y}}{\partial l^2}=-\int \stackrel{\sim }{N}(E){[m^{\prime }(E)]}^2{e}^{-m^{\prime }(E)l}dE.$$ (28)

Using the Cauchy’s inequality and the relationships in (27) and (28), it can be shown that

$${\left(\frac{\partial \overline{Y}}{\partial l}\right)}^2\le \overline{Y}\frac{{\partial }^2\overline{Y}}{\partial l^2}.$$ (29)

Since we have a maximization problem, we require C(l_n) > 0. One choice of C(l_n) that satisfies the condition in (24) was given in [15] and [25]

$$C(l_n)=-\underset{l\ge 0}{inf}\ddot{\mathrm{\Phi }}(l).$$ (30)

However, Φ̈(l) may not be bounded from below for l > 0. This can be seen by using the special case, a monotonic model, for Ȳ. Instead of finding a global condition as in (30), we consider a local region [l_n − ε, l_n + ε] around l_n for some ε > 0, and look for a curvature such that

$$C(l_n)\ge -\underset{l\in [l_n-\epsilon ,l_n+\epsilon ]}{min}\ddot{\mathrm{\Phi }}(l).$$ (31)

This curvature will define the quadratic surrogate as specified in (24). In case l_n = 0, an asymmetric region can be used such as [0, l_n + ε].

If we replace the first term in (26) by the inequality (29), we will have

$$\begin{array}{l}\ddot{\mathrm{\Phi }}(l)\ge \frac{(p-1)}{{\overline{Y}}^p}\left(1-\frac{y}{\overline{Y}}\right){\left(\frac{\partial \overline{Y}}{\partial l}\right)}^2+\left(-\frac{1}{{\overline{Y}}^{p-1}}\right)\frac{{\partial }^2\overline{Y}}{\partial l^2}\\ \ge -\frac{(p-1)}{{\overline{Y}}^p}\frac{y}{\overline{Y}}{\left(\frac{\partial \overline{Y}}{\partial l}\right)}^2+\left(-\frac{1}{{\overline{Y}}^{p-1}}\right)\frac{{\partial }^2\overline{Y}}{\partial l^2},\text{since}1<p<2.\end{array}$$

Let l₁ = l_n − ε, and l₂ = l_n + ε. Since the quantities Ȳ, −∂Ȳ/∂l, and ∂²Ȳ/∂l² are all nonincreasing functions of l, the curvature C(l_n) can be obtained by

$$\begin{array}{l}\underset{l\in [l_1{l}_2]}{min}\ddot{\mathrm{\Phi }}(l)\ge -\frac{(p-1)y}{{\overline{Y}}^{p+1}{\mid }_{l_2}}{\left({\frac{\partial \overline{Y}}{\partial l}|}_{l_1}\right)}^2+\left(-\frac{1}{{\overline{Y}}^{p-1}{\mid }_{l_2}}\right){\frac{{\partial }^2\overline{Y}}{\partial l^2}|}_{l_1}\\ \triangleq -C(l_n).\end{array}$$ (32)

Appendix B Special Case p = φ = 1

In this special case, the exponential dispersion log-likelihood in (23) degenerates to the Poisson log-likelihood, since

$$\underset{t\to 0}{lim}\frac{x^t-1}{t}=\frac{e^{\mathit{t}logx}-1}{t}=logx,x>0.$$

The second order derivative in (26) can be simplified as

$$\begin{array}{l}\ddot{\mathrm{\Phi }}(l)=-\frac{y}{{\overline{Y}}^2}{\left(\frac{\partial \overline{Y}}{\partial l}\right)}^2+\left(\frac{y}{\overline{Y}}-1\right)\frac{{\partial }^2\overline{Y}}{\partial l^2}\\ \ge -\frac{y}{\overline{Y}}\frac{{\partial }^2\overline{Y}}{\partial l^2}+\left(\frac{y}{\overline{Y}}-1\right)\frac{{\partial }^2\overline{Y}}{\partial l^2}\\ =-\frac{{\partial }^2\overline{Y}}{\partial l^2}\ge -{\frac{{\partial }^2\overline{Y}}{\partial l^2}|}_{l=0}\\ =-\int \stackrel{\sim }{N}(E){[m^{\prime }(E)]}^{2}dE\\ \triangleq -C_1(l^n)=\text{const}.\end{array}$$

As a side note, we point out that our derivation of the quadratic surrogate function is slightly different than those used in [6] and [15], where the quadratic surrogate is obtained, not for the original objective function, but for a separable, first surrogate function of the original objective function derived using convexity arguments. In the special case where p = φ = 1, these two approaches can result in the same surrogate. If we identify I_ib_ij in [6] with Ñ (E) in our model, and the linear model f_i(l^mono) ≜ m′ (E) l^mono instead of the identity function used in ([6], Approach 2), then it can be seen that C₁(l_n) corresponds to the maximum curvature (slowest convergence) in [6(24)].