Predicting Skin Permeability from Complex Chemical Mixtures: Dependency of Quantitative Structure Permeation Relationships on Biology of Skin Model Used

Abstract

Dermal absorption of topically applied chemicals usually occurs from complex chemical mixtures; yet, most attempts to quantitate dermal permeability use data collected from single chemical exposure in aqueous solutions. The focus of this research was to develop quantitative structure permeation relationships (QSPR) for predicting chemical absorption from mixtures through skin using two levels of in vitro porcine skin biological systems. A total of 16 diverse chemicals were applied in 384 treatment mixture combinations in flow-through diffusion cells and 20 chemicals in 119 treatment combinations in isolated perfused porcine skin. Penetrating chemical flux into perfusate from diffusion cells was analyzed to estimate a normalized dermal absorptive flux, operationally an apparent permeability coefficient, and total perfusate area under the curve from perfused skin studies. These data were then fit to a modified dermal QSPR model of Abraham and Martin including a sixth term to account for mixture interactions based on physical chemical properties of the mixture components. Goodness of fit was assessed using correlation coefficients (r²), internal and external validation metrics ($q_{\text{LOO}}^{\text{2}}$, $q_{\text{L25\%}}^{\text{2}}$, $q_{\text{EXT}}^{\text{2}}$), and applicable chemical domain determinations. The best QSPR equations selected for each experimental biological system had r² values of 0.69–0.73, improving fits over the base equation without the mixture effects. Different mixture factors were needed for each model system. Significantly, the model of Abraham and Martin could also be reduced to four terms in each system; however, different terms could be deleted for each of the two biological systems. These findings suggest that a QSPR model for estimating percutaneous absorption as a function of chemical mixture composition is possible and that the nature of the QSPR model selected is dependent upon the biological level of the in vitro test system used, both findings having significant implications when dermal absorption data are used for in vivo risk assessments.

Predicting the degree of dermal absorption of topically exposed chemicals is an important issue in both environmental and occupational risk assessment. Most risk assessment approaches are based on data obtained from dosing chemicals neat or in simple aqueous vehicles, yet most exposures are to more complex mixtures. Numerous studies have demonstrated that vehicles may have significant effects on modulating chemical absorption (Bliss, 1939; Cross et al., 2001; Idson, 1983; Qiao et al., 1996; Rosado et al., 2003; Sloan et al., 1986). In fact, this is the prime strategy behind developing pharmaceutical formulations (Augustijns and Brewster, 2007). Today, there is little doubt that vehicle and formulation components modulate dermal absorption or transdermal delivery of topically applied drugs and solutes. Despite the intellectual certainty of this effect, most attempts in risk assessment modeling to quantitate dermal absorption using quantitative structure permeability relationships (QSPR) are based on defining linear free-energy relationships (LFER) using data obtained from single compound exposure in simple aqueous solutions (Abraham and Martins, 2004; EPA, 2004; Geinoz et al., 2004; Hostynek and Magee, 1997; Neuman, 2008; Potts and Guy, 1992).

Because the vast majority of occupational and environmental exposure to chemicals is in the form of mixtures, understanding the mechanism operative in modulating chemical penetration into and absorption through the skin is crucial to predicting toxicological effects. Limited work has been done to broadly incorporate the effect of mixture interactions seen in more complex but realistic formulations (Baynes et al., 2008; Gregoire et al., 2009). What is required for realistic risk assessments on topical mixtures is a general approach that at a minimum indicates whether a specific mixture would be expected to increase or decrease absorption through the skin. A quantitative indication of the extent of modulation would be optimal.

We have previously reported on a straightforward approach to incorporate physiochemical properties of a mixture into existing QSPR models. These studies were focused on an initial set of 12 penetrants in 24 mixtures for 288 treatment combinations (complete factorial experimental design) based on data collected using in vitro porcine skin flow-through (PSFT) diffusion cells and the five descriptor linear free-energy QSPR relationship of Abraham and Martins (2004) (Riviere and Brooks, 2005). This approach was subsequently expanded using data from the more biologically sophisticated isolated perfused porcine skin flap (IPPSF) model (10 penetrants in five mixtures for 50 treatment combinations). The IPPSF is an ex vivo biologically intact perfused tissue preparation that has previously been shown to correlate to in vivo human dermal absorption (Riviere, 2006; Riviere et al., 1986, 1992; Riviere and Monteiro-Riviere, 1991; Wester et al., 1998). The use of this model assures that chemical mixture interactions involving the stratum corneum as well as viable epidermis and dermis would be detected because such interactions which would occur in vivo could confound solvatochromatic interactions detected using nonbiological systems, necessitating that such an approach be used if the goal is to reliably predict in vivo effects. The approach's applicability to other QSPR models was assessed by also applying it to the QSPR models of Hostynek and Magee (1997) as well as Potts and Guy (1992) (Riviere and Brooks, 2007).

The present study significantly expands on this analysis by increasing the number of penetrants studied in the in vitro porcine skin diffusion cells to 16 for a total of 384 treatment combinations and in the IPPSF to 20 penetrants dosed in a total of 119 treatment combinations. These larger data sets expand the chemical inference space to which such analyses can be applied but more importantly allow for comparison between QSPR model structures across experimental systems and begin to offer validation of the concept that such an approach is applicable to modifying the dermal risk assessment paradigm now rooted in simple single chemical aqueous exposures. The goal of this analysis was to confirm that this approach is valid across a more diverse group of chemicals and determines if mixture-based QSPR models can be extrapolated across in vitro model systems of different biological complexity.

MATERIALS AND METHODS

Study chemicals.

The chemical compounds used in the studies are listed in Table 1 along with their specific radioactivity, purity, and source.

TABLE 1.

Identity, Specific Activity, Purity, and Source of Study Compounds

Compound	mCi/mmol	Purity (%)	Source
Atrazine-ring-UL-14C	15.1	98.1	SCC
MethylParathion-ring-UL-14C	13.8	99.5	SCC
4-Nitrophenol-UL-14C	6.4	99.6	SCC
Parathion-ring-UL-14C	9.2	97.1	SCC
Pentachlorophenol-ring-UL-14C	11.9	98	SCC
Permethrin-benzyl-ring-UL-14C	10.9	96.1	SCC
Phenol-UL-14C	9	98.5	SCC
Simazine-ring-UL-14C	15.5	99	SCC
Chlorpyrifos [pyridine-2,6-14C]	32	99	ARC
Fenthion-ring-UL-14C	55	98.5	ARC
Propazine-ring-UL-14C	15	96.6	ARC
1,3,5,-Triethyl hexahydro-S-triazine [methylene-14C]	10	98.6	ARC
Ricinoleic acid [12-3H]	20,000	99	ARC
Caffeine [8-14C]	52	99	ARC
Octanol [1-14C]	5	99	ARC
Testosterone [4-14C]	55	99	ARC
Codeine [N-methyl-14C]	50	99	ARC
4-Chlorophenol [14C(U)]	20	99	ARC
4-Cyanophenol [cyano-14C]	20	99	ARC
4-Phenoxyphenol [phenol-ring-14C(U)]	77	99	ARC
2,4-Dimethylphenol [phenol-ring-14C(U)]	75	99	ARC
Chlorfenvinphos [ethyl-1-14C]	7.9	99.7	IOI
Dimethoate [carbonyl-14C]	6.6	98.2	IOI
Metribuzin [ring-6-14C]	10.6	98.7	IOI
Diazinon [pyrimidine-6-14C]	53	96.3	MB
p-Nonylphenol-ring-14C	76.6		BDR
Sodium 2-dodecylbenzene sulfonate-ring-UL-14C	50.77	99.1	WL
DEET	Not radiolabeled	98	CSC
Absolute ethyl alcohol (200 proof)	Not radiolabeled	100	AA
Propylene glycol	Not radiolabeled	99	SCC
Sodium lauryl sulfate	Not radiolabeled	99	SCC
Methylnicotinic acid	Not radiolabeled	99	SCC
Water	Not radiolabeled		House

Note. SCC, obtained from Sigma Chemical Co., St Louis, MO; ARC, obtained from American Radiolabeled Chemicals, Inc., St Louis, MO; IOI, obtained from Institute of Isotopes Co., Ltd. Budapest, Hungary; MB, obtained from Moravek Biochemicals, Inc., Brea, CA; BDR, obtained from BioDynamics Radiochemicals, Billingham, UK; WL, obtained from Wizard Laboratories, Sacramento, CA; CSC, obtained from Chem Service Company, West Chester, PA; AA, obtained from Aaper Alcohol and Chemical Co. Shelbyville, KY. Water was distilled in our in-house still. N,N diethyl-m-toluamide (DEET) was not radiolabeled and was analyzed via high performance liquid chromatography (HPLC).

In vitro PSFT diffusion cell.

The flow-through diffusion cell was used to perfuse porcine skin obtained from the dorsal area of weanling female Yorkshire pigs (Sus scrofa) according to protocols approved by the North Carolina State University Institutional Animal Care and Use Committee (Bronaugh and Stewart, 1985; Chang and Riviere, 1991). Skin was dermatomed to a thickness of 500 μm with a Padgett Dermatome (Padgett Instruments, Inc., Kansas City, MO). Each circular skin disk was punched to provide a dosing surface area of 0.64 cm² and then placed into a two-compartment Teflon flow-through diffusion cell (Crowne Glass, Somerville, NJ). Skin was perfused using a Krebs-Ringer bicarbonate buffer spiked with dextrose and bovine serum albumin. The skin was topically dosed nonoccluded with 20 μl of one of 16 marker penetrant compounds listed in Table 2 formulated in one of 24 specified mixtures also listed in Table 2. This resulted in a training set of 384 treatments with n = 4–5 replicates per treatment designed as a randomized complete factorial experiment. The target dose concentration was 20 μg/cm². Perfusate flow rate was 4 ml/h, and perfusate samples were collected every 15 min for 2 h and every hour thereafter until the end of the 8-h dosing period.

TABLE 2.

Identity of 16 Training Set Compounds Investigated in 384 Mixtures in the PSFT

Substituted phenols	Organophosphates	Triazine herbicides	Selected compounds
Phenol	Methylparathion	Atrazine	Caffeine
Pentachlorophenol	Ethylparathion	Propazine	Octanol
4-Nitrophenol	Chlorpyrifos	Simazine	Testosterone
4-Nonylphenol	Fenthion	Triazine	Codeine
Composition of 24 training set mixtures investigated in the PSFT
EtOH		PG
EtOH + MNA		PG + MNA
EtOH + SLS		PG + SLS
EtOH + MNA + SLS		PG + MNA + SLS
EtOH + water		PG + water
EtOH + water + MNA		PG + water + MNA
EtOH + water + SLS		PG + water + SLS
EtOH + water + MNA + SLS		PG + water + MNA + SLS
EtOH + PG		Water
EtOH + PG + MNA		Water + MNA
EtOH + PG + SLS		Water + SLS
EtOH + PG + MNA + SLS		Water + MNA + SLS

Note. MNA, methylnicotinic acid; PG, propylene glycol (1,2-propanediol); SLS, sodium lauryl sulfate.

Because we used finite doses, pseudo–steady state flux was determined from the slope of the cumulative perfusate flux profile versus time. The concentration was the initial chemical concentration in the vehicle at the start of the experiment. We assessed percutaneous absorption by calculating flux into perfusate normalized to applied surface concentration. This generates an operational or apparent permeability constant ($k_{\text{p}}^{\text{*}}$) for a penetrant from a specific vehicle exposure scenario that parallels calculation of a formal k_p defined by Fick's First Law of Diffusion determined using infinite dosing under occluded conditions from a single vehicle. We are using $k_{\text{p}}^{\text{*}}$ as an operational absorption metric that normalizes flux by the applied surface concentration at application time. We conducted these studies using finite doses under nonoccluded conditions to model the occupational exposure scenario, which unfortunately does not allow for preventing loss of volatile compounds.

The validation set is made up of PSFT experiments run prior to and with a similar experimental design to that of the training set. Table 3 lists the identity of seven validation set compounds investigated in 89 mixtures created from differing combinations of 14 validation set mixture components in the PSFT.

TABLE 3.

Identity of Seven Validation Set Compounds Investigated in 89 Mixtures in the PSFT

Benzidine	LAS	Permethrin
Carbaryl	Pentachlorophenol	Triazine
DEET
Composition of 14 validation set mixture components investigated in the PSFT
Acetone	Mineral oil	SLS
DEET	MNA	Triazine
DMSO	Permethrin	Triethanol amine
EtOH	Polyethylene glycol	Water
LAS	Ricinoleic acid

Note. DEET, N,N diethyl-m-toluamide; DMSO, Dimethylsulfoxide; LAS, linear alkylbenzene sulfonate; MNA, methylnicotinic acid; SLS, sodium lauryl sulfate.

IPPSF studies.

The IPPSF is a single-pedicle, axial pattern tubed skin flap obtained from the abdomen of female weanling Yorkshire pigs (S. scrofa). This model system contains a functional microcirculation and an anatomically intact and viable epidermis and dermis. Two flaps per animal, each lateral to the ventral midline, were created in a single surgical procedure using protocols approved by the North Carolina State University Institutional Animal Care and Use Committee. The procedure involved surgical creation of the flap (measuring 4 × 12 cm) perfused primarily by the caudal superficial epigastric artery and its associated paired venae comitantes followed by arterial cannulation and harvest in 48 h (Bowman et al., 1991). The IPPSF was then transferred to a perfusion apparatus that is a custom-designed temperature- and humidity-regulated chamber. Perfusion media consisted of a modified Krebs-Ringer bicarbonate buffer spiked with dextrose and bovine serum albumin. Normal perfusate flow rate was maintained at 1 ml/min/flap (3–7 ml/min/100 g) with a mean arterial pressure ranging from 30–70 mmHg, targets consistent with in vivo values reported in the literature. Viability for up to 24 h has been confirmed through biochemical studies and extensive light and transmission electron microscopy studies (Monteiro-Riviere et al., 1987). Radiolabeled compounds were topically applied in their respective vehicle under ambient, nonoccluded conditions. These techniques are fully described in the literature (Riviere et al., 1986; Riviere and Monteiro-Riviere, 1991).

The skin was topically dosed with 100 μl of one of 20 marker penetrant compounds listed in Table 4 formulated in one of five or six specified mixtures also listed in Table 4. This resulted in a training set of 119 treatments with n = 3 replicates per treatment. The target dose concentration was 20 μg/cm². Perfusate flow rate was 1 ml/min, and perfusate samples were collected every 15 min for 2 h and every half hour thereafter until the end of the 8-h dosing period.

TABLE 4.

Identity of 20 Training Set Compounds Investigated in 119 Mixtures in the IPPSF

Substituted phenols		Organophosphates		Triazine herbicides
Phenola		Methylparathion		Atrazine
Pentachlorophenola		Ethylparathiona		Propazinea
4-Nitrophenola		Chlorpyrifos		Simazinea
4-Nonylphenol		Fenthiona		Triazinea
Composition of five training set mixtures investigated in the IPPSF
EtOH	EtOH + water	Water		Water + SLS	PG
4-Chlorophenol		Diazinon		Metribuzin
4-Cyanophenol		Chlorfenvinphos
4-Phenoxyphenol		Dimethoate
2,4-Dimethylphenol
Composition of six training set mixtures investigated in the IPPSF
EtOH	EtOH + water	Water	Water + SLS	EtOH + MNA	MNA + SLS

Note. Pentachlorophenol was also investigated in EtOH + MNA, EtOH + water + MNA, PG + SLS, and water + PG. 4-Nonylphenol was not investigated in PG. MNA, methylnicotinic acid; SLS, sodium lauryl sulfate.

^aEight compounds were also investigated in water + linear alkylbenzene sulfonate.

For the IPPSF experiments, perfusate flux logAUC (area under the curve) rather than $\log k_{\text{p}}^{\text{*}}$ was employed because it better represents the total transdermal flux across this more complex, vascularized model system. AUC (%D h/ml) was calculated using the trapezoidal rule, wherein the mean of the concentration of two adjacent time points was multiplied by the elapsed time of those two samples and added to the remaining means. Table 5 lists the identity of 10 validation set compounds investigated in 40 mixtures created from combinations of the six validation set mixture components in the IPPSF.

TABLE 5.

Identity of 10 Validation Set Compounds Investigated in 40 Mixtures in the IPPSF

4-Nitrophenol	Octanol	Permethrin
Carbaryl	p-Aminobenzoic acid	Phenol
Ethylparathion	Pentachlorophenol	Theophylline
Methyl salicylate
Composition of six validation set mixture components investigated in the IPPSF
Acetone	EtOH	SLS
DEET	MNA	Water

Note. DEET, N,N diethyl-m-toluamide; MNA, methylnicotinic acid; SLS, sodium lauryl sulfate.

Radioisotope counting.

Compounds used in these studies were radiolabeled (¹⁴C), and the perfusate flux was determined using liquid scintillation counting on a Packard 1900TR Tricarb Liquid Scintillation Counter (Packard Instruments, Inc., Downers Grove, IL).

QSPR modeling approach.

Multiple regression analysis was carried out using SAS 9.1 for Windows (SAS Institute, Cary, NC). We have used stepwise regression (SAS 9.1) with each model in addition to the two or five parameters established by the model authors to determine the best mixture factor (MF) for each biological system. The two parameters utilized in the model of Potts and Guy (1992) are logK_ow (log of the octanol:water partition coefficient) and the molecular weight (MW). The five model parameters utilized in the model of Abraham and Martins (2004) are $\Sigma {\text{α}}_{\text{2}}^{\text{H}}$ (hydrogen bond donor acidity), $\Sigma {\text{β}}_{\text{2}}^{\text{H}}$(hydrogen bond acceptor basicity), ${\text{π}}_{\text{2}}^{\text{H}}$ (dipolarity/polarizability), R₂ (excess molar refractivity), and V_x (McGowan volume). The MF is a third term added to the model of Potts and Guy (1992) or a sixth term added to the model of Abraham and Martins to account for mixture interactions based on physical chemical properties of the mixture components. Goodness of fit was assessed using coefficients of variation (r²) and internal and external validation metrics ($q_{\text{LOO}}^{\text{2}}$, $q_{\text{L25\%}}^{\text{2}}$, and $q_{\text{EXT}}^{\text{2}}$). Stepwise regression was used to select the best MF, based on r² values, from among the following physicochemical properties: water solubility, Henry's law constant, polarizability, partition coefficient, LogD, ovality, MW, molecular volume, topical polar surface area (TPSA), refractive index, molar refractivity, hydrogen bond acceptors, hydrogen bond donators, boiling point, melting point (MP), boiling point minus MP, vapor pressure, Connolly accessible area, Connolly molecular area, Connolly solvent excluded volume, pKa, number of atoms, number of rotatable bonds, Lipinski number, fugacity, bioconcentration factor, and atmospheric hydroxyl radical rate constant.

In Tables 6, 7, and 8, we report each model without and with the MFs. Tabulated statistics include the number of treatments (n), the coefficient of variation (r²), the square of the correlation coefficients adjusted to the number of degrees of freedom (adj. r²), the cross-validation square of the correlation coefficients using the “leave-one-out” ($q_{\text{LOO}}^{\text{2}}$) and the “leave-a-random-25%-out” ($q_{\text{L25\%}}^{\text{2}}$) techniques, the standard deviation (s), and the Fischer's statistical test (F) for each equation. Also listed in Tables 6, 7, and 8 are the p values associated with each model component. The capability of the models to predict the treatments of the validation set was determined by the external validation parameter ($q_{\text{EXT}}^{\text{2}}$). The $q_{\text{EXT}}^{\text{2}}=1-\text{PRESS/SD}$, where PRESS is the sum of the squared differences between the observed data and the predicted data for each treatment in the validation set and SD is the sum of the squared differences between the observed validation set treatments and the mean observed data of the training set treatments.

TABLE 6.

LFER Values for Pig Skin Diffusion Cells (PSFT) Logk_p (n = 384)—Abraham and Martins (2004) Model

r2	Adj. r2	$q_{\text{LOO}}^{\text{2}}$	$q_{\text{L25\%}}^{\text{2}}$	$q_{\text{EXT}}^{\text{2}}$	s	F	i	m	MF	$a\times \Sigma {\text{α}}_{\text{2}}^{\text{H}}$	$b\times \Sigma {\text{β}}_{\text{2}}^{\text{H}}$	$s\times {\text{π}}_{\text{2}}^{\text{H}}$	e × R2	v × Vx
0.53	0.52	0.51	0.51	0.41	0.36	83	2.55(0.19)	No MF		−1.45(0.21)	0.01(0.14)	0.27(0.12)	−0.55(0.13)	−1.39(0.09)
							p < 0.001	No MF		p < 0.001	p = 0.933	p = 0.020	p < 0.001	p < 0.001
0.71	0.70	0.69	0.69	0.44	0.23	151	3.14(0.15)	77.66(5.08) × 1/MP		−1.47(0.17)	−0.01(0.11)	0.27(0.09)	−0.56(0.10)	−1.39(0.07)
							p < 0.001	p < 0.001		p < 0.001	p = 0.963	p = 0.004	p < 0.001	p < 0.001
0.73	0.73	0.73	0.72	0.61	0.21	173	4.25(0.17)	−1.21(0.07) × HBAcc		−1.40(0.16)	0.03(0.10)	0.27(0.09)	−0.55(0.10)	−1.38(0.07)
							p < 0.001	p < 0.001		p < 0.001	p = 0.748	p = 0.002	p < 0.001	p < 0.001
0.73	0.73	0.72	0.72	0.61	0.20	208	4.27(0.16)	−1.21(0.07) × HBAcc		−1.44(0.11)	No $\Sigma {\text{β}}_{\text{2}}^{\text{H}}$	0.28(0.09)	−0.55(0.10)	−1.38(0.07)
							p < 0.001	p < 0.001		p < 0.001	No $\Sigma {\text{β}}_{\text{2}}^{\text{H}}$	p = 0.001	p < 0.001	p < 0.001

Note. SE in parentheses. HBAcc, number of hydrogen bond acceptors (calculated by www.molinspiration.com); 1/MP, inverse of the melting point (literature values from Syracuse University PhysProp Database http://esc.syrres.com/interkow/physdemo.htm).

TABLE 7.

LFER Values for Isolated Perfused Porcine Skin (IPPSF) LogAUC (n = 119)—Abraham and Martins (2004) Model

r2	Adj. r2	$q_{\text{LOO}}^{\text{2}}$	$q_{\text{L25\%}}^{\text{2}}$	$q_{\text{EXT}}^{\text{2}}$	s	F	i	m	MF	$a\times \Sigma {\text{α}}_{\text{2}}^{\text{H}}$	$b\times \Sigma {\text{β}}_{\text{2}}^{\text{H}}$	$s\times {\text{π}}_{\text{2}}^{\text{H}}$	e × R2	v × Vx
0.60	0.58	0.56	0.56	0.72	0.15	34	1.61(0.34)	No MF		−2.00(0.34)	−0.39(0.14)	0.04(0.14)	0.38(0.21)	−1.54(0.15)
							p < 0.001	No MF		p < 0.001	p = 0.005	p = 0.774	p = 0.067	p < 0.001
0.62	0.60	0.57	0.57	0.70	0.14	30	1.91(0.36)	−0.27(0.12) × HBAcc		−2.02(0.33)	−0.41(0.14)	0.07(0.14)	0.38(0.20)	−1.55(0.15)
							p < 0.001	p = 0.028		p < 0.001	p = 0.003	p = 0.610	p = 0.062	p < 0.001
0.69	0.68	0.66	0.66	0.81	0.12	42	1.79(0.30)	35.93(6.20) × 1/MP		−2.02(0.30)	−0.40(0.12)	0.09(0.13)	0.38(0.18)	−1.57(0.14)
							p < 0.001	p < 0.001		p < 0.001	p = 0.001	p = 0.475	p = 0.039	p < 0.001
0.69	0.68	0.66	0.66	0.81	0.12	51	1.81(0.30)	35.63(6.17) × 1/MP		−2.01(0.30)	−0.35(0.10)	No ${\text{π}}_{\text{2}}^{\text{H}}$	0.47(0.13)	−1.61(0.13)
							p < 0.001	p < 0.001		p < 0.001	p < 0.001	No ${\text{π}}_{\text{2}}^{\text{H}}$	p = 0.001	p < 0.001

Note. SE in parentheses. HBAcc, number of hydrogen bond acceptors (calculated by www.molinspiration.com); 1/MP, inverse of the melting point (literature values from Syracuse University PhysProp Database http://esc.syrres.com/interkow/physdemo.htm).

TABLE 8.

LFER Values for Pig Skin Diffusion Cells (PSFT) Logk_p (n = 384)—Potts and Guy (1992) Model

r2	Adj. r2	qLOO2	q1.25%2	qEXT2	s	F	i	m	MF	a × logKow	b × MW
0.33	0.33	0.32	0.32	NA	0.51	94	1.13(0.13)	No MF		−0.10(0.02)	−0.0058(0.0006)
							p < 0.001	No MF		p < 0.001	p < 0.001
0.55	0.54	0.54	0.54	NA	0.35	152	2.89(0.17)	−1.23(0.09) × HBAcc		−0.10(0.02)	−0.0058(0.0005)
							p < 0.001	p < 0.001		p < 0.001	p < 0.001

Note. SE in parentheses. HBAcc, number of hydrogen bond acceptors (calculated by www.molinspiration.com); 1/MP, inverse of the melting point (literature values from Syracuse University PhysProp Database http://esc.syrres.com/interkow/physdemo.htm). NA, not applicable.

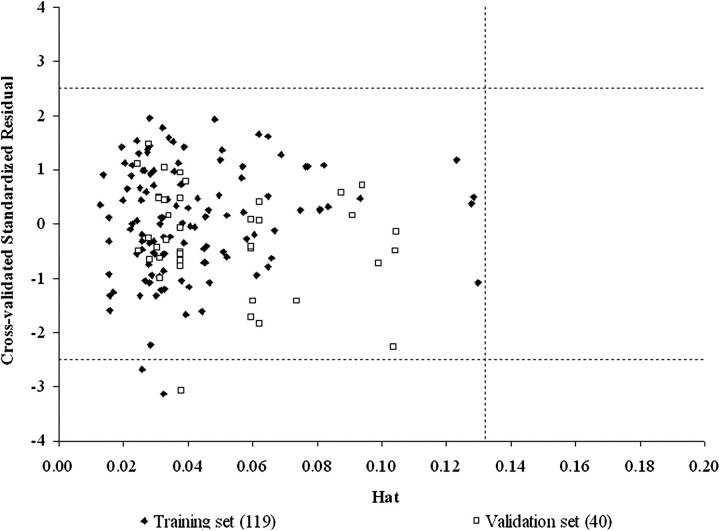
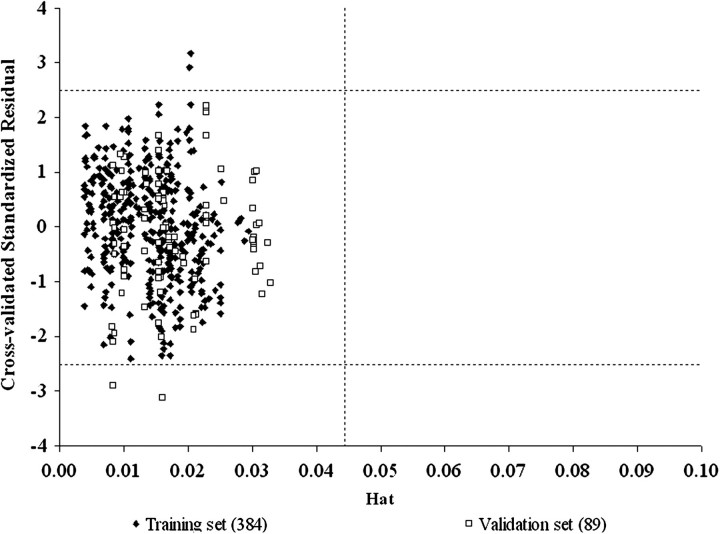
The Williams' Plot was used to visualize the applicability domain (AD). It is a plot of the standardized cross-validated residuals versus the leverage hat diagonal values (h). The standardized cross-validated residuals result from the $q_{\text{LOO}}^{\text{2}}$ calculations. The hat diagonal is calculated using the hat matrix: H = X(X^TX)⁻¹X^T, where H = Y^ (“y-hat” the predicted value of y), X is the (m × n) matrix, and X^T is the transpose of the X matrix (n × m). X is defined as the matrix of m covariate values for each of the n subjects, whereas Y is the dependent variable of interest. h* = 3(m + 1)/n, where, in this case, m is the number of model variables and n is the number of objects used to calculate the model. The AD is the area of the plot where h < h* (Gramatica, 2007; Papa et al., 2005).

RESULTS

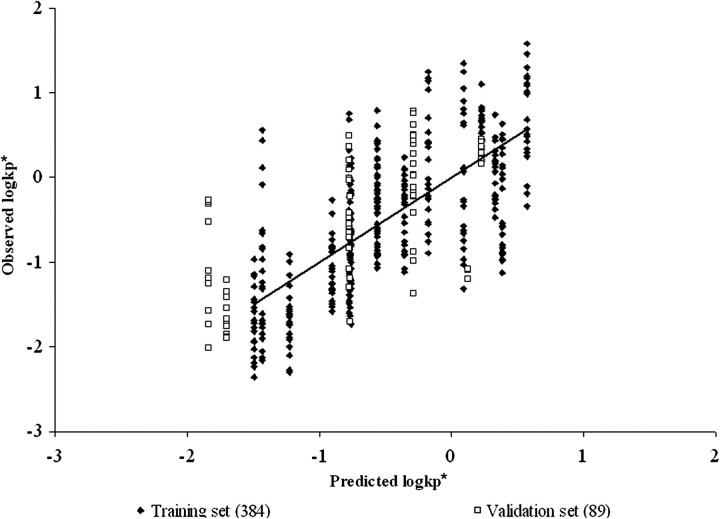
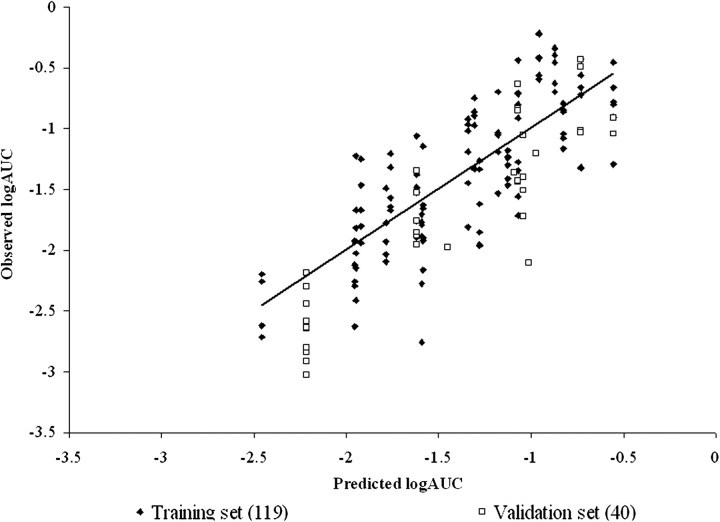
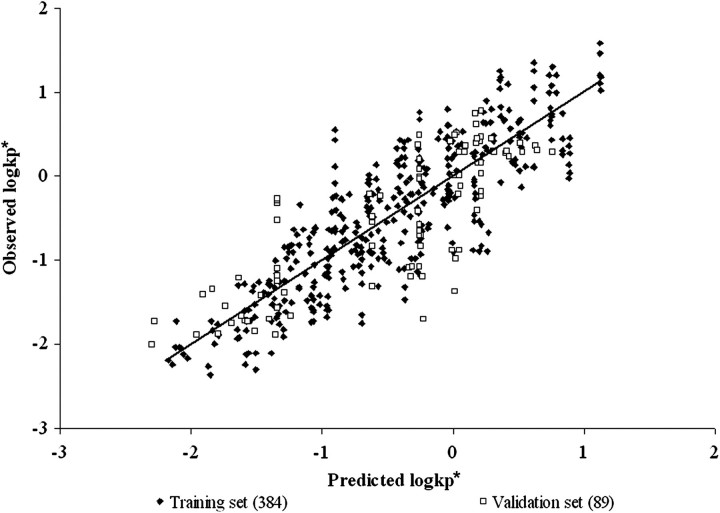
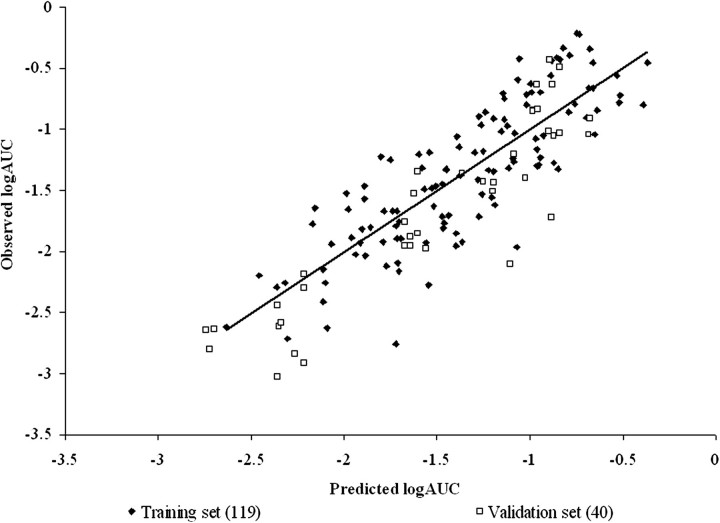
The best MFs of those evaluated were HBAcceptor (the number of hydrogen bond acceptors) and 1/MP (the inverse of the MP) for PSFT and IPPSF biological systems, respectively. Tables 6, 7, and 8 present the final LFER model fits for PSFT and IPPSF experiments for both MFs in both models. Figures 1–6 illustrate the goodness of fit (including training data and validation data points) of the Abraham's LFER model with no MF and best MF and the Williams' leverage plot showing the chemical AD for the final MF-containing model for PSFT and IPPSF fits, respectively.

FIG. 1.

Model of Abraham and Martins of the PSFT training and validation set data with no MF. r² = 0.53, adj. r² = 0.52, $q_{\text{LOO}}^{\text{2}}=0.51$, $q_{\text{L25\%}}^{\text{2}}=0.51$, and $q_{\text{EXT}}^{\text{2}}=0.41$.

FIG. 6.

Williams' leverage validation plot of the model of Abraham and Martins of the IPPSF training and validation set data with MF = 1/MP (the inverse of the MP). h* = [3(6 + 1)]/159 = 0.1321.

As can be seen from examining goodness of fit statistics as well as observed versus predicted plots, use of an MF in both systems significantly improved the ability of an LFER QSPR model to describe compound permeability compared with models that ignored the application mixture. This is best evidenced in the general improvement of r² and q² statistics when comparing models. In models that do not take into account mixture composition, the only predictor of the normalized absorptive flux $k_{\text{p}}^{\text{*}}$ are the physicochemical properties of the penetrant molecules that determine the slope of the mean regression relation. In addition, this results in the plots of Figures 1 and 4 having columns of data located at the penetrant's descriptor values, where the vertical height of each penetrant's column reflects the vehicle effect. In many cases, this vehicle effect is greater than the vertical component of the slope resulting from mean permeability. As can be seen in Tables 6, 7, and 8, the MF is not LFER model dependent as fits were also improved when the data were analyzed using the model of Potts and Guy (1992).

FIG. 4.

Model of Abraham and Martins of the IPPSF training and validation set data with no MF. r² = 0.60, adj. r² = 0.58, $q_{\text{LOO}}^{\text{2}}=0.56$, $q_{\text{L25\%}}^{\text{2}}=0.56$, and $q_{\text{EXT}}^{\text{2}}=0.72$.

A closer examination of the data presented in Tables 6, 7, and 8 for PSFT versus IPPSF model systems illustrates that different optimal MFs are needed for each model, with HBAcceptor being best for the PSFT and 1/MP best for the IPPSF data. In addition, if one examines the SE of the molecular descriptor coefficients, as well as the resultant p values, across models, it becomes evident that $\Sigma {\text{β}}_{\text{2}}^{\text{H}}$ (hydrogen bond acceptor basicity) in the PSFT and ${\text{π}}_{\text{2}}^{\text{H}}$ (dipolarity/polarizability) in the IPPSF models have errors that exceed the mean, with p values greater than α = 0.05, suggesting that these descriptors are not needed in the base LFER equation. We have reported the models with and without these terms. This is supported when these parameters are removed from the equations and the analysis repeated using the reduced model of Abraham and Martins.

The ability of the models to predict the validation data sets was determined by the external validation parameter ($q_{\text{EXT}}^{\text{2}}$). Tables 6, 7, and 8 list the $q_{\text{EXT}}^{\text{2}}$ for each model. In the PSFT section of Tables 6, 7, and 8, it can be seen that the model with the best MF resulted in a $q_{\text{EXT}}^{\text{2}}=0.61$, whereas the IPPSF model with the best MF resulted in a $q_{\text{EXT}}^{\text{2}}=0.81$. The PSFT validation set used was not as well predicted by the equation determined from the training set as the validation data set predicted by the IPPSF model. This is largely a function of the validation sets used, which were data previously conducted by our laboratory which included different marker and mixture components. The training sets were full factorial combinations more balanced for model definition. The $q_{\text{LOO}}^{\text{2}}$ and $q_{\text{L25\%}}^{\text{2}}$ statistics support the use of these models in the training sets consisting of similar penetrants and mixture components. In contrast, the validation sets are relatively imbalanced yet provide a broader chemical diversity in terms of both penetrants and mixture components.

Finally, the Williams' plots for both final models (Fig. 3 for PSFT and Fig. 6 for IPPSF data) indicate that the training and validation compounds fall within an appropriate chemical AD for the model defined by the descriptors of the model and modeled response. Data points for which a compound or mixture are not appropriate based on the defined model would fall to the right of the critical hat value (h*) and be excluded from the analysis. This provides an easy test of whether an unknown compound has a reasonable chance to be included in the AD of an existing analysis.

FIG. 3.

Williams' leverage validation plot of the model of Abraham and Martins of the PSFT training and validation set data with MF = HBAcc (the number of hydrogen bond acceptors). h* = [3(6 + 1)]/473 = 0.044.

CONCLUSIONS

These studies clearly demonstrate that components of a topical chemical mixture may modulate the dermal absorption of penetrants dosed in a mixture. In addition, the approach of using a composite MF, which takes into account the physical chemical properties of the mixture, allows for a mixture's potential effect on absorption to be quantitated in the framework of an accepted QSPR dermal absorption model. We use an LFER approach because numerous basic and theoretical studies have shown that multiple mechanisms of chemical penetration through skin may be operative preventing use of a single parameter to adequately predict absorption of a wide variety of substances. We have chosen the model of Abraham and Martins because of its wide use in this field. Recent work on diffusion cell studies have shown that one can formulate a reduced QSPR model based on simultaneous analysis of both penetrant and mixture data (Ghafourian et al., 2010); however, our goal was to determine how a mixture impacts on a QSPR model determined from single penetrants that is widely adopted in risk assessments.

These studies involve toxicologically relevant lipophilic compounds studied across various vehicles using an albumin-containing perfusate that contrasts with the more hydrophilic drugs dosed in aqueous vehicles using aqueous receptor fluids studied in other QSPR analyses largely targeted to drug development endpoints. Our focus is to develop an approach to handle vehicle interactions, which would be applicable to other data sets and be relevant to occupational and/or environmental exposure scenarios. Our study chemicals are relatively more lipophilic than those modeled in many QSPR studies, which were designed to predict absorption of relatively hydrophilic drug molecules (Ghafourian et al., 2010). Investigators have long known that there exists a parabolic relationship between the flux of chemicals across skin and logK_ow, peaking at a logK_ow of approximately 2–3, a value approximating the lipophilicity of the stratum corneum barrier lipids (Cross et al., 2003b; Roberts and Walters, 1998; Scheuplein and Blank, 1971). In fact, it has been shown that this relationship shifted to a lower logK_ow when lauric acid was added to an aqueous ethanol vehicle (Lee et al., 1994), supporting the MF concept that vehicles modulate the k_p − K_ow relationship. Permeability of more lipophilic penetrants in any vehicle becomes increasingly reduced because of resistance from dermal elements. Another difference with our work and those targeted toward drug delivery is that our studies use albumin-containing perfusate. This facilitates absorption of lipophilic compounds (Bronaugh and Stewart, 1984; Cross et al., 2003a) and generates data that can be directly compared across both PSFT and IPPSF model systems because the vascularized IPPSF requires albumin in the perfusate to maintain sufficient oncotic pressure to maintain capillary perfusion. Finally, use of albumin-containing perfusate is also more closely related to the in vivo scenario.

We estimate transdermal absorption in the PSFT system using an operational or apparent $k_{\text{p}}^{\text{*}}$ determined from the initial applied surface concentration in a specific mixture and the observed pseudo–steady state flux. We do not estimate a true steady state flux from an infinite dose exposure. Likewise, we do not conduct the studies occluded, which although would prevent evaporative loss, also occludes the stratum corneum barrier altering its inherent permeability. Finally, as discussed above, albumin is present in the media that alters the dermal penetration phenomenon away from those conditions that would be optimal to define a true Fickian permeability coefficient. The conditions employed in our study closely mimic natural occupational or environmental exposures. Unlike the design inherent to infinite dose studies, skin is not prehydrated in our experiments. Differences in the vehicle effects on percutaneous absorption of lactic acid were seen under finite versus infinite dosing designs (Sah et al., 1998). We hypothesize that the nature of our MF identifies rate-limiting processes involved in modulating penetrant absorption from a complex vehicle (e.g., altered solubility, binding, etc.) that may differ from exposures dosed under more artificial conditions.

One approach, which has been used to predict absorption from complex vehicle mixtures, is to experimentally estimate maximum flux determined from a saturated solution of a penetrant in a study mixture, a scenario that reflects maximum thermodynamic activity of the penetrants (Cross et al., 2001). This exposure scenario would be expected to be predictive of subsequent dermal absorption from a saturated solution; however, it may not be applicable to nonsaturated solutions and requires experimental studies, making the approach not amenable to estimating absorption from different mixtures, a major goal of our approach.

The primary finding of the present study is the difference in QSPR model structure between PSFT and IPPSF experiments, which implies different modulating factors in a system whose absorptive flux is primarily restricted by stratum corneum resistance (PSFT) versus one which also has dermal and vascular elements present (IPPSF). This is evidenced both by the requirement of different base QSPR descriptors needed for the systems (no $\Sigma {\text{β}}_{\text{2}}^{\text{H}}$ in PSFT and no ${\text{π}}_{\text{2}}^{\text{H}}$ in IPPSF) as well as the different MFs for both systems (Tables 6, 7, and 8). This comparison is relatively robust because all exposures use porcine skin from the same strain of pigs, use identical dosing conditions (concentration, finite dose, and no occlusion) to mimic in vivo exposures, and use the same perfusate and analytical technique.

This finding has many implications beyond its relevance to predicting absorption from a mixture in two different experimental model systems because the implication is clearly that physicochemical factors that are rate limiting in the simpler in vitro system may not be directly transferable to the more complex perfused skin system and, by extension, to the in vivo exposure scenario. Obvious differences would include interactions with dermal elements in the vascularized model, which are not operative in the diffusion cell system. The pharmacokinetics of penetration through a dermatomed skin model versus an intact epidermal-dermal skin barrier may also be significantly different and affect rate-limiting processes detectable in this pseudo–steady state experiment. All vehicle effects may not exhibit this biological system dependency, as we recently showed when low-level single-dose surfactant effects on dermal absorption in the IPPSF could be predicted from an inert membrane fiber model (Riviere et al., 2010), suggesting only solution effects were operative.

The MF approach confounds solvatochromatic effects of penetrant-vehicle interactions in solution (altered solubility, etc.) with vehicle interactions with the skin barrier. Workers have previously shown that vehicle pretreatment modulates subsequent absorption (Rosado et al., 2003). Although this reduces the ability of the model to assign specific mechanisms for the mixture effects seen, it also is more relevant in determining the nature of the effects expected when in vivo exposures to complex mixtures occur. The difference in both underlying model structure (four- vs. five-term model) and different MFs selected suggests that the rate-limiting process for a mixture's effect on absorption differs between the two biological systems studied, implying vehicle effects on skin and not simply solubility effects in solution, which is controlled across our biological systems. In our previous analysis of these data using a smaller set of penetrants, a similar phenomenon was detected where the best factors for PSFT were refractive index and TPSA of mixture components, whereas for IPPSF, it was log water solubility and ovality. The present study, consisting of a much larger number of chemicals conducted under identical controlled conditions, allows a specific test of this hypothesis to be conducted.

There are several implications resulting from this study. The most obvious conclusion is that knowledge of permeability from a simple vehicle is not sufficient to predict absorption from a more complex multicomponent vehicle. This is best seen comparing Figures 1, 2, 4, and 5. In many cases, the vertical height of the penetrant-specific columns in Figures 1 and 4 are greater than the vertical rise determined from the slope of the predicted absorptive flux for that penetrant. The vehicle effect dominates over inherent permeability. This is the scenario that this research is attempting to consider. The second implication is that the nature of the optimal QSPR model for in vitro diffusion cells versus an ex vivo isolated perfused skin model is different, suggesting that different rate-limiting processes are operative in both systems. This has a direct effect on using in vitro data to estimate in vivo exposures. For both implications, absorption data from a specific formulation or mixture exposure would be preferred and when available should be used. In the case when no data except knowledge of an apparent $k_{\text{p}}^{\text{*}}$ or absorptive flux from a single vehicle exposure in an in vitro system are available, an approach such as discussed in this paper needs to be developed.

FIG. 2.

Model of Abraham and Martins of the PSFT training and validation set data with MF = HBAcc (the number of hydrogen bond acceptors). r² = 0.73, adj. r² = 0.73, $q_{\text{LOO}}^{\text{2}}=0.73$, $q_{\text{L25\%}}^{\text{2}}=0.72$, and $q_{\text{EXT}}^{\text{2}}=0.61$.

FIG. 5.

Model of Abraham and Martins of the IPPSF training and validation set data with MF = 1/MP (the inverse of the MP). r² = 0.69, adj. r² = 0.68, $q_{\text{LOO}}^{\text{2}}=0.66$, $q_{\text{L25\%}}^{\text{2}}=0.66$, and $q_{\text{EXT}}^{\text{2}}=0.81$.

FUNDING

National Institute of Occupational Safety and Health Grant (R01 07555).