Design issues for population growth models

Abstract

We briefly review and discuss design issues for population growth and decline models. We then use a flexible growth and decline model as an illustrative example and apply optimal design theory to find optimal sampling times for estimating model parameters, specific parameters and interesting functions of the model parameters for the model with two real applications. Robustness properties of the optimal designs are investigated when nominal values or the model is mis-specified, and also under a different optimality criterion. To facilitate use of optimal design ideas in practice, we also introduce a website for generating a variety of optimal designs for popular models from different disciplines.

1 Introduction

Non-linear models are ubiquitous in all biological areas of science. Lindsey (2001) provided an eclectic collection of non-linear models used in areas such as epidemiology, ecology, pharmaceutical and biomedical areas. Motulsky and Christopoulos (2004) is another exemplary monograph that catalogues applications of nonlinear models in various disciplines. In toxicology, risk assessment models are frequently used to study dose-response relationship. Our interest is in growth models that appear in numerous disciplines, such as animal science, plant growth and cell proliferation. For example, Jolicoeur el at. (1992) reviewed and proposed new models for longitudinal growth of human stature. More general reviews of growth models include Fujii (2006) and Karkach (2006). Fujii (2006) reviewed the numerous and ever-growing growth models in auxology aimed at studying human time-series variations. Karkach (2006) also provided an in-depth review of models for individual growth rates for various species in animals, plants and human. The author noted that one reason for the abundance of research in this area is that different parts of the organisms, such as in plants, can grow with different patterns. There are many additional growth models proposed and they include Jolicoeur, Pontier and Pernin (1988), Jolicoeur and Pontier (1989), Jolicoeur, Pontier and Abidi (1992), and, Martin, Hauspie and Ranke (2005), just to name a few. It should be noted that longitudinal growth of stature of individuals (i.e. body growth) and growth in numbers of individuals in a population are different proceses. The former case is essentially a biologically continuous process, but population growth model is a continuous approximation to a discrete process that models increase of individuals in large populations.

Design issues for experiments in the biological sciences seem to be generally given short shrift. Many scientific papers do not justify the design employed for their studies even though the cost is readily acknowledged. In some studies, the study cost can be prohibitive because it requires a long time to obtain an appropriate number of observations. Statistical considerations can be incorporated in the construction of the designs that result in improved inference without increasing cost. For example, López-Fidalgo and Wong (2002) applied optimal design theory and constructed a variety of efficient designs for the widely used Michaelis-Menten model. Specifically, they found optimal designs for the Michaelis-Menten model for estimating one or two parameters and/or when there are competing interest in the two parameters. The authors showed that the optimal designs required fewer design points and offered substantial saving over designs implemented in the studies, including the popular uniform designs that take equal number of observations over a set of equally-spaced points.

In this paper, we are interested in addressing design issues for models that study growth and decline of a population. Like in many other applied disciplines, the bulk of the papers in the growth literature addressed modeling and estimation issues but not on design issues. Our goal is to choose optimal sampling times and how many to select at each time point. To fix ideas, we choose the model proposed by Jolicoeur and Pontier (1989) as an illustrative case to find an optimal design for estimating model parameters and interesting functions of model parameters. The mathematical model is

$$\text{E}(Y_t)=\frac{1}{C_1{e}^{t/D_1}+C_2{e}^{-t/D_2}},t\in [0,\infty ),$$ (1)

where C₁, C₂, D₁, D₂ ≥ 0, t is the time and Y_t the size or the proportion of the population at time t. The parameter D₁ is responsible of the growth of the population, D₂ measures the decline rate and C₁ and C₂ simultaneously control the relative rates of increase, decrease and height of the curve, that is the population size. This model is parsimonious and is used in ecology for studying population growth and decline in animals, or for studying the growth and decline of molecular or cellular populations within individual organisms.

Model (1) reduces to the logistic growth curve when (D₁ → ∞) and to the logistic decline curve when (D₂ → ∞). It also reduces to the growth exponential model when (C₁ = 0) and to the decline exponential model when (C₂ = 0). These limiting forms for the proposed model are given explicitly in Table 1 in Jolicoeur and Pontier (1989). Figure 1 shows the illustrative behaviors of these four cases subsumed in model (1).

Figure 1.

Comparison of the behavior of four particular cases of model (1): exponential growth (—), logistic growth (…), exponential decline (– –) and logistic decline (— - —).

Our purpose is to construct efficient designs for estimating model parameters (D-optimality) or specific parameters or linear combination of the model parameters (c-optimality). D-optimality is used when interest is in estimating all model parameters. A D-optimal design minimizes the volume of the confidence ellipsoid of the parameters, thereby ensuring that we have the most precise estimates for the parameters. Sometimes, a function of the model parameters is of interest. In this case, c-optimality is the design criterion typically used for this purpose and its name comes from the optimal design literature. As an example, consider model (1) and we want to estimate the time to maximal population growth or decline in model (1). In this case, time to maximal growth may be found by first differentiating the function in (1) with respect to t and solving the resulting equation. This means time to maximal growth or decline is a function of the model parameters and our interest is to estimate this function accurately. A c-optimal design fulfills this purpose by minimizing the variance of the estimate of this function. Such optimal designs can offer substantial savings in time, labor and cost and at the same time produce the most precise estimates by careful choice of the design. In our present context, such an optimal design will provide guidance on the number of sampling time points, the time points and how many to sample at each of these optimal sampling time points to get the most precise estimate once we are given a fixed amount of resources.

In the next section we describe the statistical set up and briefly review optimal design theory. Because of the complexity of the model, we only present numerically optimal designs, i.e. no analytical formulae for the optimal designs. The optimal designs provide valuable guidance for researchers in terms of cost savings and also a meaningful way for evaluating alternative designs. In Section 3, we present two illustrative examples that will be used to construct locallyD and c-optimal designs for model (1). Section 4 discusses properties of locallyD– and c–optimal designs for model (1) and their robustness properties to model assumptions. We conclude with an appendix that provides some technical justifications for our results.

2 Background

We assume that the total number of observations is N and is pre–determined by experimental cost constraints. An experimental design consists of a collection of points t₁, t₂,…, t_N, in a given interval 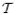. A convenient way to understand designs is to treat a design as a collection of different points from 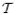, along with the proportion of the N observations allocated at these points. These are so–called approximate designs and they are essentially probability measures on 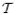. Symbolically, we denote an n-point approximate design by ξ, its design points by t₁,…,t_n and its weight distribution over these points by ξ(t₁),…,ξ(t_n). In practice, such a design takes approximately Nξ(t_i) observations at t_i,i = 1,…,n subject to Nξ(t₁)+…+Nξ(t_n) = N. As an example, suppose we have a model to represent growth of deer population in a region over time and we want to estimate the peak population in the region over a time period 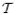. Assume further that we have resources to sample N = 100 deers from the region during this time period. The research question is how to sample these 100 deers over the time period 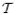? The c-optimal design ξ tells us to take a sample at n time points and roughly Nξ(t_i) deers at time t_i,i = 1,…,n subject to the restriction that Nξ(t_i)+…+Nξ(t_n) = N.

Approximate designs have increasingly proven to be an effective tool for studying design issues (Silvey, 1980, Stehlík, el at., 2008, and, Berger and Wong, 2007). This approach allows us to find optimal designs for many problems that were otherwise impossible to determine and more importantly, there are algorithms for finding a variety of optimal designs. Another advantage of this approach is that the theory is well developed; in particular, it allows us to search for the optimal design within approximate designs with a small number of support points. This simplifies and speeds up the search for the optimal design and in many cases enables us to find the optimal design analytically as well.

Throughout we suppose our mean outcome, i.e. average population growth can be adequately described by a regression model with time t as the single variable in the model. All random errors in the model are assumed to normally and independently distributed, each with mean 0 and constant variance. The mean outcome denoted by η(t, θ) is assumed known apart from the vector of model parameters θ. The design points are to be selected from a given time interval 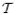and they represent sampling time points to observe the population growth.

Let f (t, θ) = ∂η(t, θ)/∂θ. Under the normality assumption, the Fisher information matrix of a design ξ is given by

$$M(\xi ,\theta )=\sum _{t\in \mathcal{T}}f(t,\theta )f^T(t,\theta )\xi (t),$$ (2)

apart from an unimportant multiplicative constant. The inverse of this matrix is asymptotically proportional to the variance-covariance matrix of the estimated parameters. For this reason, many design optimality criteria are formulated in terms of the information matrix. We sometimes denote M(ξ, θ) simply by M(ξ) when there is no confusion.

Unlike linear models, the information matrix of a design for a non-linear model depends on the model parameters. This means that our optimal design depends on the parameters that we are trying to estimate! Frequently, as a first step, we assume nominal values of the parameters are available either from similar studies or from pilot studies. Nominal values represent the best guesses for the true values of the parameters based on existing knowledge. Local optimal designs are then constructed based on nominal values (Chernoff, 1953). In practice, after the locally optimal design is determined from the nominal values, we use data from the design to estimate the parameters again. This iterative procedure is repeated and usually converges to some stable values for the parameters. This roundabout approach may seem awkward but frequently is a first and effective step in designing for a nonlinear model.

We consider only locally optimal approximate designs and focus on two optimality criteria in this work: D-optimality for estimating the model parameters θ and c-optimality for estimating a user-selected function of the model parameters. The D-optimality criterion minimizes the first-order approximation of the volume of the confidence ellipsoid of θ and is given by Φ_D[M(ξ)] = det M^−1/m(ξ), where m is the number of parameters in the model. D–optimal designs are popular and some argued that they are over-used. c–optimality, on the other hand, minimizes the asymptotic variance of a user-selected function in terms of θ, say c(θ). For instance, we may want to estimate the turning point of η(t, θ) or its maximum, or simply a linear combination of the model parameters. In the latter case, the function we want to estimate is c^Tθ and the vector c is user-selected. Our goal is to find a design that minimizes the asymptotic variance of the estimated c^Tθ and the optimality criterion is Φ_c[M(ξ)]=c^TM⁻¹(ξ)c.

It is known that these criteria are convex and differentiable functions of the information matrices (Silvey, 1980). Designs that minimize the above two criteria are called a D- and c-optimal designs, respectively. To verify whether a given design is optimal, one resorts to standard convex analysis arguments via directional derivatives and show that when the convex criterion Φ is differentiable, the design ξ* is Φ–optimal if and only if,

$$\Psi \left(t,{\xi }^{\ast }\right)=f^T\left(t\right)\nabla \Phi \left(M\left({\xi }^{\ast }\right)\right)f\left(t\right)-\text{tr}M\left({\xi }^{\ast }\right)\nabla \Phi \left(M\left({\xi }^{\ast }\right)\right)\ge 0,t\in \mathcal{T},$$

with equality at least at the support points of ξ*. Here ∇Φ(ξ) denotes the gradient of Φ(ξ) and the above inequality is referred to, in optimal design literature, as an Equivalence Theorem. Details are available in design monographs by Fedorov (1972) and Silvey (1980), for example, where algorithms and convergence issues for generating D and c-optimal designs are also discussed.

Following convention, the worth of a design ξ is measured by its efficiency. If the criterion is Φ(M(ξ)) and ξ is an arbitrary design, the Φ-efficiency of ξ is defined by eff_Φ(M(ξ)) = Φ(M(ξ*))/Φ(M(ξ)). For a statistical interpretation this definition requires a positively homogeneous criterion, that is Φ(λM) = Φ(M)/λ, λ > 0. The efficiency is usually multiplied by 100 and reported in percentage. If the value is 50%, this means that the design ξ has to replicated twice to perform as well as the optimal design ξ*.

3 Optimal experimental designs

We now provide two illustrative examples how optimal sampling times for estimating model parameters in the model (1) used by Jolicoeur and Pontier (1989) to study growth and decline rate for Paramecium caudatum and Meromyza variegata. The first concerns an experimental population in a mixed culture where that species competed unsuccessfully with another species and the second concerns the seasonal increase and decrease of the numbers of male flies of the species. Further details of the study are given in Gause (1934) and Hughes (1955). These two populations have very different behavior. The fitted model (1) for the two populations are respectively

$${\widehat{Y}}_t=\frac{1}{0.010e^{t/7.192}+0.538e^{-t/0.862}}$$

and

$${\widehat{Y}}_t=\frac{1}{0.009e^{t/21.419}+1.740e^{-t/3.280}}.$$

Figure 2 shows that there is a growth at the beginning from zero to some maximum point when the size of the population starts to decline to zero asymptotically. The rates of increase and decrease in the curves depend on the population, and for these two populations, both growth rates exhibit a steep increase to their peaks and followed by a gradual decline.

Figure 2.

Comparison of the estimated models for the populations of Paramecium (—) and Meromyza (- -).

Model (1) is non-linear in the four unknown parameters (C₁,C₂, D₁, D₂). Frequently, as in this case, we reparametrize the model to one with fewer nonlinear parameters; in this case, we have B = D₁, D = D₂ and C = C₂/C₁, and one linear parameter A = 1/C₁:

$$\text{E}(Y_t)=\frac{A}{e^{t/B}+C{e}^{-t/D}}.$$ (3)

Two important features of model (1) are the maximum response (population size) Y (t_max) and the point where this maximum is reached, t_max. A direct calculation shows

$$t_{\mathit{\text{max}}}=\frac{D_1{D}_2}{D_1+D_2}ln\frac{C_2{D}_1}{C_1{D}_2},$$ (4)

$$Y(t_{\mathit{\text{max}}})=\frac{D_2}{C_2(D_1+D_2)}{\left(\frac{C_2{D}_1}{C_1{D}_2}\right)}^{\frac{D_1}{D_1+D_2}}$$ (5)

The expression of t_max does not depend on C₁ or A but depends on C₁ and C₂ only through the ratio C = C₂/C₁. In terms of the new parameters, we have

$$t_{\mathit{\text{max}}}=\frac{BD}{B+D}ln\frac{BC}{D}\text{and}Y\left(t_{\mathit{\text{max}}}\right)=\frac{AD}{C(B+D)}{\left(\frac{BC}{D}\right)}^{\frac{B}{B+D}}.$$

Both these quantities are functions of the model parameters and the design problem is to find a design that minimizes the asymptotic variance of each of the estimates.

To determine optimal designs for model (3), we first calculate the Fisher information matrix defined in (2). This Fisher information matrix uses the linearized model obtained from the first order Taylor expansion. For the re-parametrized model (3), the parameter vector is θ = (A,B,C, D)^T and the vector of partial derivatives with respect to the parameters is

$$f\left(t,\theta \right)=\frac{1}{e^{t/B}+C{e}^{-t/D}}{\left(1,\frac{A{e}^{t/B}t}{B^2(e^{t/B}+C{e}^{-t/D})},\frac{-A{e}^{-t/D}}{e^{t/B}+C{e}^{-t/D}},\frac{-AC{e}^{-t/D}t}{D^2(e^{t/B}+C{e}^{-t/D})}\right)}^T.$$

Because of the complexity of this function, we applied an algorithm to find the optimal design numerically. The optimality or proximity of the generated design to the optimal (without knowing its optimum) is then verified using an equivalence theorem.

3.1 D–optimal designs

Let $C_1^{(0)},C_2^{(0)},D_1^{(0)}$ and ${\mathit{\text{D}}}_2^{(0)}$ be nominal values of the parameters for the original model (1) and A⁽⁰⁾, B⁽⁰⁾, C⁽⁰⁾ and D⁽⁰⁾ for the re-parametrized model (3). LocallyD–optimal designs were computed for the re-parametrized model using the software Gauss for a wide range of the nominal values. The main general characteristics of the locallyD-optimal designs are:

1. The D–optimal design has four equally weighted support points.

2. The D–optimal design depends on B⁽⁰⁾, C⁽⁰⁾ and D⁽⁰⁾ but not on A⁽⁰⁾.

3. The larger the value of either B⁽⁰⁾ or C⁽⁰⁾ is, the larger the D–optimal design support points are.

4. The smaller the value of either B⁽⁰⁾ or C⁽⁰⁾ is, the more likely 0 is a support point of the D-optimal design.

5. The four support points increase as D⁽⁰⁾ increases. Beyond a certain value of D⁽⁰⁾, which depends on B⁽⁰⁾ and C⁽⁰⁾, 0 is again a support point of the D-optimal design and the other three points also increase but more slowly.

Some of these characteristics can be proved to be true and actually applies more generally to many other models using algebra. For example, Property (1) asserts locally D-optimal designs are equally weighted, meaning that the design requires and equal number of observations at each time point. The mathematical justification for Property (1) relies on the arithmetic-geometric inequality and is given in Silvey (1980). These properties similarly apply to the optimal design for the original model. The D–optimal design for the original model is the same as the one found here except for a constant ratio $C_2^{(0)}/C_1^{(0)}$ because the D–optimal design for the re-parametrized model does not depend on A⁽⁰⁾. In both cases, the locallyD–optimal designs are equally weighted at 4 points; for the Paramecium caudatum example, these points are at 1.9,3.5,5.7 and 13.2 and for the Meromyza variegata example, the four points are at 10.58, 16.40, 23.87 and 46.55. We alert the reader that these are locally D-optimal designs and so these optimal sampling time points do depend on the nominal values assumed. If the nominal values for any of the parameters A⁽⁰⁾, B⁽⁰⁾,C⁽⁰⁾ and D⁽⁰⁾ change, the optimal sampling time points may also change.

It is interesting to set certain parameters in the model to selected values as described in Section 1 and consider the simpler and commonly used submodels in practice. The locally D-optimal designs for these models are reported below:

• Exponential growth model: If t ∈ [0,b], the D–optimal design has the same weight at b − D(0) and b when b − D⁽⁰⁾ ≥ 0 and at points 0 and b if b − D⁽⁰⁾ < 0.

• Logistic growth model: The D–optimal design is equally supported at three points. On the design interval [0,b], the points may be either 0, t₂ and b or t₁, t₂ and b depending on the nominal values of C⁽⁰⁾ and D⁽⁰⁾. The latter case occurs when C⁽⁰⁾ is much larger than D⁽⁰⁾ and the interior point is a solution of a complex equation derived from an equivalence theorem. For example, in the former case, the interior support point t₂ is the solution of the equation:

  $$b\left[e^{t_2/D^{(0)}}+C^{(0)}(-1+2e^{t_2/D^{(0)}})\right]=(-1+e^{b/D^{(0)}})\left[e^{t_2/D^{(0)}}(D^{(0)}-t_2)+C^{(0)}(D^{(0)}+t_2)\right].$$

  Conradie (2003) used this model to study the changes in the population of Leysera gnaphalodes. The response variable Y_t is the frequency of the population at time t in years, A is the ecological capacity and 1/D is the maximal annual rate growth in a non–restricted population. When t = 0, Y₀ = A/(1 + C) and we have C = A/Y₀ − 1. Thus C is determined by the initial size of the population. The fitted model is Ŷ = 89.30/(1 + 656.78e^−3.40t), t ∈ [0,7] and the D–optimal design is equally supported at 1.6, 2.2 and 7.

• Exponential decline model: If t ∈ [0,b] the D–optimal design is equally supported at either 0 and B⁽⁰⁾ or at 0 and b; the former occurs if b − B⁽⁰⁾ ≥ 0 and the latter occurs if b − B⁽⁰⁾ < 0 (see Müller and Pázman, 1998). Dette et al. (2006) provided D–optimal designs for other forms of the design intervals.

• Logistic decline model: On the interval [0,b], the D–optimal design is equally supported at three points and two of them are at the extreme ends of the design interval. This model was used by Straetemans et al. (2005) in a drug combination experiment as part of an oncology study to examine the inhibition effect of a combination of two compounds. The response variable Y is the measured radioactivity and the independent variable was the logarithm of the concentration, t. Data from the oncology study were used and the fitted homoscedastic model is approximately Ŷ_t = 7080/(1.9 + e^t/1.12), t ∈ [−2.5,2.1]. Straetemans et al. used a 9-point design. The locallyD–optimal design obtained numerically is equally supported at the points -2.5, -0.1 and 2.1. The D-efficiency of the design used in Straetemans et al. is about 77%.

3.2 Locallyc–optimal designs

Locallyc-optimal designs are used to estimate a function of the model parameter. This function depends on the object of interest and can be (i) simply a linear function or (ii) a nonlinear function of the model parameters. We discuss these two cases separately. A simple example for case (i) is when each parameter of the original model represents a characteristic of the population and so it makes sense to find an optimal design to estimate the particular parameter as precise as possible. In this case, we want to estimate c^Tθ and c is the zero vector but with one of its entries equal to one. The c-optimal design minimizes the variance of the estimate over all designs on the design interval. Using nominal values from the two examples in Jolicoeur and Pontier (1989), we determine locallyc-optimal designs for different vectors c. Table 1 shows that all the locallyc-optimal designs for each example are supported at the same points with different weights. In both examples, the distribution of the design weights are similar even though the optimal design points are quite different. A reason for this is the different nominal values used in each example.

Table 1.

Locallyc–optimal designs for the Paramecium caudatum example with sampling times at 1.27,3.38,5.85 and 16, and locallyc-optimal designs for the Meromyza variegata example with sampling times at 8.15,16, 24.57 and 55.50. All locally c-optimal designs were found using nominal values from Jolicoeur and Pontier (1989).

	Types of Optimal Designs	Weights
Paramecium caudatum	cC1 –optimal design	0.07, 0.06, 0.37, 0.50
	cC2 –optimal design	0.74, 0.14, 0.07, 0.05
	cD1 –optimal design	0.04, 0.03, 0.20, 0.73
	cD2 –optimal design	0.50, 0.24, 0.15, 0.11
Meromyza variegata	cC1 –optimal design	0.08, 0.06, 0.33, 0.53
	cC2 –optimal design	0.67, 0.16, 0.10, 0.07
	cD1 –optimal design	0.05, 0.04, 0.20, 0.71
	cD2 –optimal design	0.50, 0.23, 0.15, 0.12

Case (ii) arises when we are interested to estimate the maximum response Y(t_max) or the point t_max where the maximum is reached. In such cases, we want a design that minimizes the asymptotic variance of the estimated quantity of interest. Specifically, if c(θ) is the function of interest, we want to find a design ξ* that minimizes $\frac{\partial c(\theta )}{\partial \theta }M{(\xi ,\theta )}^{-1}\frac{\partial c(\theta )}{\partial {\theta }^T}$ when θ is set equal to the nominal value.

The above numerically optimal designs were found using a computer algorithm. Details of the algorithm can be found in standard design monograph such as Fedorov (1972) and Silvey (1980). For completeness, we provide the justifications of the optimal designs in the Appendix. The optimal designs for estimating the maximum response are one-point designs; at 4.7 for the Paramecium caudatum example and 20.5 for Meromyza variegata example. For both examples, the c–optimal designs for estimating t_max, the point where the maximum is reached have 3 optimal sampling time points. For the Paramecium caudatum example, the points are 1.32, 3.45 and 6.15 with corresponding weights 0.19, 0.4 and 0.41, respectively. For the Meromyza variegata example, the points are 21, 52 and 54 with corresponding weights 0.17, 0.41 and 0.42, respectively.

4 Discussion

We now study robustness properties of optimal designs for model (1). It is obvious all optimal designs are constructed from an assumed model and the important question to ask is how sensitive the optimal designs are to model mis-specification. To investigate this issue, we evaluate the efficiencies of the locally D-optimal designs under three common and important situations: (1) when there are mis-specifications in nominal values for the model parameters, (2) the model is mis-specified and (iii) under a different optimality criterion or goal. These are useful studies to undertake to gain further insights into the optimal design before implementation (Wong, 1994, Moerbeek, 2005). We also briefly discuss alternative and more complicated designs for the model.

4.1 Efficiencies under mis-specification of the model parameters

The nominal values for the model parameters used in the Paramecium caudatum data from Jolicoeur and Pontier (1989) were A⁽⁰⁾ = 98.56, B⁽⁰⁾ = 7.19, C⁽⁰⁾ = 53.00 and D⁽⁰⁾ = 0.86. Nominal values are usually available from pilot studies or similar studies. The locallyD–optimal design depends on B⁽⁰⁾, C⁽⁰⁾ and D⁽⁰⁾ and it is interesting to investigate whether there is a substantial loss in efficiency when these nominal values are mis–specified. To do this, we first find the numerically local D–optimal designs for a set of different nominal values,say, B⁽⁰⁾ = 7.19 ± 3, C⁽⁰⁾ = 53.00 ± 25 and D⁽⁰⁾ = 0.86 ± 0.2. These ranges were based on the standard errors for the estimated parameters reported in Jolicoeur and Pontier (1989), but other ranges can be used as well. We then calculated the D-efficiencies of these D–optimal design relative to the one with the original nominal values B⁽⁰⁾ = 7.19, C⁽⁰⁾ = 53.00 and D⁽⁰⁾ = 0.86. Table 2 displays these efficiencies.

Table 2.

D–efficiencies of D–optimal design for the Paramecium caudatum example when the nominal values B⁽⁰⁾, C⁽⁰⁾ and D⁽⁰⁾ change.

C(0)	28	28	28	53	53	53	78	78	78
D(0)	0.66	0.86	1.06	0.66	0.86	1.06	0.66	0.86	1.06
B(0) = 4.19	0.37	0.65	0.82	0.54	0.82	0.91	0.64	0.88	0.89
B(0) = 7.19	0.62	0.92	0.98	0.82	1	0.90	0.91	0.97	0.78
B(0) = 10.19	0.70	0.94	0.91	0.88	0.95	0.77	0.94	0.88	0.64

Table 2 shows efficiencies of the locallyD-optimal design under nominal mis-specification mis-specification. The main and clear message from the table is that the optimal design performs in a non-systematic way when nominal values of the full set of parameters are varied. As an example, we observe that when C⁽⁰⁾ = 78 and D⁽⁰⁾ = 0.86, the efficiencies vary from 88% to 97% and B⁽⁰⁾ varies from 4.19 to 10.19, suggesting that the optimal design is quite robust when B⁽⁰⁾ is mis-specified at this specific set of nominal values for C⁽⁰⁾ and D⁽⁰⁾. When this set of nominal values is C⁽⁰⁾ = 28 and D⁽⁰⁾ = 0.66, mis-specification in B⁽⁰⁾ will cause the D-efficiencies of the D-optimal design for model (1) to vary from 37% to 70%. For this example, the lowest efficiency of the locallyD-optimal design is 37%, suggesting that mis-specification in nominal values can result in an unacceptable loss in efficiency. It is therefore prudent to always perform a robustness study before the design is implemented.

We computed the efficiencies of the locallyD– and c–optimal designs for the Paramecium caudatum example when they are used to estimate the model for the Meromyza variegata example, and vice versa. All the efficiencies are almost zero. This is not surprising because the nominal values in both examples are quite different and nominal values for the model parameters can have a substantial impact on the resulting design.

4.2 Efficiencies under different a model assumption

We also computed D-efficiencies of the D–optimal designs for model (1) when they are used for the submodels. In order to obtain D–optimal designs for the submodels, we assume the time intervals over which we can sample are [0, 13.2] and [0, 46.55], respectively for the Paramecium and Meromyza populations. Table 3 shows the efficiencies of the designs when a submodel holds. It is remarkable that the D-optimal designs for model (1) have very low efficiencies for the growth exponential model in both populations. The practical implication here is that optimal design can be very sensitive to model specification, and generally does not perform well under another model, even within the same class of models as we see here.

Table 3.

D–efficiency of the D–optimal design for model (1) when a submodel is assumed.

	Growth Exp.	Growth Log	Decline Exp.	Decline Log.
D–optimal (Paramecium)	0.00	0.82	0.45	0.58
D–optimal (Meromyza)	0.01	0.82	0.29	0.56

4.3 Efficiencies under another criterion

We now compare the performance of the D– and c–optimal designs under a variation of optimality criteria (Table 4). The behavior of the efficiencies is very similar in both examples even though the assumed nominal values are quite different. The largest efficiencies correspond to c_Ci–optimal designs when they are used to estimate D_i, i = 1,2. The lowest efficiencies are those corresponding to the c–optimal designs for estimating D_i (respectively C_i) when they are used to estimate D_j (respectively C_j), i, j = 1,2, i ≠ j.

Table 4.

Efficiencies of the optimal designs for the Paramecium caudatum (Meromyza variegata) population.

	D–eff	cC1–eff	cC2–eff	cD1–eff	cD2–eff
D–optimal	1 (1)	0.60 (0.60)	0.48 (0.54)	0.46 (0.47)	0.67 (0.67)
cC1–optimal	0.60 (0.61)	1 (1)	0.12 (0.16)	0.83 (0.88)	0.22 (0.23)
cC2–optimal	0.50 (0.59)	0.15 (0.20)	1 (1)	0.09 (0.14)	0.77 (0.89)
cD1–optimal	0.42 (0.45)	0.80 (0.86)	0.07 (0.10)	1 (1)	0.12 (0.14)
cD2–optimal	0.76 (0.76)	0.31 (0.32)	0.81 (0.90)	0.20 (0.22)	1 (1)

The locallyc-optimal designs for estimating the maximum response and time to maximal response can be found directly using standard algorithms for generating them as described in design monographs such as Fedorov (1972), Silvey (1980) and Pazman (1986). For the two examples, these c-optimal designs are one-point designs but the optimal designs for estimating the time to maximum are supported at 3 points with uneven weights. We computed the efficiencies of the above optimal designs for estimating the maximum response and all of them are near zero. This means that the D– and c–optimal designs are not adequate at all to estimate the maximal mean response. The take-home message here is that optimal design provides the most accurate estimate or estimates but can perform abysmally under another design criterion. This observation does not apply specifically to model (1) but more generally to all nonlinear models as well.

In summary, design issues are under-addressed in many applied fields. We illuminated these issues using a popular population growth/decline model with two real examples from the biological sciences. We constructed locallyD and c-optimal designs for estimating model parameters, singly or all the parameters in the model. We also found optimal designs for estimating the maximum population growth and time to maximum growth in the population; interestingly, the former requires one time point and the latter requires 3 time points. Our robustness study shows that optimal designs are generally sensitive to model mis-specification, optimality criteria and also perform unpredictably when the model for the mean response is changed. The practical implication is that while the optimal design is constructed from theory, it is always important to conduct a robustness study to ascertain its utility in practice. In most cases, the optimal design should be modified to meet practical concerns. One common modification is to add more points to be able to conduct a lack of fit test. The purpose of the optimal design then is to make sure the modified optimal design does not stray too far from the optimum as judged from its efficiency relative to the optimum. We advocate that this approach be applied to all general design problems.

The above optimal designs require nominal values for construction and implementation. One common way to circumvent this dependence is to use a Bayesian approach or a maximin approach. In the former case, we assume a prior distribution on the unknown parameters is available and we construct the information matrix by averaging over the prior information. The maximin approach assumes a certain range of plausible values for each parameter is available and the maximin optimal design maximizes the minimal efficiency regardless the true values of the model parameters as long as they are within the plausible region. Alternatively, minimax optimal design minimizes the worst possible outcome in the sense that it minimizes the maximal inefficiency that can arise from wrong nominal values. Our experience is that minimax or maximin optimal designs are more appealing to practitioners who have less difficulty in specifying a range of plausible values for each model parameter of interest. This is in contrast to asking practitioners to come up with a single best possible value for the parameter in the case of locally optimal design, or a distribution of possible values of the parameter for Bayesian optimal design. Minimax or maximin optimal design represents a compromise for the two extreme cases. However they are usually much more difficult to find and defy analytical descriptions except for the simplest case. Some useful references for minimax optimal design are Wong (1992), Müller (1995), Müller and Pazman (1998), King and Wong (1998, 2000) and, Tommasi and López-Fidalgo (2004).

For applied statisticians or practitioners, optimal designs for specific models are not easily available. The theory behind the construction of the optimal design can be difficult and even when it is possible to do so, the task can be a time consuming undertaking. With this in mind, the third author has constructed a web site for generating a variety of optimal designs for several commonly used models in different fields. This free interactive site is at http://optimal-design.biostat.ucla.edu/optimal/ and it requires the user to first select a statistical model from a list of available models and also an optimality criterion. The user then supplies design parameters to generate an optimal design. The site also enables the user to evaluate efficiency of any design of interest. In particular, this option evaluates the efficiency of the modified optimal design when the user finds it necessary to make changes to the optimal design. We hope this site will facilitate and encourage practitioners to incorporate optimal design ideas in their work.

Appendix

Suppose Y is normally distributed with mean E(Y) = η(t,θ), t ∈ 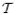and Var(Y) = 1, say. Let f(t) = ∂η(t,θ)/∂θ. The Fisher in formation matrix at point t is defined as I(t,θ) = f(t)f^T(t). Suppose that there is interest in estimating a local extremum of the mean response function. The point where the extremum is reached v(θ) solves the equation $\frac{\partial \eta (t,\theta )}{\partial t}=0$. The goal is to find a c-optimal design to estimate the maximal response given by ψ(θ) = η[v(θ),θ]. The vector c has to satisfy $c={\psi }_{\theta }=\frac{\partial \psi (\theta )}{\partial \theta }=\frac{\partial v(\theta )}{\partial \theta }{\left(\frac{\partial \eta (t,\theta )}{\partial t}\right)}_{t=v(\theta )}+{\left(\frac{\partial \eta (t,\theta )}{\partial \theta }\right)}_{t=v(\theta )}={\left(\frac{\partial \eta (t,\theta )}{\partial \theta }\right)}_{t=v(\theta )}=f[v(\theta )]$.

Using a celebrated geometric argument from Elfving theorem, it follows that if f[v(θ)] is a point on the boundary of the convex hull of the Elfving set, the c–optimal design is a one-point design concentrated at v(θ). The optimal design for estimating v(θ) is the c–optimal design where the vector c is given by

$$c=v_{\theta }=-\frac{{\left(\frac{{\partial }^2\eta (t,\theta )}{\partial t\partial \theta }\right)}_{t=v(\theta )}}{{\left(\frac{{\partial }^2\eta (t,\theta )}{\partial t^2}\right)}_{t=v(\theta )}},$$

which is obtained from the equation

$$0=\frac{\partial }{\partial \theta }\left[{\left(\frac{\partial \eta (t,\theta )}{\partial t^2}\right)}_{t=v(\theta )}\right]=\frac{\partial v(\theta )}{\partial \theta }{\left(\frac{{\partial }^2\eta (t,\theta )}{\partial t^2}\right)}_{t=v(\theta )}+{\left(\frac{{\partial }^2\eta (t,\theta )}{\partial t\partial \theta }\right)}_{t=v(\theta )}.$$