How Spacing of Data Collection May Impact Estimates of Substance Use Trajectories

Abstract

The goal of this study is to provide an empirical example using longitudinal cigarette smoking data that compares results of growth mixture trajectory models based on contiguous measurements and snapshot measurements. Data were drawn from an intensive longitudinal study of college freshman (N=905) with a previous history of smoking. Participants provided weekly smoking reports for 35 consecutive weeks. We found that using contiguous weekly data (35 waves) or 6-wave, or 4-wave snapshot data provided similar trajectory curves and proportions. However, there were notable differences in individual trajectory assignments based on contiguous and snapshot measurements.

Introduction

Over the past two decades, the development of substance use behavior has been evaluated through numerous prospective studies aimed at characterizing population subgroups that follow distinct trajectories of use (Costello et al., 2008, Chassin et al., 2002, Ellickson, Martino, & Collins, 2004), and abuse or dependence (Chung, Maisto, Cornelius, Martin, & Jackson, 2005; Hu, Muthen, Schaffran, Griesler, & Kandel, 2008; Jackson, Sher, & Wood, 2000) over time. Recently, growth mixture trajectory methods (Jones and Nagin, 2001; Muthén and Muthén, 2000; Nagin, 2005) have become the analyses of choice for evaluating these trajectory subgroups across diverse samples (e.g. Ellickson et al., 2004; Costello et al., 2008; Delucchi et al. 2004). Often termed growth mixture modeling or semiparametric group-based modeling, these methods identify unique trajectories, assess each individual’s probability of following each trajectory and evaluate whether potential predictors are associated with the likelihood of trajectory membership.

Studies in which growth mixture trajectory methods have been employed have utilized a diverse array of longitudinal designs defined according to such features as the number of prospective assessments (e.g. from 3 to more than 50), the time between assessment points (e.g. days, weeks, months or years), the regularity of assessment waves (e.g. evenly spaced or irregular) and the total duration encompassed by the measurement periods (e.g. from less than 1 year to more than 50 years). Despite this variability, the vast majority of prospective studies aimed at elucidating developmental substance use trajectories have been based on “snapshots” of behavior followed by rather long periods between subsequent assessment waves (i.e. 1 or more years). This is particularly true of studies of smoking behavior, the most extensively studied substance use to date. These studies typically have assessment periods that are at least 1 year apart and have a varying number of assessment waves ranging from 3 (Costello, Dierker, Jones, & Rose, 2008, Chassin, Presson, Pitts, & Sherman, 2000) to 10 (Lessov-Schlaggar et al., 2008, Orlando, Tucker, Ellickson, & Klein, 2004). In these studies, current smoking is typically defined based on recall of smoking behavior over the past 30 days. Some of these studies have taken advantage of a cohort-sequential design which permits modeling of more time points based on age instead of actual assessment waves (Abroms, Simons-Morton, Haynie, & Chen, 2005, Chassin, et al., 2000, Costello, Dierker, Jones, & Rose, 2008). Snapshot smoking trajectory studies have provided evidence for three (White, Pandina, & Chen, 2002), four (Audrain-McGovern et al., 2004), five (Abroms, et al., , 2005; Colder, 2001; Guo et al., 2002), and six (Chassin, et al., 2000; Costello, et al., 2008; Lessov-Schlaggar et al., 2008; Orlando, Tucker, Ellickson, & Klein, 2004; Stanton, Flay, Colder, & Mehta, 2004) distinct smoking trajectory groups. Recently, the increased use of newer technologies such as web-based surveys and palm pilots have made both shorter intervals between assessments and more frequent waves of data collection feasible (Dierker et al., 2006; Tan et al., under review). Thus, in many cases, the careful study of substance use onset, maintenance, cessation, and relapse can now include measurement intervals more on the order of monthly, weekly, or even daily (Dierker et al., 2006; Freedman, Lester, McNamara, Milby, & Schumacher, 2006; Hopper et al., 2006), making it possible to move away from sole reliance on widely spaced snapshots toward a more contiguous or proximal assessment of substance use behavior across time (Colder et al. 2008)

To date, the impact of this theoretically more informative design which includes contiguous or near contiguous measurement is unknown and the empirical question remains regarding how contiguously measured substance data might compare to the more traditional snapshot approach to assessment in growth mixture trajectory modeling. Despite the improved feasibility of frequent prospective behavioral measurement, given the cost as well as the increased burden to study participants, it is important to evaluate what, if any improvement in classification might be achieved through contiguous measurement of behavior, allowing us to better inform the design of studies whose primary aim is to characterize substance use trajectories.

Summary

The present study draws on data from an intensive longitudinal study with reports of smoking behavior collected contiguously at weekly intervals across the entire freshman year of college. Our specific goal was to evaluate the results and interpretation of growth mixture trajectory models to determine: 1) whether a snapshot approach yields comparable results, with respect to estimated trajectory curves and individual trajectory assignments, to that of a more contiguous approach to assessment and 2) under what conditions a snapshot assessment is most similar to contiguous measurement. In this study, we varied both the number and timing of assessments for a snapshot approach and compared the results to those of a contiguous weekly assessment approach.

Method

Participants

Details regarding selection and retention in the UpTERN study are available in an earlier publication (Tiffany et al., 2004). Briefly, participants were selected from responses to a screener survey (N=4690) administered to incoming college students during the orientation program in the summer of 2002 (response rate 71%). Two thousand and one individuals completing the screener reported at least some experience with smoking (i.e. one or more puffs lifetime) and were invited to participate in the study (43%). The first 912 of these individuals were enrolled and completed the baseline survey and 905 took part in weekly web-based surveys throughout their first year in college (45%). The sample is 48% female and largely Caucasian.

Procedure

Each week, participants were asked to provide 7-day time-line follow-back reports on their cigarette smoking. Using a web-based survey protocol, participants were first asked about whether they smoked in the past week. Positive responses to these questions were followed by a 7-day follow-back calendar requesting the “number of cigarettes you smoked” on each day of the preceding week. A total of 35 weeks of data were available with an average response rate for the sample slightly over 90% for each week of the study.

Measures

Smoking Quantity

We calculated weekly quantity as the average number of cigarettes smoked on days during each week (weekly quantity) on which smoking quantity (could be 0) was reported. For example, suppose one subject reported past week smoking quantities (from Monday to Sunday) as: 3, 5, 10, NA, 0, NA, 5, where “NA” denotes missing value, then the averaged daily smoking quantity for the past week for this subject is: (3+5+10+0+5)/5 = 4.6. Because average negative smoking is never negative, these data could not be considered normally distributed. Therefore, as many previous applications have done, we log-transformed quantity to normalize the data in order to meet the assumption of normality for these data. Zeros were transformed to −5.5, i.e., log(1/254), to avoid infinities. Average smoking quantity was treated as missing if all smoking data were missing in that week.

To evaluate the impact of timing and spacing of measurements on our analysis, we chose two snapshot schedules: first, a 6-wave snapshot, consisting of past week smoking quantities at week 1, 8, 15, 22, 29, 35 (nearly 2 months between assessments); second, a 4-wave snap-shot consisting of smoking quantities at week 1, 12, 23, 34 (nearly 4 months between assessments). In addition, we analyzed the full design consisting of 35 consecutive weekly measurements (i.e., no gap between adjacent assessments) of smoking quantity.

Analytic Plan

The semi-parametric group-based approach, see Nagin (1999, 2005), was used to classify participants into discrete trajectory groups based on the three smoking data sets. This was implemented by using the SAS procedure PROC TRAJ (http://www.andrew.cmu.edu/user/bjones/index.htm).

Based on previous smoking trajectory research, which has identified a number of trajectory groups ranging from three (White et al., 2002) to seven (Colder et al., 2008), we tested each of these models for a range of trajectory groups (3-8 groups). We used combination of criteria to choose the number of trajectory groups to retain, including 1) statistical fit (Bayesian Information Criteria, BIC), 2) the average posterior probability of trajectory group membership, where an average value of .70 for all groups has been suggested as a minimum indicator of adequate model fit (Nagin, 2005), 3) parsimony and 4) interpretability of the trajectories.

Like Tan et al. (2009), we began by specifying a three-group model, and systematically increased the number of groups to eight. We assume all trajectory curves are polynomial of order up to 3 (cubic) and used a censored normal model in PROC TRAJ. That is, we assume any observed measurement, conditioning on membership and time, was from certain censored normal distribution. Results for the best fitting snapshot and contiguous models were then compared with respect to: 1) number and shape of the trajecties, and 2) consistency in individual assignment to trajectories, which was based on model estimated posterior probabilities for most likely class membership for each individual.

Results

Smoking Trajectory Analysis

Plots of the BIC values for all models are shown in Figure 1. Overall, BIC increased as the number of groups increased for all three data sets. In addition, there was a marked deceleration in change on the BIC between the 5 and 6 group models, and between 7 and 8 group models for each data set (Figure 1), suggesting that either the 5-group or 7-group model might be the best fitting for all the three data sets. The range of average group posterior probabilities for the models based on the contiguous 35 weeks of data was slightly higher for the 5-group model (.967 to .998 vs. .942 to .990 for the 7-group model), and comparable for the 6-wave snapshot data (.918 to .994 for the 5-group model and .934 to .995 for the 7-group model), and 4-wave snapshot data (.935 to .987 for the 5-group model and .920 to .982 for the 7-group model). Given that both the 5- and 7-group models fit well, the 5-group models were selected for each data set as best fitting based on parsimony.

Fig. 1.

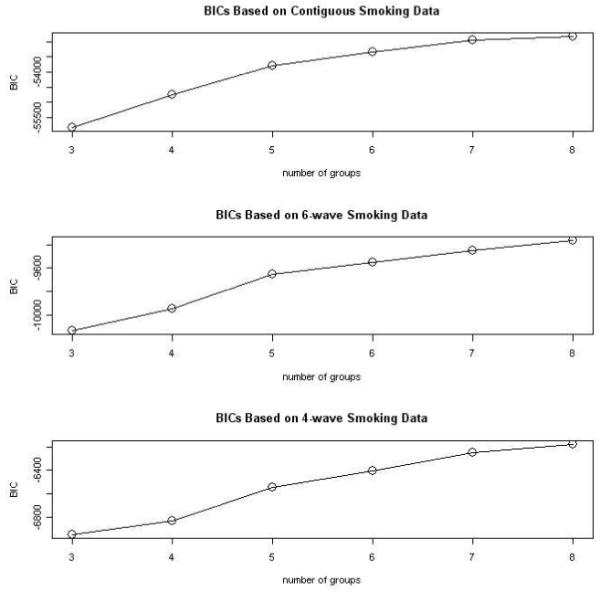
Plots of BIC’s for different models using contiguous (upper plot), 6-wave (middle plot), 4-wave data (lower plot)

Trajectory curves

For the contiguous (Figure 2), 6-wave (Figure 3) and 4-wave (Figure 4) smoking quantity data sets, the 5 group models revealed similar predicted smoking trajectories in terms of level of use and pattern of increase or decrease in smoking behavior, with comparable proportions (Table 1). In each model, the nonsmokers (trajectory 1 in Figures 2 to 4) represented the largest group (67.2% for contiguous data, 59.4% for 6-wave snapshot data, and 58.7% for 4-wave snapshot data). Also seen were two quitter groups. The early quitter (trajectory 2) group (11.3% for contiguous data, 17.0% for 6-wave snapshot data, and 18.5% for 4-wave snapshot data) was characterized in both contiguous and snapshot models by decreases in smoking quantity soon after the beginning of the academic year, while the late quitter (trajectory 3) group (6.3% for contiguous data, 8.2% for 6-wave snapshot data, and 6.9% for 4-wave snapshot data) showed declines in smoking quantity later in the academic year. A group of increasers (trajectory 4) (5.8% for contiguous data, 5.1% for 6-wave snapshot data, and 5.8% for 4-wave snapshot data) was also predicted in both contiguous and the snapshot smoking quantity models. This trajectory was characterized by increasing levels of smoking behavior across the academic year. Finally, a group of stable high smokers (trajectory 5) (9.4% for contiguous data, 10.4% for 6-wave snapshot data, and 10.1% for 4-wave snapshot data) showed a relatively steady pattern of cigarette use across the academic year.

Fig. 2.

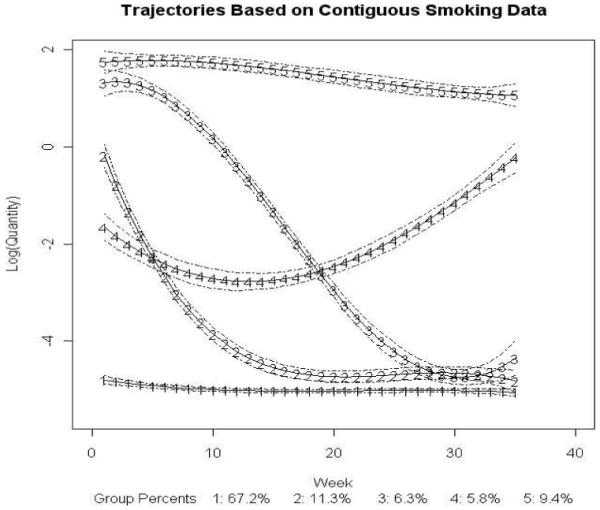
Trajectories of weekly average smoking quantity (contiguous data, 5-group cubic)

Fig. 3.

Trajectories of weekly average smoking quantity (6-wave data, 5-group, cubic)

Fig. 4.

Trajectories of weekly average smoking quantity (4-wave data, 5-group, cubic)

Table 1.

Coefficients of estimated Trajectories based on contiguous data and snapshot data (for each sub-group, the 4 coefficients in order are intercept, and linear, quadratic, cubic coefficient, the p-values for testing the significance of the coefficients are in the parenthesis)

	Contiguous		6-wave snapshot		4-wave snapshot
	Coefficient	Proportion	Coefficient	Proportion	Coefficient	Proportion
Non-smoker	−4.96(.00) −0.06(.00) 0.00(.00) −0.00(.00)	67.2%	−5.48(.00) 0.02(.26) −0.00(.41) 0.00(.48)	59.4%	−5.56(.00) 0.05(.04) −0.00(.20) 0.00(.40)	58.7%
Increaser	−1.45(.00) −0.22(.00) 0.01(.00) −0.00(.15)	5.8%	−1.82(.00) −0.43(.00) 0.03(.00) −0.00(.00)	5.1%	−2.55(.00) 0.13(.10) −0.03(.00) 0.00(.00)	5.8%
Early Quitter	0.47(.00) −0.68(.00) 0.03(.00) −0.00(.00)	11.3%	0.17(.20) −0.89(.00) 0.04(.00) −0.00(.00)	17.0%	0.50(.00) −0.89(.00) 0.04(.00) −0.00(.00)	18.5%
Late quitter	1.25(.00) 0.10(.01) −0.03(.00) 0.00(.00)	6.3%	1.30(.00) 0.08(.16) −0.02(.00) 0.00(.00)	8.2%	1.13(.00) 0.43(.00) −0.05(.00) 0.00(.00)	6.9%
Stable high	1.73(.00) 0.02(.42) −0.00(.15) 0.00(.21)	9.4%	1.78(.00) −0.04(.41) 0.00(.73) −0.00(.78)	10.4%	1.40(.00) −0.08(.15) 0.00(.30) −0.00(.49)	10.1%

Classifications

To evaluate the most likely trajectory followed by each participants in each data set, we next compared trajectory assignment based on maximum posterior probability. First, we compared trajectory assignment based on the 35 week contiguous data to that of the 6-wave snapshot data (Table 2). Overall, comparative assignment was excellent with about 81% overlap (the sum of diagonal numbers in Table 2 divided by 905) between trajectory assignment based on contiguous and that based on the 6-wave snapshot data. Specifically, 97% (513 of 531) of the individuals in the non-smoker group and 81% (79 of 97) of the individuals in the stable high group based on 6-wave snapshot data assigned to the corresponding trajectory groups based on the contiguous data. On the other hand, there were also notable exceptions: 1) of the 162 individuals assigned to the early quitter trajectory based on the 6-wave snapshot data, only 66 (41%) were classified as early quitter and 87 (54%) were classified as non-smoker based on the contiguous data; 2) of the 72 individuals assigned to the late-quitter trajectory based on the 6-wave snapshot data, only 45 (63%) were classified as late-quitter, while 17(24%) were classified as early-quitter based on contiguous data, and 3) of the 43 individuals assigned to the increaser trajectory based on the 6-wave snapshot data, only 26 (60%) were classified as increasers, while 9 were classified as early-quitter based on contiguous data. We also compared the trajectory assignment using contiguous data to that using the 4-wave snapshot data (Table 3) and found similar patterns of agreement and disagreement.

Table 2.

Confusion Matrix for Membership based on 6-wave data and that based on contiguous weekly data.

	6-wave
Contiguous	Non-smoker(1)	Early Quitter(2)	Late Quitter(3)	Increaser(4)	Stable High(5)	Marginals
Non-smoker(1)	513	87	4	6	0	610(67.4%)
Early Quitter(2)	10	66	17	9	0	102(11.3%)
Late quitter (3)	3	2	45	1	5	56(6.2%)
Increaser (4)	5	6	2	26	13	52(5.7%)
Stable high (5)	0	1	4	1	79	85(9.4%)
Marginals	531(58.7%)	162 (17.9%)	72 (8.0%)	43(4.8%)	97 (10.7%)

Table 3.

Confusion Matrix for Membership based on 4- and 6-wave data and that based on contiguous weekly data.

	4-wave
Contiguous	Non-smoker(1)	Early Quitter(2)	Late Quitter(3)	Increaser(4)	Stable High(5)	Marginals
Non-smoker(1)	516	82	2	10	0	610(67.4%)
Early Quitter(2)	9	73	7	10	3	102(11.3%)
Late quitter (3)	4	10	38	2	2	56(6.2%)
Increaser (4)	5	3	1	28	15	52(5.7%)
Stable high (5)	0	1	8	0	76	85(9.4%)
Marginals	534(59.0%)	169 (18.7%)	56(6.2%)	50 (5.5%)	96 (10.6%)
6-wave
Non-smoker(1)	519	0	0	11	1	531(58.7%)
Early Quitter(2)	2	142	5	10	3	162(17.9%)
Late quitter (3)	4	22	40	2	4	72(8.0%)
Increaser (4)	7	4	2	23	7	43(4.8%)
Stable high (5)	2	1	9	4	81	97(10.7%)
Marginals	534(59.0%)	169 (18.7%)	56(6.2%)	50 (5.5%)	96 (10.6%)

In addition, we compared the trajectory assignment using the 6-wave snapshot data to that using the 4-wave snapshot data (Table 3). This time, the overlap was about 90%, which was higher than the overlap of assignments based on contiguous and snapshot data, and group-specific overlaps were typically about 85% or greater. The most notable exception was, among 50 individuals assigned to the increaser trajectory based on the 4-wave snapshot data, only 23 (46%) were classified as increaser while 10 (20%) were classified as early-quitter based on 6-wave snapshot data.

To further check the disagreement of classifications, we compared observed smoking paths to estimated trajectory curves based on different datasets for all subjects assigned to different trajectories based on different data. Figures 5-6, summarize two typical situations. The upper plot in Figure 5 plots the observed contiguous trajectory and observed 6-wave trajectory of an individual who was assigned to group 1 (non-smoker) based on the contiguous cubic model, and group 2 (early quitter) based on the 6-wave cubic model. In addition, the two estimated mean trajectories (for group 1 and group 2, respectively) based on the contiguous cubic model are presented. The lower plot in Figure 5 plots the same observed trajectories, as well as the two estimated mean trajectories (for group 1 and group 2, respectively) based on the 6-wave cubic model.

Figure 5.

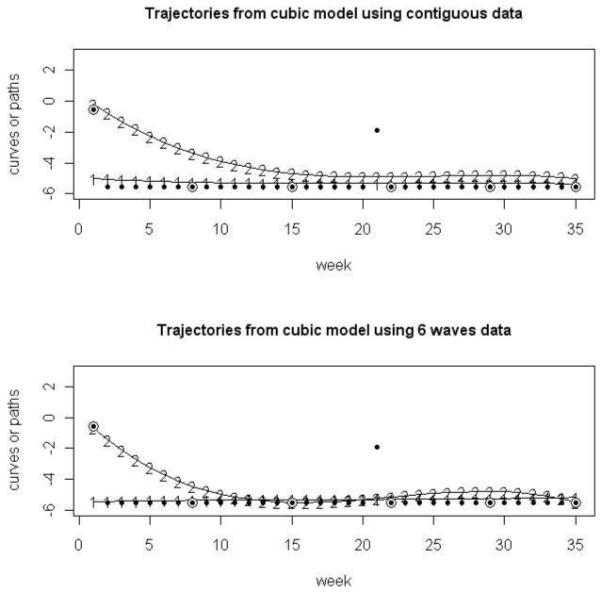
Typical Case 1: Observed versus contiguous estimated trajectories for a subject classified in group 1(non-smoker) based on the contiguous data model and in group 2(early quiter) based on 6-wave data.

Note: The observed contiguous trajectory is represented by small black dots and the observed 6-wave snapshot trajectory is represented by the encircled black dots. The estimated trajectories for groups 1(non-smoker) and 2(early quitter) based on contiguous data or 6-wave data are represented by the numbers 1 and 2, respectively.

Figure 6.

Typical case 2: Observed versus contiguous estimated trajectories for a subject classified in group 1(non-smoker) based on the contiguous data model and in group 2(early quitter) based on 6-wave data model.

Note: The observed contiguous trajectory is represented by small black dots and the observed 6-wave snapshot trajectory is represented by the encircled black dots. The estimated trajectories for groups 1(non-smoker) and 2(early quitter) based on contiguous data or 6-wave data are represented by the numbers 1 and 2, respectively.

This individual was assigned to group 1 (non-smoker) based on contiguous observation because for 33 out of 35 weeks this individual didn’t smoke. He/she was assigned to group 2(early quitter) based on 6-wave observation because this individual smoked in the first observation time, but didn’t smoke for the latter 5 observation times. Based on this plot, it’s easy to conclude that this individual should be assigned to non-smoker trajectory.

Figure 5 describes one typical situation of mismatched classification based on different data sets. The other typical situation is represented in Figures 6 which shows the observed trajectory of a different individual who was also assigned to group 1 based on contiguous data, but group 2 based on 6-wave snapshot data, with estimated mean trajectories from contiguous (upper plot) and 6-wave (lower plot) data models, respectively. This individual didn’t smoke for 27 out of the 35 weeks, and most of his/her smoking occurred in the first 12 weeks. This individual’s observed path indicated intermittent smoking for the first several weeks, but a relatively consistent nonsmoking pattern the rest of the time. Thus, the 6-wave assignment into the late quitter groups was reasonable. Because the contiguous data provided a greater proportion of nonsmoking time points compared to the 6-wave assessment, however, it is not surprising that this individual was assigned to the nonsmoking in the contiguous data model.

It is important to note that, despite some inconsistencies in terms of classification of individuals, the two estimated mean trajectories based on contiguous data were almost identical to the corresponding trajectories based on 6-wave snapshot data. This is consistent with our claim that comparable trajectories were revealed using different measurement waves.

Discussion

Despite the availability of excellent technical papers describing this method (Jones and Nagin, 2001; Muthén and Muthén, 2000) and even more numerous substantive papers that have applied growth mixture trajectory models to available substance use data, little information currently exists evaluating the impact of design and/or measurement decisions on the results and corresponding interpretation of these models (for an exception see Nylund, 2007). The goal of the present paper was to begin to fill this important gap through empirical analysis of longitudinal smoking data that compared the results and interpretation of trajectory models based on contiguous and snapshot measurements. Specific questions were: how spacing of observations affects 1) estimation of trajectory curves, and 2) individual assignments to trajectories.

Based on our empirical study, we found that if we assume a common model that can be estimated based on both contiguous and snapshot data, then we obtain comparable estimates of trajectory curves. Mathematically, the estimated curves (based on maximum likelihood principle) would converge to the “optimal” cubic curves that best approximate the underlying (true) trajectory curves (White, 1982), even when the true trajectories are more complicated than cubic curves. Based on the same model assumptions, e.g., cubic trajectory curves in our example, the advantage of using contiguous data over snapshot data is that the variance of the estimated trajectory curves based on contiguous data should be smaller than that of the estimated curves based on snapshot data, since more observations are available in contiguous data set.

The spacing of observations affects the individual assignment more fundamentally, despite consistencies across models in trajectory curves and in the proportions of individuals assigned to each trajectory group. As shown in our example, using snapshot data could cause serious misclassification of individuals, especially for individuals with non-stable behavior during the study period. Mathematically, classifications are based on the relative distances between the observed measurements and the group trajectory curves. Specifically, an individual is assigned to the trajectory which best describe the observed pattern of measurements. Snapshot measurements could pick points which make an individual’s observed trajectory different to that based on contiguous observations, and hence assign the individual to a different group than based on contiguous observations. It can be shown that, this type of misclassification is more likely to happen if an individual’s behavior is changeable (or non-stable) over the study period. This explains why the disagreement of assignments is more evident for individuals belong to the three changeable trajectories: increaser, early quitter, and late quitter, but much less evident for the two stable trajectories: non-smoker and high stable smokers (Table 2-3). Again, when simpler functional forms are estimated for trajectories, the advantages of contiguous assessment, at least in terms of sensitivity to changes in behavior, are diminished.

Future work

One important advantage of using more intensive contiguous measurements over a few widely spaced snapshot measurements is, given appropriate methodology, e.g., non-parametric approach, it allows more complex growth curves to reveal themselves, in addition to that simpler growth curves will be estimated with added precision (Collins, 2002). On the contrary, it is impossible to reveal complex growth curves with snapshot data which typically has only a few widely spaced measurements at pre-specified time points. Another disadvantage of using scheduled snapshot design is that such design may miss certain features that could affect the behavior of interest. For example, major holidays, breaks, and academic events may influence college students’ smoking behavior.

However, the benefits of intensive contiguous measurements need not always come with the cost of heavy participant burden pertaining to contiguous measurements. For example, one potential data collection strategy, which may maintain the advantages of contiguous data collection at a cost similar to a scheduled snapshot design, is to randomly assign a few measurement times for each subject so that different subjects don’t necessarily share common measurement times. Intuitively, this strategy enables the revelation of complex trajectories through combining observations from different subjects, avoids the risk of missing or over-emphasizing important features during a study period. Careful research on the advantages and disadvantages of this strategy should be further explored.

Powerful analysis methods are keys to revealing complex trajectories using contiguous data or data collected at random times. This study evaluated a traditional parametric growth mixture method capable of testing only a limited number of pre-specified trajectory forms. However, non-parametric growth mixture models, in which trajectory forms are unspecified, may prove to be a better choice for contiguous data than parametric growth mixture models, in which trajectories are assumed to have certain parametric forms. To date, little work has been done in this direction (Shedden and Zucker 2008 is the only one we could find). The continued development of methods in this direction is greatly desired, as advances in data collection technology will bring more intensive longitudinal data, making more salient the need for powerful statistical methods that fully capitalize on the advantages of such data.

Finally, other approaches, for example, dynamic cluster analysis (Huizinga, 1979; Velicer & Rossi, 1986; Hoeppner et al, 2008) and tree-structured methods (Segal, 1992), can also be used to estimate trajectory curves and to assign subjects to different trajectories. How the spacing of observations affects the conclusions of analysis when these approaches are used is largely unknown and awaits future systematic research. Although our intent with this paper was to explore this issue more rigorously using a real example applying one well-accepted and frequently used approach, we hope this paper can serve as a starting point to inform the decisions of other researchers, and to stimulate systematic research on the design of longitudinal research studies.