Density Functional Theory Study of an All Ferrous 4Fe-4S Cluster

Abstract

The all-ferrous, carbene-capped Fe₄S₄ cluster, synthesized by Deng and Holm (DH complex), has been studied with density functional theory (DFT). The geometry of the complex was optimized for several electronic configurations. The lowest energy was obtained for the broken-symmetry (BS) configuration derived from the ferromagnetic state by reversing the spin projection of one of the high spin (S_i = 2) irons. The optimized geometry of the latter configuration contains one unique and three equivalent iron sites, which are both structurally and electronically clearly distinguishable. For example, a distinctive feature of the unique iron site is the diagonal Fe⋯S distance, which is 0.3 Å longer than for the equivalent irons. The calculated ⁵⁷Fe hyperfine parameters show the same 1:3 pattern as observed in the Mössbauer spectra and are in good agreement with experiment. Broken-symmetry analysis of the exchange interactions in the optimized geometry for the 1:3, M_S = 4, BS configuration confirms the prediction of an earlier study that the unique site is coupled to the three equivalent ones by strong antiferromagnetic exchange (J > 0 in JΣ_j<4Ŝ₄ · Ŝ_j) and that the latter are mutually coupled by ferromagnetic exchange (J′ < 0 in J′Σ_i<j<4Ŝ_i · Ŝ_j). In combination, these exchange couplings stabilize an S = 4 ground state in which the composite spin of the three equivalent sites (S₁₂₃ = 6) is antiparallel to the spin (S₄ = 2) of the unique site. Thus, DFT analysis supports the idea that the unprecedented high value of the spin of the DH complex and, by analogy, of the all-ferrous cluster of the Fe-protein of nitrogenase, results from a remarkably strong dependence of the exchange interactions on cluster core geometry. The structure dependence of the exchange-coupling constants in the Fe^II-(μ₃-S)₂-Fe^II moieties of the all-ferrous clusters is compared with the magneto–structural correlations observed in the data for dinuclear copper complexes. Finally, we discuss two all-ferric clusters in the light of the results for the all-ferrous cluster.

1. Introduction

Presently the all-ferrous state of a Fe₄S₄ cluster with tetrahedral coordination sites has been established in four molecules. These systems include the Fe-protein of nitrogenase in Azotobacter vinelandii,¹ the activator protein of the dehydrogenase from Acidaminococcus fermentans,² and the synthetic complexes [Fe₄S₄(CN)₄]^{4- 3} and [Fe₄S₄(Prⁱ₂NHCMe₂)₄]⁰ (Prⁱ₂NHCMe₂ = 1,3-diisopropyl-4,5-dimethylimidazol-2-ylidene);⁴ the latter complex being hereafter referred to as the Deng–Holm (DH) complex. The observation of a [Fe₄S₄]⁰ state in the Fe-protein raised the possibility that an Fe₄S₄ cluster, which normally delivers one electron at a time by alternating between [Fe₄S₄]^1+/2+, may also donate two electrons in a concerted manner, using the redox couple [Fe₄S₄]^0/2+, thereby doubling the efficiency of the nitrogen reduction process in terms of the number of Mg-ATP molecules hydrolyzed.⁵ A recent comparison of the structural and spectroscopic data for the all-ferrous Fe-protein and the DH complex has revealed that their [Fe₄S₄]⁰ clusters are remarkably similar.⁶ Crystal structure and Mössbauer spectra show that the irons in the all-ferrous state appear as two subsets with a 1:3 ratio. A similar pattern has been observed in all-ferrous Fe₈S₈ clusters, suggesting a modular formulation of these super clusters in terms of their cubane constituents.⁷ The system spins of the DH complex and the protein bound clusters are 4. The S = 4 ground-state spin results from anti-parallel alignment of the spin of the unique iron to the three parallel aligned spins of the equivalent irons: S = 3 S_loc – S_loc = 2 S_loc = 4. The same expression for the system spin in terms of the local spins was found to hold for an all-cobaltous (S_loc = 3/2) [Co₄S₄]⁰ cluster with spin S = 3.⁸ Analysis of the spin-state energies with the Heisenberg–Dirac–van Vleck (HDvV) Hamiltonian, $\widehat{\mathscr{H}}=\sum _{\text{j}>\text{i}=1}^4{\text{J}}_{\text{ij}}{\widehat{\mathbf{\text{S}}}}_{\text{i}}\cdot {\widehat{\mathbf{\text{S}}}}_{\text{j}}$, shows that the condition for having the 1:3, S = 4 ground state is a combination of three strong antiferromagnetic exchange-coupling constants (J = J_4,i > 0 for i = 1, 2, 3) and three weaker antiferromagnetic (or even ferromagnetic) couplings between the equivalent sites (0 < J′ = J_ij ≪ J or J′ < 0 for i < j < 4).⁶ To investigate if this strong condition, which stipulates highly dissimilar coupling constants for rather similar superexchange units, can be fulfilled in a computational setting, we have performed broken-symmetry density functional calculations. The quality of the broken-symmetry DFT approximation for the S = 4 state has been monitored by comparing the predictions for the cluster structure and the ⁵⁷Fe hyperfine parameters with the experimental data. The results will be discussed in the context of magneto–structural data available in the literature.

2. Methods

The DFT calculations were performed with the Amsterdam Density Functional package (ADF 2008 version 01).⁹ The geometries for three electronic configurations, labeled M_S = 8, M_S = 4, and M_S = 0 according to their total magnetic quantum number, were optimized using the functional/basis set VWNBP/TZP. The M_S = 8 configuration represents the magnetic substate |S = 8, M_S = 8> of the ferromagnetic state and the other two are broken-symmetry configurations.¹⁰ The total magnetic quantum number, M_S, of these configurations is the sum of the local magnetic quantum numbers (M_S1, M_S2, M_S3, M_S4), which are given by (2, 2, 2, 2) for M_S = 8, (2, 2, 2, −2) for M_S = 4, and (2, 2, −2, −2) for M_S = 0. The calculations for the BS configurations were initiated using the keyword SPINFLIP. The lowest energy was obtained for the M_S = 4 configuration with the optimized M_S = 8 and M_S = 0 configurations being, respectively, 10,447 cm^-1 and 819 cm^-1 higher in energy. To test for trapping in local minima, we initiated the geometry optimization for the lowest M_S = 4 configuration with two geometries, a structure obtained from the X-ray structure by truncating the side chains of the carbene ligands (see Figure 1) and the same truncated structure in which the core was symmetrized by averaging iron–iron distances to 2.70 Å. The two optimizations yielded the same optimized geometry. The M_S = 4 configuration has preponderant S = 4 character (∼70%, see Supporting Information), suggesting that the S = 4 state is the ground state of the cluster and that both the geometry and the properties calculated for the M_S = 4 configuration are good approximations for those for the ground state. In order to verify whether the S = 4 state is the ground state we have evaluated the exchange-coupling constants appearing in the HDvV Hamiltonian (see Introduction). Since the HDvV Hamiltonian gives a valid description of the exchange splittings only when the spin state energies have been determined for the same geometry (cf. refs. 6 and 11), we have evaluated the SCF energies for the M_S = 8, M_S = 4, and M_S = 0 configurations in single point calculations for the same structure, for which we have adopted the optimized geometry of the M_S = 4 configuration. These three energies allowed us to evaluate the exchange-coupling constants J and J′ in the M_S = 4 optimized structure as described in section 3.3.

Figure 1.

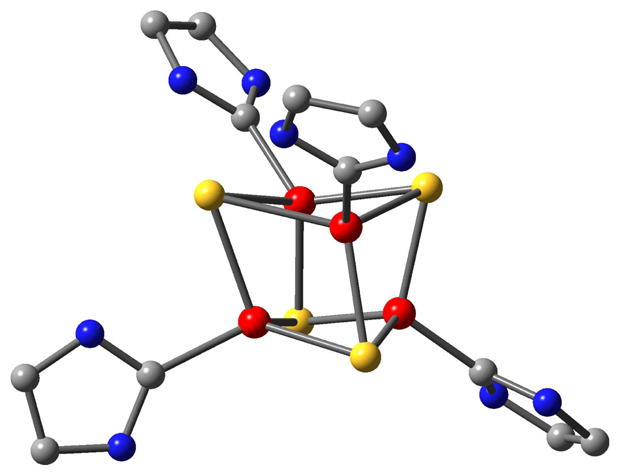
Optimized structure of [Fe₄S₄(imidazol-2-ylidene)₄]⁰, the computational model used for the DH complex. The unique iron site, labeled Fe₄ in the text, is located at the bottom on the right. Color code: carbon (grey), nitrogen (blue), iron (red), and sulfur (yellow). Hydrogen atoms are not shown for the sake of clarity.

The exchange-coupling constants were also calculated with the OPBE functional, which has been recommended for evaluating relative spin state energies,¹² to estimate the functional dependency of the results. In these calculations J and J′ were evaluated from the OPBE/TZP SCF energies for the M_S = 8, M_S = 4, and M_S = 0 configurations obtained from single point calculations for the same VWNBP/TZP-optimized M_S = 4 structure used above.

The magnetic hyperfine coupling (A) and electric field gradient (EFG) tensors of the ⁵⁷Fe sites in the optimized geometry for the M_S = 4 configuration were evaluated with the keywords ESR and QTENS. Relativistic effects were accounted for in scalar ZORA (thus, excluding small contributions from spin–orbit coupling induced orbital momentum to the A values).

All calculations were spin unrestricted and used for the SCF convergence and integration accuracy parameters the settings 10^-5 and 4.0, respectively.

3. Results and Discussion

In the following sections we present the DFT results for the structure, the ⁵⁷Fe hyperfine parameters, and the exchange-coupling constants for the optimized M_S = 4 configuration of the (truncated) DH complex and compare them with X-ray and spectroscopic literature data for this system.

3.1 Structure

The DFT optimized geometry for the M_S = 4 configuration (II in Figure 2) has an approximately C_3v symmetric core with the three-fold axis running through one of the irons (Fe₄); the remaining irons (Fe_1-3) are nearly equivalent by symmetry. Averages and standard deviations for selected metric parameters for the two types of site are listed in Table 1. The DFT distances between equivalent sites are shorter than the distances between the unique site and the equivalent sites by 0.09 Å. Concomitantly, the Fe_iSFe_j (i < j < 4) angles are smaller than the Fe₄SFe_j angles by 6.0°. The corresponding differences for the X-ray structure of the DH complex, also listed in Table 1, are 0.10 Å and 3.6°. The changes in the Fe⋯Fe distances as obtained by DFT are about equal to the changes observed in the X-ray structure but the angular changes predicted by DFT are considerably larger. At constant Fe-S bond length, small changes in Fe_i⋯Fe_j distance, Δ(Fe_iFe_j), are related to changes in the Fe_iSFe_j angle, Δ(Fe_iSFe_j), by the expression

Figure 2.

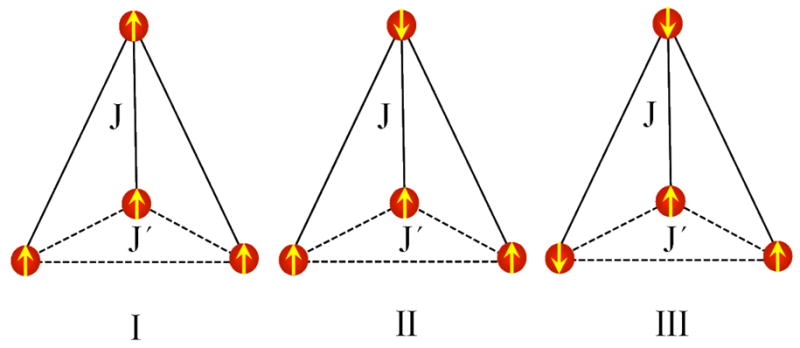
Spin configurations with magnetic quantum numbers M_S = 8 (I), 4 (II), and 0 (III) for which the energies (E_I, E_II, and E_III) were calculated with DFT in the optimized geometry for II (see section 2) to obtain the exchange-coupling constants J and J′ for the 1:3 structure (section 3.3). The unique site (Fe₄) is located at the top.

Table 1. Selected Structural Parameters for S = 4 Ground State of DH Complex.

Fei (Fej) site(s)	Fei⋯Fej (Å)		FeiSFejb (°)		Fei⋯Sic (Å)		Si⋯Sjc (Å)		Fei-S f (Å)		Fei-Ci (Å)
	X-ray a	DFT	X-ray a	DFT	X-ray a	DFT	X-ray	DFT	X-ray	DFT	X-ray	DFT
i = 4, j < 4 d	2.732 e	2.631	72.09	70.53	4.06	4.15	3.804	3.951	2.312	2.242	2.07	1.93
i < j < 4 d	2.633	2.552	68.411	64.522	3.894	3.822	3.683	3.631	2.341	2.367	2.121	2.051

^aFrom ref. 4.

^bAverage over two bridges.

^cSulfide S_i is diagonal to Fe_i.

^dAverage over three equivalent irons.

^eSubscript gives standard deviation in the least significant decimal(s).

^fAverage over bound sulfurs.

$$\mathrm{\Delta }({\text{Fe}}_{\text{i}}{\text{Fe}}_{\text{j}})=2^{-1}(\text{FeFe})coth[(\text{FeSFe})/2]\mathrm{\Delta }({\text{Fe}}_{\text{i}}{\text{SFe}}_{\text{j}}).$$ (1)

Using this expression we obtain for the DFT / X-ray angular increments Δ(Fe_iSFe_j) = 6.0° / 3.6° the distance changes Δ(Fe_iFe_j) = 0.20 Å / 0.12 Å. Thus, the increments in the Fe_iSFe_j bond angle and the associated Fe_i⋯Fe_j distance occur in the X-ray structure at approximately fixed Fe-S distances but are in the DFT structure accompanied by changes in the Fe-S bond length (see Table 1). This discrepancy between the DFT and X-ray structures is also reflected in the diagonal Fe_i⋯S_i distances (Table 1), which for the unique site (i = 4) are longer than for the equivalent sites (i = 1-3) by 0.33 Å and 0.17 Å in the DFT and X-ray structures, respectively. The larger distortion in the DFT structure may be related to an overestimation of the exchange-coupling constants by this method (see section 3.3). The average DFT / X-ray values for the Fe⋯Fe and S⋯S distances are 2.59 Å / 2.68 Å and 3.79 Å / 3.74 Å, respectively, showing that the tetrahedron defined by the four irons is smaller than the one spanned by the four sulfurs as in all known Fe₄S₄ clusters.¹³ The edges of the 4-Fe tetrahedron in the DFT structure are shorter than in the X-ray structure by 0.09 Å, while those for the 4-S tetrahedron are 0.05 Å longer. Thus, the DFT structure displays a more pronounced size difference between the 4-Fe and 4-S tetrahedra than the X-ray structure. This feature is reflected in the average FeSFe angles, 67.5° / 70.2° (DFT / X-ray), which are more acute in the DFT structure than in the X-ray structure. Despite these differences, the agreement of the DFT structure with the X-ray structure is quite satisfactory.

3.2 Hyperfine parameters

Table 2 lists the values for the ⁵⁷Fe quadrupole splitting (ΔE_Q), the asymmetry parameter of the EFG (η), and the isotropic contribution to the magnetic hyperfine coupling constants for the unique and equivalent iron sites in the DH complex as obtained from Mössbauer (Mb) spectroscopy and DFT calculations for the M_S = 4 configuration (II in Figure 2). The overall agreement between the DFT and Mössbauer results for these parameters is excellent, which inspires confidence in the quality of the DFT solution. Both methods give a large, positive ΔE_Q for the unique site and a negative ΔE_Q of about half the magnitude for the equivalent sites. The isotropic contribution to the local magnetic hyperfine coupling constants for the unique site is about half the value for the equivalent sites, both in experiment and theory. The discrepancy between the Mb and DFT results for a^iso is actually larger than apparent from Table 2 due to the presence of a positive orbital contribution that is not included in the DFT number.¹⁴ The Fermi contact term obtained from DFT is often smaller than observed as this method has the propensity to overestimate the covalent reduction of the spin population in the iron 3d shell. The results of Table 2 reveal that the 1:3 differentiation of the iron sites in the structure of the DH complex must have a marked impact on their orbital structures. The parameter values in Table 2 can be compared with the Mössbauer parameters for the two high-spin Fe^II sites in the [Fe₄S₄]¹⁺ cluster in the ferredoxin from reduced Bacillus stearothermophilus:¹⁵ ΔE_Q = 1.89 mm/s, η = 0.32, a^iso = −88 kG,¹⁶ and isomer shift δ = 0.58 mm/s. The quadrupole splitting in the ferredoxin is positive, like for the unique site in the DH complex but smaller in size (Table 2). The a^iso value for the ferrous sites in the [Fe₄S₄]¹⁺ cluster is close to the value listed for the unique site in Table 2, suggesting that the unique site in the DH complex has a greater resemblance with the ferrous sites in common ferredoxins than the equivalent sites. The ⁵⁷Fe isomer shift for the ferrous sites in [Fe₄S₄]¹⁺ (0.58 mm/s) is bracketed by the values δ₄ = 0.54 mm/s and δ_1-3 = 0.61 mm/s for the DH complex. The difference in the latter values correlates with a small difference in the Fe–carbene distances (Table 1). In absence of an isomer-shift calibration for the computational procedure described in section 2, we give here no computational estimate for this quantity.

Table 2. ⁵⁷Fe Quadrupole splitting, Asymmetry Parameter, and Isotropic Contribution to Magnetic Hyperfine Coupling of Iron Sites in DH Complex.

Fei site	ΔEQ (mm/s)		ηd		aisoie (kG)
	Mb c	DFT b	Mb c	DFT	Mb c	DFT f
i = 4	2.96	2.51	0.59	0.57	−78	−66
i = 1-3 a	−1.53	−1.26	0.07	0.22	−156	−113

^aAverage over equivalent sites.

^bΔE_Q = 2^-1 e Q V_zz (1 + η²/3)^1/2, using ⁵⁷Fe (I = 3/2) quadrupole moment Q = 0.17 barn.

^cTaken from Mössbauer study in ref. 6; A-values in Table 1 of ref. 6 are presented in the coupled-spin Ŝ · A_i · Î_i convention (S = 4) and have been converted here to local a-values, using spin projection factors: a₄ = −(5/2)A₄ and a_1-3 = (15/7) A_1-3.

^dAsymmetry parameter of EFG, η = (V_xx − V_yy)/V_zz where the V_qq are the eigenvalues of the EFG tensor, using convention |V_xx| ≤ |V_yy| ≤ |V_zz|.

^eIsotropic part of magnetic hyperfine coupling tensor in the convention ${\widehat{\mathbf{\text{S}}}}_{\text{i}}\cdot {\text{a}}_{\text{i}}^{\text{iso}}\cdot {\widehat{\mathbf{\text{I}}}}_{\text{i}}$ with S_i = 2 and I_i = 1/2 (nuclear ground state) and 3/2 (nuclear excited state) are the electronic and nuclear spins of ⁵⁷Fe site i.

^fValues obtained from the A_i-values listed in ADF output for the BS M_S = 4 configuration II (S = 4 convention), with the relations a₄ = −2 A₄ and a_1-3 = +2 A_1-3.

3.3 Exchange-coupling constants

As the [Fe₄S₄]⁰ core in the optimized structure for the BS, M_S = 4 configuration (II in Figure 2) has approximately C_3v symmetry, the HDvV Hamiltonian for describing the exchange interactions between the iron sites can be expressed as

$$\widehat{\mathscr{H}}=\text{c}+\text{J}\sum _{\text{j}=1}^3{\widehat{\mathbf{\text{S}}}}_4\cdot {\widehat{\mathbf{\text{S}}}}_{\text{j}}+{\text{J}}^{\prime }\sum _{\text{i}>\text{j}=1}^3{\widehat{\mathbf{\text{S}}}}_{\text{i}}\cdot {\widehat{\mathbf{\text{S}}}}_{\text{j}},$$ (2)

where c is a spin-independent constant and J and J′ are exchange-coupling constants. The expectation values of the HDvV Hamiltonian for the spin configurations of Figure 2, E_n = 〈n|ℋ̂|n〉, n = I, II, and III, are given by the expressions E_I = c + 12J + 12J′, E_II = c − 12J + 12J′, and E_III = c − 4J − 4J′. These equations can be solved to obtain c and the exchange-coupling constants, yielding c = (E_I + 3 E_III)/4, J = (E_I − E_II)/24, and J′ = (E_I + 2 E_II − 3 E_III)/48. The configurational energies obtained with VWNBP/TZP (section 2) are E_I = −277.9169 eV, E_II = − 279.8062 eV, and E_III = −278.8276 eV. Substitution of these values in the expressions for couplings gives J = 635 cm^-1 (antiferromagnetic) and J′ = −176 cm^-1 (ferromagnetic). With these exchange-coupling constants, the |S₁₂₃ = 6, S = 4> state is free of spin frustration and is the ground state of the HDvV Hamiltonian. (In the case that J′ is a weak antiferromagnetic coupling, this state may remain the ground state but the couplings between S_i and S_j (i < j < 4) will then be “frustrated”.) The first two excited states of ℋ̂ are |S₁₂₃ = 5, S = 3> and |S₁₂₃ = 6, S = 5> with excitation energies of 2326 cm^-1 and 3175 cm^-1, respectively. The OPBE results (see section 2) are J = 469 cm^-1 and J′ = −229 cm^-1, which yield again a |S₁₂₃ = 6, S = 4> ground state and excitation energies of 2312 cm^-1 and 2345 cm^-1, respectively.

The large difference between the values for J and J′ implies a remarkably strong dependence of the exchange-coupling constants on the structure of the associated Fe^II (μ₃-S)₂Fe^II units. Assuming that the exchange-coupling constant between any pair of irons in the [Fe₄S₄]⁰ cluster is given by the same function, denoted (θ), of the average bond angle, θ = (FeSFe)_av, taken over the two ligand bridges connecting the irons, and adopting the linear approximation (θ) ≈ (d /dθ) (θ − θ_o), the angular slope can be expressed as d /dθ ≈ (J − J′)/[(Fe₄SFe_i)_av − (Fe_iSFe_j)_av], (i < j < 4). Substitution of the DFT values for J ≡ (70.5°) and J′ = (64.5°) and the angular DFT averages, 70.5° and 64.5°, listed in Table 1, gives the slope d _DFT/dθ = 135 cm^-1/degree and yields, after a simple evaluation, the value for the zero point θ_o = 65.8° where (θ) vanishes (for OPBE: d _DFT/dθ = 116 cm^-1/degree and θ_o = 66.5°). The d _DFT/dθ value for the DH complex is comparable to the steep slope observed for the Cu^II(μ₂-OH)₂Cu^II bridges reported by Hatfield, Hodgson, and coworkers¹⁷ for which d /dθ ≈ 80 cm^-1/degree, where θ is the CuOCu angle. However, the rate of change in the total exchange splitting between the top and ground levels of the spin ladder for a Fe^II-(μ₃-S)₂-Fe^II unit in the DH complex (which is 10 × d /dθ vs. d /dθ in dicopper(II) complexes), is predicted to be more than an order of magnitude larger than in the copper complexes.

The X-ray value Δθ_X-ray ≡ [(Fe₄SFe_i)_av − (Fe_iSFe_j)_av] = 3.6° (i < j < 4) is smaller than the DFT value Δθ_DFT = 6.0°, by a factor of 0.6 (Table 1). This factor may arise from the propensity of DFT calculations to overestimate the exchange-coupling constants in iron–sulfur clusters.¹⁸ If we assume that the DFT value for the exchange-coupling constant for any given geometry of the Fe^II(μ₃-S)₂Fe^II unit is off by a constant factor q, then the angular dependence of the true J must be given by (θ) = q × _DFT(θ), leading to the expression d /dθ = q × d _DFT/dθ for the slope. Given their strong dependence on molecular geometry it seems plausible that the exchange energies have an effect on the structure of the cluster. In a previous study⁶ we showed that the angular dependence of the exchange-coupling constants gives rise to a spontaneous lowering of the symmetry of the [Fe₄S₄]⁰ core in the S = 4 state to C_3v. The associated angular difference Δθ = (Fe₄SFe_i)_av − (Fe_iSFe_j)_av (i < j < 4) was directly proportional to the force d /dθ driving this distortion. Since the X-ray value for the angular difference, Δθ_X-ray = C (d /dθ), is smaller than the DFT value, Δθ_DFT = C (d _DFT/dθ), by a factor of 0.6,¹⁹ we arrive at the relation d /dθ = 0.6 × d _DFT/dθ, allowing us to identify the factor q in (θ) = q × _DFT(θ) with the factor 0.6 for the distortions: q = 0.6. Noticing that J − J′ ≈ (d /dθ) Δθ_X-ray ≈ q² (d _DFT/dθ) Δθ_DFT ≈ q² (J − J′)_DFT, it follows that (J − J′)_DFT has to be reduced by the factor q² to obtain the true value for the difference J − J′ in the physical system. Applying this factor to the individual coupling constants, we obtain J = 0.6² × 635 cm^-1 = 229 cm^-1, J′ = 0.6² × (−176) cm^-1 = −63 cm^-1, and d /dθ = 0.6 × 135 cm^-1/degree = 81 cm^-1/degree (for OPBE: J = 169 cm^-1, J′ = −82 cm^-1, and d /dθ = 70 cm^-1/degree). Thus, the DFT values for J and J′ have a large margin of uncertainty. Somewhat accidentally, perhaps, the latter d /dθ values are close to the slope for the aforementioned dicopper(II) complexes. In contrast, the zero point of the function (θ) for the DH complex (θ_o ≈ 66°) differs significantly from the one for the bis-μ-hydroxo-copper(II) dimers (θ_o ≈ 97°).¹⁷ The DFT estimates given here are approximate since, (1) the geometry optimizations not only affect the Fe_iSFe_j bond angles and associated Fe_i⋯Fe_j distances, but also alter the Fe-S bond distances (see section 3.1), and (2) the large magnitude of the J changes raises concerns about the validity of the assumed linearity of the magneto–structural correlations considered here, although this is not unprecedented as we have seen in the copper dimers. As experimental J values for the Fe^II-(μ₃-S)₂-Fe^II bridges in Fe₄S₄ clusters are lacking, the DFT calculations of J are not well calibrated in these systems. The only J value for a Fe₄S₄ cluster currently available, J = 280 cm^-1, is for the coupling between two high-spin Fe^III sites and has been obtained from magnetic susceptibility measurements on the Fe^III₂(Fe^II(CN)₃)₂S₄ cluster, in which the Fe^II sites are low-spin.¹⁸ This value is larger than the above estimate of 229 cm^-1 for J in the DH complex, which seems reasonable given the higher oxidation state of the metal.

The strong magneto–structural correlation between J and the metal–ligand–metal bond angle in Fe^II-(μ₃-S)₂-Fe^II units stands in stark contrast to the reported lack of a demonstrable angular correlation for supported Fe^III-(μ₂-O-X)-Fe^III bridges (O-X = oxo, hydroxo, alkoxo, …),²⁰ possibly because of geometric constraints. Thus, if the sign change of J in a Fe^III-(μ₂-O)₂-Fe^III bridge were to occur at a bond angle of ∼70° as in the Fe^II-(μ₃-S)₂-Fe^II units of the all-ferrous clusters, this event would elude observation in any of the reported Fe^III-(μ₂-O-X)₂-Fe^III complexes, simply because their bond angles (98° − 160°)²⁰ are far from the zero point in the angular dependence of J.

Simultaneously with the reports of the synthetic all-ferrous clusters,^3,4 two all-ferric cubane clusters appeared in the literature, including an [Fe₄O₄]⁴⁺ cluster that is the core of an extended 8Fe^III structure²¹ and a [Fe₄S₄]⁴⁺ cluster that is stabilized by bis(trimethylsilyl)amide terminal ligands.^22,23 The Fe^III(μ₄-O)₂Fe^III coupling constants in the [Fe₄O₄]⁴⁺ moiety are weak (J ≈ 2 cm^-1),²¹ probably due to the long Fe-O distances in this unit rather than to the nearness of the FeOFe angle (≈ 98°) to a zero point in bond-angle dependence of J. (We are not aware of any Fe^III-O₍₂₎-Fe^III bridge with ferromagnetic coupling.) The J value for [Fe₄O₄]⁴⁺ is consistent, at least qualitatively, with the empirical relationship of ref. 20 between J and average Fe-O bridging bond length, which yields J ≈ 9 cm^-1 for the distances (Fe_core-O ≈ 2.05 Å) in this cluster, if one considers that the difference between 2 and 9 cm^-1 is small on the scale of observed J[Fe^III-O-Fe^III] values, i. e., 15 cm^-1 − 260 cm^-1.²⁰ The empirical J–(Fe-O) correlation predicts a value of 18 cm^-1 for the coupling constants between the terminal and core irons of the 8Fe cluster (the value obtained by substituting the average, 2.00 Å, of the Fe-O distances in the Fe_terminal-O-Fe_core bridges into the empirical correlation), which is clearly smaller than the value of ≈ 50 cm^-1 deduced from magnetic susceptibility analysis,²¹ leaving room for some degree of bond-angle dependence of J. The [Fe₄S₄]⁴⁺ cluster has an S = 0 ground state with a D_2d structure, in agreement with one of the two possible ground states predicted by the theoretical model presented in ref. 6 as applied to this system. However, to obtain two long and four short Fe⋯Fe distances, as observed, the model requires a negative slope, d /dθ < 0, at the bond angle in the all-ferric system, which is about 8° larger than in the all-ferrous cluster. Establishing the interesting and consequential magneto–structural correlations in these and other metal clusters is the subject of a future investigation.