Estimation of Model Parameters for Steerable Needles

Abstract

Flexible needles with bevel tips are being developed as useful tools for minimally invasive surgery and percutaneous therapy. When such a needle is inserted into soft tissue, it bends due to the asymmetric geometry of the bevel tip. This insertion with bending is not completely repeatable. We characterize the deviations in needle tip pose (position and orientation) by performing repeated needle insertions into artificial tissue. The base of the needle is pushed at a constant speed without rotating, and the covariance of the distribution of the needle tip pose is computed from experimental data. We develop the closed-form equations to describe how the covariance varies with different model parameters. We estimate the model parameters by matching the closed-form covariance and the experimentally obtained covariance. In this work, we use a needle model modified from a previously developed model with two noise parameters. The modified needle model uses three noise parameters to better capture the stochastic behavior of the needle insertion. The modified needle model provides an improvement of the covariance error from 26.1% to 6.55%.

I. INTRODUCTION

Needle insertion is one of the most common minimally invasive medical procedures. It is used in many medical applications such as biopsy, local anesthesia, drug delivery, and brachytherapy. Rigid needles are typically used, which are unable to maneuver around bones, nerves, and other obstacles. However, a flexible needle with an asymmetric tip can be steered inside tissue. In recent years, steerable needles have drawn considerable attention due to their simple structure and maneuverability [4], [5], [8], [10], [12], [17], [18]. The needle’s steerability allows corrections to the needle path during an insertion, so fewer insertion attempts are required to position the needle tip at the desired location. The maneuverability of steerable needles can also improve the accuracy of the insertion, which may reduce the possibility of misdiagnosis during a biopsy, or delivery of therapy to the wrong location. Potential applications of bevel-tipped flexible needles include brachytherapy [1] and brain surgery [6].

The steerability of a flexible needle comes from the interaction between the asymmetric bevel tip and the tissue surrounding the needle. When the needle is inserted into soft tissue, the bevel tip generates an asymmetric force on the needle, which causes the tip to follow a nearly circular arc [11]. The direction of the bending is determined by the direction of the bevel tip. Rotating the needle base around the needle tangent rotates the bevel edge at the needle tip and, thus, the direction of future bending. If the rotation angle is held constant during an insertion, the tip of the needle will approximately follow a circular arc with constant curvature κ. The specific value of the constant κ depends on parameters such as the angle of the bevel, sharpness of the needle tip, and properties of the tissue. Suppose that a bevel-tipped flexible needle is rotated with an angular speed ω(t) around its insertion axis while it is inserted with translational speed υ(t). Using the geometric bending curve of the needle and the two inputs, ω(t) and υ(t), a nonholonomic kinematic model predicts the time evolution of the position and orientation of the needle tip [21].

Based on the nonholonomic kinematic model, a stochastic model for the steering of bevel-tipped flexible needles has been developed and used in [13]–[16]. It uses the unicycle nonholonomic kinematic model [21] and includes white noises weighted by constants to capture the nondeterministic behavior of the needle insertion. More accurate models would improve both image-guided control and path planning. The main purpose of this work is to determine the model parameters (curvature and noise parameters) using experimental data. These parameters will be used to inform the path planner of the likely needle tip position following a planned insertion.

The Fokker-Planck equation (see [3] for general description) corresponding to the stochastic needle model defines the probability density function (PDF) of the needle tip pose. The propagation of the covariance of the PDF was previously formulated with first-order accuracy for robot arms with discrete joints in [19]. Using that formula, we analytically compute the covariance as a function of parameters for the needle model. Then we match the theoretical covariance and the experimentally obtained covariance to compute the model parameters.

II. MATHEMATICAL MODEL FOR NEEDLE STEERING

A. Review of Rigid-Body Motions

The special orthogonal group, SO(3), is the space of 3 × 3 rotation matrices, together with the operation of matrix multiplication. Any element of SO(3) can be written using the Euler angles as [2]

$$R=R_z(\alpha )R_x(\beta )R_z(\gamma ),$$

where α, β and γ are the ZXZ Euler angles, 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, 0 ≤ γ ≤ 2π. The matrices R_x(θ) and R_z(θ) represent the rotations by θ around the x and z axes, respectively.

The Euclidean motion group, SE(3), describes rigid-body motions in three-dimensional (3D) space. It is the semi-direct product of ℝ³ with SO(3). The elements of SE(3) can be written as [2], [3]

$$g=\left(\begin{array}{cc}\hfill R\hfill & \hfill \mathbf{t}\hfill \\ \hfill {\mathbf{0}}^T\hfill & \hfill 1\hfill \end{array}\right),$$ (1)

where R ∈ SO(3) is the 3 × 3 rotation matrix, t ∈ ℝ³ is a 3D translation vector and 0^T denotes the transpose of the 3D zero vector.

Given a time-dependent rigid-body motion g(t), the velocity of the body-fixed frame written in body-fixed coordinates can be computed as

$$g^{-1}\dot{g}=\left(\begin{array}{cc}\hfill R^T\dot{R}\hfill & \hfill R^T\dot{\mathbf{t}}\hfill \\ \hfill {\mathbf{0}}^T\hfill & \hfill 0\hfill \end{array}\right)\in \mathit{\text{se}}\left(3\right)$$

where a dot represents the time derivative and se(3) is the Lie algebra associated with SE(3).

The two mappings ^∨ : se(3) → ℝ⁶ and ^: ℝ⁶ → se(3) relate se(3) and ℝ⁶ as

$$\widehat{\mathit{\xi }}=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill -{\xi }_3\hfill & \hfill {\xi }_2\hfill & \hfill {\xi }_4\hfill \\ \hfill {\xi }_3\hfill & \hfill 0\hfill & \hfill -{\xi }_1\hfill & \hfill {\xi }_5\hfill \\ \hfill -{\xi }_2\hfill & \hfill {\xi }_1\hfill & \hfill 0\hfill & \hfill {\xi }_6\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\in \mathit{\text{se}}(3)$$

and ξ̂ ^∨ = ξ, where ξ = (ξ₁ ξ₂ ξ₃ ξ₄ ξ₅ ξ₆)^T. The vector ξ = (g⁻¹ġ)^∨ contains both the angular and translational velocities of the motion g(t) as seen in the body-fixed frame of reference.

Let e_i, i = 1,…,6 denote the standard basis for ℝ⁶. The basis given by a set of matrices E_i = ê_i, i = 1,…,6 produce elements of se(3), when linearly combined. The elements of SE(3) then can be obtained by the exponential mapping exp : se(3) → SE(3) as [2], [16]

$$g=g(x_1,x_2,\dots ,x_6)=\text{exp}\left({\displaystyle \sum _{i=1}^6{x}_i{E}_i}\right).$$

Therefore, the vector x = (x₁ x₂ … x₆)^T can be obtained from g ∈ SE(3) by x = (log g)^∨.

The adjoint matrix Ad_g is defined by the expression

$${\mathit{\text{Ad}}}_g=\left(\begin{array}{cc}\hfill R\hfill & \hfill 0\hfill \\ \hfill \mathit{\text{TR}}\hfill & \hfill R\hfill \end{array}\right),$$

where g ∈ SE(3) is given as in (1), and the skew-symmetric matrix T is given as T = t̂.

B. Nonholonomic Stochastic Needle Model

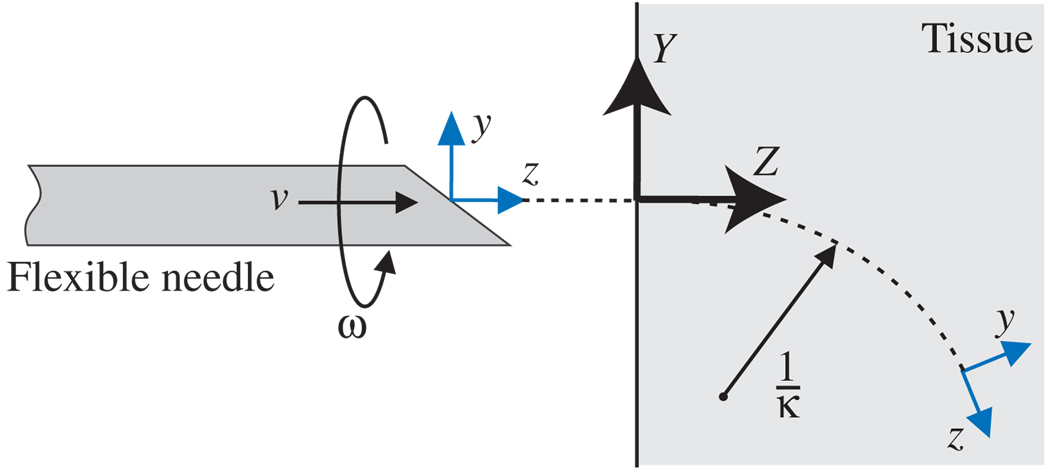
Let us consider a reference frame attached to the needle tip as shown in Fig. 1. The z axis denotes the tangent to the needle tip trajectory, and the x axis is orthogonal to the direction of infinitesimal motion induced by the bevel tip. The needle bends in the y-z plane. A nonholonomic kinematic model for the evolution of the frame at the needle tip was developed in [15], [21] as:

$$\mathit{\xi }={\left(g^{-1}\dot{g}\right)}^{\vee }={(\kappa \upsilon (t)0\omega (t)00\upsilon (t))}^T$$ (2)

where κ is the curvature of the needle trajectory and the two inputs, ω(t) and υ(t) are the rotating and insertion velocities, respectively.

Fig. 1.

The definition of parameters, inputs and frames in the nonholonomic needle model. Y-Z denotes the world frame and y-z denotes the body-fixed frame attached to the needle tip.

If everything were certain, and this model were exact, then g(t) could be obtained by simply integrating the ordinary differential equation in (2). However, in practice we obtain an ensemble of slightly different trajectories when we repeatedly insert a needle into a soft medium used to simulate soft tissue [21]. The deviation between the trajectories at the insertion location can be negligible and will increase as the insertion length increases. A simple stochastic model for the needle [15], [16] is obtained by letting:

$$\omega (t)={\omega }_0(t)+{\lambda }_1{w}_1(t),\text{\hspace{1em}and\hspace{1em}}\upsilon (t)={\upsilon }_0(t)+{\lambda }_2{w}_2(t).$$

Here ω₀(t) and υ₀(t) are what the inputs would be in the ideal case, ω_i(t) are uncorrelated unit Gaussian white noises, and λ_i are noise parameter constants.

By adding one more noise parameter λ₃, we define a new nonholonomic needle model with noise as

$$\mathit{\xi }={(g^{-1}\dot{g})}^{\vee }\mathit{\text{dt}}={\left({\kappa }_0{\upsilon }_0(t)0{\omega }_0(t)00{\upsilon }_0(t)\right)}^T\mathit{\text{dt}}+{\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \kappa {\lambda }_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)}^T\left(\begin{array}{c}\hfill {\mathit{\text{dW}}}_1\hfill \\ \hfill {\mathit{\text{dW}}}_2\hfill \\ \hfill {\mathit{\text{dW}}}_3\hfill \end{array}\right)$$ (3)

where dW_i = W_i(t + dt) − W_i(t) = w_i(t)dt are the non-differentiable increments of a Wiener process W_i(t). The noise parameter λ₃ is expected to capture the stochastic behavior in the rotation around the x axis that the needle model with the constant curvature cannot capture. The needle model (3) is a stochastic differential equation (SDE) on SE(3). As shorthand, we write this as

$${(g^{-1}\dot{g})}^{\vee }\mathit{\text{dt}}=\mathbf{h}(t)\mathit{\text{dt}}+\mathit{\text{Hd}}\mathbf{W}(t).$$ (4)

Similar models arise in various applications [3], [22].

III. COVARIANCE PROPAGATION

We now consider how to determine the model parameters, κ, λ₁, λ₂ and λ₃. In the literature [13], [15], [16], the noise parameters were set artificially because experimental data was not available at that time. However, it is desirable to extract the parameters from experimental data obtained for a specific system. This section derives the equation that relates the distribution of trajectories and the model parameters.

Corresponding to the SDE (4) is the Fokker-Planck equation that describes the evolution of the probability density function ρ(g; t) of the ensemble of tip positions and orientations at each value of time, t [3]:

$$\frac{\partial \rho (g;t)}{\partial t}=-{\displaystyle \sum _{i=1}^d{h}_i(t)}{\tilde{E}}_i^r\rho (g;t)+\frac{1}{2}{\displaystyle \sum _{i,j=1}^d{D}_{\mathit{\text{ij}}}{\tilde{E}}_i^r}{\tilde{E}}_j^r\rho (g;t)$$ (5)

where $D_{\mathit{\text{ij}}}={\displaystyle {\sum }_{k=1}^m{H}_{\mathit{\text{ik}}}{H}_{\mathit{\text{kj}}}^T}$ and ρ(g; 0) = δ(g). In (5), the ‘right’ Lie derivative ${\tilde{E}}_i^r$ is defined for any differentiable function f(g) as

$${\tilde{E}}_i^{r}f(g)={\left(\frac{d}{\mathit{\text{dt}}}f(g\circ \text{exp}({\mathit{\text{tE}}}_i))\right)|}_{t=0}.$$

For a small amount of diffusion, the solution for the Fokker-Planck equation (5) can be approximated by a shifted Gaussian function [13], [14], [16]:

$$\rho (g,t)=\frac{1}{{(2\pi )}^3{|\text{det}(\Sigma (t))|}^{\frac{1}{2}}}{e}^{(-\frac{1}{2}{\mathbf{y}}^T\sum {(t)}^{-1}\mathbf{y})},$$ (6)

where y = (m(t)⁻¹ ∘ g)^∨, and m(t) and Σ(t) are the mean and the covariance of this PDF, respectively. This approximation is based on the fact that for small diffusion the Lie derivative is approximated as ${\tilde{E}}_i^{r}f(g)\approx \frac{\partial f}{\partial x_i}$ [16]. Using this, the Fokker-Planck equation (5) becomes a diffusion equation in ℝ⁶. Therefore, (6) is the solution for the diffusion equation. The probability density function (6) plays an important role in the path planning algorithm that appears in [13], [14], [16].

We now develop the relationship between (m, Σ) and (h, H) below. m is called the mean of a probability density function ρ(g) on SE(3), if

$${\displaystyle {\int }_{\text{SE}(3)}{(\text{log}(m^{-1}\circ g))}^{\vee }\rho (g)\mathit{\text{dg}}=\mathbf{0}}.$$ (7)

In addition, the covariance about the mean is computed as

$$\sum ={\displaystyle {\int }_{\text{SE}(3)}\text{log}{(m^{-1}\circ g)}^{\vee }{[\text{log}{(m^{-1}\circ g)}^{\vee }]}^T\rho (g)\mathit{\text{dg}}.}$$ (8)

This covariance matrix can also be computed by covariance propagation. The covariance propagation in [19] is based on the concatenation of a finite number of noisy motions. In the limiting case of a time-parameterized path of noisy motions, the covariance propagation formula can be written as [19]

$$\sum (t)={\displaystyle {\int }_0^t{\mathit{\text{Ad}}}_{m{(\tau )}^{-1}\circ m(t)}^{-1}{D}_0{\mathit{\text{Ad}}}_{m{(\tau )}^{-1}\circ m(t)}^{-T}d\tau }$$ (9)

where D₀ = HH^T. In principle, m(t) ∈ SE(3) is the mean which is defined in (7). However, we approximate it using the noise-free path assuming the small diffusion. The noise-free path can be obtained by integrating (3) with λ₁ = λ₂ = λ₃ = 0. This approximation enables the closed-form formula for (9) as below.

Consider the special case of insertion with a constant speed (υ₀(t) = υ) without rotating (ω₀(t) = 0). In this case, we can write the homogeneous transformation matrix m(τ) as

$$m(\tau )=\text{exp}(\widehat{\mathbf{h}}\tau )=\left(\begin{array}{cc}\hfill R_x(\kappa \upsilon \tau )\hfill & \hfill \mathbf{p}(\tau )\hfill \\ \hfill {\mathbf{0}}^T\hfill & \hfill 1\hfill \end{array}\right)$$

where h = (κυ 0 0 0 0 υ)^T, κ is the curvature of the needle trajectory, υ is the constant insertion speed and p(τ) = (0, (cos(κυτ) − 1)/κ, sin(κυτ )/κ)^T. The rotational part and the translational part of m(τ)⁻¹ are $R_x^T(\kappa \upsilon \tau )\text{and}-R_x^T(\kappa \upsilon \tau )\mathbf{p}(\tau )$, respectively.

Since m(τ)⁻¹ ∘ m(t) = m(t − τ) in this special case, the covariance (9) can be rewritten as

$$\Sigma (t)={\displaystyle {\int }_0^t{\mathit{\text{Ad}}}_{m(\tau )}^{-1}{D}_0{\mathit{\text{Ad}}}_{m(\tau )}^{-T}d\tau }$$

by changing variables, τ′ = t − τ, and then replacing τ′ with τ.

Since D₀ = HH^T, D₀ can be written as

$$D_0=\left(\begin{array}{cc}\hfill D_{11}\hfill & \hfill D_{12}\hfill \\ \hfill D_{21}\hfill & \hfill D_{22}\hfill \end{array}\right),\text{where}{D}_{12}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \kappa {\lambda }_2^2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),$$

$D_{21}=D_{12}^T,D_{11}=\text{diag}([{\kappa }^2{\lambda }_2^2+{\lambda }_3^2,0,{\lambda }_1^2]),D_{22}=\text{diag}([0,0,{\lambda }_2^2])$. λ_i are the noise parameters in (3). Therefore, we have

$${\mathit{\text{Ad}}}_{m(\tau )}^{-1}{D}_0{\mathit{\text{Ad}}}_{m(\tau )}^{-T}=\left(\begin{array}{cc}\hfill S_{11}\hfill & \hfill S_{12}\hfill \\ \hfill S_{21}\hfill & \hfill S_{22}\hfill \end{array}\right)$$

where

$$S_{11}=R^T{D}_{11}R,S_{12}=R^T{D}_{11}\widehat{\mathbf{p}}R+R^T{D}_{12}R=S_{21}^T,S_{22}=-R^T\widehat{\mathbf{p}}{D}_{11}\widehat{\mathbf{p}}R+R^T{D}_{21}\widehat{\mathbf{p}}R-R^T\widehat{\mathbf{p}}{D}_{12}R+R^T{D}_{22}R.$$

The covariance can be given as a closed form:

$$\begin{array}{cc}\Sigma (t)\hfill & ={\displaystyle {\int }_0^t{\mathit{\text{Ad}}}_{m(\tau )}^{-1}}{D}_0{\mathit{\text{Ad}}}_{m(\tau )}^{-T}d\tau \hfill \\ \hfill \hfill & \hfill =\left(\begin{array}{cccccc}\hfill {\alpha }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_2\hfill & \hfill {\alpha }_3\hfill \\ \hfill 0\hfill & \hfill {\alpha }_4\hfill & \hfill {\alpha }_5\hfill & \hfill {\alpha }_6\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\alpha }_5\hfill & \hfill {\alpha }_7\hfill & \hfill {\alpha }_8\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\alpha }_6\hfill & \hfill {\alpha }_8\hfill & \hfill {\alpha }_9\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\alpha }_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_{10}\hfill & \hfill {\alpha }_{11}\hfill \\ \hfill {\alpha }_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_{11}\hfill & \hfill {\alpha }_{12}\hfill \end{array}\right),\hfill \end{array}$$ (10)

where

$$\begin{array}{c}{a}_1=({\kappa }^2{\lambda }_2^2+{\lambda }_3^2)t,a_2=-{\kappa }^{-2}{\upsilon }^{-1}{\lambda }_3^2(1-C)\hfill \\ a_3=\kappa {\lambda }_2^{2}t-{\kappa }^{-1}{\lambda }_3^2({(\kappa \upsilon )}^{-1}S-t)\hfill \\ a_4={\lambda }_1^2(\frac{1}{2}t-\mathit{\text{SC}}{(2\kappa \upsilon )}^{-1}),a_5={\lambda }_1^2{S}^2{(2\kappa \upsilon )}^{-1}\hfill \\ a_6={\kappa }^{-2}{\upsilon }^{-1}{\lambda }_1^2(1-C-\frac{1}{2}{S}^2),a_7={\lambda }_1^2(\frac{1}{2}t+\mathit{\text{SC}}{(2\kappa \upsilon )}^{-1})\hfill \\ a_8={\kappa }^{-1}{\lambda }_1^2(S{(\kappa \upsilon )}^{-1}-\frac{1}{2}t-\mathit{\text{SC}}{(2\kappa \upsilon )}^{-1})\hfill \\ a_9={\kappa }^{-2}{\lambda }_1^2(\frac{3}{2}t-2S{(\kappa \upsilon )}^{-1}+\mathit{\text{SC}}{(2\kappa \upsilon )}^{-1})\hfill \\ a_{10}={\kappa }^{-2}{\lambda }_3^2(\frac{1}{2}t-\mathit{\text{SC}}{(2\kappa \upsilon )}^{-1})\hfill \\ a_{11}={\kappa }^{-3}{\upsilon }^{-1}{\lambda }_3^2(\frac{1}{2}{S}^2+C-1)\hfill \\ a_{12}={\kappa }^{-2}{\lambda }_3^2(\frac{3}{2}t-2S{(\kappa \upsilon )}^{-1}+\mathit{\text{SC}}{(2\kappa \upsilon )}^{-1})+{\lambda }_2^{2}t\hfill \end{array}$$

Here S and C denote sin(κυt) and cos(κυt), respectively.

IV. EXPERIMENTS

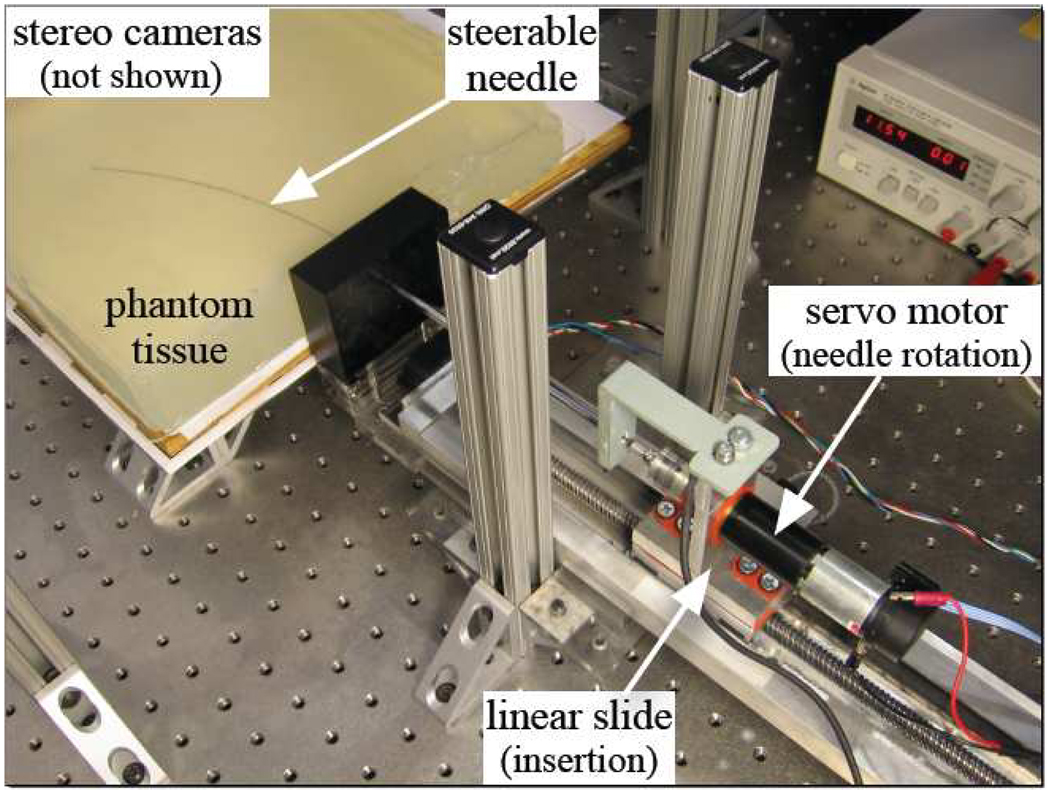
We used the device shown in Fig. 2 to perform repeated needle insertions. The needle was inserted into the artificial tissue by a DC servo motor attached to a linear slide. An additional DC motor rotates the needle shaft, but this was only used to orient the needle before insertion in these experiments. A stepper motor attached to the platform holding the artificial tissue was used to move the tissue between trials. We used a 0.57 mm diameter Nitinol wire (Nitinol Devices and Components, Fremont, CA, USA) with a bevel angle of roughly 45°. A telescoping support sheath prevented the needle outside the artificial tissue from buckling during insertion.

Fig. 2.

Experimental setup used to perform 100 needle insertions.

During insertion, images were acquired at 7 Hz from a pair of XCD-X710 firewire cameras (Sony Corporation, Tokyo, Japan) mounted above the artificial tissue. The image pairs were then triangulated offline to determine the tip position using a sub-pixel corner finder, which resulted in sub millimeter accuracy in Cartesian space. We used a transparent plastisol artificial tissue (M-F Manufacturing Co., Inc., Fort Worth, TX) manufactured from plastic and softener in a ratio of 4:1. The artificial tissue was approximately 40 mm thick and was sufficiently transparent for the needle tip to be easily identified. The artificial tissue had a refractive index of 1.3 and triangulation accounted for refraction assuming that the artificial tissue’s top surface was horizontal.

The experiment consisted of 100 needle insertions. We inserted the needle 150 mm at 2.5 mm/sec while keeping the rotation angle constant. The needle base then remained stationary for 1 second to allow the artificial tissue and needle to relax to their final positions. Then the needle was retracted and the artificial tissue was moved 5 mm perpendicular to the initial insertion direction to allow the next insertion to generate a new path. The artificial tissue was moved far enough to ensure that the subsequent insertions did not overlap with previous paths. This procedure was repeated until 100 trials had been completed. After the first 50 trials were obtained, the artificial tissue was rotated by 180° on the plane so that the final 50 trials were done on the opposite side of the artificial tissue. The artificial tissue and needle were not replaced during the experiment in order to maintain consistency in the data and model parameters.

V. DATA PROCESSING AND RESULTS

The needle trajectory near the wall of the artificial tissue cannot be clearly detected by the vision system for the first 1 to 2 cm because the artificial tissue has limited transparency and bubbles form around the edge of the artificial tissue. Thus, the first detected position of the needle tip during each insertion is not exactly the insertion position.

We estimate the insertion point at time t = 0 by extrapolating. First, we fit a circle to the needle position readings. The use of a circle for extrapolation is reasonable because we observe a circular trajectory in the needle insertion system. Computation of the best-fit circle is implemented using the code in [7]. Then we compute the closest point on the circle to the first detected point. By checking the encoder counts for the insertion length, we can compute the insertion length for the first detected point. By backtracking from the closest point on the circle to the first detected point by the recorded length, we can estimate the insertion point. Each insertion trajectory is translated so that the estimated insertion points for all insertion trajectories are placed at (0 0 0)^T.

In addition to translational matching of the insertion point, we need to align the insertion directions. Due to the variability of the puncture event at the start of each trial, which is not modeled here, the directions of repeated insertions are not identical. We can estimate the actual insertion direction by computing the tangential direction of the best-fit circle at the insertion point. Let z be this actual direction. We can compute a vector u as

$$\mathbf{u}=\frac{\mathbf{z}\times {\mathbf{z}}_0}{\Vert \mathbf{z}\times {\mathbf{z}}_0\Vert }$$

where × denotes the cross product and z₀ is the unit vector along the z axis. The rotation matrix for alignment is defined as R_a = exp(ûθ) where θ is the angle between z and z₀. We obtain the aligned data by applying this rotation matrix to all position data from each insertion.

We obtain only the position information of the needle tip using the stereo vision system. The orientation information can be easily estimated using the best-fit circle again. If we assume that needle torsion is negligible, the input angle is propagated to the needle tip without delay or discrepancy. Using this, we can compute the homogeneous transformation matrices for the needle tip poses.

Let us assume g_i(T) represents the ith needle tip pose at time T. Based on (7), we can define a sample mean m_s of g_i(T) as

$$\frac{1}{N}{\displaystyle \sum _i\text{log}}{(m_s^{-1}\circ g_i(T))}^{\vee }=\mathbf{0}.$$

where N is the number of samples. m_s can be computed using the iterative method in [20]. Using (8), the sample covariance can be computed as

$${\sum }_s=\frac{1}{N-1}{\displaystyle \sum _i\text{log}{(m_s^{-1}\circ g_i(T))}^{\vee }{[\text{log}{(m_s^{-1}\circ g_i(T))}^{\vee }]}^T.}$$

To evaluate our method, we first tested its performance using simulation data. For given model parameters, we generate many needle paths by numerically integrating the stochastic differential equation (3) using the Euler-Maruyama method [9]. We set the time to T = 60 s and the insertion speed to υ = 2.5 mm/s.

Table I shows 8 cases with different model parameters. In each case, 100 trajectories are generated, the covariance of the needle tip pose is obtained, and then the model parameters are computed by matching the covariances obtained by the simulated trajectories and the analytic equation (10). We implement this matching process by minimizing the following cost function:

$$C(\kappa ,{\lambda }_1,{\lambda }_2,{\lambda }_3)={\Vert \sum (T)-{\Sigma }_s\Vert }^2.$$

As shown in Table I, the model parameter estimates show that the error is less than 10% compared to the given values for the parameters.

TABLE I.

EIGHT CASES FOR TESTING WITH SIMULATED TRAJECTORIES.

Given parameters					Estimated parameters
κ	λ1	λ2	λ3		κ	λ1	λ2	λ3
0.005	0.01	0.1	0.002		0.0048	0.0097	0.1048	0.0020
0.005	0.01	0.1	0.004		0.0049	0.0103	0.0949	0.0043
0.005	0.01	0.2	0.002		0.0049	0.0099	0.1809	0.0020
0.005	0.01	0.2	0.004		0.0050	0.0105	0.1846	0.0041
0.005	0.02	0.1	0.002		0.0051	0.0201	0.1061	0.0020
0.005	0.02	0.1	0.004		0.0053	0.0199	0.0930	0.0043
0.005	0.02	0.2	0.002		0.0051	0.0185	0.2069	0.0019
0.005	0.02	0.2	0.004		0.0051	0.0189	0.1933	0.0039

In order to apply our parameter estimation method to the experimental data, we compute the covariance of the needle tip pose using the postprocessed experimental data as

$${\sum }_s=\left(\begin{array}{cccccc}\hfill 0.0019& \hfill -0.0002& \hfill -0.0002& \hfill -0.0130& \hfill -0.1049& \hfill 0.1069\\ \hfill -0.0002& \hfill 0.0044& \hfill 0.0053& \hfill 0.3357& \hfill 0.0062& \hfill -0.0195\\ \hfill -0.0002& \hfill 0.0053& \hfill 0.0064& \hfill 0.4029& \hfill 0.0055& \hfill -0.0250\\ \hfill -0.0130& \hfill 0.3357& \hfill 0.4029& \hfill 25.4651& \hfill 0.5003& \hfill -1.3393\\ \hfill -0.1049& \hfill 0.0062& \hfill 0.0055& \hfill 0.5003& \hfill 7.0490& \hfill -2.5077\\ \hfill 0.1069& \hfill -0.0195& \hfill -0.0250& \hfill -1.3393& \hfill -2.5077& \hfill 15.6076\end{array}\right)$$ (11)

By matching (10) and (11), the following system parameter estimates are obtained:

$${\lambda }_1=0.0219,{\lambda }_2=0.4937,{\lambda }_3=0.0043,\kappa =0.0062.$$ (12)

For the verification of these parameters, we evaluate the closed-form covariance matrix (10) using these estimated parameters. The normalized least-squared error (NLSE) of the closed-form covariance relative to the sample covariance (11) is 0.0655. The NLSE of Σ₂ relative to Σ₁ is defined as ‖Σ₁ − Σ₂‖/‖Σ₁‖.

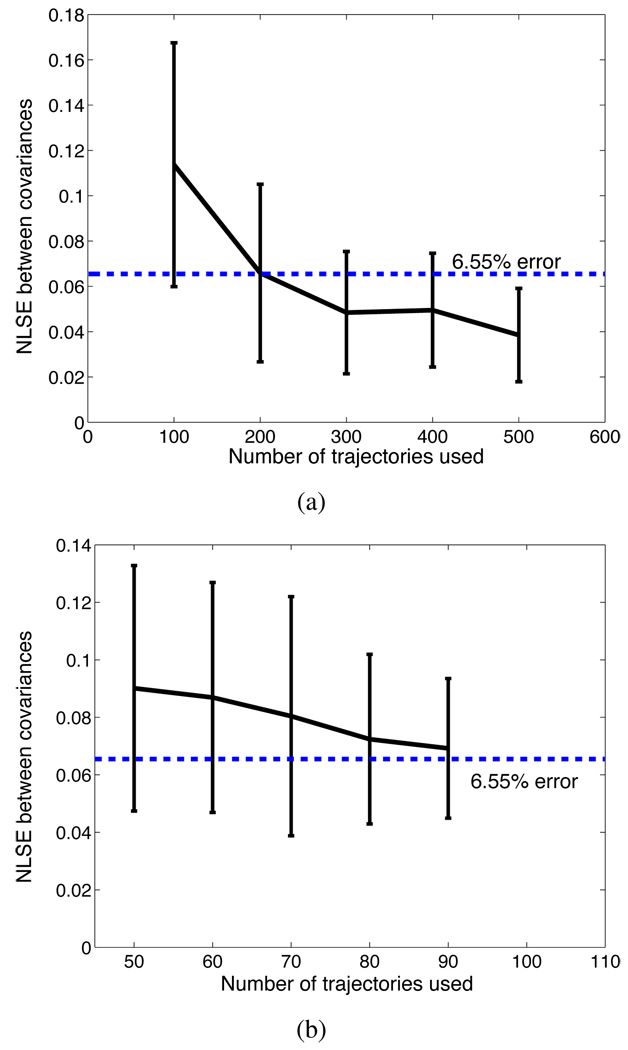
We now assess the 6.55% error in the covariance given by our stochastic model. We consider whether this error is due to modeling, experimental error, or the relatively small number of samples used to compute 6D data. Since the quantity of experimental data that can be obtained from the same artificial tissue is limited, we use numerically generated data to investigate the effect of the number of samples. Suppose that our stochastic model with four parameters (λ₁, λ₂, λ₃ and κ) perfectly describes the needle insertion system. Then using the parameters in (12) and the Euler-Maruyama method [3], [9], we generate many needle paths. Taking these paths as experimental data, we follow the same procedure that we used to estimate the model parameters and the corresponding closed-form covariance. The difference between the covariance obtained using artificial experimental data (which is assumed to be perfectly simulated by the Euler-Maruyama method) and the covariance computed using the closed-form formula is computed. We use 100 sets of 100 needle trajectories to compute the NLSEs of the covariances and have the mean μ = 0.1137 and the standard deviation σ = 0.0538 for the NLSEs. It is shown as the first error bar in Fig. 3(a). After the tests with the different numbers (200, 300, 400 and 500) of sample trajectories, we also plot the error bars as shown in Fig. 3(a). These error values show the accuracy level that we can expect when the needle model is perfect. Furthermore Fig. 3(b) shows the error bars for the NLSEs between the sample covariances and the closed-form covariances. In this test, we resample the experimental data obtained in Section IV. The NLSEs gets smaller as the resampling size increases. Comparing Fig. 3 and the 6.55% error that we achieved, and noticing the decreasing error with the increasing sampling size, we can conclude that the error is in large part due to sampling effects.

Fig. 3.

(a) Error bars for the NLSEs between the two covariances obtained by the simulated paths and by the closed-form formula. (b) Error bars for the NLSEs between the two covariances obtained by the experimental trajectories and by the closed-form formula.

Let us revisit our previous needle model in [13] and [16]. In this model, we employed two noise parameters λ₁ and λ₂. By fitting this model to our experimental data, we can estimate the parameters and obtain the closed-form covariance. The NLSE of the closed-form covariance relative to the sample covariance (11) is 0.261 (=26.1%), which is much higher than the error (6.55%) by our new model (3). Therefore, our new model better fits to the experimental data than the previous one.

VI. CONCLUSION

Using the experimentally obtained trajectories of a bevel-tipped flexible needle, we estimated the model parameters that are embedded in the stochastic nonholonomic needle model. We derived the equation that describes how the covariance of the need tip pose is related to the model parameters. This formulation is based on the theory of error propagation [19]. The closed-form covariance as a function of the model parameters was derived for the case in which the needle is inserted into tissue with constant insertion speed (υ(t) = υ₀) and without rotating (ω(t) = 0).

Using the stereo vision system, the 3D position data of the needle tip were recorded while the needle was inserted without rotating. Repeating the insertion, we obtained 100 sets of insertion data. Matching the covariances obtained by the closed-form formula and the experimental data, we determine the curvature of the needle trajectory and the three noise parameters which represent the amount of uncertainty in the insertion system. We also confirmed that our modified needle model in (3) with three noise parameters better fits to the experimental data than the previous model with the two noise parameters in [13], [16]. The parameter values that we estimated in this paper were used for needle path planning [14].

The method proposed here may be improved in several ways in the future. First, we can employ different baseline trajectories. In this paper, we consider only one circular baseline trajectory. For example, if we insert the needle with a constant rotation velocity ω(t) = ω₀ ≠ 0, we will obtain a covariance matrix which will be a different form from (10). Considering both this new covariance and the current covariance (10) may lead to more accurate determination of the model parameters. Second, the anisotropic property of real tissues should be considered. The current model (3) assumes that the artificial tissue is isotropic, although real tissue is anisotropic. Modeling the anisotropy is challenging, but it will be an essential step for needle insertion to real tissue. Finally, we can increase the accuracy of the closed-form covariance using a second-order approximation [20]. We leave this work for the future.