Host resistance and coevolution in spatially structured populations

Abstract

Natural, agricultural and human populations are structured, with a proportion of interactions occurring locally or within social groups rather than at random. This within-population spatial and social structure is important to the evolution of parasites but little attention has been paid to how spatial structure affects the evolution of host resistance, and as a consequence the coevolutionary outcome. We examine the evolution of resistance across a range of mixing patterns using an approximate mathematical model and stochastic simulations. As reproduction becomes increasingly local, hosts are always selected to increase resistance. More localized transmission also selects for higher resistance, but only if reproduction is also predominantly local. If the hosts disperse, lower resistance evolves as transmission becomes more local. These effects can be understood as a combination of genetic (kin) and ecological structuring on individual fitness. When hosts and parasites coevolve, local interactions select for hosts with high defence and parasites with low transmissibility and virulence. Crucially, this means that more population mixing may lead to the evolution of both fast-transmitting highly virulent parasites and reduced resistance in the host.

1. Introduction

Understanding the interactions between hosts and parasites, particularly the factors influencing the evolution of host defence and parasite virulence, is crucial to our management of natural systems. It is clear that most populations are characterized by spatial and social structures. For example, hosts may be more likely to contract disease from nearby infected individuals or those within their own social groups than spatially or socially more distant infected individuals. The impact of this within-population structure on the evolution of parasites is being increasingly recognized both theoretically [1–4] and empirically [5,6]. However, less attention has been focused on how the evolution of host defence may be affected by the structuring that results from local interactions. This is important as we need to understand how spatial structure may affect the coevolution of host defence in combination with parasite virulence in order to determine the overall effect on disease.

There has been substantial theoretical work on the evolution and coevolution of parasites and their hosts [7–11] in a non-spatial, or ‘mean-field’, setting. Many such studies within the gene-for-gene or matching-allele frameworks focus on how genotype-specific interactions between hosts and parasites maintain and generate diversity [12,13]. Studies on the evolution of ‘general’, non-parasite specific, host defences have mainly focused on avoidance of infection (e.g. lowered transmission rate; [9,14,15]), although alternative defence mechanisms, such as clearance (e.g. increased recovery; [10,16]) and tolerance (e.g. lowered virulence; [17,18]) have also been examined. These models show how the level of defence to parasitism that evolves depends on ecological parameters, host life history and the evolutionary costs of defence. Moreover, it has been shown that resistance mechanisms (for example, avoidance or clearance) allow for diversity to arise through negative frequency dependence leading to evolutionary branching, whereas tolerance mechanisms to parasite-induced mortality do not [9,17–19]. However, the mean-field assumption of complete population mixing in these studies, while allowing increased tractability, does limit their application to real ecological systems. In natural systems hosts are likely to create their own spatial and social structures through local reproduction and transmission.

There is a growing body of literature which recognizes that parasites within spatially structured host populations may exhibit markedly different evolutionary dynamics to those in the mean-field [1–4,20–22]. In particular, theoretical [1–4] and empirical studies [5,6] have suggested that parasites should be expected to be more ‘prudent’ when infection occurs locally, evolving lower transmission and virulence than in well-mixed populations. However, at intermediate parasite dispersal, between the completely local and completely mixed limiting cases, virulence may evolve to higher levels than predicted by non-spatial theory [4]. The evolution of parasites in spatially structured host populations is determined by the interplay of genetic and demographic spatial structuring, which in turn depends on the details of the ecological dynamics [23]. For example, demographic turnover is needed for local interactions to select for prudence [23], while in human diseases with little demographic turnover, only parasites causing diseases with long-lived immunity are likely to be prudent in space [23,24].

While the effect of metapopulation structure on local adaptation and diversity in gene-for-gene and matching alleles models has been well studied [25–27], there is little understanding of what effect local interactions between individuals within a population may have on the evolutionary dynamics of general host defence. Given that the majority of natural and managed systems have some degree of population structure, and that the coevolution of host defence with parasite virulence is crucial to an understanding of host–parasite systems, it is important to examine a within-population spatially explicit evolutionary model of host resistance. Using a classical susceptible-infected (SI) framework [28], we introduce spatial structure by assuming that hosts exist on a regular lattice and that the ecological interactions may occur locally, between neighbouring sites, or globally, across the lattice. We are, therefore, able to examine the role of structure across the full range from completely mixed to completely local populations that may occur in nature. Using a pair approximation [4,29], we numerically produce pairwise invasion plots (PIPs) [30] to identify the evolutionary behaviour and verify these findings with stochastic simulations of the full spatial system. We then assess the outcome when the host and parasite coevolve. Our key result is that increasingly global interactions select for both higher parasite virulence and transmission, and lower host defence, leading to the coevolution of highly infectious and deadly disease.

2. Model

Denoting susceptible (uninfected) hosts by X and infected hosts by Y, the classical mean-field equivalent of our model is given by the equations,

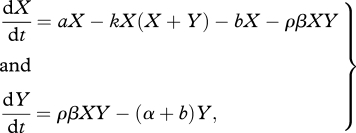2.1

with the parameter definitions as given in table 1. To construct the spatial model, we assume a regular lattice of sites, such as that shown in figure 1, where each site has four ‘neighbours’ highlighted by the lines between sites. Each site may be occupied by a susceptible host (X, light grey site on figure 1), an infected host (Y, black site) or may be unoccupied (0, white site). Susceptible hosts reproduce at birth rate a. If reproduction is local, an empty site is filled by an offspring from a (randomly chosen) neighbouring susceptible parent (i.e. in figure 1 the central susceptible may only reproduce into the free site to its right), while if it is global, offspring are born into a random unoccupied site. All hosts die at natural death rate b, and that site then becomes unoccupied. Transmission of disease occurs at a fixed rate β. If transmission is local an infected host may only transmit disease to a neighbouring susceptible (i.e. in figure 1 the central susceptible may only be infected by the two infected hosts above and below it), whereas if it is global it may infect any susceptible on the lattice. Host resistance occurs through reducing transmission (avoidance). We introduce a susceptibility scaling factor ρ (note that a low value of ρ indicates high resistance) where total transmission is given by ρ × β. Infection causes an increased death rate (defined as virulence) α and there is no recovery. We note that without recovery or reproduction from infected hosts we treat the parasite as an obligate killer and infected hosts make no direct contribution to host fitness, but this allows greater tractability to the model. We move between fully local and fully global interactions through parameters G_R and G_T, which describe the proportion of global reproduction and transmission, respectively—for example G_T = 0 gives 100 per cent local transmission, G_T = 1 gives 100 per cent global transmission (note these are equal to L_R and L_T as used by others [2,4,31]).

Table 1.

Definitions of the model parameters and variables.

a	host birth rate
k	density-dependence on host birth (mean-field only)
b	host death rate
β	transmission rate
α	parasite-induced death rate (virulence)
ρ	host susceptibility
GT	proportion of transmission occurring locally
GR	proportion of reproduction occurring locally
Pi	probability that a chosen site on lattice is in state i
Pij	probability that a chosen pair of sites on lattice are in states i and j
qi/j	conditional probability that a site is in state i given that its neighbour is in state j

Figure 1.

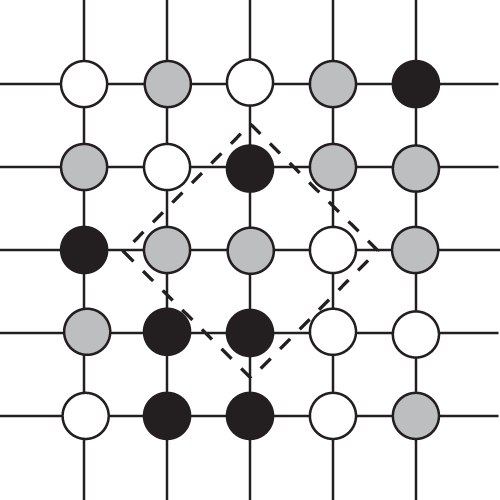
Susceptible and infected hosts exist on a lattice of sites. Grey circles denote a site occupied by a susceptible host, black circles a site occupied by an infected host and white circles an empty site. Each site has four neighbours shown by the lines between sites. The local neighbourhood of the central host is marked by the dashed lines. Local interactions occur only between the four neighbouring sites, while global interactions can occur between any sites on the lattice.

Fully spatially explicit stochastic simulations of this model are carried out by establishing an explicit lattice of sites and allowing the ecological processes to occur probabilistically in each site (see the electronic supplementary material for a detailed description of the simulation procedure). We can also approximate the spatial model through a set of ordinary differential equations that not only track the densities of susceptible, infected and empty sites, but also of neighbouring pairs of sites (i.e. how many susceptible hosts neighbour infected hosts). In particular, the probability that some site on the lattice is in a particular state (i.e. X, Y or 0) is given by, for example, P_X for state X, and the probability that a neighbouring pair of sites are in say states X and Y by P_XY. We also consider the conditional probability that given the focal site is in state X it has a neighbour in state Y, given by q_Y/X = P_XY/P_x. We then use a pair approximation [29] to represent the dynamics of the system (approximating higher order effects than between neighbouring pairs of sites). See the electronic supplementary material for more details.

We assume an evolutionary trade-off between susceptibility (ρ) and reproduction (a) such that a = f(ρ), where extreme values (ρ_max, a_max) and (ρ_min, a_min) are joined by a smooth curve. Taking an adaptive dynamics approach, we presume that the ecological dynamics are fast such that when a new mutant host appears, the lattice is at equilibrium. We then consider a mutant host strain, , which enters the population with some alternate strategy (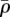, ), that differs slightly from that of the resident population strategy (ρ, a). The invasion fitness of the mutant host is defined as its growth rate when rare. From our set of equations (see the electronic supplementary material) we can calculate this to be,

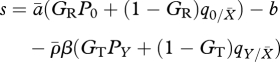2.2

(see table 1 for parameter definitions). For a range of resident and mutant parameters, as well as explicit trade-offs between susceptibility and reproduction, we numerically solve our differential equations and substitute the resulting equilibrium quantities into the fitness function (2.2). We can then produce PIPs [30] that will allow us to understand the evolutionary dynamics. In particular, we can find the position and nature of ‘evolutionarily singular points’, potential ‘stopping points’ of evolution.

3. Results

(a). Local-to-global reproduction

We first address the evolution of host resistance against a non-evolving parasite. Initially, we fix transmission to always be fully local (G_T = 0), such that transmission is only between neighbouring contacts. We then plot PIPs for varying local–global reproduction (G_R). Taking a trade-off a = f(ρ) where increased resistance incurs weakly accelerating costs to reproduction (−c < f″(ρ) < 0, where c is a small constant), we find in all cases either a Continuously Stable Strategy (CSS)—an attracting and uninvadible level of resistance—or that resistance is maximized/minimized (i.e. no singular strategy exists in our trade-off range). We plot the predicted level of resistance (susceptibility, ρ) from the PIPs with the black dots in figure 2a. As reproduction becomes increasingly global (moving from left-to-right in the figure) the host is predicted to evolve lower resistance (high values of ρ). The grey dots show the outcome from the fully spatial stochastic simulations. These show good agreement with our analytic results, and in particular agree that local reproduction selects for higher resistance. Further work (not shown) finds that the pattern of higher host resistance with local reproduction is preserved for any ratio of local : global transmission.

Figure 2.

The predicted (CSS) levels of resistance in the host as local–global reproduction and transmission are varied. Black dots show predictions from the PIPs, and grey dots the results from stochastic simulations. (a) Local–global reproduction (G_R) varies, with fixed fully local transmission G_T = 0 (a_min = 4, a_max = 8). As reproduction becomes increasingly local (right-to-left), resistance increases (ρ decreases). (b) Local–global transmission (G_T) varies, with fixed fully local reproduction G_R = 0 (a_min = 3, a_max = 8). As transmission becomes increasingly local, resistance increases. (c) Local–global transmission (G_T) varies, with fixed fully global reproduction G_R = 1 (a_min = 4.2, a_max = 8). As transmission becomes increasingly local, resistance decreases (ρ increases). Further parameters: b = 0.1, α = 0.1, β = 1, ρ_min = 1, ρ_max = 2, p = 0.1. The extremes of a in the trade-off were varied to keep the CSS within the range of 0–1.

(b). Local-to-global transmission

We now fix reproduction to be fully local (G_R = 0) and vary local–global transmission (G_T) in figure 2b. Again, the PIPs predict a clear trend that as transmission becomes increasingly global (moving from left-to-right), host resistance decreases (ρ increases). However, in figure 2c, we now fix reproduction to be fully global (G_R = 1) and again plot the resistance predicted from the PIPs for varying local : global transmission. We now see the opposite trend, that as transmission becomes increasingly global, resistance increases (ρ decreases). Further investigation finds that the threshold between these two behaviours, while parameter dependent generally occurs at roughly G_R ≈ 0.65 (i.e. 35% local reproduction). Thus if reproduction is predominantly local, local transmission selects for higher resistance, while if reproduction is predominantly global, local transmission selects for lower resistance. Once more, the fully spatial simulation results mimic the patterns from the analytic approximation in both figure 2b,c, although there are discrepancies in the actual values.

(c). Fitness gradient

We can understand the factors influencing selection by considering the selection gradient [23]. By taking the derivative of the fitness (equation (2.2)) with respect to mutant resistance, we find this to be,

3.1

(see table 1 for parameter definitions). The fitness gradient is made up of four terms. The first term is the direct fitness benefit (or, rather, reduced fitness loss) of increased resistance and is proportional to the (local or global) density of resident infected hosts. The second term is the direct fitness cost of reduced reproduction and is proportional to the (local or global) density of free space on the lattice. In a completely global system (G_R = 1, G_T = 1) the host's strategy would simply be the balance of these two factors. However, there are two further terms that are entirely local effects. The third term concerns the effect the mutant strategy has on the local density of infected hosts (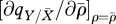). When reproduction is predominantly local, mutants will appear in clusters on the lattice. Where these mutants have higher resistance, this will create regions of low local parasite prevalence relative to the lattice mean, with the mutants protecting each other from local parasitism. This thus creates a further benefit to the mutants of increased resistance when transmission is local. When reproduction is predominantly global, mutants are likely to be surrounded by resident hosts and do not gain the same increased protection. Moreover, it is likely that a mutant with higher resistance may in fact offer slight protection to neighbouring residents from local parasites, offering an advantage to strains that ‘cheat’ by investing in lower resistance but getting protection from neighbours with higher resistance. The final term in equation (3.1) concerns the effect of the mutant strategy on the local density of free sites (). The reduction in birth rate as an evolutionary cost to resistance will create more free sites and thus, reduce local competition for reproduction. Again, this effect is likely to be amplified by local reproduction.

(d). Evolutionary branching

Until now, we have focused on long-term uninvadible attractors of evolution, CSSs. In figure 3a, we show a PIP for the fully global model (G_R = 1, G_T = 1) that predicts an evolutionary branching point—an attracting but invadible point where hosts undergo disruptive selection and branch into two coexisting strains. This result matches with mean-field models of host evolution that also predict evolutionary branching of resistance [11,12]. In figure 3b, we also show a PIP for the fully local model (G_R = 0, G_T = 0) that again predicts an evolutionary branching point, suggesting that branching may occur in a fully spatial system, although the branching point in the fully local model requires higher virulence and a more strongly decelerating trade-off than that of the global model. We also find branching points predicted for a range of intermediate values of G_R and G_T. Evolutionary branching proved difficult to achieve in the fully spatial stochastic simulations, which may be owing to there being low local population densities.

Figure 3.

PIPs predicting branching points (attracting but invadible singular strategies), where dimorphic host populations may be expected to evolve. Black areas denote regions of positive mutant invasion fitness (s > 0) and white areas regions of negative mutant invasion fitness (s < 0). Given small mutational steps, the host population will evolve up or down the diagonal. (a) the fully global model (G_R = 1, G_T = 1), (b) the fully local model (G_R = 0, G_T = 0). Parameters: in (a), α = 0.7, a_max = 8, a_min = 4.2, p = −0.3; in (b), α = 0.1, a_max = 5.2, a_min = 2.8, p = −0.002. Other parameters: b = 0.1, β = 1, θ = 0.25, ρ_max = 2, ρ_min = 1.

(e). Coevolution

Given the results of previous studies on the evolution of parasites in spatially structured host populations [4], we can now consider the effects of spatial structure on the fully coevolutionary outcome of disease interactions. We assume trade-offs, between resistance (ρ) and reproduction (a) in the host, and between transmission (β) and virulence (α) in the parasite, that predict CSS levels of resistance and virulence in the host and parasite, respectively. Plotting each species' CSS while varying the other's trade-off we can find the coevolutionary CSS where the host and parasite strategies cross (see the electronic supplementary material). Assuming fully local reproduction [4], we plot the final relative virulence (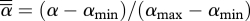) and relative total transmission (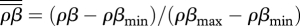) for varying local–global transmission (G_T) in figure 4. As transmission becomes increasingly global, the total transmission (black dots) increases. Virulence (grey dots) also initially rises with increasingly global transmission, before dropping slightly at high degrees of global transmission. Compared with when only the parasite evolves [4], the coevolution of the host does not affect the pattern of virulence, but it does change the pattern of transmission from a humped function of local interactions to a strictly increasing function. Global interactions thus select for disease interactions with low host defence, high parasite transmission and high virulence.

Figure 4.

The coevolutionary outcome of the spatial host–parasite interaction. We show the relative total transmission (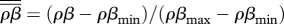, black dots) and the relative virulence (, grey dots) at varying levels of local–global transmission (G_T). As transmission becomes increasingly global (moving from left to right), both transmission and virulence increase. Parameters: b = 0.1, ρ_min = 1, ρ_max = 2, a_min = 3, a_max = 8, p = 0.1, α_min = 0.3, α_max = 0.6, β_min = 1.31, β_max = 2.7, C = 5, G_R = 0.

4. Discussion

All ecological systems are likely to exhibit at least some degree of spatial structure through localized interactions between individuals. However, the majority of evolutionary models take the extreme limit of assuming completely global, mean-field, interactions. Here, we have examined the effects of different degrees of spatial structure on the evolution of host resistance to parasitism, and on the coevolution of host resistance and parasite virulence. We have found that for the host, local reproduction will always select for higher resistance, as does local transmission provided that reproduction is also predominantly local. Our key result is that increasingly globalized interactions will select for disease characterized by low host defences, high disease transmission and high parasite virulence. As such, we have shown that spatial structure has a fundamental impact on the coevolutionary dynamics of hosts and parasites.

We have explicitly examined the factors driving increased host resistance in local populations by studying the fitness gradient. In fully mixed populations, the host's strategy is a balance between the benefit of reduced transmission (and reduced global parasite prevalence) and the cost of this increased investment. In spatially structured populations, however, the story is more complex. When reproduction occurs locally, host strains form clusters such that when a mutant appears it is likely to be surrounded by other related mutants. When transmission also occurs locally, a cluster of mutants with high resistance will reduce the local parasite prevalence, reducing the mutants' exposure to disease and thus strengthening the selection for higher resistance. Conversely, when reproduction occurs globally, mutants are likely to be surrounded by non-related (resident) host strains. In this case, when transmission is local, mutants may be at an advantage by investing in lower resistance yet benefitting from the lowered local parasite prevalence, owing to the higher resistance of the surrounding residents. A further spatial ecological feedback occurs from the reduction in birth rate as an evolutionary cost to resistance, as the increase in the number of empty sites around resistant individuals reduces local competition and density-dependence on reproduction. Both ecological structuring (the spatial pattern of susceptible and infected hosts) and genetic structuring (local clusters of related hosts) are, therefore, important in determining the level of resistance in spatially structured host populations [2,3,23,32]. Frank [33] showed that higher relatedness increased selection for resistance in a non-spatial model that assumes constant infection risk. The results of our model could also be further understood in a kin selection framework [23], but we found that collecting terms in the fitness gradient that involve some measure of relatedness did not add greater insight into the results, with the various terms being more complex than in the case of the evolution of the parasite [23]. The evolutionary outcomes of spatial models can be understood in a number of different frameworks, but fundamentally they result from both ecological and genetic structuring.

The way in which spatial structure is incorporated into evolutionary models has important implications to the outcome [34]. Spatial structure where patches with within-population mixing are linked by dispersal is well known to have important effects on coevolution resulting in ‘genetic mosaics’ [26,35]. Such metapopulation models have been studied extensively where infection depends on a match between host and parasite genotypes [25,27,36]. These studies have shown how this form of spatial structure can have important implications to diversity and local adaptation between hosts and parasites. By contrast, our model focuses on quantitative changes to the absolute level of host defence within finite populations in response to differing scales of interactions between individuals. A key finding from mean-field models in this evolutionary ecology framework has been the potential for evolutionary branching through disruptive selection [9,30]. Although branching has been found in spatially explicit ecological models [37,38], it has been suggested that it is less likely to occur in spatial models than in the mean-field [34,39]. We have predicted here that evolutionary branching in host resistance may still occur when transmission and reproduction are local but for different parameter values and trade-off shapes to the mean-field. Despite these results, we found evolutionary branching difficult to achieve in stochastic simulations, seemingly fitting with previous findings [39,40] that small population sizes may delay or inhibit branching (although the former study assumed fixed population sizes). Interestingly, although Magori et al. [37] did find branching in stochastic simulations of their spatial model, they found that the pair approximation was a poor predictor of the location of the branching point. It thus seems that, although evolutionary branching may occur in spatially structured systems, it may only occur for a restricted set of parameter values and pair approximation analysis does not predict this parameter set accurately. More broadly, our model of within-population structuring owing to local interactions predicts that spatial structure makes diversity through evolutionarybranching less likely, contrasting with the predicted effects on diversity in gene-for-gene with metapopulation structure [27]. This emphasizes not only the importance of the infection genetics to the coevolution of diversity in hosts and parasites [41] but also the fact that different forms of spatial structure may cause different selective pressures [34].

Although empirical studies in the gene-for-gene framework often include a spatial element [42], there have been few explicit experiment tests of the effects of spatial structure on the evolution of host resistance as a quantitative trait. Two studies [5,6] have investigated the effects of spatial structure on the evolution of pathogen infectivity, in a bacteria–phage and insect–virus system, respectively, and both found that their results agreed with the theoretical prediction that local interactions select for lower pathogen infectivity. Further experimental work is needed, addressing the evolution of hosts as well as parasites, to further understand the effects of spatial structure.

Our analytic approach was only an approximation to the full spatial dynamics, as higher order effects than pair relationships were ignored [29,43]. However, the results from fully spatially explicit simulations of our system closely mirrored our analytic results. In some cases there were discrepancies in the actual level of host resistance predicted between the two methods, but crucially the key patterns of how resistance varied with increasingly local interactions were preserved. By using a simple SI framework with no recovery or reproduction from infected hosts, the parasite was treated as an obligate killer in our model. It is important to apply the results to more general host–parasite systems by extending the model to incorporate processes such as recovery, infected reproduction and immunity. Furthermore, modification to the analysis should also study the evolution of alternate modes of defence, such as tolerance [15,16] or acquired immunity [44] in a spatial setting. In particular, tolerance is likely to have very different evolutionary dynamics when compared with resistance, as it will increase local prevalence which would select against defence in a local population.

We live in an increasingly globalized world, with many populations exhibiting a mix of local and global interactions [45]. We have found that local interactions and spatial structure generate greater levels of defence, while previous theoretical [2–4] and empirical [5,6] studies have also suggested that parasites will be selected to have lower transmission and lower virulence in populations with local interactions. As such, much more benign infectious disease interactions are likely to coevolve in spatially structured populations. Crucially, this of course also means that if populations become more connected, parasites are selected to be more acute while hosts will reduce their defence, leading to the coevolutionary emergence of highly prevalent, highly virulent disease. These predictions will depend critically on the ecology of the disease interactions and on whether there is demographic turnover in the population [23,31,34]. Nevertheless, with the increasing mixing of human, animal and plant populations it is vital that the implications of these changing interactions between hosts to the nature of disease are better understood.