Abstract
A widely held assumption is that metabolic rate (Ėmet) during legged locomotion is linked to the mechanics of different gaits and this linkage helps explain the preferred speeds of animals in nature. However, despite several prominent exceptions, Ėmet of walking and running vertebrates has been nearly uniformly characterized as increasing linearly with speed across all gaits. This description of locomotor energetics does not predict energetically optimal speeds for minimal cost of transport (Ecot). We tested whether large bipedal ratite birds (emus and ostriches) have gait-specific energetics during walking and running similar to those found in humans. We found that during locomotion, emus showed a curvilinear relationship between Ėmet and speed during walking, and both emus and ostriches demonstrated an abrupt change in the slope of Ėmet versus speed at the gait transition with a linear increase during running. Similar to human locomotion, the minimum net Ecot calculated after subtracting resting metabolism was lower in walking than in running in both species. However, the difference in net Ecot between walking and running was less than is found in humans because of a greater change in the slope of Ėmet versus speed at the gait transition, which lowers the cost of running for the avian bipeds. For emus, we also show that animals moving freely overground avoid a range of speeds surrounding the gait-transition speed within which the Ecot is large. These data suggest that deviations from a linear relation of metabolic rate and speed and variations in transport costs with speed are more widespread than is often assumed, and provide new evidence that locomotor energetics influences the choice of speed in bipedal animals. The low cost of transport for walking is probably ecologically important for emus and ostriches because they spend the majority of their active day walking, and thus the energy used for locomotion is a large part of their daily energy budget.
Keywords: gait, cost of transport, energetics, locomotion, preferred speeds
1. Introduction
Current opinion regarding locomotor energetics and mechanics presents a conundrum regarding preferred speeds and gaits. Freely moving animals are known to exhibit gait-specific preferred speeds, both in nature [1] and under more controlled conditions [2–4]. A widely held opinion is that one major reason animals choose particular speeds and gaits is to minimize their cost of transport (Ecot), the energy used to move a unit distance [5]. In the most often-cited study supporting this conclusion, Hoyt & Taylor [2] found a correlation between the preferred speeds of walking/trotting horses and the speeds that minimized the Ecot. However, metabolic rate (Ėmet) of most vertebrates, including bipedal birds, has almost always been described as increasing linearly with speed across all gaits [6–9]. Also, using this linear model, the slope of the increase in Ėmet with speed has been taken as the net Ecot [7,8]. This analysis results in an identical value of net Ecot across all speeds and gaits (i.e. there is no optimal speed that minimizes the net Ecot and costs are identical for walking and running). This approach assumes: (i) a straight line describes the Ėmet data across speeds and gaits; and (ii) any difference between the resting metabolic rate and the y-intercept of the line is not part of the transport costs. This simple analysis has proved very useful in making broad comparisons among vertebrate runners and delineating body size as a major factor determining locomotor energetics [8,10], but it may also obscure biologically important variation in cost both within and among species [11,12].
Exceptions to the linear increase in Ėmet with speed in walking and running have been noted in some mammals and recently in one avian biped. Numerous studies spanning almost 100 years have found that the Ėmet of humans increases curvilinearly with speed during walking, has an abrupt change in slope at the gait transition and increases linearly during running [13–15]. A recent study found that the relation of Ėmet with speed is curvilinear in running as well, if individual data are examined [16]. Because of this pattern of energy use, humans have an optimal walking speed that minimizes net Ecot, and the net Ecot (calculated by subtracting resting metabolic rate) for walking is lower than that found during running [12]. The complete biomechanical determinants of the locomotor energy use during walking and running are not known with certainty, but it is perhaps not surprising that the effect of speed is different between walking and running because the overall movements of the centre of mass are fundamentally different (reviewed in [14]). Walking uses an inverted pendulum mechanism, and running is a bouncing gait with greater possibility of elastic energy exchange. The basic mechanics of walking and running are shared by bipeds and quadrupeds, and gait-specific energy use has also been described in horses [2,17] and two smaller quadrupeds [18,19]. A curvilinear relation of Ėmet and speed has also been measured in walking elephants [20]. The authors of two studies of cervids (reindeer and elk) also noted a curvilinear increase in Ėmet with speed in some individuals, but they used a linear relation and a single value of net Ecot to describe the data for the species [21,22]. Recently, Ecot has been found to vary with gait in the ostrich [23]. Despite these exceptions, the assumption that metabolism varies linearly across gaits is still widely used in treatments of the locomotor costs in extant birds and mammals, and in predicting the locomotor energy use by extinct species [24,25]. Our focus here is on walking and running gaits and we do not consider the unusual pattern of locomotor energetics in hopping macropod marsupials [26,27].
Among extant vertebrates, striding bipedal locomotion occurs primarily in humans and birds. Large ratite birds are of particular interest because they and humans represent the outcome of independent evolution of bipedal locomotion in similar-sized animals. We asked here whether, despite differences in limb morphology, humans and large avian bipeds share a common pattern of energy use in walking and running. We hypothesized that Ėmet would not be a uniform linear function of speed across both gaits in large avian bipeds. We further hypothesized that Ėmet during walking would exhibit curvilinear function with speed if a sufficiently large range of speeds was measured. We predicted (i) that these relations would result in an energetically optimal speed for walking (i.e. minimum net Ecot) and (ii) that the minimum net Ecot would be lower for walking than for running. These data are of interest not only because they may improve our understanding of locomotion in living bipeds, but because the energetics of locomotion in large ratites may provide clues regarding energy use and optimal speeds of extinct large bipedal birds and dinosaurs, as well as extinct hominids.
2. Material and methods
(a). Animals
The protocol for this study was reviewed and approved by the Animal Care and Use Committee of California State Polytechnic University, Pomona. Five ostriches (Struthio camelus; body mass 58 ± 6.5 s.e.m. kg; range 36–75 kg; two males, two females and one unknown sex) and six emus (Dromaius novaehollandiae; body mass 25.7 ± 0.89 s.e.m. kg; range 24–30 kg; three males and three females) obtained from local farmers were housed in outdoor enclosures at the California State Polytechnic University in Pomona and provided with commercial ratite pellets and fresh water ad libitum. Starting at approximately six months of age, the birds were trained to walk and run on a large motorized treadmill (Equine Dynamics Inc., Kansas City, MO, USA) inside a custom-made mobile wooden box. The birds were trained for at least 20 min per day three to four times per week in the month before data collection. Also included in the results are metabolic rates for the ostriches (n = 4) used by Rubenson et al. [23] to calculate cost of transport.
We chose to work with sub-adult animals because this allowed us to raise the animals to experimental size within a year and because they were somewhat more tractable than sexually mature animals. Their tractability allowed us to obtain reasonable sample sizes. Available evidence suggests that our animals have locomotor energetics similar to larger adults. First, our measurements are in substantial agreement with measurements of larger representatives of the same species (see §§3 and 4). Second, for the ostriches we collected metabolic data for animals ranging from 36 to 75 kg and found no systematic change with body mass in the mass-specific metabolic rate during walking and running.
(b). Metabolic rates
Oxygen consumption (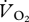 ) was measured using an open flow system with a loose-fitting mask and downstream measurement of flow. The ostrich mask consisted of a canopy supported from above and enclosing the head and neck of the bird. The lightweight emu mask was constructed from two 1 l soda bottles, covered just the head, and was connected to a cantilever that supported the mask and connecting tubing. Air was pulled into the mask and through a mass flow meter (Omega Engineering, Inc, Stamford, CT, USA) at a rate that was dependent on bird size and running speed (200–800 and 70–120 l min−1 for ostriches and emus, respectively). Dry gas flow was calculated by correcting the measured flow for the partial pressure of water vapour, which was calculated from relative humidity as measured with an Omega digital hygrometer. In the ostrich measurements, continuous sub-samples of expired gases were passed through Drierite before passing sequentially through O2 and CO2 gas analysers (Sable Systems, Las Vegas, NV, USA). For emus, the sub-sampled gas was passed through Drierite and Ascarite, and then through the Sable Systems O2 analyser. The appropriate mass-balance equations of Withers [28] were used to calculate
) was measured using an open flow system with a loose-fitting mask and downstream measurement of flow. The ostrich mask consisted of a canopy supported from above and enclosing the head and neck of the bird. The lightweight emu mask was constructed from two 1 l soda bottles, covered just the head, and was connected to a cantilever that supported the mask and connecting tubing. Air was pulled into the mask and through a mass flow meter (Omega Engineering, Inc, Stamford, CT, USA) at a rate that was dependent on bird size and running speed (200–800 and 70–120 l min−1 for ostriches and emus, respectively). Dry gas flow was calculated by correcting the measured flow for the partial pressure of water vapour, which was calculated from relative humidity as measured with an Omega digital hygrometer. In the ostrich measurements, continuous sub-samples of expired gases were passed through Drierite before passing sequentially through O2 and CO2 gas analysers (Sable Systems, Las Vegas, NV, USA). For emus, the sub-sampled gas was passed through Drierite and Ascarite, and then through the Sable Systems O2 analyser. The appropriate mass-balance equations of Withers [28] were used to calculate 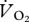 . Metabolic rate in Watts was calculated assuming 20.1 J (ml O2)−1.
. Metabolic rate in Watts was calculated assuming 20.1 J (ml O2)−1.
Resting metabolic rate was estimated as the lowest steady-state value reached while the bird stood quietly in the darkened box on the treadmill. During locomotion, steady-state metabolic rates were measured over 3–5 min periods of constant speed running. The values reported for individual emus are mean values from two to three treadmill sessions on different days. The species mean values and standard errors reported for both emus and ostriches were calculated by taking the mean of the mean values for individuals across days, and thus the sample size is equal to the number of animals measured.
(c). Preferred speeds
To determine preferred overground walking and running speeds, four of the emus used for metabolic rate measurements were videoed with a high-speed digital camera (Mikrotron EoSens CL) operated by the application StreamPix v. 4 (Norpix) as they moved through a narrow passageway. The camera operated at 500 frames per second and a pixel resolution of 1280 × 300 (horizontal × vertical) with a field of view of approximately 3 m. Video data collection and metabolic rate measurements occurred on different days. A 10-m-long passageway was constructed in the outdoor emu enclosure. One wall of the passageway was constructed of opaque-coated fabric and the other wall consisted of the chain-link fencing material of the enclosure. The entrance of the passageway was 1.8 m wide and tapered over 3.25 m to 0.9 m wide. For all runs analysed the animals ran straight through the passageway and did not contact the walls. The camera was placed outside the animal enclosure orthogonal to the centre of the passageway and captured a lateral view. Birds were fitted with reflective markers on the dorsal surface of the pelvis and gently herded through the passageway. A calibration grid was also filmed at the beginning of each session. Emus walked through the passageway unless they were encouraged to run by human assistants. Videos of the birds moving through the passageway were downloaded to a Macintosh computer and the pelvic markers tracked using ImageJ (Wayne Rasband, NIH).
(d). Dimensionless speed defined from Froude number
We calculated the dimensionless speed for the gait transition of ostriches and emus as the square root of the Froude number (v/(gLh)−0.5), where v is the horizontal velocity, g acceleration owing to gravity and Lh the hip height. Standing hip height (distance from the ground to the joint centre) for the emus and ostriches was 0.85 and 1.1 m, respectively.
(e). Analysis of covariance to test for nonlinearity
To distinguish statistically between a linear or curvilinear relationship in the metabolic rate versus speed curves for walking emus, we performed an analysis of covariance (ANCOVA) in which the independent variables were the linear and quadratic terms as covariates, and an identifier for the individuals was a factor.
3. Results
(a). Estimated gait transition
Using centre-of-mass mechanics, the gait transition in ostriches was defined by Rubenson et al. [23] as occurring at a speed of approximately 2.1 m s−1, which corresponds to a dimensionless speed (see §2) of 0.45. They found that over a small range of speeds below this value the kinetic and potential energy terms changed abruptly from out of phase to in phase. We found that the gait transition in the centre-of-mass movements in these large birds could be detected visually during the treadmill runs and on this basis noted that the gait transition in emus during treadmill locomotion occurred at approximately 1.9 m s−1, which corresponds to a dimensionless speed of 0.43. At this speed, the emus often alternated walking and running while moving backward and forward on the treadmill, and the metabolic rates at this speed were excluded from the statistical analyses of the metabolic rates during walking and running.
(b). Metabolic rates
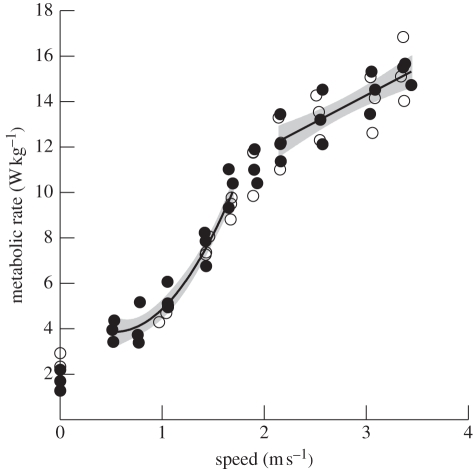
Three of our six emus walked steadily from very low speeds up to the gait transition speed, and showed what appeared to be a curvilinear relation between Ėmet and speed during walking (figure 1). We tested whether this relation was curvilinear using an ANCOVA model (see §2). In this model, all of the interactions (animal × linear; animal × quadratic; animal × linear × quadratic) were not significant, which allowed them to be removed from the model, producing a simplified model. This model indicated that inclusion of the quadratic term was highly significant, a finding that supported our interpretation that metabolic power was a curvilinear function of walking speed in emus. The remaining three emus had similar values of Ėmet for the speeds at which they walked steadily, and all of the data were taken together to calculate the overall relations of Ėmet with speed (figures 1 and 2).
Figure 1.
Mean mass-specific metabolic rate (Ėmet) of individual emus as a function of speed (v). Individuals that walked and ran over the full range of speeds (including the slowest speeds) and were used in the ANCOVA (see §3) are shown as black circles. Lines are regressions fitted separately to the walking and running data for all individuals: walking, Ėmet = 5.17 − 4.89v + 4.59v2 (r2 = 0.94); running, Ėmet = 7.19 + 2.36v (r2 = 0.60). Shaded bands indicate the 95% confidence intervals of the predicted mean values from the regressions. The zero speed values represent the metabolic rates for animals standing quietly on the treadmill and are not included in the regression analysis.
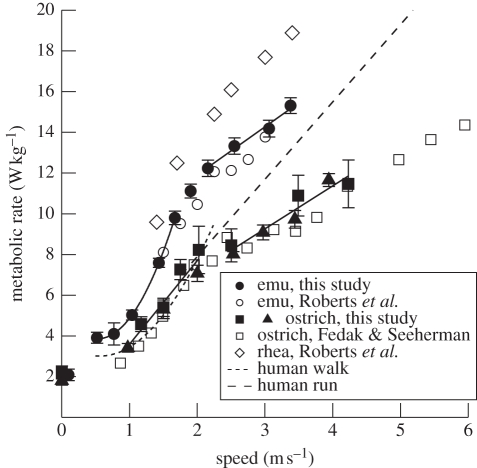
Figure 2.
Mass-specific gross metabolic rate (Ėmet) as a function of speed (v) in large ratite birds and humans. The species mean values for emus (n = 6) from this study are shown as black circles. Data from the emu measured by Roberts et al. [30] are represented by white circles (original data provided by Thomas Roberts). Mean values for ostriches from this study are shown as black squares (new data collected in California, n = 5) and black triangles (data collected in Western Australia and used previously to calculate cost of transport by Rubenson et al. [23]; n = 4). Data from the ostrich studied by Fedak & Seeherman [29] are represented by white squares. Rhea data (n = 3) collected by Roberts et al. [30] are shown as white diamonds (original data provided by Thomas Roberts). Metabolic rates plotted for human walking (short-dashed line) and running (long-dashed line) data are regressions through the data from 33 publications, most of which are cited in Rubenson et al. [12]. Solid lines through the emu data from this study are regressions fitted separately to the walking and running data (see figure 1 for equations). Solid lines through the ostrich data are regressions fitted separately to the combined mean walking and running data from this study: walking, Ėmet = −0.50 + 4.10v (r2 = 0.93); running, Ėmet = 2.95 + 2.11v (r2 = 0.92). Values at zero speed are mean values from this study (emu value offset for clarity) for animals standing quietly on the treadmill and are not included in the regression analyses.
The ostriches did not walk steadily over as large a range of speeds as did the emus. Within the range of steady walking speeds that we acquired for ostriches, the relationship between Ėmet and speed was linear (figure 2), but the slope was significantly different from that found for running (ANCOVA, p < 0.001). However, we infer that a curvilinear relation would be evident in walking ostriches if reliable data were collected at lower walking speeds because the linear relation for walking at speeds greater than 1.0 m s−1 extrapolates to a negative metabolic rate at zero speed and we assume that the metabolic rate during walking probably cannot be lower than the resting rate at zero speed. During running Ėmet increased linearly with speed for both ostriches and emus (figure 2).
(c). Cost of transport
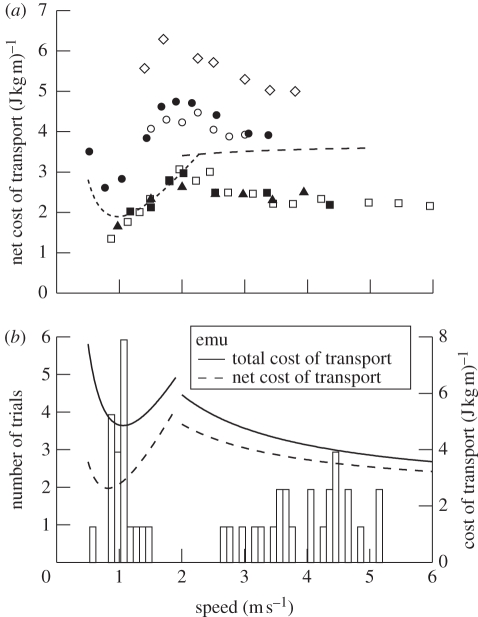
The net Ecot was calculated after subtracting resting metabolic rate during standing. For the ostriches, net Ecot increased steeply with walking speed, reached a peak at the gait transition (figure 3a) and declined with increasing running speed. The changes in net Ecot with speed were similar in emus, except a minimum value was found in walking at approximately 0.7 m s−1, below which net Ecot was higher (figure 3a). In both species the minimum net Ecot for walking was lower than the minimum value in running.
Figure 3.
(a) Mass-specific net cost of transport (J kg−1 m−1) plotted as a function of speed (m s−1) for rheas, emus, ostriches and humans. Symbols are as defined in figure 2. (b) Bars show the number of trials (left axis) recorded at different speeds for emus moving freely through a passageway in a large pen. Solid and dashed curves show the total and net cost of transport, respectively (right axis), for emus calculated from the relations of metabolic rate versus speed for walking and running.
(d). Preferred speeds of emus
Freely moving emus walked within a tightly clustered range of speeds with a mean of 1.0 m s−1 (figure 3b). No trials were recorded with a speed between 1.5 and 2.5 m s−1. When running, emus used a wide range of speeds above 2.6 m s−1.
4. Discussion
Our findings agree with most of the previous metabolic data collected on large ratites before the work of Rubenson et al. [23] (figure 2), but the change in the slope of Ėmet versus speed at the walk–run transition was not emphasized in these earlier studies. Fedak & Seeherman [29] commented on an apparent inflection in the metabolic rate versus speed data at the walk–run transition for the single ostrich in their study (figure 2), but they summarized their data with a linear fit through all of the data. Roberts et al. [30] focused on metabolic rates during running after subtracting out the intercept value, but their original data (T. J. Roberts 2009, personal communication) for an individual emu are consistent with a difference in slope at a gait transition of approximately 1.9 m s−1 (figure 2). Although a more limited speed range was examined, the data on rheas (figure 2) from the same study also suggest a change in slope at 1.7 m s−1, which corresponds to the biomechanically defined gait transition for this species [31]. We have not included in figure 2 the data on rheas from Taylor et al. [32], because the values appear to us to be anomalously high compared with the other ratite values. Their values during locomotion are approximately 30 per cent greater than the other metabolic data on running rheas [30], and their resting values are approximately 20 per cent higher than previously recorded [33]. The reason for the discrepancy is not clear; however, Taylor et al. [32] ran their birds for long intervals at each speed, and noted that the birds were fatigued and had elevated body temperatures at the end of the runs. They also adjusted the metabolic rates found during running for the elevated post-exercise oxygen consumption, assuming the post-exercise increase was an oxygen debt. They do not specify the magnitude of this adjustment.
Although the overall pattern of a changing Ėmet with speed is similar in large ratites and humans, the birds show greater changes in slope at the walk–run transition, and this difference affects the transport costs during running. In humans, the net Ecot increases with speed up to the gait transition, and then remains approximately constant across all running speeds (figure 3a). In contrast, net Ecot declines with increasing running speed above the gait transition in ostriches and emus. This difference leads to substantially lower transport costs during running in ostriches compared with humans, who have similar body masses. Humans and ratites appear to have a similar capacity to minimize Ecot during walking, perhaps by effective use of the pendulum mechanism [23]. However, during running, ostriches are more economical, probably because of differences in morphology leading to differences in the biomechanics of movement. The hypothesis that biomechanical differences explain this difference in running energetics has received support from a recent study showing that, compared with humans, ostriches store and release more net mechanical energy elastically in their legs during running and, therefore, the mechanical power produced by the muscle fibres is reduced [34].
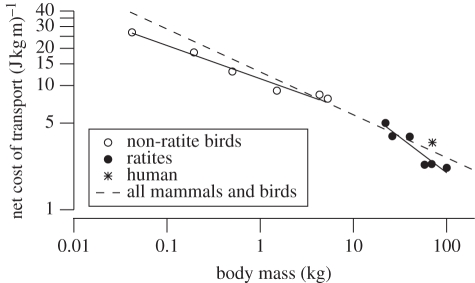
The comparison of cost of transport in ostriches and humans seems to reinforce the generally cited conclusion that humans are energetically economical walkers, but have poor running economy for their size. However, this conclusion has been biased by the particular human study often used for comparison [15], which found a higher-than-average cost of running, and the use of the slope of the linear relation of Ėmet and speed to represent the net cost [8]. With these biases removed, net Ecot of humans averages only 17 per cent higher than predicted from the allometric scaling of all vertebrates [12]. On the other hand, the net Ecot of running ostriches is at least 20 per cent below that predicted from general vertebrate scaling and 40 per cent below the value predicted from smaller non-ratite birds (figure 4). Thus, humans use much more energy per unit distance when running than do ostriches, but their net Ecot is similar to mammalian quadrupeds of the same body mass.
Figure 4.
Allometry of minimal cost of transport in running birds. Non-ratite values (galliform birds considered to be specialized for running) and the regression line for all birds and mammals are from Rubenson et al. [12]. Solid lines are regression lines fitted separately through the non-ratite (11.4Mb−0.27, r2 = 0.97) and ratite (27.7Mb−0.57, r2 = 0.89) data.
In both emus and ostriches, the minimum net Ecot for walking was lower than the minimum value in running (figure 3a). The steep rise in Ėmet (and thus net Ecot) at fast walking speeds has been attributed to a decline in the effectiveness of the inverted pendulum mechanism used by walking animals [23,31]. The switch to a running gait occurs at a dimensionless speed of approximately 0.5 and corresponds approximately to a speed above which the extrapolated Ėmet during walking would exceed that found for running. This correlation of energy use and the transition speed does not, of course, mean that energy use is the proximate trigger for the gait transition. The nature of this trigger, particularly for humans, has been subject to considerable debate [14,35], and remains controversial [36]. However, regardless of the proximate trigger for the gait transition, the choice of speed and gait can have substantial energetic consequences and could be subject to natural selection, depending on the amount of energy used for locomotion and the available energy in the environment.
The choice of economical speeds and the low minimal cost of transport in walking ostriches and emus are probably ecologically relevant for these animals. For emus, walking speeds were tightly clustered with a mean of 1.0 m s−1, which was intermediate between the speeds at which net Ecot and total Ecot were minimized (figure 3b). When running, emus used a wide range of speeds above 2.6 m s−1. Noticeably, the birds did not use a range of speeds immediately above or below the gait transition within which transport costs are highest. Predicting optimal speeds of animals in nature is context-specific and depends on whether energy or time is more important. However, one would expect that energetic considerations would be particularly important in species for which locomotion is a significant part of their daily energy budgets, which is the case in large ratites. Free-living ostriches have been found to spend 60 per cent of the daytime hours walking [37], and emus walk almost continuously during the day [38].
5. Conclusion
By re-examining the energetics of locomotion in large ratite birds, we have uncovered an ecologically relevant variation in locomotor energetics with speed and gait in these animals. This variation was obscured by previous studies, which assumed a linear relation of energy use and speed. Gait-specific optimal speeds that minimize the cost of transport and correlate with preferred speeds have been documented previously mainly for horses and humans. We suggest that gait-specific locomotor energetics may be more common than has been generally realized, and investigators should consider this possibility when examining the energetics of locomotion, preferred speed and gait selection, particularly in larger vertebrates for which the cost of transport for walking is predicted to be lower than the cost of running [12].
Acknowledgements
This project was funded by NSF grant IOB-0542795 to R.L.M. and D.F.H.; NIH grant AR47337 to R.L.M.; and funds from the College of Science, California State Polytechnic University at Pomona. We thank Thomas Roberts for supplying his original emu and rhea data; Melissa Shea and Jennifer Carr for help with measurements; Holly Greene for her aid in all aspects of the study; and numerous Cal Poly Pomona undergraduate volunteers for their assistance. This project was initiated in collaboration with the late Steven J. Wickler, to whose memory this publication is dedicated with deep appreciation for his expertise and friendship.
References
- 1.Pennycuick C. J. 1975. On the running of the gnu (Connochaetes taurinus) and other animals. J. Exp. Biol. 63, 775–799 [Google Scholar]
- 2.Hoyt D. F., Taylor C. R. 1981. Gait and the energetics of locomotion in horses. Nature 292, 239–240 10.1038/292239a0 (doi:10.1038/292239a0) [DOI] [Google Scholar]
- 3.Perry A. K., Blickhan R., Biewener A. A., Heglund N. C., Taylor C. R. 1988. Preferred speeds in terrestrial vertebrates: are they equivalent? J. Exp. Biol. 137, 207–219 [DOI] [PubMed] [Google Scholar]
- 4.Wickler S. J., Hoyt D. F., Cogger E. A., Hall K. M. 2001. Effect of load on preferred speed and cost of transport. J. Appl. Physiol. 90, 1548–1551 [DOI] [PubMed] [Google Scholar]
- 5.Alexander R. M. 1989. Optimization and gaits in the locomotion of vertebrates. Physiol. Rev. 69, 1199–1227 [DOI] [PubMed] [Google Scholar]
- 6.Fedak M. A., Pinshow B., Schmidt-Nielsen K. 1974. Energy cost of bipedal running. Am. J. Physiol. 227, 1038–1044 [DOI] [PubMed] [Google Scholar]
- 7.Taylor C. R. 1994. Relating mechanics and energetics during exercise. In Comparative vertebrate exercise physiology: unifying physiological principles (eds Jones J. H., Cornelius C. E., Marshak R. R., Melby E. C.), pp. 181–215 New York, NY: Academic Press [Google Scholar]
- 8.Taylor C. R., Heglund N. C., Maloiy G. M. O. 1982. Energetics and mechanics of terrestrial locomotion. I. Metabolic energy consumption as a function of speed and body size in birds and mammals. J. Exp. Biol. 97, 1–21 [DOI] [PubMed] [Google Scholar]
- 9.Taylor C. R., Schmidt-Nielsen K., Raab J. L. 1970. Scaling of energetic cost of running to body size in mammals. Am. J. Physiol. 219, 1104–1107 [DOI] [PubMed] [Google Scholar]
- 10.Kram R., Taylor C. R. 1990. Energetics of running: a new perspective. Nature 346, 265–267 10.1038/346265a0 (doi:10.1038/346265a0) [DOI] [PubMed] [Google Scholar]
- 11.Hoyt D. F., Wickler S. J., Dutto D. J., Catterfeld G. E., Johnsen D. 2006. What are the relations between mechanics, gait parameters, and energetics in terrestrial locomotion? J. Exp. Zool. A Comp. Exp. Biol. 305, 912–922 [DOI] [PubMed] [Google Scholar]
- 12.Rubenson J., Heliams D. B., Maloney S. K., Withers P. C., Lloyd D. G., Fournier P. A. 2007. Reappraisal of the comparative cost of human locomotion using gait-specific allometric analyses. J. Exp. Biol. 210, 3513–3524 10.1242/jeb.000992 (doi:10.1242/jeb.000992) [DOI] [PubMed] [Google Scholar]
- 13.Brezina E., Kolmer W. 1912. Über den Energieverbrauch bei der Geharbeit unter dem Einfluss verschiedener Geschwindigkeiten und verschiedener Belastungen. Biochem. Z. 38, 129–153 [Google Scholar]
- 14.Saibene F., Minetti A. E. 2003. Biomechanical and physiological aspects of legged locomotion in humans. Eur. J. Appl. Physiol. 88, 297–316 10.1007/s00421-002-0654-9 (doi:10.1007/s00421-002-0654-9) [DOI] [PubMed] [Google Scholar]
- 15.Margaria R., Cerretelli P., Aghemo P., Sassi G. 1963. Energy cost of running. J. Appl. Physiol. 18, 367–370 [DOI] [PubMed] [Google Scholar]
- 16.Steudel-Numbers K. L., Wall-Scheffler C. M. 2009. Optimal running speed and the evolution of hominin hunting strategies. J. Hum. Evol. 56, 355–360 10.1016/j.jhevol.2008.11.002 (doi:10.1016/j.jhevol.2008.11.002) [DOI] [PubMed] [Google Scholar]
- 17.Griffin T. M., Kram R., Wickler S. J., Hoyt D. F. 2004. Biomechanical and energetic determinants of the walk–trot transition in horses. J. Exp. Biol. 207, 4215–4223 10.1242/jeb.01277 (doi:10.1242/jeb.01277) [DOI] [PubMed] [Google Scholar]
- 18.Hoyt D. F., Kenagy G. J. 1988. Energy costs of walking and running gaits and their aerobic limits in golden mantled ground squirrels. Physiol. Zool. 61, 34–40 [Google Scholar]
- 19.Williams T. M. 1983. Locomotion in the North American mink, a semi-aquatic mammal. II. The effect of an elongate body on running energetics and gait patterns. J. Exp. Biol. 105, 283–295 [DOI] [PubMed] [Google Scholar]
- 20.Langman V. A., Roberts T. J., Black J., Maloiy G. M., Heglund N. C., Weber J. M., Kram R., Taylor C. R. 1995. Moving cheaply: energetics of walking in the African elephant. J. Exp. Biol. 198, 629–632 [DOI] [PubMed] [Google Scholar]
- 21.Parker K. L., Robbins C. T., Hanley T. A. 1984. Energy expenditures for locomotion by mule deer and elk. J. Wildl. Manage. 48, 474–488 10.2307/3801180 (doi:10.2307/3801180) [DOI] [Google Scholar]
- 22.Fancy S. G., White R. G. 1987. Energy expenditures for locomotion by barren-ground caribou. Can. J. Zool. 65, 122–128 10.1139/z87-018 (doi:10.1139/z87-018) [DOI] [Google Scholar]
- 23.Rubenson J., Heliams D. B., Lloyd D. G., Fournier P. A. 2004. Gait selection in the ostrich: mechanical and metabolic characteristics of walking and running with and without an aerial phase. Proc. R. Soc. Lond. B 271, 1091–1099 10.1098/rspb.2004.2702 (doi:10.1098/rspb.2004.2702) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pontzer H. 2007. Effective limb length and the scaling of locomotor cost in terrestrial animals. J. Exp. Biol. 210, 1752–1761 10.1242/jeb.002246 (doi:10.1242/jeb.002246) [DOI] [PubMed] [Google Scholar]
- 25.Pontzer H., Allen V., Hutchinson J. R. 2009. Biomechanics of running indicates endothermy in bipedal dinosaurs. PLoS ONE 4, e7783. 10.1371/journal.pone.0007783 (doi:10.1371/journal.pone.0007783) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Baudinette R. V., Snyder G. K., Frappell P. B. 1992. Energetic cost of locomotion in the tammar wallaby. Am. J. Physiol. 262, R771–R778 [DOI] [PubMed] [Google Scholar]
- 27.Dawson T. J., Taylor C. R. 1973. Energetic cost of locomotion in kangaroos. Nature 246, 313–314 10.1038/246313a0 (doi:10.1038/246313a0) [DOI] [Google Scholar]
-
28.Withers P. C. 1977. Measurement of
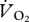 ,
, 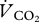 , and evaporative water loss with a flow-through mask. J. Appl. Physiol. 42, 120–123 [DOI] [PubMed] [Google Scholar]
, and evaporative water loss with a flow-through mask. J. Appl. Physiol. 42, 120–123 [DOI] [PubMed] [Google Scholar] - 29.Fedak M. A., Seeherman H. J. 1979. Reappraisal of energetics of locomotion shows identical cost in bipeds and quadrupeds including ostrich and horse. Nature 282, 713–716 10.1038/282713a0 (doi:10.1038/282713a0) [DOI] [PubMed] [Google Scholar]
- 30.Roberts T. J., Kram R., Weyand P. G., Taylor C. R. 1998. Energetics of bipedal running. I. Metabolic cost of generating force. J. Exp. Biol. 201, 2745–2751 [DOI] [PubMed] [Google Scholar]
- 31.Cavagna G. A., Heglund N. C., Taylor C. R. 1977. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. 233, R243–R261 [DOI] [PubMed] [Google Scholar]
- 32.Taylor C. R., Dmi'el R., Fedak M., Schmidt-Nielsen K. 1971. Energetic cost of running and heat balance in a large bird, the rhea. Am. J. Physiol. 221, 597–601 [DOI] [PubMed] [Google Scholar]
- 33.Crawford E. C., Jr, Lasiewski R. C. 1968. Oxygen consumption and respiratory evaporation of the emu and rhea. Condor 70, 333–339 10.2307/1365927 (doi:10.2307/1365927) [DOI] [Google Scholar]
- 34.Rubenson J., Lloyd D. G., Heliams D. B., Besier T. F., Fournier P. A. In press Adaptations for economical bipedal running: the effect of limb structure on three-dimensional joint mechanics. J. R. Soc. Interface. 10.1098/rsif.2010.0466 (doi:10.1098/rsif.2010.0466) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hanna A., Abernethy B., Neal R. J., Burgess-Limerick R. 2000. Triggers for the transition between human walking and running. In Energetics of human activity (ed. Sparrow W. A.), pp. 124–164 Chicago, IL: Human Kinetics [Google Scholar]
- 36.Van Caekenberghe I., De Smet K., Segers V., De Clercq D. 2010. Overground vs. treadmill walk-to-run transition. Gait Posture 31, 420–428 10.1016/j.gaitpost.2010.01.011 (doi:10.1016/j.gaitpost.2010.01.011) [DOI] [PubMed] [Google Scholar]
- 37.Williams J. B., Siegfried R. W., Milton S. J., Adams N. J., Dean W. R. J., du Plessis M. A., Jackson S. 1993. Field metabolism, water requirements, and foraging behavior of wild ostriches in the Namib. Ecology 74, 390–404 10.2307/1939301 (doi:10.2307/1939301) [DOI] [Google Scholar]
- 38.Dawson T. J., Read D., Russell E. M., Herd R. M. 1984. Seasonal variation in daily activity patterns, water relations and diet of emus. Emu 84, 93–102 10.1071/MU9840093 (doi:10.1071/MU9840093) [DOI] [Google Scholar]