Cycles, stochasticity and density dependence in pink salmon population dynamics

Abstract

Complex dynamics of animal populations often involve deterministic and stochastic components. A fascinating example is the variation in magnitude of 2-year cycles in abundances of pink salmon (Oncorhynchus gorbuscha) stocks along the North Pacific rim. Pink salmon have a 2-year anadromous and semelparous life cycle, resulting in odd- and even-year lineages that occupy the same habitats but are reproductively isolated in time. One lineage is often much more abundant than the other in a given river, and there are phase switches in dominance between odd- and even-year lines. In some regions, the weak line is absent and in others both lines are abundant. Our analysis of 33 stocks indicates that these patterns probably result from stochastic perturbations of damped oscillations owing to density-dependent mortality caused by interactions between lineages. Possible mechanisms are cannibalism, disease transmission, food depletion and habitat degradation by which one lineage affects the other, although no mechanism has been well-studied. Our results provide comprehensive empirical estimates of lagged density-dependent mortality in salmon populations and suggest that a combination of stochasticity and density dependence drives cyclical dynamics of pink salmon stocks.

1. Introduction

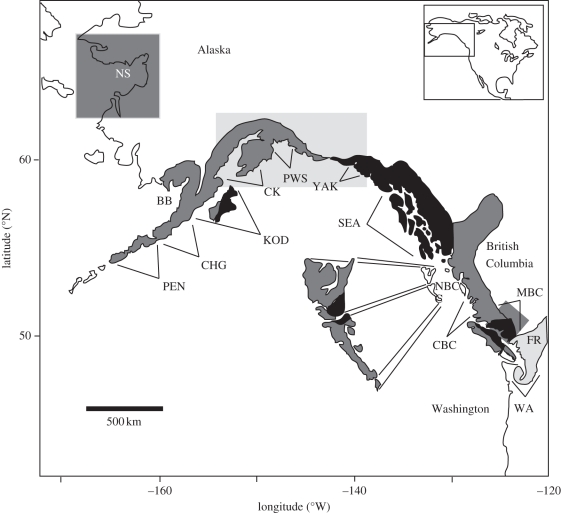
Complex population dynamics have long fascinated and challenged biologists [1,2]. Nonlinear deterministic processes such as overcompensation and delayed density-dependent mortality can produce complicated dynamics [3,4], even without environmental stochasticity. The latter can influence dynamics of natural populations, such as by synchronizing fluctuations [5,6] or by perturbing equilibria [7,8]. Thus, disentangling the deterministic and stochastic components of population dynamics is a central challenge [9,10]. One interesting example has long escaped attention: the cyclical population dynamics of pink salmon (Oncorhynchus gorbuscha). This anadromous and semelparous fish exhibits enormous variation in the existence and amplitude of 2-year cycles in abundance throughout its range in the Pacific Ocean [11,12]. Pink salmon have a 2-year life cycle with migration between coastal and offshore waters such that odd- and even-year lineages are reproductively isolated and sympatric only during short periods in coastal marine environments [13]. Despite occupying the same habitats in alternate years, one lineage often dominates (i.e. is numerically more abundant) and there are phase switches in dominance between odd- and even-year lineages. In some regions, the weak lineage is absent and in others there are no cycles and both lineages are abundant (figure 1).

Figure 1.

Map of the study area. The shaded watershed regions are adapted from Ricker [12], which he identified as odd-year dominant with respect to abundance (light grey), even-year dominant (dark grey) and no dominance (black). The shaded grey rectangles show regions that were not covered in Ricker [12] but show even-year dominance (NS), areas that Ricker [12] considered even-year dominated and now appear to be odd-year dominated (CK, PWS, YAK), or now appear to be odd-year dominated (MBC). Regions and stocks in the database are Washington (WA, stocks 1–7), Fraser River (FR, stock 8), Mainland B.C. (MBC, stock 9), Central B.C. (CBC, stocks 10–12), Northern B.C. (NBC, stocks 13–14), Southeast Alaska (SEA, stocks 15–17), Yakutat (YAK, stocks 18–19), Prince William Sound (PWS, stocks 20–22), Lower Cook Inlet (CK, stocks 23–25), Kodiak Island (KOD, stocks 26–30), Chignik (CHG, stocks 31–35), Alaska Peninsula (PEN, stocks 36–38), Bristol Bay (BB, stock 39) and Norton Sound (NS, stocks 40–43). See the electronic supplementary material for stock identities and associated information.

Almost 50 years ago, Ricker [12] proposed eight hypotheses to explain dominance in pink salmon stocks. The first two hypotheses involved depensatory mortality of juvenile salmon in (i) freshwater and (ii) coastal marine waters. The reasoning here, for both hypotheses, is that small populations may experience higher per capita percentage mortality from predation than large populations [14]. A stochastic environmental disturbance that drastically reduces one line could therefore lead to long-term suppression of the affected line through depensatory mortality within the depressed line, creating a pattern that is qualitatively cyclic. Thus, cyclic patterns in this scenario would be a transient dynamic that resulted from a random historical event, which was then perpetuated by within-line depensatory mortality. However, these hypotheses have been discounted owing to the absence of a mechanism that actively maintains distinct population sizes between lines [13].

Three of Ricker's [12] hypotheses involved density independence or fishery dependence. The density independence hypothesis posits that odd- and even-year lines may have separate migration routes at sea, which may lead to differences between odd- and even-year lines in the environmental conditions they experience. This hypothesis has been discounted because tagging studies suggest odd- and even-year lines follow similar migration routes [13]. The first fishery hypothesis suggested that fishing mortality, in early years, may have been depensatory because weaker stocks likely experienced higher per capita fishing mortality, similar to the first two hypotheses about natural predators. The second fishery hypothesis involves the possibility that suppression of a weak stock could occur even when per capita fishing mortality is equally distributed between strong and weak stocks. While these hypotheses may reinforce dominance, they have also been discounted because dominance between lines likely occurred before intensive, industrial-scale fishing began [13].

Ricker's [12] final three hypotheses involved density-dependent mortality between odd- and even-year lines. The proposed mechanisms were (i) cannibalism of juveniles by adults during summer sympatry in coastal marine waters, (ii) fouling of spawning habitat between years by mortality and persistence of decayed eggs within gravel and (iii) competition for food between odd- and even-year lines. To these hypotheses, we add the transmission of parasites from adult to juvenile salmon during summer sympatry [15]. All of these hypotheses are appealing in that they involve a nonlinearity which would suppress a weak line by an abundant line. Despite the plausibility of these mechanisms, there remains a paucity of empirical evidence with which to evaluate the presence, magnitude and generality of these effects [13]. Furthermore, there has been no quantitative analysis of pink salmon stock and recruitment data to test for the presence of between-line density-dependent mortality.

Differential adaptation to geographical clines is an alternative hypothesis to consider because odd-year lines tend to dominate in the southern part of the North American range, whereas even-year lines tend to dominate in the north. Odd- and even-year lines could be differentially adapted to latitudinal or geographical clines in habitat if they emerged from different glacial refuges. If even-year lineages colonized the Eastern Pacific from northern glacial refuges (e.g. Queen Charlotte Islands) and odd-year lineages from southern ones (e.g. Columbia River), then there may be residual adaptation to habitats associated with those refuges. Such an effect might give rise to systematic geographic trends where productivity declines with distance or latitude from the location of refuges. This trend could create differences in productivity between lines sharing the same habitats and yield cyclical population dynamics that are not related to population dynamic mechanisms. The plausibility of this hypothesis is supported by evidence that odd- and even-year lines within a river differ in numerous traits such as morphology [16] and development [17]. Further, the many failed transplants of even-year fish to Puget Sound suggest that there may be some inherent barriers [18].

In this paper, we use hierarchical multi-stock models to analyse data from pink salmon stocks from the Eastern North Pacific to evaluate the evidence for interline density dependence and/or adaptive geographical clines. Through a combination of parameter estimation, model analysis and stochastic simulation, we then compare model dynamics with the data. Finally, we discuss the plausibility of the ecological mechanisms that may underlie the patterns in the data and the structure of the best-supported model.

2. Methods

The data used in this paper come from a stock-recruit database of 43 stocks of pink salmon in Washington, British Columbia and Alaska (figure 1). The time series range in length from 17 to 47 years and are described in the electronic supplementary material (electronic supplementary material, table S1) and elsewhere [6,19,20]. Ten stocks were excluded because they lacked data on either the odd- or even-year lineages because the weak line was absent or stock assessment of the weak line was poor. We refer to a stock by its geographical location, i, and further differentiate the stock into odd- or even-year lineage, j. Thus, there are two distinct populations occupying each geographical location, which are separated by time into odd- or even-year lineages. Also, note that our usage of the term population actually corresponds to an aggregation of spawning populations within a fisheries management unit.

The model typically used for pink salmon population dynamics is the Ricker equation [2], which relates the spawning stock abundance of a population S with the resulting recruitment R 2 years later as R_t = S_{t −2} exp[r − bS_{t −2} + ɛ_t], where r is the population growth rate and b determines density-dependent mortality. Time, t, is measured in years and is lagged 2 years for the 2-year life cycle of pink salmon. This model captures environmental stochasticity in the term ɛ_t, which is a normal random variable. The standard way of applying the Ricker model to stock recruit data is to transform the model to ln[R_t/S_{t −2}] = r−bS_{t −2} + ɛ_t and fit it to data using simple linear regression [21].

For the multi-stock hierarchical models of pink salmon, the population growth rate, r, is an intrinsic quantity that has an overall mean value with some random variation among populations. In contrast, the density-dependent mortality parameter, b, is considered an extrinsic quantity determined by the set of local environmental features, such as the amount of spawning habitat, which affects density-dependent mortality in a given population. Given this interpretation, odd- and even-year lines occupying the same habitat should have the same values for r and b, but these parameters may vary among locations. These assumptions lead to the null model in our set of candidate models, giving

2.1

where i identifies the geographical region of the stock. For this model, r and b take the same value for odd- and even-year populations within a stock but vary among stocks. The population growth rate r takes an average value for the species but varies randomly among locations i according to θ_i, which is normally distributed with a mean of 0 and variance to be estimated. In contrast, b_i is a fixed factor specific to stock locations, which represents variation among stocks in the amount and quality of habitat. Finally, we assume that environmental stochasticity acting on stock i is autocorrelated according to a first-order auto-regressive process AR1.

An alternate model maintains the assumption that r and b are equal between odd- and even-year lines of a stock, but allows for density-dependent interactions between odd- and even-year lineages of a stock. The corresponding hierarchical multi-stock model for this hypothesis is

2.2

where we scale the conventional density-dependent mortality term b by the average magnitude of delayed density-dependent mortality, c, from returning adults that escape the fishery to become spawners. This model assumes that the average magnitude of density-dependent mortality, b_iS_{i,t −2}, is proportional to density-dependent mortality between odd- and even-year lineages but also varies among stocks according to γ_i, which is normally distributed with mean equal to zero and variance to be estimated.

While model (2.2) assumes that spawner abundance of returning salmon is the relevant metric for density-dependent mortality, it may be that adult recruitment is the more appropriate quantity. This hypothesis depends on the timing of the fishery relative to the period of sympatry between adults and juveniles in marine coastal waters. It follows then that an alternative model could be

2.3

in which recruitment replaces spawner abundance in equation (2.2). Model (2.2) could be more appropriate if fishing mortality occurs prior to or very early in the period of sympatry between returning adults and outmigrating fry, whereas model (2.3) could be more appropriate if fishing occurs late in that period. We evaluate both models.

To consider the hypothesis that odd- and even-year lines have differential adaptation to latitude, we include latitude as a covariate in the multi-stock model, giving

2.4

where L_i is the latitude of the stock. The coefficient that tunes the magnitude of the position in the geographical cline on productivity, l_j, is estimated separately for odd- and even-year lines, j.

Because the along-shore distance among stocks may be a more relevant measure than the latitude of a stock in affecting the productivity of the population, we considered another alternate model

2.5

where D_i is the distance of stock i from the southern-most stock and d_j determines the magnitude of the effect of distance on productivity for odd or even lineage j.

Finally, we consider combinations of models (2.2)–(2.5) as candidate models for pink salmon population dynamics. These models are

2.6

2.7

2.8

and

2.9

where the ɛ_i,t term follows a first-order autoregressive process AR1 in all models (2.1)–(2.9). Models (2.1) through (2.9) represent the set of candidate hypotheses for the 2-year cycles in the population dynamics of pink salmon, ranging from conventional density dependence, to delayed density-dependent models, to differential geographical clines in productivity between odd- and even-year lineages, and, finally, combinations of these effects. To evaluate the relative support contained in the stock-recruit data for the competing models (2.1) through (2.9), we fit the models using the principles of maximum likelihood and compared the models using the Akaike Information Criterion (AIC) and likelihood-ratio (LR) tests.

3. Results

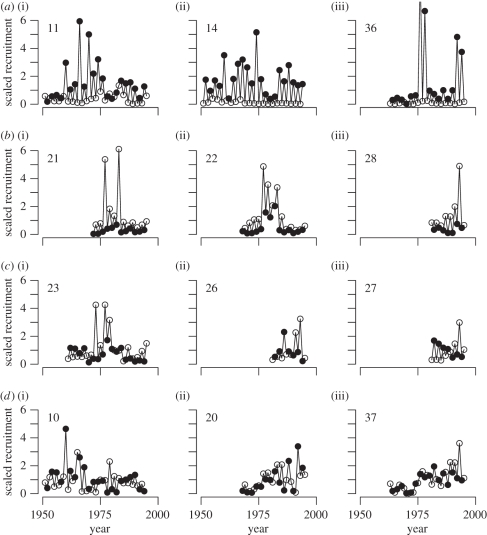
Pink salmon stocks exhibit complex patterns in their population dynamics, including sustained oscillations, phase switching and aperiodic behaviour (figure 2). Sustained oscillations consisted of 2-year cycles where either the odd- or even-year lineage was numerically dominant for most of the time series (figure 2a,b). Phase switching occurs when 2-year cycles in a time series switch in numerical dominance from odd- to even-year lineages, or vice versa (figure 2c). The population dynamics also include aperiodic fluctuations in recruitment (figure 2d). The spatial distribution of population dynamic characteristics indicates that aperiodic dynamics and cyclical dynamics occur throughout the species range (figure 1 and electronic supplementary material, figures S1 and S2). Within the cyclical dynamics, even-year dominance tends to occur in the northern end of the species range, whereas switching and odd-year dominance tends to be more common in the central portion of the species range (electronic supplementary material, table S1). In the southern part of the species range, there is even-year dominance in the datasets we analysed but also strong odd-year dominance in the Fraser River and Puget Sound region of Washington (electronic supplementary material, table S1).

Figure 2.

Examples of characteristics of pink salmon population dynamics, showing 2-year cycles with even-year dominance (a (i–iii)), 2-year cycles with odd-year dominance (b (i–iii)), 2-year cycles with switching between odd- and even-year dominance (c (i–iii)) and aperiodic dynamics (d (i–iii)). Identities of the stocks are given by the stock number in the upper left corner of each panel (electronic supplementary material, table S1). Black dots are even-year lines, open circles are odd-year lines. Stock-specific recruitment is scaled by the average recruitment over both lineages of a stock.

The multi-stock analysis did not reveal a systematic geographical trend in productivity that differed between odd- and even-year lineages. Inclusion of latitude or along-shore distance as covariates of productivity for odd- and even-year lineages (equations (2.4)–(2.9)) was not supported by the data, as measured by AIC and LR tests (table 1).

Table 1.

Model selection statistics for competing (models (2.1)–(2.9)) as defined in the main text. Model 2.1 is the null model with alternate (models (2.2)–(2.8)) containing terms for delayed density dependence (models (2.2)–(2.3)), differential geographical clines in productivity between odd- and even-year lineages (models (2.4) and (2.5)), and combinations of delayed density dependence and geographical clines in productivity (models (2.6)–(2.9)). The column identifying model terms shows the covariates used in the models: spawning escapement (S) or recruitment (R) as the metric for adult abundance in the inter-brood line density-dependent term, and L (latitude) or (D) along shore distance as the covariate for differential productivity between odd- and even-year lines. Model selection statistics include the negative log-likelihood (NLL), AIC, AIC differences (ΔAIC), models compared in likelihood-ratio (LR) tests, the LR statistic and the p-value from the LR test.

model	terms	NLL	AIC	ΔAIC	test	LR	p
2.1	null	1314.1	2702.2	12.9	—	—	—
2.2	S	1304.7	2689.3	0	2 versus 1	18.9	0.0003
2.3	R	1309.5	2699.0	9.7	3 versus 1	9.2	0.03
2.4	L	1313.7	2705.5	16.2	4 versus 1	0.7	0.71
2.5	D	1314.0	2706.1	16.7	5 versus 1	0.1	0.94
2.6	L + S	1304.3	2692.6	3.3	6 versus 2	0.7	0.70
2.7	D + S	1304.4	2692.9	3.5	7 versus 2	0.5	0.79
2.8	L + R	1308.7	2701.4	12.1	8 versus 3	1.6	0.44
2.9	D + R	1308.6	2701.1	11.8	9 versus 3	1.9	0.38

However, the multi-stock analysis suggests that density-dependent mortality acting between odd- and even-year lineages was evident in the data. This can be seen from the AIC values and LR tests of models (2.2) and (2.3) relative to model (2.1), for which model (2.1) had no interaction between odd- and even-year lineages, whereas models (2.2) and (2.3) included density-dependent mortality between odd- and even-year lineages. Further, because model (2.2) was the best-supported model, this suggests that the effect is probably linked to spawner abundance rather than recruitment, indicating that the mechanism of mortality involves the abundance of adult fish that escapes fisheries (table 1).

Parameter estimates from the best-supported models (based on LR tests)—equations (2.2) and (2.3)—were fairly consistent between models. Both models gave similar point estimates and variances for productivity, r, of pink salmon (table 2). Ranks of models by AIC scores (table 1) indicate that models (2.6) and (2.7) (which involve spawners just like model (2.2)) were superior to model (2.3), emphasizing that spawner abundance (equation (2.2)) rather than recruitment (equation (2.3)) is the most appropriate covariate for density-dependent mortality between lineages. Furthermore, equations (2.6) and (2.7) are just slight variants on equation (2.2); there is apparently little gained by adding the spatial terms latitude or alongshore distance to equation (2.2). Therefore, the next-best model after equation (2.2) is equation (2.3).

Table 2.

Estimates of the population growth rate, r, and standard deviation of θ_i among stocks as well as the delayed density-dependent mortality parameter, c, and standard deviation of γ_i among stocks from the best supported models ((2.2) and (2.3)). Also shown in parentheses are the 95% CI on the fixed effects r and c.

model	r	θi sd	c	γi sd
2.2	1.36 (1.13,1.59)	0.51	0.34 (0.21, 0.46)	0.00002
2.3	1.35 (1.16, 1.55)	0.39	0.16 (0.087, 0.23)	0.098

The best-supported model (equation (2.2)) indicated that the strength of inter-lineage density-dependent mortality was approximately one-third of the conventional within-lineage density-dependent mortality, as measured by c, with very small variance among stocks in the value of this parameter (table 2). The second best-supported model (equation (2.3)) that models inter-lineage density dependence using recruitment as opposed to the spawner data, had a lower value of c, which is consistent with model (2.2) in that the recruitments are larger than corresponding spawner data. The parameter c, estimated using recruitment data, was 47 per cent of c estimated using escapement data, which is consistent with the average harvest rate of 43 per cent over all the stocks and years. Models (2.2) and (2.3) did vary markedly in the among-stock variance associated with c (table 2). The best-fit model (2.2) had a correlation coefficient of 0.246 for the lag-1 temporal autocorrelation in residual errors and a standard deviation of 1.0023 in the normally distributed error term.

The estimated variance for the random effect on c of model (2.2) was very small (table 2). To check whether inclusion of the random effect on c in this model was supported by the data, we compared models that included a random effect on c with those that did not. We did this for model formulations for which the random effect was distributed among stocks, as well as when it was distributed among populations where each lineage was considered a separate population. The results indicated that a random effect on c was not supported by the data (table 3), indicating that variation in c among stocks is very similar to direct density dependence b_i.

Table 3.

Comparison of variations in the random effects structure of model (2.2). Random effects were distributed over stock and over each population (i.e. odd- and even-year lines within a stock), with and without application of the random effect on the delayed density-dependent term. For random effects structured by population, odd- and even-year lineages were treated as independent in the application of the random effects on model parameters. The column ‘term’ identifies which model parameters were modelled with the random effect. Also shown are the negative log-likelihood value (NLL), AIC, LR test statistic and the p-value for the likelihood ratio test.

model	RE	term	NLL	AIC	test	LR	p
2.2a	stock	r	1304.664	2688.993
2.2b	stock	r and c	1304.496	2688.993	2.2a versus 2.2b	0.33511	0.8457
2.2c	population	r	1329.355	2734.711
2.2d	population	r and c	1329.355	2738.711	2.2c versus 2.2d	0.00003	1

It was possible to analyse the stability of the deterministic and single-stock version of the best-supported model (equation (2.2)) and thereby place the empirical results above within the context of the dynamics of the underlying deterministic model. To do so, we write

3.1

as the deterministic version of equation (2.2), where N_t is abundance in year t. In the electronic supplementary material, we show that the quantity

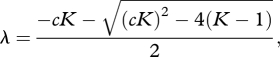3.2

is the per-year rate at which a population approaches the carrying capacity after a small perturbation away from the carrying capacity, where the carrying capacity is K = r[(1 + c)b]⁻¹. That is, η_t = η₀λ^t, where η is the displacement of the population from the carrying capacity and η₀ is the initial perturbation away from the carrying capacity. Equation (3.2) reveals that the deterministic dynamics of equation (2.2) consist of damped period-two oscillations when the absolute value of λ is less than one and more complex dynamics as the absolute value of lambda is greater than one (electronic supplementary material, model analysis).

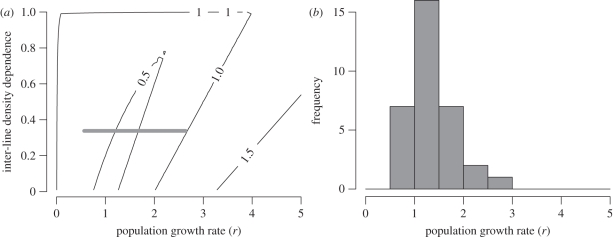
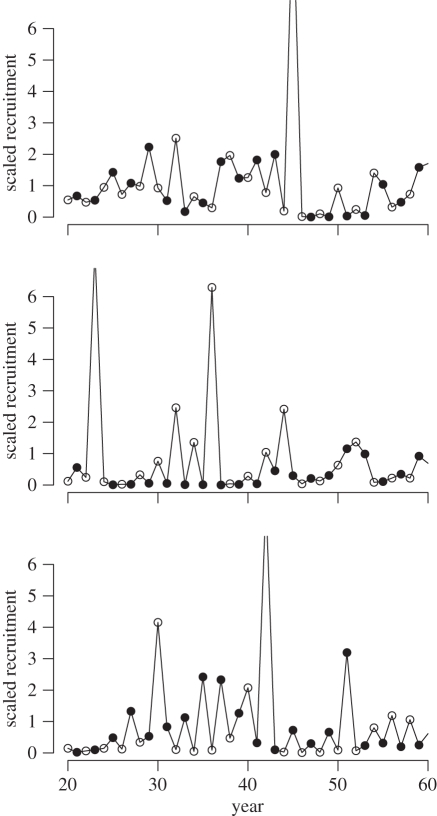
According to parameter estimates for equation (2.2), the population dynamics predicted by the deterministic component of the model include damped oscillations of period two (electronic supplementary material). The region of parameter space containing damped period-two oscillations is large relative to the parameter values for pink salmon from model (2.2) (figure 3). Regions outside of this parameter space where the absolute value of λ is larger than one correspond to instability of the carrying capacity equilibrium and more complex dynamics. Regions of parameter space where the absolute value of λ is equal to one correspond to sustained oscillations of period two. All 33 stocks of pink salmon in our analysis lie in the parameter space where damped oscillations of period two are expected (figure 3). However, the full model (2.2) contains a temporally autocorrelated environmental stochasticity term in addition to the nonlinear dynamics in the underlying deterministic model. Simulations of the full stochastic model confirm that the dynamical patterns in the data can occur in the model (figure 4).

Figure 3.

Parameter space of model (2.10). (a) Showing a contour plot of the absolute value of λ (equation (2.11)) and the range of estimates of the population growth rate (r + ϕ_i) at the estimated value of c = 0.34 (solid grey line). Regions where the contours are less than one consist of damped oscillations of period two in the deterministic dynamics of equations (2.2) and (2.10). (b) The frequency distribution of empirically estimated population growth rates (r + ϕ_i) across the 33 pink salmon populations.

Figure 4.

Simulations of the best-fit model, equation (2.2), showing characteristics that frequently occur in simulations as well as in pink salmon stock-recruit data, including 2-year population cycles, phase switching between odd- and even-year dominance, emergence and loss of dominance, and aperiodic behaviour. Parameter estimates used in the model were those as estimated from the data, with r = 1.36 and c = 0.34 (table 3). Because the within-lineage density-dependent mortality term is arbitrary for the simulations, we set it to unity (b = 1). Further parameters are for simulating the first-order autoregressive process AR(1) used to model environmental stochasticity, which were obtained from the parameter estimates of model (2.2). These were a standard deviation of 1.0023 for the Gaussian noise term and a correlation coefficient of 0.246 for the temporal autocorrelation. The first 20 iterations of the model were used as a burn-in period and hence are not plotted.

4. Discussion

The interacting influences of environmental stochasticity and nonlinear deterministic dynamics make ecological dynamics unique [9,10]. Examples from natural populations include the interaction of rainfall and density-dependent mortality that regulate the abundance of the African rat Mastomys natalensis [22], lagged density dependence through competition or predation and environmental stochasticity that affects periodicity of lemming cycles [23], and density-dependent reproduction and cannibalism combined with environmental stochasticity that may drive population dynamics of Dungeness crab [24]. In controlled laboratory conditions where environmental stochasticity is negligible, populations of flour beetles, Tribolium, follow the bifurcations and complex population dynamics predicted by the deterministic components of mathematical models [25]. Our results suggest that dominance of odd- or even-year lineages in pink salmon stocks and the resulting 2-year population cycles may be owing to a mixture of environmental stochasticity and damped oscillations caused by density-dependent mortality between odd- and even-year lineages of a stock.

The combined effects of stochasticity and density-dependent mortality between odd- and even-year lineages of a pink salmon stock can produce 2-year cycles, phase switching, disappearance of cycles and aperiodic behaviour. Cycles can appear because environmental stochasticity acts to separate the abundance of odd- and even-year lineages, after which inter-lineage density-dependent mortality maintains dominance. However, the deterministic model and the parameter estimates indicate that 2-year cycles are transient phenomena; cycles are damped and should eventually converge to a carrying capacity. The high level of environmental stochasticity inherent in salmon survival rates from parents to recruitment of their offspring likely prevents a stable carrying capacity from being reached. Previous theoretical analyses have suggested that stochastic excitation of the stable node in the Ricker model could be responsible for 4-year cycles observed for some sockeye salmon (O. nerka) populations [8]. Others have also suggested that density-dependent mortality between age classes may underlie the 4-year cycles in sockeye salmon [3,26]. To our knowledge, our results provide the most comprehensive empirical estimates of lagged density-dependent mortality in salmon populations and suggest that a combination of stochasticity and density dependence drives the cyclical dynamics of pink salmon stocks.

While our results suggest that density-dependent mortality occurs between odd- and even-year lineages of pink salmon stocks, they do not identify the mechanism of mortality. Of the hypotheses put forward for this, two would occur during summer sympatry of adult and juvenile pink salmon in coastal marine waters—cannibalism and disease transmission. Cannibalism could occur in theory because adult pink salmon are piscivorous and juvenile pink salmon during summer sympatry are a suitable size of prey [13]. Nevertheless, we were unable to find any published accounts of cannibalism. One PhD dissertation that analysed stomach contents from pink salmon in coastal purse seine catches, including catches where adult and juvenile salmon were both present, did not find evidence of cannibalism [27]. Transmission of pathogens may be plausible, particularly for marine parasites with salmonid-specific host ranges, because transmission among age classes is required for parasite population persistence. In salmon lice, Lepeophtheirus salmonis, a marine salmonid ectoparistic copepod, transmission from returning adult Chinook salmon (O. tshawytscha) to juvenile pink salmon has occurred in each of 3 years in Chatham Sound, British Columbia [15].

Density-dependent mortality between odd- and even-year lineages of pink salmon may also occur in coastal marine waters through competition for food. Though Ricker [12] discounted this hypothesis as ‘far fetched’, a plausible mechanism has been established. In 1970, Russian scientist L. D. Andrievskaya found that in the Sea of Okhotsk, adult pink salmon feed on the adult hyperiid amphipod, Parathemisto japonica, and juvenile pink salmon feed on the larval stage of the same species. Thus, large abundances of adult pink salmon could depress adult populations of amphipods, thereby reducing the supply of larval amphipods available to juvenile pink salmon [13]. Hyperiid amphidods are a key component of the diets of juvenile pink salmon [28,29] and are common in the stomach contents of adult pink salmon [13]. Depending on the demographic rates of amphipods and the timing of ontogenetic diet shifts in juvenile pink salmon relative to the return migration of adult pink salmon, the prey depletion effect could be in either direction—juveniles depleting the prey available to adults (less likely) or adults depleting the prey available to juveniles (more likely). Further data and models are needed to evaluate whether the density-dependent mortality would act in the direction from adults to juveniles.

The final hypothesis suggested to explain density-dependent mortality between odd- and even-year lineages of pink salmon was the fouling of spawning habitat by eggs that die and then decay in the gravel at sufficiently slow rates that they affect survival of eggs the following year [12]. Evidence reviewed by Heard [13] is equivocal on this hypothesis. While eggs may persist for a year in gravel [30,31], there are numerous cases of high spawner densities in both odd- and even-year lines in the same gravel and no evidence of dominance. Were this hypothesis to find support, it may not be independent of the disease-transmission hypothesis if the mortality mechanism is an increased exposure of eggs to egg pathogens, such as fungi, owing to residual decayed egg masses deposited a year earlier. In general, there is little evidence in the literature to support any of the hypotheses that we have considered for inter-line density-dependent mortality, but this is largely owing to a lack of research designed to test these hypotheses. Thus, there are opportunities for future research to test these hypotheses as well as to estimate the magnitude of the associated inter-line density-dependent mortality. If the effect of each mortality mechanism is weak, the cumulative effect may still be large.

We also considered the hypothesis of different adaptive clines, which seems reasonable given the cline in dominance that switches from odd years in Washington and southern British Columbia to even-year dominance, which occurs in northern British Columbia and Alaska (figure 1). However, upon inspection of the data for central Alaska that start in 1962 or later (electronic supplementary material, figure S1), it appears that central Alaska (Yakutat, Prince William Sound and Lower Cook Inlet) may now be dominated by odd-year runs rather than even-year runs as originally described by Ricker [12]. This switch in dominance rules out the possibility of a cline in latitude or along-shore distance that would be associated with separate glacial refuges and differential adaptations between odd- and even-year lines to latitude or along-shore distance. Furthermore, the spatial patterns of dominance originally described by Ricker [12] extend through Russia and Asia where there were interesting patterns not related to distance or latitude such as even-year dominance east of the Kamchatka peninsula and odd-year dominance to the west of it. Given these spatial patterns, and the phenomenon of phase-switching between odd- and even-year dominance within a region, these patterns appear to be variable in time, and therefore favour an explanation that the dynamics are transients caused by stochasticity and inter-line density dependence instead of being a legacy of historical origin. Nevertheless, the occurrence of differences in morphological and developmental traits between lineages within rivers [16,17] indicates that there is clearly something different between them.

There are interesting characteristics of cycles and dominance in pink salmon population dynamics that we have not considered. Occurrences of complete dominance, where the weak line is absent, may not be satisfactorily explained by our analysis. For example, numerous attempts to establish populations in rivers of British Columbia and Washington where the weak line is absent and the dominant line is abundant have all failed [32]. Our model cannot explain these occurrences, which may be owing to depensatory mortality (Allee effects) that is associated with possible maladaptation of the introduced populations to the habitats. Furthermore, the spatial characteristics of dominance, such as abrupt borders between odd-dominated and even-dominated regions beg explanation, as do the spatial details of phase switching between regimes of odd-year and even-year dominance. Because pink salmon do not perfectly home to natal rivers, there is straying that connects populations. Furthermore, stocks may interact at sea via competition or disease, though detailed data of migration routes and timing are lacking. These characteristics may necessitate a metapopulation approach to analysing the spatial characteristics of pink salmon cycles [33,34]. While our results have shed fresh light on a 50-year-old problem in population ecology, they also point to numerous future research directions to develop a quantitative and mechanistic theory for cycles in pink salmon population dynamics.