Use of the Frank Sequence in Pulsed EPR

Abstract

The Frank polyphase sequence has been applied to pulsed EPR of triarylmethyl radicals at 256 MHz (9.1 mT magnetic field), using 256 phase pulses. In EPR, as in NMR, use of a Frank sequence of phase steps permits pulsed FID signal acquisition with very low power microwave/RF pulses (ca. 1.5 mW in the application reported here) relative to standard pulsed EPR. A 0.2 mM aqueous solution of a triarylmethyl radical was studied using a 16 mm diameter cross loop resonator to isolate the EPR signal detection system from the incident pulses.

1. Introduction

Coded pulse sequences have long been used in communications, radar, and other fields to distinguish signals from noise and other interfering signals, and there is a very extensive literature in this field. The use of phase-incremented pulses in NMR was reviewed by Zhang [1]. The sequences proposed by Heimiller [2], Frank [3], and Chu [4] have been judged to have good correlation properties, and Blümich et al. [5] demonstrated that the use of the Frank sequence facilitated NMR FID detection with very low power excitation pulses. The final step in the data analysis involves the well-known Fourier transformation of an FID to obtain the absorption and dispersion spectra (see, e.g. [6]). The Frank sequence appears to encode magnetic resonance signals more effectively than other methods, such as the Hadamard transform [7]. The Blümich et al. (2009) paper [5] stimulated our labs to examine the extent to which the Frank phase sequence could be applied to pulsed EPR. Initial consideration of the fact that electron spin relaxation times are shorter than nuclear spin relaxation times by about a factor of 10³ or more, and that consequently the spectrometer dead time following a pulse is a much larger fraction of available observation time in EPR than in NMR, suggested that success was unlikely. However, this paper reports successful application of a Frank sequence of pulse phases to EPR FID detection of a triaryl methyl radical. This was accomplished by recording the signal continuously, including during the pulses, and subtracting an off-resonance signal to reduce the background.

2. Experimental

The sample used was a 0.2 mM aqueous solution of deuterated symmetric trityl (sometimes called Finland trityl) (methyl tris(8-carboxy-2,2,6,6-tetramethyl(d3)-benzo[1,2-d:4,5-d′]bis(1,3)dithiol-4-yl)-tripotassium salt) in a 10 mm o.d. tube, purged with N2 and flame-sealed. This sample has T₂ about 11 μs [8], and was chosen because it has sufficiently long T₂ to facilitate demonstration of the Frank sequence for EPR.

Experiments were performed at 256 MHz RF frequency (ca. 9.1 mT magnetic field) using components of the VHF spectrometer and air-core magnet previously described [9; 10]. Isolation (ca. 40 db) of the detected signal from the RF pulses in a wire cross-loop resonator (CLR) [11] contributed to the success of this experiment. The sample resonator is 16 mm in diameter and 15 mm long and the orthogonal excitation resonator consists of two coils 32 mm in diameter and spaced 20 mm apart. The resonator Q was reduced to about 50 by inserting the 10 mm diameter sample into a 16 mm tube with the annular space filled with water.

2.1 Phase-stepped pulses

The phase-stepped RF pulses were generated with a Tektronix arbitrary waveform generator, AWG2041, at 1023.12 MHz clock frequency, which is near the instrument’s maximum. To facilitate creation of the waveforms, a Matlab program was written to produce AWG compatible files. The 8-bit signal channel was used to form the pulse sequence. The r.f. frequency carrier was one fourth of the AWG clock frequency, so there were only 4 points per sinusoidal cycle. The lack of resolution could have produced higher harmonics of the fundamental frequency if it were not for the resonator, which when tuned to the carrier frequency acted as a pass-band filter. Consequently, all of frequencies higher or lower than the resonator bandwidth were strongly suppressed. One marker output from the AWG was used to produce a constant 255.78 MHz signal for the LO side of the double-balanced mixer (DBM) that was used to detect the EPR signal. The output of the DBM has signals at baseband and 511.56 MHz, but the bandwidth of the amplifier (~10 MHz) passes only the baseband signal. The second marker output was used to trigger the digitizer. Synchronization of the signal channel and the two markers by the same AWG clock made possible successive data averaging by a Bruker SpecJet II digitizer that was run at the 250 MS/s sampling rate.

The AWG waveform for the Frank sequence of 256 pulses was computed using a Matlab program. Each pulse was formed by 112 points. It was followed by 112 zeros. The total number of points in the waveform was 224×256=57344, which for the 1024 MHz clock frequency is 56 μs. This sequence length was about 5 T₂ for the trityl radical. The phase of each individual pulse was calculated based on the Frank sequence of 16²=256 elements [3]. There were 16 different RF phases distributed among the 256 pulses, and the phase increments are multiples of 360°/16 = 22.5° (Fig. 1). The length of each pulse was about 109 ns, which produces a 3 dB excitation bandwidth of about 8 MHz. For the resonator Q about 50 at 250 MHz resonance frequency, the 3 dB bandwidth is 5 MHz. Thus the bandwidth of each pulse is larger than the bandwidth of the resonator. The power incident on the excitation resonator was about 1.5 mW. This power was demonstrated to be within a few dB of that required to achieve the desired 90°/256 (0.35°) turning angle for the electron spins for the pulse length and resonator Q. With an isolation of about 40 dB between the excitation and detection CLR resonators, the ‘leakage’ power at the detector was on the order of 150 nW. Such a low power is many orders of magnitude smaller than would occur for a single high power pulse. A power of 150 nW would not damage the detection system, so there was no need for detector protections. Consequently, the signal could be measured even during the pulse. In spite of the isolation, a background signal produced by transition effects in the CLR was much larger than the EPR signal. In order to reduce the background, data collected off-resonance were subtracted from the on-resonance signal. The resultant complex signal was cross-correlated with the Frank sequence to produce an FID, the Fourier transform of which revealed the absorption and dispersion components of the EPR spectrum (Figure 2).

Figure 1.

The pulse sequence that was used to produce the spectra in Figure 2 consisted of 256 pulses of 109 ns with the 16 different phases selected as shown in part a. The time required for the complete sequence was about 56 μs. The detailed timing of the first 2 and last 2 pulses is shown in part b. Data were acquired continuously at 4 ns intervals during the entire pulse sequence, but only the signal corresponding to times between the pulses was analyzed.

Figure 2.

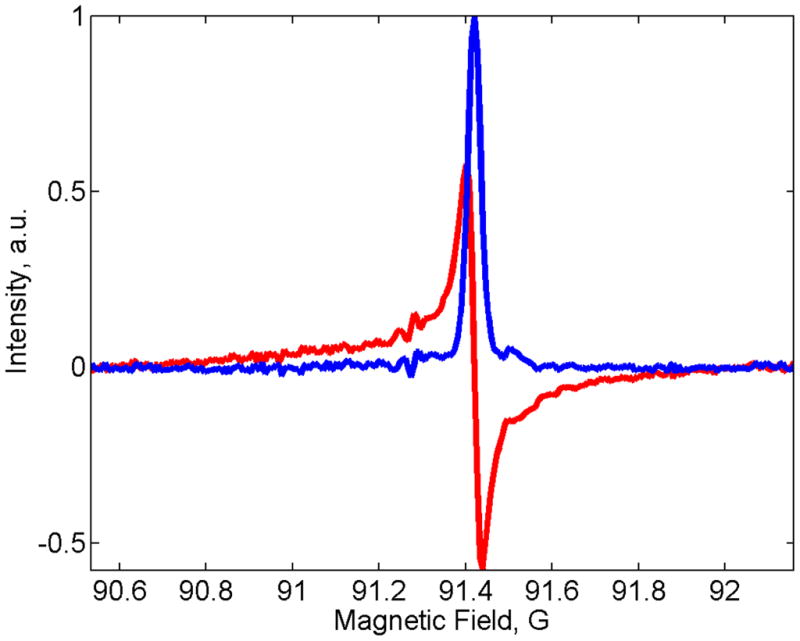
EPR spectrum of the trityl radical obtained by means of Frank Sequence EPR. The blue line is the absorption component and the red line is the dispersion component.

Three full cycles of data (3 × 56 μs) were digitized by a SpecJet II with 1024 on-board averages. In order to improve background subtraction, a ProDel program was used to alternate between on-resonance and off-resonance data that were each collected 40 times creating a 2D array. The on- and off-resonance spectra were subsequently subtracted. Thus, the total number of signal averages was 3×1024×40 = 122880 for both on-resonance and off-resonance. The total data acquisition time was about 122880×2×56μs ≅14 s. The time required to change the magnetic field from the resonance to off-resonance is not included in the time estimate.

In the Frank Sequence NMR paper [5] it was suggested that to minimize the background signal, a single data point of the resonance response to the train of preceding pulses could be measured, just before the beginning of the next pulse. It was found that in the case of EPR, where relaxation times are much shorter, better results could be obtained if more data points were averaged. Because of the isolation in the CLR the data were collected continuously, including at times during the pulses. Using a larger fraction of the points between the pulses improves the signal-to-noise. The spectra in Figure 2 were obtained by averaging all 25 points of the EPR response in the 109 ns interval between pulses to define a single point in the 256pt array that was correlated with the Frank sequence to calculate the FID.

2.2 Residual background signal

The subtraction of the off-resonance signal did not completely remove the background signal. The problem would be worse for weak EPR signals with short relaxation times. Different kinds of residual background signals produce different kinds of artifacts. The peculiarity of the Frank sequence method is that the background signal is basically a filtered Frank sequence, so cross-correlation with the Frank sequence produces ‘EPR-like’ features in the spectrum, which are due to the native response of the resonator. One approach to the problem is to reduce resonator Q, which shortens the resonator ringing time, and decreases its impact on the FID. The drawback to lowering Q is that it also decreases the intensity of the EPR signal. Alternatively, omission of the first few points of the FID decreases the impact of the residual background. The optimum Q value will depend on experimental conditions: relaxation times, spectral window, spectral resolution, etc. In our experiments a resonator with a non-optimized Q value of about 50 was used. The resonator was initially designed for rapid scan EPR [12–14] and was used in these proof-of-principle experiments because it was available. For a standard pulse EPR experiment, following an impulse to the resonator, the signal detection system is usually overwhelmed for at least five time constants of the resonator impulse response or until the EPR signal is comparable in intensity with the resonator ring-down. In the Frank sequence the single 90° pulse is replaced by a series of low power pulses that turn the spins by a much smaller angle. For the short relaxation times of many paramagnetic species, this EPR signal may be so small relative to background that detection may not be possible.

3. Results and Discussion

The results of the Frank sequence with 256 pulses, including subtraction of the off-resonance background, are shown in Fig. 2. The spectra show some oscillations on the low-field side of resonance that are attributed to a small non-orthogonality of the two channels. There is some correlation in the baselines for the dispersion and absorption signals, which also is attributed to non-orthogonality of the signal channels. The line width of the trityl signal in Figure 2 agrees well with the linewidth in a standard CW EPR measurement of the same trityl sample.

Although 256 pulses for EPR signal detection is large relative to normal pulsed spin echo and saturation recovery EPR, there is precedent for using large numbers of pulses in EPR. Morton et al. [15] showed that in a favorable case, up to 1000 refocusing pulses could be applied in a Carr-Purcell-Meiboom-Gill (CPMG) sequence.

In the Frank sequence with n phases, the number of pulses increases proportional to n² (where n is an integer). Experiments were tried with n = 5, 7, … up to 16 phases, which therefore required 25, 49, …, 256 pulses, while keeping the total length of the pulse sequence at 5 T₂. As the number of pulses increased, the pulse length decreased, which increased the bandwidth excited. It would be possible to increase the number of pulses even further, but it would not be useful to use shorter pulses in these experiments because the bandwidth of the resonator, ca. 5 MHz, would be a limiting factor.

Spectral resolution is equal to the reciprocal of the pulse sequence duration. The suggested value is 1/(5 T₂) [5]. Simulations show that the resolution can be increased by stretching the sequence to more than 5 T₂. This result might be important if the Frank Sequence EPR method is applied to a sample containing spins with different relaxation times. The example shown here is of a homogenous O₂-free solution of trityl. Samples that contain species with different relaxation times or are inhomogenous will have different T₂ values for different parts of the spectra, and consequently, the intensity and resolution will not be optimized for all parts of the sample simultaneously. The ability to discriminate based on T₂ may be an advantage for some studies. The Frank sequence may also be run under partially saturating conditions to add T₁ weighting, which might provide e.g. better pO₂ contrast for oximetry.

The major obstacle for practical use of the Frank sequence of RF pulses is that the background signal is large with respect to the EPR component signal. When the isolation between the two resonators of the CLR resonator was poor, the background increased and the EPR signal was distorted.

The primary goal of this paper is to demonstrate feasibility of this method for EPR. The experimental setup was not optimized. In order to optimize the experiment, the focus should be on solving two basic problems: (i) background reduction by increasing isolation between the excitation and detection resonators of the CLR, (ii) fast switching of the magnetic field system to decrease delay between on- and off-resonance data collection. In addition, using a lower Q resonator would reduce the dead time. This might provide a non-linear increase in signal, enhancing the signal-to-noise ratio.

Although the Frank sequence used in the present application requires that the numbers of pulses in the sequence be the squares of the number of phases, Chu [4] showed that sequences can have any number of pulses and still have the desired correlation properties. Fan et al. [16] showed that combined Frank and Chu sequences have correlation properties similar to the original sets. Thus, the restriction to squares of integers in the present work is not necessary, and a large number of sequences with desirable correlation properties can be constructed in the future.

The key conclusion of this paper is that in EPR, as in NMR, use of a Frank sequence of phase steps permits pulsed FID signal acquisition with very low power microwave/RF pulses. Relative to standard pulsed EPR, which requires high-power pulsed RF/microwave amplifiers (see, e.g., [17; 18]), much lower power can be used with the Frank sequence. Relative to normal CW operation, the present method shares with normal high-power pulse FID detection the advantage that the magnetic field is not scanned and magnetic field modulation is not required. Relative to rapid scan EPR (see, e.g. [12–14]) no auxiliary rapid magnetic field scan coils are required. Balanced against these advantages are the limitations that the spectral bandwidth will usually be determined by the resonator Q. There are many paramagnetic species, especially defect centers and doped solids, with sufficiently long T₂ that application of the method described here is not restricted to the triaryl methyl radical chosen for initial demonstration of the phenomenon.

The experiments reported here demonstrate the feasibility of low-power EPR FID spectroscopy using the Frank sequence of phases. To compare these experiments with a standard pulse experiment in which an FID is created with a 90° pulse, the two types of experiment were performed using the same 0.2 mW trityl sample in the same 16 mm diameter CLR. The resonator Q was the same, pulse lengths of ca. 108 ns were used in both experiments, the detector bandwidth was the same, and data were acquired for the same total time for each experiment. The power required to achieve maximum FID was 1.5 mW with 50% duty cycle for the Frank sequence experiment and that for the standard experiment was 12.5 W with 108 ns pulses, limited by the spectrometer hardware. Under these conditions, significantly better S/N was achieved in the standard pulse FID experiment. For the experimental parameters of the comparison as performed, if the power had all been absorbed in the sample (e.g., the hypothetical in vivo experiment where the animal determines the resonator Q), the specific absorption rate (SAR) would be about 7 times higher for the pulse experiment. The relaxation time of trityl-CD₃ in the absence of O₂ was long enough that there was very little decay during the ca. 1 μs deadtime following the high-power pulse. There was close to zero deadtime in the Frank sequence, so the relative S/N would change for a sample with shorter relaxation time.