Abstract
Purpose: The authors use reduced-order constrained optimization (ROCO) to create clinically acceptable IMRT plans quickly and automatically for advanced lung cancer patients. Their new ROCO implementation works with the treatment planning system and full dose calculation used at Memorial Sloan-Kettering Cancer Center (MSKCC). The authors have implemented mean dose hard constraints, along with the point-dose and dose-volume constraints that the authors used for our previous work on the prostate.Methods: ROCO consists of three major steps. First, the space of treatment plans is sampled by solving a series of optimization problems using penalty-based quadratic objective functions. Next, an efficient basis for this space is found via principal component analysis (PCA); this reduces the dimensionality of the problem. Finally, a constrained optimization problem is solved over this basis to find a clinically acceptable IMRT plan. Dimensionality reduction makes constrained optimization computationally efficient.Results: The authors apply ROCO to 12 stage III non-small-cell lung cancer (NSCLC) cases, generating IMRT plans that meet all clinical constraints and are clinically acceptable, and demonstrate that they are competitive with the clinical treatment plans. The authors also test how many samples and PCA modes are necessary to achieve an adequate lung plan, demonstrate the importance of long-range dose calculation for ROCO, and evaluate the performance of nonspecific normal tissue (“rind”) constraints in ROCO treatment planning for the lung. Finally, authors show that ROCO can save time for planners, and they estimate that in the clinic, planning using their approach would save a median of 105 min for the patients in the study.Conclusions: New challenges arise when applying ROCO to the lung site, which include the lack of a class solution, a larger treatment site, an increased number of parameters and beamlets, a variable number of beams and beam arrangement, and the customary use of rinds in clinical plans to avoid high-dose areas outside the PTV. In the authors previous work, use of an approximate dose calculation in the hard constraint optimization sometimes meant that clinical constraints were not met when evaluated with the full dose calculation. This difficulty has been removed in the current work by using the full dose calculation in the hard constraint optimization. The authors have demonstrated that ROCO offers a fast and automatic way to create IMRT plans for advanced NSCLC, which extends their previous application of ROCO to prostate cancer IMRT planning.
Keywords: optimization, IMRT, constrained optimization, dimensionality reduction
INTRODUCTION
Intensity-modulated radiotherapy (IMRT) has revolutionized the treatment of cancers in the last decade. It allows a higher dose to be delivered to a tumor while protecting nearby radiation-sensitive normal tissues, yielding better local control and fewer post-treatment complications than previous techniques.1, 2, 3 However, the process of obtaining a clinically acceptable IMRT plan for a difficult treatment site is often slow and labor-intensive, requiring hours of expert time in a manual trial-and-error loop in which the parameters of the optimization score function are repeatedly adjusted. Long planning times place a severe stress on available resources in a busy clinic, and can result in treatment delays, acceptance of suboptimal plans or, in the worst case, errors due to time pressure. In this paper, we apply a method called reduced-order constrained optimization (ROCO) to greatly reduce the amount of time required to obtain a clinically acceptable IMRT plan. By minimizing the trial-and-error effort characteristic of current IMRT planning, it allows treatment planners to focus on clinical tradeoffs between tumor coverage and normal organ doses. We have previously applied ROCO to prostate cancer cases;4 in this paper, we improve our application of ROCO and report new results on a more challenging treatment site, the lung.
Lung cancer accounts for the most cancer-related deaths in both men and women in the United States. An estimated 157,300 deaths, accounting for about 28% of all cancer deaths, are expected to occur in 2010.5 Radiation therapy is the main curative treatment for inoperable non-small-cell lung cancer (NSCLC), but it remains a technically challenging procedure with very low 5-year survival rates (<10%).6 IMRT is promising for treatment of NSCLC compared to traditional radiotherapy or 3D-CRT since it may enable dose escalation to the tumor;7 however, the organs at risk (OARs) are sensitive to radiation, including the lungs, esophagus, and spinal cord. Since the sizes and locations of lung cancers are diverse, unlike prostate cancer, a standard multifield class solution for IMRT is not used. Typical treatment plans for locally advanced (stage III) lung cancer feature prescription doses of 1.8–2 Gy∕fraction delivered by 3–7 coplanar treatment beams of 6 MV photons, occasionally with the addition of noncoplanar beams. For the locally advanced NSCLC cases we examine in this paper, we estimate that it takes an expert planner around 3 h to create a clinically acceptable IMRT plan (not counting time spent contouring structures and selecting beam directions).
In this paper, we describe our implementation of ROCO, which we have integrated with the clinical treatment planning system (TPS) at Memorial Sloan-Kettering Cancer Center (MSKCC), and our results from retrospective application of ROCO to 12 locally advanced lung cancer cases. The anonymized clinical data (image sets, structure contours, and clinical treatment plans) for these patients were provided by MSKCC under IRB approval. ROCO consists of three main steps, after beam directions have been selected. First, random sets of score function parameters are chosen via Latin hypercube sampling, and these plans are optimized using the clinical score-function-based optimization. Second, principal component analysis (PCA) isolates the important modes of variation in the intensity matrices, which shifts the independent variables of the problem to the few dominant PCA modes. Sampling and PCA modes are generated for each patient individually, not as class solutions. The third step is hard-constrained optimization. Dimensionality reduction by PCA makes it feasible to rapidly and automatically locate plans with clinically acceptable PTV coverage and normal tissue protection in the space spanned by the sampled plans. Using the MSKCC planning system, the overall process takes approximately 30 min per patient on a modest desktop workstation (an Intel Core 2 Duo, clock speed 2.33 GHz, with 3.5 GB of RAM).
Advanced lung cancer cases present new challenges when compared to our previous work on the prostate. For prostate cases, because the relationship between the PTV and the rest of the anatomy varies relatively little from patient to patient, the same beam directions were used for each patient. Stage III lung tumors, on the other hand, show extremely variable geometries and can grow to considerable size, growing outside of the lung proper and into the mediastinum; additionally, single or multiple tumors can appear in a variety of geometries near OARs such as the heart, esophagus, spinal cord, and brachial plexus. Because of this, ROCO used the clinical beam directions chosen by the planner in each case. Our current implementation is integrated with the clinical MSKCC treatment planning system in order to make it flexible enough to deal with different treatment sites besides the prostate, whereas the software previously described used data exported from, and performed calculations outside of, the treatment planning system4 (which caused difficulty because of discrepancies in dose calculation).
Figure 1 shows three image sections of a representative lung cancer patient in our study, with contours for the different OARs, together with a 3D representation of the CT images showing the tumor wrapping around the esophagus. The dimension of the space of possible treatments is larger for these locally advanced lung cases than for prostate cases, because the larger treatment fields contain a greater total number of beamlets. For prostate cases there are on the order of 103 beamlets, and for the lung cases that we consider, there are about 104. Finally, IMRT for NSCLC often includes “rind” structures to prevent hot spots in nonspecific normal tissues. Table Table I. summarizes the major differences pertaining to treatment planning between the prostate cases we had considered previously and the stage III NSCLC cases considered in this paper.
Figure 1.
The left three panels show CT image slices in the coronal, sagittal, and transverse planes for patient 8 in our study; the rightmost panel shows a beam’s eye view of the same case. The PTV is shown in red, the lungs in yellow, the spinal cord in green, the heart in pink, and the esophagus in cyan. The solid lines in the third panel show the beam directions.
Table 1.
Comparison of IMRT treatment planning complexity in prostate and lung treatments. Hot spots in nonspecific normal tissues around the prostate are avoided by beam arrangements and small PTV size, so rinds are not usually required.
| Criterion | Prostate case | Lung case |
|---|---|---|
| Beams (geometry) | 5 (class solution) | 4–9 |
| Beamlets | ~103 | ~104 |
| Median PTV volume | ~160 cm3 | ~380 cm3 |
| PTV∕OAR relationships | Similar | Variable |
| Nonspecific normal tissue sparing | Beam arrangement | “Rind” structures |
| Optimization parameters | ~30 | ~50 |
| OARs | 3–5 | 5–10 |
The standard clinical approach to inverse IMRT planning is to combine all the evaluation criteria specified by the physician into a scalar value using a weighted sum of several terms (i.e., costlets8). Each term includes a dose parameter (i.e., a minimum or maximum limit) or a pair of dose-volume parameters (i.e., a point on a DVH curve), and reflects a clinical objective. The weight of each term is the relative penalty imposed by the planner for not satisfying each objective. Such a formulation is easy to implement and can be optimized quickly using gradient information, e.g., by Newton’s methods9 or conjugate gradient algorithms.10 Because the result of a penalty-based optimization that does not include hard constraints is not guaranteed to satisfy the clinical criteria, such an optimization scheme is known as “unconstrained optimization.”
In practice, unconstrained optimizations require a great deal of heuristic trial and error to arrive at parameter settings such that the resulting plan is clinically acceptable.11 The planner uses the weights (or “importance factors”) in the objective function to try to “steer” the optimization algorithm to more clinically desirable solutions,12 but this can be difficult since the process of adjusting these weights is inherently imprecise and unintuitive.13 The role of dose limits in IMRT optimization is also confusing, since it has been observed that in an unconstrained optimization, dose limits more stringent than the clinical limits are required to obtain convergence to an acceptable plan (see, e.g., Refs. 10, 14, 15). The inverse planning process of obtaining a clinically acceptable IMRT plan for a difficult site can take several hours, largely due to the manual process of adjusting the parameters in the objective function.10, 13, 16
In our previous work,17 we applied sensitivity analysis to identify key parameters of an unconstrained IMRT objective function that have a strong impact on the resultant dose distribution. We then applied an outer loop over the sensitive parameter set to find the parameters such that the minimizer of the corresponding objective function gave the best score of a scalar function of plan quality. While this method quickly produced plans that generally satisfied the clinical constraints, it still suffered from (1) using a scalar-valued objective function to approximate a fundamentally hard-constrained problem and (2) requiring training data to identify the sensitive set, assuming a generalizable class solution for the treatment site. The ROCO algorithm has neither shortcoming.
While hard-constrained optimization for IMRT planning has been proposed previously (e.g., using mixed-integer programming18), it is typically prohibitively time-consuming due to the huge dimensionality of the problem and the difficulty in implementing dose-volume constraints. Another recent focus of interest is multiobjective (MO) optimization, which allows the planner to choose from a family of Pareto-optimal plans (that is, plans in which no criterion can be improved without worsening the others).19, 20
The ROCO algorithm makes constrained optimization computationally tractable using four steps:
-
1.
Select the targets and OARs to be included in the score function, and choose the beams whose intensities are to be optimized.
-
2.
Randomly sample sets of score function parameters, apply the clinical optimization to each set, and store the resulting intensity patterns.
-
3.
Apply principal component analysis (PCA) to this set of intensity profiles. The resulting principal components form a basis for the space of plans that contains the optimal plan.
-
4.
Compute the coefficients of the basis vectors that optimize target coverage, subject to clinical constraints.
In Sec. 2, we briefly review each of these steps, placing emphasis on the new features we have added; a more complete treatment is given in our previous paper.4
SUBJECTS AND METHODS
We used the MSKCC treatment planning system for our study, which uses a radiological pathlength corrected pencil beam algorithm for dose calculation.21 The optimization algorithm employed by default in the TPS is conjugate-gradient minimization of a quadratic score function, which has been previously described.6, 10 At MSKCC, stage III NSCLC IMRT plans are delivered at 2 Gy∕fraction with the sliding window technique. Up to seven planner-chosen 6 MV beam directions concentrated on the ipsi-lateral side to geometrically protect the contra-lateral lung are used (in our set of patients, up to six beam directions are used). The ROCO algorithm used these beam directions to retrospectively replan 12 NSCLC patients who had already been treated with IMRT; PTV volumes ranged from 194 to 820 cm3 (median 383 cm3), with some patients having two PTVs (the tumor and nodal metastases). These patients were selected to have challenging clinical scenarios, i.e., large tumors with mediastinal extent, where the treatment planner had required from 10 to 50 optimization cycles to come up with an acceptable plan.
Treatment plan criteria
The current MSKCC clinical evaluation protocol requires that the plan for IMRT treatment of primary lung tumors to 50–80 Gy for the PTV satisfies the conditions in Table Table II.. The mean dose constraint on the paired lungs usually ensures that the Lyman–Kutcher–Burman lung NTCP (Refs. 22, 23) is ≤25%. The hard constraint on the esophagus Dmean is only used clinically by the planner if it can be met without compromising target coverage. Target Dmin is not included as a hard constraint on the clinical plans; if D95 and V95 are ~95% or better, we deem coverage sufficient.
Table 2.
Clinical organ constraints to be implemented by ROCO for lung plans. The lung mean dose constraint is a proxy for NTCP ≤25% (see text); the esophagus constraint is not enforced clinically by the planner if it cannot be met without compromising coverage. Not shown in the table are nonspecific normal tissue maximum dose constraints: major hot spots (>110%) outside the PTV are not tolerated, and if the dose distribution is insufficiently conformal more than ~0.5 cm beyond the PTV, then the plan will be rejected by the treatment planner.
| Structure | PTV | Lungs | Esophagus | Spinal cord | Brachial plexus | |
|---|---|---|---|---|---|---|
| Constraint | Dmax<110% | Dmean<20 Gy | Dmean<34 Gy | Dmax<50 Gy | Dmax<65 Gy, D05<60 Gy |
The dose to nonspecific normal tissue surrounding the PTV is also of concern: “hot spots” above 100% of prescription outside the PTV are discouraged in clinical plans, while those above 110% are not tolerated. If the dose distribution is insufficiently conformal more than ~0.5 cm beyond the PTV, then the plan will be rejected by the treatment planner. For each patient in our study, the treatment planner had created customized rind structures to control the doses to the tissue outside of the PTV; we set aside these rinds which had been previously created for each patient by the treatment planners, and instead created standardized rind structures for each patient by leaving a 4 mm margin outside of the PTV, and then selecting a 3 cm annulus of tissue outside of this margin. We define this 4 mm margin in order to avoid compromising target coverage: hot spots that are only slightly outside the PTV are not a clinical problem at the treatment doses used in our study. In three of the patients in our study, hot spots persisted in regions further outside of the PTV than were covered by this 3 cm annulus, so for patients 9, 10, and 12, we instead used a somewhat larger rind (4–5 cm annulus) that the treatment planner had defined (the results shown below for patients 9, 10, and 12 are calculated using these larger rinds). We note that on the whole, ROCO is able to function with smaller rinds than those used by the treatment planners: for the ROCO plans, we used one rind structure, with volumes ranging from 852–3113 cm3, while the treatment planners used 1–5 rinds totaling 1213–5646 cm3. The median clinical rind size was 2562 cm3, and the median for ROCO was 1510 cm3 (difference is significant to P<0.01 by Wilcoxon signed-rank test).
A difficulty in creating a treatment plan is that the definition of “clinically acceptable” can change depending upon the specific situation under consideration. Certain dose constraints are inflexible (e.g., in our clinic, the spinal cord maximum dose is never permitted to go above 50 Gy). Other constraints, however, such as restrictions on nonspecific normal tissue maximum dose (“hot spot” constraints), or mean dose constraint to the esophagus, may be relaxed if the physician is unhappy with the tradeoffs in the plan and desires to improve the coverage of the PTV. Excessive modulation of the intensity profiles, which can lead to delivery problems and unnecessarily increased delivery time, is also not permitted in the clinic.
Unconstrained optimization
For every patient, we sample the solution space by varying the parameters of a quadratic dose-based objective function, and subjecting it to the unconstrained optimization that has been used for many years in clinical practice at MSKCC.6, 10 This optimization is referred to as “unconstrained” because while the objective function parameters influence the doses to the various structures, an intensity distribution that minimizes such an objective function is not guaranteed to obey any particular constraint.
For the kth target, the corresponding objective function term is
| (1) |
where Nk is the number of points in the target, Di is the dose to the ith point in the target, is the prescription dose, and are the minimum and maximum dose allowed without penalty, and and are the penalties (weights) for under- and over-dosing. The parameter set completely specifies the objective function for target k. A similar objective function term is defined for each OAR and rind structure (see Sec. 2 and Table Table II.), which also includes parameters , , , and , that define the dose-volume-histogram (DVH) and mean dose constraints:
| (2) |
The sum in the second term is carried out over the lowest doses that are greater than and is the minimum number of point dose changes required to bring the kth organ into compliance with the DVH constraint.10 Mean dose to the kth organ is denoted by ; the heaviside step function Θ ensures that this term only contributes to the score function when . Score functions of this type are standard in external beam treatment planning optimization.24, 25
Sampling
Let Iopt be an intensity distribution that optimizes PTV coverage while obeying clinical constraints; further suppose that some unknown set of score function parameters Popt cause this plan to be generated by unconstrained optimization. Then we conjecture that if we randomly choose parameter sets Pq in the neighborhood of Popt, the resulting Iq from unconstrained optimization will define a small basis which spans a space containing such an Iopt.26
We choose this neighborhood from clinical experience to include the range of values that planners have used for similar cases. Once a range of parameters has been chosen, Latin hypercube sampling is used to choose Nsamp parameter sets at which to sample; Latin hypercube sampling is a particular case of stratified sampling that achieves an efficient coverage of the space of input parameters.27
Dimensionality reduction and dose calculation
Given Nsamp optimized intensity distributions {I1,I2,…,INsamp} resulting from the unconstrained optimization using score function parameter sets {P1,P2,…,PNsamp}, the dimensionality of the intensity space can be reduced by linear or nonlinear feature extraction methods. Here, we use principal component analysis (PCA)28 for the reduced-order approximation. PCA is an orthogonal linear transformation that maps the data to a new coordinate system, such that the dimension with the kth greatest variance is oriented to lie on the kth coordinate (i.e., the kth principal component). This procedure shifts the independent variables of the problem from the approximately 104 beamlets that specify the intensity profile of a treatment plan to the Nmodes PCA modes with the greatest variance. These modes Uk span a reduced solution space.
During unconstrained optimization with conjugate-gradient methods, the MSKCC treatment planning system uses an approximate, short-range kernel for the purposes of calculating the doses to the targets and OARs, so that many evaluations of the dose calculation can be executed rapidly.10 Once optimization has completed, a long-range full dose calculation is performed, and then the plan is evaluated based on this calculation.
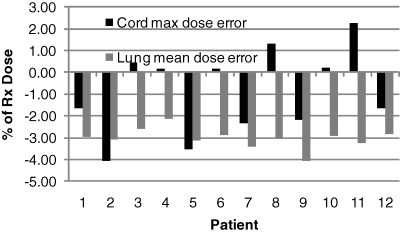
We have found that, while this approach is sufficient for the sampling step, it is inadequate for the subsequent steps of ROCO. After the Uk are determined, it is critical to make the dose calculation for the PCA modes as accurate as possible, so that during the constrained optimization, the solver has accurate information about OAR doses and target coverage. Figure 2 shows that lung mean doses are systematically underestimated by up to 4% when using the short-range approximate dose calculation normally used during the clinical score-function-based optimization. This would result in a systematic overdosing of these tissues in ROCO plans, which was a limitation in our previous work.4 We have addressed this issue here by using the long-range dose calculation to evaluate the dose distributions for the PCA modes, which costs some time: finding the optimal basis requires less than a minute to complete, but calculating the full dose distributions corresponding to the modes requires another 5–10 min. Nevertheless, this constitutes a major improvement in our implementation of ROCO, and makes ROCO optimization suitable for large targets.
Figure 2.
Importance of long-range dose calculation. The figure shows ΔD=(Dshort range-Dfull dose)∕DRx for the spinal cord Dmax (black) and mean lung dose (gray) for each patient using the ROCO intensities. In order to get accurate results from ROCO, the dose calculation for each PCA mode used by the constrained optimization must be performed with the full long-range dose kernel.
Constrained optimization
Given the reduced-dimension space that captures the effective degrees of freedom in the intensity variables, our final task is to find a clinically acceptable solution in terms of the reduced basis. For this step, the optimizer has Nmodes degrees of freedom: the coefficients of the PCA modes. The goal of the optimization is specified as
| (3) |
for the voxels T in the target structures. This causes the optimizer to work toward uniform PTV coverage. The doses to voxel i are given by
| (4) |
In this equation, the ξk are the coefficients of the principal components, which are the independent variables of the optimization. Vik is the dose to voxel i from principal component k, and υi is the dose to this voxel from the mean of the samples. The intensities of these modes were determined during the dimensionality reduction step, and the Vik and υi are obtained by calculating the doses for each intensity mode (the Uk from Sec. 2) and for the mean.
For each organ, the point dose hard constraints are specified by
| (5) |
where i runs over the set of voxels in each organ or target. While it is possible to use Dmin constraints for targets, in our study, we did not find it necessary: adequate dose homogeneity was reached via the optimization goal in Eq. 3 without an explicit Dmin constraint. Mean dose constraints are given by
| (6) |
where Nvox is the number of voxels in the structure. DVH constraints are implemented using an iterative scheme;4 briefly, on the first iteration of optimization, no DVH constraints are implemented. If a DVH constraint of the form DV≤Y for a dose Y and volume fraction V is then found to be violated after optimization, we apply the constraint Di≤Y, where i consists of the hottest NvoxV voxels, and repeat the optimization, applying DVH constraints as needed at each step.
There is also an additional constraint, which is that
| (7) |
where Ujk is the value of beamlet j in mode k, and μj is the value of beamlet j in the mean of the samples. This ensures that the set of ξk in the solution results in a nonnegative intensity distribution.
The dimensionality reduction by PCA makes it feasible to use a quadratic programming solver (ILOG CPLEX) to solve this hard-constrained problem. This step took 1–10 min when using 25 PCA modes, and we have found that the calculation time required is approximately linear for up to 200 degrees of freedom. Total time required was therefore approximately 30 min per patient; if it is desired to adjust the hard constraints, only the last step needs to be repeated. At the end of the process, the ROCO-optimized plans were leaf-sequenced for clinical delivery and the final clinical dose calculation was performed.
Rind structures
An important aspect of current techniques for lung cancer treatment planning is the creation of nonspecific normal tissue structures (referred to here as “rinds”) that help avoid regions with undesirable high doses surrounding the PTV (“hot spots”). To make treatment planning less labor-intensive, it would be an advantage to use a standardized rind structure if it could be effective at avoiding hot spots, or if suitable plans could be created without such structures altogether. More generally, we would like to know whether adding constraints on new structures, such as a planner might impose after seeing an initial treatment plan, must be incorporated from the very beginning of the ROCO process, or if the lower-dimensional space generated by the sampling phase may already contain feasible solutions for the new constraints.
We performed an experiment in which we evaluated PTV D95 and dose distribution outside the PTV with and without the presence of rinds. For the purposes of this experiment, the resulting plans were not evaluated by a treatment planner to confirm clinical acceptability, focusing instead on the performance of the algorithm. Once the standardized rinds were in place, we used ROCO to plan patients, first without the rind structures present, and then with the standardized rinds in place during both the sampling and constrained optimization, and finally leaving them out during the sampling and including them in constrained optimization only. Table Table III. summarizes the results from this experiment. Without the rind structures in place, hot spots were found outside of the PTV in four of the patients. After we ran ROCO with the standardized rind structures in place, we found that the hot spots in the 3 cm region outside of the PTV were successfully suppressed. Further, we found that it was not necessary to include the rind structures during the sampling stage: the optimizer had sufficient freedom to honor the rind constraints even if they had not been included when the sampling for the PCA basis was performed.
Table 3.
ROCO target coverage and rind maximum dose for three different cases: in the first row, no rinds are included in the optimization; in the second row, rind constraints are included in both the sampling and hard constraints; and in the third row, rind constraints are present in the hard constraint optimization step only. Patients 5, 7, 8, and 10 had unacceptable hot spots outside the PTV when rind structures were not included in the ROCO constraints. Rind constraints reduced these doses to acceptable levels (110% of PTV max dose), and the optimizer had sufficient freedom to do this even without the presence of rinds during sampling.
| Patient | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rinds: | No rinds present. | |||||||||||
| PTV D95 | 100.6 | 100.2 | 100.9 | 100.4 | 95.4 | 101.0 | 91.7 | 99.2 | 100.6 | 99.3 | 100.6 | 99.0 |
| Rind Dmax | 109.6 | 107.4 | 106.1 | 106.2 | 119.9 | 104.5 | 115.5 | 110.7 | 108.5 | 114.3 | 107.5 | 109.9 |
| Rinds: | Rinds present in both sampling and constrained optimization. | |||||||||||
| PTV D95 | 100.6 | 100.2 | 100.9 | 99.6 | 95.1 | 101.0 | 91.6 | 99.2 | 100.6 | 98.9 | 100.6 | 99.0 |
| Rind Dmax | 109.6 | 107.4 | 106.1 | 105.6 | 107.0 | 104.5 | 110.0 | 110.0 | 108.5 | 110.0 | 107.5 | 109.9 |
| Rinds: | Rinds in constrained optimization only. | |||||||||||
| PTV D95 | 100.1 | 100.1 | 100.7 | 100.4 | 98.1 | 101.0 | 93.2 | 98.9 | 100.5 | 98.0 | 100.5 | 98.7 |
| Rind Dmax | 109.0 | 108.4 | 105.7 | 106.2 | 110.0 | 104.5 | 106.8 | 106.2 | 106.6 | 110.0 | 106.1 | 107.0 |
RESULTS
Nsamp and Nmodes
In order to help determine the optimal value for Nsamp, in Fig. 3 we studied how coverage for the final ROCO plan varies with number of samples for all the patients in our study. These results show that 50 samples are sufficient to achieve the desired 95% PTV coverage, and that a larger number of samples is not likely to result in much improvement. Obtaining the intensity profiles of the 50 samples requires 10–15 min of computer time.
Figure 3.
PTV coverage (solid lines) achieved by ROCO vs number of samples for each patient in our study. After about 50 samples, almost no benefit is seen as the number of samples used is increased. No renormalization of the plans (as in Fig. 6) is performed.
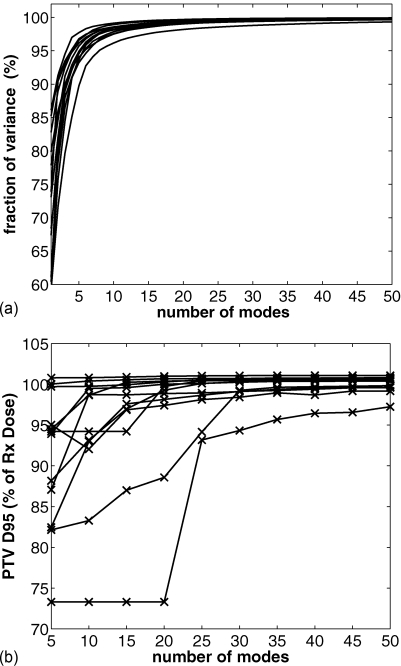
We also studied the characteristics of the solutions from ROCO as we vary Nmodes in two ways. First, we examined how much of the variance in the samples was recovered using the PCA decomposition. The top panel of Fig. 4 shows the fraction of the variance recovered for each patient as a function of the number of modes used, using an original set of 500 samples. From this we determined that 25 modes were sufficient to recover 98% of the variance of the samples in all cases. The bottom panel shows the PTV coverage that we achieved as a function of the number of modes used in the plan. For Nmodes>25 we observed only a few percentage increase in PTV coverage for these patients. While we fixed 25 modes per patient for this study, we note that for some patients, excellent performance was achieved by ROCO for several patients using a surprisingly small number of modes. For example, patient 6 only required two modes to obtain a plan that was close to acceptable.
Figure 4.
Top panel: Cumulative fraction of variance in intensity profiles of sampled plans recovered, plotted against Nmodes used. 25 modes are sufficient to capture 98% of the variance of the samples for all the patients in our study. Bottom panel: target coverage vs Nmodes used; for these patients, Nmodes = 25 was sufficient to achieve adequate coverage.
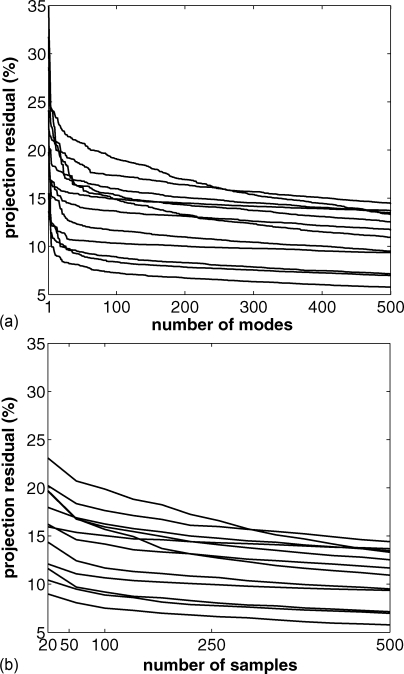
Next, for each patient, we took the intensity vector for the clinical plans used by the treatment planners Icl, and projected it into the reduced-dimension space, which allowed us to measure the projection residual R
| (8) |
The top panel of Fig. 5 shows how R behaves as a function of Nmodes. In this plot, we see that there is initially a decrease in R as we increase the number of modes. Less improvement is seen after 10–25 modes. We chose to use 25 PCA modes for the patients in our study. Similarly, the bottom panel of Fig. 5 shows how R behaves as we vary Nsamp; around Nsamp = 50, the behavior of R is smooth, so we used Nsamp = 50 in our subsequent experiments.
Figure 5.
Projection residual R [see Eq. 8] plotted against the number of modes used (top panel; using 500 samples) and number of samples used (bottom panel; using Nmodes = Nsamples).
Clinical plan comparison
In this section, we compare the ROCO plans to the plans that were used to treat these 12 patients in the clinic. In order to prepare for this comparison, the ROCO plans were evaluated by an experienced treatment planner at MSKCC to ensure clinical acceptability, i.e., compliance with the criteria mentioned in Sec. 2. For the purposes of this comparison, the ROCO plan was normalized to have the same D95 value as the plan used for treatment. All ROCO plans were inspected to confirm that the intensity profiles were sufficiently smooth, i.e., there were no large peaks in the intensity profiles, and that the plans did not require an excessive number of monitor units (MU) to deliver. Table Table IV. shows that the ROCO and clinical plan MUs were similar: ROCO plans required a median of 15% more MU, but this was not found to be a statistically significant difference.
Table 4.
Total monitor units required to deliver the IMRT plans produced by ROCO and by the standard planning method for each patient. Median MU required for ROCO was 749; the clinical plans required a median of 651 MU. The difference is not found to be significant at the P<0.1 level using the Wilcoxon signed-rank test.
| Patient | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROCO MU | 750 | 613 | 824 | 807 | 768 | 909 | 699 | 690 | 652 | 753 | 616 | 748 |
| Clinical plan MU | 548 | 608 | 635 | 898 | 773 | 785 | 869 | 578 | 531 | 861 | 496 | 667 |
In all cases, ROCO achieved a plan satisfying the given input constraints, which is the primary goal of using hard-constrained optimization. However, after the plan was normalized to have the same D95 as the treatment planner’s plan, it was not unusual for the constraints to be violated; for example, if the D95 achieved by the ROCO plan was smaller than the treatment planner’s D95, then after normalization, the lung mean dose constraint might be violated. This is not a failure of ROCO but rather a consequence of the difficulty of directly comparing two plans, a difficult and well-known problem.29, 30, 31, 32 As a result, it was sometimes necessary to reoptimize patients using lower organ dose constraints or a lower PTV max dose constraint. When ROCO is used as a standalone planning tool, without the intention of comparing to a reference plan, this step is not necessary, because the ROCO D95 would be clinically acceptable.
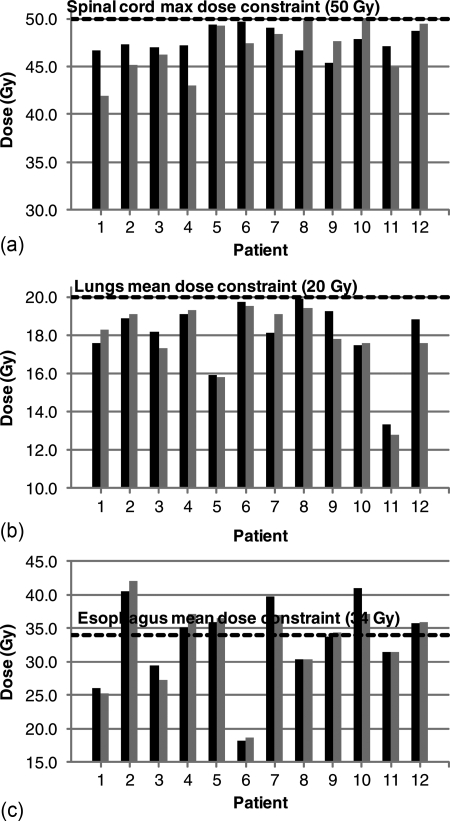
The plots in Fig. 6 show that for each case in our study, ROCO plans are competitive with the treatment planner’s plans. The required clinical constraints for the spinal cord maximum dose and lung mean dose are satisfied in each case; the esophagus mean dose constraint was satisfied when it was clinically possible to do so without sacrificing coverage. In Table Table V., we summarize ROCO’s performance with a figure of merit D*: for the PTV Dmin, D* = (DROCO – Dplanner)∕DRx, while for all other measures, D* = (Dplanner – DROCO)∕Dconstraint. D* is therefore a fractional measure of target coverage or sparing, normalized to the prescription dose or clinical constraint; positive numbers are better for ROCO. Table Table V. shows the median D* for each structure: we tested the differences in the medians for statistical significance using the Wilcoxon signed-rank test.33 We have found that differences in doses to the OARs (i.e., differences between the median values of D*) for the clinical plans and for ROCO are not statistically significant.
Figure 6.
Comparison of ROCO and treatment planner plans. Black bars show doses to organs for ROCO plans, and gray bars show the doses for the planner’s plans. ROCO plans are normalized to have the same D95 as the planner’s plan for each patient. The black dashed lines indicate the relevant clinical constraint. ROCO plans satisfy the same clinical constraints as the planner’s plan in all cases.
Table 5.
Median differences between ROCO plans and plans produced by treatment planners. D* is a target or organ dose normalized by the prescription dose (for PTVs) or clinical constraints (for organs); see text. Positive values of D* indicate either improved dose homogeneity in the PTVs, or better sparing of the OARs in ROCO plans, when compared to the treatment planner’s plans. Significance was evaluated with the Wilcoxon signed-rank test; for ROCO, the median difference in doses to targets and organs was not significantly different from the treatment planner’s.
| Structure | Median D*(%) | P < 0.1? |
|---|---|---|
| PTV Dmax | −0.9 | No |
| PTV Dmin | 0.2 | No |
| Lung | −0.9 | No |
| Cord Dmax | −1.5 | No |
| Esophagus | 0.0 | No |
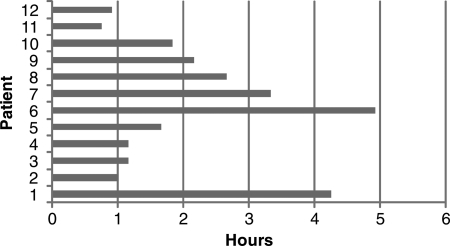
These plans were generated in a short time, requiring around 30 min of CPU time. In contrast, treatment planners using conventional IMRT optimization required around 3 h for the same task, which is an important amount of time in a busy clinic. ROCO can thus save a great deal of planner time: assuming that each readjustment-reoptimization cycle requires 10 min for a treatment planner to complete, Fig. 7 shows that ROCO saves a median of 1.75 h.
Figure 7.
Time saved by ROCO. ROCO requires about 30 min (unsupervised) to compute a treatment plan. This plot shows the time saved assuming that each adjustment-reoptimization cycle undertaken by the planner takes 10 min. The median time saved is 105 min.
ROCO plans have spared the OARs as well as the treatment planner’s plans have, but as we can see from Fig. 5, the PCA modes from which the ROCO plans are constructed cannot be used to completely reconstruct the clinical plan: 10%–20% of the intensity profile that the treatment planners use lies outside of the space spanned by these modes. However, the clinical plan should not be viewed as a “ground truth” correct answer; several authors have noted a high degree of degeneracy in IMRT plans, which result in similar objective function values but different clinical tradeoffs.26 We conjecture that the degree of this degeneracy is greater for lung patients than for prostate patients, because our PCA modes are not able to represent the clinical plan as well: the value of the projection residual R [see Eq. 8 and Fig. 5] is much larger in the current study than it was found to be for prostate patients, where fewer than 25 modes sufficed to bring the projection residual to less than 1%. ROCO does not guarantee the generation of an optimal intensity distribution (e.g., the Iopt defined in Sec. 2); rather, ROCO generates a treatment plan that satisfies the specified constraints while optimizing PTV coverage for specified targets.
DISCUSSION AND CONCLUSIONS
In this paper, we extended our previous work on ROCO in several important ways. First, we applied ROCO to a more complicated treatment site: the lung rather than the prostate, and showed that the same general algorithmic strategy produced clinically acceptable plans. We analyzed tradeoffs in sampling and dimensionality reduction and showed that acceptable plans could be obtained in about 30 min, a major time savings over the manual trial-and-error process of unconstrained optimization. ROCO plans satisfy all of the clinical constraints that were satisfied by the planner’s plans; with the same PTV D95, there were no significant differences between the OAR sparing achieved by ROCO and the organ sparing achieved by the clinical plans. From these results, we are confident that ROCO will be flexible enough for general external beam radiation therapy planning, and is not confined to simpler treatments such as prostate cancer.
A major improvement we made to ROCO in our current work is our incorporation of ROCO into MSKCC’s clinical treatment planning system. ROCO is now capable of reading and writing beam and dose information directly to∕from the treatment planning system. Most importantly, ROCO uses the clinical full dose calculation to evaluate the dose distributions corresponding to each PCA mode. Using an approximate truncated dose kernel resulted in an inaccurate dose calculation, which proved to be a major difficulty in our previous work.
Ideally, ROCO would return a solution satisfying the specified hard constraints if any such feasible solution exists, and a satisfactory plan would result. In clinical practice, some iterative modification of parameters is inevitable: the notion of clinical acceptability—which varies from clinic to clinic or even planner to planner—is extremely difficult to pose either as an objective function or a hard constraint. In the future, we need to develop new constraints (e.g., rind-type structures to suppress hot spots in normal tissue) or objective function terms (e.g., to try and bias the solution towards more uniform PTV coverage).
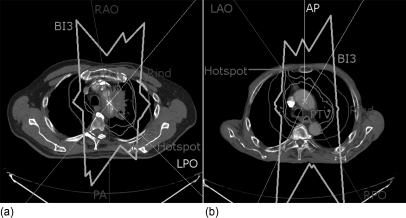
Three patients (9, 10, and 12), which required the use of a larger rind to protect the tissue outside of the PTV, have highlighted the issue of nonspecific normal tissue constraints in ROCO. The doses to the hot spots in these patients were approximately 95% of the prescription dose, which did not violate the explicit 110% limit. Rather, the treatment planner felt that they violated the conformality requirement. In each case, the hot spot appeared in the chest wall near the intersection of two beam edges, which was far enough outside of the PTV that it was not covered by the 3 cm rind, and it was necessary to use a larger rind to produce a clinically acceptable plan. Because the hotspots appeared in areas covered by at least three beams, this suggested a strategy that might be used in the future to generate rinds to deal with this problem. This is illustrated in Fig. 8, in which transverse slices of patients 10 and 12 are shown. The “BI3” line shows a structure that includes the volume within the patient that is covered by at least three beams; this structure includes the hot spots in each case, and could be defined as a standardized rind for future cases. Note that in these patients, the planner chose beam arrangements that have (close to) parallel-opposed fields in an effort to spare healthy lung tissue. The resulting BI3 has a large volume, which suggests that planners should be alert to the possibilty of distant hot spots when such arrangements are used.
Figure 8.
Transverse slices of patients 10 (left) and 12 (right). The thin lines from the edges of the panels show the central axis of the treatment beams chosen by the planner, and the three beams that contribute to the hot spot in each case are labeled. The PTV and 3 cm rind structures are labeled, and the 95% isodose line is also shown. Both of these patients (as well as patient 9) had a hot spot in the chest wall, which was far enough outside of the PTV that it was not covered by the 3 cm rind. The thick line labeled “BI3” shows the area that includes at least three beams; in each case, the hot spot lies inside this region.
The key advantage of ROCO with respect to the trial-and-error loop typical of conventional soft-constrained IMRT is that the normal tissue constraints can be posed and a solution found within a few minutes. This is true because the time-consuming parameter-sampling step to generate the PCA vectors is only done once, independent of the constraints; the constrained optimization is performed quickly in the low-dimensional space, and the new solution, if one exists, is guaranteed to satisfy the constraints. This makes any trial-and-error much less tedious and the control over the solution much more direct.
Improving planner time savings is one of the primary goals of our future work with ROCO. We plan to apply ROCO to head and neck cancer, which remains a challenging site for current IMRT planning techniques: because of the complexity of dose-painting and the large number of OARs in treatment fields, head and neck plans can require days of planner time, and even then the space of clinical tradeoffs between OAR sparing and target coverage may not have been fully explored. ROCO will be able to improve these limitations by reducing the time it takes to obtain a plan that satisfies clinical constraints.
ACKNOWLEDGMENTS
This publication was supported in part by Grant No. 1R01CA148876 from the National Cancer Institute (NCI), a grant from Varian Medical Systems, and by a private donor to Rensselaer Polytechnic Institute. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Cancer Institute, National Institutes of Health. The authors would like to thank Gig Mageras, Perry Zhang, Joseph McNamara, Howard Amols, Margie Hunt, and Chen Chui for helpful discussions.
References
- Zelefsky M. J., Reuter V. E., Fuks Z., Scardino P., and Shippy A., “Influence of local tumor control on distant metastases and cancer related mortality after external beam radiotherapy for prostate cancer,” J. Urol. (Baltimore) 179, 1368–1373 (2008). 10.1016/j.juro.2007.11.063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuban D. A., Tucker S. L., Dong L., Starkschall G., Huang E. H., Cheung M. R., Lee A. K., and Pollack A., “Long-term results of the M. D. Anderson randomized dose-escalation trial for prostate cancer,” Int. J. Radiat. Oncol., Biol., Phys. 70, 67–74 (2008). 10.1016/j.ijrobp.2007.06.054 [DOI] [PubMed] [Google Scholar]
- Yom S. S., Liao Z., Liu H. H., Tucker S. L., Hu C.-S., Wei X., Wang X., Wang S., Mohan R., Cox J. D., and Komaki R., “Initial evaluation of treatment-related pneumonitis in advanced-stage non-small-cell lung cancer patients treated with concurrent chemotherapy and intensity-modulated radiotherapy,” Int. J. Radiat. Oncol., Biol. Phys. 68, 94–102 (2007). 10.1016/j.ijrobp.2006.12.031 [DOI] [PubMed] [Google Scholar]
- Lu R., Radke R., Happersett L., Yang J., Chui C., Yorke E., and Jackson A., “Reduced-order constrained optimization in IMRT planning,” Phys. Med. Biol. 53, 6749–6766 (2008). 10.1088/0031-9155/53/23/007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Society A. C., “Cancer facts and figures 2010,” http://www.cancer.org/acs/groups/content/@epidemiologysurveilance/documents/document/acspc-026238.pdf (2010).
- Ling C. C.et al. , A Practical Guide to Intensity-Modulated Radiation Therapy (Medical Physics Publishing, Madison, WI, 2004). [Google Scholar]
- Yorke E., Jackson A., Braban L., Rosenzweig K., and Ling C., “Advantages of IMRT for dose escalation in radiation therapy for lung cancer [abstract],” Med. Phys. 28, 1291 (2001). [Google Scholar]
- Kessler M. L., Mcshan D. L., Epelman M. A., Vineberg K. A., Eisbruch A., Lawrence T. S., and Fraass B. A., “Costlets: A generalized approach to cost functions for automated optimization of IMRT treatment plans,” Optim. Eng. 6, 421–448 (2005). 10.1007/s11081-005-2066-2 [DOI] [Google Scholar]
- Wu Q., Mohan R., Niemierko A., and Schmidt-Ullrich R., “Optimization of intensity-modulated radiotherapy plans based on the equivalent uniform dose,” Int. J. Radiat. Oncol., Biol. Phys. 52, 224–235 (2002). 10.1016/S0360-3016(01)02585-8 [DOI] [PubMed] [Google Scholar]
- Spirou S. V. and Chui C. S., “A gradient inverse planning algorithm with dose-volume constraints,” Med. Phys. 25, 321–333 (1998). 10.1118/1.598202 [DOI] [PubMed] [Google Scholar]
- Purdy J. et al. , “Intensity-modulated radiotherapy: current status and issues of interest,” Int. J. Radiat. Oncol., Biol. Phys. 51, 880–914 (2001). 10.1016/S0360-3016(01)01749-7 [DOI] [PubMed] [Google Scholar]
- Webb S., Intensity-Modulated Radiation Therapy (Taylor & Francis, London, 2001). [Google Scholar]
- Bedford J. L. and Webb S., “Elimination of importance factors for clinically accurate selection of beam orientations, beam weights, and wedge angles in conformal radiation therapy,” Med. Phys. 30, 1788–1804 (2003). 10.1118/1.1582471 [DOI] [PubMed] [Google Scholar]
- Samuelsson A. and Johansson K., “Intensity modulated radiotherapy treatment planning for dynamic multileaf collimator delivery: influence of different parameters on dose distributions,” Radiother. Oncol. 66, 19–28 (2003). 10.1016/S0167-8140(02)00264-5 [DOI] [PubMed] [Google Scholar]
- Starkschall G., Pollack A., and Stevens C. W., “Treatment planning using a dose-volume feasibility search algorithm,” Int. J. Radiat. Oncol., Biol. Phys. 49, 1419–1427 (2001). 10.1016/S0360-3016(00)01547-9 [DOI] [PubMed] [Google Scholar]
- Bortfeld T., Küfer K.-H., Monz M., Trofimov A., and Niemierko A., “Problems with current IMRT prescription practices and planning systems [abstract],” Med. Phys. 31, 1761 (2004). [Google Scholar]
- Lu R., Radke R. J., Happersett L., Yang J., Chui C.-S., Yorke E., and Jackson A., “Reduced-order parameter optimization for simplifying prostate IMRT planning,” Phys. Med. Biol. 52, 849 (2007). 10.1088/0031-9155/52/3/022 [DOI] [PubMed] [Google Scholar]
- Lee E. K., Fox T., and Crocker I., “Integer programming applied to intensity-modulated radiation therapy treatment planning,” Ann. Oper. Res. 119, 165–181 (2003). 10.1023/A:1022938707934 [DOI] [Google Scholar]
- Halabi T., Craft D., and Bortfeld T., “Dose-volume objectives in multi-criteria optimization,” Phys. Med. Biol. 51, 3809 (2006). 10.1088/0031-9155/51/15/014 [DOI] [PubMed] [Google Scholar]
- Spalke T., Craft D., and Bortfeld T., “Analyzing the main trade-offs in multiobjective radiation therapy treatment planning databases,” Phys. Med. Biol. 54, 3741 (2009). 10.1088/0031-9155/54/12/009 [DOI] [PubMed] [Google Scholar]
- Mohan R., Barest G., Brewster L. J., Chui C. S., Kutcher G. J., Laughlin J. S., and Fuks Z., “A comprehensive three-dimensional radiation treatment planning system,” Int. J. Radiat. Oncol., Biol. Phys. 15, 481–495 (1988). 10.1016/S0360-3016(98)90033-5 [DOI] [PubMed] [Google Scholar]
- Lyman J., “Complication probability as assessed from dose-volume histograms,” Radiat. Res. 104, S13–S19 (1985). 10.2307/3576626 [DOI] [PubMed] [Google Scholar]
- Burman C., Kutcher G., Emami B., and Goitein M., “Fitting of normal tissue tolerance data to an analytic function,” Int. J. Radiat. Oncol., Biol. Phys. 21, 123–135 (1991). 10.1016/0360-3016(91)90172-Z [DOI] [PubMed] [Google Scholar]
- Wang X.-H., Mohan R., Jackson A., Leibel S. A., Fuks Z., and Ling C. C., “Optimization of intensity-modulated 3d conformal treatment plans based on biological indices,” Radiother. Oncol. 37, 140–152 (1995). 10.1016/0167-8140(95)01636-U [DOI] [PubMed] [Google Scholar]
- Wu Q., Manning M., Schmidt -Ullrich R., and Mohan R., “The potential for sparing of parotids and escalation of biologically effective dose with intensity-modulated radiation treatments of head and neck cancers: a treatment design study,” Int. J. Radiat. Oncol., Biol. Phys. 46, 195–205 (2000). 10.1016/S0360-3016(99)00304-1 [DOI] [PubMed] [Google Scholar]
- Alber M., Meedt G., Nüsslin F., and Reemtsen R., “On the degeneracy of the IMRT optimization problem,” Med. Phys. 29, 2584–2589 (2002). 10.1118/1.1500402 [DOI] [PubMed] [Google Scholar]
- Saltelli A., Tarantola S., Campolongo F., and Ratto M., Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models (Wiley, New York, 2004). [Google Scholar]
- Shawe-Taylor J., Kernel Methods for Pattern Analysis (Cambridge University Press, New York, NY, 2004). [Google Scholar]
- Menhel J., Levin D., Alezra D., Symon Z., and Pfeffer R., “Assessing the quality of conformal treatment planning: a new tool for quantitative comparison,” Phys. Med. Biol. 51, 5363 (2006). 10.1088/0031-9155/51/20/019 [DOI] [PubMed] [Google Scholar]
- Feuvret L., Nol G., Mazeron J.-J., and Bey P., “Conformity index: A review,” Int J. Radiat. Oncol., Biol. Phys. 64, 333–342 (2006). 10.1016/j.ijrobp.2005.09.028 [DOI] [PubMed] [Google Scholar]
- Leung L. H. T., Kan M. W. K., Cheng A. C. K., Wong W. K. H., and Yau C. C., “A new dose-volume-based plan quality index for IMRT plan comparison,” Radiother. Oncol. 85, 407–417 (2007). 10.1016/j.radonc.2007.10.018 [DOI] [PubMed] [Google Scholar]
- Tang G., Earl M. A., Luan S., Wang C., Mohiuddin M. M., and Yu C. X., “Comparing radiation treatments using intensity-modulated beams, multiple arcs, and single arcs,” Int. J. Radiat. Oncol., Biol. Phys. 76, 1554–1562 (2010). 10.1016/j.ijrobp.2009.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher L. and van Belle G., Biostatistics: A Methodology for the Health Sciences (Wiley-Interscience, New York, NY, 1939). [Google Scholar]