Use of RNA structure flexibility data in nanostructure modeling

Abstract

In the emerging field of RNA-based nanotechnology there is a need for automation of the structure design process. Our goal is to develop computer methods for aiding in this process. Towards that end, we created the RNAJunction database, which is a repository of RNA junctions, i.e. internal, multi-branch and kissing loops with emanating stem stubs, extracted from the larger RNA structures stored in the PDB database. These junctions can be used as building blocks for nanostructures. Two programs developed in our laboratory, NanoTiler and RNA2D3D, can combine such building blocks with idealized fragments of A-form helices to produce desired 3D nanostructures. Initially, the building blocks are treated as rigid objects and the resulting geometry is tested against the design objectives. Experimental data, however, shows that RNA accommodates its shape to the constraints of larger structural contexts. Therefore we are adding analysis of the flexibility of our building blocks to the full design process. Here we present an example of RNA-based nanostructure design, putting emphasis on the need to characterize the structural flexibility of the building blocks to induce ring closure in the automated exploration. We focus on the use of kissing loops (KL) in nanostructure design, since they have been shown to play an important role in RNA self-assembly. By using an experimentally proven system, the RNA tectosquare, we show that considering the flexibility of the KLs as well as distortions of helical regions may be necessary to achieve a realistic design.

1. Introduction

Nucleic acids, DNA and RNA, have been established as versatile building materials for programmable self-assembling nanostructures. We do not intend to review DNA nanotechnology here, but we would like to direct readers interested in that topic to see the review written by the pioneer of the field and use it as a gateway to the rich literature on the subject [1]. RNA is a very versatile molecule, which can serve as an information storage medium as well as a functional agent, as exemplified by aptamers, siRNAs, riboswitches or ribozymes. It can naturally fold into complex structures. This can be viewed as a process of structural self-assembly controlled by the base pairing of the primary sequence into secondary structure, further stabilized by higher order interactions (tertiary interactions, pseudoknots, kissing-loops, stem stacking) [2–4]. What is more, multiple RNA chains may interact to form larger structures. Thus RNA has the potential to be programmed into a self-assembling therapeutic agent, potentially environment-triggered, to affect the targeted cells when and only when disease conditions are present. Combinations of siRNA and aptamers or other functional agents may be fine tuned to that effect [5]. While the ultimate goal is the development of smart agents capable of disrupting oncogenic or disease pathways, there are many engineering issues associated with the design of self-assembling nano-scale structures. The RNA-based designs described in the literature and the experimentally verified RNA nanostructure examples point to the potential benefits of using computer assistance in the process [3,6–22]. A recent review of RNA-based nanotechnology summarizes nanostructure design and building strategies and discusses potential applications in nanomedicine and challenges remaining on the road to RNA-based therapeutics [23].

As a first step, we have developed a database of potential RNA building blocks extracted from experimentally obtained structures (NMR, X-ray crystallography, cryo-EM) deposited in the PDB database [24]. This RNAJunction database stores RNA junctions, i.e. internal and multi-branch loops, as well as kissing-loops (i.e. fragments with hairpin loop-loop interactions between two chains) with short stem fragments emanating from them. Some of these junctions have been shown to have very specific topological properties [25]. These junctions can be used as building blocks for larger nanostructures. Currently there are on the order of 13,000 entries in the database, both in the form extracted from the larger structural context as well as energy minimized, which was a first step to screen for potential changes in the junctions removed from their larger structural contexts. One of the most useful features from the nanostructure design point of view is the ability to query the database for junctions based on the angles between the emanating stems. Further characterization of all these building blocks is a daunting task, and was left to be considered in specific cases of the most promising building blocks. We will discuss this issue in this paper based on a specific design study.

The RNA-based structure design methodology we are pursuing starts with combining a selection of RNA junctions with idealized helices used as linkers to achieve the designed structure shape (geometry). One approach is to take what building blocks are available in the experimentally solved RNA structures, treating them as static junction points of a shape under design and to link them with idealized helices or single strands. One cannot expect a perfect geometric fit in the majority of cases, and some degree of distortion in the linking helices or the junctions may need to be introduced to connect all the blocks [26]. Following such a procedure, the full structure should be “relaxed” via the use of molecular mechanics and dynamics, which, depending on the size of the designed structure can be computationally intensive and time consuming. Another option is to consider the flexibility of the junction building blocks as well as the linkers. One can explore the geometry and potential flexibility ranges of elements used in nano-scale designs by reviewing the experimental structures, such as, for example, alternative NMR structures, if the data is available. In the case of tectosquare modeling which is the subject of this article, and an example of a class of closed ring structures, both the X-ray crystallography based structures (PDB:2B8R) and NMR based structures (PDB:2F4X) are available for the kissing loop elements crucial to the design. We discuss the results of this approach in Section 4.2. Such structures may not directly affect a closure of a designed ring shape. Therefore subjecting them to molecular dynamics (MD) simulations to see if their dynamic states can achieve a closure of the design is desirable. In general, even if the design appears to be geometrically compatible with the building blocks extracted from experimental structures, it is prudent to evaluate the stability of the full structure by explicit molecular dynamics or coarse-grained methods. Thus the building blocks taken from a database and subassemblies of larger structures, which may combine the experimental and idealized elements, can be characterized before the full assembly is tested by joining all the elements together.

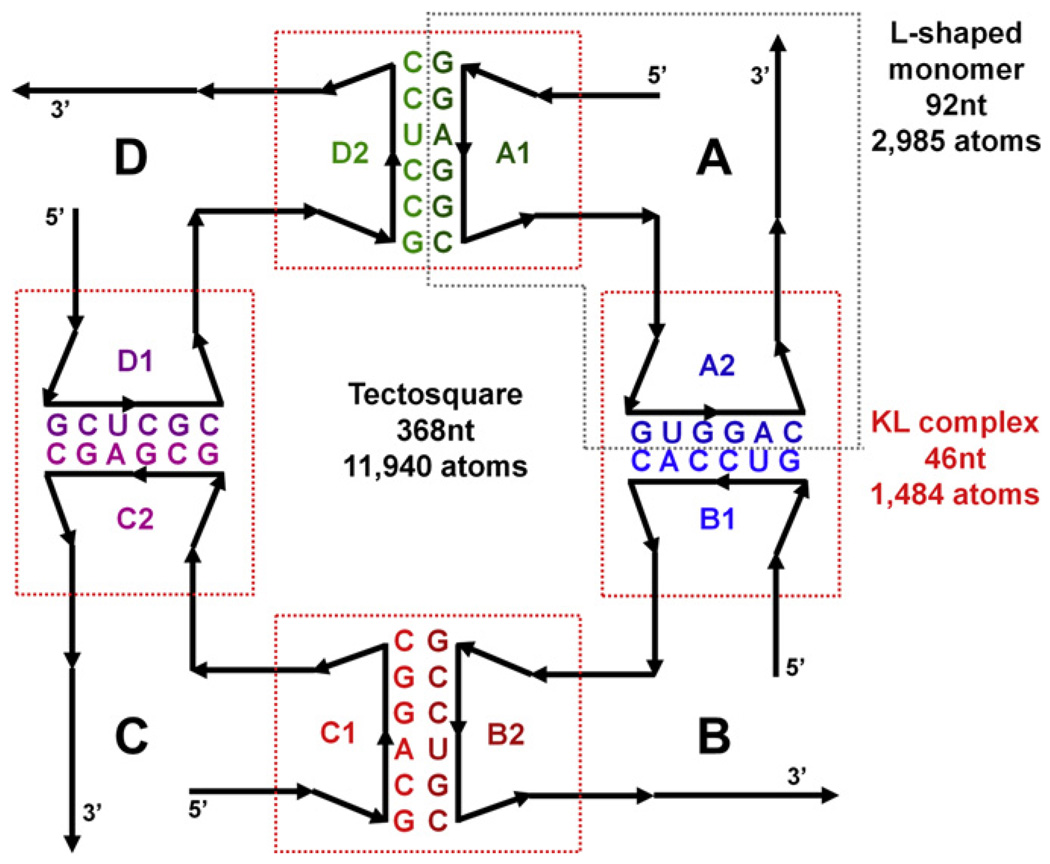
For this study of methodological approaches we have selected a tectosquare design [15] as a positive test of an experimentally verified nanostructure, which presented unique modeling problems. The basic idea of the design is illustrated in a cartoon form in Fig. 1. Four identical L-shaped monomers (called tectoRNAs in the original publication) maintaining a right angle by incorporating a junction from the large ribosomal subunit of Haloarcula marismortui (PDB: 1JJ2) are connected via kissing loops adapted from the HIV-1 kissing loop (KL) complex (PDB: 2B8R), but reprogrammed (mutated) to yield unique hairpin-to-hairpin interactions. A goal is to control the orientation of the single-stranded 3′ tails, which can pair with uniquely programmed 3′ tails of other tectosquares to form meshes of designed patterns. Different types of tectosquares have different orientations of the 3′ tails. The one shown in Fig. 1 is of type V, design LT17, with two 15 base pair long helices in each L-shaped monomer.

Fig. 1.

A 2D cartoon representation of a tectosquare design (type V). The full tectosquare is an assembly of four L-shaped monomers, labeled A through D, connected with each other via the engineered HIV-1 kissing loop structures. The kissing loop sequences (color-coded in the same way throughout all the figures) were mutated to assure unique interactions and control of the orientations of the 3′ tails, which facilitate interactions with other tectosquares. The right angles within each L-shaped monomer incorporate a right angle junction extracted from the PDB structure 1JJ2 (see the text). Loop labels within each monomer indicate the hairpins at the end of the 5′ and 3′ helical arms of each monomer. Thus the A1-D2 interaction indicates the pairing of the 5′ H-loop from monomer A with the 3′ H-loop from monomer D. This labeling scheme is used in all the figures. The dashed-line boxes indicate the elements of the tectosquare subjected to MD simulations; red boxes for the four kissing loop complexes and the gray box for the monomer A.

Modeling by utilizing RNA junctions combined with idealized helices or idealized kissing loops yielded structures which would not close the full tectosquare, (see Fig. 2, Fig. 3A and refer to Section 4.2). Given that a full LT17 tectosquare is built out of 368 nucleotides (11,940 atoms, without any solvent considerations), but it is a modular design, we subdivided further characterization of the dynamic characteristics of its building blocks into smaller sub-problems upon which the full tectosquare dynamic characteristics could be assessed (approximated). Thus we performed molecular dynamics simulations on one full L-shaped monomer (92nt) and four reprogrammed KL complexes (46nt each), which is also indicated in Fig. 1. Several approaches to characterization of the flexibility of the building blocks and ways of assembling them together into closed tectosquare structures are discussed in this paper. First, we show how to use an idealized model to estimate the extent of flexibility needed to achieve full structure closure. Next, guided by these parameters, we analyze MD data and show which elements contribute most to the overall structure flexibility. Finally, we illustrate approaches to automated searching for dynamic states yielding full nanostructure closure with the emphasis on reducing the combinatorics of the applied search methods.

Fig. 2.

An overview of the modeling methodology including flexibility data from MD simulations and optional helical linkers subject to controlled distortions. RNA building blocks obtained from a structural database, such as RNAJunction or PDB, are used to build a rigid model of a nanoparticle. In case the full structure model does not close, the junctions used and/or subassemblies of the full nanostructure can be subjected to Molecular dynamics (MD) simulations in order to characterize their flexibility. One can also explore the structural parameters required to affect closure with the help of a program such as RNA2D3D, using the results as parameters in searches for MD states of the building blocks that could assemble into a fully closed structure (bottom left and Fig. 7A). Combinatorial searches can be utilized to explore the entire set of MD trajectories of the building blocks (with or without any parameter constraints) in order to find structure closing combinations (bottom center and Fig. 8). The most flexible approach combines the MD states of junctions or subassemblies with the linker helices which can be distorted independently of the MD states, but within the MD-indicated range of distortions, in order to affect full nanostructure closure (bottom right and Fig. 9). The last two closure search schemes were accomplished with PyMOL and NanoTiler scripts.

Fig. 3.

Modeling the LT17 type V tectosquare with RNA2D3D. The tectosquare is built out of four L-shaped monomers with the shaped H-loops and PDB-based RA motifs (1JJ2-50S ribosomal unit of Haloarcula marismortui). Full structure connectivity is specified in a topology script file. (A) The initial model does not close the tectosquare. (B) Adding 1 base pair to every 5′ ideal A-form helix of every L-shaped monomer induces effective rotation of every tectosquare side and causes the A1 and D2 H-loops to move past each other. (C) Co-axial rotation of each side (via the 5′ arm) by +22° brings the A1 and D2 H-loops into coaxial orientation and closes the full tectosquare structure. One L-shaped monomer modified in this way can then be used as a reference structure in search for the equivalent dynamic states of an unmodified monomer subjected to molecular dynamics simulation.

The overview of the methodology (with variants) used in this study is shown in Fig. 2. Approaches leading to the three models illustrated at the bottom of this figure are presented in the text.

2. RNA structure modeling tools

RNA2D3D is a 2D to 3D RNA structure modeling program with some nano-design capabilities [27]. It takes a sequence and a secondary structure representation (including pseudoknots) and rapidly generates a first-pass, three-dimensional model by converting base-paired regions into standard A-form helices (automatically stacked in the case of pseudoknots). Further refinements can be performed interactively by a large set of tools facilitating structural adjustments and refinements via molecular mechanics and dynamics. Two features that were utilized in modeling of the tectosquare building blocks (monomers) were the ability to substitute parts of the modeled structure with known structural elements from a database and the loop shaping option that extends helix geometry into a loop from its 3′ end up to a user-selected position within it. Such shaped loops can be used to model idealized kissing loops via interactive base-pairing options or via topology file commands. This facilitates the building of multi-chain RNA assemblies, such as tectosquares or tectosquare meshes [15,17,27]. Once connected into a nanostructure, further manipulations of individual building blocks are applied symmetrically to all the other monomers. The symmetric nature of the tectosquare designs lends itself well to such modeling actions.

The NanoTiler program was specifically built for RNA nanostructure design, implementing the design philosophy outlined in Section 1 [26]. It can utilize junctions and kissing loops from the RNAJunction DB and other sources or generate artificial junctions to fulfill design constraints [22]. Given a target topology and a set of junctions, this program can attempt to fit linking helices between the junctions to form the specified shape. Distortions in the linking helices may be introduced if the use of the ideal A-form helices doesn’t produce the desired result. A “distortion score” is returned as a measure of the design quality. The score is based on the distance of a gap (or multiple gaps) that needs to be closed and, ultimately on the distance and the angle differences which need to be applied as distortions to linker helices. NanoTiler can also generate structures using combinatorial search among junctions and connecting helices to explore, for example, which combinations yield closed ring structures. It is capable of performing 3D nucleotide mutations based on substitutions of idealized helix nucleotides or best matches from a selection of experimental structures. It can also perform sequence optimization for the design of self-assembling structures. It offers a graphical user interface mode and a scripting language interpreter. This last capability was used to perform automated surveys of the studied tectosquare building block elements subjected to MD simulations and mated together with the aim of producing a closed nano-scale structure.

A molecular visualization system PyMOL was used to produce all the 3D figures shown in this paper (http://www.pymol.org/). The ability to extend its functionality via scripting was employed to assemble tectosquare models from various building blocks, including the molecular dynamics states of the kissing loops and the L-shaped monomers.

3. Methods

3.1. Modeling

Tectosquare LT17 monomers (A3s, B1s, C8s, D6s), each 92nt in size, were modeled in RNA2D3D true to the LT17 tectosquare sequence design [15], with the 5′ and 3′ helices 15 base-pairs long. The right angle (RA) motif (PDB: 1JJ2) was incorporated to form a log-cabin like corner piece, as indicated in the original publication. The hairpin loops at the end of each helical arm of the monomer were shaped using the RNA2D3D tool described in Section 2. Adding the experimentally determined kissing loop structures (PDB: 2B8R and 2F4X) did not produce closed nanostructures, as is explained in Section 4.2. The exploratory tectosquare modeling using the L-shaped monomers and the idealized kissing loops showed that such a model does not achieve full structure closure either (see Fig. 3A). On the other hand, by using RNA2D3D to create the tectosquare model, we could easily probe the closure issue further by symmetrically applying deformations to the sides of the structure. The flexibility required to affect closure was found to be less than the geometric modification to the design resulting from the addition of one base pair to each side, one of the features available in RNA2D3D (see Fig. 3B). A more precise way of assessing the closure requirements without adding new base-pairs is to apply rotations to the sides of the tectosquare. Co-axial rotations by +22° applied to each side demonstrated full structure closure (see Fig. 3C). A single L-shaped monomer structure modified in this way was then used as a reference structure in the exploration of the MD trajectory computed for an idealized monomer (i.e. one without any rotational modifications) to see if the MD simulation contains states equivalent to the reference structure, based on the RMSD between the reference and the MD states (see Section 4.1 for details).

3.2. Molecular dynamics simulations

The X-ray crystallography structure of the HIV-1 kissing loop complex (PDB: 2B8R), 46nt in size, was used as a starting point for the molecular dynamics studies. After it had been subjected to MD simulation, four mutated KLs used in the tectosquare designs were created by editing (3D mutations) the 2B8R MD minimized average structure’s kissing loop sequences. These were then treated as input structures and subjected to the full protocol described below (RNA minimization, equilibration in solvent, and MD production runs). In the mutated KLs the flanking stems were left unchanged from the WT (2B8R) structure, which means that the two base pairs nearest the hairpin loops of the KL complex were the same as those used in the fully designed L-shaped monomer helices. These two matching base pairs were later used as the interface points between the monomers and the kissing loop complexes in the exploration of the full tectosquare assembly (see Section 4.1).

All the MD simulations were performed with Amber 9 and 10, utilizing the Cornell force field for RNA, and the Particle Mesh Ewald summation method to calculate the electrostatic interactions [28–30]. The non-bonded interactions were truncated at 9 Å. RNA backbone phosphate charges in all the contiguous chains of length n were neutralized by the addition of n-1 Na⁺ ions. For the kissing loop complexes consisting of two chains that meant 44 Na⁺ neutralizing ions for the combined chain length of 46nt. Neutralized RNA molecules were placed in solvent boxes with explicit TIP3P water molecules and additional Na⁺/Cl⁻ ion pairs added to solvate the system to a 0.1 mol/L relative salt concentration. Prior to solvation the RNAs were subjected to energy minimization runs, and the minimized molecules were then solvated as described above. The equilibration protocol consisted of multiple stages in which the constraints on the RNA were initially imposed to equilibrate the solvent and then slowly released to equilibrate the whole system at 300 K, at which temperature it was maintained throughout all the MD runs using the Berendsen thermostat [31]. SHAKE was applied to all hydrogen bonds in the system. Pressure was maintained at 1.0 Pa using the Berendsen algorithm [31], and a periodic boundary condition was imposed. Following the equilibration, the production simulation was performed for 20 to 30 ns, depending on the molecule size, all with a 2 fs time step. While they differ in small details, all the kissing loop MD runs were performed for the systems (RNA of 46nt and solvent) of approximately 42,000 atoms enclosed in solvent boxes with the clearance distance of 15 Å (the minimum distance between the solute and the solvent box wall, also known as “buffer” in Amber), all approximately 79 Å by 100 Å by 70 Å in size. The L-shaped monomer system (RNA of 92nt and solvent) was 73,624 atoms in size, and was enclosed in a solvent box with a 10 Å buffer distance, adding up to a total size of 100 Å by 98 Å by 91 Å. Analyses of the MD results were performed with the ptraj module of the Amber package, and they excluded the equilibration stage results.

Additional MD simulations assessing potential differences between the MD characteristics of the X-ray based KL structure (PDB:2B8R) and the NMR-based structure (PDB:2F4X) were conducted. The X-ray structure was subjected to molecular dynamics with variations in the MD conditions. One run included only the neutralizing Na⁺ and water, and in another run parabolic restraints were imposed on the Watson–Crick hydrogen bonds in the closing base pairs of the kissing loop complex (i.e. the 5′ and 3′ base pairs in both chains). The idea was to examine both the impact of the restraints and the effects of NaCl in solvent on the key measured kissing loop complex characteristics. Also, since the experimental protocols for the construction of the tectosquares included Mg²⁺ ions, we evaluated the impact of them on the overall key flexibility characteristics of the wild type KL. Since the metal ions in 2B8R were reassigned in the PDB structure 1XPE [32], we used it as the wild type KL input structure. Prior to solvation, the 1XPE KL including its two coordinating Mg²⁺ ions was subjected to energy minimization. RNA backbone phosphate charges were neutralized by the addition of 40 Na+ counterions. Neutralized RNA molecules were placed in solvent boxes with explicit TIP3P water molecules and Mg²⁺/Cl⁻ ions added to solvate the system to a 0.1 mol/L relative MgCl₂ concentration. The same equilibration protocol as the one described for the 2B8R was applied to 1XPE. Results of these runs are included in Table 1.

Table 1.

Results of molecular dynamics simulations (MD) for the kissing loop complexes of the HIV-1 wild type structures and the mutants derived from it and used in tectosquare design and modeling. The redesigned sequences are listed explicitly in Fig. 1. Mean RMSDs were calculated relative to the starting states of the production MD runs. PDB ids in the parentheses indicate the NMR (2F4X) and X-ray crystallography (1PXE and 2B8R) data used as the starting structures in MD simulations. The MD Conditions column indicates variations in the neutralizing ions and salt conditions. For example, Na⁺; NaCl indicates that sodium ions were used to neutralize phosphate group charges along the backbone and Na⁺/Cl⁻ pairs were added to the solvent. The word “Restraints” indicated parabolic restrains added to the hydrogen bonds of the Watson–Crick base pairs at the 5′ and 3′ ends of each of two chains comprising the KL complex. All MD simulations were performed for approximately 20 ns, with exception of the 25 ns run for the lowest (in the table) WT kissing loop structure, from which all four mutants were derived. Refer to the text for the details of MD protocols and the definitions of the angles listed (Section 3.2 and 4.1).

Kissing loop	MD conditions	Mean RMSD, (Angstrom)	Mean Bending angle	Mean Torsion angle	Min. torsion angle	Max torsion angle
WT HIV-1 (2F4X)	Na+; NaCl	4.8 ± 1.0	139.5 ± 10.4	−8.5 ± 18.9	−57.3	+36.8
WT HIV-1 (1XPE)	Na+ and Mg2+; MgCl2	3.9 ± 0.7	155.8 ± 7.5	20.5 ± 11.6	−15.4	+61.9
WT HIV-1 (2B8R)	Na+; NaCl; Restraints	4.1 ± 1.1	160.1 ± 9.4	14.9 ± 18.1	−40.3	+60.0
WT HIV-1 (2B8R)	Na+ only	5.1 ± 1.1	160.4 ± 9.1	−8.1 ± 14.2	−54.5	+47.9
WT HIV-1 (2B8R)	Na+; NaCl	2.6 ± 0.6	161.3 ± 8.8	−5.7 ± 11.7	−40.2	+44.1
MUT A1D2	Na+; NaCl	2.3 ± 0.6	163.3 ± 10.3	11.4 ± 15.1	−37.2	+51.5
MUT A2B1	Na+; NaCl	2.6 ± 0.5	163.6 ± 7.2	1.8 ± 13.7	−39.0	+46.6
MUT B2C1	Na+; NaCl	2.5 ± 0.6	155.7 ± 11.1	−3.6 ± 11.6	−40.0	+33.3
MUT C2D1	Na+; NaCl	2.8 ± 0.7	154.5 ± 12.7	−11.3 ± 14.7	−48.1	+32.8

3.3. Automated searches for nanostructure closure

The automated assembly of full tectosquares was done with the help of PyMOL and NanoTiler. Using the scripting capability of extending standard PyMOL functions we programmed chain-docking of the L-shaped monomers and the KL complexes, using pair-fit commands which rely on RMSD minimization for best fitting. This is a relatively fast method, taking less than an hour to search an entire 20 ns trajectory (20,000 MD frames) on a PC work station with a 3.0 GHz processor. The potential problem with this method is an accumulation of fitting approximations in the chain of pair-fitting commands. Refer to Section 4.1 for details and to Section 4.3 and Fig. 8 for results.

Fig. 8.

A near-closed tectosquare found in an automated search for such combinations of the building blocks (KL and L-shaped monomers) performed with the aid of PyMOL scripts. Four sets of mutated KL-complexes (green, blue, red, magenta) to be used in the best closure search were selected in preliminary runs (refer to Sections 4.1 and 4.3 for details). These sets of solutions with gaps within 6 Å were then used as input to search for best closures including the dynamic states of L-shaped monomers. In the final phase the best scoring KL and L-shape MD states were used in a search for the best closure combinations. Note that the improvement in the gap score over the parameter-guided search illustrated in Fig. 7 came from a selection of more distorted MD states with lower torsion angles (listed under every KL label). The RMSD values of each fit in the chain assembly are listed next to each side of every KL. The overall improvement in the quality of closure fit over the structure shown in Fig. 7 is best captured in the C2D1 edge view, in which the final gap is seen on the left side of the C2D1 KL complex.

The NanoTiler program was employed to improve on the PyMOL-based automated searches by employing a global optimization of building blocks fits in searches for full structure closure. Briefly, idealized helices were first fit to the selected building blocks (junctions), using optional ideal helix linkers (see Fig. 5), and leaving one gap or a steric clash between the first and the last building blocks. This one gap can be then quantified by a “helix constraint score” and used as a measure of the existing blocks’ quality and/or used further to evenly spread the fitting errors between all the connections. The helix constraint score is generated by computing the largest square distance between the C4′ atoms of the residues that are involved in the final ring closure (assuming a 1-residue overlap between the connecting structural elements). Simulated annealing optimization is applied to all building block positions to minimize the sum of the “helix constraint scores” of the full tectosquare assembly. This score is used to determine the building blocks corresponding to the least amount of structural problems with regard to ring closure. The final refinement of connections adjusts parameters of the linker helices to accommodate small structural errors by applying bending, twisting, compression or stretching to them and connects the junctions and linkers. A sample result of such a full procedure is illustrated in Fig. 2 and 9 and presented in Section 4.3.

Fig. 5.

A 2D cartoon representation of a tectosquare assembly protocol used by NanoTiler. Only two out of four L-shaped monomers are shown. The full tectosquare is built out of the right angle (RA) junctions and kissing loop (KL) complexes (gray boxes) which are connected by idealized linker helices (red arrows and boxes). A linker helix of size 0 may be viewed as a special case where only the RA and KL building blocks are best-fit together. Linker helices are used by NanoTiler to introduce small distortions required to connect all the building blocks together. By default the junctions used in the design are not subjected to any adjustments by the program. Our mating of the MD states of the junctions with the adjustable linkers increases the versatility of the overall approach.

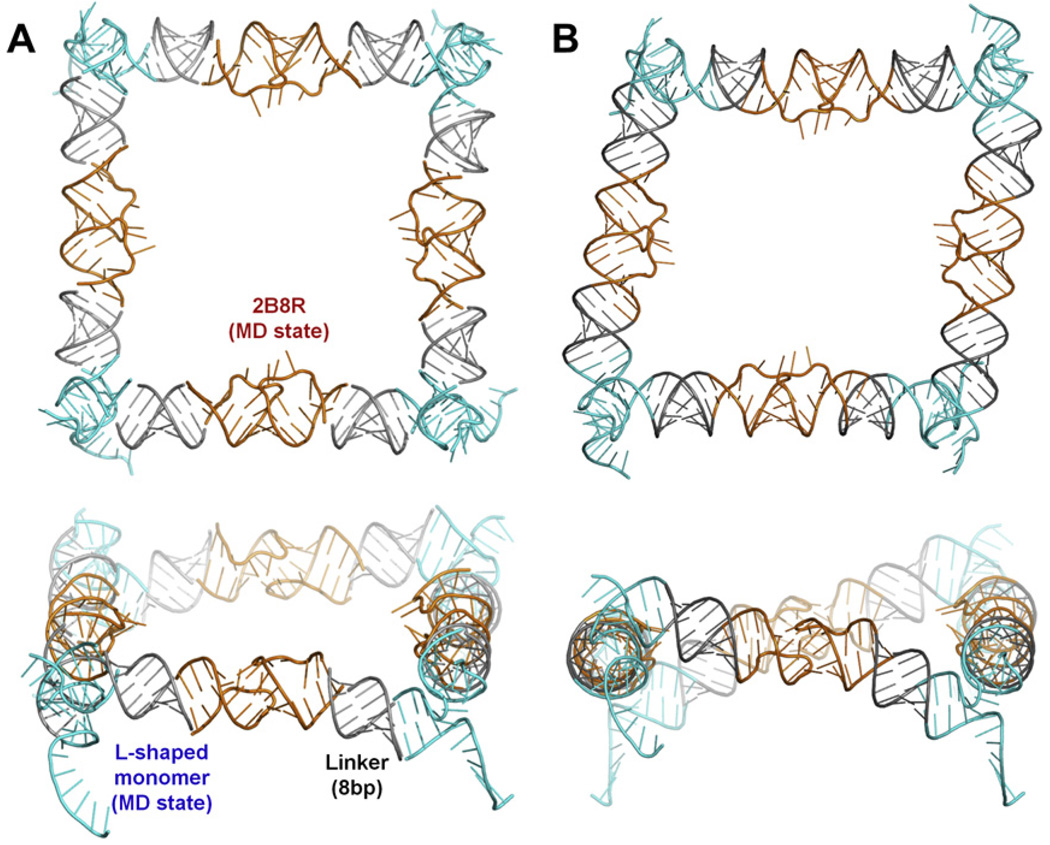
Fig. 9.

A closed tectosquare found in an automated NanoTiler search for KLs and L-shaped monomers linked with idealized helices to form the full structure closure. (A) The HIV-1 wild type kissing loop structure 2B8R (orange) was selected in the first round of searches where four copies of the 2B8R KLs were fit to four copies of idealized L-shaped monomers (created by RNA2D3D). The best scoring 2B8R MD state was then used in a search of the best tectosqure closing states in the L-shaped monomer MD trajectory. The monomers (cyan) were truncated to 4 base pairs in each arm and connected to the KLs via 8 bp long idealized helix linkers (gray). MD frame from the 7.6 ns point in the trajectory was selected (cyan). (B) The structure of the same combinations of the tectosquare building blocks as in A, after distortion of the linker helices performed by the NanoTiler to achieve the best fit, followed by the full structure energy minimization in Amber.

4. Analysis and results

4.1. Analysis

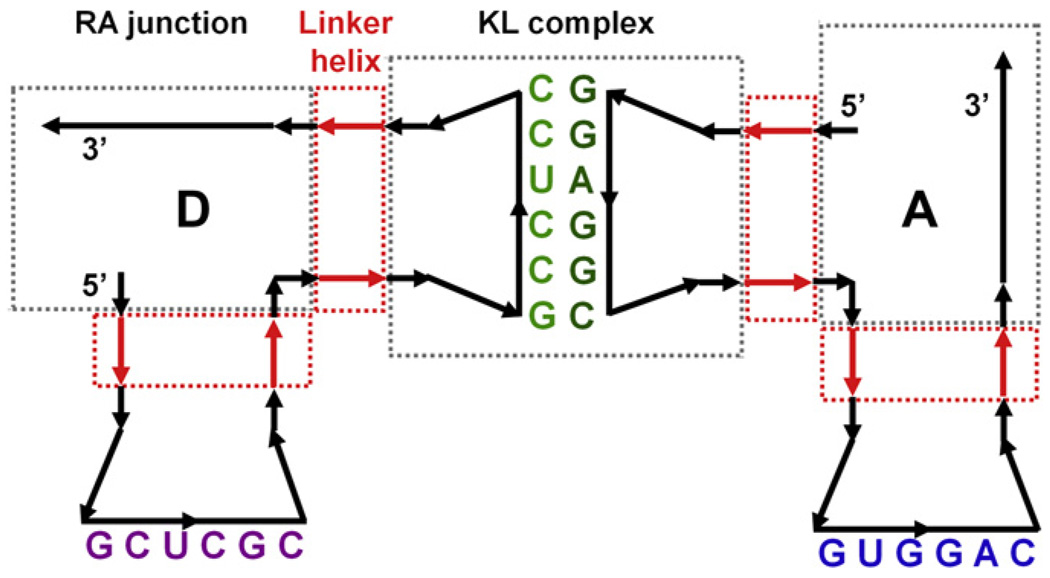
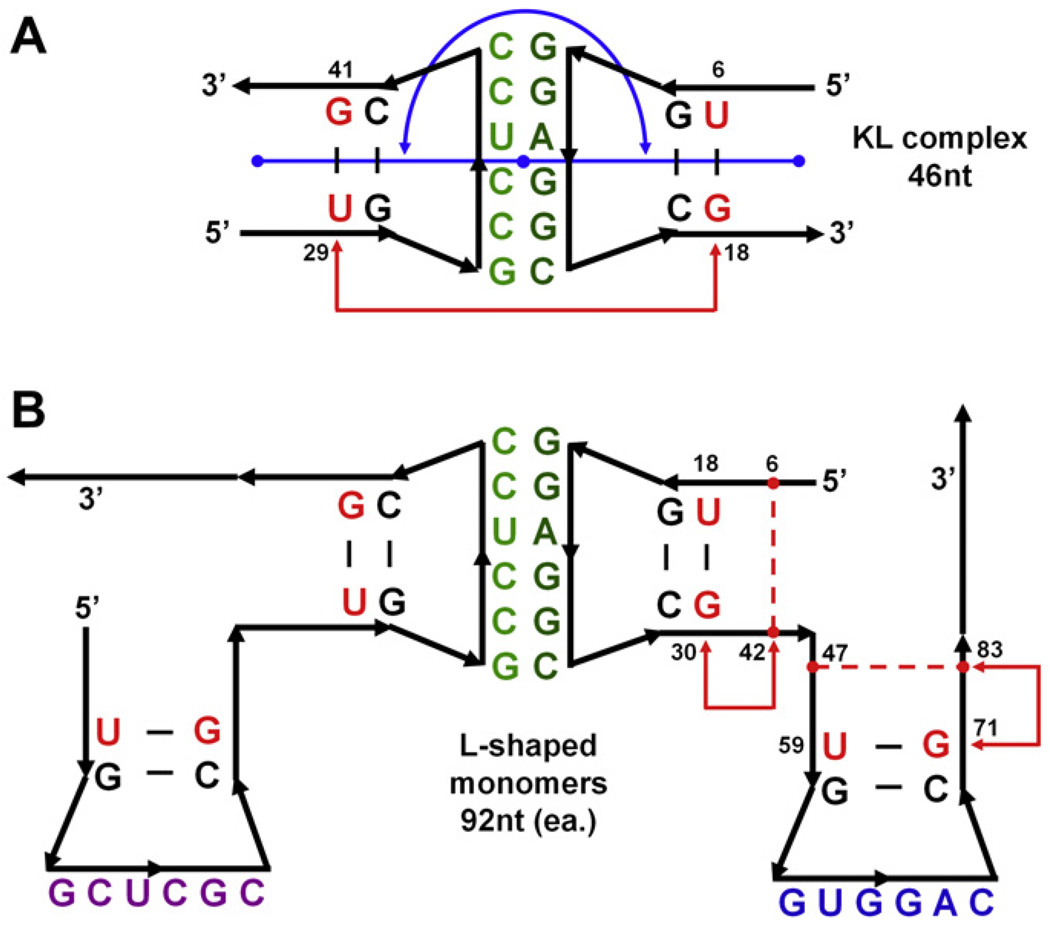
Building full tectosquares from the modules subjected to molecular dynamics required a decision on what the interface points between the modules should be. Based on the observation and the analysis of the results we decided that the regions of the two base pairs nearest to the interacting hairpin loops were subject to the least distortions of their helicity in the kissing loop MD simulations. We measured the dihedral angle variations between the four base pairs nearest to the hairpin loops in the MD simulations of the KL complexes and the L-shaped monomer and determined that they were comparably stable in all the cases (results not shown). Thus from the structural point of view, it is an interface which displays similar dynamic characteristics. Additionally, sequences in the two base pairs closest to the hairpin loops are the same in the KL and monomer simulations. Thus a set of four backbone P atoms in the nucleotides of the second base pairs away from the hairpin loops was selected to be used as the interface between the L-shaped monomers and the KL complexes for the purpose of joining these building blocks into full tectosquares. We will refer to it in the text as the L-KL interface. These are positions 18 and 30, in the 5′ helix, and 59 and 71 in the 3′ helix of the L-shaped monomer (see Fig. 4B). Corresponding interface positions for the KL complexes were adopted, and the dihedral angle measured for these four points across the kissing loop complexes is referred to in the text as the KL torsion angle (see Fig. 4A).

Fig. 4.

2D cartoon representations of tectosquare building blocks subjected to MD simulations. (A) Kissing loop complex, 46nt in two 23nt chains, mutated to match the A1D2 tectosquare interactions. Nucleotide labels indicate helix bases shared between the monomers (B) and kissing loop complexes. Bases highlighted in red indicate the nucleotides used as measuring points for the KL torsion angle (backbone P atoms of nucleotides 6, 18, 28 and 41 – refer to the text). The blue line and arc indicate the KL bending angle measured between the center of mass of the three base pairs at the end of each helix, with the mid-point at the center of mass of the six kissing loop base pairs, all represented with blue dots. (B) Two L-shaped monomers, each 92nt long (one was subjected to MD simulation). Nucleotides highlighted in red correspond to the red-labeled nucleotides in the KL complex (A) and were used as the L-KL interface points in combining the dynamic states of KLs and L-shaped monomers in searches for full structure closure. All the labeled nucleotides (red and black) within the L-shaped monomers and the KLs were used in chain-fitting of these blocks in PyMOL scripts, as described in the text. Red dashed lines and arrows within the two helical arms of the right monomer indicate positions used for the measurements of the helical torsion angles.

The creation of the tectosquare closing reference structure for the L-shaped monomer involved co-axial rotation of one or both of its helices adding up to +22°, relative to the unmodified monomer. Therefore, we monitored the torsional flexibilities of the KL complexes and of the L-shaped monomers’ helical arms. It is much easier and faster to measure and monitor dihedral angles based on specific atom selections than to calculate co-axial rotations in the structural elements distorted by MD simulation. The KL torsion angle was measured across the KL complexes, for positions 6, 18, 29, and 41, in their frame of reference. These correspond to L-KL interface positions 18 and 30 in the 5′ helical arm and positions 59 and 71 in the 3′ helical arm of the two L-shape monomers interacting via a kissing loop (see Fig. 4A). For the L-shaped monomer, the torsion angle changes internal to their arms were measured as dihedrals for the backbone P atoms of nucleotides 6, 42, 30, 18 within its 5′ helix, and nucleotides and 47, 83, 71, 59 in the 3′ helix (refer to Fig. 4B). We verified that the dihedral angle changes measured for these atom selections numerically closely correspond to the co-axial rotation changes despite the differences in the placement of the rotational axes and the dihedral angle edges (refer to Fig. 4). Also, the P atoms used to measure the torsional flexibility of the L-shaped monomers’ arms include positions within the RA motif (6, 42, 47, 83), for which we measured a low RMSD value (1.03 ± 0.14 Å) in the MD runs of the L-shaped monomer. Thus these positions can be used as relatively stable reference points, while the outer helical positions are the same as the interface points between the L-shaped monomers and the kissing loops. We will refer to these measurements as the L-shape monomer helical torsion angles.

Another angle we decided to monitor was the KL’s planar bending angle, which measures how close the two helices flanking the kissing loops are to ideal coaxial stacking. The working assumption was that “straight” kissing loop stacks are required for full tectosquare closure. We define it as the angle between the centers of masses of the 5′ and 3′-most three base pairs in each chain of a KL and passing through the center of mass of the six base pairs in the interacting hairpin loops (see Fig. 4A). For example, the KL bending angle between the helices flanking the idealized KL structures within a full tectosquare produced by RNA2D3D is 179.6°, while for the crystal structure helices (PDB:2B8R) it is measured as 173.1°, and for the NMR KL structure (PDB:2F4X, structure 1), it is measured as 148.4°. Note that in this nomenclature an angle close to 180° means no bending, and the smaller the value of the angle the deeper the bend.

Using the above definitions, we utilized the Amber module ptraj to collect data on the helix torsions angles in the L-shaped monomers, the KL torsion angles, and the RMSD information for the selected fragments of the structures in the MD data. The actual angles measured in the reference structures were then used to screen the MD trajectories of the kissing loop complexes for candidate building blocks to be assembled into full tectosquares. Similarly, dynamic states of the L-shaped monomers indicated by the RMSD minima in the comparison to the reference structures were selected for evaluation in the full tectosquare assembly.

PyMOL scripts were used to build full tectosquares from the experimental KL complexes and the L-shaped monomers with idealized helical arms, as well as from the selected KL and L-shaped monomer trajectory frames. The assembly was done by chain-docking (via the pair_fit command) the L-shaped monomers and the KL complexes, using the 4 backbone P-atoms from the 2 base pairs closest to the hairpin loops in the KLs and L-shaped monomers. To determine the degree of tectosquare closure for the final gap in the chain-fit tectosquares we selected to monitor the distances between the 5′ and 3′-side P atoms corresponding to the L-KL interface (see Section 4.1), as well as the difference in the two measurements. A perfect fit corresponds to 0 Å in both distances and a 0 difference between them. Using this measure to evaluate tectosquare closure, we screened the dynamic states of building blocks from the available MD trajectories. First, each KL mutant’s dynamic states were searched for those that closed the tectosquares built with the idealized L-shaped monomers. Four separate searches for each KL mutant were performed to yield four sets of solutions to be used in the next phase. Next, each of these solutions sets was used to search the L-shape MD states yielding closure, using four copies of an L’s MD state and of each KL mutant in each tectosquare assembly. Solutions common to these searches were used as the L-shaped monomer’s set of MD states to be used in the final search. Thus in the third phase the program searched for the best combination of all the dynamic states in the KL and L solution sets. The best result is illustrated in Fig. 8.

Because, in principle, it is possible not to find closure based on the MD states generated in relatively short simulations, we also applied our most advanced nano-assembly tool, NanoTiler, which does not rely on the strict chain-fitting of building blocks employed in PyMOL scripts, but rather attempts global optimization (see Section 3.3). Automated screenings of the building blocks involved use of the wild type KL (2B8R) MD data, instead of all the mutants, and were performed in a simplified, two phase version of the protocol used with PyMOL (refer to Section 4.3). KL fragments with the three base pairs on each side of the complex were used, since NanoTiler requires this as a minimum helix size for its scoring scheme to work accurately. The most advanced variant of the search used the best MD state of the KL complex being mated to the MD trajectory of the L-shaped monomer, with its helical arms shortened to 4 base pair-long stubs and linked to the KL by idealized helix linkers. These linkers were subjected to distortions guided by the MD simulations, but not limited to any particular dynamic states of the L-shaped monomers. This method effectively enlarges the search space provided by short MD simulations.

4.2. Results of molecular dynamics simulations

The exploratory modeling of the LT17 tectosquare in RNA2D3D utilized four copies of its A3s monomer and four copies of the HIV-1 kissing loop X-ray crystallography structure of the HIV-1 kissing loop (PDB:2B8R). The result was a near-square nanostructure missing the planar closure by the angle comparable to the RNA2D3D’s tectosquare model with one base pair added to each side (shown in Fig. 3B). Considering that the idealized KL’s torsion angle is −0.5°, while it is 33.0° for the X-ray structure, the similarity between the model with an added base pair (+33.6°) to each side and the model with the 2B8R KLs is a good verification of the overall modeling fundamentals. Other modeling artifacts, such as the RMS-based fitting of the experimental KLs to the idealized helices, contribute to the small discrepancies in the compared structures. Since the crystal structure kissing loop data yielded results improving the tectosquare closure and being close to the idealized model-based estimates, we further pursued the MD simulations based on it. The NMR-based KL structure (PDB#: 2F4X (18 files)) yielded superhelical structures, instead of planar tectosquares, nearly triangular in their cross section projection. The decision to utilize the X-ray based structure as the starting point for further MD explorations in this study is not meant to indicate dismissal of the NMR data. In several MD simulations, not directly related to this paper, we observed the KL complex bending angles oscillating between 140° and 180°, and the mean KL torsion angle higher than in the majority of the X-ray structure based MD runs (10.2° ± 12.0°). We return to the potential importance of these results in Section 5.

The results of the X-ray structure kissing loop (2B8R) MD simulations are summarized in Table 1. They illustrate large variations in the KL torsion angles and in the bending angles. The RMSD variations relative to the initial state of the MD production runs do not differ significantly between the wild type and the mutant KLs. The largest distortions away from the A-form helix were observed at the ends of the stems. The mean bending angles are smaller for the mutants B2C1 and C2D1; however, in all cases there are a large number of peak values approaching 180°. The KL mean torsion angles vary most visibly between the different mutants, with two of them having positive values (A1D2 and A2B1), and the other two being nearly symmetrically negative (B2C1 and C2D1). The maximum and minimum values listed in Table 1 illustrate the large degree of flexibility observed in all of them. The KL torsion angles measured for each trajectory exceed at multiple points the +22° estimated to affect the full tectosquare closure based on the idealized RNA2D3D models. Keeping these two key measures (KL bending angle and torsion angle) in mind, one would expect a large number of states within each MD trajectory that would yield closed tectosquares.

The analysis of the MD simulation of the LT17 L-shaped monomer (design A3s) built with the aid of RNA2D3D (see Section 3.1) shows that the RA junction (including two flanking base-pairs) is very stable with low RMSD and standard deviation (1.03 ± 0.14 Å) and is therefore a good reference point (or a substructure) for measurements of motions relative to it (see Fig. 6). From the RMSD data analysis for the full A3s monomer and measurements of selected angles between the helices of the L-shaped monomer (data not shown), it is apparent that most of the motions within the helical arms of the monomer happen outside the RA.

Fig. 6.

Plots of the RMSD values measured for the entire L-shaped monomer and its structure subsets relative to the starting state of the MD run of the full L-shaped monomer (tectosquare design LT17, monomer A3s). Shown in black are the RMSD values for the entire monomer (92nt), with the mean value of 6.11 ± 0.91 Å. Shown in red are the RMSD values of the helical arms and the connecting right angle junction (RA), a total of 62nt. Excluded are the 5′ and 3′ single strands and the hairpin loops. The mean RMSD value is 3.63 ± 0.90 Å. Thus the movements and distortions of the relatively short, disjoint, single-stranded elements excluded from consideration in the red plot contribute significantly to the full structure RMSD measure. Shown in blue are the RMSD values for the RA junction including the two proximal base pairs in each helical arm (total of 10nt), with the mean value of 1.03 ± 0.14 Å. The RA junction distortions measured in different ways (not shown) also show it to be the most stable subset of the entire L-shaped monomer.

Helical torsion angles measured for each of the two arms of the RNA2D3D-created L-shaped monomer subjected to MD simulation show a large degree of flexibility but a limited degree of angle increase, about +7°, in the direction aiding square closure.

The RMSD data for the L-shaped monomer’s interface points at the end of each arm (nucleotide positions 18,19,29,30 and 59,60,70,71) versus the reference structure with +22° added to the 5′ helical arm shows the best fit of 2.33 Å around the 3.2 ns point in the MD trajectory point. The results are better for the reference structure with +11° added to its 5′ helical arm, with a 1.32 Å RMSD around the 3.2 ns MD trajectory point, and multiple points within the trajectory with RMSD between the 2 and 3 Å. The +11° reference structure was used to assess if an effective midway state is reached more often than the full closure (+22°) state. The RMSD minima for these two reference structure measurements coincide closely in time and are infrequent within the time scale of the performed MD simulations (data not shown). However, the measured ranges of individual motions, i.e. torsional changes in each arm (5′ and 3′ helices) of the L-shaped monomer and the variations of the planar angle between the arms appear to be sufficient to affect closures (factoring in the KL torsional angle data). The coincidences of the necessary events can be assumed to be sufficiently frequent for closure on experimental time-scales as evidenced by the actual experimental results.

Another important observation is that many L-shaped monomer motions contribute to the effective torsional state changes at the interface points. Helical torsion angles alone show potential for aiding the closure by approximately +7°, and the RMSD matches to the reference structures with the added +11° twist indicate good fit up to this (+11°) effective angle increase. Principal component analysis (data not shown) also indicates diverse motions (multiple eigenvectors) contributing to the effective helical torsion angle changes.

Using the combination of the KL bending angles close to the “straight” stacking of the reference structure and the KL torsion angle of +22° as the guiding parameters, we first searched the MD trajectories for KL MD states that would produce tectosquare closure in combination with the idealized L-shaped monomers. MD data for one of the engineered KL complexes is shown in Fig. 7B. Fig. 7A shows a set of KL MD states found in that parameter-guided search combined with an MD state of the L-shaped monomer trajectory (used in four copies), thus assembling a full closed tectosquare from the MD states of all the building blocks. The L-shaped monomer MD state was selected based on its low RMSD relative to the idealized L-shape created in RNA2D3D. The actual bending angles in the final selection of KL states varied from 170.3° to 178.9°, while the KL torsion angles varied from +15.1° to +19.2°, i.e. their values were lower than the +22° assumed to be necessary to affect the tectosquare closure (see Section 4.1). The final L-KL interface gaps were 5.3 and 4.9 Å for the 5′ and 3′ sides, respectively. Several error minimizing steps were required to arrive at the solution illustrated in Fig. 7A. The insight gained from this exercise was that a combination of KL torsion and bending angle is a good approximation of the geometric constraints required for full structure closure, but is not sufficiently accurate to directly guide searches of tectosquare closing solutions in a precise analytical fashion. As in the case of the L-shaped monomers, the KL motions ultimately contributing to a tectosquare closure are complex. Best fitting KLs and L-shaped monomers show different RMSD fitting values for each side of the KL, underscoring the asymmetry of MD states for all the building blocks at their interfaces. As the fitting approximations must ultimately compensate each other to affect closure, which increases combinatorics of fitting, the most efficient search procedure appeared to be automation of the process.

Fig. 7.

A tectosquare built out of MD states of four kissing loop models and one MD state of the L-shaped monomer used four times. (A) The KL states come from the following points in their respective trajectories: A1D2 – 4.0 ns, A2B1 – 4.5 ns, B2C1 – 18.9 ns, and C2D1 – 1.8 ns. Listed under each KL label are the actual KL torsion angles measured for each of them. The MD state of the L-shaped monomer comes from the 3.2 ns point in its trajectory. The color-coded KL fragments were truncated for display purposes to include only the two base pairs closest to the interacting hairpin loops, which were used as reference points in a chain-fitting of the building blocks together. The last KL in this procedure, C2D1, was fit to the monomer C and the gap between the KL and the D monomer was used as a measure of the overall closure quality. The gap distances were measured for the corresponding KL complex’s and L-shaped monomer’s 5′ and 3′-side P atoms of the second base pairs from the KL’s H-loops (L-KL interface points). A perfect fit would measure 0 Å for both gaps. The RMSD values of each fit in the chain assembly are listed next to each side of every KL. (B) A plot of the KL bending angle (red) and the KL torsion angle (black) in the MD simulation of the KL complex B2C1. A point in the trajectory corresponding to 18.917 ns is marked with the blue vertical line for which the KL bending angle is 177.9° and the KL torsion angle is 17.4°. This MD state was used as one of the kissing loops yielding the closed full tectosquare shown in (A).

4.3. Results for automated closure searches

Even though, guided by the torsion and bending angle parameters, we found a set of MD states which produced a closure with approximately 5 Å gaps, it might have been impossible to find all the matching dynamic states with parameters close to the estimates based on the idealized model. Therefore, to improve on the parameter-guided MD state search scheme described in Section 4.2, we employed two types of automated searches described in Section 4.1. First, the MD trajectories of the four mutated kissing loops were searched for best closures of tectosquares utilizing the L-shaped monomers with idealized helical arms. Keeping in mind that the best results of these four searches may not yield best fits to the MD states of the L-shaped monomers, we included solutions with gap measures within 6 Å. For each KL mutant solution set, a KL dynamic state was used in four copies to find the best L-shaped monomer MD states affecting closure. Repeatedly, a small set of the L-shape dynamic states was indicated, corresponding to the RMSD trough around the 3.2 ns MD trajectory point (see Section 4.2). For the input sets of KL and L-shaped monomer dynamic states selected in the first two phases, the third phase found multiple solutions with gaps of less than 2.5 Å and a difference between them (5′ and 3′ gaps, refer to Section 4.1) of less than 0.5 Å. Worth noting is the fact that the kissing loops yielding the best closure results show lots of compensating distortions relative to the idealized parameters and the results shown in Fig. 7A. The best result of using this three-stage protocol is shown in Fig. 8.

Finally, the NanoTiler program was employed to automatically test the MD trajectories, as described in Section 4.1. It implements a nanostructure closure scoring scheme based on the gap distance and angular differences between the open ends of the full nanostructure and assembles the building blocks in a globally optimized scheme (thus less restrictive than the chain assembly employed in PyMOL). Not to duplicate the work described in the Section 4.2 and above, we selected the HIV-1 wild type kissing loop (PDB:2B8R) MD trajectory for examination, as its KL torsion angle and KL bending angle measurements placed it within the results for the mutants. The 2B8R MD trajectory of over 25 ns was sampled in 0.1 ns steps (every 100 MD trajectory steps) in search of the best KL MD states bringing a tectosquare assembled from four copies of such a state and four idealized L-shaped monomers (kept constant throughout the search) to a closure, or closest to it. Next, using the KL state selected in this first phase, we searched the 30 ns MD trajectory of the LT17 A3s monomer, using the same 0.1 ns sampling steps, for the states closing the tectosquare when mated with the previously selected kissing loop MD state. Despite the relatively sparse sampling, imperfect but well scoring MD states for the KL and L-shaped monomer were identified (results not illustrated). A variant of the second procedure was tested, in which the best KL MD state from the first search was used, but the L-shaped monomer fragments were shortened to four base pairs in each helix emanating from the right angle junction, leaving 8 bp spaces to be filled with idealized helix linkers. Using this method another (truncated) L-shaped monomer MD state was identified as the best candidate for the full tectosquare closure. Fig. 9A illustrates this solution. Use of helical linkers also allowed us to take advantage of the refinement procedure in NanoTiler in which they are subjected to small distributed distortions in order to close the remaining gaps in the best identified set of building blocks for the full nanostructure. Following this step, the full tectosquare was subjected to energy minimization in Amber, and the result of that procedure is shown in Fig. 9B.

It is worth noting that in both of the automated search schemes, but especially in the NanoTiler results, the shape of the minimized tectosquare has shifted from the near-perfect square towards a rhomboid, thus revealing the advantage of these methods in finding closed states that are not limited to structures matching the near-square reference tectosquares constructed for the preliminary closure problem evaluation. What is more, this shape agrees with the experimental results observed by Atomic Force Microscopy [15,21]. We verified that the distortions of the helical linkers are within the range of distortions of the corresponding 8 base pair sections of the helical arms in the full L-shaped monomer MD trajectory (RMSD relative to the first frame of the production MD run). It is worth stressing that by default NanoTiler does not perturb the junction structures and uses the linker helices to introduce small distortions required to connect all the building blocks together. Thus the NanoTiler scheme combining the MD states of the junctions with the adjustable linkers increased the scope of search for closure states and can be viewed as an extension of the MD states-based search scheme, but within the MD trajectory boundaries.

5. Discussion and future plans

We have demonstrated that RNA structure flexibility plays an important role in the design and assembly of nano-scale structures. Data obtained from the MD simulations on selected structural motifs can help in the design of nanostructures from building blocks which, without it, may yield no static, geometric fit. This idea applies as much to the available experimental structures, as it does to idealized junctions that may be introduced into designs, in cases in which no fitting building blocks are available in a database. In the case of RNA tectosquare design the assembly of the L-shaped building blocks appears to benefit mostly from the torsional flexibility in the kissing loop motifs, aided by the more limited flexibility in the direction of the tectosquare closure in the L-shaped monomer’s helical arms. The right angle junction shows the least amount of flexibility. MD results also show that the mutations programmed into the HIV-1 kissing loops influence their stability relative to the wild type structure, but not to the point of interfering with full structure assembly.

An issue that was found to be potentially important in this methodology is the role of subtleties in molecular dynamics simulations. MD simulation of the HIV-1 WT kissing loop (PDB:2B8R) with only the neutralizing Na⁺ ions showed deep relaxation of the KL torsion angle (i.e. more negative mean value than with additional NaCl in the solvent) with increased standard deviation (see Table 1). The importance of Mg²⁺ to the full tectosquare assembly was clearly indicated by the experimental data [15], but it is very difficult to simulate accurately, even with partial ion placement based on the experimental X-ray crystallography data, which we used in the WT kissing loop simulation. It is worth noting, that our best approximation of molecular dynamics conditions in the presence of MgCl₂ yielded a much higher KL torsion angle than the MD runs without the Mg²⁺ ions (see Table 1). Since this result is closer to the starting crystal structure value, it appears that Mg²⁺ stabilizes the entire KL complex. From the modeling point of view, the mean KL torsion angle measured for this simulation is very close to the closing target value based on the exploratory modeling with RNA2D3D, which should help in finding full tectosquare structure closing MD states. However, given that the mutations within the hairpin loops used in the tectosquare design are in the vicinity of one of the experimentally placed Mg²⁺ ions, we could not be certain that the wild type ion placement data (PDB:1XPE) could be used in the reengineered KL complexes. Therefore, we settled on a compromise approach by using neutralizing Na⁺ augmented with Na⁺ and Cl⁻ ions added to the solvent, on the assumption that they will add to the stability of the full KL complex [33,34]. As the data in Table 1 shows, some degree of KL stabilization was achieved, relative to the MD results using only the neutralizing ions. Another evaluated MD option was the addition of parabolic restraints on the hydrogen bond distances in the closing base pairs of the WT kissing loop complex, which increased the mean KL torsion angle (closer to the results including Mg²⁺ in the simulation), but also added to the standard deviation. While the range of motions, including the effective KL torsion angle changes, required for the closure of large tectosquares (such as the LT17 design studied here) was sufficient in the MD simulations employed, one has to keep in mind the above mentioned differences in the MD results dependent on the ionic conditions or restraints employed, or re-consider as a starting structure the NMR-based experimental data. For example, a variant of the tectosquare design studied here utilizes L-shaped monomer helices shortened to 9 bp [15]. While we were able to find a closed state for a small tectosquare (results not shown) using the same NanoTiler protocol employed for the large tectosquare and the same MD trajectory data, the automated searches using PyMOL scripts required MD results including Mg²⁺ ions.

The basic idea of exploring the closure problem with the aid of RNA2D3D is sound. However, translating the idealized and simplified parameters obtained in the exploratory modeling into precise search criteria for the exploration of the MD trajectories limits the number of solutions since the MD motions were found to be far more complex than the exploratory manipulations. Combinations of smaller motions not captured by these measures are also important. In the final assembly process the approximations at each fitting interface between the L-shaped monomer’s arms and the emanating KL’s stems must ultimately compensate each other to affect good tectosquare closure. In this context, the parameter-guided selection of building blocks yielding full structure closure (Fig. 7) should be viewed as a verification of the flexibility parameters, rather than a method of assembly exploration. The idea of exploring the flexibility limits of multiple building blocks and then testing the full assembly by mating the available dynamic states is best suited to automated combinatorial searches.

The proof-of-concept exploration of the MD trajectories illustrated here first mated an idealized L-shape monomer with the MD states of a kissing loop in search of the best KL state closing the tectosquare. In the next step or steps, the best KL selected in step one were tested against the MD states of the L-shaped monomer, to assess if it reaches the desired state. This approach limits the search and the potential solution set to blocks yielding a square or near square final shapes. Another possible approach could reverse the order of searches, first assessing the L-shaped monomer MD states, and allow mixing of two or more MD states to explore more diverse closing structures, i.e. go beyond the symmetric use of one MD state and reliance on the best solution from such an approach. We plan to refine this methodology and include it in the future releases of NanoTiler, either as an explicit tool or a sample script that could be adapted by users to the specific problems.

Another issue that may be easier to assess by an automated assembly process, rather than by an analysis of the full building blocks subjected to MD, is the potential problem of very few and maybe even no dynamic states fulfilling the structure closure criteria within the relatively short time of MD simulations, which may be orders of magnitude shorter than the time scales of the experiments. One option we demonstrated is to utilize NanoTiler’s capability to link smaller versions of RNA junctions with ideal or deformed helices in order to affect structure closure and judge how “strained” (or far away from the target) the solution is, based on the deformation score calculated by the program. If the scores indicate that only minor adjustments are needed, it could be an indication of a possible closure, even when the dynamic state fulfilling all the 3D geometry criteria is not explicitly found in an MD trajectory. In this study we concluded that the distortions introduced into the helical linker fragments were acceptable and comparable to the distortions of the equivalent fragments of the full L-shaped monomers based on the comparison to explicit MD data. We plan to evaluate the distortion scoring scheme employed in NanoTiler against a set of controls, so that the acceptability of distortion levels in the linkers can be accurately judged in the absence of data for direct comparisons. Another way of substantially speeding up the whole process would be to employ coarse-grained dynamics simulations. Based on the explicit all atomic MD data obtained in this study, it should be easier to evaluate such an approach. Faster computational methods, such as elastic network modeling, could also help in exploring the impact that larger subassemblies and full nanostructures may have on the flexibility of individual building blocks and the full structure closure. The additivity of individual building block flexibilities, implicitly assumed in the methodology presented here, could and should be further examined with the aid of methods permitting larger scale dynamics simulations.

In summary, we have demonstrated the importance of incorporating structural flexibility data in the design and modeling of modular RNA-based nanostructures. First, we showed that an idealized model can be used to develop parameters for assessing flexibility boundaries needed to achieve full structure closure. Next, we presented MD data analysis guided by these parameters which can be used to analytically assess the closure and search for the dynamic states yielding a closed structure. Finally, we showed two approaches to perform an automated search for the full structure closure. Depending on the amount of information one wants to obtain to characterize building blocks of a larger nanostructure, one or all of these methods can be employed. By substituting other topologies (connectivity specifications) in place of the tectosquare design illustrated here, one could apply the same approaches to other modular nanostructure design evaluations. In general, base composition of the helical regions can be altered and other motifs can be inserted to affect torsional and angular flexibility of the helical regions [25,35–37].