Patient-Specific Non-Linear Finite Element Modelling for Predicting Soft Organ Deformation in Real-Time; Application to Non-Rigid Neuroimage Registration

Abstract

Long computation times of non-linear (i.e. accounting for geometric and material non-linearity) biomechanical models have been regarded as one of the key factors preventing application of such models in predicting organ deformation for image-guided surgery. This contribution presents real-time patient-specific computation of the deformation field within the brain for six cases of brain shift induced by craniotomy (i.e. surgical opening of the skull) using specialised non-linear finite element procedures implemented on a graphics processing unit (GPU). In contrast to commercial finite element codes that rely on an updated Lagrangian formulation and implicit integration in time domain for steady state solutions, our procedures utilise the total Lagrangian formulation with explicit time stepping and dynamic relaxation. We used patient-specific finite element meshes consisting of hexahedral and non-locking tetrahedral elements, together with realistic material properties for the brain tissue and appropriate contact conditions at the boundaries. The loading was defined by prescribing deformations on the brain surface under the craniotomy. Application of the computed deformation fields to register (i.e. align) the preoperative and intraoperative images indicated that the models very accurately predict the intraoperative deformations within the brain. For each case, computing the brain deformation field took less than 4 s using a NVIDIA Tesla C870 GPU, which is two orders of magnitude reduction in computation time in comparison to our previous study in which the brain deformation was predicted using a commercial finite element solver executed on a personal computer.

1. Introduction

Surgery planning is typically conducted using high quality preoperative radiographic images. Craniotomy (i.e. surgical opening of the skull) and other surgical procedures result in brain deformations that lead to misalignment between the actual position of pathology and critical healthy tissues and their positions determined from the preoperative images (Warfield et al., 2002). Therefore, predicting the intraoperative brain tissue deformations to align the high-quality preoperative images to the intraoperative geometry (in a process known as non-rigid registration) is recognised as a critical tool in image-guided neurosurgery (Fedorov et al., 2008).

In the past non-rigid registration relied solely on image processing methods that predict the deformation field within the brain without taking into account the brain tissue mechanics (Beauchemin and Barron, 1995; Viola and Wells III, 1997; Warfield et al., 2001). As such methods do not ensure plausibility of the predicted deformations, biomechanical models, in which predicting the brain deformations is treated as a computational problem of solid mechanics, have been introduced (Archip et al., 2007; Edwards et al., 1998; Hu et al., 2007; Kyriacou and Davatzikos, 1998; Kyriacou et al., 1999; Miga et al., 1998; Miga et al., 2000; Miga et al., 2001; Skrinjar et al., 1998; Skrinjar et al., 2001; Warfield et al., 2002). In most practical cases, such models utilise the finite element method (Bathe, 1996) to solve sets of partial differential equations of solid mechanics governing the behaviour of the analysed continuum. The finite element method has been verified in numerous applications in computer-aided engineering and biomechanics. However, its application in neurosurgery poses new challenges as the deformation field within the brain must be computed within the real-time constraints of image-guided neurosurgery. A precise definition of such constraints is still lacking, and values varying from tens of seconds (Grimson et al., 1998; Platenik et al., 2002; Warfield et al., 2002) to tens of minutes, for slowly occurring brain deformations, (Miga et al., 1999; Skrinjar et al., 2002) have been suggested. In this study, we follow a definition of real-time constraints of image-guided neurosurgery suggested by Chrisochoides et al. (2006) who stated that the computation time of the registration application should not exceed the time of acquisition of the intraoperative magnetic resonance images and less time the computation takes the better. Similar opinion has been expressed by Jalote-Parmar and Badke-Schaub (2008) who listed timely providing the surgeons with the intraoperative organ position among the key factors influencing intraoperative surgical decision making. Thus, the studies by Chrisochoides et al. (2006) and Jalote-Parmar and Badke-Schaub (2008) place the real-time constraints of image-guided neurosurgery within an order of seconds or tens of seconds rather than tens of minutes and highlight the importance of reducing the computation time of the registration algorithms.

So far, real-time prediction of the brain deformation has relied on linear finite element procedures in which the deformation is assumed to be infinitesimally small (i.e. the equations of solid mechanics are integrated over the undeformed preoperative brain geometry) and the brain tissue is treated as a continuum exhibiting linear stress–strain relationship (Archip et al., 2007; Clatz et al., 2005; Ferrant et al., 2001; Skrinjar et al., 2002; Warfield et al., 2002). However, the brain surface deformations due to craniotomy can exceed 20 millimeters (Roberts et al., 1998) and tend to be above 10 millimeters for around 30% of patients (Hill et al., 1998). These values are inconsistent with the infinitesimally small deformation assumption that implies that geometry changes of the analysed continuum are negligible and equations of continuum mechanics can be solved over the initial (undeformed) geometry. Therefore, in several studies (Hu et al., 2007; Wittek et al., 2007; Wittek et al., 2009; Xu and Nowinski, 2001) finite element models utilising geometrically non-linear (i.e. finite deformations) formulation of solid mechanics have been applied to compute deformation field within the brain for neuroimage registration. Despite facilitating accurate predictions of the brain deformations, the non-linear biomechanical models have been, so far, of little practical importance as the algorithms used in such models led to computation times greatly exceeding the real-time constraints of neurosurgery. For instance, Wittek et al. (2009) reported the computation time of over 1700 s on a standard personal computer when predicting the brain deformations using a model with around 50 000 degrees of freedom implemented in the commercial non-linear finite element solver LS-DYNA™.

Recently our group developed and implemented specialised non-linear finite element algorithms and solvers for real-time computation of soft tissue deformation. Verification of the numerical accuracy and numerical performance of these algorithms have been previously reported in the literature (Miller et al., 2007; Joldes et al., 2009a; Joldes et al., 2009b; Joldes et al., 2010a). In this study, following our recent work (Joldes et al., 2009c), we evaluate their accuracy and performance in a practical context through application in predicting deformation fields within the brain for six cases of craniotomy-induced brain shift. In the accuracy evaluation, the preoperative image data warped using the deformations predicted by means of our models and algorithms are compared with the intraoperative images. The results demonstrate that biomechanical models using specialised non-linear finite element algorithms facilitate accurate prediction of deformation field within the brain for computation times below 40 s on a standard personal computer and below 4 s on a graphics processing unit (GPU).

2. Material and Methods

2.1 Medical context

We analysed six cases of craniotomy-induced brain shift that represent different situations that may occur during neurosurgery as characterised by tumours located in different parts of the brain: anteriorly (for Cases 1, 2 and 6), laterally (for Case 3) and posteriorly (for Cases 4 and 5) (Fig. 1). Case 6 was investigated in our previous studies (Joldes et al., 2009a; Joldes et al., 2009b; Wittek et al., 2007; Wittek et al., 2009). In this paper, the previously obtained results for Case 6 are presented in a format consistent with a new analysis we conduct here for Cases 1 to 5.

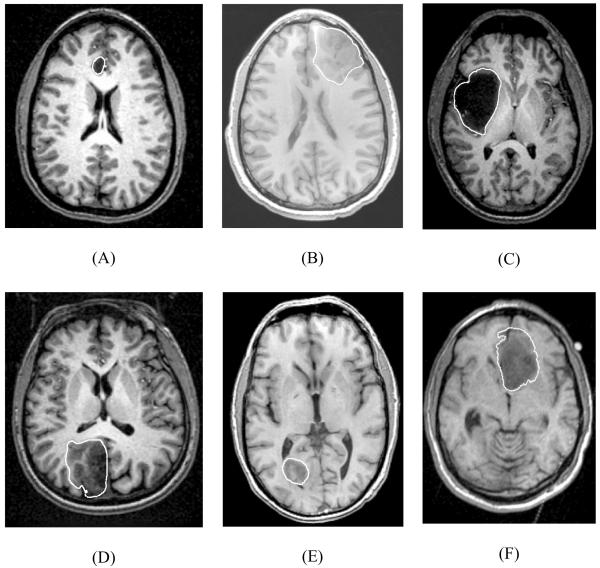
Fig. 1.

Preoperative T1 magnetic resonance images showing tumour location in the craniotomy cases analysed in this study. White lines indicate the tumour segmentations. (A) Case 1; (B) Case 2; (C) Case 3; (D) Case 4; (E) Case 5; and (F) Case 6. Case 6 was used in our previous studies (Joldes et al. 2009a; Joldes et al. 2009b; Wittek et al., 2007; Wittek et al., 2009).

2.2 Biomechanical models for computing brain deformation

2.2.1 Brain tissue constitutive modelling for biomechanical models

Despite continuous efforts (Sinkus et al., 2005; Turgay et al., 2006), commonly accepted non-invasive methods for determining patient-specific constitutive properties of the brain and other soft organs’ tissues have not been developed yet. Constitutive models of the brain tissue applied for computing the brain deformation for non-rigid registration vary from simple linear-elastic model (Warfield et al., 2000) to Ogden-type hyperviscoelasticity (Wittek et al., 2007) and bi-phasic models relying on consolidation theory (Miga et al., 2000; Miga et al., 2001). However, as explained in more detail in section Loading and Boundary Conditions, the strength of the modelling approach used in this study is that the calculated brain deformations depend very weakly on the constitutive model and mechanical properties of the brain tissues. Therefore, following Joldes et al. (2009a), we used the simplest hyperelastic model, the neo-Hookean (Yeoh, 1993). The rationale for selecting the hyperelastic constitutive model was that it has been indicated in the literature (Miller and Chinzei, 1997) that such models very well represent the behaviour of the brain tissues undergoing large deformations.

Based on the experimental data by Miller et al. (2000) and Miller and Chinzei (2002), the Young’s modulus of 3000 Pa was assigned for the brain parenchyma tissue. For tumour, we used the Young’s modulus two times larger than for the parenchyma, which is consistent with the experimental data of Sinkus et al. (2005). There is strong experimental evidence that the brain tissue is (almost) incompressible (Pamidi and Advani, 1978; Sahay et al., 1992; Walsh and Schettini, 1984) so that we used the Poisson’s ratio of 0.49 for the parenchyma and tumour. Following Wittek et al. (2007), the ventricles were assigned the properties of a very soft compressible elastic solid with Young’s modulus of 10 Pa and Poisson’s ratio of 0.1 to account for possibility of leakage of the cerebrospinal fluid from the ventricles during surgery.

2.2.2 Loading and boundary conditions

As explained in the previous section, there are always uncertainties regarding the patient-specific properties of the living tissues. To reduce the effects of such uncertainties, we loaded the models by prescribing displacements on the exposed (due to craniotomy) part of the brain surface (Fig. 2). It has been suggested by Skrinjar et al. (2002) and shown by Wittek et al., (2009) that for this type of loading, the unknown deformation field within the brain depends very weakly on the mechanical properties of the brain tissues. The displacements for loading the models were determined from distances between the preoperative and intraoperative cortical surfaces segmented in the T1 MRIs. The correspondences between the preoperative and intraoperative surfaces were determined by applying the vector-spline regularisation algorithm to the surface curvature maps (Arganda-Carreras et al., 2006; Joldes et al., 2009d).

Fig. 2.

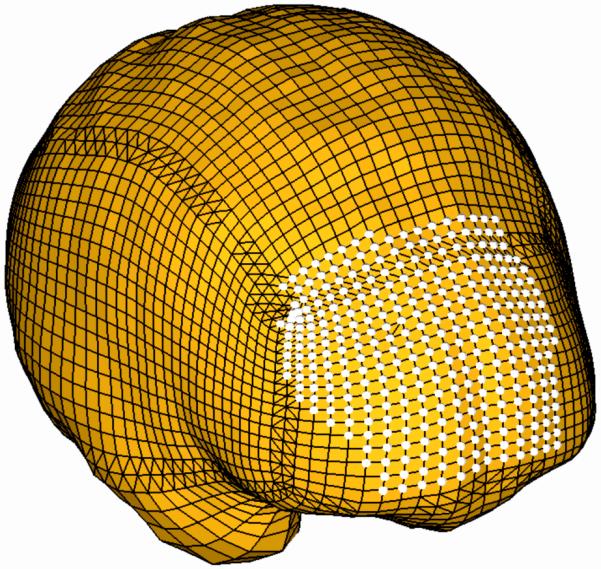
Model (Case 1) loading through prescribed nodal displacements on the part of the brain surface exposed during the craniotomy. White circles indicate the nodes where the displacements were applied.

To define the boundary conditions for the remaining nodes on the brain model surface, a contact interface was defined between the rigid skull model and areas of the brain surface where the nodal displacements were not prescribed. The contact formulation described in Joldes et al. (2009a) was used. This formulation prevents the brain surface from penetrating the skull while allowing for frictionless sliding and separation between the brain and skull. Although modelling of the brain-skull interactions through a sliding contact with separation may be viewed as oversimplification since the anatomical structures forming the interface between the brain and skull are not directly represented, such modelling has been widely used in the literature when computing the brain deformations during brain shift (Hu et al., 2007; Skrinjar et al., 2002; Wittek et al., 2007).

2.2.3 Computational grids; Construction of patient-specific finite element meshes

Three-dimensional patient-specific brain meshes were constructed from the segmented preoperative magnetic resonance images (MRIs) obtained from the anonymised retrospective database of Computational Radiology Laboratory (Children’s Hospital, Boston, MA). The parenchyma, ventricles and tumour were distinguished in the segmentation process.

Because of the stringent computation time requirements, the meshes had to be constructed using low order elements that are not computationally expensive. The under-integrated hexahedron with linear shape functions is the preferred choice due to its superior convergence and accuracy characteristics (Shepherd and Johnson, 2009). Many algorithms are now available for fast and accurate automatic mesh generation using tetrahedral elements, but not for automatic generation of hexahedral meshes (Viceconti and Taddei, 2003). Template based meshing algorithms could not be used here because of the presence of irregularly placed and shaped tumours. Our previous experience (Wittek et al., 2007) indicated that it can take several weeks of work of an experienced analyst to manually build a patient-specific hexahedral mesh of the brain with a tumour. Therefore, to partly automate the meshing, we used mixed meshes consisting of both hexahedral and tetrahedral elements with linear shape functions (Fig. 3, Table 1). The meshes were built using IA-FEMesh (a freely available software toolkit for hexahedral mesh generation developed at the University of Iowa) (Grosland et al. 2009) and HyperMesh™ (a high-performance commercial finite element mesh generator by Altair, Ltd. of Troy, MI, USA). Following the literature (Ito et al., 2009; Shepherd et al., 2007), hexahedral elements with Jacobian of below 0.2 were regarded as of unacceptably poor quality and replaced with the tetrahedral elements. Because of irregular geometry of ventricles and tumour, vast majority of tetrahedral elements were located in the ventricles and tumour as well as in the adjacent parenchyma areas. It took between one and two working days for a graduate student (assisted by an experienced finite element analyst) to generate the brain mesh for each of the craniotomy cases analysed in this study.

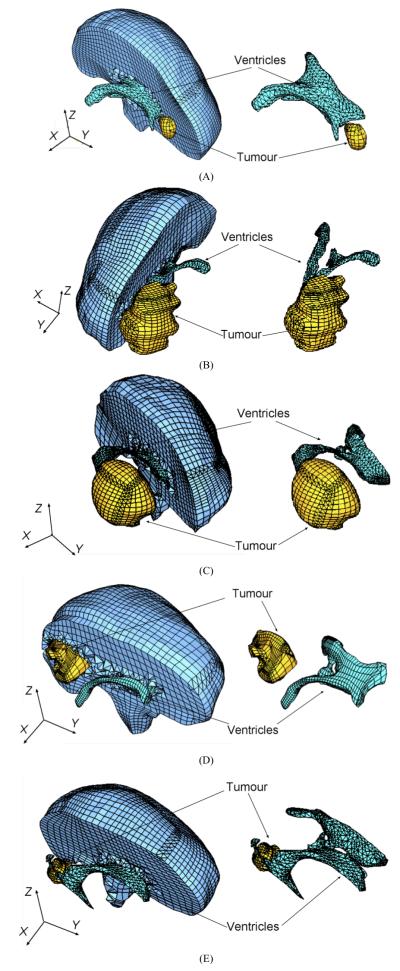
Fig. 3.

Patient-specific brain meshes built in this study. (A) Case 1; (B) Case 2; (C) Case 3; (D) Case 4; (E) Case 5. Because of the complex geometry of ventricles and tumours, tetrahedral elements were mainly used for discretisation of the ventricles and tumours as well as the adjacent parenchyma areas.

Table 1.

Summary of the patient-specific brain meshes used in this study. Every node in the mesh has three degrees of freedom. Case 6 was used in our previous studies (Joldes et al. 2009a; Joldes et al. 2009b; Wittek et al., 2007; Wittek et al., 2009).

	Case 1	Case 2	Case 3	Case 4	Case 5	Case 6
Number of Hexahedral Elements	14447	10258	10127	9032	8944	15032
Number of Tetrahedral Elements	13563	20316	23275	23688	21160	54
Number of Nodes	18806	15433	15804	14732	14069	16710

As the parenchyma was modelled as an incompressible continuum, average nodal pressure (ANP) formulation by Joldes et al. (2009a) was applied to prevent volumetric locking (i.e. artificial stiffening due to incompressibility) in the tetrahedral elements. We refer to these elements as non-locking ones.

To eliminate instabilities (known as zero-energy modes or hourglassing) that arise from one-point integration, the stiffness-based hourglass control method by Joldes et al. (2009a) was used for underintegrated hexahedral elements.

2.3 Algorithms for integration of equations of solid mechanics for computing soft tissue deformation

The details (including verification and validation) of the applied algorithms have been previously described in the literature (Joldes et al., 2009a; Joldes et al., 2009b; Joldes et al., 2010a; Miller et al., 2007, Miller et al., 2010). Therefore, only a brief summary is given here. Computational efficiency of the algorithms for integrating the equations of solid mechanics used in this study has been achieved through the following two means:

1. Total Lagrangian (TL) formulation for updating the calculated variables (Miller et al., 2007);

2. Explicit integration in the time domain combined with the algorithm employing transient terms that optimise convergence to steady state (Joldes et al., 2009b; Joldes et al., 2010a).

2.3.1 Total Lagrangian formulation

In the total Lagrangian formulation, all the calculated variables (such as displacements and strains) are referred to the original configuration of the analysed continuum. The decisive advantage of this formulation is that all derivatives with respect to spatial coordinates can be pre-computed. As indicated in Miller et al. (2007), this greatly reduces the computation time in comparison to the updated Lagrangian formulation used in vast majority of commercial finite element solvers (such as e.g. LS-DYNA™, ABAQUS™). An additional advantage is that application of the total Lagrangian formulation simplifies the material law implementation since the hyperelastic material models, such as the neo-Hookean model we used here, can be easily described using the deformation gradient.

2.3.2 Explicit integration in time domain with mass proportional damping

In explicit time integration, such as the central difference method applied in this study, the treatment of non-linearities is very straightforward as even for non-linear problems, no iterations are required for a solution during a time step. The displacement and velocity at a given time step n+1 are calculated by incrementing the solution at the previous step n:

$${\mathit{u}}_{n+1}={\mathit{u}}_n+\Delta t{\stackrel{.}{\mathit{u}}}_n+1∕2\Delta t^2{\ddot{\mathit{u}}}_n\text{and}$$ Eq. (1)

$${\stackrel{.}{\mathit{u}}}_{n+1}={\stackrel{.}{\mathit{u}}}_n+1∕2\Delta t({\ddot{\mathit{u}}}_{n+1}+{\ddot{\mathit{u}}}_n),$$ Eq. (2)

where u is the nodal displacement, u̇ is the nodal velocity, ü is the nodal acceleration, and Δt is the time step. Using Eq. (1) and Eq. (2), time stepping scheme for solving the equations of motion of the analysed continuum can be expressed as

$${\mathit{u}}_{n+1}={\mathit{M}}^{-1}({\mathit{R}}_n-{\mathit{F}}_n)\Delta t^2+(2{\mathit{u}}_n-{\mathit{u}}_{n-1}),$$ Eq. (3)

where R is the vector of externally applied nodal forces, F is the vector of internal nodal forces, and F=K(u) u (where K is the stiffness matrix). For nonlinear problems, such as the one analysed in this study, the stiffness matrix K depends on deformation u, which is indicated by notation K(u).

For the lumped (diagonal) mass matrix M we used in this study, the time stepping scheme given in Eq. (3) can be decoupled and solution is done at the nodal level (Belytschko, 1976). Therefore, no system of equations must be solved and the global stiffness matrix of the entire model does not have to be built.

In consequence, application of explicit integration alone can reduce by an order of magnitude the time required to compute the brain deformations in comparison to implicit integration typically used in commercial finite element codes (such as e.g. LS-DYNA™, ABAQUS™) for steady state solutions (Wittek et al., 2007).

In dynamic relaxation, a mass proportional damping component is added to the equations of motion (Joldes et al., 2009b) and Eq. (3) becomes

$${\mathit{u}}_{n+1}={\mathit{u}}_n+\alpha ({\mathit{u}}_n-{\mathit{u}}_{n-1})+\beta {\mathit{M}}^{-1}({\mathit{R}}_n-{\mathit{F}}_n),$$ Eq. (4)

where

$$\alpha =(2-c\Delta t)∕(2+c\Delta t),\text{and}$$ Eq. (5)

$$\beta =\left(2\Delta t^2\right)∕(2+c\Delta t).$$ Eq. (6)

In Eqs. (4) – (6), c is the damping coefficient. We use the lumped (i.e. diagonal) mass matrix for which the algorithm defined in Eq. (4) is explicit. The mass matrix M does not affect the steady state solution. Therefore, the damping coefficient c, integration time step Δt and mass matrix M are computed to maximise the convergence rate to steady state and improve the computational efficiency without compromising the solution accuracy (Joldes et al., 2009b; Joldes et al., 2010a).

2.4 Implementation of algorithms for computing soft tissue deformation on Graphics Processing Unit (GPU)

Recent examples of implementation of non-linear finite element algorithms for computing soft tissue deformation for non-rigid registration on Graphics Processing Unit (GPU) include Noe and Sørensen (2010) and Joldes et al. (2010b). The first implementation of our basic total Lagrangian explicit dynamics algorithm on GPU has been presented by Taylor et al. (2008). The implementation by Taylor et al. (2008) proved that the algorithm is very well suited to execution on GPUs and other parallel hardware and shown 16 times computational speed gain compared with the corresponding implementation on a Central Processing Unit (CPU) from a typical personal computer. However, it exhibits several key limitations: it can handle only linear locking tetrahedral elements and a single material type, contains no features for modelling contact interaction, has no integration step control, and cannot compute steady state solution. In this study, we use the GPU implementation of our finite element algorithms summarised in Joldes et al. (2010b) who utilised the NVIDIA Compute Unified Device Architecture (CUDA), see reference NVIDIA (2008). This implementation does not suffer from the limitations of the study by Taylor et al. (2008) as it includes dynamic relaxation that facilitates fast convergence to steady state solution, brain – skull contact model, several non-linear materials, and supports hexahedral and non-locking tetrahedral elements that are very efficient and robust in modelling of incompressible continua such as the brain and other soft tissues. As the details have been given in Joldes et al. (2010b), only a brief summary is presented here.

As explained in Section 2.3.1, we employ total Lagrangian formulation that allows precomputation of all derivatives with respect to spatial coordinates in our finite element algorithms. Therefore, we focused on applying GPU to increase computation speed of the algorithms’ iterative component (see Eq. 4) that cannot be pre-computed and has to be performed intraoperatively. As GPUs offer high computation efficiency through their parallel architecture, at first we identified data-parallel parts of this component. Since each element and/or node can be seen as a data structure on which computations are made, we identified the following iterative parts of our algorithms for implementation as GPU kernels (i.e. separated codes executed on GPU):

1. Computation of the element pressure for non-locking tetrahedral elements;

2. Computation of the nodal pressure for non-locking tetrahedral elements;

3. Computation of nodal forces for hexahedral and non-locking tetrahedral elements (considered separately in GPU implementation as different integration formulae are used for hexahedral and tetrahedral elements);

4. Computation of new displacements (Eq. 4) for all nodes in the brain mesh;

5. Enforcing contact conditions with the rigid skull for the nodes located on the brain surface.

In order to obtain high computation performance, strict guidelines must be followed when programming a GPU using CUDA (NVIDIA, 2008). One of the most critical guidelines refers to data transfers between the CPU (that runs a program from which a GPU kernel is launched) and GPU. Such transfers are relatively slow and in order to minimise them, in the GPU implementation of our finite element algorithms, all the information needed for the computations is transferred to the GPU in the initialisation stage (i.e. the transfer occurs only once).

Complete GPU implementation of the finite element algorithm used in this study for computing the steady state deformations can be summarised as follows:

1. Initialisation:

   • Compute the damping coefficient c, the time step Δt and mass matrix M that facilitate the fastest convergence to the steady state.
   • Precompute all other needed quantities/variables such as the element shape functions, hourglass shape vectors for underintegrated hexahedral elements, initial volumes of the elements etc.
   • Transfer all the needed data to the GPU memory.
2. For every iteration step:

   1. Apply current loading (in this study the loading is defined by prescribing the displacements).
   2. Compute the nodal forces F corresponding to the current displacement u_n.

      • ○
        Run the GPU kernel that computes the element pressure.
      • ○
        Run the GPU kernel that computes the nodal pressure.
      • ○
        For each element type:

        • - Run the GPU kernel that computes the nodal forces and saves them in the GPU memory.
   3. c) Compute the next displacement vector.

      • ○
        Run the GPU kernel that computes the next displacements using Eq. (4). This kernel also assembles the force vector and mass matrix.

   • e) Run the kernel that enforces the contacts.
   • f) Check for convergence. If the convergence criteria are satisfied, finish the analysis.

3. Read final displacements from the GPU.

4. Clean up the GPU memory.

2.5 Evaluation of the modelling results accuracy

In image-guided surgery, accuracy of tissue motion prediction is typically assessed by evaluating the accuracy of alignment between the registered position of the preoperative image predicted by the non-rigid registration algorithm and the actual patient position established by an intraoperative image or navigation system. Universally accepted “gold standards” for such evaluation have not been developed yet (Chakravarty et al., 2008). Objective metrics of the images alignment can be provided by automated methods using image similarity metrics, such as e.g. Mutual Information (Viola and Wells III, 1997; Wells III et al., 1996), Normalised Cross-Correlation (Rexilius et al., 2001) and Dice similarity coefficient (Dice, 1945; Zou et al., 2004). From the perspective of validation of biomechanical models for computing the deformation field within the brain, one of the key deficiencies of such metrics is that they quantify the alignment error in terms that do not have straightforward geometrical interpretation in terms of Euclidean distance. Therefore, validation of predictions obtained using biomechanical models has been often done using landmarks manually selected by experts in the MRIs (Ferrant et al., 2002; Hu et al., 2007). Although interpretation of the results of landmarks-based validation is very straightforward, the method provides accuracy estimation only at the landmark locations. Furthermore, determining these locations is typically very time consuming and its accuracy relies on the experience of an expert (Miga et al., 1999).

When evaluating the accuracy of the predicted brain deformation, we followed the studies by Archip et al. (2007) and Oguro et al. (2010) who used 95-percentile Hausdorff distance as the registration error measure. The Hausdorff distance H(A, B) (Hausdorff, 1957; Fedorov et al., 2008) between set A (in this study: non-rigidly registered preoperative surface of the ventricles) and set B (in this study: surface of the ventricles obtained from the intraoperative image segmentation) is denoted as:

$$H(A,B)=\max \left\{h\right(A,B),h(B,A\left)\right\},$$ Eq. (7)

where h(A,B) is the maximum distance from any of the points in set A to set B, and h(B,A) is the maximum distance from any of the points in set B to set A. h(A,B), and analogically h(B,A), is calculated using the following formulae (Fedorov et al., 2008):

$$h(A,B)={\max }_{a\in A}\left\{d\right(a,B\left)\right\},$$ Eq. (8)

where a is a point in set A, and d is the Euclidean distance from point a to the nearest point b in set B:

$$d(a,B)={\min }_{b\in B}\Vert a-b\Vert .$$ Eq. (9)

Predicting the tumour’s intraoperative position is one of the key motivations of image-guided neurosurgery. However, as it is very difficult to reliably determine tumour boundaries in intraoperative images, we do not provide Hausdorff distances for tumour surfaces. From our experience, the segmentation uncertainty dominates this measure and consequently its utility in assessing tumour registration accuracy would be doubtful. Instead we provide qualitative evidence of the appropriateness of our methods by showing detailed intraoperative images with overlaid contours of tumours and ventricles predicted by our models.

3. Results

For Cases 1 to 5, it took between 30 s (Case 1) and 38 s (Case 5) of computation on a standard personal computer (Intel E6850 dual core 3.00 GHz processor, 4 GB of internal memory, Windows XP operating system) to predict the brain deformations using our specialised finite element algorithms. The computations using the NVIDIA CUDA implementation of our algorithms were performed on a NVIDIA Tesla C870 graphics processing unit, which resulted in computation times of less than 4 s for all the analysed craniotomy cases.

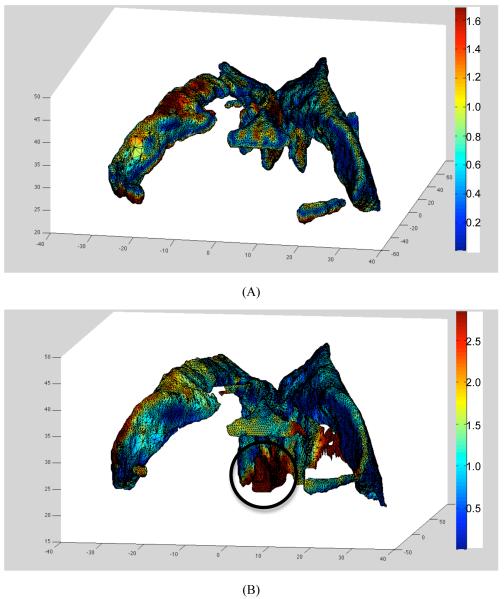
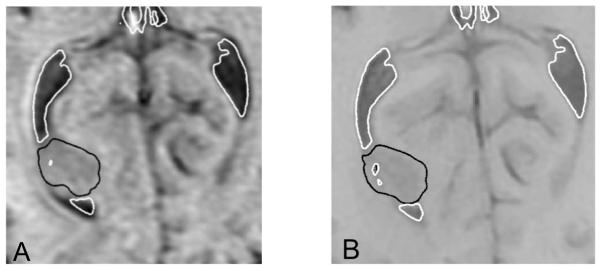
The 95-percentile Hausdorff distance (used here as the registration error measure) between surface of the ventricles obtained by registration (i.e. warping using the predicted deformation field) of the preoperative segmentation and intraoperative surface of the ventricles determined from the intraoperative image segmentation was between 0.9 mm (for Case 4) and 2.8 mm (for Case 2), see Table 2. This compares well with the voxel size (0.86×0.86×2.5 mm³) of the intraoperative MRIs. Furthermore, the 75-percentile Hausdorff distance was at most 1.2 mm which is well within the intraoperative MRI voxel size. Some of the registration errors reported in Table 2 could be related to the differences in segmentation of the preoperative and intraoperative images. As segmentation is a difficult and subjective process and quality of the intraoperative images in terms of the resolution and contrast is inferior to that of the preoperative images, some uncertainties are unavoidable. For instance, in Case 2 for which the largest (2.8 mm) 95-percentile Hausdorff distance between the registered and intraoperative surfaces of ventricles was observed, the differences between the registered and intraoperative surfaces are localised in the third ventricle area (Fig. 4B). Comparison of Fig. 4A and Fig. 4B clearly suggests that this localisation is due to the differences in ventricles’ segmentation in the preoperative and intraoperative images rather than actual non-rigid registration error caused by inaccuracies in predicting the intraoperative deformations.

Table 2.

95-, 75-, 50- and 25-percentile Hausdorff distance between surface of the ventricles obtained by registration (i.e. warping using the predicted deformation field) of the preoperative segmentation and intraoperative surface of the ventricles determined from the intraoperative image segmentation. The 95-percentile Hausdorff distance (numbers in bold font) was used as the registration error measure. Case 6 was analysed in our previous studies (Joldes et al. 2009a; Joldes et al. 2009b; Wittek et al., 2007; Wittek et al., 2009). The results are presented to one decimal place as we previously determined (Wittek et al., 2007) that this is approximately the accuracy of computations using finite element algorithms of the type applied in this study (i.e. explicit integration in the time domain and elements with linear shape functions).

	95-percentile distance [mm]	75-percentile distance [mm]	50-percentile distance [mm]	25-percentile distance [mm]
Case 1	1.3	0.6	0.4	0.3
Case 2	2.8	1.2	0.8	0.4
Case 3	1.9	1.1	0.6	0.4
Case 4	0.9	0.5	0.4	0.2
Case 5	1.5	0.8	0.5	0.3
Case 6	2.0	1.2	0.8	0.6

Fig. 4.

Registration results for Case 2. (A) Surface of the ventricles obtained by registration (i.e. warping using the predicted deformation field) of the preoperative segmentation with distance distribution (magnitude in millimetres in a colour code) to surface of the ventricles determined by segmentation of the intraoperative images. This is the distance h(A,B) as defined by Eq. (8). (B) Surface of the ventricles determined by segmentation of the intraoperative images with distance distribution (magnitude, up to 95-percentile distance, in millimetres in a colour code) to surface of the ventricles obtained by registration. This is the distance h(B,A) in Eq. (7). In this case, the Hausdorff distance H(A,B) equals the distance h(B,A), see Eqs. (7), (8) and (9). Note the concentration of misaligment between the registered and intraoperative surfaces in the third ventricle area (indicated by a circle) due to the differences between preoperative (A) and intraoperative (B) segmentations.

The conclusions derived using the 95-percentile Hausdorff distance as the registration error measure are consistent with those obtained through detailed comparison of the contours of ventricles in the intraoperative images and the ones predicted by the finite element brain models developed in this study. The comparison indicates good overall agreement between the predicted and actual intraoperative contours (Figs. 5 and 6). However, some local misalignment between these contours is clearly visible. Examples of such misalignment include the third ventricle area in Case 2 (Fig. 4 and Fig. 5B), discussed in the previous paragraph, and the posterior horn of the left lateral ventricle in the area adjacent to the tumour in Case 5 (Fig. 8) discussed in detail in the next paragraph.

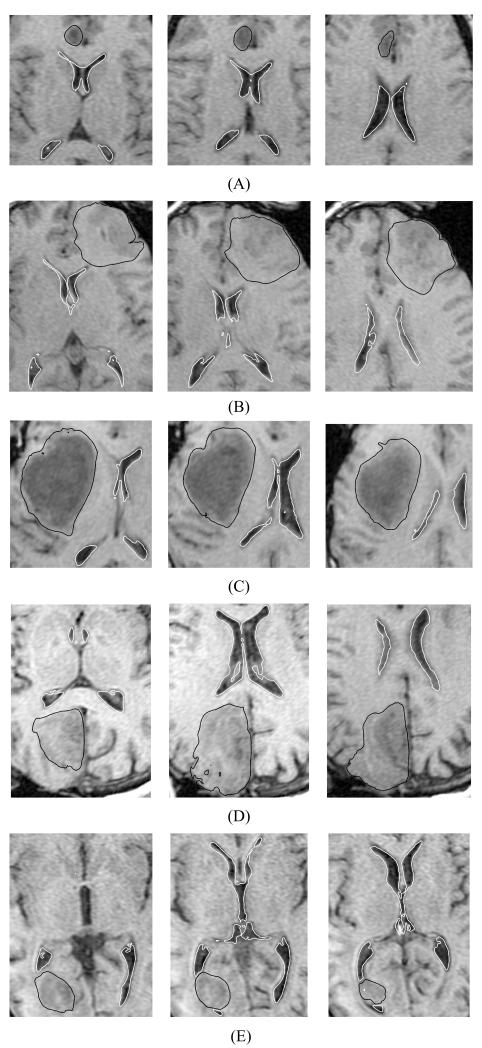
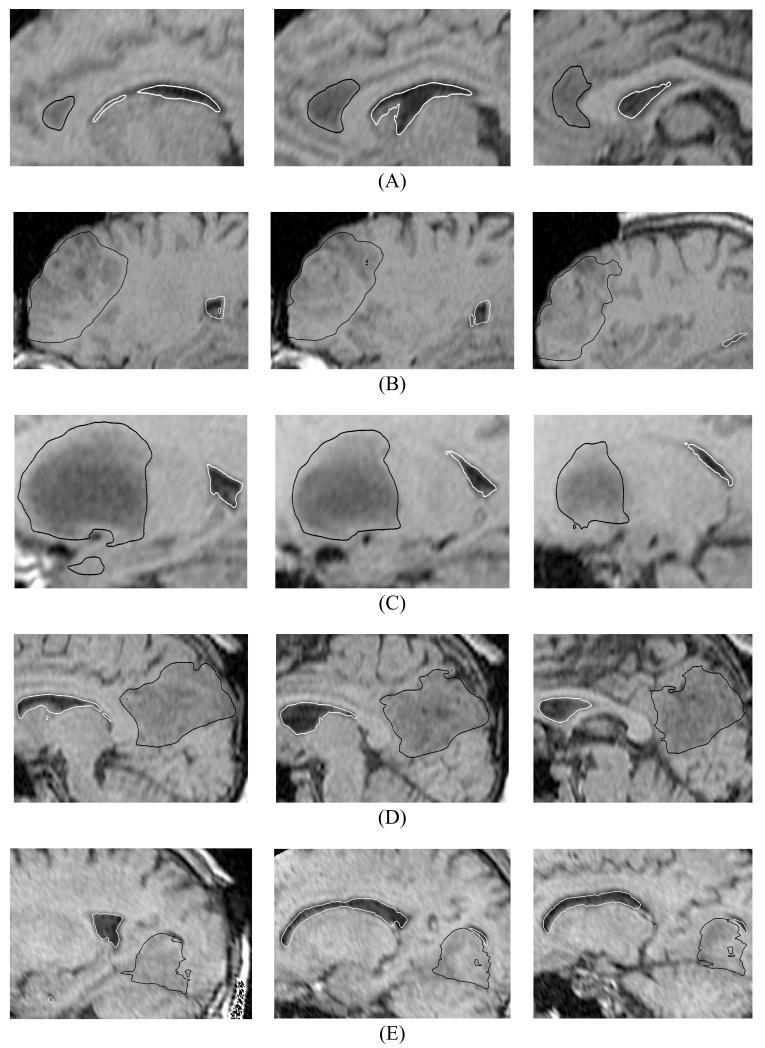
Fig. 5.

The registered (i.e. deformed using the calculated deformation field) preoperative contours of ventricles (white lines) and tumour (black lines) overlaid on the intraoperative magnetic resonance images. Three transverse image sections are presented for each case, selected so that the tumour and ventricles are clearly visible. The images were cropped and enlarged. (A) Case 1; (B) Case 2; (C) Case 3; (D) Case 4; and (E) Case 5. The sections’ location is explained in Fig. 7. For Case 2 (row B – left-hand-side figure), note the differences between registered contours and intraoperative image in the third ventricle area.

Fig. 6.

The registered (i.e. deformed using the calculated deformation field) preoperative contours of ventricles (white lines) and tumour (black lines) overlaid on the intraoperative magnetic resonance images. Three sagittal image sections are presented for each case, selected so that the tumour and ventricles are clearly visible. The images were cropped and enlarged. (A) Case 1; (B) Case 2; (C) Case 3; (D) Case 4; and (E) Case 5. The sections’ location is explained in Fig. 7.

Fig. 8.

Case 5, section H3 (for section H3 definition see Figure 7E): (A) The registered (i.e. deformed using the calculated deformation field) preoperative contours of ventricles (white lines) and tumour (black lines) overlaid on the intraoperative magnetic resonance images. Note local misregistration in the posterior left horn area. This figure highlights also the difficulties with reliable tumour segmentation in the intraoperative images (the tumour boundaries are very difficult to distinguish). (B) The segmented preoperative image. Segmentation of the ventricles is indicated by white lines, and segmentation of the tumour — by black lines. Note appreciable differences in shape and size of the posterior horn of left lateral ventricle between the intraoperative and preoperative images in the area adjacent to the tumour. The horn is appreciably larger in the intraoperative than preoperative image, which indicates that it was compressed by the tumour.

Six cases of craniotomy-induced brain shift analysed here are characterised by tumours located in different parts of the brain (for details see Medical Context section). The results presented in Table 2 exhibit no correlation between the tumour location and registration errors measured by 95-percentile Hausdorff distance that tends to estimate the maximum misalignment between the intraoperative and registered preoperative images. However, comparison of the preoperative, intraoperative and registered images indicates that detailed information about anatomical structures required for building accurate biomechanical models may be difficult to obtain for tumours that affect geometry of such structures. For instance, in Case 5, the posterior horn of the left lateral ventricle was compressed by the tumour. Consequently, large part of the horn could not be seen in the preoperative images (Fig. 8). This, in turn, limited the accuracy when simulating the posterior horn of the left lateral ventricle in the biomechanical model for predicting the brain deformations in Case 5, which led to local misregistration (Fig. 8).

4. Discussion

In this study, we used finite element meshes consisting of hexahedral and tetrahedral elements combined with the specialised non-linear (i.e. including both geometric and material non-linearities) finite element algorithms to predict the deformation field within the brain for six cases of craniotomy-induced brain shift. Despite abandoning unrealistic linearisation (i.e. assumptions about infinitesimally small brain deformations during craniotomy and linear stress–strain relationship of the brain tissues) typically applied in biomechanical models to satisfy real-time constraints of neurosurgery we were able to predict deformation field within the brain in less than 40 s using a standard personal computer (with a single 3 GHz dual-core processor) and less that than 4 s using a graphics processing unit (NVIDIA Tesla C870) for finite element meshes of the order of 18 000 nodes and 30 000 elements (~50 000 degrees of freedom). This computation times compare well with the times reported in the studies using linear finite element procedures and advanced computation hardware. For instance, Warfield et al. (2002) reported the time of 27 s when computing the linear finite element brain model consisting of 43584 nodes using the Sun Microsystems Sun Fire 6800 workstation with twelve 750 MHz UltraSPARC-III processors. Similarly, the computation times reported here for the NVIDIA CUDA implementation of our finite element algorithms, indicate dramatic improvement in computation speed in comparison to our previous results obtained using commercial non-linear finite element solvers: Wittek et al. (2009) reported computation time of over 1700 s when predicting the brain deformations using a model with around 50 000 degrees of freedom implemented in non-linear finite element solver LS-DYNA™.

Despite that we used only very limited intraoperative information (deformation on the brain surface exposed during the craniotomy) when prescribing loading for the models and did not have patient-specific data about the tissues mechanical properties, our application of the specialised non-linear finite element algorithms made it possible to obtain a very good agreement between the observed in the intraoperative MRIs and predicted positions and deformations of the anatomical structures within the brain (Figs. 5 and 6, Table 2). This is confirmed by the fact that 95-percentile Hausdorff distance between surface of the ventricles obtained by registration and intraoperative surface of the ventricles determined from the intraoperative images was at most 2.8 mm which compares well with the voxel size (0.86×0.86×2.5 mm³) of the intraoperative images. As explained in Results section, the alignment errors (as measured by 95-percentile Hausdorff distance) reported in Table 2 could be related to the differences in segmentation of the preoperative and intraoperative images.

In this study, we demonstrated the utility of specialised non-linear finite element algorithms for soft tissue modelling in real-time predicting of the deformation field within the brain for six cases of craniotomy-induced brain shift. Before non-linear biomechanical models using state-of-the-art finite element algorithms, such as those applied in this study, can become a part of clinical systems for image-guided neurosurgery, reliability and accuracy of such models must be confirmed against much larger data sample than six cases of craniotomy-induced brain shift analysed here.

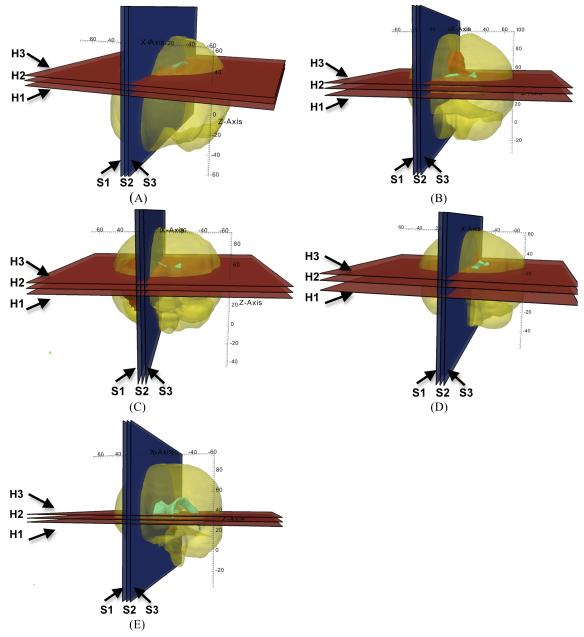
Fig. 7.

Location of the planes for sections shown in Figs. 5 and 6. (A) Case 1; (B) Case 2; (C) Case 3; (D) Case 4; and (E) Case 5. H1: section shown in the left-hand-side column of Fig. 5; H2: section shown in the central column of Fig. 5; H3: section shown in the right-hand-side column of Fig. 5; S1: section shown in the left-hand-side column of Fig. 6; S2: section shown in the central column of Fig. 6; and S3: section shown in the right-hand-side column of Fig. 6. The axes’ coordinates are in millimetres.