Genetic analysis of biological pathway data through genomic randomization

Abstract

Genome Wide Association Studies (GWAS) are a standard approach for large-scale common variation characterization and for identification of single loci predisposing to disease. However, due to issues of moderate sample sizes and particularly multiple testing correction, many variants of smaller effect size are not detected within a single allele analysis framework. Thus, small main effects and potential epistatic effects are not consistently observed in GWAS using standard analytical approaches that consider only single SNP alleles. Here we propose unique methodology that aggregates variants of interest (for example, genes in a biological pathway) using GWAS results. Multiple testing and type I error concerns are minimized using empirical genomic randomization to estimate significance. Randomization corrects for common pathway-based analysis biases such as SNP coverage and density, linkage disequilibrium, gene size and pathway size. PARIS (Pathway Analysis by Randomization Incorporating Structure) applies this randomization and in doing so directly accounts for linkage disequilibrium effects. PARIS is independent of association analysis method and is thus applicable to GWAS datasets of all study designs. Using the KEGG database as an example, we apply PARIS to the publicly available Autism Genetic Resource Exchange (AGRE) GWA dataset, revealing pathways with a significant enrichment of positive association results.

Introduction

Genome wide association studies (GWAS)have successfully identified numerous genetic risk factors for many common diseases, however, only single nucleotide polymorphisms (SNPs)with the strongest p-values are generally declared significant due to issues arising from multiple testing and type I error concerns(Manolio et al., 2008). Many biologically meaningful associations of lower effect size are thus left languishing in the sea of false-positive associations. Systematic grouping of these SNPs could reveal novel biological pathways or systems underlying disease susceptibility. To detect these effects, multiple methods have been proposed(Askland et al., 2009; Holmans et al., 2009; Hong et al., 2009; Lesnick et al., 2007; O’Dushlaine et al., 2009; Wang et al., 2007), most focusing on examining a subset of genes functionally related in biological pathways.

Pathway-based analyses of GWA data are subjected to multiple biases including gene size, pathway size, chip coverage and linkage disequilibrium (LD)patterns. At a standard type I error rate of α=0.05, each SNP tested has a 5% chance of being associated with disease by chance alone. Testing more SNPs therefore increases the number of false positive associations. Thus, genes with more SNPs tested have an a priori increased likelihood of having a greater number of markers associated by chance. Larger pathways with more genes similarly increase this potential bias. Furthermore, if a SNP is falsely associated, it is likely that other SNPs in LD with it will be falsely associated as well. The aforementioned pathway analysis methods elegantly control for the issues related to multiple testing biases. Several of the more cited methods (and the one presented in this manuscript) are described in Table 1.

Table 1.

Pathway-based analysis from GWA data methods comparison

Method Used	Pathway Databases available for use	Requires original dataset	LD correction	Gene Size Correction	Study designs allowed	Reference
PARIS	any	No	genomic randomization	yes	any	Yaspan, 2010
SRT	any	Yes	case-control status randomization	yes	case-control§	O’Doulishaine, 2009
EVA	any	Dependent on correction (LD)	done prior to EVA analysis	Done prior to EVA analysis	any	Askland, 2009
ProxyGeneLD	any	No	Bonferroni-type based # SNPs typed in areas of LD and LE	yes	any	Hong, 2009
ALIGATOR	GO	No	none (assumes LD = across pathways)	yes	any	Holmans, 2009
Modified GSEA	GO, KEGG	Yes	case-control status randomization	yes	case-control§	Wang, 2007

^§modifiable for use with family-based datasets by using non-transmitted alleles to create pseudo-controls

We sought a pathway analysis method that would operate independent of study design and would be fully and easily customizable while maintaining independence of the statistical methodology used to calculate single locus association values. This method would regard the pathway as a single unit, rather than a collection of the genes within. Several existing methods have been designed specifically for pathway enrichment analysis from GWA data, but each has its limitations. For example, many require the original dataset for a computationally intensive permutation of case-control status to account for multiple testing, gene size/SNP coverage and LD biases. In this design, datasets arising from family based designs are converted to case-pseudo control structure and re-analyzed for current pathway analysis algorithms. Other methodologies are independent of study design, but are limited by use of specific pathway databases. An ideal method would function similarly regardless of study design, and therefore would need to control for multiple testing, gene size/SNP coverage and LD biases in novel fashion. PARIS (Pathway Analysis by Randomization Incorporating Structure) is a pathway analysis algorithm that functions independently of study design and assigns significance to a pathway through permutation of the genome rather than permutation of affectation status. Such a design does not require the original dataset and is far less computationally intensive than methods requiring permutation of affectation status. In this paper we utilize the KEGG collection of pathways, but in theory, this method can be applied to any pre-existing database or novel gene-set. To our knowledge, PARIS represents the first methodological attempt at permutation of the genome to account for potential biases in analysis.

Methods

Concept of Features

Pathway analysis algorithms assess the presence of significant entities, usually either gene or SNP, over-represented within a biological pathway or ad hoc gene-set. Throughout this paper our references to “pathway” include both concepts. PARIS also assesses the presence of significant entities; however, PARIS approaches this somewhat differently by counting the number of significant p-value associations in a pathway for independently inherited “features” rather than using a gene-based p-value or individual SNPs. Features are defined as blocks of linkage disequilibrium (LD) and individual SNPs in linkage equilibrium (LE). Therefore, we refer to LD blocks as ‘LD Features’ and SNPs in regions of LE as ‘LE features’. LD feature boundaries were generated using Hapmap CEPH samples (release 27) using the Gabriel et. al method as implemented in Haploview using the default parameters(Barrett et al., 2005). LD boundaries are determined by the 5′ and 3′ SNP positions of the LD block. LE boundaries were the genomic inverse to areas of LD. Conceptually, PARIS allows for analysis of different ancestral populations and LD calculation algorithms, however, as proof of concept, we chose the Gabriel et. al method as it is widely used and straightforward(Gabriel et al., 2002). Block calling approaches such as the Gabriel et. al method generally look for patterns of high LD among sequential SNPs and thus do not require that all SNPs in an LD block be in high LD with all other SNPs of the LD block. Therefore in some instances, a single LD feature may represent a somewhat heterogeneous collection of signals. We continue to explore alternative LD-based methods to better accommodate this scenario. Features are visualized and further described in Figure 1.

Fig. 1. Visual representation of genomic ‘features.’.

Depicted is an interval on chromosome 2 containing 18 SNPs. After applying the algorithm of Gabriel et. al, as implemented in Haploview, we identified four regions of LD and two SNPs that do not reside in areas of LD (denoted by arrows). Thus, this region of the genome has four LD features and two LE features for a total of six features. On the matrix, red indicates D′ = 1 (LOD ≥ 2), periwinkle indicates D′ = 1 (LOD < 2), shades of pink indicate D′ < 1 (LOD ≥ 2), and white indicates D′ < 1 (LOD < 2). Numbers in the squares indicate the r² value between the two SNPs tested. A blank red square indicates an r²=1

Binning of LD Features

PARIS first determines the structure of the pathway being tested by determining the number and size of its features based on the genomic positions of the genes within the pathway. If any part of the feature overlaps the 5′ to 3′ position of the gene, it is said to reside in that gene and is included in its feature count. Using this information, PARIS creates randomized feature collections culled from the remainder of the genome that mimic the size and number of features of the actual pathway being tested. For example, if a pathway has 100 SNPs categorized as LE features, PARIS would select 100 LE features at random from the genome (not including the 100 SNPs in the pathway being tested). Unlike single SNPs, LD features vary in size, so the distribution of LD feature size (measured as the number of SNPs tested within the feature) should be similar to the distribution of LD features size from the actual pathway. Complicating random selection is the fact that there are a far greater number of smaller features than larger ones. A distribution of block sizes throughout the genome as calculated by the Gabriel et. al method using the default parameters in Haploview is shown in Table 2. Consider a large LD feature consisting of 101 SNPs as tested in a dataset, in this case the CEU HapMap samples. Looking at Table 2, a comparable block of 101 SNPs or greater is relatively rare in the genome (n=898 of 134,305 total LD features). As a result, selecting a sufficient number of unique blocks of equal size for permutation tests that estimate an empiric p-value for a pathway is not possible. While there are considerably more SNPs typed in the HapMap samples than in a standard dataset, this observation is inherent to any genome-wide dataset regardless of genotyping platform. Therefore PARIS places (by size)LD features containing two or more typed SNPs into bins of roughly 10,000 features each. To accomplish this, PARIS assigns each LD feature a unique ID and first sorts by feature size. Next, the order of features within each size is randomized. For example, PARIS randomly sorts all of the LD features of SNP size 2, 3, 4, etc, separately so that the list is still in order by size, but LD features of each size are randomly ordered. PARIS assigns features to bins in this order, making cutoffs to achieve the desired feature per bin size. This is done uniquely for each GWAS as differing SNP chips and quality control efforts will cause the SNP distribution within and across features to vary from dataset to dataset. Features are compared to other features in their same bin by random selection, enabling comparison of similarly sized LD features. Through the creation of bins with approximately 10,000 LD features each we enable unique selection of LD features of similar, although not exact, size with which to compare across the full range of observed sizes. Table 3 shows the LD feature size distribution in an example GWAS dataset that uses the Illumina 550k genotyping platform.

Table 2.

LD Feature Distribution in CEU HapMap Samples

Number of SNPs per Feature	# Features
2	24386
3	16771
4	8461
5	8003
6	7605
7	6346
8	5612
9	4828
10	4226
11–20	24091
21–30	10202
31–40	5287
41–50	2998
51–60	1813
61–70	1177
71–80	788
81–90	486
91–100	327
101–150	693
151–200	154
201–323	51

Table 3.

Binned LD feature distribution

Bin	Feature Count	Avg. LD Feature Size (# SNPs)	LD Feature Size Distribution (# SNPs)
1	9986	2	2-2
2	9986	2	2-2
3	9985	2.76	2–3
4	9985	3.25	3–4
5	9985	4.15	4–5
6	9985	5.34	5–6
7	9985	7.04	6–8
8	9985	12.03	8–53

PARIS Methodology

Using the unique LD and LE feature-based signature of the actual pathway as a template, PARIS is designed to create multiple randomized collections of features culled from the remainder of the genome to mimic the size and number of features of the actual pathway under investigation. The overall methodology of PARIS is depicted in Figure 2. PARIS calculates an empiric p-value for each pathway under investigation through comparison of the number of statistically significant features in the actual pathway and the multiple randomized collections of features. We deemed a feature to be statistically-significant if it contains at least one SNP having a p-value of < 0.05(a user defined criterion). Randomization of LD and LE features drawn from the entire genome allows PARIS to control for gene and pathway size biases inherent to pathway analysis of GWAS data. It is important to note that although PARIS calculates empiric p-values within each pathway, the testing of multiple pathways by PARIS must still be taken into account.

Fig. 2. Flowchart describing overall methodology of significance assignment to a pathway.

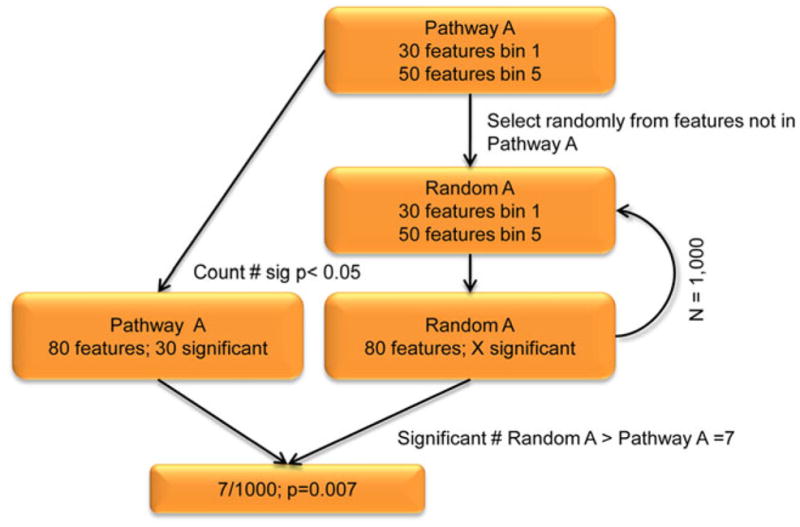
As an example, we analyze “Pathway A”, consisting of 80 total features (30 from bin 1 and 50 from bin 5). We consider a feature significant if any SNP found within has a p<0.05, and perform 1,000 permutation tests to assign significance to Pathway A. In our example Pathway A, we count 30 significant features. We randomly select from bins 1 (n=30 features) and 5 (n=50 features) to mimic the structure of Pathway A, creating “Random A”. Features are selected without replacement. We then count the number of significant features in Random A, replacing all features to their respective bins for the next iteration. We then create 999 more Random A pathways, tallying the number of times there are more significant features (p<0.05) in Random A than in Pathway A. This happens seven times in our hypothetical example giving us a p-value for Pathway A of 0.007.

Detailed Analysis of Pathways of Interest

Once pathways of interest are identified, PARIS conducts a detailed analysis of each pathway. In a predefined pathway database, it is possible for a single gene to be present in multiple pathways. It is of interest to look at each pathway in detail to identify the source of the signal. For example, is the pathway seen as significant because of one gene with many significant features or are many genes in the pathway contributing to the signal? Through an examination of each gene in the pathway we can determine which genes are responsible for the significant pathway signal. To assess the contribution of each gene to the overall pathway signal, we perform a permutation test based on the features present in the single gene to assign an empirical p-value to each gene in the pathway, referred to the “Gene P-value”. This analysis can be thought of, and is methodologically identical to a PARIS pathway analysis in which the pathway contains one gene. It should be noted that this statistic is meant to assess contribution of the features within a gene to the significance of the overall pathway and is not designed to test for significance within any given gene. Sample output from this procedure of PARIS is seen in Table 4, and visualized in Figure 3.

Table 4.

Detailed analysis of KEGG hsa:00072 (Synthesis and degradation of ketone bodies)

Gene Name	Ensembl ID	Feature Count (Total)	Simple Feature§ Count	Simple Feature§ Count p<0.05	Complex Feature‡ Count	Complex Feature‡ Count p<0.05	Gene P-value	Other Pathways (path:hsa)
HMGCS2	ENSG00000134240	12	5	0	7	0	1	00280,00650,00900,01100,03320
HL	ENSG00000117305	1	0	0	1	1	< 0.001	00280,00650,01100
OXCT2	ENSG00000198754	5	2	0	3	0	1	00280,00650
ACAT1	ENSG00000075239	3	0	0	3	1	0.114	00071,00280,00310,00380,00620, 00640,00650,00900,01100
BDH1	ENSG00000161267	14	7	0	7	4	0.005	00650,01100
BDH2	ENSG00000164039	5	1	1	4	2	< 0.001	00650,01100
OXCT1	ENSG00000083720	5	2	1	3	2	0.001	00280,00650
HMGCS1	ENSG00000112972	2	1	0	1	0	1	00280,00650,00900,01100
ACAT2	ENSG00000120437	9	6	0	3	1	0.211	00071,00280,00310,00380,00620, 00640,00650,00900,01100

^§a single SNP in an area of LE

^‡an LD block containing two or more typed SNPs

Fig. 3. Visual representation of hsa0072: Synthesis and degradation of ketone bodies.

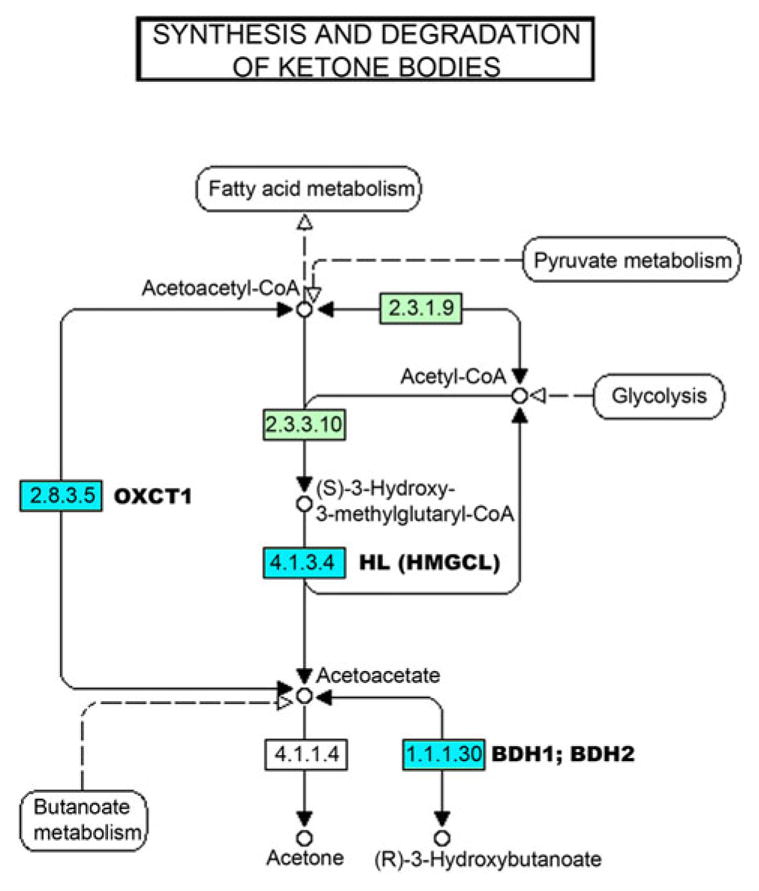
Modified from the Kyoto Encyclopedia of Genes and Genomes website(http://www.genome.jp/kegg-bin/show_pathway?hsa00072) (Kanehisa and Goto, 2000), we present a visual depiction of the data from Table 4. In green are genes annotated in the KEGG database, in white are genes not annotated in the KEGG database. In blue are genes that show nominal significance in the “Gene p-value” test in the detailed pathway analysis, and the gene symbols for the nominally significant genes are listed beside the KEGG annotation. Genes that were not nominally associated, but in the pathway are: 2.3.1.9 = ACAT1 and ACAT2; 2.3.3.10 = HMGCS1 and HMGCS2; 2.8.3.5 = OXCT2.

Results

Methodology Testing and Bias Reduction

We performed tests to assess bias reduction using the publicly available Autism Genetic Resource Exchange (AGRE) GWAS dataset genotyped on the Illumina 550k platform and analyzed by Ma et. al(Ma et al., 2009). Full details of the GWAS analysis are available in that manuscript. This analysis consists of 487 Caucasian AGRE families. We first tested the efficacy of our method through a negative control by creating collections of randomly culled features to mimic the structure of all actual KEGG pathways. For example, if a KEGG pathway was comprised of 10 features from bin 1 and 10 features from bin 5, we selected 10 features randomly from both bins 1 and 5 to mimic the genetic architecture of the pathway; the end result being 204 collections of randomly culled features with the same feature structure as the 204 actual KEGG pathways. This provides an estimate of the false positive rate. This analysis was repeated 100 times. For 204 KEGG pathways we expect to see on average ~10 significant at p<0.05. We saw, on average, 11.9 pathways associated per repetition at p<0.05. Thus, our method sees 5.9% pathways as significant by chance.

We assessed the impact of PARIS on gene size, pathway size and LD block structure on PARIS. We reasoned that if these variables were confounding the results it would be evident in the final empiric p-values assigned to each pathway. To test the effect of gene size, pathway size and LD block structure, we compared PARIS results to a simple method in which we deemed a particular gene in a pathway statistically significant if two or more SNPs tested had p<0.05 in the single-allele analysis. We performed a χ² test on the number of genes in the pathway meeting this criterion relative to the expected number of significant genes. The expected number of significant genes was based on the pathway size in number of genes. For example, in a pathway of 100 genes, the expectation is 5 significant genes by chance alone at p<0.05. In this scenario, the number of SNPs tested per gene and the number of genes in the pathway should affect the empiric p-value assigned to each pathway.

Linear regression analyses of the p-value assigned to a particular pathway on gene size, pathway size and LD block structure variables were calculated (Stata intercooled for Windows 9.0). The linear regression coefficients and p-values for these analyses are indicated in Table 5. Results for log-transformed and untransformed p-values were similar. Results for untransformed p-values are presented. It is apparent that the p-value assigned to a pathway is significantly correlated with pathway size and LD structure(“Comparison Method” in Table 5) whereas the implementation of PARIS(“PARIS” in Table 5) removes these significant relationships.

Table 5.

Linear Regression of Final P-Value assigned to a pathway with size and LD biases

	No. Features/Pathway		Avg. Feature Size (No. SNPs)		No. Genes/Pathway
Analysis	Coef	P>t	Coef	P>t	Coef	P>t
PARIS	2.52E-05	0.093	−6.70E-06	0.382	9.10E-04	0.126
Negative Control	1.31E-05	0.502	−1.86E-05	0.063	2.53E-04	0.744
Biased Negative Control	−1.34E-04	0.000	−4.30E-06	0.711	−5.34E-03	0.000
Comparison Method	−1.31E-03	0.000	2.90E-04	0.000	−3.88E-02	0.000

We also slightly altered the negative control described previously to intentionally introduce a size-related bias. By inflating the size of the LD features, we reasoned we should see a return of size related biases to final p-values of a pathway. Thus, instead of selecting LD features from bins at random to create a random collection of features, we created a size-biased collection of features by selecting the largest features in their respective bins. For example, if a pathway had 7 features from bin 9, instead of choosing 7 features from bin 9 at random, we chose the 7 largest features from bin 9. We observed that by artificially inflating LD feature size, bias could be reinstated (“Biased Negative Control” in Table 5).

Thus, PARIS reduces bias in a quantifiable manner lessening the effect on p-value assigned to the pathway from the parameters tested by roughly two orders of magnitude when compared to our simple χ² based method. Notably, the trend of each relationship was reversed. While the relationship of number of features per pathway to p-value trends towards significance (p=0.093), bias is substantially reduced from the comparison method. Furthermore, by artificially inflating pathway feature size, we were able to re-insert bias related to gene and pathway size, suggesting that our method appropriately confronts these issues.

We observed that as the size of the LD features increases, their distribution within the bins widens. For example, bin 8 (Table 3) has a LD feature size distribution of 8–53 SNPs. We considered the possibility that altering the number of bins could affect results as it would alter the distribution of feature sizes. We therefore tested the number of bins, examining 5, 10 (as described) and 20 bins. For all KEGG pathways tested, the empiric p-value assigned to the pathway varied only slightly as a result of doubling or halving the number of bins (data not shown).

Application of PARIS

As an example of applying PARIS, we used single-SNP data from a family-based study design dataset; the AGRE autism study as analyzed by the pedigree disequilibrium test (PDT) from ananalys is that includes only the Caucasian AGRE families(Ma et al., 2009). Samples were genotyped on the Illumina 550k gene chip and full quality control and analysis methods are described elsewhere (Ma et al., 2009). We used a threshold of p<0.05 to determine feature significance and extended the boundaries of each gene by 50 kb in each direction to account for possible promoter variation effects.

Using PARIS, we found 17 of 204 (8.3%) KEGG pathways in which nominally significant single-allele p-values were enriched (Table 6). Upon closer inspection many pathways are interrelated and driven by signals from features in the same genes. For example, four pathways(hsa00040, hsa00053, hsa00980, hsa00860) are driven by signals in the same core set of genes, those in the uridine diphosphate glycosyltransferase 2 family of proteins (UGT2A1, UGT2A3, UGT2B4, UGT2B7, UGT2B11, UGT2B28). These genes are located contiguously within a 2 MB region at chromosome 4q13.2. The pathway incorporating these genes and the smallest number of other genes is the most statistically significant (hsa00040; p<0.001). As more genes are added to this core set and the pathways increase in size, significance diminishes. Full detailed output for each pathway (by gene) identified by PARIS as nominally significant is seen in the Supplemental Tables.

Table 6.

Nominally significant KEGG pathways identified by PARIS in the AGRE autism GWAS

Pathway Name	Total SNP Count	Description	P-Value	Gene Count	Gene Count p<0.05	Simple Feature§ Count	Simple Feature§ Count p<0.05	Complex Feature‡ Count	Complex Feature‡ Count p<0.05
path:hsa00040	370	Pentose and glucuronate interconversions	< 0.001	16	10	52	6	53	16
path:hsa04120	3803	Ubiquitin mediated proteolysis	< 0.001	133	62	709	49	538	117
path:hsa00072	219	Synthesis and degradation of ketone bodies	0.001	9	6	24	2	32	11
path:hsa00740	476	Riboflavin metabolism	0.001	16	6	114	14	73	13
path:hsa00053	458	Ascorbate and aldarate metabolism	0.008	16	10	71	8	69	16
path:hsa04060	5911	Cytokine-cytokine receptor interaction	0.011	262	105	1266	67	921	161
path:hsa04710	414	Circadian rhythm-mammal	0.011	13	8	10100	7	66	15
path:hsa05211	2323	Renal cell carcinoma	0.011	70	43	516	32	338	62
path:hsa05221	1792	Acute myeloid leukemia	0.012	56	25	423	30	259	45
path:hsa00534	1242	Heparan sulfate biosynthesis	0.014	26	18	258	18	201	37
path:hsa05220	2558	Chronic myeloid leukemia	0.018	75	42	567	33	376	69
path:hsa04330	1521	Notch signaling pathway	0.019	46	26	356	23	217	40
path:hsa00980	1180	Metabolism of xenobiotics by cytochrome P450	0.02	58	21	201	13	174	36
path:hsa00480	1021	Glutathione metabolism	0.03	47	24	215	11	152	32
path:hsa00860	808	Porphyrin and chlorophyll metabolism	0.037	32	19	138	11	127	24
path:hsa00760	763	Nicotinate and nicotinamide metabolism	0.039	24	14	171	11	122	23
path:hsa00730	307	Thiamine metabolism	0.048	8	3	84	10	43	5

^§a single SNP in an area of LE

^‡an LD block containing two or more typed SNPs

Discussion

Here we present a novel method for identification of pathways or gene-sets by analysis for overrepresented statistically significant SNPs. PARIS assigns significance and corrects for multiple testing by randomization of the entire genome rather than affection status. PARIS directly incorporates genomic LD structure and is not subject to bias due to number of SNPs tested in a gene nor areas of differing LD structure; the first methodology to correct for these biases in this way. A potential weakness to the PARIS algorithm is the necessary binning procedure. As the size of LD features increases, their frequency decreases in the genome. While we acknowledge that the larger LD features are compared to a wider array of LD feature sizes(SNPs tested) than smaller ones due to binning, we did not observe bias in increasing (or decreasing) statistical significance towards pathways which contain the largest LD features. Conversely, features of modest size are numerous within the genome and are spread across multiple bins. This could bias results if the distribution of p-values of the features differed between the bins. However, we did not observe any difference in the distribution of p-values between bins of similar size(data not shown).

Other publicly available pathway analysis algorithms are listed in Table 1. Some methods were originally designed to analyze microarray studies. Others, such as ALIGATOR, ProxyGeneLD, the SRT and now PARIS were designed explicitly for pathway-based analysis of GWA studies. The method closest in ideology to PARIS is ProxyGeneLD, which utilizes the concept of “features” to determine the overall significance of a gene directly incorporating LD and gene size into the calculation(Hong et al., 2009). ProxyGeneLD determines a gene-wide p-value from the lowest p-value of the individual SNPs, or the lowest p-value in a cluster multiplied by the number of individual SNPs and clusters that fall within the gene boundaries; essentially a Bonferroni-style correction for the multiple independently inherited features within a gene. The user is then able to choose a final analysis program to examine enrichment of significant genes in a pathway and the authors demonstrate use of DAVID, GSEA-P (Gene Set Enrichment Algorithm) and IPA (Ingenuity Pathway Analysis). While the concept of LD and LE features is similar, PARIS differs from this method in several ways. First, PARIS permutes the genome rather than applying a Bonferroni-type correction to correct for multiple testing. In a Bonferroni-type correction, larger genes could be overly penalized, especially in studies of modest size. Second, while in this manuscript we use the Gabriel et. al method to define LD block structure, PARIS will allow for usage of LD block structure based on different methodologies. Finally, PARIS departs from the concept of using a gene-based p-value to determine significance of the pathway and considers the structure of the pathway as a whole.

We have shown that biases related to LD, chip coverage, gene and pathway size are significantly reduced compared to a naïve analysis. As proof of concept, we applied PARIS to a GWAS analysis of the Caucasian AGRE autism families. Our exploratory analysis identified seventeen pathways with overrepresented significant SNPs in the GWA analysis. Further analysis of the genes comprising several of these pathways identifies genes in the uridine diphosphate glycosyltransferase 2 family of proteins, located contiguously at chr4p13.2, underlie the significance seen in multiple pathways. The possibility exists that either overlapping features or the close proximity of these genes in which residual LD between the genes could be causing a spurious significant signal. The first scenario is unlikely as PARIS only counts features once per pathway, regardless of the number of genes it overlaps. The latter is a possibility, and was also noticed in the work of Hong et. al (2009), in that genes in close proximity retain a higher than basal amount of residual LD which could lead to false positives.

Another significant pathway, hsa00072 – Synthesis and degradation of ketone bodies (Figure 3, Table 4), helps to illustrate the potential for biological interpretation. This pathway was chosen for presentation due to its small size, but further exploration identifies several genes involved in acetoacetate metabolism as driving the signal of the overall pathway. These genes have not been associated with autism individually, however together they could affect acetoacetate levels, which can potentially lead to an elevation of GABA (γ-aminobutyric acid) content in synaptosomes(Greene et al., 2003). Multiple studies support a role for the GABA neurotransmitter system in autism susceptibility and with epilepsy and seizures, suggesting a potential common mechanism for these often co-morbid conditions(Blatt, 2005; Delahanty et al., 2009; Dhossche et al., 2002). Analyses of additional datasets will ultimately show if these genes and pathways are implicated in autism etiology.

Although we document the use of one pre-defined set of pathways, in theory, PARIS can be applied to any pre-existing database, novel gene-set or single gene. Furthermore, PARIS is fully customizable to suit user preferences. Although the default settings mirror those described in this manuscript, PARIS can be configured to use any LD feature bin size, significance threshold, or gene boundary extension the user desires. PARIS requires a simple input file that includes chromosome, SNP name and p-value (derived from the primary GWAS single-allele analysis). Finally, PARIS currently defines LD and LE feature boundaries based on the HapMap CEU Caucasian dataset and therefore is currently useful for datasets of similar ancestry. Further optimizations of PARIS will allow for multiple ancestries and LD determination algorithms.

PARIS is available for download at http://chgr.mc.vanderbilt.edu/ritchielab/subscriptions