Effect of the microstructure on the lifetime of dental ceramics

Abstract

Objectives

To evaluate the effect of the microstructure on the Weibull and slow crack growth (SCG) parameters and on the lifetime of three ceramics used as framework materials for fixed partial dentures (FPDs) (YZ - Vita In-Ceram YZ; IZ - Vita In-Ceram Zirconia; AL - Vita In-Ceram AL) and of two veneering porcelains (VM7 and VM9).

Methods

Bar-shaped specimens were fabricated according to the manufacturer’s instructions. Specimens were tested in three-point flexure in 37°C artificial saliva. Weibull analysis (n=30) and a constant stress-rate test (n=10) were used to determine the Weibull modulus (m) and SCG coefficient (n), respectively. Microstructural and fractographic analyses were performed using SEM. ANOVA and Tukey’s test (α=0.05) were used to statistically analyze data obtained with both microstructural and fractographic analyses.

Results

YZ and AL presented high crystalline content and low porosity (0.1–0.2%). YZ had the highest characteristic strength (σ₀) value (911 MPa) followed by AL (488 MPa) and IZ (423 MPa). Lower σ₀ values were observed for the porcelains (68–75 MPa). Except for IZ and VM7, m values were similar among the ceramic materials. Higher n values were found for YZ (76) and AL (72), followed by IZ (54) and the veneering materials (36–44). Lifetime predictions showed that YZ was the material with the best mechanical performance. The size of the critical flaw was similar among the framework materials (34–48 µm) and among the porcelains (75–86 µm).

Significance

The microstructure influenced the mechanical and SCG behavior of the studied materials and, consequently, the lifetime predictions.

Introduction

The use of ceramic materials with high crystalline content for dental restorations was improved by the development of CAD/CAM (computer-aided design/computer-aided manufacturing) technology. Alumina and zirconia-based systems were introduced as framework materials to produce restorations subjected to high stress concentration, such as posterior crowns and fixed partial dentures (FPDs). These materials are available as pre-fabricated blocks for CAD/CAM. All-ceramic restorations are produced in two layers: a high strength ceramic framework is veneered with porcelain to provide a more natural-looking restoration [1]. Although clinical evaluation of zirconia-based all-ceramic FPDs showed high success rate there is still some concern about the reliability of these systems, since the follow up period reported in these studies is relatively short, around 3 to 5 years [2, 3].

The limitations of all-ceramic restorations are related to the brittle behavior of ceramic materials. Ceramics are sensitive to stress concentrations around pre-existing cracks. The stress field at the tip of a crack can be described by the stress intensity factor (K_I) that is controlled by the loading in Mode I (opening mode). The flaw will propagate when the stress intensity factor reaches a critical condition, K_Ic, which is also called the critical stress intensity factor or fracture toughness and characterizes the resistance to unstable propagation of pre-existing cracks [4, 5]. These flaws form during processing (i.e. pores, inclusions) or subsequent handling, finishing, or service damage [6]. Thus, the strength of ceramic materials is limited by the presence of these pre-existing cracks associated with the relatively low fracture toughness. Large variability in strength is a consequence of the distribution in crack sizes, and the time-dependency of strength results from the material susceptibility to a phenomenon called “subcritical crack growth” [7].

Strength variability is usually characterized using the Weibull distribution, which is based on the premise that the weakest link in a body controls strength. The distribution function relates the cumulative probability of failure of a volume or area under tensile stress to two parameters, the Weibull modulus and the Weibull characteristic strength, m and σ₀, respectively. The characteristic strength or scale parameter represents the value at which 63.21% of the test specimens have fractured. The Weibull modulus or shape parameter (m) describes the relative spread of strength values in the asymmetrical distribution, with high m corresponding to less spread. A large value of Weibull modulus ensures a smaller variability in strength estimation, and greater precision [8–11].

The literature reports a large range of flexural strength and Weibull modulus values for ceramics used as FPDs framework materials. For yttria partially stabilized tetragonal zirconia ceramic (Y-TZP), the flexural strength varies from 700 to 1200 MPa and the Weibull modulus from 10 to 18 [9, 12–14]. Studies showed, for an alumina-based zirconia-reinforced glass infiltrated ceramic (In-Ceram Zirconia), lower flexural strength values (440–620 MPa) than the ones found for Y-TZP [13, 15–19]. However, the Weibull modulus values obtained were in the same range as YZ, from 9 to 14 [13, 16, 18]. A polycrystalline alumina ceramic (Vita In-Ceram AL) can also be used as framework material for FPDs. Although the manufacturer reported a mean flexural strength of 500 MPa, there is a lack of studies that characterize the mechanical performance of this ceramic material.

“Subcritical crack growth” (SCG) is a process that involves the stable growth of pre-existing flaws at stress intensity factor (K_I) levels lower than that necessary for the flaw to become unstable (K_Ic) [20, 21]. In the case of stress-corrosion, this phenomenon can result from a water-assisted breakage of silicate or oxide bonds at the crack tip under applied stress. Catastrophic failure will occur once the crack has grown to a critical size, at a given stress [22]. SCG can be determined by direct measurement of the crack velocity as a function of stress intensity factor. Otherwise, inferences about crack propagation can be made using indirect methods such as dynamic, cyclic and static fatigue tests [11]. The coefficient of subcritical crack growth, n, represents the inverse of degree of susceptibility of a material to SCG in a particular environment. Therefore, high n values correspond to lower susceptibility to the subcritical growth [23]. Studies showed for alumina polycrystalline ceramic n value of 44, and values varying from 29 to 57 for Y-TZP [14, 24, 25]. For In-Ceram Zirconia, the literature reported n values around 20 [18, 26].

A strength test produces two important information: the strength data and the fracture origin or flaw. Quantitative fracture surface analysis can be used to identify the size and location of the fracture initiating crack, the stress at failure, the nature of the stress state, the existence of residual stress or SCG, and knowledge of local processing anomalies that affect the fracture process [10, 21].

A combination of high fracture toughness, high resistance to stress corrosion, and lack of severe flaws is required for structural reliability [27]. However, few studies systematically evaluated all the factors necessary to predict the behavior of framework and veneer materials. Therefore, the first objective of this study was to analyze the microstructure of three ceramics used as framework material for FPDs and of two veneering porcelains in order to establish a relationship with the results obtained in the fracture strength test and Weibull analysis. The tested hypothesis was that the materials’ microstructures affect their mechanical behavior. The second objective was to determine the SCG parameters of these materials, testing the hypothesis that the materials’ microstructures influence the slow crack growth behavior. The third objective was to perform lifetime predictions for the studied materials combining both the SCG and Weibull parameters. The hypothesis was that the microstructure of the material significantly affects the lifetime of specimens predicted in vitro.

Materials and Methods

Three ceramics used as framework materials for FPDs and two veneering porcelains were studied. The materials and the experimental groups are described in Table 1.

Table 1.

Materials identification and experimental groups

Group	Material*	Composition	Indication
YZ	Vita In-Ceram YZ	yttria partially stabilized tetragonal zirconia polycrystal	framework
IZ	Vita In-Ceram Zirconia	alumina-based zirconia-reinforced glass infiltrated ceramic	framework
AL	Vita In-Ceram AL	alumina polycrystal	framework
VM7	Vita VM7	feldsphatic porcelain	veneer
VM9	Vita VM9	feldsphatic porcelain	veneer

^*Materials are manufactured by Vita Zahnfabrik, Bad Sackingen, Germany.

YZ, IZ and AL bar-shaped specimens were obtained by cutting pre-sintered blocks using a diamond disc in a precision cutting machine (Isomet 1000, Buehler, Lake Bluff, USA) at 275 rpm. YZ and AL specimens were sintered in the Zyrcomat furnace (Vita Zahnfabrik, Germany) at 1520°C for 2 h. IZ material was infiltrated with glass (Zirconia Glass Powder, Vita Zahnfabrik, Germany). The infiltration cycle was performed in the Inceramat 3 furnace (Vita Zahnfabrik, Germany), and the excess glass was removed with burs. The glass infiltration cycle was performed at 1110°C for 6 hours, according to the manufacturer’s instruction. VM7 and VM9 specimens were fabricated by mixing ceramic powder with distilled water. The mixture was poured into a metallic mold and condensed with manual vibration. The excess water was blotted out with absorbent paper. Keramat I furnace (Knebel, Porto Alegre, Brazil) was used for the porcelain sintering as follows: pre-drying at 500°C for 6 min, heating to 910°C at a rate of 55°C/min under vacuum, heating at 960°C for 1 min and slow cooling (~6 min).

After YZ, AL, VM7 and VM9 sintering and IZ glass infiltration, all specimens were ground to their final dimensions (2 mm × 4 mm × 16 mm). The 4-mm wide face was polished to 1 µm finish using a polishing machine (Ecomet 2, Buehler, Lake Bluff, USA). All edges were chamfered at a 0.1 mm wide chamfer, following the ISO 6872:2008 standard.

The SCG parameters were evaluated by the constant stress-rate test using five different rates: 10⁻², 10⁻¹, 10⁰, 10¹ and 10² MPa/s. For all groups, ten specimens were tested at each stress rate. Except for 1 MPa/s stress rate, in which thirty specimens were tested to perform Weibull analysis [7, 8]. The mechanical testing was performed according to the ISO 6872:2008 standard. The flexural strength (σ_f) was determined using a three-point flexure fixture in a universal testing machine (Sintech 5G, MTS, São Paulo, Brazil) at constant stress rates, in 37°C artificial saliva with the following composition [28]: 100 mL of KH₂PO₄ (2.5 mM); 100 mL of Na₂HPO₄ (2.4 mM); 100 mL of KHCO₃ (1.50 mM); 100 mL of NaCl (1.0 mM); 100 mL of MgCl₂ (0.15 mM); 100 mL of CaCl₂ (1.5 mM); and 6 mL of citric acid (0.002 mM). The three-point flexural strength (σ_f, MPa) was calculated using the following equation:

$${\sigma }_f=\frac{3\mathit{\text{Pl}}}{2{\mathit{\text{wb}}}^2}$$ (1)

where P is the fracture load (N), l is the span size (12 mm), w is the specimen width (mm) and b is the thickness of the specimen (mm).

The parameters n (stress corrosion susceptibility exponent) and σ_f0 (scaling parameter) and standard deviation were calculated according to ASTM C 1368-00 equations [29], where σ̇ is the stress rate (MPa/s):

$$\text{log}{\mathrm{\sigma }}_{\mathrm{f}}=\left(\frac{1}{\mathrm{n}+1}\right)\text{log}\dot{\mathrm{\sigma }}.\text{log}{\mathrm{\sigma }}_{\mathrm{f}0}$$ (2)

According to the ASTM C 1368-00 standard, a pre-load up to 80% of the material fracture load has little effect on the results of dynamic fatigue testing, since significant crack growth only occurs at load values that are close to the fracture load. Therefore, to reduce the testing time, a pre-load was used when the specimens were tested with a stress rate of 10⁻² MPa/s (approximately 50% of the fracture load). The pre-load was calculated based on a regression analysis using the results obtained in the other stress rates [30]. Lifetime curves were drawn using the correlation between log of fracture stress and log of time to failure of the specimens tested at constant stress rates [31].

Weibull analysis was performed with Weibull++ software (Reliasoft, Tucson, USA). The parameters were calculated based on the maximum likelihood method, and the 95% upper and lower confidence bounds were calculated using the likelihood ratio. The strength, at a failure probability of 5% (σ_5%) was also determined. Weibull and constant stress-rate data were used to estimate stress-probability-time (SPT) diagrams for three different times to failure (1 day, 1 year and 10 years), according to the theory proposed by Davidge et al. [32]. The SPT diagrams are based on the assumption that the specimen is under constant load.

Fracture surfaces were examined using a stereomicroscope (Olympus SZ61, Olympus, Japan) to determine the mode of failure based on the fracture origin and fractographic principles [33, 34]. Five specimens of each experimental group were sputter-coated with gold-palladium and examined using a scanning electron microscope (SEM) (Stereoscan 440, LEO Electron Microscopy Ltd, Cambridge, England) to identify and measure the critical flaw (c). The equivalent semi-circular flaw was determined using the following equation:

$$c=\sqrt{\mathit{\text{ab}}}$$ (3)

where, a is the crack depth and b is half crack width. This approximation is suitable for many fracture mechanics crack problems provided that the cracks are not too elongated (e.g., b ≤ 5a). In the case of a corner crack, c corresponds to the distance from the crack corner to the limit of the critical flaw-mirror region. Fracture mechanics was used to calculate the fracture toughness (K_Ic), following Griffin-Irwin equation [35, 36]:

$$K_{\mathit{\text{IC}}}=Y{\sigma }_f\sqrt{c}$$ (4)

where Y is a geometric factor, which accounts for the shape of the fracture-initiation crack and loading condition, and also depends on the ratio a/b. For semicircular cracks Y is approximately 1.24 and for corner cracks is equal to 1.4 [27, 36].

Microstructural analysis was performed using SEM (JEOL-JSM 6300, Peabody, MA, USA) coupled with an energy dispersive spectroscope (EDS) (Noran Instruments, Middletown, WI, USA). Before the analysis, YZ and AL polished specimens were submitted to a thermal treatment at 1470°C for 30 min, revealing the grain boundaries. VM7 and VM9 were etched with 2% hydrofluoric acid (HF) for 15 s [30]. No surface treatment was performed on IZ. The area fraction and the size of crystals and pores were estimated using stereology principles along with Adobe Photoshop (Photoshop 7.0, Adobe, USA) and Image J software.

The values of fracture toughness (K_Ic), critical flaw (c), area fraction and size of pores were analyzed with one-way analysis of variance. Tukey’s test with a global significance level of 5% was used for multiple comparisons.

Results

The estimated mean and standard deviation values of area fraction of crystalline phase (A_A), crystal size (Ā), area fraction of pores (A_O) and pore size (Ō) for the studied materials are presented in Table 2. IZ showed the highest mean area fraction of pores. YZ and AL had the lowest mean A_O, followed by the porcelains. IZ, VM7 and VM9 presented higher mean size of pores than YZ and AL.

Table 2.

Crystalline phase(s), estimated mean and standard deviation values of area fraction of crystalline phase (A_A), crystal size (Ā), area fraction of pores (A_O) and pore size (Ō) for the materials studied.

	Materials
	YZ	IZ	AL	VM7	VM9
Crystal	zirconia	alumina; zirconia	alumina	-	leucite
AA (%)	100	alumina: 46.0 (3.3) zirconia: 20.2 (2.1)	100	0	4.6 (1.9)
Ā (µm)	0.7 (0.1)	alumina: 2.5 (0.3) zirconia: 1.3 (0.6)	2.3 (0.1)	-	1.4 (0.2)
AO (%)	0.1 (0.1)c	5.4 (1.5)a	0.2 (0.1)c	2.7 (0.7)b	2.6 (1.0)b
Ō (µm)	7.1 (0.5)c	10.2 (0.3)a	8.9 (1.5)b	11.2 (1.3)a	10.4 (1.2)a

^*Values followed by the same letter in the line are statistically similar (p≥0.05).

Figure 1 shows representative SEM microstructure images for the framework and veneering materials. Zirconia grains (Zr and O elements detected by EDS) with a mean crystal size of 0.7 µm were observed in YZ. Alumina crystals (Al and O elements detected by EDS) with a mean size of 2.3 µm constitute the AL ceramic. IZ ceramic presented two types of crystals (alumina and zirconia) and a glass phase (lanthanum oxide-based glass). Mean crystal size values of 2.5 µm and 1.3 µm were measured for alumina and zirconia, respectively (Figure 1C). These crystal phases were surrounded by a glass phase, in which the following elements were identified: C, O, La, Al, Si and Ca. VM7 porcelain presented a microstructure constituted only by a glass phase, no second-phase particles were detected (Figure 1D). VM9 porcelain showed a glass matrix reinforced with leucite crystals with a mean size of 1.4 µm. It was possible to observe clusters of leucite crystals distributed on an amorphous matrix (Figure 1E). A leucite area fraction of 4.6% was estimated for VM9 and EDS analysis indicated that this crystalline phase contained the following elements: Si, Al, K, Na, Ca and O. Similar glass phase composition was found for both porcelains. The composition of crystalline and glass phases were confirmed by EDS analyses.

Figure 1.

Representative SEM images for the ceramic materials. A- YZ; B- AL; C- IZ showing alumina crystals (black), zirconia crystals (white) and the glass phase (gray); D- VM7 and, E – VM9.

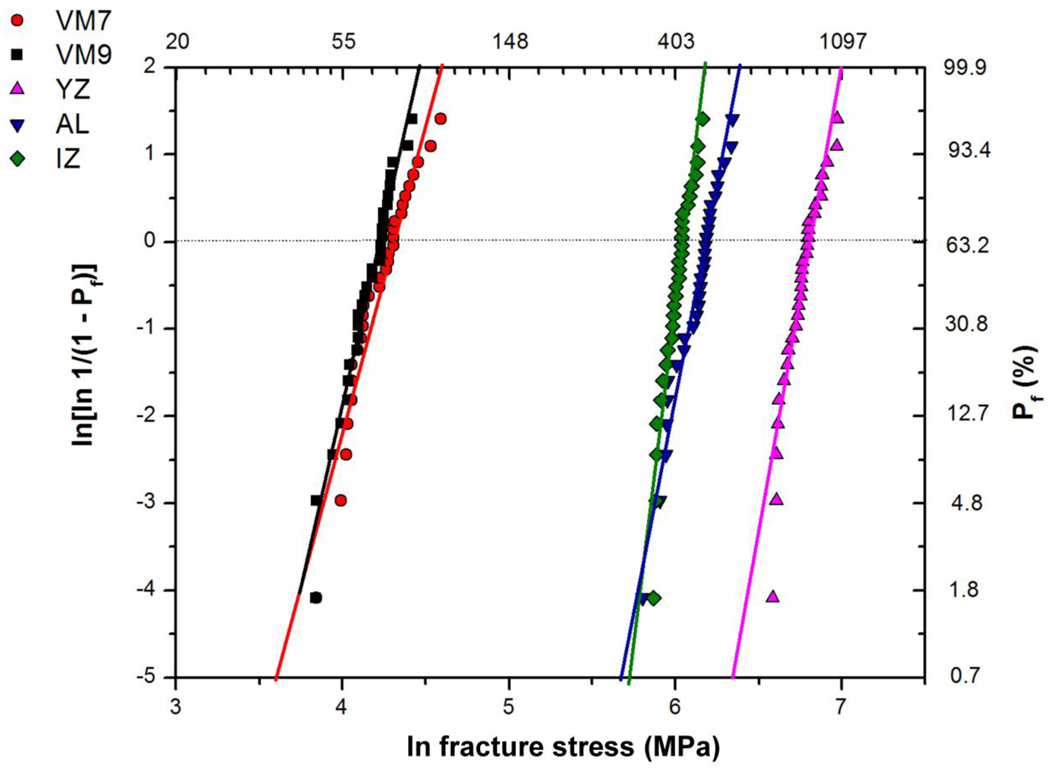
Table 3 shows the Weibull modulus (m), characteristic strength (σ₀) and the flexural strength for a failure probability of 5% (σ_5%). The Weibull parameters are statistically different when the confidence bound values fail to overlap. YZ showed the highest σ₀ value, followed by AL and IZ, that presented significant differences. Lower σ₀ values were observed for the veneering materials (VM7 and VM9). Considering the Weibull modulus, there was statistical difference only between IZ and VM7. For each material, the position and slope of the curve in the Weibull plot (Figure 2) are determined by σ₀ and m values, respectively. The curve of a material that has a high m value is steeper than the curve of a material with low m value. In addition, the curve of a material with higher σ₀ value, such as YZ, is located more to the right of the curve of a material with low σ₀, such as VM7 and VM9 porcelains.

Table 3.

Weibull parameters (m, σ₀ and σ _5%) and statistical grouping for the experimental groups (95% confidence intervals in parentheses). Subcritical crack growth parameters (n and σ_f0) and fracture stress corresponding to a lifetime of 10 years (σ_10y) (standard deviation in parentheses).

	m	σ0 (MPa)	σ5% (MPa)	n	σf0 (MPa)	σ10y(MPa)
YZ	10 (7–12)a,b	911 (874–947)a	673	76 (38)	880	770
IZ	16 (10–17)a	423 (411–436)c	340	54 (10)	408	320
AL	9 (7–12)a,b	488 (467–508)b	355	72 (27)	467	400
VM7	6 (5–8)b	74.7 (69.9–79.5)d	45.9	36 (11)	65.1	46.2
VM9	8 (6–11)a,b	68.5 (65.2–71.7)d	47.8	44 (12)	60.6	44.3

^*Values followed by the same letter in the column are statistically similar (p≥0.05).

Figure 2.

Weibull plot showing the fracture stress as a function of the failure probability (P_f).

Table 3 also shows the subcritical crack growth parameters¹ (n, stress corrosion susceptibility exponent, and σ_f0, scaling parameter) for the experimental groups. YZ and AL presented high n values (76 and 72, respectively), which were approximately two times higher than the n values of porcelains (around 40). IZ showed an intermediate n value (54). The highest σ_f0 value was obtained for YZ, followed in decreasing order by AL, IZ, VM7 and VM9.

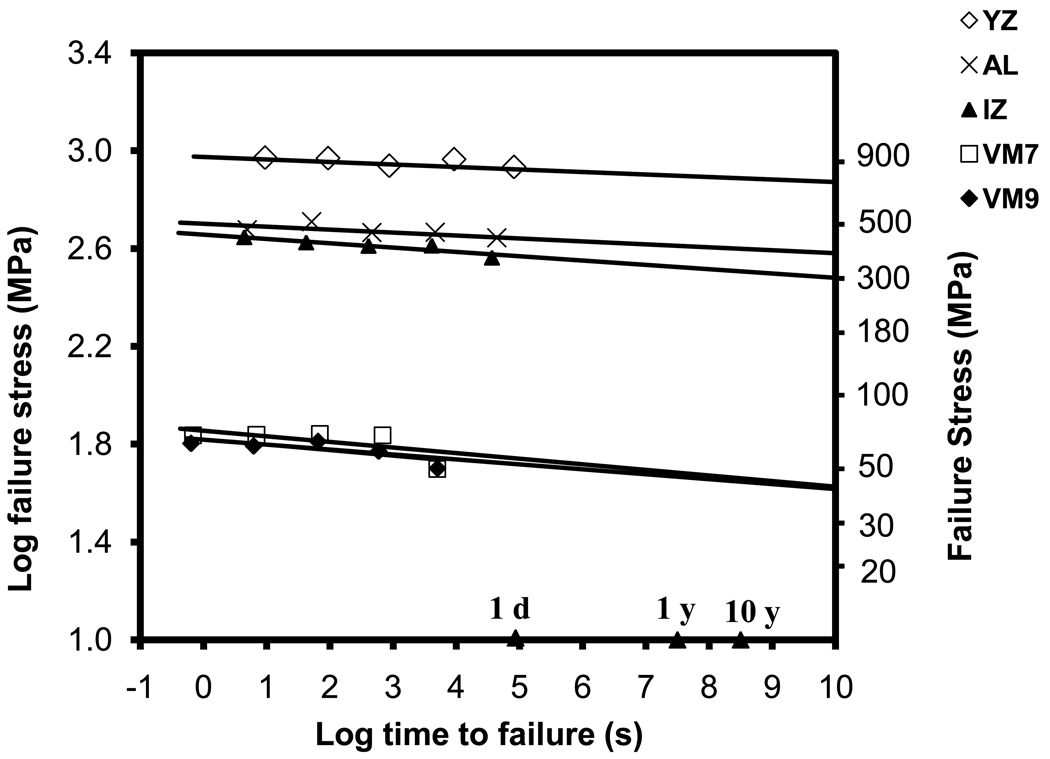
Lifetime curves for the experimental groups are presented in Figure 3 and were extended above 10 years to make possible the prediction of the average fracture strength after longer lifetimes. The slope of the curve is related to the material’s slow crack growth susceptibility; a high slope corresponds to a low n value. Therefore, the strength degradation after 10 years for YZ and AL materials was lower than the degradation observed for the porcelains.

Figure 3.

Lifetime curves drawn for the experimental groups using the correlation between the log of time to failure and the log of failure stress. The x-axis is labeled for 1 day (1d), 1 year (1y) and 10 years (10y).

The fracture stress after 10 years (σ_10y) for each material was predicted using the dynamic fatigue data (Table 3). The σ_10y for YZ was approximately two times higher than the σ_10y estimated for IZ and AL. The σ_10y values predicted for VM7 and VM9 were lower than the other groups, around 45 MPa.

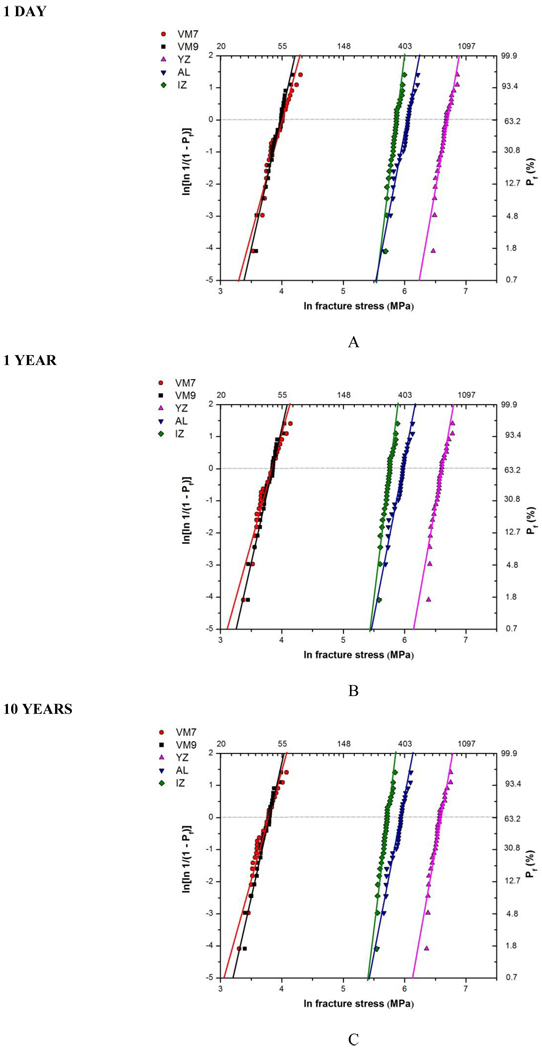
The SPT diagrams are presented in Figure 4. The slope of the curve is related to the m value of each material and is similar for different lifetimes since it is assumed that this value is constant with time. The curves change position for 1 day, 1 year and 10 years according to each material subcritical crack growth susceptibility. YZ and AL curves move in the same proportion because the n values are similar. The distance between IZ and AL curves increases with time due to IZ higher n value. Table 4 shows the fracture stress values for 1 day, 1 year and 10 years with a probability of failure of 5% for the experimental groups that were estimated using the SPT diagrams. For each material, the difference in the fracture stress between 1 day and 10 years is related to the n value.

Figure 4.

SPT (stress-probability-time) diagrams for 1 day (A), 1 year (B) and 10 years (C).

Table 4.

Fracture stress values (MPa) corresponding to 5% failure probability at 1 day (σ_1d), 1 year (σ_1y) and 10 years (σ_10y) for the experimental groups, and the relative difference (decay) between σ_1d and σ_10y (%). Values obtained from the SPT diagrams (Figure 3).

	Materials
	YZ	IZ	AL	VM7	VM9
σ1d	840	370	450	60	57
σ1y	780	330	420	50	50
σ10y	760	320	400	47	47
Relative decay between σ1d and σ 10y	9%	13%	11%	22%	17%

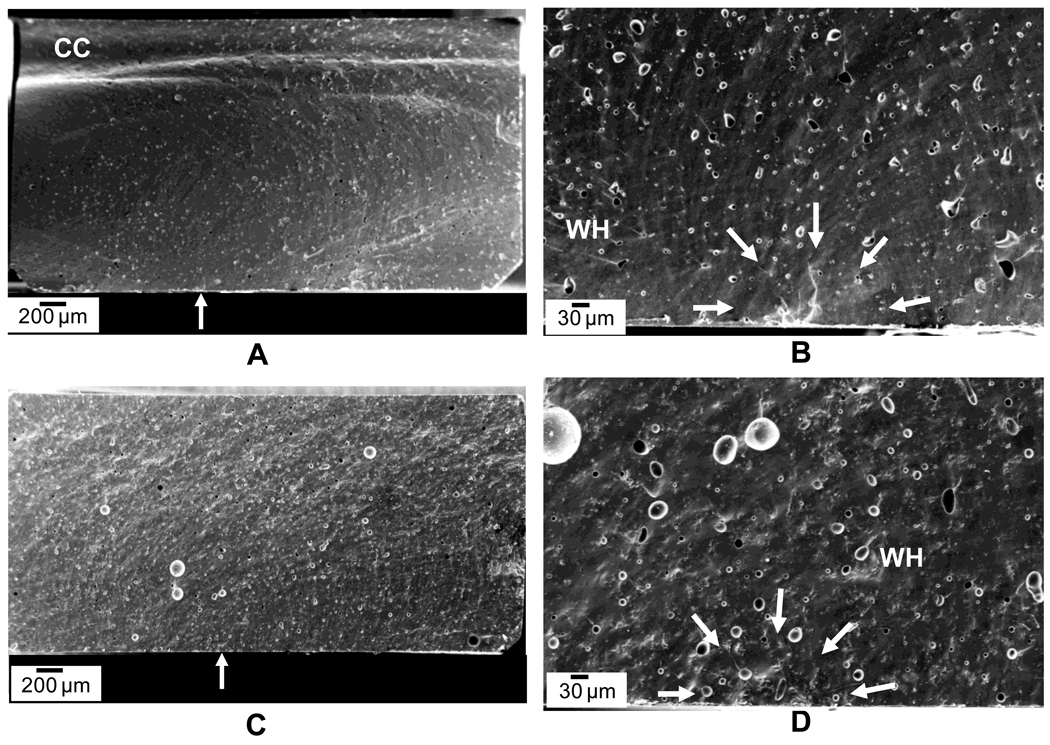
Figure 5 shows the fracture surface of the framework materials (YZ, IZ and AL). The fracture mode was similar for all materials. The initial flaw was located in the surface subjected to tension during testing and propagated throughout the material. For the framework materials, all flaws originated from the surface (no internal or corner cracks were observed). Yet, for the porcelains, both surface and corner cracks were identified (Figure 6).

Figure 5.

SEM images of the fracture surface of the framework materials. A – B) YZ. C – D) IZ. E – F) AL. It is possible to observe fractographic features, such as compression curl (CC) and hackle lines (HL). Arrows point to the critical flaw.

Figure 6.

SEM images of the fracture surface of the porcelains. A – B) VM7. C – D) VM9. It is possible to observe fractographic features, such as compression curl (CC) and wake hackles (WH). Arrows point to the critical flaw.

The framework materials presented a rougher surface corresponding to their microstructural composition. It was possible to observe hackle lines that run in the direction of fracture origin, separating parallel, noncoplanar portions of the crack surface, and compression curl in the opposite side of the critical flaw (Figure 5). The porcelains showed a smoother surface with many wake hackles connected to the pores (Figure 6).

The mean critical flaw (c) and fracture toughness (K_Ic) values for the materials studied are presented in Table 5. There were no significant differences between mean c values for the framework materials (YZ, IZ and AL). The mean c values for the porcelains were similar and statistically higher than the mean values obtained for the framework materials. YZ showed the highest mean K_Ic value. IZ and AL presented similar K_Ic values. The lowest mean K_Ic values were observed for the porcelains. In addition, it is possible to observe an increase in the critical crack size with a decrease in the stressing rate (Table 5).

Table 5.

Mean critical flaw size (c) and fracture toughness (K_Ic) values, standard deviation and statistical grouping for the materials studied (n=25). It is also shown c as a function of the stress rate for each material studied.

		Materials
c (µm)	Stress rate	YZ	IZ	AL	VM7	VM9
	0.01	46	60	43	85	84
	0.1	32	51	41	78	100
	1	37	37	40	58	101
	10	31	47	38	85	77
	100	28	44	34	77	70
	Mean	34 (9)b	48 (10)b	40 (8)b	75(16)a	86 (25)a
KIc (MPa·m1/2)		6.5 (0.3)a	3.6 (0.2)b	3.6 (0.2)b	0.7 (0.1)c	0.7 (0.1)c

^*Values followed by the same letter in the line are statistically similar (p≥0.05).

Discussion

In the present study, materials with different microstructures resulted in significantly different values of flexural strength and fracture toughness. Therefore, the first study hypothesis was accepted. The microstructural analysis showed that the high crystalline content ceramics,YZ and AL, have very low porosity (0.1–0.2%, Table 2). Yet, YZ showed superior values of σ₀ (Table 3) and K_Ic (Table 5). The superior mechanical behavior of YZ compared to AL can be attributed to a well-known toughening mechanism that is associated to the transformation of the zirconia crystals. When stabilized zirconia is subjected to tension (i.e. chewing, grinding, polishing), a transformation from tetragonal to monoclinic crystal structure is induced in regions of enhanced stress concentration, such as around a crack tip. This transformation results in internal compressive stresses that oppose crack propagation, increasing the material’s fracture toughness and strength [37].

Although IZ has about 20 vol% of ceria-stabilized zirconia crystals, the characteristic strength (σ₀) was significantly lower than that obtained for AL. The mechanical behavior of IZ is probably jeopardized by some of the microstructural characteristics described in Table 2, such as the high fraction of pores (5.4%) and large pore sizes, and also the presence of an amorphous phase (lanthanum oxide-based glass). Pores can act as crack initiators with high stress concentration and reduce the cross-section area subjected to loading, decreasing the fracture strength [38]. In addition, it has been reported that the mechanical properties of IZ can be degraded by the porosity, if there is a poor distribution of alumina and zirconia particles or a poor solubility between the glassy phase and the crystal phases [15].

The porcelains VM7 and VM9 showed the lowest σ₀ values among the materials studied, which can be credited to their composition. Although the microstructural analysis showed a lower fraction of pores than IZ, the porcelains are constituted mainly by glass matrix, which is highly susceptible to crack propagation, as indicated by their low fracture toughness values (0.7 MPa·m^1/2).

In dentistry, the fracture strength for a failure probability of 5% (σ_5%) is considered to be more clinically relevant than for 63.2% (σ₀) [14]. Therefore, the values for σ_5% were obtained using Weibull analysis. YZ showed the highest σ_5% value, which follows the greatest σ₀ and K_Ic values. When materials with similar mean or characteristic fracture strength are considered for clinical application the material with larger Weibull modulus (m) value should be chosen since a more reliable prognosis is expected. However, for a material such as YZ, the high fracture strength provides a margin of safety that supports the use of this system, even if low m values are observed. In addition, the fact that there was no significant difference between the m values for the studied groups further support the use of YZ as the material of choice for large all-ceramic restorations.

The porcelains (VM7 and VM9) showed mean σ_5% values below 50 MPa. Considering that stresses of 27–31 MPa are estimated for the posterior area [39], the values obtained for porcelains are critical and may compromise the clinical performance, resulting in premature failure of monolithic porcelain restorations or chipping of layered structures.

The fractographic analysis showed that the critical flaw size was similar among the framework materials (34 to 48 µm) and between the porcelains (75 to 86 µm). The smaller flaw sizes found in the framework materials could be attributed to the fact that these specimens were produced from CAD-CAM blocks that are processed in optimal conditions, in a industrial environment, what may guarantee a more uniform microstructure and lower porosity [19]. In fact, YZ and AL showed the lowest number and size of pores. However, IZ was the material with the highest fraction of pores. This may be explained by the difference in processing steps. Zirconia and alumina powders are pressed and pre-sintered to produce YZ and AL blocks. After the machining process, the restoration is sintered at 1530°C, reaching its final density and significantly reducing the porosity. IZ blocks are produced by dry-pressing a mixture of alumina and zirconia particles and firing to maintain an open-pore microstructure. The porous structure gains strength by infiltration with a lanthanum-containing glass [15, 19]. Although the porosity is reduced by the infiltration process, the final IZ microstructure still shows higher fraction of pores than the single-phase polycrystalline microstructure of YZ and AL. Thus, different flaw populations were expected for these ceramics. Yet, the critical flaw size was similar among the three framework materials in the present study.

The high n values observed for YZ and AL show that the microstructure of polycrystalline ceramics, without a glass phase, are a more efficient barrier to crack propagation than the microstructure of porcelains and glass-containing composites (IZ). Therefore, the second study hypothesis was also accepted.

The high resistance to slow crack growth observed for YZ and AL could also be attributed to mechanisms such as transformation toughening and microcrack nucleation that are related to the zirconia particles, and crack deflection and contact shielding that are related to the alumina particles [15]. These toughening mechanisms could also be responsible for the R-curve behavior, since they act shielding the crack tip and increasing the fracture toughness as consequence of the increase in crack size [40, 41]. Thus, the high n values observed for AL and YZ groups may also be related to this increase in the resistance to crack growth during crack extension [37]. Previous studies reported on the mean n values of ceramics [14, 24, 25] and found higher n values for alumina and zirconia polycrystalline ceramics than for porcelains [14]. Besides the fact that YZ exhibits a higher fracture toughness (K_Ic) than AL, an investigation reported similar values of stress intensity factor threshold (K_I0), which means that the stress at the crack tip necessary to initiate crack growth is the same in both materials [20]. Alumina has a lower susceptibility to water degradation and thus to stress assisted corrosion. Otherwise, zirconia bonds are prone to chemical reactions with water molecules. Therefore, the fracture energy of zirconia is lower in the presence of water or body fluid [20]. For YZ, the same toughness mechanism that improves its mechanical performance can result in an undesirable behavior called low temperature degradation (LTD). The zirconia LTD mechanism was well discussed in a review by Chevalier and Gremillard [42] and could partially explain why, in the present study, AL showed a similar n value to YZ even though its mechanical properties were inferior.

The intermediate n values observed for IZ are mainly attributed to the presence of a glass phase. It was expected that the toughening mechanisms associated with alumina and zirconia grains would interact with the crack front improving the resistance to slow crack growth of this material. However, the effect of these toughening mechanisms apparently fails to compensate for the presence of an amorphous phase. The glass phase is more susceptible to stress-corrosion, and SCG occurs through the bulk glass phase or the glass-ceramic interface [18, 21, 26]. Previous studies also observed significant influence of the glass matrix in the slow crack growth behavior of these glass-infiltrated composites [26, 42, 43].

The low n values found for porcelains are also related to the fact that the microstructure of these materials is constituted mainly by a glass phase. The literature reports n values from 15 to 41 for porcelains [23, 30, 31, 44]. These results are similar to the n values observed for silicate glasses (15 to 19), which are among the most fatigue-susceptible of all ceramics [45]. Thus, the slow crack growth behavior observed for the porcelains is critical considering that these materials are directly exposed to humidity and loading in the oral cavity.

The occurrence of slow crack growth was further evidenced by a decrease in the mean flexural strength values and an increase in the critical flaw size with decreasing stress rates. This behavior can be attributed to the fact that when specimens are tested with high stress rates, there is less time for stress-corrosion to increase the crack size, consequently, higher fracture strength values are found [31]. These findings are in agreement with a study by Taskonak et al. [21] that also observed a stressing rate dependence of strength.

The third hypothesis of this study was also accepted since the lifetime predictions showed different rates of strength degradation for the five materials studied, as shown in Figures 3 and 4 and Tables 3 and 4. To provide a ceramic material with high strength and low slow crack growth susceptibility, high values of both parameters, n (stress corrosion susceptibility exponent) and σ_f0 (scaling parameter), should be obtained. Therefore, YZ was the material with the best mechanical performance. Even though the mean n value observed for AL was similar to YZ, the σ_f0 value was lower. In the lifetime graph (Figure 3), YZ showed the highest fracture strength after 1 day and the lowest slope, which means low degradation over time. The difference in fracture strength values between IZ and AL increased from 1 day to 10 years (Fig. 3) due to IZ higher SCG susceptibility. The fracture stress after 10 years (σ_10y) was predicted for each material using the lifetime curves (Table 3). Through the analysis of these results it is possible to notice that the values of σ_10y for the porcelains (around 45 MPa) are in the same range of the stress reported for the posterior area (27–31 MPa) [39], suggesting a higher probability of failure during clinical application than the framework materials.

The SPT diagram is another tool used to estimate the lifetime of a material as a function of stress. Besides time and stress, the SPT diagram allows the evaluation of different failure probabilities. Therefore, the fracture stress for 1 day, 1 year and 10 years with a probability of failure of 5% was estimated for each material (Table 4). The difference in the fracture stress between 1 day and 10 years was smaller for YZ (9%) and AL (11%) (Table 4), which is related to the highest values of stress-corrosion coefficient (n). The porcelains showed a greater strength degradation from 1 day to 10 years.

One limitation of these lifetime estimations is the fact that stress is considered to be constant during time. However, for a 10-year period, an individual stays in occlusion only 1 to 4% of this time, which corresponds to a period of constant stress application between 38 and 152 days [30]. Thus, using the SPT diagrams, the probability of failure for the materials studied was estimated for 10 years of clinical use and a constant stress between 27 and 31 MPa (chewing stress). For the framework materials, the probability of failure was negligible (0%). Even for the porcelains, the probability of failure was small, from 2 to 5% for VM7 and from 1 to 3% for VM9. The results suggested a good clinical prognosis for these ceramic systems. The direct extrapolation of these estimations to clinical application should be done with caution. In the oral environment, the restoration will fail when the critical crack size is achieved for an applied stress at any period of time. Clinical stresses are complex, therefore is difficult to determine the exact stress condition in which the restoration is subjected. Yet, these parameters can be very useful to compare different materials [31].

Conclusion

The results of this study showed that the microstructure significantly influenced the mechanical and slow crack growth behavior of the dental ceramics evaluated and, consequently, the strength degradation over time (lifetime). The high crystalline content and low porosity found for the polycrystalline ceramics (YZ and AL) resulted in high values of flexural strength, low susceptibility to slow crack growth and low strength degradation over time. Although IZ showed a high crystalline content, this material had intermediate values of flexural strength and SCG coefficient, which is related to the presence of a high fraction of pores and of an amorphous phase. The porcelains showed the lowest values of flexural strength and resistance to crack propagation, resulting in high strength degradation over time. The mechanical and SCG behavior of the porcelains may be attributed to the fact that these materials are constituted mainly by a glass matrix.