Relating reflex gain modulation in posture control to underlying neural network properties using a neuromusculoskeletal model

Abstract

During posture control, reflexive feedback allows humans to efficiently compensate for unpredictable mechanical disturbances. Although reflexes are involuntary, humans can adapt their reflexive settings to the characteristics of the disturbances. Reflex modulation is commonly studied by determining reflex gains: a set of parameters that quantify the contributions of Ia, Ib and II afferents to mechanical joint behavior. Many mechanisms, like presynaptic inhibition and fusimotor drive, can account for reflex gain modulations. The goal of this study was to investigate the effects of underlying neural and sensory mechanisms on mechanical joint behavior. A neuromusculoskeletal model was built, in which a pair of muscles actuated a limb, while being controlled by a model of 2,298 spiking neurons in six pairs of spinal populations. Identical to experiments, the endpoint of the limb was disturbed with force perturbations. System identification was used to quantify the control behavior with reflex gains. A sensitivity analysis was then performed on the neuromusculoskeletal model, determining the influence of the neural, sensory and synaptic parameters on the joint dynamics. The results showed that the lumped reflex gains positively correlate to their most direct neural substrates: the velocity gain with Ia afferent velocity feedback, the positional gain with muscle stretch over II afferents and the force feedback gain with Ib afferent feedback. However, position feedback and force feedback gains show strong interactions with other neural and sensory properties. These results give important insights in the effects of neural properties on joint dynamics and in the identifiability of reflex gains in experiments.

Introduction

During posture control, humans have two strategies to counteract unexpected disturbances and keep their equilibrium position. Co-contraction of the muscles increases joint viscoelasticity, while maintaining equilibrium. Co-contraction provides instantaneous viscoelasticity at the expense of high metabolic energy consumption. Sensory feedback is energy efficient, although effectiveness is limited due to the inherent neural time delays.

In the presence of fast unpredictable disturbances in the upper extremity, reflexes through afferent feedback provided by muscle spindles and Golgi tendon organs are the major contributors to sensory feedback. Muscle spindles are located in the muscles and provide feedback on stretch and stretch velocity. Golgi tendon organs are located in the junction between muscle and tendon, providing feedback on muscle force. Reflexes are involuntary responses to stimuli, and their strength is known to be modulated. Experiments have shown that different task instructions (Doemges and Rack 1992a, b; Abbink et al. 2004), disturbance properties (de Vlugt et al. 2002) and dynamic properties of the environment (Van der Helm et al. 2002) all elicit adaptation of the reflexive contribution to joint dynamics. Model simulations have indicated that these reflex settings are close to optimal for suppressing the disturbances (Schouten et al. 2001).

Additional to the many studies that quantify reflexive behavior by directly deriving metrics like integrated EMG after the application of a mechanical or electrical stimulus (e.g. Dewald and Schmit 2003; Schuurmans et al. 2009; Kurtzer et al. 2008; Nielsen et al. 2005), other studies use a control engineering approach to parameterize joint dynamics. A combination of system identification and modeling is then used to separate muscular and reflexive contributions (Kearney et al. 1997; Perreault et al. 2000; Van der Helm et al. 2002; Ludvig and Kearney 2007; Schouten et al. 2008a). The dynamic behavior of the joint is estimated by perturbing the joint with a random force disturbance using a robotic manipulandum and recording displacement and interaction force between the subject and the manipulandum. The joint dynamics are expressed in terms of the mechanical admittance, describing the amount of displacement per unit force. To separate reflexive contributions from muscle viscoelasticity, lumped parameters (Schouten et al. 2008b) can be fitted to the mechanical admittance. The resulting set of parameters quantify the joint inertia, the muscle viscoelasticity and the reflexive gains of the force, position and velocity feedback pathways.

There are multiple mechanisms that affect the strength of the reflex pathway. Fusimotor drive (Crowe and Matthews 1964; Ribot-Ciscar et al. 2009) modulates the muscle spindle’s sensitivity to stretch and stretch velocity, therewith altering the gain of the reflex pathway. With presynaptic inhibition (Rudomin and Schmidt 1999; Rudomin 2009; Baudry et al. 2010), the efficacy of transmission between primary afferent fibers and the receiving neurons can be centrally modulated. The strengths of interneuronal connections in the spinal cord affect the net amount of activation of the motoneuron pool due to the sensory feedback. All these mechanisms contribute to the joint dynamics as determined experimentally.

Despite the known neural mechanisms of reflex modulation and the available identification techniques, there are still many unknowns on how exactly neural mechanisms affect the measured joint dynamics. The goal of this study was to investigate how neural and sensory properties could map onto the (limited) set of reflex gains as obtained from joint dynamics, using a neuromusculoskeletal model. In other words: how do the underlying, physical neural and sensory properties effectively link to the lumped reflex gains? We used a neuromusculoskeletal model of a spinal neural network controlling an antagonistic pair of muscles with afferent feedback (Stienen et al. 2007). In a sensitivity analysis, sensory and neural properties in the model were systematically varied and reflex experiments were simulated to determine reflex gains. The results showed that besides the expected mappings, there also exist intricate, counterintuitive relationships between neural and sensory properties and reflex gains that need to be taken into account when interpreting experimental results.

Methods

Approach

Posture control experiments around the shoulder joint (Van der Helm et al. 2002) were mimicked on a neuromusculoskeletal (NMS) model. In these types of experiments, a subject holds the handle of a linear manipulator and minimizes deviations while being perturbed with a random force disturbance. This type of posture control experiment was mimicked by perturbing a joint in a neuromusculoskeletal model with a continuous random force disturbance. The reflexive contributions to the dynamic behavior of the joint were determined using system identification techniques identical to experiments in vivo. The reflexive component was expressed in terms of reflex gains, which gave a quantitative measure for the amount of stretch, stretch velocity and force related reflex action. In the sensitivity analysis the model parameters were systematically varied and the effects on task performance, joint admittance and the reflex gains were determined.

Model description

The NMS model is briefly described here; for full details see Stienen et al. (2007). Posture control of the shoulder was modeled as a one degree of freedom joint (inertia m = 0.18 kg m²), actuated by an antagonistic pair of muscles (moment arm r _m = 30 mm). Since the experiment involved only small deviations around a constant level of co-contraction (≈40% of maximal force), a linearized muscle model was used. The viscoelasticity due to muscle co-contraction was set, such that the rotational viscoelasticity of the model was equivalent to the translational viscoelasticity taken from experimental data (Van der Helm et al. 2002): the endpoint stiffness and viscosity of the arm were respectively 800 N/m and 40 Ns/m. Stiffness and viscosity represented cross-bridge viscoelasticity, which is dominant in an experiment with co-contraction and relatively small displacements. The muscle activation dynamics were of first order with a time constant of 30 ms.

Afferent feedback to the spinal network was provided by Golgi tendon organs (force, through Ib afferents) and muscle spindles (stretch velocity and stretch, through Ia and II afferents). Each of the 121 Golgi tendon organs per muscle fired a spike train with a spike rate r _Ib that was proportional (Crago et al. 1982) to the muscle force with a constant c _Ib in spikes/s (Eq. (1)).

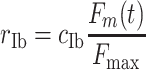1

where F _m is the muscle force, F _max is the maximal muscle force (800 N) and t denotes time. A Poisson process was used to convert spike rate r _Ib to the spike trains of the individual fibers. The afferent time delay of the Ib fibers was 15 ms.

A model of the muscle spindle (Prochazka and Gorassini 1998) was used to determine the firing rates of the 121 Ia and II afferent fibers per muscle as a function of muscle stretch (x _m) and stretch velocity (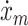). The Ia afferent firing rate r _Ia was the summation of a background firing rate (constant a _Ia), a linear length dependent part (c _Ia) and an exponential stretch velocity dependent part (constants d _Ia, e _Ia). For the II afferents (r _II), which were assumed to only transmit length-dependent information, the same model was used without the velocity-dependent part.

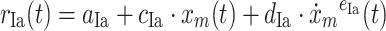2

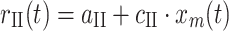3

The afferent time delays of the group Ia and II fibers were respectively 15 ms and 30 ms.

The spinal neural network, which integrated the afferent input to generate the efferent control signals to the muscles, was based on Bashor (1998) and presented before in Stienen et al. (2007). The model consisted of six pairs of spinal neuron populations, i.e. motoneurons, Renshaw cells, group Ia and Ib interneurons and inhibitory and excitatory interneurons (see Fig. 1). Each population consisted of either 169 or 196 individual spiking neurons (MacGregor and Oliver 1974). These neurons have four state variables, i.e. membrane potential, variable threshold, potassium conductance and synaptic conductance. Whenever the membrane potential reached threshold, the neuron fired a discrete spike which was transmitted to the connected synapses. The synaptic connections between the neurons were created according to the connection scheme in Fig 1. Tonic, descending excitation (TDE) provided background activity to the motoneurons (resulting in co-contraction) and to some of the other neural populations. Each neuron in a receiving population was connected to 34–232 neurons, afferent fibers or descending fibers. Generally, the afferent input fans out over the populations. The connections with the lower number of synapses are closer to the afferent input than the connections with high number of synapses (the interneuronal connections). A full overview of synapse count can be found in Stienen et al. (2007). The individual projections were randomized. Five pre-set types of synaptic connections were used: single, double and triple strength excitatory synapses, excitatory synapses a with long time constant (to the Renshaw cells), and inhibitory synapses. No network training or any form of neural plasticity was implemented. Since the many motoneurons in a population all activated a single, lumped muscle (no individual muscle fibers and a single neuromuscular junction), the input signal to the muscle activation dynamics was obtained by taking a 20 ms moving average of the summed spike output of the motoneuron populations. Efferent time delay was 10 ms.

Fig. 1.

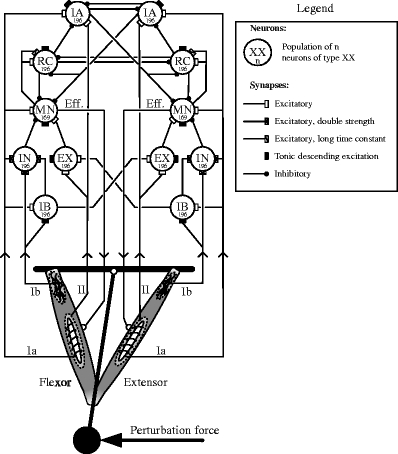
Neuromusculoskeletal model. A muscle pair actuated a one degree of freedom joint while being controlled by a spinal network with populations of motoneurons (MN), group Ia interneurons (IA), Renshaw cells (RC), inhibitory interneurons (IN), excitatory interneurons (EX) and group Ib interneurons (IB). Feedback is provided by Ia, Ib and II afferents

Simulation of the neuromuscular model

Similar to posture control experiments a crested multi-sine disturbance signal (Pintelon and Schoukens 2001) with a flat power spectrum between 0.5 Hz and 20 Hz was applied to the joint of the NMS model. The magnitude of the disturbance was chosen such that the root mean square (RMS) of the endpoint displacements was approximately 4 mm, similar to experiments on human subjects (Van der Helm et al. 2002). A single model run simulated a 9 second perturbation experiment. The model was run with a discrete time step of 1 ms. To prevent transient behavior from influencing the results the first 808 ms were rejected, leaving exactly 2¹³ data samples. To account for possible variability due to the random processes involved in the generation of the force disturbance and the Poisson spike trains, each simulation was repeated eight times with a different initial seed of the random generators.

Lumped reflex gain model

After simulation of a perturbation experiment, reflex gains were determined by fitting a lumped reflex gain model onto the joint dynamics. The reflex gain model is illustrated in Fig. 2. The model input was disturbance force d and output was joint position 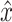. The intrinsic dynamics were parameterized by the inertia of the arm m and the muscle stiffness k and viscosity b. Reflexive feedback consisted of position feedback (with a gain k _p), velocity feedback (gain k _v) and force feedback (gain k _f). A single reflexive feedback neural time delay τ _del is represented by H _del. Like in the simulated NMS model, the muscle activation dynamics H _act were represented by a first order system with time constant τ _act.

Fig. 2.

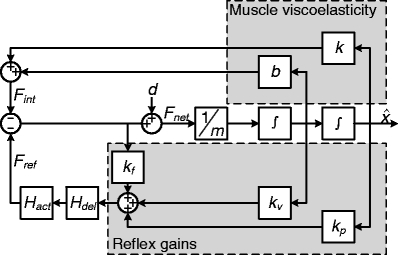
Lumped reflex gain model used to fit reflex gains onto the output of the perturbation experiments of the neuromusculoskeletal model. In this lumped model, the force disturbance d is applied to a single inertia m. Muscle viscoelasticity is represented by a stiffness k and viscosity b. Reflexive feedback is represented by a positional feedback gain k _p, a velocity feedback gain k _v and a force feedback gain k _f. A single reflexive feedback neural time delay τ _del is represented by H _del. The first order muscle activation dynamics are H _act. Output of this lumped model is joint position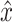

The reflex gain model transfer function H _mod was described by:

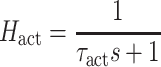4a

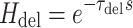4b

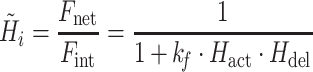4c

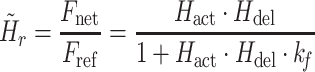4d

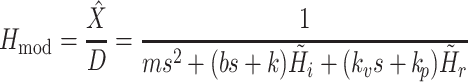4e

For convenience, two intermediate variables 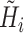and 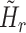describe the effect of the force feedback loop on the afferent and reflexive velocity and position feedback loops (from intrinsic muscle force F _int and reflexive muscle force F _ref to net force F _net). Using these intermediate variables, the entire model transfer function H _mod can be expressed in a form similar to that of a mass-spring-damper system (see also Schouten et al. 2008b).

The eight model parameters m, b, k, k _p, k _v, k _f, τ _del and τ _act (see also Table 1) were fitted onto the data with a criterion function J which minimized the error between arm position x of the neuromusculoskeletal model and the output of the lumped reflex gain model :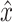

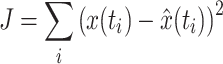5

where i indexes the time vector t. For efficiency, lumped reflex gain model output 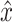was first determined in the frequency domain and then inverse Fourier transformed to obtain:

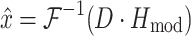6

where D is the Fourier transform of disturbance force d. The criterion J was minimized using the least squares algorithm

lsqnonlin

from the Matlab optimization toolbox.1 The result of the fitting procedure was a set of 8 parameters that describe the joint dynamics, including reflexive contribution, in the same way as done in experiments.

Table 1.

Parameters of the lumped reflex gain model

Lumped parameter	Unit	Description
m	kg·m 2	Joint inertia
b	Nm·s / rad	Muscle viscosity
k	Nm / rad	Muscle stiffness
k p	Nm / rad	Position feedback gain
k v	Nm·s / rad	Velocity feedback gain
k f	Nm / Nm	Force feedback gain
τ del	s	Neural time delay
τ act	s	Muscle activation time constant

After fitting, the goodness of fit was expressed in variance accounted for (VAF):

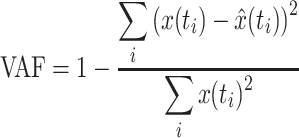7

A VAF value of 1 indicates a perfect match between the lumped reflex gain fit and the NMS model output. Besides the parameters of the lumped reflex gain model and the VAF, the RMS value of the joint deviation (in radians) was determined to get a measure of performance in counteracting the disturbance.

Data analysis

A sensitivity analysis was performed where the neural and sensory parameters in the NMS model were systematically varied. The effects on the lumped reflex gains (Table 1) and the performance in terms of disturbance suppression (RMS) were determined. The 36 parameters included in the analysis were: muscle spindle constants (6), the Golgi tendon organ constant (1), synaptic weights between afferents and the neuron populations (8), synaptic weights between the neuron populations (12), synaptic weights between descending excitation and each neuron population separately (4), synaptic weights between descending excitation and all neuron populations simultaneously (1), and afferent and efferent time delays (4). A complete overview of the parameters including their description is listed in Table 2.

Table 2.

Model parameters in the sensitivity analysis and their description

Neural model parameter	Description
Sensory constants
a Ia	Muscle spindle constant a Ia (Eq. (2))
c Ia	Muscle spindle constant c Ia (Eq. (2))
d Ia	Muscle spindle constant d Ia (Eq. (2))
e Ia	Muscle spindle constant e Ia (Eq. (2))
a II	Muscle spindle constant a II (Eq. (3))
c II	Muscle spindle constant c II (Eq. (3))
c Ib	Golgi tendon organ constant c Ib (Eq. (1))
Transport delays
τ Ia	Ia afferent transport delay
τ Ib	Ib afferent transport delay
τ II	II afferent transport delay
τ Eff	Efferent transport delay
Synaptic weights (between neurons)
w RC − MN	Synaptic weight Renshaw cell → motoneuron
w IA − MN	Synaptic weight Ia interneuron → motoneuron
w IN − MN	Synaptic weight inhibitory interneuron → motoneuron
w EX − MN	Synaptic weight excitatory interneuron → motoneuron
w MN − RC(L)	Synaptic weight motoneuron → Renshaw cell (long time constant)
w MN − RC(S)	Synaptic weight motoneuron → Renshaw cell (short time constant)
w RC − RC	Synaptic weight Renshaw cell → Renshaw cell (reciprocal)
w IA − RC	Synaptic weight Ia interneuron → Renshaw cell
w RC − IA	Synaptic weight Renshaw cell → Ia interneuron
w IA − IA	Synaptic weight Ia interneuron → Ia interneuron (reciprocal)
w IB − IN	Synaptic weight Ib interneuron → inhibitory interneuron
w IB − EX	Synaptic weight Ib interneuron → excitatory interneuron
Synaptic weights (afferents to neurons)
w ia − IB	Synaptic weight Ia afferent → Ib interneuron
w ia − IN	Synaptic weight Ia afferent → inhibitory interneuron
w ia − MN	Synaptic weight Ia afferent → motoneuron
w ia − IA	Synaptic weight Ia afferent → Ia interneuron
w ib − IN	Synaptic weight Ib afferent → inhibitory interneuron
w ib − IB	Synaptic weight Ib afferent → Ib interneuron
w ii − EX	Synaptic weight II afferent → excitatory interneuron
w ii − IA	Synaptic weight II afferent → Ia interneuron
Tonic descending excitation
w td − MN	Synaptic weight descending excitation → motoneuron
w td − RC	Synaptic weight descending excitation → Renshaw cell
w td − IA	Synaptic weight descending excitation → Ia interneuron
w td − EX	Synaptic weight descending excitation → excitatory interneuron
w td − ALL	Synaptic weight descending excitation → all receiving neurons

One by one each parameter was simulated at 0.5, 0.9, 1.0, 1.1, 1.5 and 2.0 times its nominal value, with all other parameters kept to their nominal value. For each value, a single set of reflex gains was fitted onto the data of the eight simulation repetitions. A sensitivity measure was defined by taking the slope of a linear regression through the six resulting reflex gain values (Fig. 4). To allow for comparisons between the different sensitivities the sensitivity measure was normalized with the reflex gain value when all neural parameters had their default, nominal value (relative sensitivity, see Frank 1978). So the sensitivity measure gave the relative amount of change in a fitted lumped reflex gain as the result of a changing neural or sensory parameter. Figure 4 illustrates this process for the three reflex gains k _p, k _v, k _f and the RMS of joint deviation.

Fig. 4.

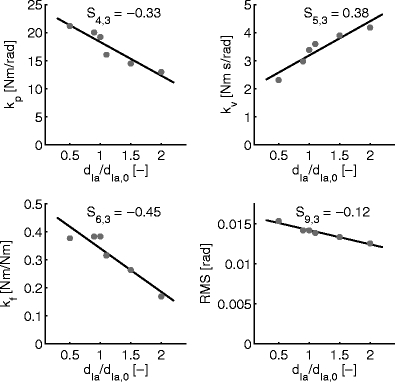
Sensitivity of reflex gain parameters k _p, k _v, k _f and RMS of joint deviation to the velocity component d _Ia of the muscle spindle. Lines indicate the linear regression fit; the normalized slope determined the sensitivity measure S _ij

Results

Figure 3 illustrates the results of a single model simulation. The top panel shows the multisine disturbance force d(t) acting on the joint. The resulting joint rotation x(t) of the NMS model is illustrated in the bottom panel, together with the reflex gain model fit 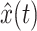. Of all reflex gain model fits, one fit with a VAF of 0.48 was rejected. This was the condition in which tonic descending excitation (TDE) was minimal, causing some of the neural populations to completely cease activity. The average VAF of the remaining 215 fits was 0.95 with a standard deviation of 0.014 and a minimum of 0.84.

Fig. 3.

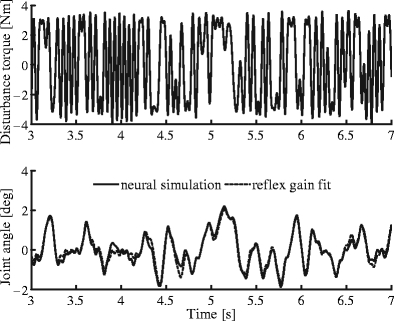
Four-second segment of a perturbation experiment on the NMS model and the output of the lumped reflex gain fit for a single condition. Disturbance torque (top) and resulting arm motion (bottom). Simulation experiment with the NMS model (solid) and the fit of the lumped reflex gain model (dashed). In this case VAF of the fit was 0.95

Table 3 lists the lumped reflex gains resulting from a simulation run with all neural and sensory parameters at their nominal values. The simulation results are generally close to the experimental results (within one SD of the experiments by Schouten et al. 2008a), except for neural time delay τ _del, which seems to be underestimated in the model simulation result.

Table 3.

Estimated lumped reflex parameters of the neuromuscular model with all neural parameters at their nominal values

Lumped reflex gain	Value	Unit
m	0.178	kg·m 2
b	2.99	Nm·s / rad
k	90.5	Nm / rad
k p	19.2	Nm / rad
k v	3.39	Nm·s / rad
k f	0.384	Nm / Nm
τ del	15.0	ms
τ act	47.5	ms

As an example, Fig. 4 shows how lumped reflex gains were modulated by varying neural parameter d _Ia; the velocity component of the muscle spindles. The sensitivity measure S _ij is indicated in the figure. The example shows that when the velocity component d _Ia in the output of the muscle spindle increases, velocity feedback gain k _v increases as expected. Position and force feedback gains k _p and k _f both decrease, demonstrating that position feedback gain k _p and force feedback gain k _f also depend on velocity component d _Ia of the muscle spindle. Performance increased with d _Ia, indicated by the decreasing RMS value of the joint deviation: as the amount of velocity feedback from the muscle spindles increased, joint deviations decreased. In a position task, small deviations indicate good performance.

The sensitivity of the lumped reflex gains to variations in the neural and sensory parameters of the NMS model is illustrated in Fig. 5. For each of the parameters of the lumped reflex gain model and the RMS of the joint deviation, the eight neural and sensory parameters with the largest effect (per parameter) are shown. The height of the bars shows the magnitude of the sensitivity metric S _ij, plus and minus signs above the bars indicate the sign of S _ij.

Fig. 5.

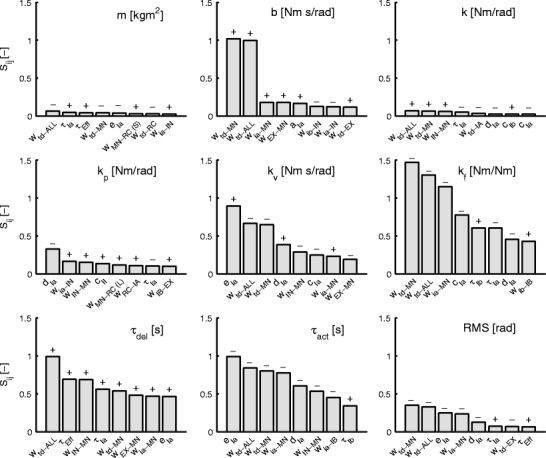
Sensitivity measure S _ij for the eight lumped reflex gain model parameters (m, b, k, k _p, k _v, k _f, τ _del, τ _act) and RMS of the joint position. Low RMS indicates high task performance: the force disturbances result in small deviations. For each graph, only the eight parameters with the highest sensitivity values are shown

The top row in Fig. 5 shows the sensitivity of the intrinsic parameters: inertia m, joint viscosity b and joint stiffness k. Sensitivity of the inertia estimate is low for all parameters (sensitivity in the order of 0.05) as can be expected, since mass was not varied. Joint viscosity b is mainly affected by tonic descending excitation. Increasing TDE to specifically the motoneurons or to all populations increased viscosity by increasing the tonic muscle activation. Further, viscosity was increased by various excitatory pathways to the motoneurons and decreased by inhibitory pathways via the inhibitory interneuron populations. Sensitivity of stiffness k is remarkably low (in the same order of magnitude as that of inertia m). Because of the linearized muscle model, one might expect similar sensitivity of stiffness and viscosity. The difference is due to the relatively high value of stiffness k in the nominal condition, decreasing the normalized sensitivity.

The middle row in Fig. 5 illustrates the sensitivity of reflex gains k _p, k _v and k _f to the eight parameters that they were most sensitive to. Velocity feedback over the Ia afferent decreased k _p. This is indicated by the negative sensitivity to muscle spindle constant d _Ia, and also by the positive sensitivity to inhibitory pathways from Ia afferents to motoneurons. Group II afferent feedback increased k _p as expected. Renshaw cell activation increases position feedback gain k _p, both through the long latency constant synapse (w _{MN − RC(L)}) and the synapse between the Renshaw cells and the IA interneuron (w _{RC − IA}). Velocity reflex gain k _v increases with the stretch velocity components in the Ia afferent pathway (d _Ia, e _Ia) and with increasing strength of the synapse between Ia afferent and motoneuron. TDE to either the motoneurons alone or to all populations decreases k _v. Further, k _v decreases with the stretch component of the Ia afferent, and the pathway over inhibitory interneurons. Activation by excitatory interneurons decreased k _v, which might be caused by these interneurons receiving stretch feedback from the II afferent and no velocity feedback from the Ia afferent. Force feedback gain k _f strongly decreased with TDE and Ia afferent feedback and increased with Golgi tendon organ (GTO) feedback over the Ib afferent pathway. The neural time delay of the Ib afferent increased k _f as well.

The bottom row in Fig. 5 illustrates the sensitivities of neural time delay τ _del, muscle activation time constant τ _act and the RMS of joint deviation. Neural time delay estimate τ _del was highly sensitive to the Ia afferent and efferent neural time delays as expected, and further to a mixture of neural and sensory parameters. The high sensitivity of the estimated muscle activation time constant τ _act to a wide range of neural and sensory parameters is surprising (note that muscle activation was not varied in the simulations).

The bottom-right panel in Fig. 5 shows how the RMS of the joint deviations changed with the neural parameters. TDE had the strongest effect on performance, by increasing motoneuron activity and therewith co-contraction. Further, Ia afferent feedback (both synaptic strength and muscle spindle properties) improved performance while neural time delays decreased performance. Force feedback over Ib afferents and position feedback over II afferents only had a small effect on performance.

Figure 5 demonstrates that most lumped reflex gains were sensitive to a mixture of neural and sensory parameters. To elucidate the relation between the properties of the proprioceptors and the estimated reflex gains, Fig. 6 shows a subset of the data: the sensitivity of k _p, k _v and k _f to only the sensory constants of the muscle spindle and GTO. The velocity components of the muscle spindle (constants d _Ia and e _Ia) positively correlated with velocity gain k _v, with relatively low interaction with the other reflex gains. Position feedback gain k _p and force feedback gain k _f however did not show such a distinct sensitivity. There was positive sensitivity of k _p to the stretch component of the muscle spindle c _II, but k _p decreased with velocity component d _Ia as well. The GTO constant c _Ib led to an increase of k _f, but the spindle parameters a _Ia, c _Ia and d _Ia have a far stronger negative (decreasing) effect on k _f. Summarizing, Fig. 6 demonstrates that k _v and k _f are mostly influenced by muscle spindle feedback, while k _p is influenced by a mixture of afferent feedback pathways.

Fig. 6.

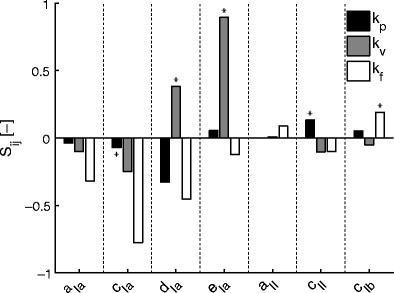
Sensitivity measure S _ij of the lumped reflex gains k _p, k _v, k _f to the sensory parameters of the muscle spindle and Golgi tendon organs. The most closely related neural substrates of each reflex gain parameter are indicated with an asterisk (*), e.g: velocity feedback gain k _v is expected to be closest related to the velocity components d _Ia and e _Ia. (See Eqs. 1–3 and Table 1 for a list of these parameters)

Discussion

Multiple mechanisms contribute to posture maintenance. Perturbation experiments and system identification are widely used to assess posture maintenance in humans (e.g. Kearney et al. 1997; Perreault et al. 2000; Van der Helm et al. 2002; Ludvig and Kearney 2007). System identification and neuromuscular modeling pose a powerful tool for quantifying posture maintenance with a small set of control parameters. For instance, a position feedback gain expresses force buildup related to muscle stretch. However, many neural and sensory properties contribute to these feedback gains. When posture maintenance is captured in such a small set of reflex parameters, interaction could be expected. For instance, both decreasing presynaptic inhibition of the Ia afferent and increasing fusimotor drive can increase the velocity feedback gain, since the net amount of velocity related feedback in the control action to the muscle increases. These interactions complicate the interpretations of the results from reflex experiments. Neural and sensory mechanisms might affect multiple parameters of the lumped reflex model (see Figs. 5 and 6). Since direct in vivo measurements of neural and sensory properties are unfeasible during posture control experiments in humans, the goal of this study was to investigate how neural and sensory properties could map onto the (limited) set of reflex gains. Or, in the example of presynaptic inhibition and fusimotor drive, investigate how the net synaptic weights between afferents and motoneurons or the parameters of the muscle spindle model affect the lumped reflex gains.

We simulated posture control experiments with a neuromusculoskeletal model. In the NMS model, spinal cord circuitry controlled a joint, while receiving feedback from muscle spindles and Golgi tendon organs in the activated muscles. The joint was perturbed with a random force disturbance. Like in experiments, the posture control behavior of the simulated NMS model was captured by fitting the parameters of a lumped reflex gain model onto the simulated data. The high VAF of the reflex gain model fits onto the output of the NMS model indicated that the linear reflex gain model was able to adequately capture the behavior of the strongly nonlinear NMS model. This was greatly due to the conditions in the simulated experiment (and commonly used in in vivo experiments): during a posture control task (minimize deviations), there is a constant level of muscle co-contraction with small deviations around the equilibrium position of the joint. Therefore, the experimental conditions linearize the behavior of the non-linear neural system. A comparison to actual experimental data showed that the reflex gains fitted from the neuromuscular model closely resembled reflex gains identified in vivo.

The results showed a dominant role of tonic descending excitation (TDE) on the parameters of the lumped reflex gain model. TDE to the motoneurons (parameter w _{td − MN}) increases tonic muscle activation (co-contraction) and therewith the muscle viscoelasticity, expressed in parameters b and k. Parameter w _{td − ALL} simultaneously increased the amount of TDE to both motoneurons and all other populations receiving TDE. Besides viscoelasticity, also reflex gains k _v and k _f were influenced by these two TDE parameters; these reflex gains decreased with TDE. In the simulations of the NMS model, TDE increased activation of the receiving populations. As a result, the neural network received relatively less afferent input than tonic input, which could explain the decreasing reflex gains with TDE.

The results have shown that each of the lumped reflex gain parameters is positively sensitive to its most direct neural substrate: k _v increases with parameters related to Ia afferent stretch velocity feedback pathway, k _p with the II afferent stretch feedback pathway, and k _f with Ib afferent force feedback pathway. For k _v this most direct substrate was also the most dominant and interaction with other pathways was low. In contrast, k _p and k _f showed stronger sensitivities to other (and less directly related) neural and sensory mechanisms, which makes accurate identification difficult in the given experimental conditions. Both k _p and k _f decreased with velocity feedback over the Ia afferent pathway. Additionally, force feedback gain k _f strongly decreased with TDE. This is in concordance with experimental findings: force feedback modulation in humans was strongest in an experimental condition with low co-contraction and low-frequent (slow) perturbations (Mugge et al. 2010). Position feedback gain k _p was remarkably less sensitive to neural and sensory property changes than k _v and k _f. In the posture control task used in the experiments deviations were small, while high muscle stretch velocities resulted from the disturbance force. Therefore muscle length information played a lesser role during the posture control task than velocity feedback. These results suggest that to effectively identify k _p experimentally, stretch velocities need to be kept small to minimize the interactions between velocity and position feedback.

Summarizing, the sensitivity analysis demonstrated dominance of muscle spindle velocity feedback and tonic descending excitation. Velocity feedback gain k _v was distinctly influenced by afferent velocity feedback and TDE, while position and force feedback gains k _p and k _f depended on a wide variety of neural properties. The results of this modeling study contribute to determining experimental conditions suited for studying reflex modulation in vivo. From reflex experiments (de Vlugt et al. 2002; Schouten et al. 2001), we know that experimental conditions like level of co-contraction, perturbation velocities and amplitudes, but also task instruction induce reflex gain modulation. When the relationship between neural properties and reflex gains is better understood, experimental conditions can be adapted to the type of reflex modulation that is being studied. Furthermore, it is important to know if the experimentally estimated reflex gains are the result of the expected neural mechanism or may be a combination of interacting mechanisms. For example, one must be aware that modulation of k _v can, besides Ia afferent feedback, be caused by tonic descending excitation to the motoneurons. It could therefore be important to control the level of co-contraction in such an experiment.

Like most models, the model presented here has many simplifications. Starting at the sensory level, a straightforward feline muscle spindle was chosen, together with a linear Golgi tendon organ model. Because of the modeled task (a position task with co-contraction and small, continuous perturbations with fixed frequency content) both sensors operate with small deviations around a relatively steady state. We argue that under these conditions, the simple models capture sufficient detail to describe the afferent feedback triggered by the perturbations, although we are aware of the intricate dynamics that muscle spindles and Golgi tendon organs can demonstrate (Mileusnic et al. 2006; Mileusnic and Loeb 2006). The sensory models used had their output in spikes per second and a Poisson process was used to convert output to spike trains. Halliday and Rosenberg (1999) presented a point-process spectral estimate on a human Ia afferent spike train, that closely matched the spectral properties of recorded spike trains, indicating that a point process could describe the Ia afferent dataset.

The spinal neural model was relatively straightforward. The spinal populations in the neural model were homogeneous, and connections between the individual neurons in the populations were assigned using a random process. The neuron model was a simple point neuron, without spatial representations like a dendrite structure. These are important simplifications, and more detailed models of the individual components of our neural model do exist. Nevertheless, this simplicity serves a purpose. The main goal was to determine how changes in velocity-, position- and force-related neural feedback map onto the limited set of reflex gains that are used in experiments. The main question was: which neural pathways could be contributing when changes in reflex gains are observed in an experiment? Unlike a lumped reflex gain model, where each feedback channel has a distinct pathway, biological afferent feedback fans out in the spinal populations before finally converging at the motoneurons. The multitude of pathways and their interactions are the cause of most lumped reflex gains being sensitive to multiple neural and sensory parameters. Each detail added to the neural model adds one or more parameters and thus might add a new relationship with one of the reflex gains. However, the main phenomenon that was demonstrated here can be captured with a relatively simple model that includes at least the afferent feedback pathways, fan-out and convergence in the spinal populations and output to a musculoskeletal model.

We conclude that with postural control tasks and wide-bandwidth force perturbations, parameters of the Ia afferent feedback pathway largely contribute to the task performance enabling accurate identification of k _v. In these conditions of high stretch velocities, but low stretch and fairly constant muscle activation, parameters of the II and Ib afferent feedback pathways hardly contribute to task performance. Because of this low contribution to task performance, the amount of position and force related information in the measured joint deviations is low, resulting in poor identifiability of k _p and k _f. This is expressed by the high sensitivity to other, seemingly non-related feedback pathways. Identification of k _p and k _f probably needs an experimental design that decreases the effects of interaction from velocity feedback, like Mugge et al. (2010) suggests for k _f.