Radiofrequency Ablation at Low Frequencies for Targeted Tumor Heating: In-vitro and computational modeling results

Abstract

Radiofrequency (RF) ablation uses RF current to heat and kill cancer applied via an electrode inserted under image-guidance. Tumor has about half the electrical resistivity of normal tissue below 20 kHz, but similar resistivity above 500 kHz. We placed normal porcine liver tissue in contact with Agar gel having similar resistivity as tumor within 20-450 kHz. A needle electrode was placed with half of the electrically active tip in each layer. We performed ablation with electric current applied for 12 min at 30W, either at 20 kHz or 450 kHz (n=7 each) while measuring temperature via thermocouples 4 and 8mm from the electrode. Mathematical heat-transfer models were created of an equivalent configuration and temperature profile determined at both frequencies. At 8 mm distance, at 450 kHz, tumor gel phantom and normal tissue obtained similar temperatures (57.5±1.4 vs 58.7±2.5°C); at 20 kHz, tumor phantom obtained significantly higher temperatures than normal tissue (65.6±2.0 vs 57.2±5.6°C, p<0.01). Computer models confirm these results, and show the ablation zone diameter to be larger within the tumor phantom at 20 kHz compared to 450 kHz. Heating at low radio frequencies may thus allow targeted heating of tumor tissue and reduced heating of normal tissue.

I. Introduction

Radiofrequency (RF) ablation employs electric current in the radiofrequency range (450 – 500 kHz) to heat, and destroy cancer tissue. It is in clinical use for treatment of primary and metastatic liver tumors, as well as tumors in kidney, lung, bone, and adrenal gland tissue [4-9]. During RF ablation, an electrode is inserted into the tumor under imaging guidance (typically CT or Ultrasound), and tissue surrounding the electrode is heated and destroyed. The radiofrequency range was chosen for these devices because electrosurgery devices, which served as predicate devices and use essentially the same type of RF generators, operate in this frequency range and therefore simplified regulatory approval of RF ablation devices.

When tissue is heated via application of electric current from an electrode, the heating profile around the electrode depends on the electrical resistivity of the adjacent tissue. Tissue electrical resistivity is frequency dependent and varies by tissue type; of particular interest for this study is the variation of resistivity between normal and cancerous tissue [10-15]. A prior in vivo animal tumor study found that the electrical resistivity of tumor tissue is significantly lower than normal tissue over the 10 kHz to 1 MHz frequency range, with a more pronounced difference at lower frequencies, where tumor has approximately half the resistivity of normal tissue (Figure 1) [11]. Subsequent ex vivo measurements in human tumors have shown an even more pronounced difference in electrical resistivity between normal and tumor tissue [10, 15, 16], but ex vivo tissue measurements are typically less accurate, since the dielectric properties of tissue change rapidly and considerably after removal from the body [17]. Previously published studies employing mathematical modeling suggest that this difference between normal and cancer tissue in the frequency range below 100 kHz may be exploited to preferentially heat tumor tissue [18, 19], and recent preliminary in-vitro studies at low temperature exposures (< 50 °C) support this hypothesis [20].

Fig. 1.

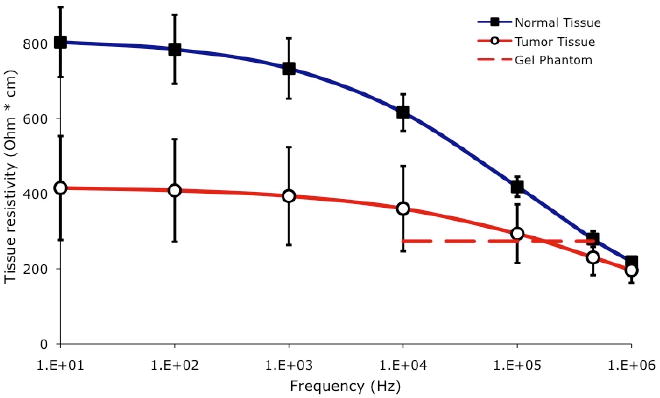
Electrical resistivity of tumor and normal liver tissue. Each data point represents average of measurements in 24 tumors measured in-vivo in 17 rats, with error bars indicating standard error (SE); data reproduced from a prior study [11]. Dashed line shows electrical resistivity of the tumor gel phantom used in this study for comparison.

Here we report in-vitro experimental results on animal tissue and corroborating mathematical models comparing RF ablation between standard, and low radio frequencies.

II. Materials and Methods

A. Ex Vivo Experiments

A.1. Experimental Setup

We created an ex vivo model consisting of a layer of excised porcine liver tissue and a layer of tumor phantom made of Agar gel. This two-layer setup was used in this study instead of a setup involving a spherical tumor phantom surrounded by normal tissue for two reasons: (1) there is no animal model with tumors sufficiently large for this study, and (2) this setup allowed us consistent positioning of temperature sensors relative to the boundary between the two materials, thus avoiding errors caused by variations in the sensor locations due to the tumor size and shape. Previous studies have demonstrated that the resistivity of tumor tissue is relatively independent of frequency in the range of 10 – 100 kHz [11]. In this study, we used agar gel (5% agar by volume) as a tumor phantom because its resistivity (as determined by the saline concentration used during its construction) is similarly independent of frequency as tumor tissue (Fig. 1).

It has been previously reported that the resistivity of liver tissue rises by approximately a factor of 2 in the first few hours after excision [17]. In preliminary experiments with fresh ex vivo porcine liver tissue obtained from a local slaughterhouse, we utilized the four-electrode method [21] to measure tissue resistivity at 20 kHz and 450 kHz approximately 2 hours after excision at the frequencies of interest (results not reported here), and obtained values similar to previous studies [17]. We used 0.12% NaCl solution for tumor phantom creation so that phantom resistivity (estimated 400 ohm·cm at 20 °C from a prior study on NaCl solutions [22]) was similar to the resistivity measured in our preliminary tissue measurements at 450 kHz. Thus, the resistivity ratio between the tumor phantom and normal tissue in our setup was analogous to the ratio published in a previous in vivo animal study (i.e. similar resistivitiy at 450 kHz, with tumor having about half resistivity of normal tissue at 20 kHz) (Fig. 1). Note that the ratio of the resistivities, and not absolute resistivity values, determines relative RF power deposition between different tissue types.

A diagram of the two-layer experimental setup is shown in Figure 2. Before each experiment, we obtained fresh porcine liver tissue from a local slaughterhouse and measured the resistivity of the tissue and gel phantom as described above. In each experiment, a block of tumor phantom measuring approximately 7 cm by 7 cm and 2 cm thick was placed flush with a piece of liver tissue that was at least 3 cm thick. A custom plexiglass template (Fig. 2, B) guided the insertion of an internally cooled RF electrode and four needle microprobe thermocouples (MT-26, Physitemp, Clifton, NJ) into the phantom and tissue. The electrode had an uninsulated (active) length of 3 cm, and was placed such that half of the active length was in each material. Two of the thermocouples were placed 4 mm from the electrode on opposite sides, with one located in the tissue 0.75 cm below the tissue/phantom boundary, and one located in the phantom 0.75 cm above the boundary. The remaining two thermocouples were placed 8 mm from the electrode in the tissue and phantom (similarly 0.75 cm from the tissue/phantom boundary) (Fig. 2). After arrangement of the template, electrode, and thermocouples, a rubberized clamp was used to apply pressure between the template and tissue, ensuring uniform contact between the layers. We then placed the two-layer setup in a plastic tank (~20 × 30 cm) containing room temperature 0.25% saline, which has similar resistivity as muscle tissue at 450 kHz (ρ = 227 ohm·cm). A sheet of aluminum foil was placed ~25 cm from the RF electrode to provide the ground electrode.

Fig. 2.

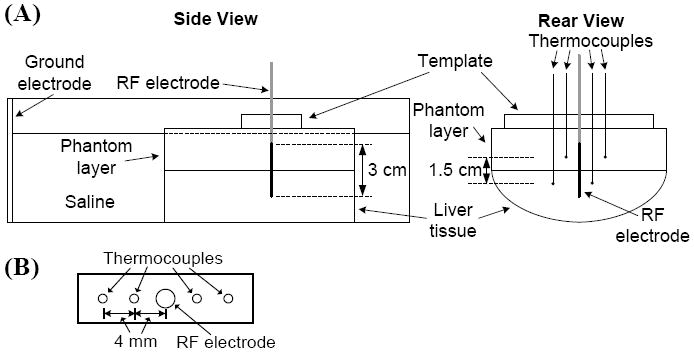
(A) Experimental setup for in-vitro study. A clamp (not shown) ensured uniform contact between tumor phantom and liver tissue. (B) Plexiglass template for thermocouple placement.

We performed a total of 14 experiments in this study. A variable frequency RF generator (AG-1014, T&C Power Conversion, Rochester, NY) was used to apply 30W at either 20 kHz (n = 7) or 450 kHz (n = 7) to the phantom and tissue setup for 12 min. A pump circulated room-temperature cooling water internally through the electrode (starting 15 s before power application) for the duration of each trial. Temperatures at each thermocouple were continuously recorded at a sampling rate of 100 Hz using a laptop PCMCIA data acquisition card (DAQ-6036E, National Instruments, Austin, TX). The initial temperature of the tumor phantom layer was 20.9 ± 0.4 °C and 21.1 ± 0.2 °C in the 20 kHz and 450 kHz trials, respectively. The initial temperature of the liver tissue layer was 21.9 ± 0.6 °C and 21.8 ± 0.4 °C in the 20 kHz and 450 kHz trials, respectively.

A.2. Measurement of Electrical Resistivity

Before each ex vivo experiment as described above, the electrical resistivity of both the liver tissue and tumor phantom were measured at ~4 locations on the surface of both materials. We used the well-known four-electrode measurement system using the same setup as in some of our prior studies [11, 17, 21]. Briefly, a linear array of four Ag/AgCl plunge-electrodes (6 mm long, 1.5 mm apart) was inserted into the gel or tissue. A function generator then injected electrical current at frequencies of 20 kHz and 450 kHz between the outer two electrodes, and the resulting voltage drop was measured between the inner two electrodes. After calibration of the measurement system in a substance of known electrical resistivity (0.9 % NaCl solution at 20°C), the electrical resistivity of the sample could be calculated based on the measured relationship between voltage and current. The average resistivity values were used in the computational modeling studies described below.

A.3. Data Analysis

We compared the temperature measurements at each measurement distance from the electrode between normal tissue and tumor phantom, for both frequencies using Student’s t-test. Statistical significance was designated as p < 0.05.

B. Computational Modeling

A number of prior studies have used the Finite Element Method (FEM) to examine tissue heating during radiofrequency ablation [19, 23-28]. We used the FEM to solve the coupled thermo-electric equations for a cooled needle electrode in a 2-layer setup of normal and tumor tissue, simulating ablations at both 20 and 450 kHz for 12 min at 30 W of power, same as in the experiments (section A1). We used COMSOL Version 3.4 (COMSOL, Stockholm, Sweden) to generate the geometric models, assign material properties, assign boundary conditions, generate mesh, and perform the coupled thermo-electrical analysis. A coupled analysis is required since electrical properties change with temperature, and therefore the electric field problem has to be modified accordingly at each time step. All analysis was performed on a PC equipped with a Pentium 4 CPU and 3 GB of memory.

B.1. Model Geometry and Boundary Conditions

We created an identical FEM model geometry to that used in the ex vivo experiments using an axisymmetric 2-D model; note that for more complex geometries, 3-D models may be preferable and required. A cooled needle electrode with an active length of 3 cm was placed in a 2- layered (top half tumor phantom, bottom half normal tissue) cylinder 40 cm high, and 25 cm in diameter, such that half of the active length was in each layer. The mesh generated by COMSOL was fine (0.2 mm spacing) near the electrode where electrical and thermal gradients are high; the mesh spacing gradually increased at greater distances from the electrode (up to 25 mm at the model boundary). We performed initial convergence tests to confirm that the mesh size was sufficiently small and that the modeling domain was sufficiently large, with tissue temperature as the convergence criterion. We assumed sufficient mesh size and domain size when changing either by a factor of two resulted in a maximum change in temperature of less than 0.1 °C. The size of the time steps during the simulation varied between 0.1 s at the beginning to a maximum of 1 s.

We applied 0 V electric potential at the outer model boundary to represent the ground electrode (Fig. 3). The initial tissue temperature was set to room temperature (21 °C), which was also applied to the outer model boundary. The electric potential boundary condition at the electrode surface was set for each simulation such that a constant power of 30 W was dissipated. The internal cooling of the needle electrode via circulating room-temperature water was simulated by applying a constant temperature boundary of 10 °C to the needle surface (note that a prior study showed that the tissue temperature profile is not sensitive to changes in cooling temperature [25]).

Fig. 3.

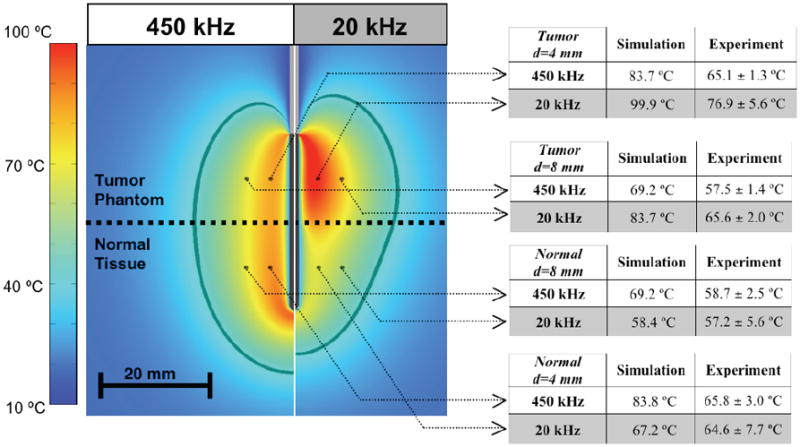
Temperature profile after heating for 12 min at 450 kHz (left), and 20 kHz (right). The table on the right shows temperatures at the marked locations (4 mm and 8 mm distance d from the electrode center) from the computer simulation compared to experimental results (average of n=7 measurements, +/- SE). The dark gray boundary marks the region within which estimated cell survival in the computer simulation is less than 1%. Experimental temperature data were not significantly different between normal tissue and tumor phantom at 450 kHz at either distance, but were significantly higher in tumor phantom at 20 kHz at both distances (p<0.01).

B.2. Computation of Electric field, Temperature, and Damage

When alternating electric fields are applied to resistive materials (like tissue), heating occurs due to both conduction losses (resistive heating from ion movement) and dielectric losses (caused by the rotation of molecules in the alternating electric field). However, in the frequency range below ~1 MHz, dielectric losses are negligible [23], and therefore we only consider resistive heating in this model.

During RF ablation a certain voltage is applied to the electrode. The resulting electric field in the tissue from the Laplace’s equation:

$$\nabla ·\frac{1}{{\rho }_e}\nabla V=0$$ (1)

where ρ_e is the electrical resistivity of the material (Ω·m) and V is the electric potential (V). The electric field intensity E (V/m) and current density J (A/m²) are then computed from:

$$\mathbf{E}=-\nabla V$$ (2)

$$\mathbf{J}=\frac{\mathbf{E}}{{\rho }_e}$$ (3)

The local power density resulting in tissue heating is the product of current density J and electric field intensity E, which is then used to calculate the temperature distribution via the heat-transfer equation:

$${\rho }_{m}c\frac{\partial T}{\partial t}=\nabla ·k\nabla T+\mathbf{J}·\mathbf{E}$$ (4)

where ρ_m is the mass density of the material (kg/m³), c is the specific heat of the material (J/(kg·K)), and k is the thermal conductivity of the material (W/(m·K)).

To determine the boundaries of cell death, we utilized an Arrhenius damage model [29, 30] as shown in Equation 5, where thermal damage Ω(t) is related to the expected cellular survival fraction as shown in Equation 6:

$$\mathrm{\Omega }(t)=\underset{0}{\overset{t}{\mathit{\int }}}{\mathit{Ae}}^{-\mathrm{\Delta }E/\mathit{RT}(\tau )}d\tau$$ (5)

$$\mathrm{\Omega }\left(t\right)=-\ln \left(c\left(t\right)/c\left(0\right)\right)$$ (6)

where A is the frequency factor (2.984 × 10⁸⁰ s^-1), ΔE is the activation energy (5.064 × 10⁵ J·mole^-1), T(τ) is the absolute temperature as a function of time, c(t) represents the concentration of living cells as a function of time, and c(0) is the initial concentration of living cells. The values for ΔE and A in Equation 5 were shown in a previous experimental study to accurately predict the cell death boundary in an animal model when used with a threshold value of 4.6 for Ω(t) (which corresponds to 99.0% cell death) [31].

B.3. Electrical and Thermal Tissue Properties

Table 1 shows the tissue and tumor phantom material properties used in the computer models. For the tumor phantom, we assumed thermal properties and their temperature dependence are the same as for water [1, 3].

TABLE I.

Material Properties Used in FEM Model

Material	ρm (kg/m3)	c (J/(kg·K))	k (W/(m·K))	ρe (Ω·cm)
Liver tissue	1060	3800 (20 °C)	0.498+0.0008·T(°C)	ρe’·(1-0.0162 · (T-20°C)
				ρe’=816 Ω·cm (20 kHz, 20°C)
				ρe’=493 Ω·cm (450 kHz, 20°C)
Agar Tumor Phantom	998 (20 °C)	4182 (20 °C)	0.60 (T=20 °C)	410 Ω·cm (20 °C)

Electrical tissue resistivity values ρ_e’ listed as measured experimentally in this study at 20 °C. Other tissue and phantom property data are taken from prior studies [1-3]. All properties except mass density ρ_m were considered temperature dependent, and either functions used for temperature dependence are listed, or the value at 20 °C is given when the references provided tabulated data at different temperatures.

The NaCl content at the concentration used in the experiments does not change heat capacity or thermal conductivity significantly [32, 33]. For electrical resistivity of both gel phantom and liver tissue, we used the average of the values we measured in the experimental part of this study, both at 20 kHz and 450 kHz (see Section A.2). For the tissue layer we assumed a temperature coefficient from a prior study for kidney [34], as no such data was available for liver. For the Agar phantom we assumed electrical resistivity to vary with temperature as it does for a NaCl solution of same salinity [22].

III. Results

The experimentally measured resistivity values of tissue and gel phantom are shown in Table II.

TABLE II.

Experimentally Measured Electrical Resistivity

Frequency	20 kHz	450 kHz
Liver tissue	816±106 Ω·cm	493±39 Ω·cm
Agar Tumor Phantom	409±18 Ω·cm	413±18 Ω·cm

Electrical tissue resistivity was measured at ~21 °C before commencing the ablation experiments.

Figure 3 shows the temperature profile at the end of the 12 min ablation determined from the computational models, both at 450 kHz (left), and 20 kHz (right). The table on the right side of Figure 3 shows temperatures measured in each layer at 4 mm and 8 mm distance from the electrode center, at both 20 kHz and 450 kHz (average of n=7 measurements, +/- SE).

Experimental temperature data were not significantly different between normal tissue and tumor gel phantom at 450 kHz at either distance, but were significantly higher in tumor phantom at 20 kHz at both distances (p<0.01). Figures 4 and 5 show the cell survival fraction after 2 min, and after 12 min heating at both frequencies as calculated from the temperature profile history data of the computational model.

Fig. 4.

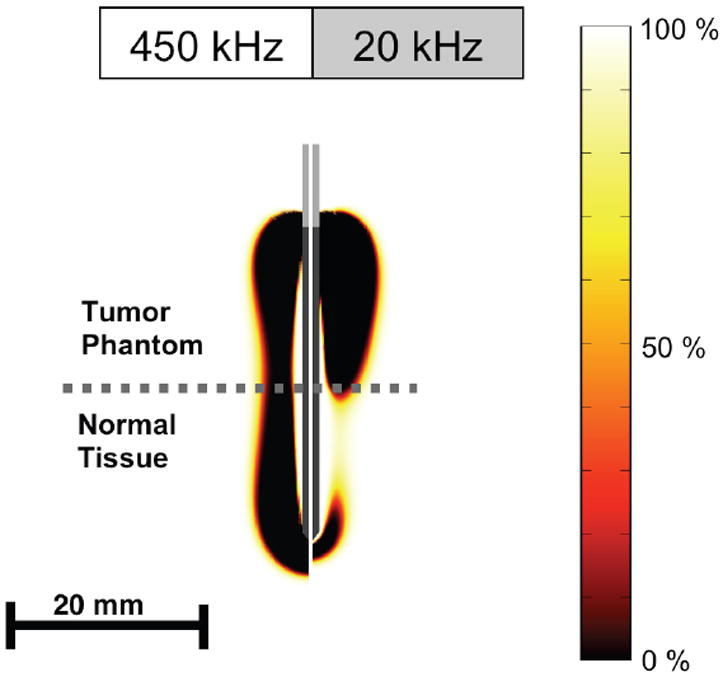
Cell survival fraction (%) after 2 min heating at both frequencies as calculated from temperature history.

Fig. 5.

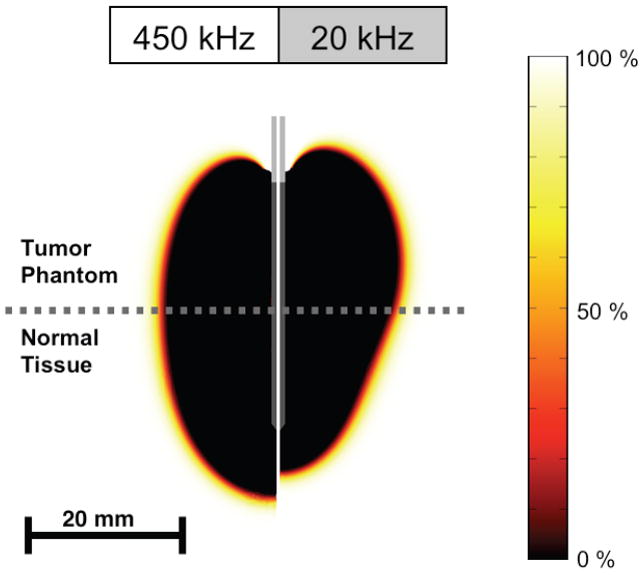
Cell survival fraction (%) after 12 min heating at both frequencies as calculated from temperature history.

IV. Discussion

RF ablation is currently in clinical use for treatment of patients with cancers in liver, kidney, lung, bone, and adrenal gland [4-9]. During the procedure, an electrode is inserted into the tumor using medical imaging (typically computed tomography (CT) or ultrasound) as guidance. Upon placement, electric current in the radio frequency range is applied to the electrode resulting in electrically resistive heating of the surrounding tissue. Devices used clinically for RF tumor ablation all operate in the frequency range of 450 – 500 kHz due to their development out of electrosurgical units. Here we examined whether ablation via electric current at lower radio frequencies provides benefits in terms of targeted tumor heating as suggested by prior results from mathematical models [19]. The potential benefit of lower frequencies than currently used stems from the frequency dependence of electrical tissue resistivity, and particularly the variation of this frequency dependence between normal and cancer tissue. Unlike most homogenous materials, the resistivity of biological tissues is frequency dependent, not unlike suspensions of dielectric particles [35]. This frequency dependence occurs because electric current in tissue is conducted via free ions (chiefly Na+, K+, Cl-), and the ensuing accumulation of ionic charges around cell membranes as described by the Wagner-Maxwell effect. A number of prior studies have measured dielectric tissue properties in the radiofrequency range and found consistently lower values for electric resistivity of tumor tissue [10-16]. While at standard ablation radiofrequencies the difference between normal and tumor tissue is modest, at low radio frequencies tumor has approximately half the resistivity of normal tissue (Figure 1).

In this study we used a gel phantom as a model for tumor tissue as there are no sufficiently large animal tumors available for this experimental setup. It should however be noted that, unlike the gel, tumor has often a considerable variability in electrical resistivity between tumors [10, 11, 16], which would affect the resulting tissue heating. In terms of frequency dependence, tumor tissue varies little in electrical resistivity within the range of 10 kHz – 500 kHz, and could be approximated closely by a gel phantom with frequency-independent electrical resistivity (Figure 1). We created the tumor gel phantoms such that the ratio between resistivity of normal tissue and the gel at both 20 kHz and 450 kHz was similar as measured in a prior in vivo animal study [11]; i.e. resistivity of the gel was similar to normal tissue at 450 kHz, and about half that of normal tissue at 20 kHz, which was confirmed by resistivity measurements we performed prior to each experiment on both materials. The differential heating pattern generated by the electric current emanating from the electrode depends on the resistivity ratio between the two materials the electrode is in contact with rather than absolute resistivity values. As a rough approximation of the electrode in contact with two material layers, we can envision two resistors (representing tumor and normal tissues) are placed electrically in parallel, with a certain voltage applied to the resistors. If the voltage is adjusted such that a certain defined magnitude of power is dissipated in total, then the power dissipated at each resistor will depend on the ratio of the resistor values but not on the absolute resistances. Therefore if we can in our experimental setup replicate the resistivity ratios that were measured in vivo, we should be able to obtain a heating pattern similar as would be observed in vivo.

The goal of our experiments was to examine the differential heating obtained on both sides of the tumor-tissue interface via a two-layer setup of fresh normal liver tissue and the tumor gel phantom (Figure 2). During application of electric current at either 450 kHz (standard radio-frequency range) or 20 kHz (low radio-frequency range), we measured the temperature in each of the layers at a distance of 7.5 mm from the interface, at two distances from the electrode (4 and 8 mm). To allow direct comparison between experimental trials as well as between experiment and computational model, we applied constant power (30W for 12 min) to the electrode placed with equal exposed lengths in each of the layers. Even though we did not employ control of applied power as is typically done in clinical devices, note that temperatures obtained are in the range of those obtained during clinical RF ablation, with temperatures measured at 8 mm distance in the range of 60 °C and diameter of the coagulation zone in the 3 cm range (Figure 3). In addition to the experiments, we used computational heat-transfer models similar to prior mathematical modeling studies [19, 23-28], to determine temperature profile around an electrode placed in a two-layer geometry replicating the experimental setup, Both experimental results and computer model are in agreement in that both layers experience similar temperatures when heated with current at 450 kHz. However, when electric current is applied at 20 kHz, significantly higher temperatures are observed in the tumor gel phantom compared to normal tissue (Figure 3). This preferential heating of the tumor phantom is due to the frequency dependence of electrical tissue resistivity, and the much higher resistivity differential between normal and tumor tissue at 20 kHz compared to 450 kHz. In the computational model we also calculated the cell survival fraction from the temperature history data using an Arrhenius damage model [29, 30], with parameters from a prior study where MR thermometry data was correlated with tissue damage [31]. The cell survival fraction images (Figures 4 and 5) show a thin transition zone between dead and live tissue, as has been reported in prior animal studies [26, 36]. After 2 min the preferential ablation of tumor is clearly visible, while the effect is less pronounced after 12 min in part due to the effects of thermal conduction. After 12 min we observe that the diameter of the ablation zone within the tumor layer is increased at 20 kHz in comparison to 450 kHz, whereas the diameter within normal tissue is smaller at the lower frequency; i.e. the higher temperatures obtained in the tumor layer result in larger ablation zones.

While we could not confirm this experimentally as the gel phantom does not allow visualization of the coagulation zone, there is agreement with the temperature data, in that the temperature within the tumor gel phantom is increased at 20 kHz compared to 450 kHz (65.6 vs. 57.5 °C at 8 mm electrode distance), whereas within normal tissue there was no significant difference between the two frequencies (58.7 vs. 57.2 °C at 8 mm electrode distance). These measured temperatures suggest a larger ablation zone diameter in the tumor created at the lower frequency.

While the setup with two adjacent layers simplifies the analysis, clinically the geometry is different in that a typically spherical tumor is surrounded by normal tissue. Depending on the specific case, the ablation electrode may or may not be located such that it crosses the tumor boundary. Often times however the electrode will necessarily have to be placed partially in normal tissue to reach the goal of killing a margin of 1-1.5 cm normal tissue surrounding the tumor, which is done to destroy any microscopic islands of cancer cells that may surround the tumor.

In a prior computer simulation study we found that there was no difference in temperature profile at low-frequency ablation in cases where the electrode is completely submerged in a tumor [19], i.e. in those cases lower frequencies likely provide no advantage. For differential heating to occur, the electrode needs to be placed partially in tumor, and partially in normal tissue [19].

Another potential application would be a RF ablation device where the applied frequency can be varied. Such a device would then provide the ability to shift the heating pattern via varying applied frequency. Particularly in combination with better intra-procedural imaging modalities as may be available in the near future (e.g. MR- or ultrasound thermometry) this would allow for intra-procedural adjustment of tissue heating.

While there is good qualitative correlation between the experimental and the computational modeling data, there is a considerable difference in terms of absolute temperature values. The reason for this deviation could be the insufficient data on exact temperature dependence of tissue, as well as the fact that we could not reproduce the exact three-dimensional geometry of the experimental setup (i.e. size and form of various layers, saline, location of ground electrode etc.); e.g. a considerable fraction of applied power may be dissipated in the saline resulting in reduced energy deposition and heating of the tissue and gel layers compared to the computer simulation. In addition, melting of the gel phantom and resulting convection may affect results.

The frequency dependence of electrical resistivity data (Fig. 1) would suggest that the use of even lower frequencies than the 20 kHz employed in this study would further enhance the effect of preferential heating of tumor tissue. However, it should be noted that further decreasing the frequency may result in stimulation of excitable tissues (heart, nerves, and muscle), and the likely small benefit may not be worth this additional risk.

V. Conclusion

Both experimental results and computational model suggest that thermal ablation employing lower radio frequencies than currently in clinical use may allow preferential heating of tumor tissue and reduced heating of normal tissue, allowing for a targeted thermal therapy. In addition, varying the frequency may allow for shifting of the heating pattern around the electrode after placement.