Thermophilic Bacteria Strictly Obey Szybalski's Transcription Direction Rule and Politely Purine-Load RNAs with Both Adenine and Guanine

Abstract

When transcription is to the right of the promoter, the “top,” mRNA-synonymous strand of DNA tends to be purine-rich. When transcription is to the left of the promoter, the top, mRNA-template strand tends to be pyrimidine-rich. This transcription-direction rule suggests that there has been an evolutionary selection pressure for the purine-loading of RNAs. The politeness hypothesis states that purine-loading prevents distracting RNA–RNA interactions and excessive formation of double-stranded RNA, which might trigger various intracellular alarms. Because RNA–RNA interactions have a distinct entropy-driven component, the pressure for the evolution of purine-loading might be greater in organisms living at high temperatures. In support of this, we find that Chargaff differences (a measure of purine-loading) are greater in thermophiles than in nonthermophiles and extend to both purine bases. In thermophiles the pressure to purine-load affects codon choice, indicating that some features of their amino acid composition (e.g., high levels of glutamic acid) might reflect purine-loading pressure (i.e., constraints on mRNA) rather than direct constraints on protein structure and function.

Duplex DNA can be represented as two horizontal lines, representing “top” (5′ → 3′) and “bottom” (3′ → 5′) strands. When transcription is to the right of the promoter, the top, mRNA-synonymous strand tends to be purine-rich. When transcription is to the left of the promoter, the top, mRNA-template strand tends to be pyrimidine-rich (Szybalski et al. 1966; Smithies et al. 1981). It follows that mRNAs, whatever the direction of their transcription, tend to be purine-rich (Bell et al. 1998; Dang et al. 1998). Usually one of the two purine bases is most heavily involved in purine-loading, and the other may appear indifferent. For organisms of low genomic (C+G)% the purine is usually A. For organisms of high (C+G)% the purine is usually G. The extra purines are located in the loop regions of computer-folded mRNA structures (Bell and Forsdyke 1999a,b).

To explain the phenomenon of purine-loading, it was pointed out that the physical and chemical state of the “crowded” cytosol (Fulton 1982; Forsdyke 1995) is probably adapted to facilitate a reaction of fundamental importance—tRNA–mRNA interaction. This connection between genotype and phenotype (mRNA translation) must occur rapidly and with high specificity. If cytosolic conditions were such as to optimize this process, then there would be an increased probability not only of efficient tRNA–mRNA interactions, but also of efficient mRNA–mRNA interactions. These would initiate by way of “kissing” between the loops of folded RNAs (Eguchi et al. 1991). Such interactions might (1) directly impede protein synthesis, and (2) generate double-stranded RNA segments of lengths sufficient to trigger various intracellular alarms (Cristillo 1998; Fire 1999; Forsdyke 1999a; A.D. Cristillo, T.P. Lillicrap, and D.R. Forsdyke, unpubl.). Thus, there would have been a selection pressure for mRNAs to be “polite” (Zuckerkandl 1986) and avoid unnecessary interactions. This would have been achieved, wherever compatible with other mRNA functions, by loading loops of all mRNAs with non-Watson–Crick pairing bases (e.g., all purines or all pyrimidines).

Exploratory kissing interactions between hybridizing nucleic acids involve transient stacking interactions (Eguchi et al. 1991), with the exclusion of structured water. Such reactions have a strong entropy-driven component (Cantor and Schimmel 1980) and so might increase as temperature increases (Lauffer 1975). Hence, perhaps counterintuitively, nucleic acids should be more “sticky” at high temperatures and the selection pressure to avoid formation of double-stranded RNA should be greater. To examine this, we compare the magnitude (evaluated as Chargaff differences) and range (one or both purines) of purine-loading in the genomes of thermophilic bacteria with those of the genomes of mesophilic bacteria, which normally exist at 37°C or lower temperatures. We also examine the extent to which the pressure to purine-load has affected codon choice, and hence, potentially, protein composition and function.

RESULTS

Large Chargaff Differences in Methanococcus jannaschii

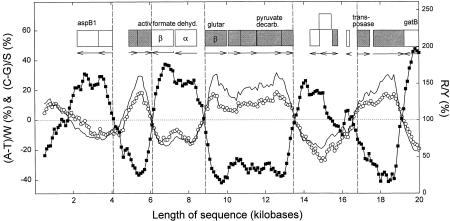
Figure 1 shows a plot of Chargaff differences (%) along a segment of the genome of the thermophilic bacterium Methanococcus jannaschii. In previous studies of nonthermophilic organisms, such plots had to be carefully examined to see whether the S or the W bases were the best predictors of transcription direction in accordance with Szybalski's transcription direction rule. Chargaff differences were seldom >20% (especially Chargaff differences for the S bases), and simply plotting the ratio of purines to pyrimidines (R/Y) was not particularly informative (Bell et al. 1998; Dang et al. 1998; Bell and Forsdyke 1999a,b). In contrast, for M. jannaschii it is observed that (1) both purines follow Szybalski's transcription direction rule, (2) the magnitude of the Chargaff differences is often >20% (especially Chargaff differences for the S bases), and (3) the R/Y ratio strongly correlates with transcription direction.

Figure 1.

Variation of Chargaff differences (%) and purine/pyrimidine (R/Y) ratios along the first 20 kb of the genomic sequence of the thermophile M. jannaschii. A 1-kb sequence window was moved in steps of 0.1 kb, and base compositions were determined in each window. From these, Chargaff differences (○ for the W bases; █ for the S bases), and R/Y ratios (continuous line), were calculated. Data points are located at the center of each window. The locations of putative ORFs are shown as boxes (open for transcription to the left; shaded for transcription to the right; orientations are also marked by horizontal arrows below each box). Although most ORFs correspond to hypothetical proteins, some tentatively identified ORFs have been labeled: (aspB1) Aspartate aminotransferase; (activ) activator of 2-hydroxyglutaryl-CoA dehydratase; (formate dehyd.) α and β subunits of formate dehydrogenase; (glutar) β subunit of 2-hydroxyglutaryl-CoA dehydratase; (pyruvate decarb.) phosphonopyruvate decarboxylase; transposase; (gatB) Asp-tRNA amidotransferase, subunit B.

Even a small rightward-transcribed ORF (in the 15.5- to 15.8-kb region), which is surrounded by leftward-transcribed ORFs, is detectable as a small dip in the S-base plot (G>C), although the W-base plot is not affected. No ORF has been reported at the beginning of the sequence (1- to 2-kb region), but the curve pattern (A>T; G>C) predicts that any ORFs found here should be transcribed to the right of the promoter.

Quadrant Analysis of M. jannaschii

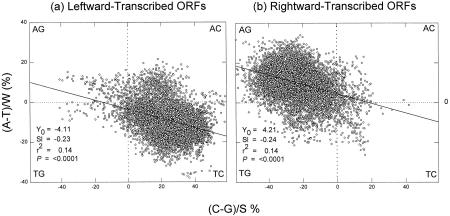
To show that these features of a 20-kb segment (Fig. 1) are typical of the whole genome, the two Chargaff differences (for the W and S bases) were plotted against each other to generate quadrant plots (Bell et al. 1998) for leftward-transcribed ORFs (Fig. 2a) and for rightward-transcribed ORFs (Fig. 2b). Each point in such plots represents a 1-kb window. Because M. jannaschii is 1.66 Mb and windows are taken at 0.1-kb intervals, there are several thousand points in each plot. For windows whose centers overlap leftward-transcribed ORFs, most points indicate enrichment both in T and C, implying that the corresponding mRNA synonymous strands would be enriched both in A and G. For windows whose centers overlap rightward-transcribed ORFs, most points indicate enrichment both in A and G, again implying that the mRNA synonymous strands are enriched both in A and G.

Figure 2.

Quadrant analysis of Chargaff differences (%) for the W and S bases in 1-kb windows from the top strand of the M. jannaschii genome. Each quadrant corresponds to windows enriched for two particular bases, as indicated at the corners. (a) The 7494 windows whose centers overlap leftward-transcribed ORFs; (b) the 8202 windows whose centers overlap rightward-transcribed ORFs. The diagonal lines are the least squares regression lines. Listed are values for intercepts at the ordinate (Y₀), slopes (Sl), squares of correlation coefficients (r²), and probabilities that slopes are not significantly different from zero (P). Similar values were obtained for plots using every tenth window to avoid window overlap (e.g., P < 0.0001).

As in Figure 1, Chargaff differences for the S bases are generally greater than those for the W bases (e.g., in Fig. 2b points are generally farther to the left of the ordinate, indicating G-richness, than they are above the abscissa, indicating A-richness). Although widely scattered, the points fit linear regressions sloping downward, so that, as suggested by Figure 1, it is likely that windows enriched in one pyrimidine are also enriched in the other (Fig. 2a) and that windows enriched in one purine are also enriched in the other (Fig. 2b).

Large Chargaff Differences in Other Thermophiles

The extreme purine-loading found for the entire genome of M. jannaschii was also found for large segments of the genomes of two other thermophilic bacteria (Table 1). The thermophilic bacteria strictly comply with Szybalski's transcription direction rule for both Watson–Crick base pairs, and the magnitude of the differences is generally greater than in the case of the nonthermophilic bacteria. The latter sometimes do not comply with respect to one Watson–Crick base pair (for the Escherichia coli segment, rightward-transcribed ORFs are slightly T-rich; for the Haemophilus influenzae segment, leftward transcribed ORFs are slightly A-rich).

Table 1.

Comparison of Chargaff Differences of Thermophilic and Nonthermophilic Bacteria

Bacterium			Chargaff difference (%)			Base composition of average 1-kb windowb								Purine-loading indexc
	Genome segment			transcriptional orientation		leftward-transcribed				rightward-transcribed
(C + G)%	length (kb)a	leftward	rightward	A	C	G	T	A	C	G	T
Thermophilic
M. thermoauto	49.5	245	(A − T)/W	T > A  −9.44 ± 0.25d	A > T  7.96 ± 0.27	229	268	227	276	273	235	260	232	153
trophicum			(C − G)/S	C > G  8.16 ± 0.21	G > C  −4.91 ± 0.21	A − T = −47		C − G = 41		A − T = 40		C − G = −25
A. aeolicus	43.4	248	(A − T)/W	T > A −12.75 ± 0.36	A > T  9.86 ± 0.36	247	239	195	319	311	199	235	255	208
			(C − G)/S	C > G 10.21 ± 0.29	G > C  −8.30 ± 0.24	A − T = −72		C − G = 44		A − T = 56		C − G = −36
M. jannaschii	31.4	genome	(A − T)/W	T > A  −9.78 ± 0.09	A > T  9.92 ± 0.09	309	195	119	377	377	119	195	309	288
			(C − G)/S	C > G 24.06 ± 0.15	G > C −24.16 ± 0.14	A − T = −68		C − G = 76		A − T = 68		C − G = −76
Nonthermophilic
E. colie	50.7	200	(A − T)/W	T > A  −1.5 ± 0.3	T > A  −1.3 ± 0.3	243	255	252	250	243	234	273	250	42
			(C − G)/S	C > G  0.5 ± 0.2	G > C  −7.6 ± 0.1	A − T = −7		C − G = 3		A − T = −7		C − G = −39
M. pneumoniae	40	genome	(A − T)/W	T > A  −5.49 ± 0.20	A > T  3.08 ± 0.28	284	204	196	316	309	197	203	291	64
			(C − G)/S	C > G  1.87 ± 0.16	G > C  −1.52 ± 0.21	A − T = −32		C − G = 8		A − T = 18		C − G = −6
H. influenzaee	38.1	350	(A − T)/W	A > T  0.3 ± 0.2	A > T  2.1 ± 0.2	310	210	171	309	316	184	197	303	64
			(C − G)/S	C > G 10.2 ± 0.2	G > C  −3.6 ± 0.2	A − T = 1		C − G = 39		A − T = 13		C − G = −13

^aAnalysis involved either entire genomes (Methanococcus jannaschii, 1665 kb; Mycoplasma pneumoniae, 816 kb) or large segments (Methanobacterium thermoautotrophicum, 374431–619430; Aquifex aeolicus, 871431–1119930; Escherichia coli, 1–200000; Haemophilus influenzae, 1–350000). 

^bBase composition for an average window in each category (leftward-transcribed or rightward transcribed), with Chargaff differences (A − T and C − G) expressed as base excesses. The mean pyrimidine excess in leftward-transcribed ORFs of the three thermophiles [(88 + 116 + 144)/(3)], is greater (P = 0.012; paired t-test with 2 df) than that of the three nonthermophiles [(10 + 40 + 38)/(3)]. The mean purine excess in rightward-transcribed ORFs of the three thermophiles [(65 + 92 + 144)/(3)] is greater (P = 0.10) than that of the three non-thermophiles [(32 + 24 + 26)/(3)]. 

^cThe purine-loading index is the sum of the four absolute Chargaff difference values (base excesses) when they relate positively to purine-loading (i.e., excess pyrimidines when transcription to the left; excess purines when transcription is to the right). All three thermophilic bacteria fulfill this criterion (mean value 216.3 ± 39.2 bases/kb). The absolute values are subtracted from the sum when Chargaff differences relate negatively to purine-loading (e.g., T > A for rightward-transcribed ORFs in E. coli). Thus, for the three nonthermophilic bacteria the mean value is 56.7 ± 7.7 bases/kb. 

^dEach Chargaff difference value (%) is presented ± the s.e. of the mean. 

^eThese data are from Bell et al. (1998). 

The difference between thermophiles and nonthermophiles was more readily appreciated when the four Chargaff differences values (base excesses) for each organism were combined to provide an index of the purine-loading of the corresponding RNAs. For the thermophiles the index is simply the sum of the four absolute Chargaff differences, as the transcription rule is followed in each of the four cases. For the nonthermophiles, in cases where the transcription rule was not followed, the corresponding values were subtracted from the overall sum. On average, the three thermophiles show more purine-loading than the three nonthermophiles (Table 1). Purine-loading in thermophiles [(153 + 208 + 288)/(3)] exceeds that of nonthermophiles [(42 + 64 + 64)/(3)] by 160 bases/kb window (P = 0.04; paired t-test with 2 df).

More Purine-Loading at Low (C+G)

For thermophiles the purine-loading index shows an inverse linear relationship to (C+G)%, with a slope that is significantly different from zero (r² = 0.994; P = 0.05). The relationship reflects purine-loading with G residues more than with A residues [i.e., with decreasing (C+G)% there is an increasing tendency for C-excess in leftward-transcribed ORFs and for G-excess in rightward-transcribed ORFs]. Thus, although there are fewer S bases available to support these excesses when the (C+G)% is low, those present are more readily utilized for the purine-loading function (i.e., they are likely to be locally unpaired in loops, rather than in stems). Whereas in their absolute numbers, the S bases and the W bases contribute about equally to purine-loading in thermophilic bacteria, usually one class dominates in the nonthermophilic bacteria.

Genome-Wide Distribution of Purine-Loading

That large segments of genomes are likely to be representative of the entire genomes with respect to purine-loading was shown for M. jannaschii. The genome was divided into six segments of approx. 276.5 kb each. At this level of resolution, there are only minor fluctuations between segments in (C+G)%, Chargaff differences, and purine-loading indices (Table 2). For example, for rightward-transcribed ORFs, the genomic average Chargaff difference (%) for the W bases is 9.92 ± 0.09 (i.e., A>T; Table 1), and corresponding values for the six segments range from 8.46 to 10.57.

Table 2.

Comparison of Chargaff Differences of Six Segments of M. jannaschii

Genome segment				Chargaff difference (%)			Base composition of average 1-kb window								Purine-loading index
no.a	(C + G) %	number of windows			transcription orientation		leftward-transcribed				rightward-transcribed
leftward	rightward	leftward	rightward	A	C	G	T	A	C	G	T
1	32.1	1370	1169	(A − T)/W	−10.66 ± 0.21	9.93 ± 0.28	303	203	118	376	373	124	197	306	298
				(C − G)/S	26.48 ± 0.33	−23.04 ± 0.40	A − T = −73		C − G = 85		A − T = 67		C − G = −73
2	31.6	1416	1257	(A − T)/W	−8.38 ± 0.22	8.46 ± 0.27	313	193	123	371	371	123	193	313	256
				(C − G)/S	21.95 ± 0.43	−22.37 ± 0.37	A − T = −58		C − G = 70		A − T = 58		C − G = −70
3	31.7	1305	1324	(A − T)/W	−9.92 ± 0.21	9.65 ± 0.20	308	197	120	375	374	121	196	309	284
				(C − G)/S	24.45 ± 0.30	−23.69 ± 0.35	A − T = −67		C − G = 77		A − T = 65		C − G = −75
4	30.9	1248	1368	(A − T)/W	−9.82 ± 0.23	10.40 ± 0.21	312	191	118	379	381	113	196	310	294
				(C − G)/S	23.34 ± 0.35	−26.64 ± 0.32	A − T = −67		C − G = 73		A − T = 71		C − G = −83
5	31.5	1180	1361	(A − T)/W	−8.80 ± 0.27	10.57 ± 0.20	312	195	120	373	379	123	192	306	278
				(C − G)/S	23.98 ± 0.33	−22.08 ± 0.35	A − T = −61		C − G = 75		A − T = 73		C − G = −69
6	30.9	975	1723	(A − T)/W	−11.48 ± 0.23	10.31 ± 0.18	306	192	117	385	381	114	195	310	306
				(C − G)/S	24.23 ± 0.40	−26.24 ± 0.30	A − T = −79		C − G = 75		A − T = 71		C − G = −81

Details are as in Table 1. 

^aThe six segments correspond to bases 1–276500, 276501–553000; 553001–829500, 829501–1106000, 1106001–1382500, and 1382501–1664970. 

The genome of M. jannaschii shows a remarkable symmetry between leftward and rightward ORFs in the actual numbers of S and W bases contributing to purine-loading (Table 1). Thus, the average 1-kb window has pyrimidine excesses of 68 (T) and 76 (C) for leftward-transcribed ORFs, and purine excesses of 68 (A) and 76 (G) for rightward-transcribed ORFs. This tendency toward symmetry also occurs in the six segments (Table 2) and is precise in segment 2.

Influence of the Origin of Replication?

Although leftward and rightward ORFs are covered by approximately equal numbers of overlapping 1-kb windows (7494 and 8202, respectively), the distribution varies (Table 2). The number of windows corresponding to leftward ORFs tends to decrease with segment number, whereas the number of windows corresponding to rightward ORFs tends to increase with segment number. Because the M. jannaschii chromosome is circular, a sharp switch is indicated between segments 6 and 1 from a predominantly purine-rich top strand (reflecting an excess of windows covering rightward ORFs in segment 6) to a predominantly pyrimidine-rich top strand (reflecting an excess of windows covering leftward ORFs in segment 1). This probably relates to the origin of replication (site not currently known), as when windows much greater than 1 kb are used for Chargaff difference analysis (thus tending to obscure the local effects of individual ORFs), the results can provide a guide to the position of the origin of replication (Smithies et al. 1981; Lobry 1996).

Same Optimum Window for Thermophiles and Nonthermophiles

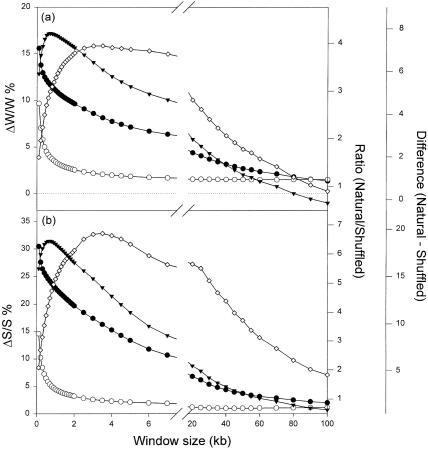
In previous studies the optimum window (1 kb) for examining Chargaff differences was determined in a range of organisms by comparing natural with the corresponding shuffled sequences (Bell et al. 1998; Dang et al. 1998; Bell and Forsdyke 1999a). A similar study of the three thermophile genomes considered above indicated that a 1-kb window would also be optimum in these organisms. For example, for Figure 3 absolute Chargaff difference values were plotted against window size in a 276.5-kb segment of M. jannaschii. The difference between values of points on the curves for the natural and shuffled sequences reaches an optimum at a window size of ∼1 kb. As with the nonthermophiles, the ratio of the values on these curves reaches an optimum at higher window sizes. It was concluded that it was appropriate to use 1-kb windows when comparing the Chargaff differences of thermophile and nonthermophile genomes.

Figure 3.

Variation of average Chargaff difference values with size of windows in M. jannaschii. Windows of varying size were moved along the first 276.5 kb of the genome in steps of 100 nucleotides, and base compositions were determined in each window. Average absolute Chargaff differences (%) for each window size are plotted either as ● (natural sequence), or ○ (shuffled sequence). (▴) The difference between these values (the average Chargaff difference for the natural sequence less the average Chargaff difference for the shuffled sequence). (⋄) The ratio of these values. The total number of windows of a given size used to calculate average Chargaff differences varied with sequence length. Thus, in a 100-kb sequence there would be 999 windows of 0.2 kb and one window of 100 kb.

Purine-Loading Affects Codon Choice

The strong pressure on thermophiles to purine-load their mRNAs, as revealed by Chargaff difference analysis, suggested that choice of synonymous codons might provide an independent measure of this evolutionary force. Furthermore, thermophiles show some regularities in amino acid compositions (Kagawa et al. 1984; Deckert et al. 1998; Jaenicke and Bohm 1998), raising the possibility that the choice of nonsynonymous codons might also be affected.

Table 3 shows data for some amino acids corresponding to purine-rich codons. In the case of glycine (4 codons) and arginine (6 codons) the opportunity is provided for choice of synonymous codon, and in both cases purine-rich codons are preferred by thermophiles. Thus, thermophiles prefer GGR over GGY, and nonthermophiles prefer GGY over GGR. This suggests a selection pressure acting at the nucleic acid level, rather than at the protein level.

Table 3.

Comparison of Amino Acid Frequency and Codon Choice of Thermophilic and Nonthermophilic Bacteria

Amino acid codonsbacterium	(C + G)%	Specific codons/1000 codons
		glycine			glutamic	aspartic	lysine	arginine
GGR	GGY	total	GAR	GAY	AAR	AGR	CGR	CGY	total
Thermophilic
M. thermoautotrophicum	49.5	38.2	41.4	79.6	81.5	59.1	45.6	53.3	5.8	8.4	67.4
A. fulgidus	48.5	41.2	31	72.2	88.7	48.7	68.3	51.7	2.4	3.3	57.4
A. aeolicus	43.4	43.5	23.6	67.1	96.2	43	94.1	44.9	1.3	2.7	49
M. jannaschii	31.4	48.8	17.2	66.1	86.2	54.9	103.6	37.4	0.5	0.4	38.3
Mean		42.9	28.3	71.2	88.1	51.4	77.9	46.8	2.5	3.7	53
Nonthermophilic
E. coli	50.7	20.5	52.5	73	56.9	51.4	45.5	5	10	40.8	55.7
M. pneumoniae	40	15.3	39.6	54.9	56.8	49.4	85.2	6.8	7.5	20.5	34.9
H. influenzae	38.1	18.4	48.2	66.6	63.8	49.8	63.8	4.6	6.6	33.3	44.4
M. genitalium	32	18.2	27.9	46.1	56.6	49	94.6	18.7	2.4	9.9	31
Mean		18.1	42	60.1	58.5	49.9	72.3	8.8	6.6	26.1	41.5
P valuea		0.003	0.03	0.09	0.0005	0.68	0.61	0.01	0.01	0.03	0.06

^aThe probabilities that differences between the means could have occurred by chance (paired t-tests). 

There is a significant increase in codons for glutamic acid in thermophiles, consistent with a selection pressure on nonsynonymous codons. However, although there is a suggestion of a similar pressure for arginine, it is not found for aspartic acid or lysine. The thermophile Archaeoglobus fulgidus is very similar to the other thermophiles (Table 3), indicating that in future work, purine-loading might also be demonstrable by the Chargaff difference method in this organism.

DISCUSSION

An Adaptation for Survival at High Temperatures

It is likely that Szybalski's transcription direction rule is a consequence of purine-loading (Bell and Forsdyke 1999b). Under this assumption, the difference between thermophilic and nonthermophilic bacteria in (1) the extent of their compliance with Szybalski's transcription direction rule (Table 1), and (2) their choice of purine-rich codons (Table 3) suggests that adaptation for survival at high temperatures requires that mRNAs be more heavily purine-loaded. Consistent with this, in a survey of 12 chloroplast genomes (R.J. Rasile and D.R. Forsdyke, unpubl.) we find that those of the thermophile Cyanidium caldarium have a greater purine-loading index (108 bases/kb) than those of 11 nonthermophilic organisms (average 41.1 ± 6.2 bases/kb). An extreme example of the latter is the genome of chloroplasts of the parasitic plant Epiphagus virginiana, in which the chloroplasts are degenerate so that pressure on mRNAs to be polite is likely to be decreased (purine-loading index only 22 bases/kb).

The Politeness Hypothesis

The Gibb's free energy equation (ΔG = ΔH − TΔS) implies that with increasing temperature, reactions with a significant entropy-driven component can occur more readily (Lauffer 1975). Because the base-pairing involved in RNA–RNA interactions has a considerable entropic component (Cantor and Schimmel 1980), such interactions, whether desirable or undesirable, should be favored at high temperatures. Thus, if chemically and biologically feasible, it is possible that RNA sequences would have adapted to avoid undesirable interactions while not impairing desirable ones. Purine-loading would seem to achieve this. In general, mRNAs “drive” politely on the purine “side of the road,” and thermophile mRNAs appear excessively polite. The politeness is not trivial (contrast the “polite DNA” of Zuckerkandl 1986). Driving on the correct side of the road is conducive to efficient highway operation. Failure to do so might be lethal if it led to the formation of dsRNA and the false triggering of intracellular alarms.

Exceptions to Szybalski's Rule

There are exceptions to Szybalski's rule (Cristillo 1998; Bell and Forsdyke 1999b; A.D. Cristillo, T.P. Lillicrap, and D.R. Forsdyke, unpubl.). Certain viruses with a prolonged period of clinical latency load their mRNAs with pyrimidines. Thus, whereas human immunodeficiency virus 1 (moderately committed to latency) is polite (mRNAs heavily purine-loaded), human T-cell leukemia virus 1 (profoundly committed to latency) is extremely impolite (mRNAs heavily pyrimidine-loaded). Epstein-Barr virus (like many other herpes viruses) is also profoundly committed to latency and pyrimidine-loads most of its RNAs. However, unlike human T cell leukemia virus 1, Epstein-Barr virus has an important transcript expressed in all forms of latency, the transcript encoding the EBNA-1 antigen. Remarkably, this transcript is polite, its purine-loading being amplified by inclusion of a simple-sequence element encoding, by preferential employment of purine-rich codons, a glycine–alanine repeat that can be removed without greatly affecting EBNA-1 function. Despite this, much current work is based on the premise that in the compact virus genome, the simple-sequence element persists because of a function at the protein level rather than at the nucleic acid level (for references, see Lee et al. 1999).

Purine-Loading Might Affect the Composition of Proteins

Conventional natural selection provides an extrinsic pressure on the phenotype and so determines which genotypes will survive. However, it has long been recognized that genomes are also molded by intrinsic forces (Romanes 1886; Forsdyke 1999b,c). One such force is a component of the base composition of DNA—(C+G)%. This can affect protein composition and, hence, possibly the phenotype (Sueoka 1961; Ball 1973; Grantham 1980; Bronson and Anderson 1994; Forsdyke 1996, 1998). In light of the present work it appears that another component of base composition, R/Y, may also affect protein composition and, hence, possibly the phenotype.

We have identified purine-loading as an evolutionary force and have suggested an adaptive basis related to the intrinsic workings of the cell (Bell et al. 1998; Bell and Forsdyke 1999b; Fire 1999; Forsdyke 1999a). Thermophilic bacteria appear particularly susceptible to this force, so that the pressure to purine-load RNA in these organisms might have been powerful enough to affect choice both of synonymous and nonsynonymous codons. In thermophiles, an increase in the proportion of glutamic acid (encoded by codons containing only purines) has been noted (Deckert et al. 1998), and this is confirmed in Table 3. Although it is tempting to believe that all such changes in the amino acid composition of proteins are related to the need to maintain protein stability and function at high temperatures (Kagawa et al. 1984; Jaenicke and Bohm 1998), our results raise the possibility that the needs of efficient mRNA function at high temperatures might also have affected the composition of proteins. However, Jaenicke and Bohm (1998) find it difficult to define what they call “traffic rules” of thermophilic adaptation in terms of significant differences in amino acid composition.

Which Purine to Use?

From our initial studies of the purine-loading phenomenon, the generalization emerged that organisms with high (C+G)% genomes would preferentially load with G residues, and organisms with low (C+G)% genomes would preferentially load with A residues (Bell and Forsdyke 1999b). This seemed logical, as organisms with a low (C+G)% would appear to have less flexibility for loading codons with scarce G residues (e.g., the Gs would be required for critically placed codons, which might not match RNA loop regions). To our surprise, the present work (Table 1) indicates either that this generalization is not valid or that thermophiles are a special case. Perhaps because the strength of bonding between the S bases is greater than that between the W bases, it may be the avoidance of C residues as much as the inclusion of G residues that generates such large Chargaff differences with respect to the S bases in thermophiles. The unpaired Gs would locate to the loop regions of stem–loop secondary structures. In considering this matter, one should also take into account the fact that nearest neighbors are of considerable importance in base-pairing interactions (Turner 1996), and in low (C+G)% DNA an S base is more likely to have a W base nearest neighbor.

METHODS

Chargaff Difference Analysis

Chargaff's first parity rule for duplex DNA (%A = %T; %C = %G) applies, to a close approximation, to ssDNA (Chargaff's second parity rule; Chargaff 1979). Deviations from parity are referred to as Chargaff differences. The base composition of successive 1-kb windows, moved in steps of 0.1 kb, was assessed as described by Dang et al. (1998). Chargaff differences were either calculated as (A − T)/W and (C − G)/S and expressed as percentages or were expressed directly as positive or negative base excesses (A − T, or C − G). Here, A, T, C, and G refer to the number of the corresponding base in a window. The direction of subtraction (A − T or T − A) is determined alphabetically. W is the sum of the W bases (A + T) and S is the sum of the S bases (C + G).

Purine-Loading

Purine-loading of mRNAs is indicated when the regions of top DNA strands corresponding to leftward-transcribed ORFs are enriched in pyrimidines and when the regions of top DNA strands corresponding to rightward-transcribed ORFs are enriched in purines. These enrichments may be assessed at the DNA level as Chargaff differences. Because the direction of subtraction is determined alphabetically, purine-loading has been supported when Chargaff differences for the W bases (A − T) are positive and/or Chargaff differences for the S bases (C − G) are negative.

An overall index of the purine-loading of RNA was obtained by summing absolute Chargaff difference values (positive or negative base excesses per 1-kb window) for the pyrimidine excess in leftward-transcribed ORFs and for the purine excess in rightward-transcribed ORFs. In circumstances where Szybalski's transcription direction rule was not followed, the corresponding absolute values were subtracted from the overall total.

When both purines contributed to purine-loading, the latter was assessed as the purine/pyrimidine ratio (Y/R; usually expressed as a percentage). In some circumstances codon choice provided a measure.

Sequences

Sequence information refers to the top strand as designated in the GenBank record. Genomic sequences examined were from Aquifex aeolicus (Deckert et al. 1998), A. fulgidus (Klenk et al. 1997), E. coli (Blattner et al. 1997), H. influenzae (Fleischmann et al. 1995), Methanobacterium thermoautotrophicum (Smith et al. 1997), M. jannaschii (Bult et al. 1996), Mycoplasma genitalium (Fraser et al. 1995), and Mycoplasma pneumoniae (Himmelreich et al. 1996). These sequences were analyzed with programs of the Genetics Computer Group (GCG, Madison, WI) and our own programs written as Unix scripts or in C++. Codon usage tables for complete genomes, calculated using the GCG program CodonFrequency, were obtained from C. Brown (Department of Biochemistry, University of Otago, Dunedin, New Zealand).