Abstract
Many models of infectious disease ignore the underlying contact structure through which the disease spreads. However, in order to evaluate the efficacy of certain disease control interventions, it may be important to include this network structure. We present a network modeling framework of the spread of disease and a methodology for inferring important model parameters, such as those governing network structure and network dynamics, from readily available data sources. This is a general and flexible framework with wide applicability to modeling the spread of disease through sexual or close contact networks. To illustrate, we apply this modeling framework to evaluate HIV control programs in sub-Saharan Africa, including programs aimed at concurrent partnership reduction, reductions in risky sexual behavior, and scale up of HIV treatment.
Keywords: Stochastic simulation, Network dynamics, Concurrent partnerships, Sexually transmitted diseases
1 Introduction
Infectious diseases such as HIV and other sexually transmitted diseases, tuberculosis, and hepatitis B pose a significant global health burden [41, 43]. However, funds for controlling such diseases fall far short of estimated need. Model-based analyses can quantify the effectiveness and cost-effectiveness of alternative control methods and thus help policy makers make the best use of limited resources for controlling infectious disease. To be useful to policy makers, a model must include sufficient detail to accurately reflect the evolution of a disease in the population and to capture the aspects of disease progression and/or transmission that a disease control policy may seek to modify. While many detailed models of disease transmission and progression exist for a variety of infectious diseases (e.g., see [2]), they often ignore the underlying contact network through which these diseases spread. However, interventions for the control of many infectious diseases, particularly sexually transmitted diseases, aim to modify the contact network or target the behavior of specific individuals in the network. To accurately evaluate the effects of such interventions, a model of the contact network is needed.
For a given population and disease, a complete network dataset is rarely available. The few existing network datasets reflect the structure of very specific communities (e.g., [15, 18, 28, 40, 44]) and may not generalize to other populations. Furthermore, network datasets typically only provide a snapshot of the network structure at a particular instant in time; however, contact networks are dynamic. In order to construct an infectious disease model that incorporates contact structure, one must infer both network structure and network dynamics from incomplete data.
Network models have been developed to simulate the spread of a variety of sexually transmitted diseases [10, 17, 20, 25, 36]. These models are often based on stylized network structures rather than empirically derived degree distributions (e.g., [17, 36]). Furthermore, many network models ignore potentially important details of disease and demographic dynamics, often assuming a susceptible-infected disease model and a closed population (e.g., [10, 20, 25]). This simplifies calculations but may not appropriately reflect the spread of the disease in a population over time.
In this paper we present a method for modeling network structure and dynamics using readily available metrics. We illustrate these ideas by describing a network-based modeling framework that captures the spread of a sexually transmitted disease in a heterosexual partnership network in an open population (Section 2). Using this framework, we developed a model to evaluate the effectiveness and cost-effectiveness of programs in sub-Saharan Africa that aim to reduce the spread of HIV (and other sexually transmitted diseases) by reducing concurrent sexual partnerships [8]. We present illustrative analyses from the model (Section 3). We then discuss potential applications of this modeling framework to the spread of other diseases and other types of partnership networks, such as homosexual partnership networks and needle-sharing networks (Section 4).
2 Model description
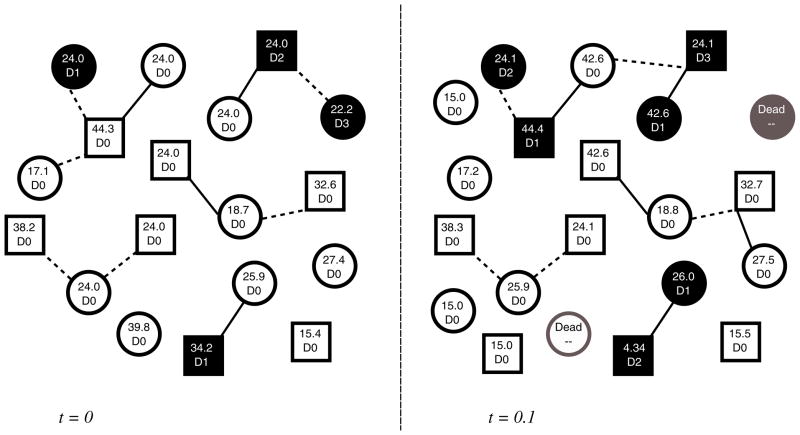
We develop a network modeling framework that captures the dynamics of a heterosexual partnership network, the spread of a sexually transmitted disease through these partnerships, and disease progression in infected individuals. (In Section 4 we describe how the framework can be modified to capture other types of diseases and other types of partnerships). We assume that the population comprises sexually active individuals (those currently engaged in a sexual partnership) and potentially sexually active individuals (those not currently engaged in a sexual partnership who could potentially form such a partnership in the future). At each time step t = 1, 2, … individuals can join or leave the network and sexual partnerships can form or dissolve. A disease model captures the spread of the disease from infected individuals to their sexual partners and the progression of the disease in each infected individual. These dynamics are illustrated in Fig. 1.
Fig. 1.
Diagrammatic representation of model dynamics. Squares denote men and circles denote women. In each time step (in this example t increments in 0.1 years), partnerships are lost and gained, individuals enter and exit the population, and individuals experience disease acquisition or progression. In this example, two types of partnerships are considered. Solid lines between individuals indicate spousal partnerships, while dashed lines denote non-spousal partnerships. Shaded squares/circles correspond to infected individuals. Inside each square/circle, we indicate an individual’s age in years (top) and disease state D ∈ {D0, D1, …, DM} (bottom), where D0 represents uninfected individuals and D1, …, DM are various states of infection (e.g., acute infection, chronic infection, infected and on treatment, etc.)
The population consists of Nm(t) nodes representing men and Nf (t) nodes representing women. The number of men and women in the population is a function of time, t, because we allow entry into the population due to birth and/or maturation, as well as exit out of the population due to death and maturation. Each node has a set of characteristics, such as age, gender, and disease state. These characteristics are initialized to match population-specific demographic data and age-and gender-specific disease prevalence.
Individuals leave the population by aging out of the population or due to death. For individuals uninfected with the disease of interest, their mortality risk is a function of their age and gender and can be determined from mortality tables. We also model individuals aging into the population. We define rm and r f to be the rates at which men and women, respectively, enter the population during each time period. These rates can be determined from demographic data. The number of new individuals entering the population at each time step is stochastic, but the expected number of men and women entering the population at time t + 1 should be Nm(t)rm and N f (t)r f respectively. The arrival of new men and women in the populationcan can therefore be modeled by sampling from a distribution (typically a binomial or Poisson distribution) with the appropriate mean.
Sexual partnerships between men and women are represented as a Nm(t) × Nf (t) adjacency matrix At, where a non-zero entry at At(i, j) indicates a sexual partnership between man i and woman j at time t. Different types of partnerships, with different dynamics and/or risk of disease transmission, can be represented by different non-zero values in At. To illustrate, we consider two types of partnerships: spousal and non-spousal partnerships. The type of partnership between man i and woman j is indicated by the value of At(i, j):
| (1) |
In general, At will be a sparse matrix for a sexual contact network, since most individuals are connected to only a few other individuals in the population. Storing At in memory as a sparse structure reduces the computational burden of simulating large population sizes, since the memory requirements to store At scale with the number of partnerships in the population, rather than with the product of the male and female population sizes, Nm N f.
2.1 Partnership degree distribution
For a disease that spreads through heterosexual contact, we are interested in the network of heterosexual partnerships. Though a complete dataset is not likely to be available, sexual behavior surveys often collect data on the number of sexual partners of respondents (e.g., [23]). This data provides a population-level degree distribution, which describes the proportion of individuals who have 0, 1, 2, or more partners concurrently during the survey period. Men and women typically have different sexual behaviors and thus different degree distributions. In our modeling framework, we allow for gender-specific degree distributions, which we denote by m(p) and f (p) for men and women, respectively; the network is initialized such that the proportion of men and women with p partners (p = 0, …, L) matches m(p) and f (p) (in expectation) at the initialization of the simulation. Because we only include heterosexual partnerships, each partnership involves exactly one man and one woman. In order for m(p) and f (p) to be feasible values with which to initialize the model, the initial number of partnerships in which men are involved, given by
must equal the initial number of partnerships in which women are involved, given by
The reported m(p) and f (p) by men and women in the literature are unlikely to satisfy this equality constraint. Sexual behavior surveys consistently find that men report a greater number of sexual partners than women. A variety of explanations have been proposed, such as sample bias, social desirability bias, recall error, differing definitions of sex, and the underrepresentation of prostitutes [9, 37]. However, it is difficult to estimate the contribution of these different factors to the sexual behavior reported by a particular population. It is therefore unclear how the discrepancy between sexual behavior reported by each gender should be reconciled. One could use the degree distribution reported by either men or women or an average of the two and apply this distribution to both genders. This would result in a population with an equal number of men and women and no differences in sexual behavior between genders. An alternative is to maintain the degree distributions reported by men and women and instead adjust the initial male-to-female ratio. No matter what adjustment method is used, it is important to evaluate the impact of this modeling decision in sensitivity analysis.
In our analysis, we choose to adjust the male-to-female ratio because it maintains the reported gender differences in sexual behavior and does not introduce potentially incorrect adjustments to the reported sexual behavior data. A similar assumption has been made in the development of other partnership network models [25]. Thus for a fixed initial number of men in the population, Nm(0), the number of women is given by
| (2) |
Generally surveys collect data only on the overall number of partners that individuals have; however, individuals may engage in different types of sexual partnerships with important differences in risk behavior and partnership duration. For example, it may be important to distinguish between spousal and non-spousal partnerships or between regular partners and brief encounters with sex workers. As a general framework, we model a network of K different partnership types. From other population-level data, such as rates of marriage or frequency of encounters with sex workers, we can estimate the joint distribution over these partnership types, dm(k1, …, kK) = dm(k) and d f (k1, …, kK) = d f (k) over all feasible k, for men and women, respectively. Here, ki is the number of partnerships of type i and k is the vector of the number of partnerships of each type. Thus dm(k) and d f (k) are the proportions of men and women, respectively, with k partnerships of each type, as estimated from empirical data. To be consistent with the overall partnership distribution, these values must satisfy
| (3) |
For simplicity below, when we refer to dm(k) and d f (k) as partnership distributions it is with the understanding that we mean the values of dm(k) and d f (k) for all feasible k.
As an example, let us consider a network of two partnership types: spousal and non-spousal partnerships. We can infer the partnership distributions from the reported gender-specific degree distributions, m(p) and f (p), and the proportion of married men and women in the population, sm and s f, respectively. Note that Nm(0)sm = N f (0)s f for consistency. In this example, we assume that individuals have at most one spousal partnership, though they may have multiple non-spousal ones. We also assume, lacking data informing us otherwise, that married men and women have the same concurrent partnership behavior as their unmarried counterparts. (The analysis here could be readily modified to relax this assumption if data were available on concurrent partnership behavior of married vs. unmarried individuals.) If k1 is the number of spousal partnerships and k2 is the number of non-spousal partnerships, then we can write the partnership distribution for men as
| (4) |
where L is the maximum number of partnerships allowed in the model. Similar equations define the proportions of women, d f (k1, k2), with k1 spousal and k2 non-spousal partnerships for all feasible (k1, k2). This is just a specific example of how partnership distributions over different types of partnerships can be inferred. The model can include an arbitrary number of different partnership types, as long as a distribution over these different partnership types can be measured or inferred for men and women from available data.
2.2 Network structure
To model a disease that is spreading in a network, a representation of the network structure is needed. Given a particular population and disease, it is often not possible to determine the full contact network. The few network datasets that do exist are for very specific communities (e.g., [15, 18, 28, 40, 44]). In the absence of complete network data, the underlying structure of the contact network must be assumed. Many stylized network structures, such as Erdős-Renyi random graphs and small-world networks, have been used to model social and contact networks (e.g., [1, 10, 17, 21, 36]). These networks represent the result of specific network formation processes and thus exhibit specific degree distributions: an Erdős-Renyi random graph (where a link exists between any pair of nodes in the network with some probability p) yields a Poisson degree distribution in the limit for large networks, while a small-world network (formed through preferential attachment, with many local connections and a few long-range connections) exhibits a power law degree distribution [16, 30, 38]. However, since an empirical degree distribution is typically available in the case of a sexual partnership network (and was available for our example application to modeling concurrency reduction in sub-Saharan Africa), we use a generalized random graph structure, which is a modified random graph that can match an arbitrary degree distribution [27, 30].
We initialize the sexual partnership network as a generalized random graph using the configuration model, which is a standard initialization procedure for a random network [16, 27]: at time t = 0, we randomly assign each individual a number of the different partnership types drawn from the empirical partnership distributions, dm(k) and d f (k). To form links between nodes, we randomly match men and women seeking partners of type i for i = 1, …, K. If individuals are matched to the same partner twice, the duplicate partner is exchanged with another random partnered individual in the population until no duplicate partnerships remain. For large population sizes, we find that the chance of duplicate partnerships is small. Furthermore, since we are exchanging duplicate partnerships and not removing them, the degree of each individual is preserved and the proportion of men and women with k partners will still match the initial degree distributions, dm(k) and d f (k), respectively.
2.3 Network dynamics
After initializing the sexual partnership network to match behavioral survey data, we must capture the evolution of the network over time. To do so, we allow old partnerships to dissolve and new partnerships to form at each time step. Thus, we need to determine the probabilities with which these events occur, while maintaining, on average, the same degree distribution observed in survey data. Again, the available data influences how we choose to model partnership dynamics.
2.3.1 Partnership dissolution
First we consider the case of partnership dissolution. Many studies report statistics on the average duration of sexual partnerships (e.g., [19, 25, 26]). A simple way to model partnership dissolution is to assume a constant hazard model, where there is a constant probability of dissolution each time step, σi for each partnership type i (i = 1, …, K). This results in average partnership lengths of 1/σi for each partnership type i, which we match to the available data. Differences in the σi’s reflect differences in average partnership duration.
2.3.2 Partnership formation
Just as in the case of partnership dissolution probabilities, partnership formation probabilities must be calibrated to observed data. Unlike partnership dissolution, however, there is often no data available describing the probability of a partnership forming between two individuals. As an alternative, we choose partnership formation probabilities such that they balance partnership dissolution, the flow of un-partnered individuals aging into the population, and partnership loss due to death; this allows us to maintain a constant degree distribution over time.
Partnership formation probabilities could be chosen in a variety of ways. For example, one could simply search over different sets of partnership formation probabilities to find appropriate values. However, searching over a continuous parameter set is computationally intensive and since the formation probabilities are specific to a specific degree distribution, these probabilities must be recomputed each time the degree distribution is modified (e.g., when evaluating behavior change interventions that modify the degree distribution). For flexibility and ease of computation we instead consider a simplified Markov model of the partnership dynamics in the population and then solve for the unknown partnership formation probabilities that achieve as steady state the partnership distributions, dm(k) and d f (k). We use the Markov model to approximate partnership dynamics at the population level. The partnership formation probabilities that we solve for then govern the chance of any individual gaining a new partnership in any time period of the simulation.
The state space of this Markov model is all allowed partnership combinations, Ω, and the state of the Markov model represents the distribution of the population over all k ∈ Ω. We denote the transition probabilities from one state to another by for men and by for women. For simplicity, we consider only transitions to adjacent states; that is, transitions that involve the loss or gain of at most one partnership at a time. We define the notation k+i to denote the state adjacent to k with an additional partnership of type i, while k−i denotes the state adjacent to k with the loss of a partnership of type i.
The probabilities of transitions that involve the dissolution of a partnership are known based on our constant hazard model of partnership dissolution. For an individual with a set of k partnerships, these transition probabilities are
| (5) |
Note that these transition probabilities are the same for men and women.
The only unknown values of and are therefore the probability of gaining additional partnerships in each of the states. We choose these such that the degree distributions, dm(k) and d f (k), are the steady-state distribution of the Markov chain. If we only needed to balance partnership dissolution, then these probabilities would need to satisfy the following steady-state equations:
| (6) |
| (7) |
However, we must also consider that men and women age into the population at a monthly rate of rm and r f, respectively. These individuals enter the population without partners; thus, they contribute a flow into the 0 state. This flow must be balanced by the partnership formation probabilities. These probabilities must therefore satisfy the following modified steady-state equations:
| (8) |
| (9) |
where δk = 1 if k1 = …= kK = 0 and δk = 0 otherwise. For simplicity, we do not include a term reflecting mortality. That is, we assume that no partnership state is affected more than any other by mortality, so no differential flows arise due to mortality. Clearly individuals with a greater number of partners are at a greater risk for infection and the associated increase in mortality. However, if the disease-related mortality is low, the partnership formation probabilities calculated under this assumption still maintain a stable partnership distribution, as we will show in the example in Section 3.
We find a set of feasible partnership formation probabilities, and , that solve the following optimization problem, P:
| (10) |
subject to
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
where again we use the notation k±i to denote the state adjacent to k with the gain/loss of a partnership of type i. Here we have relaxed the equality constraint of the modified steady-state equation to minimize the mean squared error between the achieved steady state, um(k) and u f (k), and the desired steady state, dm(k) and d f (k), for men and women, respectively. We include constraints such that transitions involving gaining or losing more than one partnership are excluded (Eq. 13). Dissolution of different partnership types is expressed by Eq. 14. Constraints 15 and 16 ensure that the elements of Pm and P f are valid probabilities. The last constraint 17 restricts the formation probabilities such that men and women gain the same number of partnerships of each type on average. This is necessary because a man cannot gain a partnership of a certain type unless a woman gains one also.
The optimization problem P is a convex quadratic program. Convexity is guaranteed because the objective function is the norm of affine functions of the optimization variables, Pm and P f. P could be solved using any quadratic programming solver. For convenience, we solved P using CVX, a parsing solver used for specifying and solving convex optimization problems [12].
To simulate partnership formation, we could simply apply the partnership formation probabilities obtained by solving P to the population at each time step and match men and women, with both gaining a partnership in the same time step. However, although men and women gain the same number of partnerships on average at each time step, in a stochastic setting they will not always gain exactly the same number of partnerships at each time step. Therefore, we need some way of reconciling this inevitable discrepancy. If we simply do not match individuals if there is no partner of the opposite sex also seeking a new partnership—that is, if we take the minimum of the number of men and the number of women seeking new partnerships—we would form fewer partnerships than the desired average number of new partnerships at each time step. To avoid this problem, for each partnership type i, we first apply the partnership formation probabilities to male individuals to determine the number of partnerships of type i to be formed. We then randomly select the same number of women to gain each type of partnership, choosing them proportionally to their formation probabilities. That is, the probability that a particular women is selected to gain a partnership of type i is the probability that she gains a partnership of type i divided by the sum of the probabilities of all women in the population gaining a partnership of type i. We then randomly pair men and women to form new partnerships, again being careful not to duplicate existing partnerships.
In practice, we have found that this method achieves relatively stable degree distributions over time.
2.4 Disease model
For each individual in the network, we model disease acquisition and progression over time. At any time step, an uninfected individual can acquire the disease from an infected partner and then, once infected, can progress through different disease states. The simplest disease model is a susceptible-infected model, where individuals are either susceptible to or infected with the disease [2]. However, in a microsimulation modeling framework, more complex disease models can easily be incorporated. Such models can include many disease states, representing different stages of disease, the presence or absence of treatment, response to treatment, other co-infections, etc. The disease states may have different infectivities, mortality risks, and/or costs, all of which can be included in this modeling framework. Because each individual is modeled separately, it is straightforward to incorporate stochastic elements of disease transmission and progression to reflect biological variability among individuals (e.g., differing levels of infectivity, rates of disease progression, responses to treatment, etc.), behavioral variability (e.g., the extent to which an individual adheres to treatment), and other types of disease variability. A disease model may employ a discrete set of disease states, D0, D1, D2, …, DM, where D0 denotes uninfected individuals and D1, D2, …, DM denote different infected states. Continuous disease states are also possible: for example, progression of HIV disease can be characterized by continuous CD4 cell counts [5]. We describe a specific disease model in the example analysis presented in Section 3.
2.5 Model calibration
An important step in constructing a model is calibration. A network-based model of this type typically incorporates a significant amount of detail and must be constructed using data from a variety of sources. To ensure that all of these components function together to reflect reality, we adjust model parameters to match salient features of the population and epidemic to be modeled [4, 32]. This process is as much art as science. First, target variables must be chosen (e.g., disease prevalence, population growth, mortality) and then selected input parameters must be adjusted to match these targets. Typically parameters of limited precision are adjusted, within a range of feasible values, in the calibration process [7].
Our modeling framework includes two model components that are independently calibrated to available data: the network model matches the population degree distribution and average partnership durations, and the disease model reflects disease transmission, progression and mortality rates reported in the literature. After these two components have been combined, adjustments may be needed to match important population features impacted by both of these components. One intuitively reasonable approach is to adjust model parameters such that the model’s projected disease prevalence trend is close to observed trends. Additional adjustment to match other key population features (e.g., population growth trends) may further improve model accuracy.
3 Example application: HIV in sub-Saharan Africa
3.1 Model instantiation
We applied the modeling framework to investigate the impact of reducing concurrent heterosexual partnerships on the HIV epidemic in sub-Saharan Africa [8]. It is believed that concurrent sexual partnerships are a key driver of the HIV epidemic in sub-Saharan Africa [6, 22, 34]. A number of countries such as Botswana, Uganda, and others have instituted behavior change campaigns that aim to reduce concurrent sexual partnerships (for example, promoting a message to “be faithful” to one partner) [14, 26, 29]. However, the effectiveness of such programs on reducing the spread of HIV is unknown.
We modeled a population of sexually active and potentially sexually active adults, aged 15–49 years old. We included two types of partnerships: spousal and non-spousal. We only allow for a single spousal partnership, though individuals may have multiple non-spousal partnerships (in addition to a spouse). Spousal partnerships are characterized by much longer durations than non-spousal ones, reflected in a much lower probability of dissolution. We estimated the joint distribution over spousal and non-spousal partnerships from the proportion of married individuals in the population.
We employed a detailed model of HIV disease, including acute HIV infection, chronic infection, and a treatment-eligible state. We used this model in order to capture important features of HIV, such as varying infectivity and HIV-related mortality by disease state. We also included HIV treatment, which extends lives and reduces the infectivity of treated individuals [13]. However, not all eligible individuals receive treatment because of the imperfect HIV treatment coverage levels in these resource-poor countries [34]. We instantiated the model for four different sub-Saharan African countries: Swaziland, Tanzania, Uganda, and Zambia. We matched country-specific demographic structure (e.g., distribution of the population by age, birth, death, and maturation rates, etc.) and concurrent partnership behaviors, and we calibrated the model to match the historical HIV prevalence trends in each country [23, 35].
We developed the model in Mathworks Matlab R2008. We initialized the model with 4,000 representative male individuals and between 4,000 and 5,000 women, depending on the country. Because men in these countries reported more sexual partnerships than women, we must have more women in the population than men in order for the model to reflect the partnership distributions reported by both the men and women [23]. A population size of 9,000 individuals was the largest that we could simulate within reasonable computation time given our computational capabilities. We found that trends in incidence and prevalence observed using this size population closely mirrored trends observed when we simulated a smaller population (e.g., 2,000 individuals).
We simulated the population over a 10-year time horizon in monthly time steps. To compute the expected value of outcomes such as number of new HIV infections and final HIV prevalence, we averaged over 500 runs. We chose 500 runs because this yielded confidence intervals of less than ±1% in our estimates. Each run was completed in 10 s on a 2.33 GHz quad-core Intel Xeon processor.
The model can be used to evaluate the potential effects of concurrent partnership reduction programs as well as the effects of other HIV prevention programs. Ongoing prevention efforts in sub-Saharan Africa include HIV awareness education, HIV testing and counseling, early and effective treatment of sexually transmitted infections, expanded access to HIV treatment, and promotion of safer sex practices through concurrency reduction and condom use [31].
3.2 Example analysis
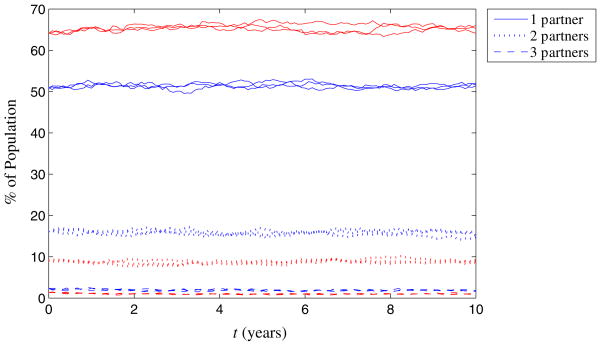
We present numerical results for Tanzania as an example. Model details and the full set of parameter values for this example are included in the Appendix. Tanzania has a population of about 43 million people and 7% overall HIV prevalence with 21% of men and 12% of women reporting more than one sexual partner according to demographic surveys completed in 2003 [24]. To be consistent with reported sexual behavior in Tanzania, we require a male-to-female ratio of 1:1.09 in the model, which is consistent with the male-to-female ratio of 1:1.02 reported in demographic data [35]. We consider 0 or 1 spousal partnerships for each individual and 0, 1, 2, 3, or 4 non-spousal partnerships, leading to ten possible partnership states, k = (k1, k2). We solved the optimization problem P with these states and with values of dm(k) and d f (k) that reflect the reported degree distributions. This led to a set of eleven calculated partnership formation probabilities that we used in the model simulation. Figure 2 shows the simulated degree distribution for men and women over time for three different simulation runs. We see that the computed partnership formation probabilities do in fact yield a relatively stable degree distribution over time.
Fig. 2.
Degree distribution of men (blue) and women (red) in Tanzania over time, shown for three different simulation runs. The degree distribution remains approximately constant over time, indicating that the dynamics of partnership formation based on the probabilities calculated in the optimization problem, P, are correctly balancing partnership dissolution
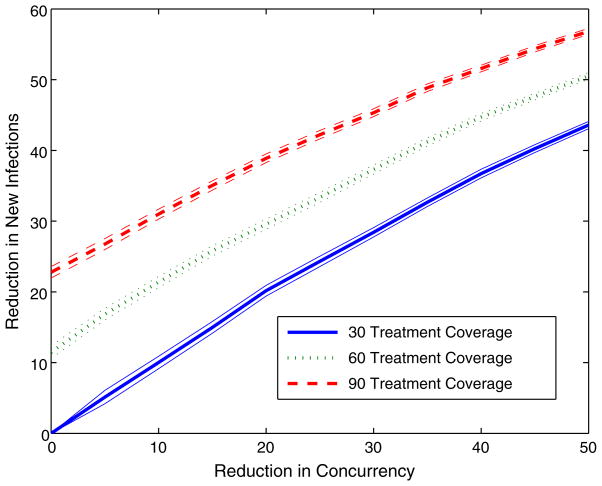
We first consider the effects of an HIV control program that includes both concurrency reduction and HIV treatment scale up. HIV treatment not only increases the lifespan of treated individuals, but also reduces their infectivity, thus preventing the spread of HIV to others [13]. In many resource-limited settings, such as sub-Saharan Africa, only a fraction of individuals eligible for HIV treatment actually receive it. In Tanzania, the current treatment coverage of eligible individuals is about 30%. Figure 3 shows the percentage reduction in new infections as a function of concurrent partnership reduction for HIV treatment coverage levels of 30% (status quo), 60, and 90%. For these examples, we define concurrent partnership reduction as the fraction of individuals with more than one sexual partner who transition to being monogamous (with a single sexual partner). Not surprisingly, a combination of increased treatment coverage and reduced concurrency results in more infections averted than either intervention alone (because treatment has a preventive effect).
Fig. 3.
Percentage reduction in new HIV infections in Tanzania for a comprehensive HIV prevention campaign targeting both concurrent partnership reduction and increased access to HIV treatment. 95% confidence intervals are indicated. We measure concurrent partnership reduction as the fraction of individuals with more than one sexual partner who transition to being monogamous with a single sexual partner. We define treatment coverage to be the fraction of individuals eligible for HIV treatment actually receiving it. In Tanzania, currently only 30% of eligible individuals actually receive HIV treatment
We observe that while the number of infections averted is greater for a higher level of treatment, the slopes of the curves for each treatment coverage level do not differ noticeably. Thus, the number of additional infections averted as concurrency is reduced is unchanged, implying a preservation of the efficiency of concurrency reduction in the presence of treatment scale up. Tanzania, like many countries in sub-Saharan Africa, has been expanding access to HIV treatment in recent years and this scale up is continuing [31]. Figure 3 shows that the benefits of concurrent partnership reduction are likely to be substantial and are likely to be similar for any level of treatment scale up.
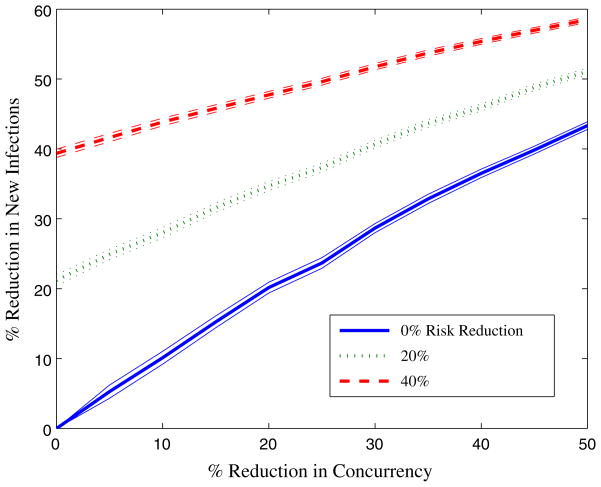
We next consider the effects of a program that combines concurrency reduction with a program that reduces HIV transmission risk in non-spousal partnerships (for example, by encouraging condom use). Figure 4 shows the percent reduction in new infections as a function of concurrency reduction for different reductions in the probability of HIV transmission within non-spousal partnerships. As for the interventions considered in Fig. 3, combinations of these two strategies avert more infections than either strategy alone. However, as the level of risk reduction increases, the slope of infections averted as a function of concurrency reduction decreases. This means that for a greater percentage risk reduction in non-spousal partnerships, reducing concurrency is less effective in averting additional infections. This makes intuitive sense: when non-spousal partnerships become less risky, there is less to be gained (in terms of HIV infections averted) from eliminating them.
Fig. 4.
Percentage reduction in new HIV infections in Tanzania for a comprehensive HIV prevention campaign targeting both concurrent partnership reduction and HIV risk reduction among non-spousal partnerships (e.g., condom use promotion). 95% confidence intervals are indicated. We measure concurrent partnership reduction as the fraction of individuals with more than one sexual partner who transition to being monogamous with a single sexual partner. We define risk reduction to be the reduction in probability of HIV transmission within non-spousal partnerships. For example, a 20% reduction in risk would be mean that the probability of HIV transmission through non-spousal partnerships is 0.8 of the base case transmission probability
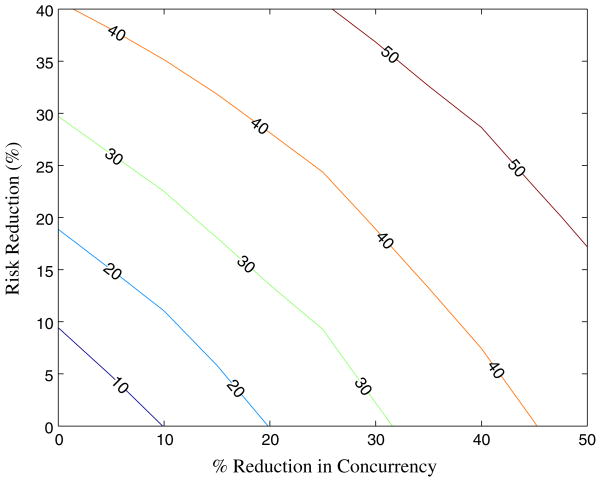
Figure 5 presents the contour lines of constant infections averted for combinations of concurrency reduction and risk reduction within non-spousal partnerships. This allows us to determine which combinations of strategies can achieve a given target reduction in new infections. For example, a 40% reduction in new infections could be achieved by a 45% reduction in concurrency, by a 41% reduction in risky behavior in non-spousal partnerships, or by a 25% reduction in concurrency and a 25% reduction in non-spousal partnership risk. Our network-based model allows us to evaluate the effects of combinations of interventions (some of which change the structure of the network) on the spread of HIV in the population and thus can be used to assist in determining appropriate portfolios of interventions to invest in.
Fig. 5.
Contours of constant HIV infections averted in Tanzania for combinations of concurrency reduction and HIV risk reduction among non-spousal partnerships. (Shown for a reduction in new infections of 10, 20, 30, 40, and 50%)
4 Conclusions
We have described a method for modeling the structure and dynamics of a heterosexual partnership network based on readily available data, such as reported degree distributions and average partnership durations. This modeling framework allows for an open population (with entry and exit) and captures multiple types of heterosexual partnerships with potentially different behaviors and disease transmission risks.
Our application of this framework to evaluate the effects on the HIV epidemic of programs to reduce concurrent partnerships, scale up treatment, and reduce risk in sexual partnerships in sub-Saharan Africa yields several policy insights. First, reducing concurrency could have a major impact on the HIV epidemic in sub-Saharan Africa, averting a large number of HIV infections. Second, comprehensive HIV control programs that combine concurrency reduction with other prevention efforts such as treatment scale up or risk reduction in non-spousal partnerships avert an even greater number of HIV infections. Third, the effects of combining multiple prevention efforts can be sub-additive because the same infection cannot be prevented twice.
We have evaluated the potential effectiveness of combinations of concurrency reduction, treatment scale up, and risk reduction in sexual partnerships, but have not evaluated their cost-effectiveness. More data about levels and types of concurrency reduction achieved as a function of expenditure is needed before the cost-effectiveness of HIV control efforts that include concurrency reduction can be evaluated. Evaluations of ongoing programs in countries such as Botswana [26] and Zambia [29] may yield such data.
Our modeling framework could be extended in a variety of ways. We did not include changes in sexual behavior with age nor did we include age-specific mixing preferences. Extending the model to incorporate these age-dependent behaviors could capture important mixing patterns, such as a tendency for older men to engage in sexual partnerships with much younger women. In addition to concurrent partnerships, these so-called cross-generational partnerships may play an important role in the continued HIV epidemic in regions like sub-Saharan Africa [33].
Our modeling framework could be applied to a variety of other settings. The framework could easily be modified to reflect the transmission and progression of other sexually transmitted diseases or even co-infections with multiple diseases. Our methodology could also be applied to a network of homosexual contacts. Such a network would involve only individuals of the same gender (either men or women) and thus would exhibit a single degree distribution. As in the heterosexual case, we could compute the partnership formation probabilities that balance partnership dissolution to maintain an approximately constant degree distribution. An individual gaining new partners would then be matched randomly with another individual also gaining a new partner in that time step (of the same gender).
Our methodology may also be applicable to other types of close contact networks, such as needle-sharing among injection drug users (IDUs). Such networks have been shown to be an essential feature of disease transmission via shared needles (e.g., HIV, hepatitis C virus) [40]. Instead of sexual contact, a link in an injection-drug using network would represent a needle-sharing relationship. One could again create a network to match an empirical degree distribution of needle-sharing partners. The duration of needle-sharing partnerships among IDUs is likely to be much shorter than the duration of sexual partnerships in the general population; this would be reflected in a higher probability of partnership dissolution each time step. Needle-sharing partnership formation probabilities could be calculated to balance partnership dissolution and, similar to the case of a homosexual network, IDUs gaining a new needle-sharing partner at a certain time step would be matched randomly with another IDU who is gaining a partner in that time step.
Different types of contact networks could also be combined within one population by overlaying each network type. For example, one could model HIV transmission in a population of sexually active IDUs by including links in the network that represent sexual partnerships and links that represent needle-sharing partnerships. As another example, one could model a population of heterosexual, homosexual, and bisexual individuals by overlaying a heterosexual partnership network with a homosexual partnership network. Bisexual individuals would be individuals participating in both networks.
Our modeling framework has wide applicability to the simulation of the spread of sexually transmitted diseases and other diseases transmitted via close contacts over networks. Though network-based simulation approaches are relatively data-intensive, our method for inferring simulation parameters relies on data that is relatively easy to collect for a given population. Such a modeling approach could be extremely useful in evaluating the efficacy of different infectious disease control policies and, in particular, those interventions that seek to modify the contact network structure as a means of controlling the spread of disease. Social networks are increasingly being recognized as factors in the spread of infectious diseases [16]. Our methodology provides a practical means of estimating network structure and network dynamics from available data, thus facilitating the simulation and evaluation of disease control policies over such networks.
Acknowledgments
This research was funded by the National Institute on Drug Abuse, Grant Number R01-DA15612. Eva Enns is supported by a National Defense Science and Engineering Graduate Fellowship, a National Science Foundation Graduate Fellowship, and a Rambus Inc. Stanford Graduate Fellowship.
Appendix: Details of Tanzania example
This Appendix describes input parameters and key assumptions for the example analysis of the effects of concurrency reduction and other HIV prevention programs in Tanzania. Values for all input parameters are shown in Table 1.
Table 1.
Input parameters for numerical example evaluating the effects of concurrency reduction and other HIV prevention programs in Tanzania
| Parameter name | Value | Source |
|---|---|---|
| Population size | ||
| Number of men, Nm | 4,000 | Assumed |
| Number of women, N f | 4,360 | Calculated |
| Female-to-Male ratio | ||
| Actual | 1.02 | [35] |
| Model | 1.09 | Calculated |
| Demographic parameters (M,W) | ||
| Age distribution (%) | [35] | |
| 15–19 | 24.1, 24.3 | |
| 20–24 | 20.5, 20.7 | |
| 25–29 | 16.8, 17.1 | |
| 30–34 | 14.1, 13.9 | |
| 35–39 | 10.6, 10.0 | |
| 40–44 | 7.9, 7.2 | |
| 45–49 | 6.0, 6.8 | |
| Annual maturation rate, rm and r f (%) | 5.5, 5.5 | [35] |
| Age-specific monthly non-HIV mortality (%) | [24] | |
| 15–19 | 0.018, 0.029 | |
| 20–24 | 0.036, 0.044 | |
| 25–29 | 0.048, 0.054 | |
| 30–34 | 0.064, 0.063 | |
| 35–39 | 0.087, 0.073 | |
| 40–44 | 0.104, 0.083 | |
| 45–49 | 0.132, 0.094 | |
| >49 | 0.170, 0.122 | |
| Sexual partnership characteristics | ||
| % Married (sm,s f) | 52, 47 | [24], Calculated |
| Partnership duration (months) | [25, 26] | |
| Spousal, σ1 | 120 | |
| Non-spousal, σ2 | 18 | |
| Concurrent partnership distributions, m(p) and f (p), (%) | [24] | |
| 0 partners | 28.5, 24.3 | |
| 1 partner | 50.9, 64.2 | |
| 2 partners | 16.2, 9.1 | |
| 3 partners | 2.3, 1.3 | |
| 4 partners | 2.1, 1.1 | |
| Monthly partnership formation probabilities (%), Pm and P f | Calculated | |
| Gain a spousal partnership with | ||
| 0 non-spousal partners | 1.1, 1.7 | |
| 1 non-spousal partner | 1.6, 0.58 | |
| 2 non-spousal partners | 1.5, 0.97 | |
| 3 non-spousal partners | 8.5, 5.4 | |
| Gain a non-spousal partnership with 0 spousal and | ||
| 0 non-spousal partners | 3.8, 6.5 | |
| 1 non-spousal partner | 4.2, 1.8 | |
| 2 non-spousal partners | 3.2, 2.8 | |
| 3 non-spousal partners | 17.6, 14.5 | |
| Gain a non-spousal partnership with 1 spousal and | ||
| 0 non-spousal partners | 1.3, 0.51 | |
| 1 non-spousal partner | 0.80, 0.71 | |
| 2 non-spousal partners | 11.4, 9.1 | |
| Tanzania-specific HIV characteristics | ||
| % HIV prevalence by age (M,W) | [24] | |
| 15–19 | 2.0, 2.0 | |
| 20–24 | 4.1, 6.0 | |
| 25–29 | 6.3, 9.3 | |
| 30–34 | 8.5, 12.9 | |
| 35–39 | 9.9, 11.7 | |
| 40–44 | 12.2, 9.9 | |
| 45–49 | 6.7, 5.9 | |
| Monthly HIV transmission risk per partnership (%) | [39], Calculated | |
| Acute phase | 18 | |
| Chronic phase | 1.5 | |
| With treatment | 0.22 | |
| Proportion of treatment eligible individuals receiving treatment (%) | 30 | [34] |
| General HIV characteristics | ||
| Monthly HIV-related mortality (%) by CD4 count | [3, 5] | |
| <50 cells/μL | 2.1 | |
| 51–200 cells/μL | 1.7 | |
| 201–350 cells/μL | 1.1 | |
| >350 cells/μL | 0.8 | |
| Risk of opportunistic infection (%) by CD4 count | [3, 5] | |
| <50 cells/μL | 10.5 | |
| 51–200 cells/μL | 2.6 | |
| 201–350 cells/μL | 1.1 | |
| >350 cells/μL | 0.26 | |
| Additional opportunistic infection mortality risk (%) by CD4 count | [5, 11] | |
| <50 cells/μL | 7.7 | |
| 51–200 cells/μL | 4.5 | |
| 201–350 cells/μL | 0.66 | |
| Monthly CD4 count progression | [5] | |
| HIV+, no treatment | CD4(t + 1) = CD4(t) − 5 | |
| HIV+, with T months on treatment | CD4(t + 1) = CD4(t) + 75 ln(T/ T − 1) | |
We initialized the model with approximately 8,000 sexually active and potentially sexually active individuals aged 15–49 years old. We matched the age distribution of this population to gender-specific age distributions of Tanzania. Individuals age into the population at age 15 with an annual maturation rate determined from Tanzania demographic data [35]. Individuals experience a baseline gender- and age-specific mortality risk determined from country-specific life tables [42]. We matched the gender-specific concurrent partnership behavior reported in the most recent Demographic Health Survey conducted in Tanzania [24].
The disease model is a simplified version of a previously developed HIV progression model [5] and is described in detail in [8].
We modeled three discrete HIV disease states: acute, chronic, and on treatment. The HIV disease state determined the risk of transmission to sexual partners, with the acute state having the highest transmission risk and the treated state having the lowest. Per-act transmission probabilities were obtained from the literature [39] and then adjusted in model calibration to account for levels of sexual activity and condom use so that model-projected prevalence matched projected HIV prevalence trends in Tanzania.
We also modeled each individual’s CD4 counts. This provides a continuous measure of an individual’s immune function. CD4 counts determined HIV-related mortality risk and risks of opportunistic infections, which also increased mortality. In the chronic HIV state, CD4 counts decline slowly over time. Once CD4 counts fall below 200 cells/μL, an individual becomes HIV treatment eligible. HIV treatment causes a recovery in CD4 counts and thus a reduction in HIV-related mortality, though not all eligible individuals receive treatment in these resource-limited settings. The level of treatment coverage in Tanzania is estimated to be about 30% [34].
Contributor Information
Eva A. Enns, Email: evaenns@stanford.edu, Department of Electrical Engineering, Stanford University, 117 Encina Commons, Stanford, CA 94035-6019, USA
Margaret L. Brandeau, Department of Management Science & Engineering, Stanford University, Huang Engineering Center, Stanford, CA 94035-4026, USA
References
- 1.Amaral LAN, Scala A, Barthlmy M, Stanley HE. Classes of small-world networks. PNAS. 2000;97(21):11,149–11,152. doi: 10.1073/pnas.200327197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anderson RM, May RM. Infectious diseases of humans: dynamics and control. Oxford University Press; Oxford: 1991. [Google Scholar]
- 3.Badri M, Lawn S, Wood R. Short-term risk of AIDS or death in people infected with HIV-1 before antiretro-viral therapy in South Africa: a longitudinal study. Lancet. 2006;368(9543):1254–1259. doi: 10.1016/S0140-6736(06)69117-4. [DOI] [PubMed] [Google Scholar]
- 4.Banks J, Carson JS, Nelson BL, Nicol DM. Discrete-event simulation. 5. Prentice Hall; 2009. [Google Scholar]
- 5.Bendavid E, Young SD, Katzenstein DA, Bayoumi AM, Sanders GD, Owens DK. Cost-effectiveness of HIV monitoring strategies in resource-limited settings: a southern African analysis. Arch Intern Med. 2008;168(17):1910–1918. doi: 10.1001/archinternmed.2008.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Carter MW, Kraft JM, Koppenhaver T, Galavotti C, Roels TH, Kilmarx PH, Fidzani B. A bull cannot be contained in a single kraal: concurrent sexual partnerships in Botswana. AIDS Behav. 2007;11(6):822–830. doi: 10.1007/s10461-006-9203-6. [DOI] [PubMed] [Google Scholar]
- 7.Drummond M, McGuire A. Economic evaluation in health care: merging theory with practice. Oxford University Press; 2001. [Google Scholar]
- 8.Enns EA, Brandeau ML, Igeme TK, Bendavid E. Working Paper. Stanford University; 2011. Assessing effectiveness and cost-effectiveness of concurrency reduction for HIV prevention. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fenton K, Johnson A, McManus S, Erens B. Measuring sexual behaviour: methodological challenges in survey research. Sex Transm Infect. 2001;77(2):84–92. doi: 10.1136/sti.77.2.84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ghani AC, Swinton J, Garnett G. The role of sexual partnership networks in the epidemiology of gonorrhea. Sex Transm Dis. 1997;24(1):45–56. doi: 10.1097/00007435-199701000-00009. [DOI] [PubMed] [Google Scholar]
- 11.Goldie S, Yazdanpanah Y, Losina E, Weinstein MC, Anglaret XRW, Hsu H, Kimmel A, Holmes C, Kaplan J, Freedberg K. Cost-effectiveness of HIV treatment in resource-poor settings–the case of Cote d’Ivoire. N Engl J Med. 2006;355(11):1141–1153. doi: 10.1056/NEJMsa060247. [DOI] [PubMed] [Google Scholar]
- 12.Grant M, Boyd S. CVX: Matlab software for disciplined convex programming, version 1.21. cvxr.com/cvx. 2010. [Google Scholar]
- 13.Gray RH, Wawer MJ, Brookmeyer R, Sewankambo NK, Serwadda D, Wabwire-Mangen F, Lutalo T, Li X, vanCott T, Quinn TC. Probability of HIV-1 transmission per coital act in monogamous, heterosexual, HIV-1-discordant couples in Rakai, Uganda. Lancet. 2001;357(9263):1149–1153. doi: 10.1016/S0140-6736(00)04331-2. [DOI] [PubMed] [Google Scholar]
- 14.Green EC, Halperin DT, Nantulya V, Hogle JA. Uganda’s HIV prevention success: the role of sexual behavior change and the national response. AIDS Behav. 2006;10(4):335–346. doi: 10.1007/s10461-006-9073-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Helleringer S, Kohler H. Sexual network structure and the spread of HIV in Africa: evidence from Likoma Island, Malawi. AIDS. 2007;21(17):2323–2332. doi: 10.1097/QAD.0b013e328285df98. [DOI] [PubMed] [Google Scholar]
- 16.Jackson M. Social and economic networks. Princeton University Press; 2008. [Google Scholar]
- 17.Kiss IZ, Green DM, Kao RR. Infectious disease control using contact tracing in random and scale-free networks. J R Soc Interface. 2006;3(6):55–62. doi: 10.1098/rsif.2005.0079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Klovdahl AS. Social networks and the spread of infectious diseases: the AIDS example. Soc Sci Med. 1985;21(11):1203–1216. doi: 10.1016/0277-9536(85)90269-2. [DOI] [PubMed] [Google Scholar]
- 19.Klusmann D. Sexual motivation and the duration of partnership. Arch Sex Behav. 2002;31(3):275–287. doi: 10.1023/a:1015205020769. [DOI] [PubMed] [Google Scholar]
- 20.Kretzschmar M, van Duynhoven YTHP, Severijnen AJ. Modeling prevention strategies for gonorrhea and chlamydia using stochastic network simulations. Am J Epidemiol. 1996;144(3):306–317. doi: 10.1093/oxfordjournals.aje.a008926. [DOI] [PubMed] [Google Scholar]
- 21.Liljeros F, Edling CR, Amaral LAN, Stanley HE, Åberg Y. The web of human sexual contacts. Nature. 2001;411:907–908. doi: 10.1038/35082140. [DOI] [PubMed] [Google Scholar]
- 22.Mah T, Halperin D. Concurrent sexual partnerships and the HIV epidemics in Africa: evidence to move forward. AIDS Behav. 2008;14(1):11–16. doi: 10.1007/s10461-008-9433-x. [DOI] [PubMed] [Google Scholar]
- 23.MEASURE DHS. [Accessed January 2009];Demographic and health surveys. www.measuredhs.com.
- 24.MEASURE DHS. Tanzania demographic and health survey. 2003 www.measuredhs.com.
- 25.Morris M, Kretzschmar M. A microsimulation study of the effect of concurrent partnerships on the spread of HIV in Uganda. Math Popul Stud. 2000;8(2):109–133. [Google Scholar]
- 26.National AIDS Coordinating Agency Botswana. National campaign plan—multiple concurrent partnerships. 2009 www.comminit.com/en/node/304747/2781.
- 27.Newman MEJ, Strogatz SH, Watts DJ. Random graphs with arbitrary degree distributions and their applications. Phys Rev E. 2001;64(2):026, 118. doi: 10.1103/PhysRevE.64.026118. [DOI] [PubMed] [Google Scholar]
- 28.Parker M, Ward H, Day S. Sexual networks and the transmission of HIV in London. J Biosoc Sci. 1998;30(1):63–83. doi: 10.1017/s0021932098000637. [DOI] [PubMed] [Google Scholar]
- 29.Serlemitsos E. Mass media campaign on multiple concurrent sexual partnerships (MCP) in Zambia. 2009 www.harvardaidsprp.org.
- 30.Strogatz SH. Exploring complex networks. Nature. 2001;410(6825):268–276. doi: 10.1038/35065725. [DOI] [PubMed] [Google Scholar]
- 31.The United Republic of Tanzania Prime Minister’s Office. National policy on HIV/AIDS. 2009 www.tanzania.go.tz/pdf/hivaidspolicy.pdf.
- 32.Troitzsch KG. Validating simulation models. Proceedings of the 18th European simulation multiconference. Society for Modeling and Simulation; Germany. 2004. [Google Scholar]
- 33.Tumbo D, Jana M, Nkambule M. One love: Multiple and concurrent sexual partnerships in southern Africa. 2008 www.onelovesouthernafrica.org.
- 34.UNAIDS. Report on the global AIDS epidemic. 2008 www.unaids.org/en/KnowledgeCentre/HIVData/GlobalReport/2008.
- 35.US Census Bureau, P.D. International data base. 2008 www.census.gov/ipc/www/idb/tables.html.
- 36.Vieira IT, Cheng RCH, Harper PR, Senna V. Small world network models of the dynamics of HIV infection. Ann Oper Res. 2010;178(1):173–200. [Google Scholar]
- 37.Wadsworth J, Johnson A, Wellings K, Field J. What’s in a mean?—an examination of the inconsistency between men and women in reporting sexual partnerships. J R Stat Soc A. 1996;159(1):111–123. [Google Scholar]
- 38.Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 39.Wawer MJ, Gray RH, Sewankambo NK, Serwadda D, Li X, Laeyendecker O, Kiwanuka N, Kigozi G, Kiddugavu M, Lutalo T, Nalugoda F, Wabwire-Mangen F, Meehan MP, Quinn TC. Rates of HIV-1 transmission per coital act, by stage of HIV-1 infection, in Rakai, Uganda. J Infect Dis. 2005;191(9):1403–1409. doi: 10.1086/429411. [DOI] [PubMed] [Google Scholar]
- 40.Weeks MR, Clair S, Borgatti SP, Radda K, Schensul JJ. Social networks of drug users in high-risk sites: finding the connections. AIDS Behav. 2002;6(2):193–206. [Google Scholar]
- 41.WHO. Removing obstacles to healthy development. 1999 www.who.int/infectious-disease-report/
- 42.WHO. Life tables for WHO member states. 2006 www.who.int/whosis/database/life_tables/life_tables.cfm.
- 43.WHO. Millennium development goals: Combat HIV/AIDS, malaria and other diseases. 2008 www.who.int/topics/millennium_development_goals/
- 44.Wylie JL, Jolly A. Patterns of chlamydia and gonorrhea infection in sexual networks in Manitoba, Canada. Sex Transm Dis. 2001;28(1):14–24. doi: 10.1097/00007435-200101000-00005. [DOI] [PubMed] [Google Scholar]