Abstract
The phase versus frequency function of the distortion product otoacoustic emission (DPOAE) at 2f1 − f2 is approximately invariant at frequencies above 1.5 kHz in human subjects when recorded with a constant f2∕f1. However, a secular break from this invariance has been observed at lower frequencies where the phase-gradient becomes markedly steeper. Apical DPOAEs, such as 2f1 − f2, are known to contain contributions from multiple sources. This experiment asked whether the phase behavior of the ear canal DPOAE at low frequencies is driven by the phase of the component from the distortion product (DP) region at 2f1 − f2, which exhibits rapid phase accumulation. Placing a suppressor tone close in the frequency to 2f1 − f2 reduced the contribution of this component to the ear canal DPOAE in normal-hearing adult human ears. When the contribution of this component was reduced, the phase behavior of the ear canal DPOAE was not altered, suggesting that the breaking from DPOAE phase invariance at low frequencies is an outcome of apical-basal differences in cochlear mechanics. The deviation from DPOAE phase invariance appears to be a manifestation of the breaking from approximate scaling symmetry in the human cochlear apex.
INTRODUCTION
Distortion product otoacoustic emissions (DPOAEs) are signals generated in the cochlea and recorded in the ear canal (Kemp, 1979). These signals are currently understood to be a by-product of the active physiological processes linked to the cochlear amplifier (Kemp, 2002). DPs are generated when a healthy cochlea is simultaneously stimulated with two tonal signals. The frequencies of these DPs are arithmetically related to those of the stimulus tones. The DP at the frequency, 2f1 − f2 (where f1 and f2 are the frequencies of the stimulus tones, f2 > f1) is widely utilized for clinical and research purposes. The study reported here records and analyzes the DPOAE at 2f1 − f2 to study aspects of apical cochlear function.
Cochlear scaling
On observing the similarity in shape of the “phase difference” curves recorded at two different locations on the basilar membrane of the squirrel monkey by Rhode (1971), Zweig (1976) conjectured that the phase response of basilar membrane motion was consistent with the scale invariance. The phase difference reported by Rhode (1971) was essentially the difference in phase observed at the malleus and at a certain location on the basilar membrane when the system was stimulated over a range of frequencies. The total phase accumulated at two basilar membrane locations appeared to be approximately equal for their respective characteristic frequencies, as did the pattern of phase accumulation as a function of frequency. From this observation, Zweig argued that phase of basilar membrane motion did not depend independently on either the stimulus frequency or the characteristic frequency of the measurement location but rather, was determined by the ratio between the two; thus satisfying the definition of a scaled variable as one which depends only on the ratio between two variables.
DPOAEs can be used as a metric of cochlear scaling. In the “fixed ratio” paradigm, the frequency ratio between the two stimulus tones (f2∕f1) is held constant as the frequencies of both tones are changed. The phase of the DPOAE recorded using this paradigm, when plotted as a function of frequency, typically remains approximately invariant above a species-dependent break in frequency (Shera et al., 2000). At frequencies below this break, the phase of the DPOAE exhibits a non-zero slope. In humans, the DPOAE phase accumulates between 0.5 and 1 cycles per octave below this break frequency, and the behavior is secular (implying a continuation of the trend as frequency decreases). This break in DPOAE phase invariance has been equated with the break in cochlear scaling.
In recording DPOAEs with a constant f2∕f1 ratio, and assuming a logarithmic frequency-place map, the relative distance between the stimulus tones is maintained on the basilar membrane. Given the definition of scaling provided above, the phases of the stimulus tones encountered by distortion generators (presumably outer hair cells) remain constant irrespective of the absolute frequencies of the stimulus tones. Thus, the phase of the DPOAE generated using a fixed-ratio paradigm remains approximately constant as a function of frequency. The reader is directed to a more in-depth description and a visual demonstration of this phenomenon in Fig. 7 of Shera and Guinan (1999). This scaling behavior has been observed and reported repeatedly in the DPOAE literature (e.g., Shera et al., 2000) and linked to the scaling that Rhode initially observed in basilar membrane mechanics.
Although there is a break from the invariant phase-frequency behavior of DPOAE at frequencies below ∼1.5–2 kHz (Shera et al., 2000; Abdala and Dhar, 2010a,b, 2), the features of this break and mechanisms contributing to it have not been well characterized, While there is no question about a link between DPOAE behavior and cochlear mechanics, the mapping of basilar membrane motion to its distant cousin, the DPOAE measured in the ear canal, is far from clear. Below we consider a potential source for the deviation from DPOAE phase invariance in the apex and its relationship to cochlear scaling.
Is the low-frequency DPOAE dominated by the component from the DP region?
The tonotopic organization of the cochlea dictates that the characteristic frequency place for DPOAEs that are lower in frequency than the stimulus tones, such as the 2f1 − f2 DPOAE, will be apical to that of the stimulus tones themselves. In these cases, the initial distortion energy is generated at the region of overlap between the mechanical disturbances caused by f1 and f2. A portion of the distortion energy generated travels back to the ear canal, but another portion travels apically to peak at the distortion product (DP) region. This apically traveling energy is subsequently reflected backward and travels basalward and into the ear canal. Thus, the DPOAE recorded in the ear canal is a mixture of two components from different cochlear sources (e.g., Talmadge et al., 1999).
A critical difference between the two DPOAE components is in their phase behavior as a function of frequency. While the phase of the component from the overlap region where the DPOAE is generated, is essentially flat as a function of frequency, phase of the component from the DP region, the putative reflection component, changes rapidly. This difference in phase behavior is thought to derive from differences in generation mechanisms (Moulin and Kemp, 1996; Talmadge et al., 1998; Mauermann et al., 1999a; Shera and Guinan, 1999; Knight and Kemp, 2000; Kalluri and Shera, 2001; Konrad-Martin et al., 2002). The component from the overlap region has been modeled to derive from a nonlinear mechanism where the phase of the DPOAE is determined entirely by the phases of the stimulus tones. The component from the DP region, on the other hand, has been modeled to derive from a linear reflection process where the phase is determined by the phase of the stimulus at a place-fixed “reflector” along the basilar membrane (Talmadge et al., 1998; Shera and Guinan, 1999).
Evidence supporting this two-component DPOAE comes from experiments where the relative contribution of one of the components is manipulated by a strategically placed suppressor tone (e.g., Heitmann et al., 1998). The component from the DP region can be successfully eliminated by a suppressor tone in close frequency proximity to 2f1 − f2, thereby eliminating the characteristic component interference pattern of oscillating peaks and valleys (i.e., fine structure) seen in the ear canal DPOAE response.
The phase of the DPOAE recorded in the ear canal is determined by and resembles that of the dominant component. Most, if not all, reports on relative contribution of DPOAE components to the ear canal measure agree on the general dominance of the nonlinear component from the overlap region at moderate and high stimulus levels, though isolated frequency regions where the reflection component dominates the ear canal signal can be identified in individual subjects (see Mauermann et al., 1999b; Talmadge et al., 1999 for examples). Because the component from the overlap region is typically dominant, the phase of the ear canal DPOAE is fairly flat as a function of frequency for most of the frequency range. This pattern changes in the lower frequencies where the rate of phase accumulation increases, producing a steeper phase-gradient, qualitatively more similar to the reflection component. Given this, one might ask: is the departure from the flat phase-frequency pattern at lower frequencies a consequence of a dominant reflection component in the apical region of the cochlea? In this paper, we report data from an experiment designed to rule out the hypothesis that a dominant reflection component produces the non-zero DPOAE phase slope observed at low frequencies. The influence and possible contribution of other factors, such as middle ear transmission are also considered.
METHODS
Subjects
Ten normal-hearing adults participated as subjects. Four of the 10 subjects were evaluated at Northwestern University and the remaining six at the House Research Institute, in accordance with the guidelines of the Institutional Review Boards of the respective institutions. The subjects were between 20 and 29 years old; three were male and seven female. All had hearing thresholds better than 20 dB hearing level (HL) between 0.25 and 8 kHz, normal middle ear function and a negative history of ear pathology. Hearing thresholds and middle ear function were determined using an Interacoustics Audio Traveler AA220 Audiometer (Interacoustics, Assens, Denmark) and the GSI Tympstar Middle Ear Analyzer (Grason Stadler Inc., Eden Praire, MN).
Instrumentation and calibration
DPOAEs were recorded using a Macintosh computer controlling a MOTU 828 MkII (Mark of the Unicorn, Cambridge MA) audio device (44.1 kHz, 24 bit). The output of the MOTU was appropriately amplified and fed to either MB Quartz (Maxxsonics, Chicago, IL) 13.01 HX drivers (Northwestern) or Etymotic Research (Elk Grove Village, IL) ER2 tube phones (House Research Institute). The output of the drivers was coupled to the subjects’ ears through the sound tubes of an Etymotic Research ER10B+ probe microphone assembly.
Stimulus levels were calibrated using a depth compensation method (Siegel, 2009). The depth of probe insertion in each subject’s ear was determined using the half-wave resonance peak in response to a chirp in the ear canal, normalized to that recorded in a 50 ft long copper tube (ID = 7.9 mm, approximating that of the average adult ear canal). The pressure response recorded for a similar depth of insertion in the Bruel and Kjaer (Naerum, Denmark) 4157 ear simulator (IEC 60318-4) was used to compensate the frequency response of the sound sources. The goal was to deliver a close approximation of the desired sound pressure level (SPL) at the subject’s tympanic membrane. The compensation factor was derived from a series of responses previously recorded with the insertion depth of the probe varying in ∼1-mm steps.
Stimuli and protocol
DPOAEs were recorded using a stimulus frequency ratio (f2∕f1) of 1.22 and stimulus levels of 65 (L1) and 55 dB SPL (L2). The stimulus tones were swept in (f2) frequency between 0.5 and 4 kHz in octave-wide segments. Breaking the stimulus sweep into octave-wide segments allowed us to perform a greater number of averages at the lowest frequencies where the data were negatively influenced by physiological noise. Because obtaining high-quality recordings in the 0.5–1 kHz octave was critical to define the break from scaling, 12 sweeps were presented to obtain an average in the low-frequency octave (compared to six sweeps presented in a typical adult protocol). Average adult signal-to-noise ratio (SNR) for the low-frequency octave was 27 dB. (Representative signal-to-noise ratios for the three, octave-wide recording bands are graphically presented in a companion paper.) DPOAE recordings were also obtained with a suppressor tone placed at 0.2-octave below 2f1 − f2. Three levels of the suppressor tone (45, 50, and 55 dB SPL) were presented. The no-suppressor condition and the conditions with the three suppressor levels were interleaved during the recording session.
DPOAE level and phase estimates were obtained using a least-squares fit algorithm (LSF) as described by Long et al. (2008) and yielded estimates every 2–4 Hz around 0.5–1 kHz and every 12 Hz around 4 kHz. The noise floor was estimated similarly after phase-inverting every alternate sweep window. The phase was “unwrapped” by sequentially subtracting 360° from all points beyond identifiable discontinuities. Additionally, the computed phases of the stimulus tones, 2φ1–φ2, where φ1,2 are phases of the lower and higher frequency stimulus tones, respectively, were subtracted from the estimated phase of the DPOAE.
Analyses
Component contribution
To determine the dominant component driving ear canal phase in the unsuppressed condition, an inverse fast Fourier transform (IFFT) was conducted on DPOAE recordings from each octave-wide frequency segment using matlab-based analysis software (NIPR) (Talmadge et al., 1999). DPOAE distortion- and reflection-source components were separated based on their respective group delays. During IFFT and DPOAE complex pressure measured in the frequency domain was multiplied by a moving hann window in overlapping 50 Hz steps. The length of the hann window was adjusted on a logarithmic scale in accordance with the cochlear frequency map and ranged from 400 Hz at the lowest DPOAE frequency to 930 Hz at the highest. Impulse response (IPR) functions were determined for each window and rectangular time-domain filters applied to each IPR to extract the desired delay. The filtered windows of data were then transformed back to the frequency domain by fast Fourier transform (FFT) and the level and phase of the distortion (around the f1, f2 overlap) and reflection (at the DP region) components were reconstructed.
Modeling the phase-frequency function
Since the phase recordings were obtained in three different octave-wide intervals to most effectively cover the frequency range, the individual segments were linked together to form a continuous phase-frequency function by aligning segments with a phase shift of ±1 full cycle if necessary. Each individual phase versus frequency function was fitted using a nonlinear regression model where the functions were allowed to change along the range of frequencies (spline or piecewise linear regression, spss version 18 for OS X). In this particular application, the slope of the function was allowed to change about inflection points (or knots) that are not fixed in frequency a priori. These knots or junctions indicate significant change in phase slope. Knots were allowed to roam in an iterative process until the best fit was obtained for phase-frequency functions from each individual subject in each suppressor condition. Single- and dual-knot solutions were compared using the coefficient of determination (R2) and resulted in mean R2 values of 0.982 and 0.983, respectively. The residuals conformed to the expectations of a normal distribution. Because the two-knot solutions did not enhance the spline fits to the phase-frequency data, the results and the statistical tests are based on one-knot analyses.
The knot values for the suppressor and no-suppressor conditions were compared using a one-way repeated measures analysis of variance (ANOVA). The slope values of both the low- and high-frequency segments of the phase-frequency function were analyzed with two-way repeated measures ANOVA.
RESULT
Component contribution
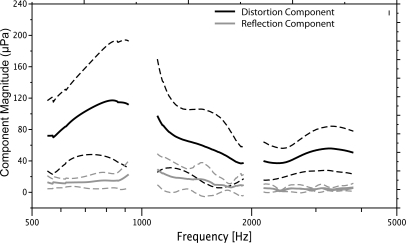
Figure 1 shows the mean amplitudes of both DPOAE components in each of three octaves (solid black, gray lines) ±1 standard deviation (dashed lines). The distortion component was dominant overall in the DPOAE ear canal recording and showed mean amplitude that was ∼20 dB higher than mean reflection component amplitude.
Figure 1.
Mean DPOAE component magnitude for three, octave-wide intervals: 0.5–1 kHz, 1–2 kHz, and 2–4 kHz. The black lines display the nonlinear component from the overlap region around f2, f1 and the gray lines represent the reflection component from the DP region at 2f1 − f2. The dashed lines outline ±1 standard deviation.
Effectiveness of suppressor tone
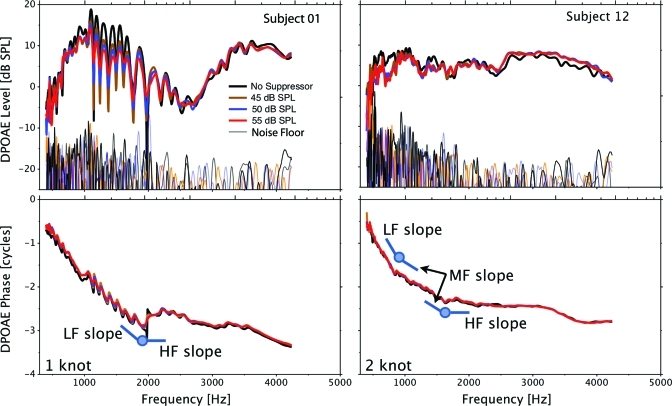
DPOAE level and phase estimates were obtained both with and without three levels of a suppressor tone, close in frequency to the DP region. Representative data from two subjects are presented in Fig. 2. The results obtained without a suppressor tone are presented in black and the colored traces represent data obtained with the three levels of suppressor tones. These two subjects were chosen because they represent two general categories of data. DPOAE level from subject 01 shows pronounced fine structure, while such fine structure is absent in data from subject 12. In the case of subject 01, the suppressor gradually reduces both level and phase fine structure depth, most notably between 1 and 2 kHz though fine structure is not completely eliminated even for the highest suppressor level. This reduction in fine structure depth represents the effectiveness of the suppressor tone in reducing the contribution of the reflection component from the DP region. The failure of the suppressor to completely eliminate fine structure points to incomplete suppression of the reflection component; however, this is inconsequential to the purpose of the current experiment. The suppressor tone was intended as a tool to bias the ear canal DPOAE signal toward the nonlinear component from the overlap region. The reduction in fine structure depth in subject 01 supports the success of this approach in reducing reflection and establishing the component from the overlap region as dominant in the ear canal DPOAE recording. The addition of the suppressor tone smoothed the “saw tooth” behavior of the phase between 1 and 2 kHz as well as shown in the bottom left panel of Fig. 2.
Figure 2.
Representative DPOAE level and phase results from two subjects presented in the top and bottom panels, respectively. Data obtained without a suppressor tone and with three levels of suppressors are presented in different colors in each panel. A one-knot spline model is schematically presented in the bottom left panel with the knot and short lines representing the slopes of the low- and high-frequency segments. A two-knot model is presented in the bottom right panel.
In contrast to subject 01, DPOAE level data recorded from subject 12 do not exhibit marked fine structure. In this case, the addition of the suppressor tone has little or no effect on either DPOAE level or phase. These results suggest that the nonlinear component was dominant in the ear canal in the baseline condition and the suppressor tone did not alter this dominance. The results from subject 01 and 12 taken together provide strong evidence that the suppressor tone served its purpose effictively; that is, when a reflection component was present in the baseline condition, the suppressor tone reduced its contribution to the ear canal DPOAE thereby guaranteeing the dominance of the nonlinear component. In the other extreme, when the reflection component was not contributing significantly in the baseline condition, the suppressor tone had no effect on the ear canal DPOAE level or phase.
Suppressed versus unsuppressed DPOAE phase
Knot frequencies represent the point on the function where the DPOAE phase-frequency relationship changed trajectory. Knots were identified using a spline model with one-knot specified. An example of this solution is schematically represented in Fig. 2, bottom left panel. The circle represents the knot frequency and the flanges represent the slopes of the two phase segments separated by the knot. The right, lower panel of Fig. 2 shows an example where an intermediate segment (denoted MF slope) of the phase-frequency function appears to be present and a two-knot solution is employed. The graphical elements representing the knot frequency and flanges are displaced from the data traces to aid visibility.
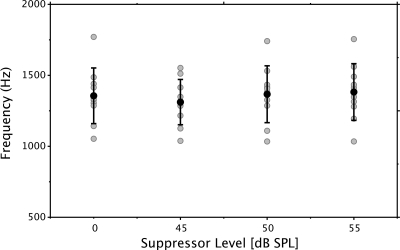
Statistical analyses were performed on spline fits using the one-knot solution only because the addition of a second knot did not enhance the model fits. The mean knot frequencies and phase slopes for the one-knot solutions are presented in Table TABLE I.. Individual and mean knot frequencies are presented in Fig. 3. The gray circles represent individual data and the black circle and error bars represent the mean and ±1 standard deviation. The mean knot frequency (without suppressor) was centered around 1.3 kHz.
Table 1.
Mean and standard deviation (SD) of knot frequencies and slope values (cycles/kHz) for spline modeling on DPOAE phase-frequency functions. The suppressor conditions are represented in the four columns. Standard deviations are encased in brackets below the corresponding mean. LF = Low frequency; HF = High frequency.
| Suppressor level (dB SPL) | 0 | 45 | 50 | 55 |
|---|---|---|---|---|
| Knot frequency (Hz) | 1356 | 1311 | 1367 | 1382 |
| SD | [196] | [160] | [200] | [200] |
| LF slope (cycles/kHz) | −1.98 | −1.96 | −1.97 | −1.92 |
| SD | [0.33] | [0.35] | [0.36] | [0.35] |
| HF slope (cycles/kHz) | −0.20 | −0.22 | −0.21 | −0.20 |
| SD | [0.14] | [0.16] | [0.14] | [0.14] |
Figure 3.
Knot frequencies derived from the one-knot spline model. The knot frequency was not constrained a priori. Gray symbols represent individual data points. Black symbols represent the mean value for each experimental condition (no-suppressor and suppressors at 45, 50, and 55 dB SPL). The error bars represent ±1 standard deviation.
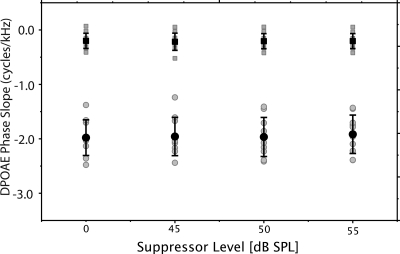
The mean slope values (cycles∕kHz) for the low- and high-frequency segments of the phase-frequency functions are presented in Fig. 4. The phase slopes measured for the segment higher in frequency than the knot are displayed with square symbols. The slope values for the frequency segment below the knot are displayed with circles. The black and gray symbols represent the mean and individual data, respectively. Slope values for the high-frequency segment approximate zero but none of the conditions is exactly zero, as would be expected if the cochlea were perfectly scaled. The slope of phase for the low-frequency segment is considerably steeper and approximates 2.0, corresponding to a mean phase-gradient delay of 2 ms.
Figure 4.
Fitted phase slopes (cycles/kHz) from the one-knot spline model. The near-zero, high-frequency slopes [squares] represent the segment above the knot frequency. The low-frequency slope values [circles] represent the segment below the knot frequency. Gray symbols display individual data points. Black symbols represent mean values and error bars, ±1 standard deviation.
There were no significant differences between knot frequencies established without a suppressor and those established in conditions with a suppressor present. Likewise, the slope of neither the low- or high-frequency segments were significantly different when measured with or without suppressor tones. This result indicates that features of the phase-frequency function were the same whether a suppressor effectively reduced the contribution of the reflection-source or not. By inference, it is assumed that DPOAE phase versus frequency functions recorded at moderate levels are driven by the nonlinear component from the overlap region of the two stimulus tones.
In summary, a phase discontinuity or “knot” was identified in the phase-frequency functions of all subjects; the slope of this function above this knot frequency was approximately zero. The slope was steeper in the low-frequency segment and approximated phase-gradient delays of 2.0 ms. Importantly, a suppressor tone did not influence the frequency of the knot or the slope of the low-frequency segment suggesting that this low-frequency phase behavior is not driven by the reflection component from the DP region. This finding is consistent with the IFFT analysis which confirms that the distortion source from around the generator region was the dominant component and thus, determined the phase characteristics of the ear canal recordings.
DISCUSSION
The phase of DPOAE recorded with a constant stimulus frequency ratio has been described as relatively invariant as a function of frequency over most of the frequency range (Shera and Guinan, 1999; Talmadge et al., 1999; Shera et al., 2000; Abdala and Dhar, 2010a). The phase invariance breaks at low frequencies and phase slope steepens. General interest in this low-frequency break is related to its putative origin in apical cochlear mechanics. However, our interest extends to recent reports of developmental differences in the phase-gradient of the low-frequency DPOAE phase-frequency function between human newborns and adults (Abdala and Dhar, 2010a). The reader is directed to a companion paper dedicated to the exploration of these developmental differences.
The non-zero DPOAE phase observed for low-frequency signals indicates a general break from scaling in the apical end of the human cochlea (Shera et al., 2000; Dhar et al., 2002). Several factors may produce or contribute to this break. Prominent amongst these are the interference from dual DPOAE components (Kim, 1980), the interactions between multiple internal reflections (Dhar et al., 2002), and the possible influence of the middle ear. Though interference from dual DPOAE components and multiple internal reflections can potentially be dismissed based on empirical observations that the ear canal DPOAE recorded with moderate to high stimulus levels is generally dominated by the nonlinear component, which drives its phase behavior (Shera et al., 2000), the contribution of either factor to the breaking of DPOAE scale invariance in the low-frequencies has not been explicitly tested. Also, while this generalization is strongly supported by data from human adults (Talmadge et al., 1999; Kalluri and Shera, 2001; Konrad-Martin et al., 2001; Johnson et al., 2006), it is not clear in newborn ears, a population that has been reported to show an enhanced reflection contribution (Abdala and Dhar, 2010b). The goal of this study was to experimentally evaluate these factors and narrow the interpretive space for the companion paper where the maturation of apical cochlear mechanics is targeted.
The middle ear
The role of the middle ear cannot be neglected as it serves as the essential way station both for stimulus tones being delivered to the cochlea and the otoacoustic emission (OAE) delivered back to the ear canal. Clearly, the properties of the middle ear transfer function are bound to impact the phase characteristics of the DPOAE in a profound manner. However, currently there does not appear to be any evidence that could support a tenfold increase in the round-trip delay through the middle ear at low frequencies. The round-trip delay through the human middle ear is currently estimated to be around 0.2 ms (Puria, 2003); this, in contrast to a DPOAE phase-gradient delay in the low-frequencies of almost 2.0 ms. The middle ear phase data extrapolated from Puria (2003; Fig. 5) were converted to group delay for the low-frequency segment of interest here (<1.4 kHz) to estimate its potential contribution to DPOAE phase. The round-trip middle ear delay was estimated to be 0.46 ms, approximately one-quarter of the observed DPOAE delay in the apical region of the human cochlea. Thus, the break from invariance observed in DPOAE phase at low frequencies appears to be cochlear in origin.
Contributions from reflection
Two possible origins of the noted break in phase invariance, i.e., that DPOAE phase was determined by the phase of the reflection component or the influence of multiple internal reflections, have a common root. They are both manifestations of activity triggered at the DP region and hence, can be eliminated by extinguishing contributions from this region. Several promising techniques of disentangling the various components in the ear canal DPOAE signal have been proposed and used in recent times (Heitmann et al., 1998; Talmadge et al., 1999; Kalluri and Shera, 2001; Konrad-Martin et al., 2001; Johnson et al., 2006; Vetesnik et al., 2009). However our goal was simpler than a perfect separation of DPOAE components from the ear canal signal. Given the fact that the phase of the DPOAE in the ear canal is determined by the dominant component, the task at hand was to ensure that the nonlinear DPOAE component from the overlap region between the stimulus tones was sufficiently dominant in the ear canal DPOAE signal. By using a suppressor tone to achieve this goal, a sufficient reduction of any influences of multi-component interaction and multiple internal reflections was also ensured.
In the present study, three levels of suppressor tone were used. Data presented by Heitmann et al. (1998) would suggest that suppressors between 40 and 60 dB SPL are sufficient in reducing or eliminating the reflection component without interfering with the nonlinear component; However, variability in the effect of a suppressor tone across subjects and across frequency within subjects has also been documented (Dhar and Shaffer, 2004). We were spared these complexities to a great extent, as complete suppression of the reflection component was not our objective. Thus, suppressor levels were chosen so that they would not interfere with the nonlinear component but still reduce contributions of the reflection component. The fact that DPOAE levels were not significantly altered in subjects, such as subject 12 (Fig. 2, top right panel) supports our choice. The fact that DPOAE level and phase fine structure was markedly diminished in subjects with prominent fine structure such as subject 01 (Fig. 2, left panels) provides evidence that the reflection component was reduced along with its influence on the ear canal DPOAE.
The IFFT results showing the distortion component to be dominant overall, combined with the ineffectiveness of a suppressor tone near the DP region in altering the slope of DPOAE phase, assures us of its origin in the phase of the nonlinear component. Stated differently, at the moderate stimulus levels used here, the contribution of the reflection component to the overall DPOAE is not significant and hence, does not determine the measured phase. The recorded DPOAE phase was derived from the nonlinear component generated in the overlap region between the stimulus tones.
Origin of break from cochlear scaling
As Shera et al. (2000) have eloquently pointed out, the explanation for the low-frequency DPOAE phase behavior need not be any more complicated than the breaking from scaling. After all, if the phases of the stimulus tones registered by DPOAE generators do not remain constant, nor can the phase of the ensuing DPOAE in the ear canal. Not only is this at the cochlear apex evident in measures of DPOAE phase, recent reports have documented similar apical-basal discontinuities in stimulus frequency OAE group delays in several species (Shera and Guinan, 2003; Shera et al., 2010).
A variety of apical-basal physiological differences have been reported in the literature. Differences in neural tuning patterns at low and high frequencies were evident in the earliest reports (Kiang and Moxon, 1974; Liberman, 1978) and are discussed in detail by Robles and Ruggero (2001). The expression of approximate cochlear scaling and its breaking at low frequencies is also evident in some of these early neural tuning reports and continue to be observed and refined even today (Temchin et al., 2008; Temchin and Ruggero, 2010). To the student of this phenomenology, the basic questions pertain to the existence of scaling in the cochlea and the reason for its breaking at the apex. Data from the auditory nerve always leaves the possibility of an unknown intermediary operating between cochlear mechanics and the neural response, as alluded to by Temchin and Ruggero (2010). This uncertainty can of course be eliminated by simultaneous measurement of mechanical and neural activity in the same animal (Narayan et al., 1998). Unfortunately, data such as these are not available from the cochlear apex at this time.
There are also clear differences in cochlear mechanics between the base and the apex, including differences in the nonlinearity of basilar membrane motion (Cooper and Rhode, 1995), an altered relationship between the movements of the tectorial membrane and sensory hair cells (Nowotny and Gummer, 2006) and significant deviations in the mode of energy propagation from the traditional traveling wave (Guinan et al., 2005; Karavitaki and Mountain, 2007b,a).
Interestingly, in some of our subjects, the phase-frequency behavior could be effectively segmented into three parts: an invariant segment above ∼2 kHz; a transitional segment between 1 and 2 kHz and a steeply sloping segment below ∼1 kHz. The three-segment model did not enhance the statistical fit significantly, indicating that this demarcation scheme was not as distinct or, perhaps, not present in all subjects; nevertheless, it may be noteworthy. It is intriguing that a similar frequency region of transition between distinct high- and low-frequency behavior has been reported recently in the auditory nerve of the chinchilla (Temchin et al., 2008) and was evident in the population statistics of a large group of animals. Here we observe a similar intermediate region within individual human ears.
CONCLUSIONS
By separating DPOAE components and by using a strategic suppressor tone we have eliminated the possibility of the reflection component from the DP region determining the phase behavior of the ear canal DPOAE at low frequencies. By extension, we have also provided evidence against the role of component interference or multiple internal reflections as the origin of this scaling break. The, noted discontinuity in the ear canal DPOAE phase around 1.3 kHz is linked to the region near f2 and f1 (the generator or overlap region) and thus, suggests a break from scaling in the human cochlea. This establishes an interpretive framework for any differences in the apical-basal transition frequency or phase slopes observed across different species or different populations within the same species, such as adults and newborns, as further explored in the companion paper.
ACKNOWLEDGMENTS
This work was supported by a grant from the National Institutes of Health, R01 DC03552 (CA) and the House Research Institute. Authors would like to thank Srikanta Mishra for assistance with data collection, Laurel Fisher, Silvia Batezati, and Ping Luo for statistical and technical expertise and Radha Kalluri for helpful comments about this manuscript.
References
- Abdala, C., and Dhar, S. (2010a). “Distortion product otoacoustic emission phase and component analysis in human newborns,” J. Acoust. Soc. Am. 127, 316–325. 10.1121/1.3268611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abdala, C., and Dhar, S. (2010b). “Differences in distortion product otoacoustic emission phase recorded from human neonates using two popular probes,” J. Acoust. Soc. Am. 128, EL49–55. 10.1121/1.3453415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper, N. P., and Rhode, W. S. (1995). “Nonlinear mechanics at the apex of the guinea-pig cochlea,” Hear. Res. 82, 225–243. 10.1016/0378-5955(94)00180-X [DOI] [PubMed] [Google Scholar]
- Dhar, S., and Shaffer, L. A. (2004). “Effects of a suppressor tone on distortion product otoacoustic emissions fine structure: Why a universal suppressor level is not a practical solution to obtaining single-generator DP-grams,” Ear Hear. 25, 573–585. 10.1097/00003446-200412000-00006 [DOI] [PubMed] [Google Scholar]
- Dhar, S., Talmadge, C. L., Long, G. R., and Tubis, A. (2002). “Multiple internal reflections in the cochlea and their effect on DPOAE fine structure,” J. Acoust. Soc. Am. 112, 2882–2897. 10.1121/1.1516757 [DOI] [PubMed] [Google Scholar]
- Guinan, J. J., Jr., Lin, T., and Cheng, H. (2005). “Medial-olivocochlear-efferent inhibition of the first peak of auditory-nerve responses: Evidence for a new motion within the cochlea,” J. Acoust. Soc. Am. 118, 2421–2433. 10.1121/1.2017899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitmann, J., Waldmann, B., Schnitzler, H. U., Plinkert, P. K., and Zenner, H. P. (1998). “Suppression of distortion product otoacoustic emissions (DPOAE) near f1 − f2 removes DP-gram fine structure-evidence for a secondary generator,” J. Acoust. Soc. Am. 103, 1527–1531. 10.1121/1.421290 [DOI] [Google Scholar]
- Johnson, T. A., Neely, S. T., Kopun, J. G., and Gorga, M. P. (2006). “Reducing reflected contributions to ear-canal distortion product otoacoustic emissions in humans,” J. Acoust. Soc. Am. 119, 3896–3907. 10.1121/1.2200048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalluri, R., and Shera, C. A. (2001). “Distortion-product source unmixing: A test of the two-mechanism model for DPOAE generation,” J. Acoust. Soc. Am. 109, 622–637. 10.1121/1.1334597 [DOI] [PubMed] [Google Scholar]
- Karavitaki, K. D., and Mountain, D. C. (2007a). “Evidence for outer hair cell driven oscillatory fluid flow in the tunnel of corti,” Biophys. J. 92, 3284–3293. 10.1529/biophysj.106.084087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karavitaki, K. D., and Mountain, D. C. (2007b). “Imaging electrically evoked micromechanical motion within the organ of corti of the excised gerbil cochlea,” Biophys. J. 92, 3294–3316. 10.1529/biophysj.106.083634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemp, D. T. (1979). “The evoked cochlear mechanical response and the auditory microstructure - evidence for a new element in cochlear mechanics,” Scand. Audiol. Suppl. 9, 35–47. [PubMed] [Google Scholar]
- Kemp, D. T. (2002). “Otoacoustic emissions, their origin in cochlear function, and use,” Br. Med. Bull. 63, 223–241. 10.1093/bmb/63.1.223 [DOI] [PubMed] [Google Scholar]
- Kiang, N. Y. S., and Moxon, E. C. (1974). “Tails of tuning curves of auditory-nerve fibers,” J. Acoust. Soc. Am. 55, 620–630. 10.1121/1.1914572 [DOI] [PubMed] [Google Scholar]
- Kim, D. O. (1980). “Cochlear mechanics: Implications of electrophysiological and acoustical observations,” Hear. Res. 2, 297–317. 10.1016/0378-5955(80)90064-7 [DOI] [PubMed] [Google Scholar]
- Knight, R. D., and Kemp, D. T. (2000). “Indications of different distortion product otoacoustic emission mechanisms from a detailed f1, f2 area study,” J. Acoust. Soc. Am. 107, 457–473. 10.1121/1.428351 [DOI] [PubMed] [Google Scholar]
- Konrad-Martin, D., Neely, S. T., Keefe, D. H., Dorn, P. A., Cyr, E., and Gorga, M. P. (2002). “Sources of DPOAEs revealed by suppression experiments, inverse fast Fourier transforms, and SFOAEs in impaired ears,” J. Acoust. Soc. Am. 111, 1800–1809. 10.1121/1.1455024 [DOI] [PubMed] [Google Scholar]
- Konrad-Martin, D., Neely, S. T., Keefe, D. H., Dorn, P. A., and Gorga, M. P. (2001). “Sources of distortion product otoacoustic emissions revealed by suppression experiments and inverse fast Fourier transforms in normal ears,” J. Acoust. Soc. Am. 109, 2862–2879. 10.1121/1.1370356 [DOI] [PubMed] [Google Scholar]
- Liberman, M. C. (1978). “Auditory-nerve response from cats raised in a low-noise chamber,” J. Acoust. Soc. Am. 63, 442–455. 10.1121/1.381736 [DOI] [PubMed] [Google Scholar]
- Long, G. R., Talmadge, C. L. and Lee, J. (2008). “Measuring distortion product otoacoustic emissions using continuously sweeping primaries,” J. Acoust. Soc. Am. 124, 1613–1626. [DOI] [PubMed] [Google Scholar]
- Mauermann, M., Uppenkamp, S., van Hengel, P. W. J., and Kollmeier, B. (1999a). “Evidence for the distortion product frequency place as a source of distortion product otoacoustic emission (DPOAE) fine structure in humans. I. Fine structure and higher-order DPOAE as a function of the frequency ratio f2/ f1,” J. Acoust. Soc. Am. 106, 3473–3483. 10.1121/1.428200 [DOI] [PubMed] [Google Scholar]
- Mauermann, M., Uppenkamp, S., van Hengel, P. W. J., and Kollmeier, B. (1999b). “Evidence for the distortion product frequency place as a source of distortion product otoacoustic emission (DPOAE) fine structure in humans. II. Fine structure for different shapes of cochlear hearing loss,” J. Acoust. Soc. Am. 106, 3484–3491. 10.1121/1.428201 [DOI] [PubMed] [Google Scholar]
- Moulin, A., and Kemp, D. T. (1996). “Multicomponent acoustic distortion product otoacoustic emission phase in humans. II. Implications for distortion product otoacoustic emissions generation,” J. Acoust. Soc. Am. 100, 1640–1662. 10.1121/1.416064 [DOI] [PubMed] [Google Scholar]
- Narayan, S. S., Temchin, A. N., Recio, A., and Ruggero, M. A. (1998). “Frequency tuning of basilar membrane and auditory nerve fibers in the same cochleae,” Science 282, 1882–1884. 10.1126/science.282.5395.1882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowotny, M., and Gummer, A. W. (2006). “Nanomechanics of the subtectorial space caused by electromechanics of cochlear outer hair cells,” Proc. Natl. Acad. Sci. U.S.A. 103, 2120–2125. 10.1073/pnas.0511125103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puria, S. (2003). “Measurements of human middle ear forward and reverse acoustics: Implications for otoacoustic emissions,” J. Acoust. Soc. Am. 113, 2773–2789. 10.1121/1.1564018 [DOI] [PubMed] [Google Scholar]
- Rhode, W. S. (1971). “Observations of the vibration of the basilar membrane in squirrel monkeys using the Mossbauer technique,” J. Acoust. Soc. Am. 49, 1218–1231. 10.1121/1.1912485 [DOI] [PubMed] [Google Scholar]
- Robles, L., and Ruggero, M. A. (2001). “Mechanics of the mammalian cochlea,” Physiol. Rev. 81, 1305–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J., Jr., (1999). “Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian OAEs,” J. Acoust. Soc. Am. 105, 782–798. 10.1121/1.426948 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J., Jr., (2003). “Stimulus-frequency-emission group delay: A test of coherent reflection filtering and a window on cochlear tuning,” J. Acoust. Soc. Am. 113, 2762–2772. 10.1121/1.1557211 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., Jr., and Oxenham, A. J. (2010). “Otoacoustic estimation of cochlear tuning: Validation in the chinchilla,” J. Assoc. Res. Otolaryngol. 11, 343–365. 10.1007/s10162-010-0217-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., Talmadge, C. L., and Tubis, A. (2000). “Interrelations among distortion-product phase-gradient delays: Their connection to scaling symmetry and its breaking,” J. Acoust. Soc. Am. 108, 2933–2948. 10.1121/1.1323234 [DOI] [PubMed] [Google Scholar]
- Siegel, J. H. (2009). “Estimating wideband eardrum sound levels in humans,” in Thirty-Second Annual Midwinter Research Meeting of the Association for Research in Otolaryngology, Baltimore, MA, pp. 11–12.
- Talmadge, C. L., Long, G. R., Tubis, A., and Dhar, S. (1999). “Experimental confirmation of the two-source interference model for the fine structure of distortion product otoacoustic emissions,” J. Acoust. Soc. Am. 105, 275–292. 10.1121/1.424584 [DOI] [PubMed] [Google Scholar]
- Talmadge, C. L., Tubis, A., Long, G. R., and Piskorski, P. (1998). “Modeling otoacoustic emission and hearing threshold fine structures,” J. Acoust. Soc. Am. 104, 1517–1543. 10.1121/1.424364 [DOI] [PubMed] [Google Scholar]
- Temchin, A. N., Rich, N. C., and Ruggero, M. A. (2008). “Threshold tuning curves of chinchilla auditory-nerve fibers. I. Dependence on characteristic frequency and relation to the magnitudes of cochlear vibrations,” J. Neurophysiol. 100, 2889–2898. 10.1152/jn.90637.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin, A. N., and Ruggero, M. A. (2010). “Phase-locked responses to tones of chinchilla auditory nerve fibers: Implications for apical cochlear mechanics,” J. Assoc. Res. Otolaryngol. 11, 297–318. 10.1007/s10162-009-0197-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetesnik, A., Turcanu, D., Dalhoff, E., and Gummer, A. W. (2009). “Extraction of sources of distortion product otoacoustic emissions by onset-decomposition,” Hear. Res. 256, 21–38. 10.1016/j.heares.2009.06.002 [DOI] [PubMed] [Google Scholar]
- Zweig, G. (1976). “Basilar membrane motion,” Cold Spring Harb Symp. Quant Biol. 40, 619–633. [DOI] [PubMed] [Google Scholar]