A Mechanical Bidomain Model of Cardiac Tissue

Abstract

Intracellular and extracellular spaces are separately considered in an electrical bidomain model of tissue. We propose a mechanical bidomain model separately considering the intracellular and extracellular spaces with a linear restoring force proportional to the displacement difference of the two spaces. We consider a mechanically passive model of heart fibers (no tension) with an action potential and an electrically passive model (no action potential) in tissue with an ischemic boundary. We find the pressure and displacement fields arising from our consideration of a bidomain instead of a monodomain and note interesting characteristics evident only with a bidomain approach.

Introduction

The electrical properties of cardiac tissue are often represented using the bidomain model [1], which takes into account the anisotropic electrical properties of both the intracellular (i) and extracellular (e) spaces. It is a continuum model, because it models the electrical behavior averaged over many cells. One formulation of the steady-state electrical bidomain equations is [1,2]

$$\nabla ·({\tilde{g}}_i\nabla {\varphi }_i)=\beta G({\varphi }_i-{\varphi }_e)-I_i$$ (1)

$$\nabla ·({\tilde{g}}_e\nabla {\varphi }_e)=-\beta G({\varphi }_i-{\varphi }_e)-I_e$$ (2)

where ϕ is the electrical potential, g̃ is the conductivity tensor, G is the membrane conductance per unit area, β is the ratio of membrane area to tissue volume, and I is the source current (as through an electrode). Interesting and unexpected behavior is predicted by the bidomain model, especially when analyzing electrical stimulation [2].

In analogy to the electrical bidomain model we propose a mechanical bidomain model to represent the elastic properties of cardiac tissue. Much research has been performed to study the biomechanical behavior of the heart [3–6], but biological tissue has traditionally been based on “monodomain” models that do not distinguish between the intracellular and extracellular spaces (see for example [7,8]). Our bidomain analysis models an intracellular space that consists of cells embedded in an extracellular matrix, and resembles superficially the classic study of Eshelby (1957) on the elasticity of inclusion bodies. There is, however, one key difference. Eshelby considered the deformation around inhomogeneities (individual cells), whereas our model represents the tissue as a continuum in which the properties of both the intracellular and extracellular spaces are averaged over many cells.

The Mechanical Bidomain Model

Cardiac tissue is largely composed of water, a nearly incompressible fluid. Like Chadwick [10], we assume the tissue is incompressible, implying that the trace of the strain tensor is zero and a hydrostatic pressure builds up as necessary to prevent volume changes. Moreover, we assume each space is individually incompressible (no fluid is transferred between the intracellular and extracellular spaces). We approximate the extracellular space as an isotropic material, so the extracellular stress tensor σ̃_e is [11,12]

$${\sigma }_{e,\mathit{\text{nm}}}=-p_e{\delta }_{\mathit{\text{nm}}}+2\mu {\epsilon }_{e,\mathit{\text{nm}}}+M_{e,\mathit{\text{nm}}}$$ (3)

where p_e is the extracellular pressure, δ_nm is the Kronecker delta, μ is the shear modulus,ε̃ is the strain tensor, and M̃ is a tensor specifying an external body force acting on the extracellular space such that F⃗_e = ∇ · M̃_e.

The intracellular space is not isotropic, and we represent its mechanical properties as a fluid-fiber continuum. Assume the myocardial fibers are directed along the unit vector τ̂, which in general can be a function of position. The intracellular stress σ̃_i is given by [10–12]

$${\sigma }_{i,\mathit{\text{nm}}}=-p_i{\delta }_{\mathit{\text{nm}}}+T{\tau }_n{\tau }_m+M_{i,\mathit{\text{nm}}}.$$ (4)

T is the fiber tension, which consists of two parts [10]: an active isometric tension at zero strain T₀ and a passive linear stress-strain relationship characterized by the Young’s modulus Y

$$T=T_0+\mathit{\text{Ye}}$$ (5)

where e is the strain along the fiber, given in terms of the displacement u as [10]

$$e=((\widehat{\tau }·\nabla )\mathit{u})·\widehat{\tau }$$ (6)

Chadwick [10] and Holzapfel et al. (2000) examine the case of curving fivers. In our analysis, we restrict ourselves to straight fibers, whence

$$e={\epsilon }_{e,\mathit{\text{kl}}}{\tau }_k{\tau }_l.$$ (7)

If the intracellular and extracellular spaces were not coupled, the quasistatic equations of equilibrium could be found by setting the divergence of the stress tensor equal to zero in each space

$$-\nabla p_i+\widehat{\tau }(\widehat{\tau }·\nabla T)=-{\overrightarrow{F}}_i$$ (8)

$$-\nabla p_e+2\mu \nabla ·{\tilde{\epsilon }}_e=-{\overrightarrow{F}}_e.$$ (9)

The intracellular and extracellular spaces are not, however, isolated from each other. These spaces interact in a number of ways, including transmembrane extensions of the cytoskeleton, transmembrane proteins, etc [13]. Therefore, we assume that displacements in the intracellular space will cause displacements in the extracellular space and vice versa through a coupling force. As a first approximation, we model this interaction by a linear restoring force similar to Hooke’s law and proportional to the displacement difference which modifies the equations of mechanical equilibrium

$$-\nabla p_i+\widehat{\tau }(\widehat{\tau }·\nabla T)=K(\overrightarrow{u}-\overrightarrow{w})-{\overrightarrow{F}}_i$$ (10)

$$-\nabla p_e+2\mu \nabla ·{\tilde{\epsilon }}_e=-K(\overrightarrow{u}-\overrightarrow{w})-{\overrightarrow{F}}_e.$$ (11)

where u⃗ is the intracellular displacement field and w⃗ is the extracellular displacement field. This pair of equations is the mechanical analog of the electrical bidomain equations in Equations 1 and 2.

Boundary conditions are that the displacements and the normal components of the stress tensor in each space are continuous across a boundary [12,14].

Example 1

We now apply our model of cardiac tissue to two specific examples. First, we examine the magnetic forces on action currents associated with a propagating action potential wave front. We restrict ourselves to the two-dimensional case (plane strain), with straight fibers along the x-axis. We also assume there is no active tension (T₀=0) and the body forces are given by the Lorentz forces [14] on the action potential currents, J_i and J_e, in a magnetic field B: F_i = J_i × B and F_e = J_e × B. If the magnetic field is perpendicular to the plane (in the z-direction), the mechanical equations become

$$-\frac{\partial p_i}{\partial x}+Y\frac{\partial {\epsilon }_{i,\mathit{\text{xx}}}}{\partial x}=K(u_x-w_x)-J_{i,y}B$$ (12)

$$-\frac{\partial p_i}{\partial y}=K(u_y-w_y)+J_{i,x}B$$ (13)

$$-\frac{\partial p_e}{\partial x}+2\mu (\frac{\partial {\epsilon }_{e,\mathit{\text{xx}}}}{\partial x}+\frac{\partial {\epsilon }_{e,\mathit{\text{xy}}}}{\partial y})=-K(u_x-w_x)-J_{e,y}B$$ (14)

$$-\frac{\partial p_e}{\partial y}+2\mu (\frac{\partial {\epsilon }_{e,\mathit{\text{xy}}}}{\partial x}+\frac{\partial {\epsilon }_{e,\mathit{\text{yy}}}}{\partial y})=-K(u_y-w_y)-J_{e,x}B.$$ (15)

Roth and Woods [15] have solved the electrical problem of an action potential propagating in the x-direction with fibers at an angle θ with respect to the x-axis as depicted in Fig. 1. The intracellular and extracellular conductivities are both of the form [16]

$$\tilde{g}=\left(\begin{array}{cc}{g}_L{\text{cos}}^2\theta +g_T{\text{sin}}^2\theta \hfill & (g_L-g_T)\text{sin}\theta \text{cos}\theta \hfill \\ (g_L-g_T)\text{sin}\theta \text{cos}\theta \hfill & g_L{\text{sin}}^2\theta +g_T{\text{cos}}^2\theta \hfill \end{array}\right)$$ (16)

where g_L and g_T are the conductivities parallel to and perpendicular to the fibers, respectively. A model for the transmembrane action potential is ${\varphi }_m=\pm \frac{{\varphi }_0}{2}=\text{constant}$ for |x| > L and ${\varphi }_m=\frac{{\varphi }_0}{4}\left(3\frac{x}{L}-{\left(\frac{x}{L}\right)}^2\right)$ for |x| ≤ L. The intracellular and extracellular current densities are given by [15] ${\mathit{J}}_{\mathit{i}}=-(f_1(\theta )\widehat{x}+f_2(\theta )\widehat{y})\frac{\partial {\varphi }_m}{{\partial }_x}\text{and}{\mathit{J}}_{\mathit{e}}=(f_1(\theta )\widehat{x}+f_3(\theta )\widehat{y})\frac{\partial {\varphi }_m}{{\partial }_x}$ where

$$f_1(\theta )=\frac{(g_{\mathit{\text{iL}}}{\text{cos}}^2\theta +g_{\mathit{\text{iT}}}{\text{sin}}^2\theta )(g_{\mathit{\text{eL}}}{\text{cos}}^2\theta +g_{\mathit{\text{eT}}}{\text{sin}}^2\theta )}{(g_{\mathit{\text{iL}}}+g_{\mathit{\text{eL}}}){\text{cos}}^2\theta +(g_{\mathit{\text{iT}}}+g_{\mathit{\text{eT}}}){\text{sin}}^2\theta }$$ (17)

$$f_2(\theta )=\frac{(g_{\mathit{\text{iL}}}-g_{\mathit{\text{iT}}})\text{sin}\theta \text{cos}\theta (g_{\mathit{\text{eL}}}{\text{cos}}^2\theta +g_{\mathit{\text{eT}}}{\text{sin}}^2\theta )}{(g_{\mathit{\text{iL}}}+g_{\mathit{\text{eL}}}){\text{cos}}^2\theta +(g_{\mathit{\text{iT}}}+g_{\mathit{\text{eT}}}){\text{sin}}^2\theta }$$ (18)

$$f_3(\theta )=\frac{(g_{\mathit{\text{eL}}}-g_{\mathit{\text{eT}}})\text{sin}\theta \text{cos}\theta (g_{\mathit{\text{iL}}}{\text{cos}}^2\theta +g_{\mathit{\text{iT}}}{\text{sin}}^2\theta )}{(g_{\mathit{\text{iL}}}+g_{\mathit{\text{eL}}}){\text{cos}}^2\theta +(g_{\mathit{\text{iT}}}+g_{\mathit{\text{eT}}}){\text{sin}}^2\theta }.$$ (19)

We will find it convenient to define the peak amplitude of the intracellular current density as $J_0=f_1(\theta )\frac{3{\varphi }_0}{4L}$.

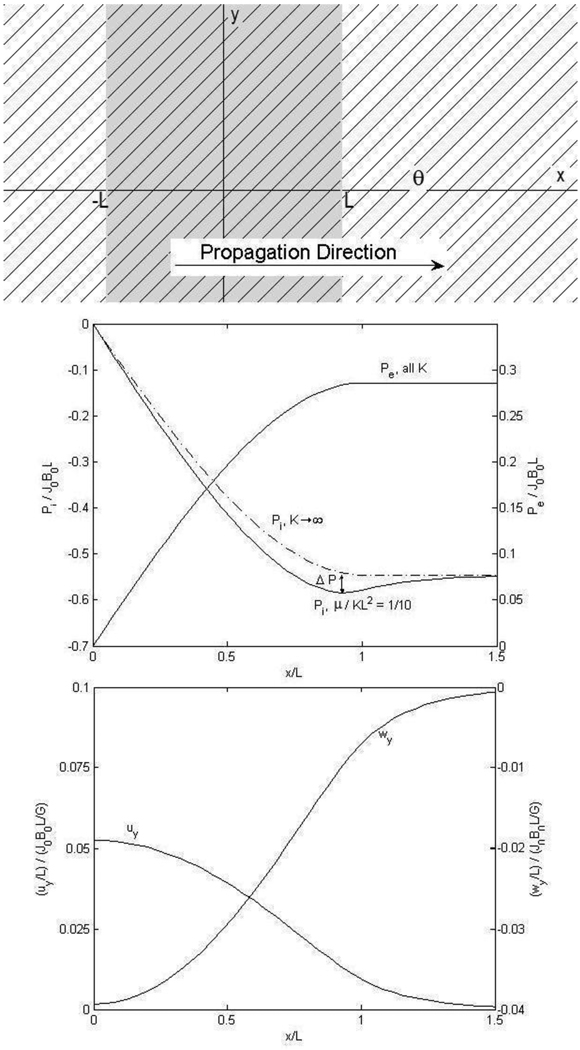
Figure 1.

Propagation of a planar cardiac action potential (shaded gray) in the x-direction, with fibers at an angle 45° with respect to the x-axis. The sum of the intracellular and extracellular current densities J_i + J_e is not, in general, zero; there is, in this case, a net current in the y-direction [15]. The intracellular and extracellular displacements, while in opposition, are not equal in magnitude; observe, however, that displacements are greatest at the site of maximum current density $\frac{x}{L}=0$, as we expect. Hydrostatic pressure is found to buildup within the region of the action potential and peak before, and not at the boundary $\frac{x}{L}=1$. We label this buildup before the boundary Δp, which diminishes with increasing K. The dashed line indicates the intracellular pressure distribution with infinite stiffness; with infinite stiffness u_y = w_y = 0 and there is no displacement, again as we expect. Our estimate of K is somewhat small to exaggerate the effects in the plot. Large K make displacements and pressure buildup significantly smaller.

Using the boundary conditions τ_xx, τ_xy, u⃗ and w⃗ continuous across x = ±L, we find solutions for the intracellular and extracellular hydrostatic pressure distributions and tissue displacement fields

$$p_i=J_0{B}_{0}L\{\begin{array}{cc}\hfill -\frac{f_2(\theta )}{f_1(\theta )}\frac{x}{L}(1-\frac{x^2}{3L^2})+\frac{2}{\text{tan}(\theta )}{\left(\frac{x_0}{L}\right)}^2\left(\right(1+\frac{x_0}{L}\left)e^{-L/x_0}\text{sinh}\right(\frac{x}{x_0})-\frac{x}{L})\hfill & \hfill |x|\le L\hfill \\ \hfill -\frac{2}{3}\frac{f_2(\theta )}{f_1(\theta )}+\frac{2}{\text{tan}(\theta )}{\left(\frac{x_0}{L}\right)}^2(\frac{x_0}{L}{e}^{L/x_0}-(1+\frac{x_0}{L}\left)\text{cosh}\right(\frac{L}{x_0}\left)\right)e^{-x/x_0}\hfill & \hfill x>L\hfill \end{array}$$ (20)

$$p_e=J_0{B}_{0}L\frac{f_3(\theta )}{f_1(\theta )}\{\begin{array}{cc}\hfill \frac{x}{L}(1-\frac{x^2}{3L^2})\hfill & \hfill |x|\le L\hfill \\ \hfill \frac{2}{3}\hfill & \hfill x>L\hfill \end{array}$$ (21)

$$w_y=\frac{2J_0{B}_0{L}^2}{\mu }{\left(\frac{x_0}{L}\right)}^2\{\begin{array}{cc}\hfill {\left(\frac{x_0}{L}\right)}^2-\frac{1}{2}(1-\frac{x^2}{L^2})-\frac{x_0}{L}(1+\frac{x_0}{L})e^{-L/x_0}\text{cosh}\left(\frac{x}{x_0}\right)\hfill & \hfill |x|\le L\hfill \\ \hfill \frac{x_0}{L}(\frac{x_0}{L}{e}^{L/x_0}-(1+\frac{x_0}{L}\left)\text{cosh}\right(\frac{L}{x_0}\left)\right)e^{-x/x_0}\hfill & \hfill x>L\hfill \end{array}$$ (22)

$$u_y=\frac{-4\mu }{Y{\text{sin}}^2(2\theta )}{w}_y$$ (23)

with no x-displacements in the intracellular or extracellular spaces. The given hydrostatic pressure functions are odd functions of x, while the displacement fields are even functions. The mechanical bidomain model introduces a new length scale into the problem

$$x_0=\sqrt{\frac{\mu Y}{K}\frac{{\text{sin}}^2(2\theta )}{4\mu +Y{\text{sin}}^2(2\theta )}},$$ (24)

analogous to the electrical length constant familiar in the electrical bidomain model [16].

Typical values for most of the mechanical parameters of cardiac tissue can be found in the literature. However, experimental evidence is lacking for an estimate of K. To illustrate behavior arising from the bidomain model we use a somewhat large value of $\frac{\mu }{{\mathit{\text{KL}}}^2}=\frac{1}{10}$, relative conductivities [16,17] $\frac{g_{\mathit{\text{iL}}}}{g_{\mathit{\text{iT}}}}=10,\frac{g_{\mathit{\text{eL}}}}{g_{\mathit{\text{eT}}}}=2.5$, and a ratio of Young’s to shear modulus [18] $\frac{Y}{\mu }=3$ for the dimensionless plots of displacements and pressures shown in Fig. 1. There is a build-up of intracellular hydrostatic pressure within the action potential before, and not at the boundary $\frac{x}{L}=1$. In Fig. 1 we observe this pressure buildup Δp depends on K, the stiffness of the coupling spring constant. As the spring is stiffened p_i approaches the dashed curve of intracellular pressure with K → ∞ and the magnitude of this pressure buildup decreases. We take note, however, of the fact that this pressure buildup is only approximately 1% of the largest pressure and that the largest pressure, itself, is only approximately half of the quantity J₀B₀L. Referring again to Fig. 1, we observe, as we expect, that the greatest displacements of tissue are in the region of greatest current densities (here at x=0) and that the magnitude of the intracellular displacement u_y is only approximately 5% of $\frac{J_0{B}_0{L}^2}{\mu }$. Evidently, displacements associated with a cardiac action potential propagating at an angle to the fibers while in an external magnetic field are very small indeed.

Example 2

Another common is a boundary between an area of ischemic tissue (T₀ = 0) and an area of healthy, uniform active tissue (T₀ = T₁) as shown in Fig. 2. We consider the area of ischemic tissue is in the region y<0 and the area of healthy tissue is in the region y>0 with fibers at an angle θ with respect to the x-axis. Again we assume plane strain, and in this case the external body forces are zero (F⃗_l = F⃗_e = 0). The equations governing the tissue are

$$-\frac{\partial p_i}{\partial x}+Y\frac{\partial {\epsilon }_{i,\mathit{\text{xx}}}}{\partial x}=K(u_x-w_x)$$ (25)

$$-\frac{\partial p_i}{\partial y}=K(u_y-w_y)$$ (26)

$$-\frac{\partial p_e}{\partial x}+2\mu (\frac{\partial {\epsilon }_{e,\mathit{\text{xx}}}}{\partial x}+\frac{\partial {\epsilon }_{e,\mathit{\text{xy}}}}{\partial y})=-K(u_x-w_x)$$ (27)

$$-\frac{\partial p_e}{\partial y}+2\mu (\frac{\partial {\epsilon }_{e,\mathit{\text{xy}}}}{\partial x}+\frac{\partial {\epsilon }_{e,\mathit{\text{yy}}}}{\partial y})=-K(u_y-w_y).$$ (28)

and the boundary conditions are τ_yy, τ_xy, u⃗, and w⃗ are continuous across the boundary y=0. The hydrostatic pressure and displacement fields are found to be

$$p_i=T_1\frac{2\mu {\text{sin}}^2(\theta )}{4\mu +Y{\text{sin}}^2(2\theta )}\{\begin{array}{cc}\hfill 2(1-\frac{1}{2}{e}^{-y/x_0})\hfill & \hfill y\ge 0\hfill \\ \hfill e^{y/x_0}\hfill & \hfill y<0\hfill \end{array}$$ (29)

$$u_x=T_1\frac{2x_0\text{sin}(2\theta )}{4\mu +Y{\text{sin}}^2(2\theta )}\{\begin{array}{cc}\hfill \frac{2\mu }{Y{\text{sin}}^2(2\theta )}{e}^{-y/x_0}-\frac{y}{x_0}\hfill & \hfill y\ge 0\hfill \\ \hfill \frac{2\mu }{Y{\text{sin}}^2(2\theta )}{e}^{y/x_0}\hfill & \hfill y<0\hfill \end{array}$$ (30)

$$w_x=-T_1\frac{x_0\text{sin}(2\theta )}{4\mu +Y{\text{sin}}^2(2\theta )}\{\begin{array}{cc}\hfill e^{-y/x_0}+\frac{2y}{x_0}\hfill & \hfill y\ge 0\hfill \\ \hfill e^{y/x_0}\hfill & \hfill y<0\hfill \end{array}.$$ (31)

In this example there are no y-displacements in the intracellular or extracellular spaces and there is no external pressure (p_e = 0). The new spatial scale parameter x₀ again appears in the solution. We assume a free boundary at infinity allowing displacement to increase with increasing y. The x-displacements are increasingly negative with increasing distance from the ischemic boundary, thus the fibers are righting themselves to be perpendicular to the ischemic boundary. The dotted line indicates displacements with infinite stiffness that are not zero. Instead, with K → ∞, we find u_x = w_x and the tissue behaves like a monodomain. For an infinite stiffness the pressure is discontinuous across the boundary, while for a finite stiffness it is smoothly varying between these two regions.

Figure 2.

Cardiac tissue with a boundary between an ischemic region (shaded gray) and a non-ischemic region with fiber angle again 45°. We assume a free boundary at infinity, allowing displacements to increase. Negative x-displacements are found to increase with distance from the ischemic boundary, suggestive of a situation where the fibers are trying to right themselves perpendicular to the ischemic boundary. The dotted line indicates displacements with infinite stiffness, which is not zero; instead, with infinite stiffness we find u_y = w_y (not necessarily zero) and the tissue behaves like a monodomain. For an infinite stiffness, we observe the pressure is discontinuous across the boundary, while for a finite stiffness it is smoothly varying between these two values.

Discussion

We have developed a bidomain mechanical model, in analogy to the well-known electrical bidomain model. Our model is similar to the monodomain mechanical model of Ohayon and Chadwick [18], who included three terms in their stress tensor: a pressure, a fiber tension, and an isotropic elastic matrix they associated with collagen. In our case, we assign the isotropic collagen matrix to the extracellular space and the fiber tension to the intracellular space. The two spaces are coupled with a term characterized by the spring constant K.

A bidomain mechanical model is particularly valuable when the intracellular and extracellular body forces are in opposite directions. For instance, in the model of magnetic forces on action currents (our example 1), the x-component of the intracellular and extracellular current densities are equal in magnitude and opposite direction. Therefore, the y-component of the magnetic force acting in the intracellular space is equal and opposite to that in the extracellular space. In a monodomain model, the net force acting on the tissue would therefore be zero, and one would not expect displacements. In the bidomain model, however, the intracellular and extracellular spaces are displaced in opposite directions. This is an example of a new effect predicted by the bidomain mechanical model that is not predicted by a monodomain model.

Another new feature of the bidomain model is the introduction of a new length scale x₀, which is inversely related to the spring constant K. Although we do not have a good value for K, we suspect that it will be large enough that x₀ is relatively small. Many of the interesting bidomain effects are confined to a distance of a few x₀.

We made a number of limiting assumptions in our analysis: 1) We considered straight fibers in the x-direction, although our model could easily handle curving fibers [10,19]. Analytic solutions might be difficult to find in that case, and numerical methods may be needed. 2) We have assumed that in the intracellular space the tension develops only along the fibers. This is an idealization that is probably more applicable to skeletal muscle where fibers are independent than in cardiac muscle. In heart tissue, there may be some intracellular mechanical coupling between fibers because of intracellular junctions coupling cells. Nevertheless, the intracellular space should be far more anisotropic that the extracellular space (the spaces have “unequal anisotropy ratios” [2]), so our model should capture any new qualitative behavior arising from the bidomain representation. 3) Our model uses linear elasticity and therefore assumes small strains. Our results indicate that often the strains are small, but a nonlinear model could be developed for large strains. 4) Treating the tissue as incompressible is probably a good assumption, but requiring both the intracellular and extracellular space to be individually incompressible is more questionable. This assumption is equivalent to saying that the intracellular volume fraction is constant, and there is no net flow of fluid from one space to the other. Brief displacements, such as those associated with an action potential, probably do not provide enough time for significant flow of water between spaces. Over longer time scales, this assumption is more suspect. 5) The central assumption in our model is that the coupling force between the two spaces can be represented by a simple Hooke’s law, with spring constant K. We have little experimental evidence to justify this assumption. Rather, this is a first order approximation and may be a first step towards a more realistic model.

We have shown through two relatively simple examples that equilibrium displacements and hydrostatic pressures of biological tissue under the action of body forces (e.g. the Lorentz force) or in response to an ischemic boundary are small. This is an important fact to recognize, as others have considered Lorentz force displacement imaging a potential use of MRI; our results suggest otherwise and are in agreement with previous mechanical analysis [20]. We note some distinct features of our bidomain results: In the two examples presented here, the intracellular and extracellular pressures are not equal in magnitude. If these pressures are maintained for a long time fluid will move from one space to the other in response to the pressure differential. Bidomain effects appear to be more important when fibers lie at an intermediate angle to either the direction of wave propagation or the boundary of the ischemic region. In our calculations if θ = 0° or 90°, effects specific to the bidomain model disappear. We consider steady-state mechanical equilibrium here. At high frequencies our model suggests a possibly new type of elastic wave with the intracellular and extracellular spaces oscillating out of phase; a large value of K would suggest fast propagation at a very high frequency. Detection of such a wave might allow the experimentalist to determine K. We have presented a first order approximation of bidomain elastic properties of cardiac tissue.