What is flux balance analysis?

Abstract

Flux balance analysis is a mathematical approach for analyzing the flow of metabolites through a metabolic network. This primer covers the theoretical basis of the approach, several practical examples and a software toolbox for performing the calculations.

Flux balance analysis (FBA) is a widely used approach for studying biochemical networks, in particular the genome-scale metabolic network reconstructions that have been built in the past decade^1–5. These network reconstructions contain all of the known metabolic reactions in an organism and the genes that encode each enzyme. FBA calculates the flow of metabolites through this metabolic network, thereby making it possible to predict the growth rate of an organism or the rate of production of a biotechnologically important metabolite. With metabolic models for 35 organisms already available (http://systemsbiology.ucsd.edu/In_Silico_Organisms/Other_Organisms) and high-throughput technologies enabling the construction of many more each year^{6, 7}, FBA is an important tool for harnessing the knowledge encoded in these models.

In this primer, we illustrate the principles behind FBA by applying it to the prediction of the specific growth rate of Escherichia coli in the presence and absence of oxygen. The principles outlined can be applied in many other contexts to analyze the phenotypes and capabilities of organisms with different environmental and genetic perturbations (a supplementary tutorial provides six additional worked examples with figures and computer code).

Flux balance analysis is based on constraints

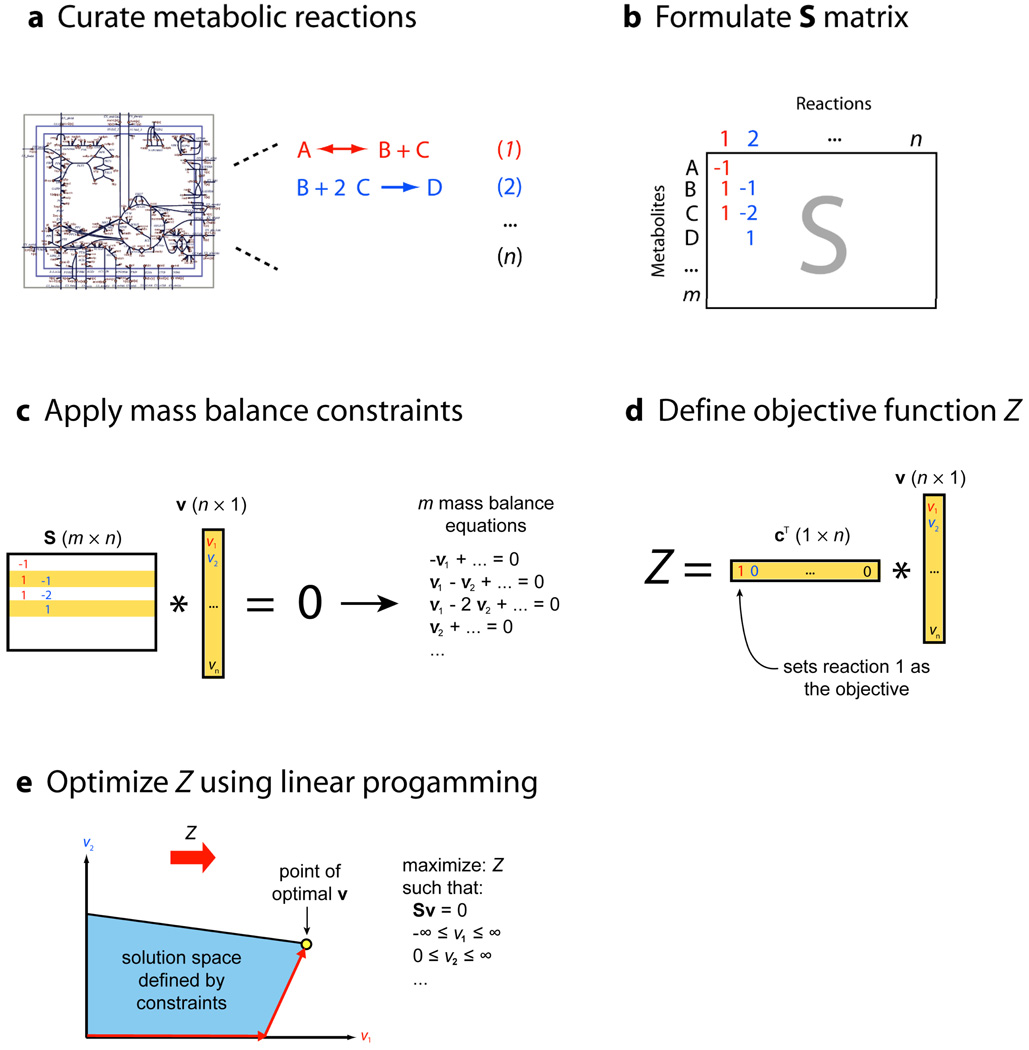
The first step in FBA is to mathematically represent metabolic reactions (Box 1). The core feature of this representation is a tabulation, in the form of a numerical matrix, of the stoichiometric coefficients of each reaction (Fig. 1a,b). These stoichiometries impose constraints on the flow of metabolites through the network. Constraints such as these lie at the heart of FBA, differentiating the approach from theory-based models based on biophysical equations that require many difficult-to-measure kinetic parameters^{8, 9}.

Box 1: Mathematical representation of metabolism.

Metabolic reactions are represented as a stoichiometric matrix (S), of size m*n. Every row of this matrix represents one unique compound (for a system with m compounds) and every column represents one reaction (n reactions). The entries in each column are the stoichiometric coefficients of the metabolites participating in a reaction. There is a negative coefficient for every metabolite consumed, and a positive coefficient for every metabolite that is produced. A stoichiometric coefficient of zero is used for every metabolite that does not participate in a particular reaction. S is a sparse matrix since most biochemical reactions involve only a few different metabolites. The flux through all of the reactions in a network is represented by the vector v, which has a length of n. The concentrations of all metabolites are represented by the vector x, with length m. The system of mass balance equations at steady state (dx/dt = 0) is given in Fig. 1c²³:

$$\mathbf{\text{Sv}}=0$$

Any v that satisfies this equation is said to be in the null space of S. In any realistic large-scale metabolic model, there are more reactions than there are compounds (n > m). In other words, there are more unknown variables than equations, so there is no unique solution to this system of equations.

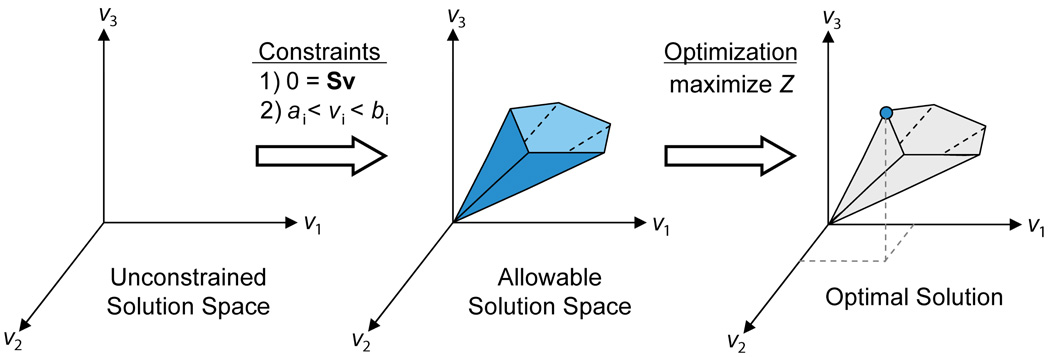
Although constraints define a range of solutions, it is still possible to identify and analyze single points within the solution space. For example, we may be interested in identifying which point corresponds to the maximum growth rate or to maximum ATP production of an organism, given its particular set of constraints. FBA is one method for identifying such optimal points within a constrained space (Fig. 2).

FBA seeks to maximize or minimize an objective function Z = c^Tv, which can be any linear combination of fluxes, where c is a vector of weights, indicating how much each reaction (such as the biomass reaction when simulating maximum growth) contributes to the objective function. In practice, when only one reaction is desired for maximization or minimization, c is a vector of zeros with a one at the position of the reaction of interest (Fig. 1d).

Optimization of such a system is accomplished by linear programming (Fig. 1e). FBA can thus be defined as the use of linear programming to solve the equation Sv = 0 given a set of upper and lower bounds on v and a linear combination of fluxes as an objective function. The output of FBA is a particular flux distribution, v, which maximizes or minimizes the objective function.

Figure 1.

Formulation of an FBA problem.(a) First, a metabolic network reconstruction is built, consisting of a list of stoichiometrically balanced biochemical reactions. (b) Next, this reconstruction is converted into a mathematical model by forming a matrix (labeled S) in which each row represents a metabolite and each column represents a reaction. (c) At steady state, the flux through each reaction is given by the equation Sv = 0. Since there are more reactions than metabolites in large models, there is more than one possible solution to this equation. (d) An objective function is defined as Z = c^Tv, where c is a vector of weights (indicating how much each reaction contributes to the objective function). In practice, when only one reaction is desired for maximization or minimization, c is a vector of zeros with a one at the position of the reaction of interest. When simulating growth, the objective function will have a 1 at the position of the biomass reaction. (e) Finally, linear programming can be used to identify a particular flux distribution that maximizes or minimizes this objective function while observing the constraints imposed by the mass balance equations and reaction bounds.

Constraints are represented in two ways, as equations that balance reaction inputs and outputs and as inequalities that impose bounds on the system. The matrix of stoichiometries imposes flux (that is, mass) balance constraints on the system, ensuring that the total amount of any compound being produced must be equal to the total amount being consumed at steady state (Fig. 1c). Every reaction can also be given upper and lower bounds, which define the maximum and minimum allowable fluxes of the reactions. These balances and bounds define the space of allowable flux distributions of a system—that is, the rates at which every metabolite is consumed or produced by each reaction. Other constraints can also be added¹⁰.

From constraints to optimizing a phenotype

The next step in FBA is to define a biological objective that is relevant to the problem being studied (Fig. 1d). In the case of predicting growth, the objective is biomass production, the rate at which metabolic compounds are converted into biomass constituents such as nucleic acids, proteins, and lipids. Mathematically, the objective is represented by an ‘objective function’ that indicates how much each reaction contributes to the phenotype. A ‘biomass reaction’ that drains precursor metabolites from the system at their relative stoichiometries to simulate biomass production is selected by the objective function in order to predict growth rates. This reaction is scaled so that the flux through it is equal to the exponential growth rate (µ) of the organism.

Taken together, the mathematical representations of the metabolic reactions and of the phenotype define a system of linear equations. In flux balance analysis, these equations are solved using linear programming. Many computational linear programming algorithms exist, and they can very quickly identify optimal solutions to large systems of equations. The COBRA Toolbox¹¹ is a freely available Matlab toolbox for performing these calculations (Box 2).

Box 2: Tools for flux balance analysis.

FBA computations, which fall into the category of constraint-based reconstruction and analysis (COBRA) methods, can be performed using several available tools^24–26. The COBRA Toolbox¹¹ is a freely available Matlab toolbox (http://systemsbiology.ucsd.edu/Downloads/Cobra_Toolbox) that can be used to perform a variety of COBRA methods, including many FBA-based methods. Models for the COBRA Toolbox are saved in the Systems Biology Markup Language (SBML)²⁷ format and can be loaded with the function readCbModel. The E. coli core model²⁸ used in this Primer is included in the toolbox.

In Matlab, the models are structures with fields, such as ‘rxns’ (a list of all reaction names), ‘mets’ (a list of all metabolite names) and ‘S’ (the stoichiometric matrix). The function ‘optimizeCbModel’ is used to perform FBA. To change the bounds on reactions, use the function ‘changeRxnBounds’. The Supplementary Tutorial contains examples of COBRA toolbox code for performing FBA.

In the growth example, suppose we are interested in the aerobic growth of E. coli under the assumption that uptake of glucose, and not oxygen, is the limiting constraint on growth. This involves capping the maximum rate of glucose uptake to a physiologically realistic level (e.g. 18.5 mmol glucose gDW⁻¹ hr⁻¹) and setting the maximum rate of oxygen uptake to an unrealistically high level, so that is does not constrain growth. Then, linear programming is used to determine the flux through the metabolic network that maximizes growth rate, resulting in a predicted exponential growth rate of 1.65 hr⁻¹. (See Supplementary Tutorial for computer code).

Anaerobic growth of E. coli can be calculated by constraining the maximum rate of uptake of oxygen to zero and solving the system of equations, resulting in a predicted growth rate of 0.47 hr⁻¹. Studies have shown that these predicted aerobic and anaerobic growth rates agree well with experimental measurements¹².

Although growth is easy to experimentally measure, computational approaches such as flux balance analysis shine in simulations to predict metabolic reaction fluxes and simulations of growth on different substrates or with genetic manipulations. FBA does not require kinetic parameters and can be computed very quickly even for large networks, so it can be applied in studies that characterize many different perturbations. An example of such a case is given in Supplementary Example 6, which explores the effects on growth of deleting every pairwise combination of 136 E. coli genes to find double gene knockouts that are essential for survival of the bacteria.

FBA has limitations, however. Because it does not use kinetic parameters, it cannot predict metabolite concentrations. It is also only suitable for determining fluxes at steady state. Except in some modified forms, FBA does not account for regulatory effects such as activation of enzymes by protein kinases or regulation of gene expression, so its predictions may not always be accurate.

The many uses of flux balance analysis

Because the fundamentals of flux balance analysis are simple, the method has found diverse uses in physiological studies, gap-filling efforts and genome-scale synthetic biology³. By altering the bounds on certain reactions, growth on different media (Supplementary Example 1) or with multiple gene knockouts (Supplementary Example 6) can be simulated¹². FBA can then be used to predict the yields of important cofactors such as ATP, NADH, or NADPH¹³ (Supplementary Example 2).

Whereas the example described here yielded a single optimal growth phenotype, in large metabolic networks, it is often possible for more than one solution to lead to the same desired optimal growth rate. For example, an organism may have two redundant pathways that both generate the same amount of ATP, so either pathway could be used when maximum ATP production is the desired phenotype. Such alternate optimal solutions can be identified through flux variability analysis, a method that uses FBA to maximize and minimize every reaction in a network¹⁴ (Supplementary Example 3), or by using a mixed-integer linear programming based algorithm¹⁵. More detailed phenotypic studies can be performed such as robustness analysis¹⁶, in which the effect on the objective function of varying a particular reaction flux can be analyzed (Supplementary Example 4). A more advanced form of robustness analysis involves varying two fluxes simultaneously to form a phenotypic phase plane¹⁷ (Supplementary Example 5).

All genome-scale metabolic reconstructions are incomplete, as they contain ‘knowledge gaps’ where reactions are missing. FBA is the basis for several algorithms that predict which reactions are missing by comparing in silico growth simulations to experimental results^{18, 19}. Constraint-based models can also be used for metabolic engineering where FBA based algorithms, such as OptKnock²⁰, can predict gene knockouts that allow an organism to produce desirable compounds^{21, 22}.

This primer and the accompanying tutorials based on the COBRA toolbox (Box 2) should help those interested in harnessing the growing cadre of genome-scale metabolic reconstructions that are becoming available.

Figure 2.

The conceptual basis of constraint-based modeling and FBA. With no constraints, the flux distribution of a biological network may lie at any point in a solution space. When mass balance constraints imposed by the stoichiometric matrix S (1) and capacity constraints imposed by the lower and upper bounds (a_i and b_i) (2) are applied to a network, it defines an allowable solution space. The network may acquire any flux distribution within this space, but points outside this space are denied by the constraints. Through optimization of an objective function, FBA can identify a single optimal flux distribution that lies on the edge of the allowable solution space.