The Growing Scope of Applications of Genome-scale Metabolic Reconstructions: the case of E. coli

Abstract

The number and scope of methods developed to interrogate and use metabolic network reconstructions has significantly expanded since the first review of the use of constraint-based analysis in Nature Biotechnology some 14 years ago. In particular, the Escherichia coli metabolic network reconstruction has reached the genome-scale and has been broadly adapted. Specifically, it has been used to address a broad spectrum of basic and practical applications, falling into five main categories: 1) metabolic engineering, 2) model-directed discovery, 3) interpretations of phenotypic screens, 4) analysis of network properties, and 5) studies of evolutionary processes. With these accomplishments in hand, the field is expected to move forward and seek to further, i) broaden the scope and content of network reconstructions, ii) develop new and novel in silico analysis tools, and iii) expand in adaptation to uses of proximal and distal causation in biology. Taken together, these efforts will solidify a mechanistic genotype-phenotype relationship for microbial metabolism.

The availability of reconstructed metabolic networks for microorganisms has increased rapidly in recent years, and a growing number of research groups are reconstructing metabolic networks for organisms of interest¹. A network reconstruction represents a highly curated set of primary biological information for a particular organism and thus can be considered a biochemically, genetically and genomically structured (BiGG) data base^{1, 2}. A curated BiGG data base (de facto a knowledge base) can be converted into a mathematical format (i.e., an in silico model), and used to computationally assess phenotypic properties using a variety of computational methods^{2, 3}. Genome-scale reconstructions are thus, a key step in quantifying the genotype-phenotype relationship and can be used to ‘bring genomes to life’⁴. The purpose of this review is to summarize and classify applications utilizing the E. coli reconstruction to answer a broad spectrum of biological questions. These studies provide both an up to date review of the applications of constraint-based analysis and a guide to similar applications for the growing number of organisms for which genome-scale reconstructions are becoming available.

The Key Steps in the Formulation of Genome-scale Metabolic Network Models

The four key steps in the formulation and use of genome-scale models are illustrated in Fig. 1. Foundational to the process is the generation of global, or genome-scale, omics data. Omics data, along with legacy information (i.e., the ‘bibliome’) and small-scale detailed experiments, can be used to define the interactions amongst the biological components that are used to reconstruct organism-specific networks¹. Network reconstruction is also an iterative, on-going process that continually integrates data in a formal fashion as it becomes available⁵. As a result, a current and well curated genome-scale network reconstruction is a common denominator for those studying systems biology of an organism. An in depth review on the bottom-up reconstruction process can be found in² and will not be described here.

Figure 1. Formulation and use of GEMs as a four-step process.

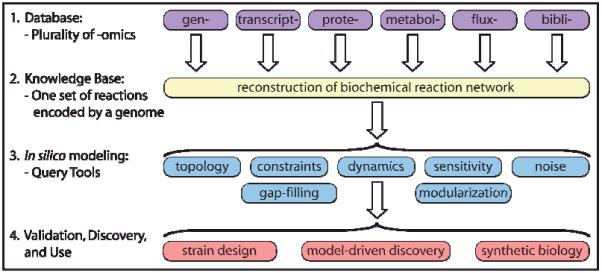
Formulation and use of GEMs as a four-step process. Step 1, the process is based on a variety of high-throughput data sets (i.e., omics data) and a comprehensive assessment of the literature (i.e., bibliomic data). Step 2, all of the data types are used to reconstruct the list of biochemical transformations that make up a network as well as their genetic basis¹. In principal, the network is unique. Step 3, the data contained in the reconstruction can be formally represented (i.e., in the form of matrices and logical statements) that can be mathematically characterized by a variety of methods. Step 4, the computational model enables a broad spectrum of applications, as reviewed in this article. Figure adapted from²

The arrow from step 2 to step 3 in Fig. 1 involves a somewhat subtle, but critical, transition. With the definition of systems boundaries and other details, a network reconstruction can be converted into a mathematical format that can be computationally interrogated and subsequently used for experimental design². Thus, a network reconstruction is converted into a Genome-scale Model (GEM)³. This arrow represents a bridge between the realms of high-throughput data/bioinformatics on one hand and systems science on the other. A network reconstruction (or BiGG knowledge base) is accessible to all and significant strides have been made to make computation with GEMs more readily accessible and free of use^6-11. This availability of both genome-scale reconstruction and GEMs has unleashed creativity in research groups around the world and resulted in the series of studies reviewed below.

The E. coli Metabolic Reconstruction

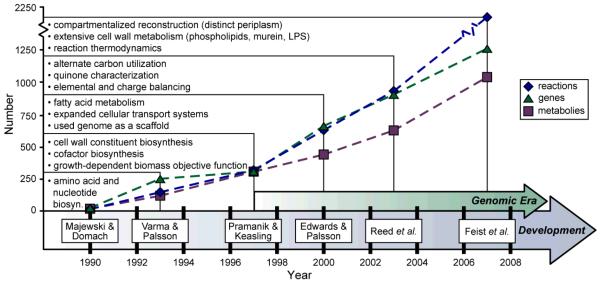
The 18-year history of reconstruction of the E. coli metabolic network (summarized in Fig. 2), has culminated in a network containing a total number of 1,260 ORF metabolic functions^12-19. This reconstruction represents 48% of the total experimentally annotated ORF functions in the E. coli genome (Table 1). It should be noted that the function of 92% of the 1,260 gene products have been experimentally verified. Reconstruction of the E. coli network has thus, approached an exhaustion of known metabolic gene functions and it is now being used in a prospective fashion to discover new metabolic capabilities (see below). The reconstruction of the E. coli metabolic network represents the best-developed genome-scale network to date and it has proven to be a platform for a variety of computational analyses. Three successive E. coli GEMs^17-19 have been used as the basis for over 60 detailed studies reviewed below.

Figure 2. The ongoing reconstruction of the E. coli metabolic network.

History of the E. coli metabolic reconstruction. Shown are six milestone efforts contributing to the reconstruction of the E. coli metabolic network. For each of the six reconstructions ^12-19, the number of included reactions (blue diamonds), genes (green triangles) and metabolites (purple squares) are displayed. Also listed are noteworthy properties that each successive reconstruction provided over previous efforts. For example, Varma & Palsson^{13, 14} included amino acid and nucleotide biosynthesis pathways in addition to the content that Majewski & Domach¹² characterized. The start of the genomic era⁹² (1997) marked a significant increase in included reconstruction components for each successive iteration. The reaction, gene and metabolite values for pre-genomic era reconstructions were estimated from the content outlined in each publication and in some cases, encoding genes for reactions were unclear.

Table 1.

Properties of the most current E. coli metabolic reconstruction¹⁹

Included Genes	1260	(28%) d
Experimentally Based Function	1161	(92%)
Computationally Predicted Function	99	(8%)
Unique Functional Proteins	1148
Multigene Complexes	167
Genes Involved in Complexes	415
Instances of Isozymes a	346
Reactions	2077
Metabolic Reactions	1387
Unique Metabolic Reactions b	1339
Cytoplasmic	1187
Periplasmic	192
Extracellular	8
Transport Reactions	690
Cytoplasm to Periplasm	390
Periplasm to Extracellular	298
Cytoplasm to Extracellular	2
Gene - Protein - Reaction associations
Gene Associated (Metabolic / Transport)	1294 / 625
Spontaneous / Diffusion Reactions c	16 / 9
Total (Gene Associated and No Association Needed)	1310 / 634	(94%)
No Gene Association (Metabolic / Transport)	77 / 56	(6%)
Exchange reactions	304
Metabolites
Unique Metabolites b	1039
Cytoplasmic	951
Periplasm	418
Extracellular	299

^atabulated on a reaction basis, not counting outer membrane non-specific porin transport

^breactions can occur in or between multiple compartments and metabolites can be present in more than one compartment

^cdiffusion reactions do not include facilitated diffusion reactions and are not included in this total if they can also be catalyzed by a gene product at a higher rate.

^doverall genome coverage based on 4453 total ORFs in E. coli; iAF1260 contains 48% of the ORFs in E coli that have been characterized experimentally (2403 ORFs)⁹⁹

Ask not what you can do for a reconstruction, but what a reconstruction can do for you

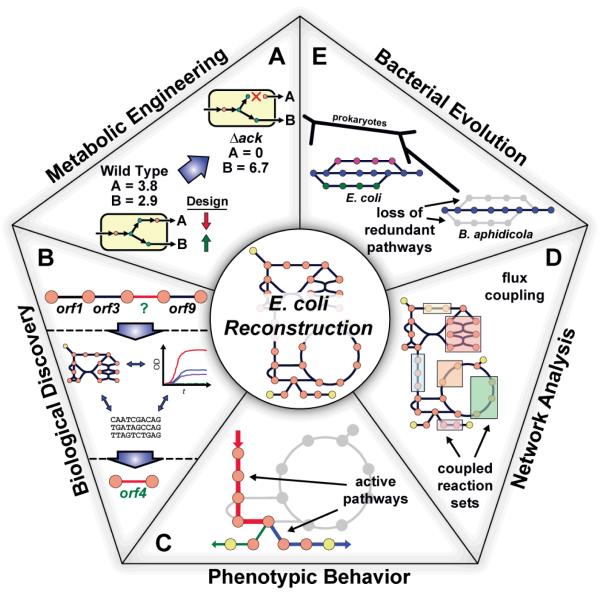
A growing number of research groups utilize the E. coli GEM for predicting, interpreting and understanding E. coli phenotypic states and function, in addition, the reconstruction itself has been used as a context for the interpretation of large amounts of experimental data. Applications of the E. coli GEM range from pragmatic to theoretical studies, and can be classified into five general categories (Fig. 3): 1) metabolic engineering^20-30; 2) biological discovery^31-37; 3) assessment of phenotypic behavior^{19, 38-63}; 4) biological network analysis^64-79; and 5) studies of bacterial evolution^80-82. The in silico methods used to probe the E. coli GEM in each study are summarized in Fig. 4. It should be noted that these methods perform an assessment of the solution spaces associated with the mathematical representation of a reconstruction²; these methods are categorized as unbiased and biased methods³. The latter category relies on an observer bias that is stated through an objective function (that is now beginning to be experimentally examined⁸³) and is utilized in most of the studies reviewed here use the general application of flux balance analysis (FBA)^84-86. Each category of application is now detailed, with emphasis on the first three that have the greatest practical utility.

Figure 3. Applications of the Genome-Scale Model (GEM) of E. coli.

Uses of the E. coli reconstructions divided into five categories. (A) A drawing of a predicted effect from a loss of function mutation in a simple system is shown. Metabolic engineering studies have investigated in silico strain design using E. coli metabolic reconstructions to overproduce desired products^20-30. (B) Recent studies utilizing the reconstruction in a prospective manner have aimed to use the current biochemical and genetic information included in the metabolic network along with additional data types to drive biological discovery, such as predicting genes encoding for orphan reactions^{32, 33, 35-37}. (C) Utilizing the reconstruction in phenotypic studies, computational analyses have examined gene^{19, 46, 51, 53, 63}, metabolite^{44, 60} and reaction^{39, 47, 48, 58} essentiality along with considering thermodynamics^{19, 40, 47, 49, 52, 54, 55, 57, 61} to make better predictions about the physiological state (i.e., the active pathways) of the cell for a given environmental condition. (D) The E. coli reconstructions have been used to analyze and interpret the intrinsic properties of biological networks. One example being finding coupled reaction activities⁶⁶ (as shown in the drawing) across different growth conditions. (E) Using the network reconstruction, evolutionary studies have examined the cellular network in the context of adaptive evolution events⁸¹, horizontal gene transfer^{80, 81} and minimal metabolic network evolution (as shown in the drawing)⁸².

Figure 4. Summary of the in silico methods utilized in published E. coli GEM studies.

This heatmap characterizes the incorporation of different computational methods into studies utilizing genome-scale models of E. coli. A dark box indicates that a particular method (one method per row) was utilized in a corresponding study (one citation per column); the frequency of usage of a particular method is given on the right. Studies were grouped into one of five general categories and studies examining phenotypic behavior were further divided into three subgroups. Studies that contributed new experimental growth data are also marked along the bottom offset row.

Applications of GEMs to metabolic engineering of E. coli

Through the application of computational methods that incorporate linear, mixed integer linear, and non-linear programming, it has been demonstrated that model-directed strain design can lead to increased metabolite production^20-30. In these studies, the E. coli GEM is principally used to analyze the metabolite production potential of E. coli and identify metabolic interventions needed to enable the production of the product of interest. Thus, E. coli strains have been systematically designed through in silico analysis to overproduce target metabolites such as lycopene^{23, 24}, lactic acid²⁵, ethanol²⁶, succinic acid^{27, 28}, L-valine²⁹, L-threonine³⁰, additional amino acids²¹, as well as diverse products from hydrogen to vanillin²². Select exemplary metabolic engineering applications will be described in more detail.

To increase the production of an already high producing strain, a systematic computational search was developed²⁴ to explore the E. coli metabolic network and report gene deletions that diverted metabolic flux towards the desired product. This process resulted a knock-out strain, that when constructed, showed a two-fold increase in the production of lycopene over the parental strain. In this analysis, the computational algorithm MOMA⁴¹ and the iJE660¹⁸ E. coli GEM were utilized to sequentially examine additive genetic deletions that would improve lycopene production while maintaining cell viability. Strain designs were constructed through genetic manipulations using the predicted modifications and it was found that this computational approach yielded the twofold increase in production rate over a previously engineered overproducing strain and an 8.5 fold increase over wild-type production harboring only a lycopene biosynthesis plasmid²⁴. Strain performance was evaluated by monitoring lycopene production through enzymatic assays and mutant growth rates. In addition, the strain designs identified computationally were compared to mixed combinatorial transposon mutagenesis and it was found that the maximum production observed could be designed solely using the systematic GEM aided computational method^{23, 24}. Furthermore, a deleterious effect was observed when targets identified in individual computational designs were combined in an attempt to achieve an overall more desirable phenotype. Thus, the overall systematic effects from individual designs were not additive and needed to be interpreted in the context of the entire network.

Two studies producing the amino acids L-valine²⁹ and L-threonine³⁰ have demonstrated the broad usage of GEM aided computation for strain design. In the first study, GEM aided modeling was employed in three different areas to increase the production of L-threonine to industrial titers³⁰. In one instance, in silico modeling was used to identify the optimal activity of a key enzymatic reaction towards maximum L-threonine production using a parametric sensitivity analysis that compared reaction activity to L-threonine production rate. The optimal activity prediction was subsequently used to tune the overexpression of the gene which encodes for this enzymatic reaction through comparison to base-line activity and the result was a production increase. This method proved to be vital to the success of this strain, as a previous transcription profiling guided attempt at overexpression resulted in an undesirable surplus of activity and was detrimental to L-threonine production. For the same strain, a GEM aided flux analysis in conjunction with mRNA expression data levels also guided the elimination of negative regulation on a gene which encoded for a reaction that channeled flux towards the final product. The third use of the GEM for the design of this strain occurred when an unwanted byproduct was observed in the culture medium and computation was utilized to divert the flux from this byproduct to L-threonine³⁰ through overexpression of another key gene encoded activity. The second analysis applied the systematic computational search algorithm previously described²⁴ to the updated E. coli GEM MBEL979⁷ (similar to the iJR904 GEM¹⁷) to improve L-valine production. The in silico analysis of beneficial knock-outs to divert flux towards the desired product once again resulted in a significant increase in the production of the desired metabolite over an existing overproducing strain; more than a two-fold increase in this case²⁹. Furthermore, in this same study, a number of additional metabolic engineering approaches to increase overproduction were performed (i.e., relieving feedback inhibition and regulation through attenuation, removing competing pathways, up-regulation of primary biosynthetic pathways, and overexpression of exporting machinery). When compared to each of the other individual strain modifications, the in silico GEM aided interventions resulted in the greatest increase in L-valine production²⁹. Taken together, these two studies demonstrate the broad applications for which GEMs can be utilized to design strains not only in a de novo fashion, but to make further improvements on strains through integrating and interpreting experimental data.

Several other strain designs utilizing E. coli GEMs have been reported. In a combined computational and experimental study, the bi-level optimization algorithm OptKnock²⁰ and iJR904¹⁷ were utilized to overproduce lactate in E. coli²⁵. The algorithm OptKnock optimizes two objective functions, biomass formation and product secretion, to produce strains that will couple the excretion of a desirable product to the growth rate. Using adaptive evolution with growth rate selection pressure, the lactate producing strains designed using OptKnock were found to possess this growth-coupling property. Growth rate, uptake and secretion rate profiles were the measures by which this property was examined and thus this study demonstrated the utility of adaptive evolution as a design tool⁸⁷. Additional noteworthy examples of GEM aided design are two studies which demonstrated^{27, 28} that GEM modeling using iJR904¹⁷ was beneficial to screen genes that were deemed to be important for succinate production. Combinatorial knock-outs that were predicted to be overproducers in silico were experimentally verified to display the same overproducing phenotype in vivo. Furthermore, this method had an advantage over using comparative genomics for strain design, which was also performed in one of the studies²⁷.

Taken together, a growing number of metabolic engineering studies demonstrate the use of GEMs to generate strain designs that are often non-intuitive and non-obvious. An excellent example of a non-intuitive strain improvement outlined in this section was when modeling was used to not only study the effect of a gene removal, but to tune the expression of a gene to an optimally predicted level, that when expressed too highly, was detrimental to product formation. Genome-scale reconstructions thus allow the examination and simulation of metabolism as an integrated network, circumventing the possible shortcomings of methods that rely on manual assessment of a limited number of interactions and fail to detect non-intuitive causal interactions. With the growing availability of organism and strain specific GEMs, applications for designing microbial strains for industrial production are expected to continue to grow. This growth expectation is in part based on the on-going reconstruction of additional cellular processes, such as transcriptional regulation and protein production. Computations based on genome-scale models are also beginning to influence other areas of industrial microbiology such as generation of renewable energy^88-90 and bioremediation⁸⁹.

Directing Discovery: GEM-driven discovery in E. coli

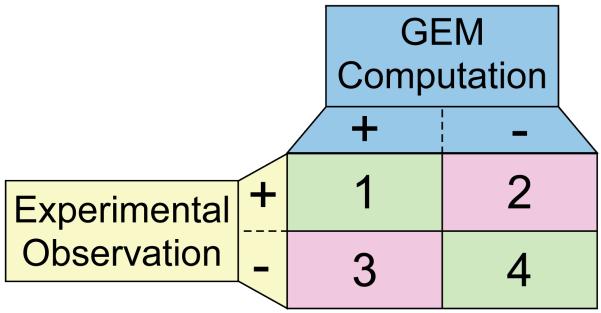
GEMs can provide a guide to biological discovery. This capability is based on comparison of computed and actual experimental outcomes. Given the fact that BiGG knowledge bases are incomplete and that they contain gaps⁹¹, they provide a context for systematic discovery of missing information. The comparison between computation and experiments are summarized in Fig. 5 highlighting how agreements and disagreements are analyzed.

Figure 5. Comparison of computation and experimental data: identification of agreements and disagreements.

The comparison of GEM computation and organism-specific experimental measurements identifies agreements and disagreements. The phenotypic outcomes are tabulated for genetic perturbations examined in a given environment (e.g., growth or no growth). A ‘+’ indicates that a given phenotype is not affected by the perturbation, and ‘−’ indicates it does. Each outcome of comparison has a different implication; 1: consistency check - a perturbation has no affect on the property being measured and modeling predicts the same; 4: validation - the perturbation affects the experimental outcome and modeling with the GEM predicts this outcome; 2: identification of missing content - when GEM modeling fails to predict the positive confirmation of the property being measured, this outcome indicates that there is missing content in the GEM and can lead to the identification of specific areas for biological discovery; 3: identification of errors, inconsistencies or missing context-specific information – a positive prediction for the measured property and an opposite experimental observation indicates a possible error in the current organism-specific knowledge or that additional context-specific information is lacking from the GEM or modeling method (e.g., transcriptional regulation).

The current area of most significant interest is to direct discovery efforts towards characterizing unknown ORFs in the E. coli genome. Ten years after the first release of the complete genome-sequence⁹², many unknown ORFs still exist in the E. coli genome (see Supplementary Table 1), with many of these likely to encode metabolic functions. ORF discovery utilizing GEMs also has significant potential to impact not only how new and less studied genomes are annotated, but to fill out the missing pieces in E. coli metabolism.

To address this challenge, algorithms have been developed to determine the probable gene candidates that fill knowledge gaps in the E. coli and other network reconstructions. These algorithms utilize global network topology and genomic correlations, such as genome context and protein fusion events³², as well as local network topology and/or phylogenetic profiles^{32, 33}. Similar tools has been developed which utilize mRNA coexpression⁹³ and which can evaluate more general metabolic pathway databases⁹⁴. In addition to these network topology-based methods, an optimization based procedure has also been developed to fill network gaps and evaluate reaction reversibility along with adding additional transport and intracellular reactions from databases of known metabolic reactions³⁶. These studies produce specific targets for drill-down experiments needed for confirmation of these computationally generated hypotheses.

Two recent studies have integrated a combined computational and experimental approach to aid the ORF discovery process in E. coli through utilizing the GEM and high-throughput phenotype data^{35, 37}. The first study utilized an iterative process³⁵ in which, 1) differences in modeling predictions and high-throughput growth phenotype data were identified, 2) potential missing reactions that remedy these disagreements were algorithmically determined, 3) bioinformatics was utilized to identify likely encoding ORFs, and 4) resulting targeted ORFs were cloned and experimentally characterized. Application of this process led to the functional characterization of eight ORFs that are involved in transport, regulatory and metabolic functions in E. coli³⁵. The discovery process was aided by a high-throughput growth phenotyping analysis and the genome-wide single-gene mutant collection⁹⁵, along with other characterization analyses such as targeted expression profiling. The second GEM-based analysis which resulted in ORF discovery utilized network topology to examine orphan reactions in the E. coli network (i.e., reactions known to exist in E. coli that have not been linked to an encoding gene) identified by the previously mentioned network topology-based gap-filling algorithms^{32, 33, 93}. The basic premise behind these algorithms is the utilization of an orphan reaction’s network neighbors as constraints to assign metabolic function. With the resulting tentative ORF assignment, biochemical characterization studies utilizing genetic mutants⁹⁵, analysis of growth under different substrate conditions, and expression data were all utilized to characterize and assign function to an orphan ORF that is responsible for a metabolic conversion that has been known for 25 years³⁷.

Further studies in this category of biological discovery applications (not focused on ORF identification) have utilized GEMs of E. coli to identify potential bottleneck reactions in the metabolic network³⁴ and as of yet uncharacterized transcription factor target interactions in E. coli³¹. The aforementioned study targeting the elucidation of regulatory and metabolic interactions in E. coli developed an iterative procedure focused on reconciling computational and experimental discrepancies stemming from high-throughput growth phenotype and gene expression data where selected expression changes were validated using RT-PCR³¹. With the advancement of high-throughput technologies to test the hypotheses generated from computational studies, these and similar algorithmic approaches are likely to continue to aid in the quest to achieve full functional annotation of the E. coli genome and its context-specific uses.

Phenotypic Functions: GEM aided assessment

The area where the E. coli GEMs has been most extensively utilized is for the examination and quantitative interpretation of metabolic physiology for wild-type, genetically perturbed and adaptively evolved strains of E. coli^{19, 38-63}. These efforts have implications in both the quantitative and qualitative understanding of physiological states of the cell. Furthermore, these efforts have examined E. coli physiology for a vast number of given genetic and environmental conditions and incorporation of the developed methods will have an impact on future design of biological systems and modeling approaches. A large subset of these studies of phenotypic behavior aim to utilize thermodynamic laws and information to refine phenotype predictions of GEMs and to incorporate metabolomic and fluxomic data into modeling^{19, 40, 47, 49, 52, 54, 55, 57, 61}.

A set of distinct computational methods using GEMs have been developed to determine the physiological state of E. coli after genetic perturbations^{41, 45, 50}. These studies have utilized ¹³C flux measurements and growth rate phenotype data to evaluate the predictability of the developed algorithms when compared to experimental observations. Whereas comparisons to flux data from wild-type and E. coli mutants reveals that the computational algorithm MOMA⁴¹ provides better predictions for transient growth rates (early post perturbation state), the algorithm ROOM⁴⁵ (and basic FBA) was found to be more successful in predicting final steady-state growth rates and overall lethality⁴⁵. These algorithms have been utilized, in addition to basic FBA, for genome-wide essentiality screens, as now outlined.

A range of computational studies have sought to understand phenotypes through determining the essential genes^{19, 46, 51, 53, 63}, metabolites^{44, 60} and reactions^{39, 47, 48, 58} in the E. coli metabolic network. A common benchmark for examining GEM predictive ability is to determine the agreement with growth phenotype data from knock-out collections of E. coli. Such studies will be further enabled by the recent availability of a comprehensive single-gene knock-out library for E. coli⁹⁵ (for example^{19, 53}). Implications for examining network essentiality in E. coli include determining network essentiality in similar organisms^{39, 48, 53, 58}, deciphering network makeup and enzyme dispensability (i.e., measures of robustness)^{46, 58, 60}, aiding in metabolic network annotation, validation and refinement⁴⁴, and even rescuing knock-out strains through additional gene deletions⁶³, to name a few. The predictive capability of the E. coli GEM, as demonstrated by these studies, has been instrumental in the adaptation of its use. One particular study examining knock-out phenotypes has demonstrated that the E. coli GEM was able to predict the outcomes of adaptively evolved strains to a high degree (78%) when knock-out E. coli strains were grown in a number of different substrate environments by examining growth rates at the beginning and end of adaptive evolution⁴³. This study represents a demonstration of a GEM’s ability to look at adaptive behavior (or ‘distal’ causation⁹⁶), in addition to immediate behavior (or ‘proximal’ causation⁹⁶). Predictive capability is expected to improve through examining growth behavior across a greater number of environments (additional phenotyping screens will be necessary) and with an increase of integration of additional cellular processes. Genetic perturbations have played a key role in the study of the genotype-phenotype relationship in biology and GEMs can be used to mechanistically interpret the results and predict the outcomes of such perturbations.

Incorporating thermodynamic information into E. coli GEMs has shown promise in narrowing predictions of allowable physiological states in a given environment^{19, 40, 47, 49, 52, 54, 55, 57, 61} and in identifying reactions likely to be subject to active allosteric or genetic regulation^{49, 54}. This field is progressing rapidly and should prove to increase the predictive capabilities of genome-scale modeling through the addition of governing thermodynamic physiochemical constrains. One particular analysis incorporating compound formation and reaction energies for the content of the GEM based on iJR904¹⁷ identified reactions that are likely to be effectively irreversible for any realistic metabolite concentration⁵⁴. The hypothesis was advanced that these reactions are candidates for cellular regulation in their respective pathways since enzyme regulation will likely be the dominant mechanism for control of flux through these reactions⁵⁴.

The addition of thermodynamics enables the analysis of metabolomic data in the context of a reconstruction. A study utilizing high-throughput metabolomic data and GEMs proposed likely regulatory interactions by deciphering the metabolite concentrations in the context of overall network functionality⁴⁹. Not only did the metabolomic data benefit computations by constraining the system using physiological measurements, but the computational predictions were also able to validate quantitative metabolomic data sets for consistency through providing a functional context to relate metabolite concentrations. This application is one example of how metabolomic data will directly influence modeling and metabolite concentration data is likely to greatly influence future metabolic modeling due to its intimate connection with GEM content. Similar work incorporating other quantitative values with FBA, such as metabolite concentrations⁵⁷ and flux ratios at branch points in metabolism⁵⁶ is also appearing.

Applying a different physiochemical constraint, molecular crowding, a framework has also been developed to incorporate spatial constraints into FBA⁵⁹. The functional states predicted with this method (i.e., FBA with molecular crowding, FBAwMC) and the E. coli GEM were validated against generated growth, substrate, and production rate data along with gene expression profiles and enzyme activity measures to demonstrate predictive accuracy, including substrate preferentiality, when examining growth in complex substrate environments^{59, 62}. Overall, these studies which incorporate reaction thermodynamics and additional cellular constraints should further narrow the range of allowable functional network states that can made based on stoichiometry alone and thus improve the utility of GEMs.

In addition to analyses on the genomic scale, a number of studies modeling the metabolism of E. coli on a smaller-scale have been performed. These analyses typically utilize models containing approximately 100 reactions or less and most often, focus on incorporating non-linear analysis to understand quantitative experimental data (e.g., isotopomer modeling). With the advancement of computational power and developed platforms, the networks that can be analyzed will grow in size⁹⁷. Given that the results produced from analyses such as isotopomer modeling have been shown to be highly dependent on the content of a reduced model, the logical starting point for building such models is the E. coli GEM⁹⁷. A number of noteworthy studies have been conducted with reduced models, but not detailed here as they are outside the scope of this review.

Systems Biology: Analysis of network properties

E. coli is generally viewed as having the most complete characterization of any model organism^{98, 99}. Due to the incorporation of thousands of metabolic interactions with relatively high reliability (e.g., 92% of the genes included in the latest reconstruction of E. coli¹⁹ have experimentally determined annotated functions⁹⁹, Table 1), validated genome-scale reconstructions of E. coli have become popular resources for the analysis of various network properties^64-79. The methods designed to analyze the underlying network structure of E. coli metabolism, some characterizing its interplay with regulation, have been developed to determine a number of physiological features. These features include the most probable active pathways and utilized metabolites under all possible growth conditions^{67, 69, 73, 75}, the existence of alternate optimal solutions and their physiological significance⁶⁵, conserved intracellular pools of metabolites⁶⁸, coupled reaction activities⁶⁶ and their relationship to gene co-expression⁷⁷, metabolite coupling⁷¹, metabolite utilization⁷², the organization of metabolic networks^{64, 76}, strategies for E. coli to incorporate metabolic redundancy⁷⁸, and the dominant functional states of the network across various environments^{70, 74, 79}. These findings are both driven by biased approaches utilizing FBA and biomass objective function optimization and by unbiased approaches such as graph-based analyses (see Fig. 4). One noteworthy study utilizing the GEM outlined network examined thousands of different potential growth conditions and observed a ‘high-flux backbone’ in E. coli that both carried high levels of flux across the different environmental conditions and was composed of a relatively small set of enzymatic reactions⁶⁷. This result can be of practical importance for synthetic biology efforts aimed towards manipulating flux within biological systems. Furthermore, this finding was hypothesized to be a universal feature of metabolic activity in all cells and was consistent with flux measurements from ¹³C labeling experiments⁶⁷.

The studies in this category have a common systems biology theme; namely the development and subsequent demonstration of methods that identify sets of reactions or metabolites with correlated or coordinated functions and systematic relationships. The systems biology that these methods enable and demonstrate has potential implications for, i) antimicrobial drug-target discovery^{68, 69}, ii) aiding the development of additional metabolic reconstructions^{66, 68}, iii) guiding genetic manipulations⁶⁶, iv) improving metabolic engineering applications^{67, 68}, and v) increasing the general understanding of biological network behavior^{65, 74, 77} and resilience⁷⁸. The role that the E. coli GEM has taken is a comprehensive and curated set of up to date metabolic knowledge; thus providing a scaffold for these large-scale computations.

Bacterial evolution: GEM aided studies of distal causation

The GEMs of E. coli have been used to examine the process of bacterial evolution^80-82. Specifically, the network reconstructions have been used to interpret adaptive evolution events⁸¹, horizontal gene transfer^{80, 81} and evolution to minimal metabolic networks⁸². These studies, which utilize the E. coli reconstruction as an organism-specific genetic and metabolic content database, and the corresponding GEM, have been able to provide insight into evolutionary events through combining known physiological data (e.g., in various environmental conditions) with hypotheses and in silico computation. Examining the evolution of minimal metabolic networks through simulation demonstrated that it was possible to predict the gene content of close relatives of E. coli by examining the necessity of genes and reactions in the overall context of the system functionality for a specific lifestyle⁸². Similarly, by re-examining network functionality in a number of different environments and through the utilization of comparative genomics, it was shown that recent evolutionary events (i.e., horizontal gene transfer) likely resulted from a response to a change in environment⁸¹. Furthermore, computational analysis led to the additional conclusion that these horizontal gene transfer events are more likely if the host organism contains an enzyme that catalyzes a coupled metabolic flux related to the transferred enzyme’s function^{80, 81}. Taken together, these studies demonstrate the importance of having high-quality curated reconstructions to enable studies on an organism’s response to environmental changes and for understanding the fundamental forces driving bacterial evolution.

Closing

The myriad of studies described in this review highlights the rapid development and use of genome-scale reconstruction and derived computational models to address a growing spectrum of basic research and applied problems. The experience with genome-scale reconstructions has demonstrated that they are a common denominator in the systems analysis of metabolic functions. With the recognition of its basic paradigms and a growing spectrum of practical uses enabled, there are several exciting challenges that this field now faces. Accordingly, further development is necessary, and three major areas where it will be influential are now discussed; i) network reconstructions and the reconstruction process, ii) computational BiGG query tools (i.e., modeling), and iii) application to proximal and distal causation in biology.

The scope of reconstructions is bound to grow, representing more and more BiGG knowledge in the structured format of a GEM⁹¹. Growth in scope in the near-term will on one front, involve the transcriptional and translational machinery of bacterial cells^100-102. Such an extension will enable a range of studies including the direct inclusion of proteomic data, fine graining of growth requirements and the explicit consideration of secreted protein products. Another expansion in scope in the near-term is the reconstruction of the genome-scale transcriptional regulatory network (TRN). Such reconstruction at the genome-scale is now enabled by new experimental technologies, such as ChIP-chip¹⁰³. Experimental interrogation of the currently available TRN suggests that we know about one-fourth to one-third of its content³¹, indicating that there is much to be discovered. Once reconstructed, the TRN will allow computational predictions of the context-specific uses of the E. coli genome and the responses of two-component signaling systems. Taken together, these near-term expansions in content will encompass the activity of apparently 2000 ORFs in the E. coli genome.

Mid-term expansions in scope will include the growth cycle, shock responses and additional cellular functions. Such a reconstruction should eventually be a comprehensive representation of the chemical reactions and transactions enabled by E. coli’s gene products. Longer-term reconstruction may begin to address the 3-dimensional organization of the bacterial cell. In particular, high-resolution ChIP-chip data on the DNA binding protein could enable the estimation of the topological arrangement of the genome, and potentially elucidate the structure of the cell wall and other cellular structures that will allow us a full 3-dimensional reconstruction of E. coli.

We now know how to represent BiGG data in either a stoichiometric format or in the form of causal relationships¹⁰⁴ and how to use them to perform several lines of computational inquiries. Computational query tools of GEMs will continue to be developed. New advances will likely include modularization methods, use of fluxomic data and eventually kinetics. As the scope and content of the reconstruction grows, the need to modularize its content becomes more pressing. Fine or course grained views of cellular processes are needed for different applications. For instance, as previously mentioned, current computational limitations force the reduction in a network for the analysis of isotopomer data, and a rational way to carry out such reduction is needed. Given the systemic nature of fluxomic data and its phenotypic relevance, there is a pressing need to increase the size of the networks that can be analyzed for experimental measurement and estimation of flux states. Finally, although detailed kinetic models of microbial functions may currently be mostly of academic interest, we will most likely be able to construct them in the mid-term based on advances with metabolomic and fluxomic data, in addition to the developments that are occurring with the incorporation of thermodynamic information. Such large-scale kinetic models are likely to differ from those resulting from traditional approaches for construction of kinetic models as, they come with different challenges.

As this review shows, the scope of applications of genome-scale reconstructions and GEMs is growing. Going forward, we wish to comment on three categories of applications: growth in coverage (i.e., gap-filling), engineering (i.e., synthetic biology), and the development of fundamental understanding. Growth in coverage will come through discovery of missing network components. For instance, the latest metabolic reconstruction, iAF1260, contains 14% blocked reactions¹⁹. This disconnected content means that we have knowledge gaps that have arisen due to characterization of individual gene products outside the context of a given physiological function (i.e., outside a defined pathway). Metabolomic profiling is one measure that will provide us with the missing upstream or downstream routes to such dead ends in the network. Also, an expansion of scope in modeling will allow for further investigation of network content, such as tRNA charging reactions that are currently in this blocked reaction set¹⁹. Furthermore, growing metabolomic data suggests that we are discovering the existence of several new metabolites. Pathways that include these metabolites need to be discovered. Methods exist to compute missing pathways between molecules¹⁰⁵ that can be applied to such data. Such pathways, in turn, will lead to experimental programs to discover novel gene functions and to validate or refute the existence of such pathways. Similarly, we expect that a number of the components of TRNs are missing, such as new sRNA molecules (see Supplementary Table 1). Clearly, well QC/QA’ed reconstructions will help in guiding us to comprehensive genome-scale representation of all major cellular processes in bacteria at the BiGG data level of resolution that, in turn, enables GEMs of growing coverage and resolution. The scope of this effort has been described as being; “… 10 times more ambitious and 100 times more important for mankind [compared with Human Genome Project]…” Hans Westerhoff¹⁰⁶.

Predictive models allow for design. In fact, in engineering, there is ‘nothing more useful that a good theory.’ As this review demonstrates, genomics and high-throughput technologies have enabled the construction of predictive computational models. The scope of such predictions is limited at the moment, but with the growing scope and coverage of genome-scale reconstructions and advancements in the development of computational tools, this scope will broaden. Not only will GEMs influence design in synthetic biology, but their influence in discovery of cellular content will provide a more complete picture of the environment (i.e., the parts list in the cell) in which future synthetically engineered constructs and circuits will be placed. The impact of GEMs on synthetic biology is thus likely to be notable; ranging from the provision of the cellular-context of a small-scale gene circuit design to engineering of the entire genome-scale network towards fundamentally new and useful (i.e., production) phenotypes.

Finally, we can speculate about the deep scientific impact that comprehensive predictive GEMs will have on our understanding of the living process. A comprehensive view of cellular functions will allow us to study the fundamental properties of both the underlying energy and information flows in living organisms. Such a view is likely to deeply affect our understanding of both distal and proximal causation in biology.