Promoter Prediction on a Genomic Scale—The Adh Experience

Abstract

We describe our statistical system for promoter recognition in genomic DNA with which we took part in the Genome Annotation Assessment Project (GASP1). We applied two versions of the system: the first uses a region-based approach toward transcription start site identification, namely, interpolated Markov chains; the second was a hybrid approach combining regions and signals within a stochastic segment model. We compare the results of both versions with each other and examine how well the application on a genomic scale compares with the results we previously obtained on smaller data sets.

Within the next year, the complete genomes of several eukaryotic organisms will be stored in the databases, and we must face the challenge that the annotation process is getting more and more complicated for higher eukaryotes such as Drosophila melanogaster. The first draft of the annotation of a newly sequenced genome is usually limited to the coding part of a gene, but a complete annotation should also contain the positions of the transcription start sites (TSSs), as most of the regulatory elements involved in gene expression are located in the promoter region upstream or close to the TSS.

The untranslated region between transcription and translation start site, the 5′ UTR region, can span up to several kilobases in higher eukaryotes—it is an average of almost 2000 bases for the TSS set compiled in the paper by Reese et al. (2000). Therefore, we cannot simply take the sequence upstream from the start codon. Methods that aim at the identification of regulatory elements in the upstream regions of coexpressed genes such as described by van Helden et al. (1998) have been shown to deliver promising results for the yeast genome, which has very short UTRs, but they will be hard to apply when the annotation only consists of the coding part of a gene. Of course, TSS identification is alleviated by full-length cDNA sequencing projects; but the sequencing always starts at the 3′ end of a gene, and we need additional methods to confirm the 5′ end of the sequences or to hunt for rarely expressed genes that are not contained in the libraries at all. We are in a desperate need to at least get a good guess where the TSS (and thus the promoter region) is located, or we will start looking for the needle in the wrong haystack.

The only available evaluation of promoter prediction tools on genomic DNA was performed by Fickett and Hatzigeorgiou (1997). At that time, no extensive unstudied genomic sequences were available for complex eukaryotic organisms, and the authors performed their evaluation on a set of 18 newly released vertebrate sequences, the longest of which comprised <6000 bp. It was, therefore, a great challenge to see how well a recently developed promoter recognition program performs on a genomic scale and what we can conclude for the annotation of complex eukaryotic genomes. We will briefly review the two versions of our promoter recognition system that we applied, discuss in detail the results that were described in the paper of Reese et al. (2000), and finally draw conclusions on the state of promoter prediction in general.

METHODS

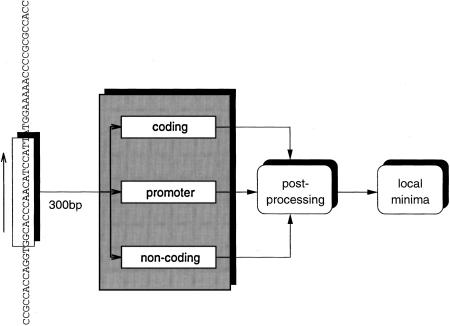
MCPromoter (Ohler et al. 1999a) is a statistical method to look for eukaryotic polymerase II TSSs in genomic DNA. It consists of a model for promoter sequences and a mixture model for nonpromoter sequences, containing submodels for coding and noncoding sequences. To localize TSSs, a window of 300 bases is shifted over the sequence in steps of 10 bases (see Fig 1). At every position, the difference between the log likelihood of the promoter and the nonpromoter model is computed. The resulting plot describes the regulatory potential over the sequence and is smoothed by a median and hysteresis filter (see Duda and Hart 1973) to eliminate single false predictions and reduce the high number of neighboring minima that are due to noise. The program then makes a prediction for each local minimum below a prespecified threshold (see Fig. 2 for an example).

Figure 1.

Structure of the MCPromoter system. A window of 300 bases is shifted over the sequence in steps of 10 bases, and the content is evaluated with the promoter and nonpromoter models. The difference between the promoter and the nonpromoter log likelihood is stored. After postprocessing, the local minima are reported as TSS predictions.

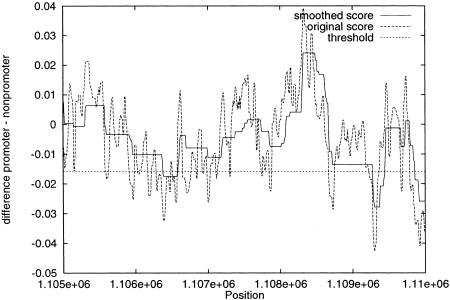
Figure 2.

Application of MCPromoter v. 2.0 on a 5000-bp long sequence of the Adh region containing the TSS for the Adh gene. We show the nonsmoothed as well as the smoothed output of the system. The strongest local minimum corresponds to the annotated TSS of Adh.

We applied two versions of MCPromoter on the Adh sequence (for a comprehensive description of the annotated genes, see Ashburner et al. 1999). The difference between the two versions lies in the structure of the promoter model, and we wanted to explore how well our more recent modeling approach improved on the recognition of TSSs. Version 1.1 of MCPromoter is a content-based approach and uses a single interpolated Markov chain (IMC) of 5th order to model promoter sequences. As such, the model does not rely on a priori knowledge about the structure of the promoters but judges the overall composition of the sequence. For the two nonpromoter components for coding and noncoding sequences, we also chose IMCs. Related methods were described by Audic and Claverie (1997) and Hutchinson (1996). In the figures of the GASP paper by Reese et al. (2000), version 1.1 is denoted by LMEIMC (Lehrstuhl für Mustererkenung–Interpolated Markov Chains). The submodels are trained using the discriminative maximum mutual information (MMI) approach. In contrast to the standard maximum likelihood (ML) parameter estimation, MMI maximizes the probability of the decision for the correct sequence class and therefore also takes negative samples into account (Ohler et al. 1999b).

In version 2.0, we replaced the single Markov chain promoter model by a more sophisticated stochastic segment model (SSM) that consists of five states for specific segments within eukaryotic promoter sequences: the upstream region, the TATA box, a spacer, the initiator, and the downstream region (Ohler et al. 2000). With this approach, we obtain more accurate statistics for those segments, combining states for regions such as the one for the upstream segment with states for signals such as the one for the TATA box. Hybrid approaches that exploit statistics for several regions were described previously by Solovyev and Salamov (1997) and Zhang (1998). Version 2.0 of MCPromoter is denoted by LMESSM in the GASP overview paper (Reese et al. 2000).

Both versions were trained on the same representative data set consisting of D. melanogaster promoter and nonpromoter sequences of 300 bases in length, obtained at http://www.fruitfly.org/sequence/drosophila-datasets.html. Cross-validation classification experiments on this data (described in Ohler et al. 2000) gave a recognition rate of 27.9% for version 1.1 and 58.8% for version 2.0 at the very low false-positive rate of 1%. We used the system at this threshold for the evaluation of the Adh region.

RESULTS

According to the results described by Reese et al. (2000), version 1.1 of MCPromoter could identify 26 (28.2%) TSS with a false-positive rate of 1/2633 bases, and version 2.0 successfully located 31 promoters (33.6%) with the slightly higher false-positive rate of 1/2437 bases. This compares well with the results described in the comparison of promoter recognition algorithms in vertebrate DNA (Fickett and Hatzigeorgiou 1997), especially considering the smaller amount of available training data for the organism of D. melanogaster.

Sixteen of the 26 predictions made by version 1.1 are contained in the set of 31 predictions from version 2.0. Considering that the methods are closely related, this number is somewhat small and could be due to the different training algorithms (MMI vs. ML parameter estimation). A negatively surprising fact for us was the small improvement of the performance that version 2.0 achieved in comparison with the earlier version. With the results from cross-validation experiments on the representative set of promoters and nonpromoters in mind, we expected the new version to localize ∼20%–30% more TSSs at the same rate of false predictions.

We also examined the accuracy of the predictions. Nine predictions from version 1.1 are located within ±40 bases of the annotated start site (mean distance 202 bases), as opposed to 13 close predictions and a mean distance of 166 bases of the predictions obtained by version 2.0. As we do not know exactly how far the true TSS differs from our current annotation, this number is encouraging to us. Concerning the identification of the exact position of the start sites, version 2.0 is clearly more successful than version 1.1.

DISCUSSION

To get a better understanding why the performance of version 1.1 and version 2.0 did not differ very much from each other, we looked at the system performance without the smoothing postprocessing steps (Table 1). When we look at the results without postprocessing, it becomes obvious that the new version is a great improvement and primarily, that the post processing is responsible for version 2.0 not performing as well as expected. The smoothing was designed specifically for a region-based approach like the Markov chains applied in version 1.1 and works less well on a hybrid approach like version 2.0 where the promoter region is divided into several distinct segments.

Table 1.

Influence of Postprocessing Methods on the Performance of the Promoter Predictors

Postprocessing	Version 1.1		Version 2.0
recognized promoters	false positive rate per base	recognized promoters	false positive rate per base
None	47	1/450	57	1/719
Hysteresis	33	1/1833	43	1/1653
Median and hysteresis	26	1/2633	31	1/2437

Shown are the results without any postprocessing (i.e., every local minimum is used as prediction), after hysteresis smoothing, and after both median and hysteresis smoothing. The postprocessing operations reduce the number of false positives for both versions, but it becomes clear that the effect is much better for the pure region-based approach of v. 1.1. 

A rough extrapolation of the cross-validation results at the currently used threshold (1% false positives) leads to a worst-case false-positive rate of 1/2000 bases. From the nonsmoothed results it becomes clear now that this is obviously not met by reality. A possible explanation is that the available training data is still not representative enough. It certainly contains too little noncoding data, and the available promoter set has a bias toward TATA box containing promoters.

We already realized a number of plans to improve the model performance of version 2.0. The first idea was to include reverse sequence models for the nonpromoter states, as we scan both directions of the sequence independently. It is well known that the reverse sequences of genes still resemble the true genes on the opposite strand and that the statistics of reverse exon and intron sequences are close to the forward sequence—hence, the problem of shadow gene predictions. Nevertheless, we added two new states for reverse exon and intron sequences to have a more accurate model for the nonpromoters.

In a second step, we increased the amount of training data. For the Adh experiment, we took the model that performed best on three cross-validation experiments and left out one third of the available data to see whether our predictions on this set were met by reality. Instead, we took the whole set and determined the 1% false-positive threshold by choosing the mean threshold of the three experiments.

Finally, we replaced the median and hysteresis filters by a simple approach to allow only one prediction below the threshold within 300 bases (the model size). A similar smoothing approach is implicitly carried out by the gene finders with integrated promoter predictors: They choose the best prediction in accordance with the model topology that allows for only one prediction before the start codon. But the question remains whether some predictions close to the best one might correspond to alternative TSSs, and whether such a reduction actually filters out useful information.

As a result of these improvements, 20 predictions instead of 13 are now located within ±40 bases from the putative start site, and we could increase the performance to 34 identified promoters with a false-positive rate of 1/3000 bases.

Conclusions and Outlook

The analysis of the Adh region clearly showed that promoter recognition by itself, without context information, still delivers too many false positives to be practically useful on a genomic scale. There is still a lot of room for improvement—we think of parallel states for the TATA box region and the downstream region, discriminative training of the segment model, and a nonlinear combination of the segment likelihoods. But the overall picture will maybe not change in the near future when we exploit only the primary sequence. We will see whether the usage of other features such as DNA bendability (Pedersen et al. 1998) can lead to the necessary improvement.

From a different point of view, though, the rate of one false positive in 3 kilobases seems reasonable if one has already an idea where the coding part of the gene is. This information can be provided both by alignments of cDNA to genomic sequence and ab initio gene finding. We therefore envision a promoter recognition system used within a gene finder that also incorporates EST and cDNA alignment information to extend the coding region on the 5′ end. The accuracy of the TSS localization of MCPromoter is good enough to then use such a preliminary annotation of the TSS for the analysis of upstream regions of coexpressed genes.

Both versions of the MCPromoter system can be accessed via the World Wide Web at http://www5.informatik.uni-erlangen.de/HTML/English/Research/Promoter.