GeneID in Drosophila

Abstract

GeneID is a program to predict genes in anonymous genomic sequences designed with a hierarchical structure. In the first step, splice sites, and start and stop codons are predicted and scored along the sequence using position weight matrices (PWMs). In the second step, exons are built from the sites. Exons are scored as the sum of the scores of the defining sites, plus the log-likelihood ratio of a Markov model for coding DNA. In the last step, from the set of predicted exons, the gene structure is assembled, maximizing the sum of the scores of the assembled exons. In this paper we describe the obtention of PWMs for sites, and the Markov model of coding DNA in Drosophila melanogaster. We also compare other models of coding DNA with the Markov model. Finally, we present and discuss the results obtained when GeneID is used to predict genes in the Adh region. These results show that the accuracy of GeneID predictions compares currently with that of other existing tools but that GeneID is likely to be more efficient in terms of speed and memory usage. GeneID is available at http://www1.imim.es/∼eblanco/GeneId.

GeneID (Guigó et al. 1992) was one of the first programs to predict full exonic structures of vertebrate genes in anonymous DNA sequences. GeneID was designed with a hierarchical structure: First, gene-defining signals (splice sites and start and stop codons) were predicted along the query DNA sequence. Next, potential exons were constructed from these sites, and finally the optimal scoring gene prediction was assembled from the exons. In the original GeneID the scoring function to optimize was rather heuristic: The sequence sites were predicted and scored using position weight matrices (PWMs), a number of coding statistics were computed on the predicted exons, and each exon was scored as a function of the scores of the exon defining sites and of the coding statistics. To estimate the coefficients of this function a neural network was used. An exhaustive search of the space of possible gene assemblies was performed to rank predicted genes according with an score obtained through a complex function of the scores of the assembled exons.

During recent years GeneID had some usage, mostly through a now nonfunctional e-mail server at Boston University (geneid@darwin.bu.edu) and through a WWW server at the IMIM (http://www1.imim.es/geneid.html). During this period, however, there have been substantial developments in the field of computational gene identification (for recent reviews, see Claverie 1997; Burge and Karlin 1998; Haussler 1998), and the original GeneID has become clearly inferior to other existing tools. Therefore, some time ago we began developing an improved version of the GeneID program, which is at least as accurate as other existing tools but much more efficient at handling very large genomic sequences, both in terms of speed and usage of memory. This new version maintains the hierarchical structure (signal to exon to gene) in the original GeneID, but we have simplified the scoring schema and furnished it with a probabilistic meaning: Scores for both exon-defining signals and protein-coding potential are computed as log-likelihood ratios, which for a given predicted exon are summed up into the exon score, in consequence also a log-likelihood ratio. Then, a dynamic programming algorithm (Guigó 1998) is used to search the space of predicted exons to assemble the gene structure (in the general case, multiple genes in both strands) maximizing the sum of the scores of the assembled exons, which can also be assumed to be a log-likelihood ratio. Execution time in this new version of GeneID grows linearly with the size of the input sequence, currently at ∼2 Mb per minute in a Pentium III (500 MHz) running linux. The amount of memory required is also proportional to the length of the sequence, ∼1 megabyte (MB)/Mb plus a constant amount of ∼15 MB, irrespective of the length of the sequence. Thus, GeneID is able to analyze sequences of virtually any length, for instance, chromosome size sequences.

In this paper we describe the “training” of GeneID to predict genes in the genome of Drosophila melanogaster. In the context of GeneID training means essentially computing PWMs for splice sites and start codons, and deriving a model of coding DNA, which, in this case, is a Markov model of order 5, similar to the models introduced by Borodovsky and McIninch (1993). Therefore, in the following sections, we describe the training data set used, particularly our attempt to recreate a more realistic scenario to train and test GeneID by generating semiartificial large genomic contigs from single-gene DNA sequences, and we briefly describe the main features of GeneID for D. melanogaster. Then, we present the results obtained in the training data set when different schemas are used to compute scores for sites and coding potential, and the results obtained on the D. melanogaster Adh region when the optimal scoring schema in the training set is used to predict genes in this region.

METHODS

Data Sets

We have merged the sets of 275 multi- and 141 single-exon sequences provided by Martin Reese (Reese et al. 2000) as a set of known D. melanogaster gene-encoding sequences into the unique MR set. From the MR set we inferred PWMs for splice sites and start codons, and the Markov model of order 5 for coding regions. The MR set contains only single-gene sequences. To assess the accuracy of the predictions in a more realistic scenario, we have randomly embedded the sequences in the MR set in a background of artificial random intergenic DNA as described (R. Guigó, P. Agarwal, J.F. Abril, M. Burset, and J.W. Fickett, in prep.). Thus, a single sequence of 5,689,206 bp embedding the 416 genes in the MR set has been used to evaluate the accuracy of the predictions. The sequence, and the coordinates of the embedded exons are available at http://www1.imim.es/∼gparra/GASP1.

GeneID

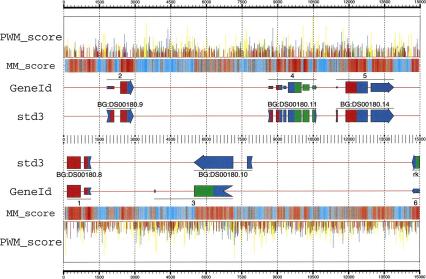
As outlined, GeneID for D. melanogaster uses PWMs to predict potential splice sites and start codons. Potential sites are scored as log-likelihood ratios. From the set of predicted sites (which includes, in addition, all potential stop codons), the set is built of all potential exons. Exons are scored as the sum of the scores of the defining sites, plus the log-likelihood ratio of the Markov model for coding sequences. Finally, the gene structure is assembled from the set of predicted exons, maximizing the sum of the scores of the assembled exons. The procedure is illustrated in Figure 1, which shows the GeneID predictions in a small region of the Adh sequence.

Figure 1.

Predictions obtained by GeneID in the region 462500–477500 from the Adh sequence, compared with the annotation in the standard std3 set. In a first step, GeneID identifies and scores all possible donor (blue) and acceptor (yellow) sites, start codons (green), and stop codons (red) using PWMs—the height of the corresponding spike is proportional to the site score. A total of 4704 sites were generated along this 15,000-bp region by GeneID, only the highest scoring ones are displayed here. In a second step, GeneID builds all exons compatible with these sites. A total of 11,967 exons were built in this particular region (not displayed). Exons are scored as the sum of the scores of the defining sites, plus the score of their coding potential measured according with a Markov model of order 5. The coding potential is displayed along the DNA sequence (MM_score). Regions strong in red are more likely to be coding than regions strong in blue. From the set of predicted exons, the gene structure is generated, maximizing the sum of the scores of the assembled exons. Exons assembled in the predicted genes are drawn with heights proportional to their scores. A two-color code is used to indicate frame compatibility: Two adjacent exons are frame compatible if the right half of the upstream exon (the remainder) matches the color of the left half of the downstream exon (the frame). Data are from the gff2ps program (available at http://www1.imim.es/∼jabril/GFFTOOLS/GFF2PS.html). The input GFF and the configuration files required for gff2ps to generate this diagram can be found at http://www1.imim.es/∼gparra/GASP1.

Predicting and Scoring Sites

Actual splice sites, and start codons were extracted from the MR set.

Donor Sites

The MR set contains 757 donor sites. From them, a frequency matrix P was derived from position −3 to +6 around the exon–intron boundary, with position 0 being the first position in the intron. P_ij is the probability of observing nucleotide i[i ∈(A,C,G,T)] at position j [j ∈(−3,…,+6)] in an actual donor site. The positional frequency Q of nucleotides in the region −3 to +6 around all dinucleotides GT was also computed (with position 0 being the position corresponding to the nucleotide G in the GT dinucleotides.) Then, a PWM for donor sites D was calculated as

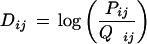1

PWMs for acceptor sites, A, and start codons, S, were obtained in a similar way. These matrices can be obtained from http://www1.imim.es/∼gparra/GASP1.

PWMs can be used to score each potential donor site (GT), acceptor site (AG), and start codon (ATG), along a given sequence. The score of a potential donor site, S = s₁s₂ . . . s₁₀ within the sequence is computed as

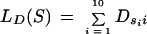2

This is the log-likelihood ratio of the probability of observing this particular sequence S in an actual site versus the probability of observing S in any false GT site. Similar scores are computed for acceptor sites (L_A) and start codons (L_B).

Predicting and Scoring Exons

GeneID distinguishes four types of exons: (1) Initial ORFs, defined by a start codon and a donor site; (2) internal ORFs, defined by an acceptor site and a donor site; (3) terminal ORFs, defined by an acceptor site and a stop codon; and (4) single ORFs, defined by a start codon and a stop codon. This corresponds to intronless genes. GeneID constructs all potential exons that are compatible with the predicted sites. (Only the five highest scoring donor sites within frame are considered for each start codon and acceptor site.)

Coding Potential

All exon and intron sequences were extracted from the MR multiexon data set. A Markov model of order 5 was estimated to model both exon and intron sequences, that is, we estimated the probability distribution of each nucleotide given the pentanucleotide preceding it in exon and intron sequences. From the exon sequences we estimated this probability for each of the three possible frames, building the transition probability matrices F¹, F², F³. F^j (s₁s₂s₃s₄s₅s₆) is the observed probability of finding hexamer s₁s₂s₃s₄s₅s₆ with s₁ in codon position j, given that pentamer s₁s₂s₃s₄s₅ is with s₁ in codon position j. An initial probability matrix, I^j, was estimated from the observed pentamer frequencies at each codon position. From the intron sequences a single transition matrix was computed F₀, as well as a single initial probability matrix, I₀. Then, for each hexamer h and frame j a log-likelihood ratio was computed:

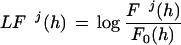3

as well as for each pentamer p and frame j

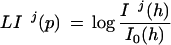4

The distributions F and I can be obtained from http://www1.imim.es/∼gparra/GASP1.

Then, given a sequence S of length l in frame j, the coding potential of the sequence is defined as

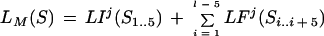5

where S_i..k is the subsequence of S starting in position i and ending in position k.

The score of a potential exon, S, L_E(S) defined by sites s_a (start/acceptor) and s_d (stop/donor) is computed as

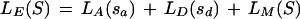6

This score can be assumed to be the log-likelihood ratio of the probability of finding such sites and sequence composition given an actual exon over the probability of finding it on a random sequence bounded by AG and GT dinucleotides. Because L_M is the logarithm of the ratio of the probability of the sequence under the coding model over the probability under the noncoding model (not under a random model), L_M only approximates such a log-likelihood ratio.

Assembling Genes

GeneID predicts gene structures, which can be multiple genes in both strands, as sequences of frame-compatible nonoverlapping exons. A minimum intron length of 40 bp and a minimum intergenic distance of 300 bp are enforced. If a gene structure, g, is a sequence of exons, e₁, e₂,…e_n, a natural scoring function is

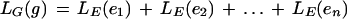7

L_G (g) can be approximately interpreted as the log-likelihood ratio of the probability of the defining sites and the hexamer composition of the resulting product given a gene sequence, over this probability given a nongene sequence. In GeneID, the gene structure predicted for a given sequence is the gene maximizing L_G(g), among all gene structures that can be assembled from the set of predicted exons for the sequence. Because the number of approximations made, the simple sum of log-likelihood ratios does not produce necessarily genes with the correct number of exons (if L_E is positive, the genes tend to have a large number of exons; if L_E is negative, the genes tend to have a small number of exons), and the score of the exons is corrected by adding a constant, IW. Thus, given an exon, e, the actual score of e is

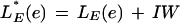8

To estimate this constant, a simple optimization procedure was performed. Genes were predicted in the training semiartificial genomic sequence for different values of IW, and the value was chosen that maximized the correlation coefficient between the actual and predicted coding nucleotides. This value was found to be IW = −7.

RESULTS

Training GeneID

We tested two additional models of coding DNA before deciding for a Markov model of order 5, a Codon usage model, and a model that combined a Markov model of order 1 of the translated amino acid sequence and a Codon preference model (see Guigó 1999 for details on these models). In both cases, log-likelihood ratios were obtained in a similar way to the Markov model log-likelihood ratios (see Methods). For instance, in the case of the Codon usage model, for each triplet s, we estimated the probabilities of the codon s in coding sequences, U(s) and the probability of the triplet in noncoding sequences, U₀(s), and built the log-likelihood ratio

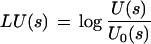Then, given a sequence, S, of length l in frame 0 (i.e., S₁S₂S₃ form a codon), the coding potential of the sequence is computed as

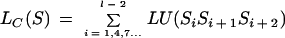The models were inferred from the MR set, as the Markov model was, and tested on the MR-set sequences embedded in the large artificial genomic contig. To test the models, genes were predicted using GeneID, but exons were scored using only the scores derived under the coding DNA model (i.e., the scores from the exon defining sites were ignored). Predictions were compared with the annotated genes, and the usual measures of accuracy were computed (Reese et al. 2000). Results are shown in Table 1. For comparison, we also show the results when only the scores of the sites are used to score the exons. As it is possible to see the Markov model of order 5 produces more accurate results than the other models, it was chosen to be used in GeneID to predict the genes in the Adh region. As described above, GeneID scores the exons as the sum of the scores of the sites and the Markov model score. Results under this scoring schema, the one effectively used to predict genes in the Adh region, are also given in Table 1.

Table 1.

Testing Different Models of Coding DNA in the Training Semiartificial Genomic Sequence

	Base level			Exon level
Sn	Sp	CC	Sne	Spe	SnSp	ME	WE
Sites–PWM	0.23	0.65	0.37	0.17	0.13	0.15	0.72	0.79
CU	0.91	0.88	0.88	0.46	0.43	0.45	0.21	0.27
DIA + CP	0.91	0.88	0.89	0.46	0.46	0.46	0.23	0.25
MM-5	0.93	0.90	0.91	0.54	0.51	0.52	0.18	0.24
PWM and MM-5	0.92	0.92	0.92	0.75	0.71	0.73	0.12	0.18

(CU) Codon usage model; (DIA+CP) combination of a Markov model of order 1 of the translated amino acid sequence and a Codon preference model; (MM-5) Markov model of order 5. Genes have been predicted using GeneID, but in each case exons have been scored on the basis solely of the coding DNA model, ignoring the contribution of the exon-defining sites. Predicted genes have been compared with the annotated ones, and the usual measures of accuracy computed. Results obtained when exons are scored as a function only of the scores of the defining sites are also given (Sites–PWM). Finally, we report the results on accuracy when the exons are scored as the sum of the Markov model score and the scores of the exon-defining sites. This is the scoring schema used by GeneID when attempting to predict genes in the Adh region. 

Results in the Adh Region

Table 2 shows the results when GeneID, with the parameters estimated above, is used to predict genes in the Adh region. Both the results originally submitted to the Genome Annotation Assessment Project (GASP) and the results obtained with the currently available version of GeneID are given (see Discussion). In addition, we provide information on execution time and memory requirements of GeneID to analyze the Adh region. The detailed exon coordinates of the predictions by GeneID can be found at http://www1.imim.es/∼gparra/GASP1.

Table 2.

Accuracy of GeneID in the Adh Region

	Base level		Exon level				CPU time (sec)	Memory (MB)
	Sn	Sp	Sn	Sp	ME	WE
(std1)	(std3)	(std1)	(std3)	(std1)	(std3)
GeneID, submitted (1)	0.48	0.84	0.27	0.29	54.4	47.9	74	∼500
GeneID, submitted (2)	0.86	0.82	0.59	0.34	21.0	48.0	74	∼500
GeneID, current	0.96	0.92	0.70	0.62	11.0	17.0	83	18.11

The std1 annotation data set was used to evaluate sensitivity; the std3 annotation data set to evaluate specificity, as in GASP1 (see Reese et al. 2000). Discrepancies between the accuracy of the submitted predictions, both the initial ones (1) and the corrected (2), and the accuracy of the predictions obtained with the current version of GeneID are due to a number of errors during the process of generating the submitted predictions (see Discussion). The decrease in the amount of memory required to obtain the predictions is due to algorithmic developments occurring after GASP1. 

DISCUSSION

The results presented above indicate that the current version of GeneID shows an accuracy, as measured by the GASP contest, comparable to the accuracy of the programs based on hidden Markov models (HMMs), which in GASP exhibited the highest accuracy. In favor of GeneID is the simplicity and modularity of its structure, which, as a consequence, is likely to make the program more efficient in terms of speed and memory usage. In GeneID the gene identification problem is stated as a one-dimensional chaining problem for which more efficient algorithms may be designed than for an aligment problem, as gene identification is implicitly formulated in HMMs. Against GeneID is the somehow less rigorous probabilistic treatement of the scoring schema. For instance, we are currently unable to justify the “magic number” (IW, see Methods), which needs to be added to the exon scores to obtain accurate predictions.

GeneID submitted rather poor predictions to GASP (see Table 2). Two bugs in the version of the program under development at that time were to blame. They were discovered and a second prediction submitted (see Table 2). After GASP we changed a rather complex schoring schema to the simpler and more natural schema described in Methods, which resulted in higher accuracy. This is the scoring schema currently in use in GeneID.

Although currently fully functional, we are still developing GeneID further. Our short-term plans include, among others, to train GeneID to predict genes in the human and the Arabidopsis thaliana genomes and to include the possibility of incorporating the results of database searches—both ESTs and proteins—in the GeneID prediction schema, which can be done rather naturally. The possibility of including external evidence to “force” known genes or exons into the prediction is already included in the working version of GeneID. This may be useful for reannotation of very large genomic sequences. Finally, the current structure of GeneID can be highly parallelized, and we are also working in this direction.