Gapped Spectral Dictionaries and Their Applications for Database Searches of Tandem Mass Spectra

Abstract

Generating all plausible de novo interpretations of a peptide tandem mass (MS/MS) spectrum (Spectral Dictionary) and quickly matching them against the database represent a recently emerged alternative approach to peptide identification. However, the sizes of the Spectral Dictionaries quickly grow with the peptide length making their generation impractical for long peptides. We introduce Gapped Spectral Dictionaries (all plausible de novo interpretations with gaps) that can be easily generated for any peptide length thus addressing the limitation of the Spectral Dictionary approach. We show that Gapped Spectral Dictionaries are small thus opening a possibility of using them to speed-up MS/MS searches. Our MS-GappedDictionary algorithm (based on Gapped Spectral Dictionaries) enables proteogenomics applications (such as searches in the six-frame translation of the human genome) that are prohibitively time consuming with existing approaches. MS-GappedDictionary generates gapped peptides that occupy a niche between accurate but short peptide sequence tags and long but inaccurate full length peptide reconstructions. We show that, contrary to conventional wisdom, some high-quality spectra do not have good peptide sequence tags and introduce gapped tags that have advantages over the conventional peptide sequence tags in MS/MS database searches.

Most peptide identification tools are rather slow because they match every tandem mass (MS/MS)¹ spectrum against all peptides in a database (subject to constraints on the precursor mass, the enzyme specificity, and the number of missed cleavages). A faster approach would be to generate a full-length de novo reconstruction of a spectrum and to match the resulting peptide against a database. The fundamental algorithmic advantage of the latter approach is that one can preprocess the database (e.g. by constructing its suffix tree) so that matching becomes instantaneous. The only reason why most MS/MS database search tools still use the former approach is because full-length de novo peptide sequencing remains inaccurate. Even the most advanced de novo peptide sequencing tools (1–3) correctly reconstruct only 30–45% of the complete peptides identified in MS/MS database searches. After decades of algorithmic developments, it seems that de novo peptide sequencing “hits a wall” and that accurate full-length peptide reconstruction is nearly impossible because of the limited information content of MS/MS spectra (other reasons include limited understanding of fragmentation rules, co-eluted peptides, etc.). We argue that regions with low information content should be represented as mass gaps (that represent two or more amino acids) and advocate use of gapped peptides as spectral interpretations.

Kim et al., 2009 (4) recently proposed to generate multiple de novo reconstructions (rather than a single one) and to match them against a database (MS-Dictionary approach). Because matching peptides against a preprocessed database is very fast, generating thousands of reconstructions still has advantages over the traditional approaches in which spectra are matched against large databases. Given an MS/MS spectrum, MS-Dictionary generates the Spectral Dictionary (4) that contains all plausible de novo reconstructions of the spectrum (i.e. with scores exceeding a given threshold) and further matches them against a database. The running time of MS-Dictionary is almost independent of the database size making it a tool of choice for peptide identification in large databases (4).

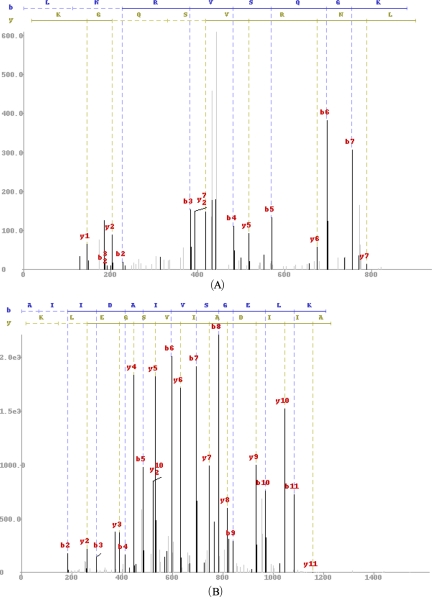
Although MS-Dictionary was proved to be useful for peptides shorter than 15 amino acids (aa), it has limitations for longer peptides with large Spectral Dictionaries. For example, the size of the Spectral Dictionary for a typical 15-aa long peptide may exceed a billion peptides making it too large for a MS/MS database search. We introduce MS-GappedDictionary that generates rather small Gapped Spectral Dictionaries (even for long peptides) thus addressing the key limitation of the Spectral Dictionaries. Gapped Spectral Dictionary is the set of gapped peptides (see (5)) that are derived from the full-length peptides in the Spectral Dictionary. Although the concept of a gapped peptide is not new (1, 2, 6–8), constructing dictionaries of gapped peptides that account for all plausible de novo interpretations was not addressed before. Gapped peptides occupy a niche between accurate but short peptide sequence tags (9) and long but inaccurate full-length peptide reconstructions. The gapped peptides are both long and accurate making them well suited for de novo-based MS/MS database searches. In difference from short peptide sequence tags, a gapped peptide typically has a single match in a database reducing peptide identification to a single database look-up. For a typical 20-aa long peptide, the size of the Spectral Dictionary exceeds 10¹⁷, whereas the size of the Gapped Spectral Dictionary is only ≈10⁴. Moreover, we show that even smaller Gapped Spectral Dictionaries with only 20–100 peptides are sufficient for most applications. At the same time, gapped peptides are sufficiently long for efficient database matching. For example, for a spectrum of 15-aa long peptide, the average length (The total number of gaps and amino acids in the gapped peptide. For example, the length of [186]DK[246]FK is 6.) of gapped peptides in its Gapped Spectral Dictionary exceeds nine. For all practical purposes, (gapped) peptides of length nine are as informative as (full-length) peptides of length 15 for matching databases (unless the database size approaches 20⁹). Table I (a) shows the Gapped Spectral Dictionary of a spectrum of peptide LNRVSQGK shown in Fig. 1A, consisting of seven gapped peptides (as compared with its Spectral Dictionary consisting of 92 peptides shown in supplemental Table S1). We describe an efficient algorithm for constructing the Gapped Spectral Dictionaries that also computes coverage of each gapped peptide, reflecting the portion of plausible de novo reconstructions represented by a gapped peptide (see below for the definition of coverage).

Table I.

(A) The Gapped Spectral Dictionary for the spectrum of peptide LNRVSQGK (consisting of seven gapped peptides) is much smaller than the Spectral Dictionary (consisting of 92 full-length peptides). For simplicity, LNRVSQGK is represented by its integer amino acid masses as follows: [113][114][156][99][87][128][57][128]. Each gapped peptide is represented by amino acids and mass gaps that represent combinations of amino acids (for example, [128] can be Q, K, GA, or AG). Either Q or K is used instead of [128] when [128] occupies the same position as Q or K on the peptide LNRVSQGK. The gapped peptides that match the correct peptide are called correct gapped peptides (like gapped peptides 1 and 6 marked with ^†). For example, the gapped peptides [113 + 114]RVSQGK or LN[156 + 99]SQGK match peptide LNRVSQGK. The second column represents the coverage of the gapped peptide (see Results section for the definition of coverage), reflecting the portion of the total probability of all full-length peptides represented by the gapped peptide (see Supplement Table S1 for an example of the calculation of the coverage of the gapped peptide [227]RVSQGK).

(B) Peptide sequence tags of length 3 derived from the Gapped Spectral Dictionary. Masses over left (right) arrows are the prefix (suffix) masses of the tags. The third column shows the coverage of each tag, where the coverage of a tag is defined by the summation of the coverages of gapped peptides covered by the tag. The fourth column shows the gapped peptides (specified by the numbers in the first column of (A)) covered by each tag. For example, a tag VRV covers two gapped peptides 3 and 5 in (A) with coverages of 13.71% and 5.71%, respectively. The coverage of the tag VRV is, thus, 13.71 + 5.71≈19.4%. Overall, only two tags (e.g. QGK and VRV) cover all gapped peptides in the Gapped Spectral Dictionary.

(C) The Gapped Spectral Dictionary for the spectrum of peptide AIIDAIVSGELK shown in Fig. 2B (16 gapped peptides represent 24,034 full length peptides). The correct gapped peptides are marked by ^†. The Gapped Spectral Dictionary for the peptide AIIDAIVSGELK reveals only three tags (GEL, ELK, and SGE), together covering only 18.59% of the Spectral Dictionary. In contrast, six (gapped tags) [273]LK, G[242]K, S[299]K, [250]SG, ELK, and [186]LK cover the entire Spectral Dictionary.

(A)
No.	Gapped Peptide (GP)	Coverage of GP *	# of peptides represented by GP
1†	[227]RVSQGK	45.69	12
2	[128] [255]VSQGK	15.99	32
3	[128]VRVSQGK	13.71	20
4	[128]VR[186]QGK	11.42	4
5	[128]VRV[215]GK	5.71	2
6†	[383]VSQGK	5.71	2
7	[128]G[198]VSQGK	1.77	20
Total	·	100	92

(B)
No.	Tag	Coverage of tag (%)	Covered GP
1	569← QGK 0→	94.3	1,2,3,4,6,7
2	383← VSQ 185→	82.9	1,2,3,6,7
3	482← SQG 128→	82.9	1,2,3,6,7
4	227← RVS 313→	59.4	1,3
5	128← VRV 400→	19.4	3,5

(C)
No.	Gapped Peptide (GP)	Coverage of GP *	# of peptides represented by GP
1	[445][250]S[186]LK	33.81	3286
2†	[695]S[186]LK	19.18	1703
3	[445][337][186]LK	13.28	255
4	[445][250][273]LK	7.67	178
5†	[782]GELK	6.10	684
6†	[695]SGELK	5.55	5563
7	[445][250]S[299]K	4.20	901
8	[445][250]SGELK	3.78	3437
9	[445][337]GELK	1.98	1072
10	[445][250]SG[242]K	1.61	3942
11†	[695]SG[242]K	0.91	1614
12	[445][394]ELK	0.91	507
13	[445][250]SG[370]	0.66	604
14	[445][250][144]ELK	0.20	91
15†	[695][144]ELK	0.07	35
16	[445][337]G[242]K	0.09	162
Total	·	100.00	24034

Fig. 1.

Spectra for the peptide LNRVSQGK (A) and AIIDAIVSGELK (B) identified by InsPecT (release 20090910) database search.

Recent proteogenomics studies highlighted the importance of MS/MS searches against the six-frame translation of genomes (10–17). However, until recently, searches against the six-frame translations of large genomes were impractical even with the fastest MS/MS search tools, let alone with traditional tools like SEQUEST and Mascot. Although MS-Dictionary enabled searches in the six-frame translation of the human genome with 40× speed-up over InsPecT (4), it loses many peptide identifications (compared with InsPecT) because Spectral Dictionaries of long peptides have to be truncated (leading to truncating the correct peptides in some cases). Gapped Spectral Dictionaries remedy this shortcoming of Spectral Dictionaries and nearly double the number of identified peptides in the six-frame translation of the human genome (as compared with MS-Dictionary (4)).

Table I (b) illustrates how gapped peptides and their coverage can be used for constructing the peptide sequence tags (9). Tanner et al., 2005 (18) introduced covering sets of tags (set of tags containing at least one correct tag) and demonstrated how such sets can greatly speed-up MS/MS database searches. However, although the sizes of covering sets may vary between spectra, Tanner et al., 2005 (18) did not describe an approach for selecting (the varying number of) tags for every spectrum and did not assign rigorous probabilities to tags. Although Gapped Spectral Dictionaries can be used for generating (varying number of) conventional peptide sequence tags along with their probabilities, Table I (c) illustrates that “good“ peptide sequence tags (representing all peptides in the Gapped Spectral Dictionary) may be difficult to find. We show that, contrary to conventional wisdom, some high quality spectra do not have good peptide sequence tags. We therefore advocate generating gapped tags representing sequences of mass gaps (like [186]LK derived from the first peptide in Table I (c)) and demonstrate that gapped tags improve the filtration efficiency of peptide sequence tags in tag-based MS/MS database searches.

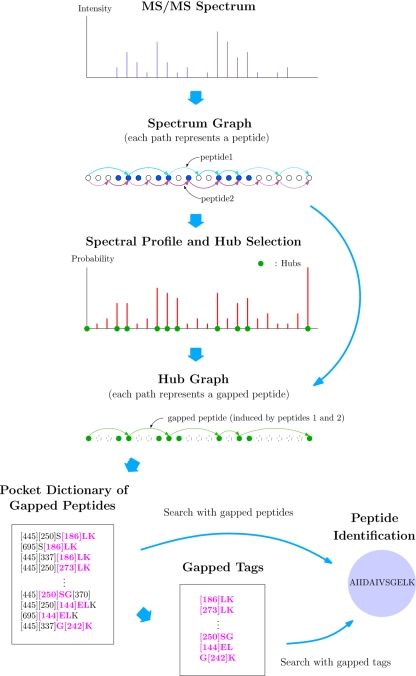
Fig. 2 illustrates different modules of MS-GappedDictionary that are described below.

Fig. 2.

Different modules of MS-gappeddictionary.

EXPERIMENTAL PROCEDURES

Path Dictionary Problem

Most de novo peptide sequencing algorithms interpret spectra by analyzing paths in spectrum graphs (19). We start by discussing the problem of finding suboptimal paths in arbitrary graphs and later describe how it relates to finding paths in the spectrum graphs.

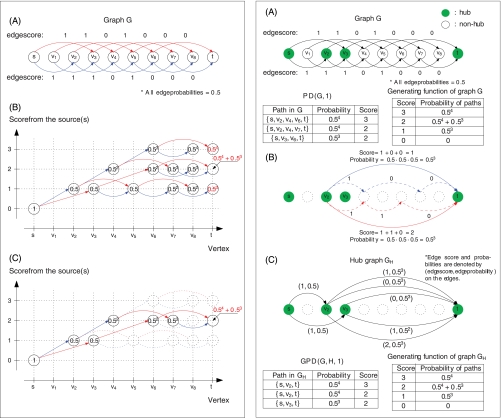
Let G(V,E,score,probability) be a directed acyclic graph with vertex set V, edge set E, and functions score and probability defined on its edges (Fig. 3 A, left panel). (At this point, the score and probability should be viewed as arbitrary numbers assigned to the edges.) Later, we will describe what score and probability mean in the context of de novo peptide sequencing. Given a path in G, the score of the path is defined as the sum of scores of its edges, whereas the probability of the path is defined as the product of probabilities of its edges. Given a graph G with selected vertices s (source) and t (sink), and a threshold MinScore, the Path Dictionary (denoted as PD(G,MinScore)) is defined as the set of all paths from s to t with scores exceeding MinScore (along with their probabilities). The following Path Dictionary Problem can be solved using standard algorithms for finding suboptimal paths (20).

Fig. 3.

Left panel: Illustration of the dynamic programming algorithm for computing the generating function of graph G shown in (A). The nodes of the dynamic programming (DP) graph (B) are defined as pairs (v,x), where v is a vertex of G and x is a score. Two nodes (v,x) and (v′,x′) are connected by an edge if and only if there exists an edge between vertices v and v′ in G with score x′-x. The probability of an edge between (v,x) and (v′,x′) in the DP graph equals to the probability of the edge (v,v′) in G. A source s in graph G corresponds to a single node (s,0) in the DP graph. A node (v,x) is present in the DP graph if and only if there exist a path from (s,0) to (v,x). In this example, red (blue) edges of the DP graph in (B) are from the red (blue) edges of the graph G in (A). All edge probabilities in (B) are 0.5 as the probabilities of edges of G are 0.5. The node probability of node (v,x) (shown inside nodes in (B) and (C)) is the total probability of the paths from the source s to v with the score x. The node probability of the source of the DP graph is initialized by 1, and the node probability of a node (v,x) is obtained by the weighted summation of the node probabilities of its predecessors (see (21)). The generating function is represented by the probabilities of the sink nodes in the DP graph. To find all paths of score x from the source to the sink in graph G one has to backtrack all paths from the node (t,x) in the DP graph. For example, if x = 2, two such paths are found: {s, v₂, v₄, v₇, t} and {s, v₃, v₆, t} as in (C). Right panel: Path Dictionary and Gapped Path Dictionary. (A) PD(G,1) and the generating function of G. (B) The construction of G_H using edges between hubs v² and t (shown as solid blue and red edges) as examples. Solid blue and red edges in G_H are induced by dashed blue and red paths in G. All paths that use only nonhub vertices in G are collapsed into edges in G_H. (C) The hub graph G_H, GPD(G,H,1), and the generating function of G_H.

Path Dictionary Problem. Given a directed acyclic graph G and a threshold MinScore, construct PD(G,MinScore).

Define the generating function p(x) as the total probability of all paths of score x from the source s to the sink t in the graph G. The generating function can be efficiently computed as the probability of node (t,x) in the dynamic programming graph as described in (4, 21) (Fig. 3, left). PD(G,MinLength) is constructed by standard backtracking in the dynamic programming graph.

For the spectrum graph of a tandem mass spectrum (19), the Path Dictionary Problem corresponds to a de novo peptide sequencing problem when multiple (suboptimal) de novo reconstructions (rather than a single one) are generated. (In the spectrum graph of a spectrum, vertices represent all (integer) masses from 0 to parent mass of the spectrum, and vertices v and v′ are connected by a directed edge (v,v′) if and only if there is an amino acid with (integer) mass (v′-v). The score of the edge (v,v′) is given by the PRM score (18) of the peak represented by the vertex v′, and the probability is given by the probability that the amino acid represented by the edge (v,v′) appears in a random database (a database with identically and independently distributed amino acids with probability 1/20).) Kim et al., 2008 (21) applied the generating function approach (Fig. 3, left) to analyze MS/MS spectra and further demonstrated (4) how to generate the Path Dictionary (termed Spectral Dictionary) that contains all plausible de novo reconstructions for a given spectrum. Each path in the Path Dictionary corresponds to a full-length peptide reconstruction in the Spectral Dictionary, and ${\displaystyle \sum _{x>MinScore}p\left(x\right)}$ corresponds to the spectral probability (p value) defined in (4). To generate the Spectral Dictionaries, a spectral probability Threshold is fixed and MinScore is selected in such a way that the spectral probability does not exceed Threshold.

This Spectral Dictionary approach, whereas useful, is not practical for long peptides (15 amino acids and longer) with large dictionaries. We bypass this problem by solving the Gapped Path Dictionary Problem defined below.

Gapped Path Dictionary Problem

Let H be a subset of vertices of a graph G containing the source s and the sink t (vertices of H are called hubs). We remark that every path on vertices in G induces a hub path on vertices in H by simply retaining only vertices from H in the original path. For example, a path s→v₁→v₂→v₃→v₄→v₅→v_6-→t that contains hubs s, v₂, v₃, v₅, t induces a hub path s→v₂→v₃→v₅→t. We define the probability of a hub path as the total probability of all paths inducing this hub path. The Gapped Path Dictionary GPD(G,H,MinScore) is defined as the set of all hub paths induced by the paths in PD(G,MinScore) (along with their probabilities).

Gapped Path Dictionary Problem. Given a directed acyclic graph G, a subset of its vertices H, and a threshold MinScore, construct GPD(G,H,MinScore).

The brute-force algorithm for constructing GPD(G,H,MinScore) (by constructing PD(G,MinScore) and generating all hub paths induced by the paths in PD(G,MinScore)) is impractical for large PD(G,MinScore). Below we describe an efficient algorithm for solving the Gapped Path Dictionary Problem that does not require the construction of PD(G,MinScore).

Given hubs h and h′, we define Path(h,h′) as the set of all paths in G between h and h′ that do not pass through other hubs. Each path in Path(h,h′) is characterized by its score and probability. Let X(h,h′) be the set of scores of all paths from Path(h,h′) and Prob(h,h′) be the total probability of all paths in Path(h,h′). If Prob(h,h′,x) is defined as the total probability of all paths of score x from the set Path(h,h′), then $\mathrm{Pr}ob\left(h,h\prime \right)={\displaystyle \sum _{x\epsilon \chi \left(h,h\prime \right)}\mathrm{Pr}ob\left(h,h\prime ,x\right)}$.

We define the hub graph G_H as a multigraph on the set of vertices H (Fig. 3, right). For every xϵX(h,h′), there exists an edge between h and h′ with score x and probability Prob(h,h′,x). (There exists X(h,h′) edges between vertices h and h′ in the multigraph G_H.) The score and the probability of a path in G_H is defined as the sum of scores and the product of probabilities of its edges, respectively.

As the hub paths (on vertices in H) are induced by the paths in G, GPD(G,H,MinScore) is the same as PD(G_H, MinScore). Therefore, the Gapped Path Dictionary Problem in G is essentially the Path Dictionary Problem in the hub graph G_H, and we only need to compute the scores and the probabilities of the edges in G_H to solve the Gapped Path Dictionary Problem. Below, we show how to compute Prob(h,h′,x) for all edges of the hub graph.

Given a hub h in the graph G(V,E,score,probability), we modify the score function by assigning score -∞ to all edges originating at all hubs other than h. Denote the resulting score function (parameterized by h) as score(h). The family of score functions score(h) for all hubs hϵH can be used to compute Prob(h,h′,x) for all pairs of hub vertices h and h′. One can prove that computing Prob(h,h′,x) (for all xϵX(h,h′)) is equivalent to computing the generating function for a graph G(V, E,score(h),probability) with source h and sink h′. Note that a single computation of the generating function from h to the sink t for the graph G(V,E,score(h),probability) gives us Prob(h,h′,x) for all h′ϵH and all xϵX(h,h′).

After constructing the hub graph G_H, GPD(G,H,MinScore) can be constructed by computing generating function for the graph G_H and generating all paths with score exceeding MinScore. Fig. 3 (right) shows an example of the Path Dictionary and the Gapped Path Dictionary.

Gapped Spectral Dictionaries

So far, we represented each path in the Gapped Path Dictionary as the sequence of edges (rather than vertices) the path traverses. Because the hub graph G_H is a multigraph (that may have multiple edges of various scores between the same vertices), there can be many paths (with different scores) with identical vertex-sets (Fig. 3, right panel (C)). We define the Compact Gapped Path Dictionary, denoted by CGPD(G,H,MinScore), as the set of vertex-sets of paths in the Gapped Path Dictionary GPD(G,H,MinScore), along with their probabilities, where the probability of each vertex-set in CGPD(G,H,MinScore) is defined as the total probability of the paths in GPD(G,H,MinScore) with the same vertex-set (see supplemental Table S1). The algorithm for efficient generation of Compact Gapped Path Dictionaries is described in the Supplement S2.

For each spectrum, we construct its spectrum graph and generate a set of hubs (prefix masses). Given a spectrum graph G and a set of hubs H, paths in G correspond to peptides whereas vertex-sets in G_H correspond to gapped peptides introduced in (5). Gapped Spectral Dictionary is defined as Compact Gapped Path Dictionary of the spectrum graph.

Although we described an algorithm for constructing the Gapped Spectral Dictionary for a given hub set H, it remains unclear how to select hubs. The hub selection has to achieve two conflicting goals: (i) minimize the number of selected hubs to ensure that the Gapped Spectral Dictionary is small, and (ii) maximize the average length of peptides in the Compact Gapped Spectral Dictionary to ensure that the reconstructed gapped peptides are sufficiently informative.

Therefore, the goal is to select k hubs that maximize the average number of vertices per path in the Gapped Path Dictionary (weighted by their probabilities). We select hubs as k most “popular” vertices in paths from PD(G,MinScore). Such ranking of vertices of the graph G can be computed by generating Spectral Profiles introduced in (5). (The Spectral Profiles provide a better hub selection than peak intensities and PRMs (18) (see Supplement Fig. S1).)

RESULTS

Data Sets

We used the previously published Shewanella, HEK, and Standard data sets to benchmark MS-GappedDictionary (see (22, 14, 23), and (24) for the details of the generation of spectra in Shewanella, HEK, and Standard data sets, respectively).

Shewanella Data Set

To benchmark the performance of MS-GappedDictionary, we adopted the Shewanella data set composed of 18,468 charge two spectra from Shewanella oneidensis MR-1, each representing a distinct tryptic peptide (22). (Although this paper focuses on doubly charged spectra, the same generating function approach works for spectra with higher charges as shown in (25).) The spectra in this data set were acquired on an ion trap MS (LCQ, ThermoFinnigan, San Jose, CA) using ESI and were identified with InsPecT 197 MS-GeneratingFunction (18, 21) to ensure that all Peptide Spectrum Matches (PSMs) have spectral probabilities below 10^–9. Note that MS-GeneratingFunction was shown to improve upon other MS/MS identification tools (InsPecT, X! Tandem, and SEQUEST/PeptideProphet (21)) and in most applications, peptide identifications with spectral probabilities above 10^–9 are of little use because they result in high FDR. (The Supplement Material Figs. S2, S3, S4 presents analysis of the same data set for spectral probabilities below 10^–10 and 10^–11.) The analysis below is based on Shewanella data set unless noted otherwise.

Standard Data Set

Shewanella data set is inadequate for benchmarking the (gapped) tag generation accuracy, because the tag-based tool InsPecT was used to identify the spectra in Shewanella data set (i.e. a correct InsPecT tag was generated for every spectrum). We obtained the data set reported in (5) collected from the Standard Protein Mix database (24). For this study, we considered only the charge-two spectra generated by LTQ, where the spectra were identified by SEQUEST (26) and PeptideProphet (27) that do not use tags for identifications. We further selected PSMs with spectral probabilities below 10^–9 and formed the data set (denoted Standard) with 990 charge-two spectra of distinct peptides.

HEK Data Set

To benchmark MS-GappedDictionary, MS-Dictionary (4), InsPecT (18), and OMSSA (28) in MS/MS searches of huge databases, we analyzed the previously published spectral data set from the human HEK293 cell line generated in Steve Briggs' laboratory (see (14, 23) for a detailed description of this data set). The spectra were acquired on an LTQ linear ion trap tandem mass spectrometer.

InsPecT and OMMSA were chosen for benchmarking because they represent some of the fastest MS/MS database search tools. (Sequest was shown to be 60 times slower than InsPecT 4 making it impractical for large proteogenomic searches.) We selected 1 million spectra from HEK293 data set (described in (14)) for analyzing proteogenomics applications of MS-GappedDictionary (see Supplement S16). Because analyzing 1 million spectra even with fast tools like InsPecT is very time consuming (estimated CPU time in the search against the 6-frame translated human genome is 9 million seconds) we further selected a single run of this data set (≈30,000 spectra) for benchmarking. We further processed this data set with PepNovo+ (Release 20091029) (3) to correct charges and parent masses and limited our analysis to 14,000 charge-two spectra (denoted HEK data set). The HEK data set was searched against the six-frame translation of the repeat-masked human genome (version GRCh37 released on March 2, 2009) using MS-GappedDictionary, MS-Dictionary, InsPecT, and OMSSA. (see supplemental Table S2 for search parameters)

To generate the Gapped Spectral Dictionaries, the spectral probability threshold is set to 10^–9 for Shewanella and Standard data sets and 10^–11 for HEK data set (assuming that the precursor mass is known). The spectral probability thresholds vary for different data sets to maintain roughly 1% FDR (see 29 for selection of the spectral probability threshold). The spectral hubs are selected based on k maximal peaks in its Spectral Profile with k varying from 20 to 40.

From Gapped Spectral Dictionaries to Pocket Dictionaries

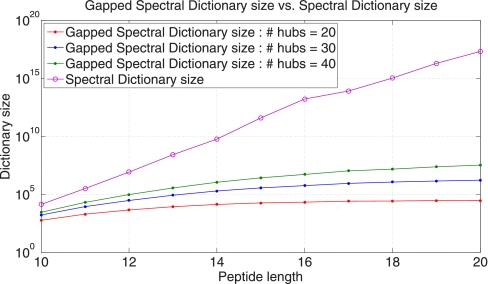
Because multiple peptides often induce the same gapped peptide, Gapped Spectral Dictionaries are typically much smaller than Spectral Dictionaries. Fig. 4 shows the sizes of Gapped Spectral Dictionaries and Spectral Dictionaries for various peptide lengths. Although the size of Spectral Dictionary grows as 20^{peptide length}, the size of the Gapped Spectral Dictionary is limited by 2 ^H, where H is the number of hubs. In practice, the size of Gapped Spectral Dictionaries is much smaller than 2 ^H for sensible values of spectral probabilities. For example, for peptides of length 20, the size of the Spectral Dictionary exceeds 10¹⁷ whereas the size of the Gapped Spectral Dictionary is on the order of 10⁴ (for H = 20).

Fig. 4.

Gapped Spectral Dictionary size versus Spectral Dictionary size (for varying peptide length and number of hubs) for the Shewanella data set.

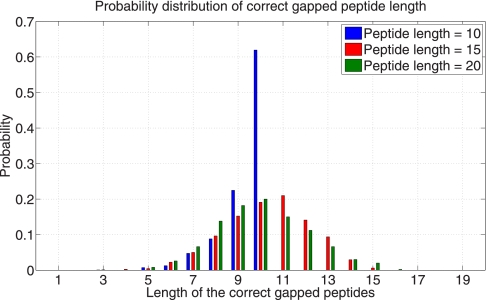
Fig. 5 shows the distribution of the lengths of the gapped peptides that are induced by the correct peptides (correct gapped peptides). The high average length of the correct gapped peptides (10–13) indicates that Gapped Spectral Dictionaries have the potential to speed up database searches. (The fraction of short gapped peptides (length less than 5) is less than 0.01 regardless of the peptide length.) Gapped peptides are classified into short (with length shorter than δ) and long (with length equal to or longer than δ), where δ is the minimum gapped peptide length threshold. Discarding short gapped peptides results in δ-reduced Gapped Spectral Dictionary.

Fig. 5.

Distribution of the lengths of the gapped peptides induced by correct peptides (for 20 hubs) for the Shewanella data set. (see Supplement Fig. S2 for different parameters).

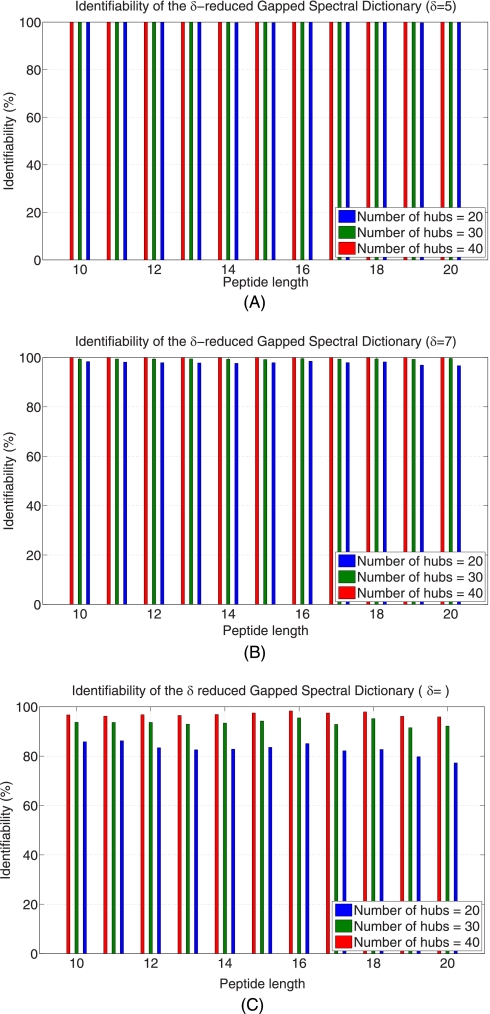
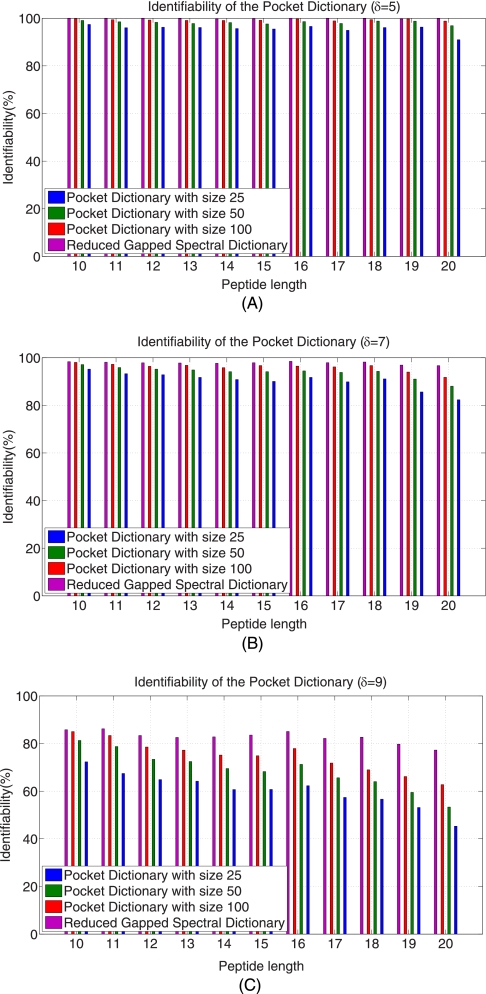
A spectrum is δ-identifiable if its δ-reduced Gapped Spectral Dictionary contains at least one correct gapped peptide. Fig. 6 shows the identifiability of spectra in the Shewanella data set. For δ = 5, the identifiability is higher than 99% for all peptide lengths. Fig. 6 illustrates that there exists a tradeoff between the identifiability and efficiency of the database search controlled by the minimum length of the gapped peptide δ (increase in δ reduces the identifiability but improves the efficiency of the database search).

Fig. 6.

Identifiability of the δ-reduced Gapped Spectral Dictionaries from the Shewanella data set for δ = 5 (A), δ = 7 (B), and δ = 9 (C).

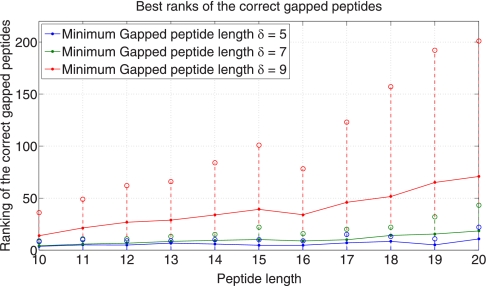
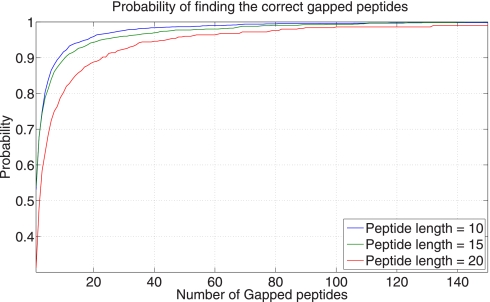
After generating the δ-reduced Gapped Spectral Dictionaries, we order all gapped peptides by their coverages, and analyze the rank of the first correct gapped peptides in this ranked list. The coverage of a gapped peptide is defined as the probability of the gapped peptide divided by the total probability of the peptides in the Spectral Dictionary. Fig. 7 shows that the average rank of the best ranked correct gapped peptides does not exceed 100 even for long gapped peptides (δ = 5,7,9). In fact, only 20–100 gapped peptides are typically sufficient to generate a correct peptide (Fig. 8). As such, it suffices to generate a small subset of the Gapped Spectral Dictionary called Pocket Dictionary by choosing the k best-ranked gapped peptides in the δ-reduced Gapped Spectral Dictionary (k is typically 20–100). Fig. 9 shows the identifiability of the Pocket Dictionaries compared with the identifiability in the (full-size) δ-reduced Gapped Spectral Dictionaries. (It turns out that selecting gapped peptides based on their coverage yields better results than selecting based on their scores (see Supplement S5).) Throughout the paper we generate Pocket Dictionaries of size 100 with δ = 5 and 20 hubs that results in high identifiability.

Fig. 7.

Average rank of (the best ranked) correct gapped peptides. The average ranking does not exceed 80 regardless of the peptide length (for δ = 5,7,9). The number of hubs is 20. The dotted lines with open circles at the ends represent the range that the rankings fall into 90% of the time.

Fig. 8.

The probability that a correct gapped peptide is found within k top-ranked peptides in the δ-reduced Gapped Spectral Dictionary. The number of hubs is 20, and δ = 5 (see Supplement Fig. S3 for different parameters).

Fig. 9.

Identifiability of the Pocket Dictionaries from the Shewanella data set for δ = 5 (A), δ = 7 (B), and δ = 9 (C). The number of hubs is 20. Even for long peptides, Pocket Dictionaries with 50 gapped peptides are sufficient to ensure the identifiability higher than 97% when δ is 5. When δ is large, larger Pocket Dictionaries are needed. (see Fig S4 in Supplemental).

Although we showed how to generate the highest-scoring gapped peptides, generation of the highest-probability vertex-sets (gapped peptides) in the δ-reduced Gapped Path Dictionary is described in Supplement S3.

From Gapped Spectral Dictionaries to Gapped Tags

Once the Pocket Dictionary is generated, one still needs to match gapped peptides in the Pocket Dictionary against the protein database. The current version of MS-GappedDictionary uses gapped tags of length three (see below) instead of gapped peptides to speed-up searches in huge databases. This is conceptually similar to InsPecT search with the only difference that InsPecT uses 3-aa long peptide sequence tags whereas MS-GappedDictionary uses gapped tags of length three for filtering the database. In Supplement S15 we sketch a more efficient algorithm (based on matching the entire gapped peptides).

Table I (C) demonstrates that many gapped peptides in the Gapped Spectral Dictionary may not contain peptide sequence tags. In contrast, allowing a single gap in tags (gapped tags) reveals a covering set of only six tags of length three: [273]LK, G[242]K, S[299]K, [250]SG, ELK, and [186]LK. In contrast with peptide sequence tags, gapped tags include both gaps and amino acid masses. Below we limit our analysis to gapped tags with gaps below 500 Da (We limit the mass of the largest gap to limit the memory requirements of MS-GappedDictionary (see Supplement S12).) and analyze gapped tags of length three with at most one gap (i.e. gapped tags with at least two amino acids). Such tags are called proper gapped tags. We demonstrate that the proper gapped tags have better filtration efficiency (defined below) than peptide sequence tags.

Some masses in a gapped peptide may represent either an amino acid or a gap because 5 amino acids (N, Q, K, R, and W with masses 114, 128, 128, 156, and 186, respectively) have composite masses equal to the (integer) sum of two amino acid masses. (In this article, we focus on ion-trap spectra and thus limit our analysis to integer amino acid masses. However, the generating function approach can be easily adjusted to more accurate mass measurements (see 21).) For example, the composite mass 114 Da could represent either N or GG. Therefore, to generate a set of proper gapped tags, one has to decide whether a composite mass in the gapped tag corresponds to a single amino acid (see Supplement section S10 for the explanation on how it is done).

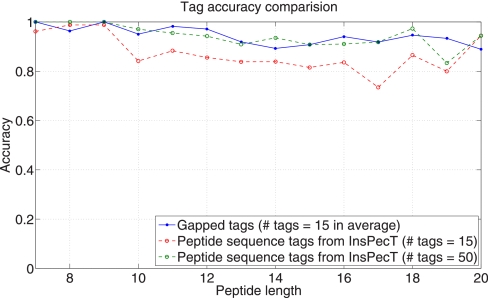
To generate the set of proper gapped tags, we select at most one proper gapped tag from each gapped peptide in the Pocket Dictionary. The greedy algorithm for selecting proper gapped tags is described in Supplement section S11. Fig. 10 compares the gapped tags generated by MS-GappedDictionary with peptide sequence tags generated by InsPecT (release 20090910). With 15 (on average) proper gapped tags generated by MS-GappedDictionary (see supplemental Table S4), the average accuracy is 94.8% whereas the accuracy of InsPecT tags is only 87.2% with 15 peptide sequence tags and 94.7% even with 50 tags. (The accuracy of tag generation is defined as the percentage of cases when the set of generated tags contains a correct tag.) MS-GappedDictionary constructs a table of proper gapped tags as described in the Supplement. Once the Table is built, finding peptides matched to a proper gapped tag is fast, and the search space for further analysis is limited to only those matched peptides. We define the filtration efficiency of a peptide sequence tag/gapped tag/peptide as the ratio of the number of its matches in the random database over the database size. Although the filtration efficiency of a peptide (i.e. an amino acid sequence) is 1/20^{peptide length} (and the filtration efficiency of amino acid is 1/20), it is easy to see that the filtration efficiency of a gap of mass m is the sum of filtration efficiencies of all amino acid sequences with mass m. It turns out that large masses typically have better filtration efficiencies than amino acids. (For example, gap mass 57 (integer mass of Gly) appears in N/20 positions in a random database of size N whereas gap mass [400] appears in ≈N/121 positions. There are 1,102 combinations of amino acids for the gap mass [400]: 42 combinations of 3 amino acids, 664 combinations of 4 amino acids, 300 combinations of 5 amino acids, and 96 combinations of 6 amino acids. Thus, the filtration efficiency of the gap mass [400] is 42 · (1/20)³ + 664 · (1/20)⁴ + 300 · (1/20)⁵ + 96 ·(1/20)⁶ = 0.0095. supplemental Fig. S6 shows the filtration efficiency of masses as compared to an amino acid, and supplemental Table S3 shows the possible aa (amino acid) combinations for each mass (from 114 Da to 250 Da). This improvement translates into a superior filtration efficiency of gapped tags as compared with peptide sequence tags (compare with (31) where database searches with similar gapped tags were introduced).

Fig. 10.

Comparison of gapped tags generated from the Pocket Dictionaries and the peptide sequence tags generated by InsPecT (on spectra from the Standard data set).

For each spectrum in Standard data set, we generated tags using MS-GappedDictionary (15 proper gapped tags per spectrum on average) and InsPecT (50 peptide sequence tags per spectrum), and measured the number of matches against the Swiss-Prot database. Although InsPecT reported ≈2 thousand peptide sequence tag matches per spectrum on average, MS-GappedDictionary reported only ≈420 gapped tag matches. (The number of peptide matches reported by MS-GappedDictionary is only about 4–6 when the gapped peptides (not gapped tags) in the Pocket Dictionaries (with size 100) are used for the same experiment. The filtration efficiency of a gapped peptide, therefore, is 10⁶ to 10⁷ times better than that of gapped tags or peptide sequence tags.) The running time to search the Swiss-Prot database was 0.36 s for MS-GappedDictionary (including the generation of the Gapped Spectral Dictionary and the gapped tags) and 0.51 s for InsPecT per spectrum on a desktop machine with a 2.67-GHz Intel processor.

Database Search with Gapped Spectral Dictionaries

To compare MS-GappedDictionary with other database search tools (for searches in huge databases), the HEK data set was searched against the six-frame translation of the human genome (2.8 billion amino acid residues) using MS-GappedDictionary, MS-Dictionary (ver. 20100415) (4), InsPecT (release 20090910) (18), and OMSSA (ver. 2.1.7) (28). The search parameters used in these searches are specified in the Supplement. We plotted the peptide level FDR curve of each tool in this search using the target-decoy database approach as described in (32). In the case of MS-GappedDictionary, two different methods to search in the database are used: the search with gapped tags and the search with gapped peptides. We use a brute-force scanning algorithm for matching gapped peptides against the database. Searching gapped peptides against a database can be done by simply scanning each gapped peptide in the Pocket Dictionary against the database. Because a more efficient search with gapped peptides will be described elsewhere, the goal of this search with gapped peptides is to study FDR rather than to establish the running time of this primitive approach.

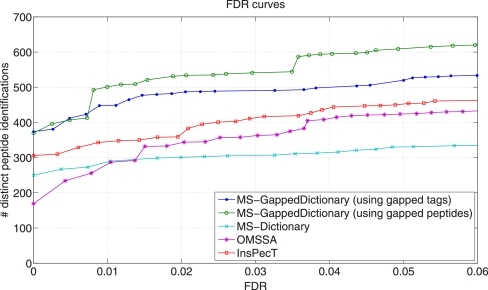
To measure the FDR of each tool, we first generated the reversed decoy database of the six-frame translation of the human genome. The spectra in HEK data set were searched against both the target and decoy databases. Fig. 11 shows the FDR curve of each tool and illustrates that MS-GappedDictionary significantly improves on all other tools in the number of reliably identified peptides for all levels of FDR (≈30% improvement in the case of 1% FDR). InsPecT is shown to improve on OMSSA and MS-Dictionary. However, MS-GappedDictionary is ≈20 times faster than InsPecT (0.8 s versus 17 s per spectrum, respectively). (All tools used in this benchmarking preprocess the protein database. Because preprocessing time is negligible (compared to the search time), we do not report the database preprocessing times. The running times include both target and decoy database search times. Except OMSSA, the six-frame translation of the human genome should be divided into small subdatabases because of the memory overhead (in MS-Dictionary and MS-GappedDictionary) or unexpected errors (in InsPecT). The running time of each tool is measured by summing the search times on the subdatabases. MS-GappedDictionary filters out poor quality spectra [23] and does not generate their Gapped Spectral Dictionaries.) OMSSA and MS-Dictionary are also fast (1.2 s and 0.8 s per spectrum, respectively) but their FDRs deteriorate significantly in comparison with MS-GappedDictionary.

Fig. 11.

The FDR curves for MS-GappedDictionary (using either gapped tag or gapped peptides), OMSSA, InsPecT, and MS-Dictionary (peptide-level FDR is reported (32)). For each spectrum, only the single best matching peptide is reported.

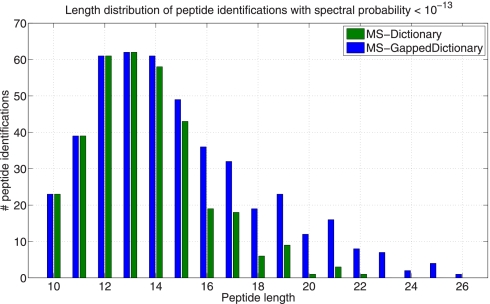
Fig. 12 shows the length distribution of peptide identifications in the HEK data set identified with MS-Dictionary and MS-GappedDictionary (in searches against the six-frame translation of the human genome). Although Both tools identified roughly the same number of short peptides (length less than 14 aa), MS-GappedDictionary significantly improves on MS-Dictionary in identifying long peptides (14 aa and longer). This is a consequence of the fact that MS-Dictionary has to truncate the (large) spectral dictionaries of long peptides resulting in loosing many peptide identifications.

Fig. 12.

The length distribution of peptides with the spectral probability less than 10^–13 (corresponding FDR ≈1%) in HEK data set identified by MS-GappedDictionary and MS-Dictionary in the six-frame translation of the human genome. MS-Dictionary identifies less peptides than MS-GappedDictionary when the peptide length is longer than 13.

In contrast to MS-Dictionary, peptides matched to gapped peptides or gapped tags generated by MS-GappedDictionary may not belong to the Spectral Dictionary. For example, a gapped peptide AT[144]GG may match to ATSGGG (in the Spectral Dictionary) and ATGSGG (not in the Spectral Dictionary). Thus, all peptides matched by MS-GappedDictionary have to be scored to remove those that are not in the Spectral Dictionary. (There may be multiple peptides in the database matched to the gapped peptides or gapped tags (see Table S6 in Supplement). However, MS-GappedDictionary never accept a PSM (Peptide-Spectrum Match) without scoring the entire spectrum against the full length peptide using MS-GF scoring function. This additional scoring step applies to all found PSMs (gapped peptides in the Pocket Dictionary are only used to filter the database). After MS-GF scoring, MS-GappedDictionary assigns p-values (spectral probability) to each PSM.) Because the number of peptides matched by MS-GappedDictionary before scoring is typically small (supplemental Table S5), the time required for removing low-scoring peptides is negligible (less than 0.01 s per spectrum).

DISCUSSION

Gapped peptides occupy a niche between accurate but short peptide sequence tags and long but inaccurate full-length peptide reconstructions. The gapped peptides are both long and accurate making them an ideal choice for de novo-based MS/MS database searches. In difference from peptide sequence tags, they typically have a few matches in a database often reducing peptide identification to a single look-up in the database. Although future work will focus on efficient matching of gapped peptides against large databases, we show how gapped tags can be generated from gapped peptides to effectively filter indexed databases. Furthermore, we show how the concept of coverage can be instrumental for ranking sparse representations of spectral dictionaries, here limited to gapped tags and gapped peptides but conceptually generalizable to any sparse representation of all plausible peptide reconstructions. We emphasize that every gapped peptide search must be complemented by rigorous scoring of all found peptide-spectrum matches (i.e. with MS-GF (21) as described above) to ensure that only statistically significant PSMs are reported. MS-GappedDictionary enables proteogenomics (e.g. searches against the six-frame translation of large genomes) and metagenomics (e.g. searches against 1000+ already sequenced bacterial genomes) analysis that is prohibitively slow for traditional MS/MS database search tools.

Although this paper focuses on nonmodified gapped peptides (proteogenomics studies are typically based on nonmodified peptides, (We remark that many modified peptides identified in typical MS/MS searches are also identified as nonmodified peptides. For example, although oxidation of Met is very common, as observed in Gupta et al. 2007 [22], for a great majority of identified peptides with Met⁺¹⁶, there exists also a nonmodified version of the same peptide (that is sufficient for proteogenomics applications). This observation applies to most chemical adducts and even some biological modifications.) MS-GappedDictionary is applicable to spectra of modified peptides as well (see Supplement Table S7). If the set of modifications is given in advance (like in traditional MS/MS search approaches), one can generate the set of modified gapped peptides by simply extending the set of masses to accommodate masses of modified amino acids. Nevertheless, the probability that the Pocket Dictionary contains a correct gapped peptide may start decreasing if diverse modifications are added to the analysis. Moreover, gapped peptides with modifications should be converted into those without modification when they are used for the database search. The algorithms that address these issues are under development.

Although MS-GappedDictionary has a potential to speed-up database searches by orders of magnitude as compared with other widely used tools such as SEQUEST and InsPecT, its performance deteriorates in the case of highly charged spectra (charge 4 and higher). This is a bottleneck for all MS/MS database search approaches based on full length peptides or peptide sequence tags (18). Further advances in design of scoring functions for highly charged spectra are needed to address this bottleneck (25).

We emphasize that the benefits of a preprocessed database are best used when the database does not need to be re-processed to reflect changes in enzyme specificity, number of missed cleavages, etc. Our approach assumes a standard combinatorial pattern matching (CPM) database preprocessing (e.g. hash tables, keyword trees, suffix trees, etc (33).) rather than a specialized MS/MS database preprocessing that may account for different search parameters such as the precursor mass or the enzyme specificity. Thus, we assume that applications of MS-GappedDictionary do not require database re-processing when the search parameters change. Although traditional MS/MS database preprocessing (e.g. by parent mass) may be more specific than a CPM preprocessing, this benefit is being offset by the universal nature of CPM preprocessing and by the fact that gapped peptide searches are much faster than the traditional database searchs (even with universal rather than specialized database indexing). In the case when the search changes to include an additional post-translational modification, we suggest to change the gapped peptide generation (i.e. to transform gapped peptides with modifications into gapped peptides without modifications) rather than to reprocess the database.