Microindentation permits biomechanical characterization of small specimens of ocular tissues and demonstrates that although properties of periocular fatty tissues vary markedly by location, comparable bovine and human tissues behave similarly.
Abstract
Purpose.
The authors applied a novel microindentation technique to characterize biomechanical properties of small ocular and orbital tissue specimens using the Hertzian viscoelastic formulation, which defines material viscoelasticity in terms of the contact pressure required to maintain deformation by a harder body.
Methods.
They used a hard spherical indenter having 100 nm displacement and 100 μg force precision to impose small deformations on fresh bovine sclera, iris, crystalline lens, kidney fat, orbital pulley tissue, and orbital fatty tissue; normal human orbital fat, eyelid fat, and dermal fat; and orbital fat associated with thyroid eye disease. For each tissue, stress relaxation testing was performed using a range of ramp displacements. Results for single displacements were used to build quantitative Hertzian models that were, in turn, compared with behavior for other displacements. Findings in orbital tissues were correlated with quantitative histology.
Results.
Viscoelastic properties of small specimens of orbital and ocular tissues were reliably characterized over a wide range of rates and displacements by microindentation using the Hertzian formulation. Bovine and human orbital fatty tissues exhibited highly similar elastic and viscous behaviors, but all other orbital tissues exhibited a wide range of biomechanical properties. Stiffness of fatty tissues tissue depended strongly on the connective tissue content.
Conclusions.
Relaxation testing by microindentation is a powerful method for characterization of time-dependent behaviors of a wide range of ocular and orbital tissues using small specimens, and provides data suitable to define finite element models of a wide range of tissue interactions.
Biomechanical properties of ocular and orbital tissues are of increasing interest in disciplines from refractive surgery to ocular motility. Accurate biomechanical properties must be known in generalized form for computational analysis of tissue responses to mechanical forces. Biomechanical characterization has been performed using a plethora of techniques for tissues such as cornea,1–3 crystalline lens,4–6 sclera,7–10 iris,11,12 orbital fat,13,14 orbital connective tissue,14,15 and extraocular muscle (EOM).16–18 However, idiosyncratic techniques used in some tissues often lead to results that cannot be generally compared among tissues.
Conventional mechanical experimental techniques such as uniaxial-tensile testing, by which strips of specimens are clamped at each end and pulled until rupture, are inappropriate for small or amorphous tissue specimens, which are frequently the only ones available. An alternative technique, fine-scale indentation, has recently emerged as a method of biomechanical characterization that can be performed in situ or with smaller and less processed specimens. Indentation produces results suitable for general comparisons in the context of Hertzian viscoelastic analysis,19–22 a general mathematical formulation that describes material stiffness in terms of the contact pressure to initiate deformation by a harder spherical body.
In this study, we developed quantitative models of multiple ocular and orbital tissues within the framework of Hertzian viscoelasticity based on experimental measures of microscale indentation. These models were validated by accurate prediction of tissue responses to a wide range of deformations and related to tissue composition by quantitative histology.
Methods
Microindentation Relaxation Testing
A custom displacement-controlled indentation load cell was assembled. Given that testing in the microscale requires fine resolution of both force and displacement, a 100-nm precision linear stepper motor and controller (Thorlabs, Newton, NJ) was synchronized with a 100-μg precision analytical balance (Mettler-Toledo, Columbus, OH). The stepper motor displaced tungsten spheres of 2-, 3-, 4-, 5-, or 6-mm diameter downward against test specimens that rested in a Petri dish on the analytical balance pan. A position servo maintained constant pan position while reading out the force exerted on the pan. The specimen was immersed in lactated Ringer solution and was maintained at 37°C by a conduction heating pad and by diffuse heat lamp illumination.
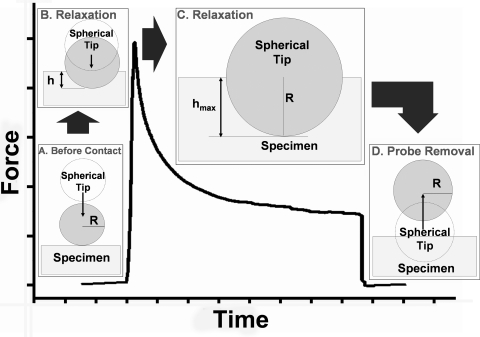
Before each test, the initial contact position for the indenter was determined. Downward force became transiently negative on initial contact of the probe with the liquid layer because of the surface tension. Initial contact of the probe with the specimen occurred when approximately 100- to 200-μg positive force was observed. Indentation was then applied at a fixed rate, optimized for each specimen type, after which the resultant indenter force was measured for approximately 100 seconds during maintenance of the fixed indentation depth. Figure 1 schematically illustrates test events.
Figure 1.
Typical microindenter data. (A) Because of downward capillary force exerted by the Ringer solution, there is a slight increase in force before imposition of physical deformation on the specimen. (B) During ramp loading, force rapidly increases because of deformation by the indenter. (C) During maintained deformation, force relaxation is observed for >100 seconds. (D) The force returns to zero after the probe is lifted from the specimen.
The force-time (P-t) data of two trials were averaged for each displacement distance. At least four displacement distances were used to compute a viscoelastic model for each tissue type.
Hertzian Viscoelasticity
Viscoelastic modeling was performed to describe indentation by a sphere of radius, R, to a depth, h, by a ramp trajectory within the framework of Hertzian contact mechanics21,23 that is derived fully in the Appendix. Briefly, a load-relaxation function consisting of three exponential terms was first fit to the experimental data using the Levenberg-Marquardt nonlinear least squares method.21 Material parameters, Ci, were determined from force-relaxation parameters, Bk. The model incorporates a ramp correction factor (RCF) that accounted for finite, rather than ideally instantaneous, ramp loading time. Short-term (E0) and long-term (E∞) elastic stiffnesses are generalized biomechanical descriptors of the tissues and can be determined from the fitted viscoelastic model with material parameters. These elastic stiffnesses constitute the primary outcome measures of the study.
Specimen Preparation
Bovine specimens were extracted fresh from local abattoir after slaughter the same morning (Manning Beef LLC, Pico Rivera, CA). Total preparation time for specimens averaged 15 ± 5 minutes (SD).
Bovine Sclera
One-centimeter–wide strips of bovine sclera were sharply excised from three different regions of the bovine globe whose mean diameter was 33 ± 2 mm. Region 1 was closest to the limbus, region 2 was from the equator, and region 3 was close to the optic nerve. Each strip was then divided longitudinally into three specimens measuring 1-cm long × 0.5-cm wide with mean thickness 1.7 ± 0.4 mm (depending on specimen location). However, in preliminary experiments, all 10 specimens from three different regions of the same globe exhibited similar elastic and viscous behaviors, indicating that the mechanical properties do not change significantly along the axial direction. Although negligible difference in mechanical properties was observed along the axial direction, large variation in mechanical properties was observed between the inner and outer scleral surfaces. Therefore, we tested differences in mechanical properties between inner scleral surface specimens and outer scleral surface specimens. After removal of external attached tissues such as tendon and Tenon's fascia, as well as the uveal tract from the inner surface, 10 specimens were prepared of each specimen type.
Bovine Iris
Bovine iris specimens were much thinner than scleral specimens at approximately 900 μm. Because it had been determined from preliminary experiments that mechanical properties were uniform throughout entire iris, iris regions were not differentiated. Once bovine corneas were excised, the iris was removed en bloc, and 3 × 3-mm strips were prepared. Ten iris specimens were tested from three globes.
Bovine Crystalline Lens
Eleven specimens were prepared from six animals. The lens was glued to a Petri dish with cyanoacrylate. The issue of possible topographic variation in local elasticity disparity remains controversial; investigations have reported difference in local mechanical properties as a function of location on the lens surface,24,25 whereas other authors have reported a single stiffness value.26,27 Because of the size of the spherical indenter and the curved shape of the lens, only the center of the lens was tested. Examinations after indentations were performed to verify that the lens capsules remained intact.
Bovine Orbital Connective and Fatty Tissues
The distribution and content of fatty and connective tissues were determined in a previous study that included histologic analysis of serial sections of the whole bovine orbit.14 Ten pulley tissue specimens extracted from the previously determined pulley and 10 fatty tissue specimens taken from the orbit between the retractor bulbi and rectus EOMs14 were prepared from four orbits. Specimens were cut to a 5-mm-diameter at 3-mm thickness.
Bovine Kidney Fat
To compare viscoelastic properties of orbital fat with nonorbital fat, experimental specimens were prepared from fresh bovine kidney fat. Ten specimens were prepared measuring 1 × 1-cm at 5-mm thickness.
Human Periocular Fat
As discarded tissue from ophthalmic surgeries, we obtained healthy human orbital fat, orbital fat from patients with thyroid eye disease, and healthy human eyelid fat. Each tissue was cut into a 4-mm cube. Time from surgical excision to analysis averaged 30 minutes. Ten healthy human orbital fatty specimens were prepared from the anterior orbital fat of four subjects. Eight specimens were prepared from the retrobulbar orbital fat of two patients with thyroid eye disease. Ten specimens were prepared from eyelid fat of patients who did not have evidence of inflammatory orbital disease.
Human Dermal Fat
We obtained subcutaneous preauricular fat as discarded tissue from facial plastic surgeries. Time from surgical excision to analysis averaged 30 minutes. Ten specimens were prepared measuring 10 × 10 × 12 mm.
Histology and Quantitative Tissue Composition
To explore the relationship between collagen content and mechanical properties, tissues were examined histologically as previously described.14 Samples were dehydrated in alcohol solutions with different concentrations from 50% to 100%. After complete dehydration, the fatty portion of the tissue was dissolved in xylene. Tissue samples were then serially sectioned at a 5-μm thickness after they were embedded in paraffin and stained with hematoxylin. Photographs in 24-bit color were made using a microscope (E800N; Nikon, Tokyo, Japan) fitted with a digital camera (D1X; Nikon). Four randomly selected micrographs were thresholded into binary images; the number of white pixels representing eluted fat was compared with the total number of tissue pixels to determine the percentage of fat in each specimen.
Results
Preliminary Validation
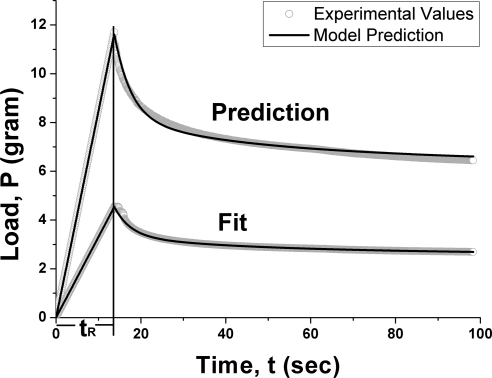
To validate the model's representation of viscoelastic behavior of a well-behaved synthetic material, indentation testing was performed on a specimen of damping foam (Confor-Foam, CF-47050; E-A-R Specialty Composites, Indianapolis, IN). Experimental results from relaxation testing for 100 seconds at two different ramp displacements are shown in Figure 2. In each case, force was observed to rise rapidly to a peak during the indentation ramp; however, as the indentation was maintained at the specified amplitude, force rapidly declined from this peak at a gradually decreasing rate. The data in Figure 2 represent the means (± SD) of three trials on the same specimen for which ramp displacements of 0.55 and 1 mm were imposed at indentation rates of 40 and 73 μm/s, respectively, during same rise time, tr, of 13.7 seconds. Viscoelastic model parameters were determine by fitting to the lower strain rate data and were used to predict the response for the higher ramp displacement. There was excellent agreement between the model and the data because the value for maximum error between the model prediction and the data were 4.9% at the higher ramp loading rate. These findings indicate general validity of the Hertzian approach with data from the custom load cell.
Figure 2.
Indentation testing of synthetic material damping foam at 40 μm/s and 73 μm/s displacement rate, resulting in 0.55- and 1-mm displacements, respectively. The viscoelastic model fit to the lower displacement rate accurately predicted the observed response to the higher displacement rate, with a maximum deviation of 0.21 g. Data average three repetitions.
Bovine Sclera
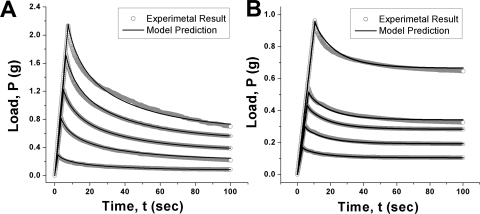
The qualitative behavior of sclera was typical of all specimens of every type tested and are described here in detail. Twenty-two scleral specimens (12 scleral inner and 10 outer surfaces) were tested at various levels of indentation. Viscoelastic mechanical models based on data from any one displacement for each specimen accurately predicted behavior for all other displacements tested, as was the case for the synthetic material in Figure 2. Figures 3A and 3B compare experimental data and model predictions for inner and outer surfaces of sclera at various indentation levels over a 100-second interval. The maximum average errors between model prediction and data for the inner and outer scleral surfaces were 6.4% and 3.2%, respectively. As further evidence of agreement between model prediction and experimental data, coefficients of determination (R2) values for all five ramp displacements exceeded 0.98 for both inner and outer scleral surfaces. Short- and long-term stiffnesses computed from the viscoelastic models were 119 ± 2.6 (± SEM), and 27.5 ± 2.5 KPa, respectively, for the inner scleral surface and 31.9 ± 1.6 and 17.0 ± 0.3 KPa, respectively, for the outer scleral surface (Table 1). Although larger ramp displacements were used for the outer than for the inner scleral surface, resultant peak forces were lower for the outer sclera, indicating that the inner scleral surface is less elastic than the outer scleral surface. In addition, both average stiffnesses for the outer scleral surface (n = 5) were significantly smaller than the stiffnesses for the inner scleral surface (t-test; P ≤ 10−8 for short-term and P ≤ 10−5 for long-term stiffness).
Figure 3.
Comparisons of model predictions and experimental results for bovine inner (A) and outer (B) scleral surfaces. Each ramp displacement represents the average of two trials. (A) Ramp displacements of 45, 92.5, 125, 160, and 190 μm were imposed on five inner scleral surfaces. The sum of squares of residuals between experimental results and model predictions for five ramp displacements were 0.028, 0.17, 0.014, 0.34, and 1.18 gm2, respectively. Coefficients of determination for all ramp displacements were >0.98. (B) Viscoelastic responses of outer surface scleral specimens to indentation. 77.5-, 116-, 150-, 170-, and 265-μm ramp displacements were imposed. The sum of squares of residuals between experimental results and model predictions for the five ramp displacements were 6.3 × 10−4, 9.2 × 10−3, 2.05 × 10−5, 0.089, and 0.14 gm2, respectively; all coefficients of determination for fits to data exceeded 0.98.
Table 1.
Summary of Parameters Viscoelastic Model Fits for All 11 Types of Specimens Tested
| Bovine Outer Sclera | Bovine Inner Sclera | Bovine Lens | Bovine Iris | Bovine Orbital Connective Tissue | Bovine Orbital Fat | Human Orbital Fat (thyroid disease) | Human Eyelid Fat | Human Orbital Fat (normal) | Bovine Kidney Fat | Human Dermal Fat | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| B0, g/mm | 0.28 | 0.35 | 1.29 | 0.03 | 0.13 | 0.27 | 0.19 | 0.15 | 0.47 | 0.02 | 0.06 |
| B1, g/mm | 0.13 | 0.58 | 36.1 | 0.22 | 0.11 | 0.12 | 0.24 | 0.30 | 4.15 | 0.48 | 0.02 |
| τ1, s | 10.2 | 7.79 | 1.51 | 3.01 | 22.5 | 34.4 | 12.91 | 13.8 | 2.04 | 2.41 | 31.7 |
| B2, g/mm | 5.06 | 1.45 | 0.24 | 0.16 | 0.20 | 0.17 | 0.14 | 9.99 | 18.6 | 0.05 | 0.02 |
| τ2, s | 1.01 | 1.56 | 1.76 | 23.9 | 3.29 | 23.5 | 111 | 1.52 | 2.86 | 9.66 | 31.7 |
| B3, g/mm | 0.09 | 0.58 | 0.77 | 0.53 | 0.56 | 6.72 | 1.85 | 0.13 | 0.62 | 0.05 | 0.37 |
| τ3, s | 19.40 | 37.5 | 23.4 | 3.01 | 0.65 | 3.33 | 1.41 | 105 | 48.5 | 84.6 | 2.37 |
| RCF1 | 1.36 | 1.40 | 6.81 | 1.65 | 1.03 | 1.09 | 1.10 | 1.22 | 10.7 | 6.20 | 1.11 |
| RCF2 | 65.5 | 7.38 | 4.97 | 1.06 | 1.21 | 1.14 | 1.01 | 9.53 | 4.92 | 1.48 | 1.11 |
| RCF3 | 1.17 | 1.07 | 1.11 | 1.65 | 2.88 | 2.87 | 2.56 | 1.03 | 1.08 | 1.04 | 5.11 |
| C0, g/mm | 1.16 | 1.87 | 0.23 | 0.02 | 0.22 | 0.03 | 0.08 | 0.03 | 0.04 | 0.05 | 0.27 |
| C1, g/mm | 0.39 | 2.23 | 1.26 | 0.07 | 0.16 | 0.02 | 0.09 | 0.04 | 0.04 | 0.08 | 0.08 |
| τ1, s | 10.2 | 7.79 | 1.51 | 3.01 | 22.5 | 34.4 | 12.91 | 13.8 | 2.04 | 2.41 | 31.7 |
| C2, g/mm | 0.32 | 1.05 | 0.01 | 0.08 | 0.22 | 0.02 | 0.08 | 0.18 | 0.26 | 0.03 | 0.08 |
| τ2, s | 1.01 | 1.56 | 1.76 | 23.9 | 3.29 | 23.5 | 111 | 1.52 | 2.86 | 9.66 | 31.7 |
| C3, g/mm | 0.30 | 2.93 | 0.16 | 0.17 | 0.41 | 0.29 | 0.38 | 0.02 | 0.04 | 0.05 | 0.30 |
| τ3, s | 19.4 | 37.54 | 23.4 | 3.01 | 0.65 | 3.33 | 1.41 | 105 | 48.5 | 84.6 | 2.37 |
| E0, KPa | 31.9 | 119 | 25.6 | 4.86 | 18.5 | 7.91 | 11.2 | 5.90 | 7.86 | 2.68 | 10.6 |
| E∞, KPa | 17.0 | 27.5 | 4.50 | 0.24 | 3.99 | 0.74 | 1.71 | 0.48 | 0.71 | 0.34 | 3.92 |
See Appendix for symbol definitions. Last two rows are bolded to indicate summary stiffness computed from parameters in preceding rows.
Similarly, multiple ramp displacements were imposed on all 11 specimen types. Based on parameters fitted to one of the data subsets, viscoelastic models were compared with experimental data for the other ramp displacements. In general, the models fit to any one ramp displacement agreed well with the data for all other ramp displacements, with R2 values consistently exceeding 0.97.
Bovine Crystalline Lens
Lens indentation was limited to 1.2 mm, beyond which the capsule ruptured. Five lenses were tested at ramp displacements of 0.47, 0.59, 0.74, 0.87, and 1.08 mm. The sum of squares of residuals between experimental results and the model predictions over all five different displacement levels were 0.025, 0.024, 0.044, 0.014, and 0.082 gm2, whereas the minimum R2 between model prediction and data for all lens specimens was 0.97, showing excellent agreement. Behavior predicted from the viscoelastic mechanical model based on data from one displacement accurately described data for all other displacements tested in each specimen. Observed short-term and long-term stiffnesses in the bovine lens were 25.6 ± 3.5 (± SEM) and 4.50 ± 1.60 KPa, respectively.
Bovine Iris
Because iris specimens were only 900-μm thick, ramp displacements were limited to 391, 436, 529, 644, and 673 μm. The sums of squares of residuals between experimental results and model predictions were 0.025, 0.024, 0.044, 0.014 and 0.081 gm2, respectively, whereas R2 values ranged from 0.97 to 0.99. The short-term and long-term elastic moduli for bovine iris specimens were 4.86 ± 0.38 (± SEM) and 0.24 ± 0.16 KPa, respectively.
Bovine Orbital Connective and Fatty Tissues
Marked differences in mechanical properties were observed between dense orbital connective tissue specimens composed of <40% fat by weight and orbital fatty tissues composed of >90% fat. For orbital connective tissue, displacements of 0.24, 0.38, 0.57, 0.81, and 1.01 mm were imposed on five specimens. Displacements of 1.21, 1.53, 1.88, 0.88, and 1.02 mm were imposed on five bovine orbital fatty tissue specimens. Model prediction showed good agreement with experimental results for both orbital connective and fatty tissue specimens at different levels of ramp displacements because most R2 values exceeded 0.95. Computed short-term and long-term stiffnesses from the model were 18.5 ± 1.8 (± SEM) and 3.99 ± 1.84 KPa, respectively, for bovine orbital connective tissue and 7.91 ± 0.41 and 0.74 ± 0.08 KPa, respectively, for bovine orbital fatty tissue. Orbital connective tissue was, therefore, stiffer than orbital fatty tissue by at least fivefold (P ≤ 10−4 for short-term stiffness and P ≤ 10−7 for long-term stiffness).
Human Orbital Fat
Human orbital fat had viscoelastic properties quantitatively similar to those of bovine orbital fat. For normal orbital fat, model predictions and experimental results for five trials agreed well; all coefficients of determination exceeded 0.95. Similar to bovine orbital fat, the short-term and long-term stiffnesses were 7.86 ± 1.00 (± SEM) and 0.71 ± 0.16 KPa, respectively, for healthy human orbital fatty specimens. However, substantial differences in biomechanical properties were observed in thyroid eye disease specimens. Long- and short-term stiffnesses for orbital fat in thyroid eye disease were substantially greater at 11.2 ± 1.3 and 1.71 ± 1.05 KPa (P < 10−3 for short-term stiffness and P ≤ 10-−4 for long-term stiffness).
Healthy Human Eyelid Fat, Dermal Fat, and Bovine Kidney Fat
Five displacements were tested on 30 specimens prepared from healthy human eyelid fat, dermal fat, and bovine kidney fat (10 specimens each). Predictions from all three models agreed well with experimental results, with coefficients of determination exceeding 0.94 for all specimens and conditions. Stiffnesses for human eyelid fat were similar in magnitude to those of human and bovine orbital fat, with short-term and long-term stiffnesses of 5.90 ± 0.98 (± SEM) and 0.48 ± 0.086 KPa, respectively (P > 0.3 for short-term stiffness and P > 0.1 for long-term stiffness). Bovine kidney fat was only approximately one-third as stiff as orbital fat, with short- and long-term stiffnesses of 2.68 ± 0.61 and 0.34 ±0.24 KPa, respectively. Both stiffnesses of bovine kidney fat differed significantly from those of human orbital fat (P ≤ 10−5 for short-term stiffness and P ≤ 0.002 for long-term stiffness). On the other hand, short-term stiffnesses of human dermal fat were twice those of lid fat at 10.6 ± 1.0 KPa (P ≤ 10−5), and the long-term stiffness of human dermal fat was nearly 10-fold higher than that of orbital fat at 3.92 ± 0.14 KPa (P ≤ 10−7).
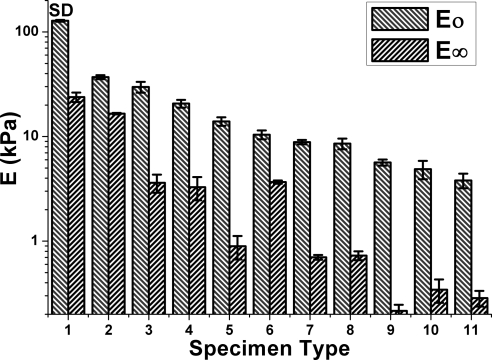
Figure 4 shows short- and long-term elastic stiffnesses for all 11 types of specimens. Bovine and human orbital fatty tissues exhibited similar short- and long-term stiffnesses. Although the greatest difference between short and long-term stiffnesses were observed in the iris, only minimal differences between short- and long-term stiffnesses were observed in the outer sclera and dermal fatty tissue.
Figure 4.
Short- (E0) and long-term stiffness (E∞) for all types of specimens. Specimen types: 1, inner surface of bovine sclera; 2, outer surface of bovine sclera; 3, bovine crystalline lens; 4, bovine orbital pulley tissue; 5, human orbital fat in thyroid eye disease; 6, human dermal fat; 7, bovine orbital fat; 8, human orbital fat; 9, bovine iris; 10, human eyelid fat; 11, bovine kidney fat.
Histology
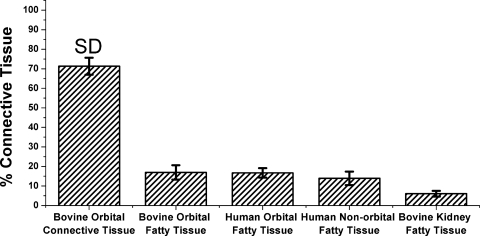
Figure 5 shows histologic sections of five tissues. As seen in Figure 5A, connective tissue stains more darkly, indicating more collagen, whereas soluble fat is eluted, leaving white voids. The connective tissue specimen (Fig. 5A) extracted from the pulley region has fewer fatty voids than does predominantly orbital fat (Fig. 5B). In addition, human and bovine orbital fatty tissue specimens contained more collagenous content than bovine kidney fat (Fig. 5E), which exhibited larger fat cells than other specimens. Four randomly taken micrographs for each specimen were analyzed to quantify fatty composition, as shown in Figure 6.
Figure 5.
Hematoxylin-stained micrographs. (A) Bovine orbital connective tissue containing 71% ± 4% collagen. (B) Bovine orbital fat containing 17% ± 2% collagen. (C) Human orbital fat containing 17% ± 2% collagen. (D) Human eyelid fat containing 14% ± 3% collagen. (E) Bovine kidney fat containing 6% ± 1% collagen.
Figure 6.
Mean fatty composition of five tissues.
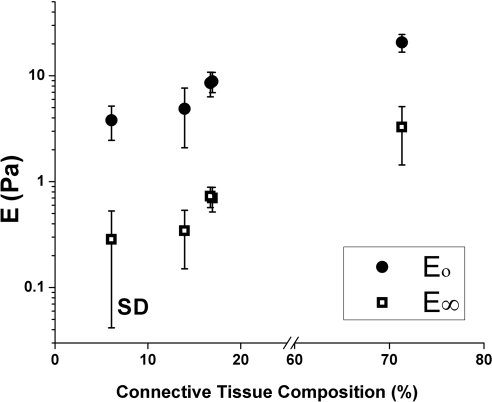
Figure 7 correlates both short-term and long-term stiffnesses for all five fatty specimens as a function of connective tissue content. Initial and long-term stiffnesses increased with increasing connective tissue composition, which necessarily implied decreasing fat composition.
Figure 7.
Short-term (E0) and long-term (E∞) stiffnesses increased with increasing connective tissue composition of tissue in (from left to right) bovine kidney fat, human eyelid fat, human orbital fat, bovine orbital fat, and bovine pulley tissue.
Discussion
Microindentation with Hertzian viscoelastic analysis proved here to be a general and practical approach by which to study the viscoelastic behavior of ocular tissues that are not suitable for conventional mechanical approaches such as uniaxial tensile testing. The viscoelastic model formulation, which incorporates elastic-viscoelastic correspondence and a relaxation function composed of the sum of exponentials, accurately described the time-dependent mechanical behavior of all the ocular tissues in the framework of Hertzian viscoelastic contact for incompressible material.23,28 Hertzian models based on parameters fit to a subset of microindentation data accurately predicted behavior over a wide range of indentation amplitudes because the coefficients of determination of model predictions and experimental results for all 11 tissues averaged 0.97. This verifies that the Hertzian model is an excellent and general description of viscoelastic behavior of ocular tissues.
In a finite element analysis of orbital tissue mechanics, Schutte et al.29 estimated the elastic modulus, which is equivalent to long-term stiffness in the present study, for intraconal and extraconal retrobulbar fat to be 0.3 and 1.0 KPa, respectively. Although “muscle cone” as a demarcating structure in the deep orbit is an anatomic fiction,30 the bovine orbital fatty tissue in current investigation may correspond to what Schutte et al.29 termed intraconal retrobulbar fat. The present study determined the long-term stiffness of human orbital fat to be 0.71 KPa, which is of similar magnitude to that reported by Schutte et al.29 A more important observation of the current investigation, however, was similarity in the stiffness of normal human and bovine orbital fatty tissue. As can be seen in Table 1, the long-term stiffness of human orbital fatty tissue and bovine orbital fatty tissue are similar at 0.74 and 0.71 KPa, respectively. Although there is <5% difference in long-term stiffness between human and bovine orbital fatty tissues, dense bovine connective tissue from around the globe equator has a much higher long-term stiffness of 3.99 KPa, which is within same order of magnitude of stiffness for extraconal retrobulbar fat reported by Shutte et al.29 The long-term stiffness of dense orbital connective tissue, also known as pulley tissue, exceeds that of orbital fatty tissue close to threefold, which agrees with the assessment of Yoo et al.14 Highly stiff connective tissue, of which pulleys are composed, must be therefore be distinguished in biomechanical models from the much less stiff orbital fat. Pulley tissue is highly collagenous (Fig. 6), making its mechanical properties markedly different from those of orbital fatty tissue.
Although several studies have measured orbital compliance in Graves' eye disease,31,32 there have been no previous in vitro measurements of elastic stiffness of orbital fat in this disorder. As seen in Figure 5, orbital fat in thyroid eye disease has significantly higher short- and long-term stiffness values at 11.2 and 1.7 KPa than those of normal human and bovine orbital fatty tissues. However, both stiffnesses are approximately half that of bovine orbital connective tissue, clearly suggesting that connective tissue content makes a more significant contribution to the structural stiffness of soft tissue than does fat, which is infiltrated by fibrosis in thyroid eye disease.
As shown in Figure 4, short- and long-term stiffnesses for the inner sclera were 119 and 27.5 KPa, but they were lower at 31.9 and 17.0 KPa for the outer sclera. Battaglioli et al.7 determined the static compressive modulus of cattle sclera range from 12 to 19 KPa, which is comparable to our long-term elastic modulus for inner sclera of 27.5 KPa. Using uniaxial tensile testing, Downs et al.9 found long-term elastic moduli of 7.46 ± 1.58 MPa for monkey eyes with early glaucoma and 4.94 ± 1.22 MPa for healthy monkey eyes. It thus appears that that scleral tissue may be 50-fold stiffer under tensile than under compressive loading.
Transverse elastic stiffness of the bovine iris has not been previously reported. Using an extension method, Heys et al.11 previously reported the radial stiffness of the iris sphincter and dilator to be 340 KPa and 890 KPa, respectively. This should not be expected to be comparable to the compressive loading data reported here. Elastic moduli for bovine iris tissue resulting from the viscoelastic model in current investigation are 4.86 and 0.24 KPa, indicating that stiffness in the radial direction is different from transverse stiffness. For bovine lens, short-term and long-term elastic moduli were found here to be 25.6 and 4.50 KPa, respectively. Fisher4 reported that the stiffness of the human lens is much lower, ranging from 0.75 to 3.0 KPa. Although there might be discrepancy between the mechanical properties of human and bovine lens, the long-term stiffness of bovine lens found in the present study certainly falls within the same order of magnitude.
One important observation made in the current investigation is how tissue stiffness varies with connective tissue versus fat composition. As can be seen in Figures 6 and 7, connective tissue content was directly correlated with stiffness in five different tissues. This seems logical if collagen and elastin, rather than lipid, constitute the elastic component of the orbital tissues.
Although not available for testing in the present study, it is likely that human orbital pulley tissue would have viscoelastic properties similar to those of bovine pulley tissue, but different from those of human and bovine orbital fat. The viscoelastic models for various orbital tissues reported in the current investigation can be used in FEA simulation of orbital biomechanical responses to compressive loads. Biomechanical responses to tensile loads might differ in some cases and should also be tested for complete tissue characterization. Implementation of accurate material properties in FEA simulations would render them more realistic.
Acknowledgments
The authors thank Manning Beef, LLC (Pico Rivera, CA), for the generous contribution of bovine specimens; Jose Martinez, Claudia Tamayo, and Ramiro Carlos for assistance with specimen preparation; and Ben Glasgow, MD, for assistance with histologic processing.
Appendix
Hertzian Viscoelastic Model
When a rigid sphere of radius, R, is pressed a distance, h, into an incompressible material with elastic modulus, E, the sphere exerts force, P, that is a function of Poisson ratio ν, the ratio of the transverse contracting strain to the elongation strain (equation 1a).
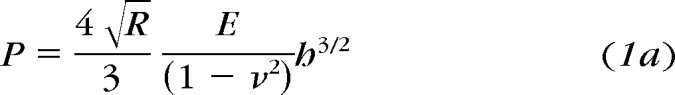 |
If the material is incompressible, as seems reasonable for biological materials, the Poisson ratio is, by definition, ν = 0.5, and the shear modulus G = E/3.
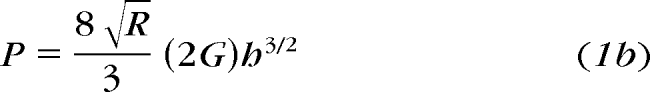 |
shows that the indenting force, P, is a nonlinear function of indenter displacement and a linear function of shear modulus.
The principle of viscoelasticity is used for modeling of time dependence.33 Instead of constants, a viscoelastic operator is substituted for the elastic modulus, E, in equation 1a, or shear modulus, G, in equation 1b.21,22,28,33 The elastic modulus and relaxation functions (represented as a Prony series, which is a sum of exponential functions) then can be fit empirically.21,23,28
The relaxation response for a step-load experiment is expressed in equation 221,22,28
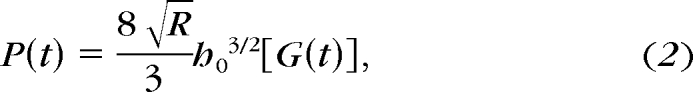 |
where G(t) is the time-dependent shear relaxation modulus. Given that ideal instantaneous step loading is not physically attainable, actual rise time (tR) for ramp loading should be considered in the derivation.21,23 Equation 3 is a viscoelastic integral operator for relaxation where u is a strain function of time dummy variable τ.
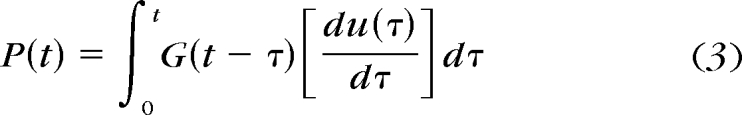 |
As suggested by Mattice et al.,21 a Boltzmann integral method23 is used here. When the time-dependent relaxation modulus in equation 2 is combined with equation 3, the resultant Boltzmann integral equation is shown in equation 4.
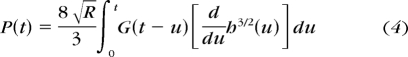 |
For ramp-loading rate k, displacement for ramp-hold relaxation can be written as
The solution for displacement-controlled relaxation is expressed as the step-loading relaxation solution adjusted by an RCF to take into account the difference in relaxation caused by noninstantaneous ramp loading.23,28 Since load P(t), is exponentially decaying during relaxation, it is expressed as
whereas the material relaxation function has the form,
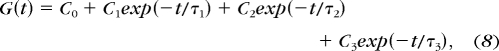 |
where τ represents each time constant for each exponential form, Bn represents a fitting constant, and Cn represents relaxation coefficients. It is parsimonious and, therefore, desirable to minimize the number of exponential terms for curve fitting. We settled on three terms that captured relaxation behavior with <6.5% error. Once all the fitting parameters (Bn) have been determined, they can be converted to material parameters (Cn) using equations 9 and 10.
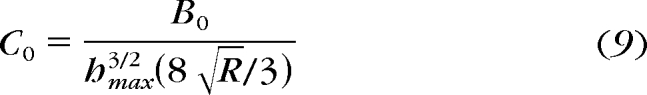 |
The equation for RCF, which compensates for actual ramp versus ideal step loading, is shown in equation 11.
Instantaneous G(0) and long-time G(∞) stiffnesses can be computed from the fitted relaxation coefficients (Ci), as shown in equations 12 and 13.
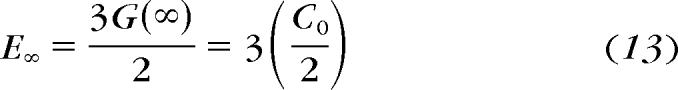 |
Footnotes
Supported by the United States Public Health Service; National Eye Institute Grants EY08313 and EY00331; and Research to Prevent Blindness. JLD is the Leonard Apt Professor of Ophthalmology at the University of California at Los Angeles.
Disclosure: L. Yoo, None; J. Reed, None; A. Shin, None; J. Kung, None; J.K. Gimzewski, None; V. Poukens, None; R.A. Goldberg, None; R. Mancini, None; M. Taban, None; R. Moy, None; J.L. Demer, None
References
- 1. Nash IS, Greene PR, Foster CS. Comparison of mechanical properties of keratoconus and normal corneas. Exp Eye Res. 1982;35:413–424 [DOI] [PubMed] [Google Scholar]
- 2. Jue B, Maurice DM. The mechanical properties of the rabbit and human cornea. J Biomech. 1986;19:847–853 [DOI] [PubMed] [Google Scholar]
- 3. Andreassen TT, Hjorth Simonsen A, Oxlund H. Biomechanical properties of keratoconus and normal corneas. Exp Eye Res. 1980;31:435–441 [DOI] [PubMed] [Google Scholar]
- 4. Fisher RF. The elastic constants of the human lens. J Physiol. 1971;212:147–180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kikkawa Y, Sato T. Elastic properties of the lens. Exp Eye Res. 1963;2:210–215 [DOI] [PubMed] [Google Scholar]
- 6. Krag S, Andreassen TT. Mechanical properties of the human lens capsule. Prog Retin Eye Res. 2003;22:749–767 [DOI] [PubMed] [Google Scholar]
- 7. Battaglioli JL, Kamm RD. Measurements of the compressive properties of scleral tissue. Invest Ophthalmol Vis Sci. 1984;25:59–65 [PubMed] [Google Scholar]
- 8. Downs JC, Suh JKF, Kevin AT, Anthony JB, Claude FB, Richard TH. Viscoelastic characterization of peripapillary sclera: material properties by quadrant in rabbit and monkey eyes. J Biomech Eng. 2003;125:124–131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Downs JC, Suh JKF, Thomas KA, Bellezza AJ, Hart RT, Burgoyne CF. Viscoelastic material properties of the peripapillary sclera in normal and early-glaucoma monkey eyes. Invest Ophthalmol Vis Sci. 2005;46:540–546 [DOI] [PubMed] [Google Scholar]
- 10. Curtin BJ. Physiopathologic aspects of scleral stress-strain. Trans Am Ophthalmol Soc. 1969;67:417. [PMC free article] [PubMed] [Google Scholar]
- 11. Heys J, Barocas VH. Mechanical characterization of the bovine iris. J Biomech Eng. 1999;32:999–1003 [DOI] [PubMed] [Google Scholar]
- 12. Yamaji K, Yoshitomi T, Usui S, Ohnishi Y. Mechanical properties of the rabbit iris smooth muscles. Vision Res. 2003;43:479–487 [DOI] [PubMed] [Google Scholar]
- 13. Schoemaker I, Hoefnagel PPW, Mastenbroek TJ, et al. Elasticity, viscosity, and deformation of orbital fat. Invest Ophthalmol Vis Sci. 2006;47:4819–4826 [DOI] [PubMed] [Google Scholar]
- 14. Yoo L, Gupta V, Lee C, Kavehpore P, Demer JL. Viscoelastic properties of bovine orbital connective tissue and fat: constitutive models. Biomech Model Mechanobiol. In press [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Van den Bedem SPW, Schutte S, Simonsz HJ. Mechanical properties and functional importance of pulley bands or ‘faisseaux tendineux.’ Vision Res. 2005;45:2710–2714 [DOI] [PubMed] [Google Scholar]
- 16. Yoo LH, Kim H, Gupta V, Demer JL. Quasilinear viscoelastic behavior of bovine extraocular muscle tissue. Invest Ophthalmol Vis Sci. 2009;50:3721–3728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Quaia C, Ying HS, Nichols AM, Optican LM. The viscoelastic properties of passive eye muscle in primates, I: static forces and step responses. PLoS ONE. 2009;4:e4850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Quaia C, Ying HS, Optican LM. The viscoelastic properties of passive eye muscle in primates, II: testing the quasi-linear theory. PLoS ONE. 2009;4:e6480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Scott ON, Begley MR, Komaragiri U, Mackin TJ. Indentation of freestanding circular elastomer films using spherical indenters. Acta Materialia. 2004;52:4877–4885 [Google Scholar]
- 20. Bryant-Greenwood GD. The extracellular matrix of the human fetal membranes: structure and function. Placenta. 1998;19:1–11 [DOI] [PubMed] [Google Scholar]
- 21. Mattice JM, Lau AG, Oyen ML, Kent RW. Spherical indentation load-relaxation of soft biological tissues. J Mater Res. 2006;21 [Google Scholar]
- 22. Johnson KL. Contact Mechanics. Cambridge, UK: Cambridge University Press; 1987 [Google Scholar]
- 23. Oyen ML. Spherical indentation creep following ramp loading. J Mater Res. 2005;20 [Google Scholar]
- 24. Heys K, Crams S, Truscott R. Massive increase in the stiffness of the human lens nucleus with age: the basis for presbyopia. Mol Vis. 2004;10:956–963 [PubMed] [Google Scholar]
- 25. Weeber H, Eckert G, Pechhold W, van der Heijde R. Stiffness gradient in the crystalline lens. Graefes Arch Clin Exp Ophthalmol. 2007;245:1357–1366 [DOI] [PubMed] [Google Scholar]
- 26. Koretz JF, Handelman GH. Model of the accommodative mechanism in the human eye. Vision Res. 1982;22:917–927 [DOI] [PubMed] [Google Scholar]
- 27. van Alphen GWHM, Graebel WP. Elasticity of tissues involved in accommodation. Vision Res. 1991;31:1417–1438 [DOI] [PubMed] [Google Scholar]
- 28. Chua W, Oyen M. Viscoelastic properties of membranes measured by spherical indentation. Cell Mol Bioeng. 2009;2:49–56 [Google Scholar]
- 29. Schutte S, Van den Bedem SPW, Van Keulen F, Van der Helm FCT, Simonsz HJ. A finite-element analysis model of orbital biomechanics. Vision Res. 2006;46:1724–1731 [DOI] [PubMed] [Google Scholar]
- 30. Demer JL. Extraocular muscles. In: Tasman W, Jaeger EA. eds. Duane's Clinical Ophthalmology. Vol. 1, ed. 2 Philadelphia: Lippincott Williams & Wilkins; 2009:1–30 [Google Scholar]
- 31. Riemann CD, Foster JA, Kosmorsky GS. Direct orbital manometry in patients with thyroid-associated orbitopathy. Ophthalmology. 1999;106:1296–1302 [DOI] [PubMed] [Google Scholar]
- 32. Frueh BR, Musch DC, Grill R, Garber FW, Hamby S. Orbital compliance in Graves' eye disease. Ophthalmology. 1985;92:657–665 [DOI] [PubMed] [Google Scholar]
- 33. Lee EH, Radok JRM. Contact problems for viscoelastic bodies. J Appl Mech. 1960;27 [Google Scholar]