Abstract
Maps of parasite prevalences and other aspects of infectious diseases that vary in space are widely used in parasitology. However, spatial parasitological datasets rarely, if ever, have sufficient coverage to allow exact determination of such maps. Bayesian geostatistics (BG) is a method for finding a large sample of maps that can explain a dataset, in which maps that do a better job of explaining the data are more likely to be represented. This sample represents the knowledge that the analyst has gained from the data about the unknown true map. BG provides a conceptually simple way to convert these samples to predictions of features of the unknown map, for example regional averages. These predictions account for each map in the sample, yielding an appropriate level of predictive precision.
The need for Bayesian geostatistics
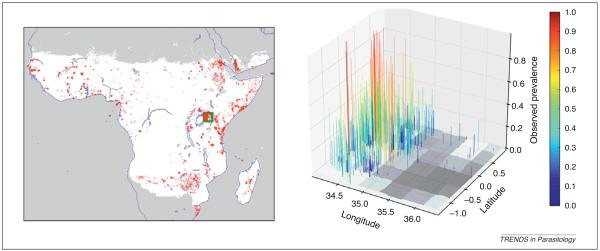
A recently described, large database of Plasmodium falciparum endemicity surveys in Africa and Yemen [1,2] is shown in Figure 1 in two and three dimensions. The data are highly clustered and coverage is sparse in Central Africa. The short-range variation in the data is striking; for example, in the small cluster to the east of Lake Victoria, where observed prevalences range widely from zero to near 80%. Efforts to account for this variability by means of environmental factors [3-5], time [2], and age [6] are ongoing, but much of it remains unexplained, possibly because local variation in environment and human activities are not captured by the environmental data available at continental scales.
Figure 1.
Spatial patterns of Plasmodium falciparum endemicity data. Visualizations of a large P. falciparum dataset [2] within the range of stable transmission in Africa. In the left-hand panel, survey locations are marked as semitransparent red dots. This panel illustrates the heavy spatial clustering in the dataset. Certain hot spots, such as East Africa and Yemen, have very dense coverage, whereas coverage in Central Africa is sparse. The data within the green square (approximately 270 km2) east of Lake Victoria are plotted in three dimensions in the right-hand panel. The z-axis and the color indicate the observed prevalence of each data point. This panel illustrates another aspect of the dataset that complicates mapping: in clusters of high coverage, there is remarkable short-range variability in prevalence.
These observations call into question the usefulness of producing a single map of P. falciparum endemicity in Africa and elsewhere. A map provides a single estimate for each location in the mapped region, and it is clearly impossible to make accurate and precise estimates of parasite rates in Central Africa based on the sparse data coverage there. Even if data coverage were uniformly dense, the unexplained short-range variability evident in data-rich East Africa indicates that no single value would capture the wide range of endemicities that might be encountered at an unsampled location. The malaria epidemiology community faces the problem of converting this patchy dataset, with substantial unexplained variation, into advice for a range of users.
Bayesian geostatistics (BG), which is becoming the standard mapping technique in certain branches of parasitology [7], is well suited to generating advice under uncertainty because it attempts to find a large sample of maps that are consistent with the dataset rather than a single map. This sample is encapsulated in the posterior distribution. This opinion is a guide to understanding and making good use of the posterior distribution for parasitologists, with examples drawn from malaria.
Posterior distributions
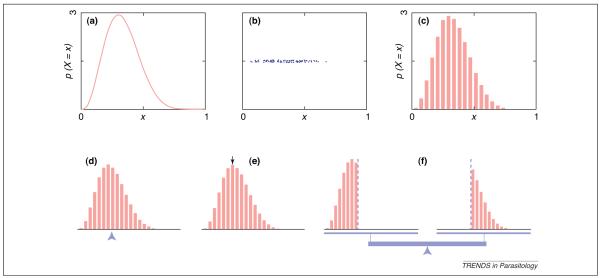
A posterior distribution, often called a posterior, is a probability distribution that has been informed by data according to the rules of Bayesian inference [8]. Figure 2 shows a probability distribution for a random number labeled X. In the Bayesian interpretation of probability, ‘random’ just means ‘unknown;’ random numbers such as X are understood to have unknown, true values. The probability distribution of X can be used to compute the probability density (intuitively speaking, the relative probability) of any given candidate value, but does not specify the value of X exactly. In Figure 2, any number between 0 and 1 is a possible value, but each alternative number has a different probability density.
Figure 2.
Probability distributions for unknown numbers and their summaries. Representations and summaries of a probability distribution for a random number. Samples (b) can be drawn from a probability distribution, shown in (a) as a probability density function (PDF). Many such samples can be compiled into a histogram (c), which approximates the original PDF (a). The representations in the top row can be summarized as, for example, the mean (d), which is the point at which the PDF would balance on a fulcrum; the mode (e), which is the highest point on the PDF; and the median (f), which is the dividing point where the two halves of the PDF have equal mass. Although the summaries on the bottom row are depicted in terms of the histogram representation (c), it is generally most convenient to compute them based on the sample representation (b).
Figure 2 shows the probability distribution as both a probability density function (PDF) and as random values (also known as realizations) generated from it. In Bayesian probability, these values can be interpreted as a sample of all the candidates for the unknown, true value of X. Values that are more probable are more likely to be represented. A long list of these candidate values can be seen as an alternative representation of the probability distribution, and in practice are usually more useful than its mathematical formula. Properties of a probability distribution such as the mean, variance, quantiles and credible intervals can be estimated readily from long lists of candidate values.
A BG analysis is an application of these ideas to an unknown map, which is made up of one unknown number for each point in the region of interest. In BG, the posterior is a probability distribution for the map that takes the data into account. It is understood that in reality there is a single true map, but that it cannot be determined exactly from the data. A vast variety of maps are possible, but a more restricted variety is probable in light of the data. It is possible to generate candidate maps (CMs, also known as realizations) from the posterior. Because random maps are much more complicated than random numbers, it is not possible to visualize their probability distributions as PDFs; the posterior is best understood as a long sequence of CMs.
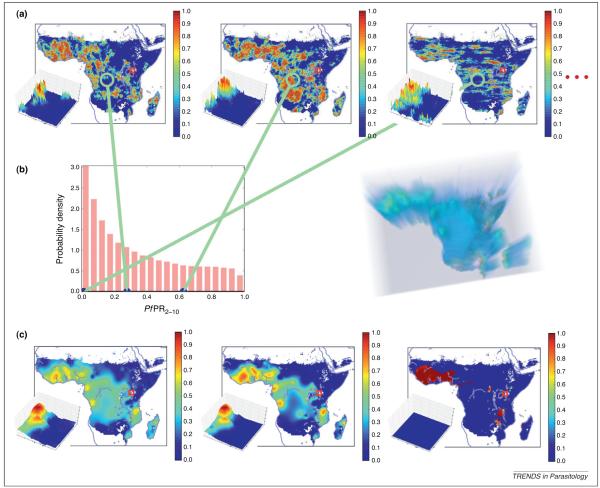
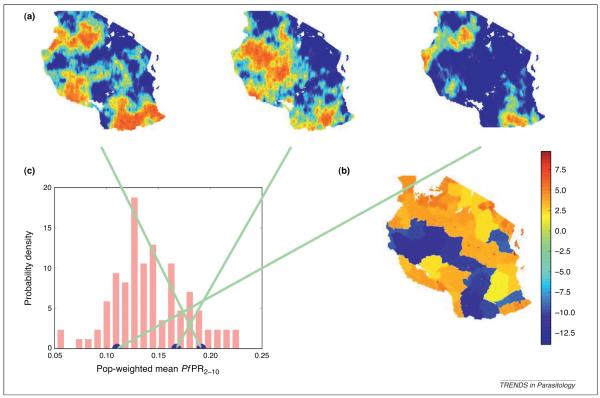
Three CMs of P. falciparum endemicity within the regions of stable malaria transmission in Africa [2] are shown in Figure 3(a). Between them, the maps convey some idea of the variety of large-scale spatial patterns that are consistent with the dataset. In Central Africa, some maps show high typical values and some show low values, reflecting the relatively large uncertainty associated with this data-poor area. In data-rich East Africa, however, the pattern is relatively consistent from map to map.
Figure 3.
Probability distributions for unknown maps and their summaries. The relation between the posterior of the map of average P. falciparum endemicity over 2007 within the areas of stable transmission in Africa in 2–10-year-olds [2], and some summaries of the posterior. The posterior of a map cannot be visualized as a probability density function or histogram, as was possible in Figure 2(a,c). The most understandable and usable representation of this complicated mathematical object is a long sequence of CMs (analogous to Figure 2(b)), three of which are shown in row (a). Each CM (or realization) in row (a) is credible given the data, meaning it reflects the long- and short-range patterns of spatial variation seen in the data and its value at each of the observation locations is consistent with the data. The maps are in relatively good agreement with one another in areas with abundant data, such as East Africa, but major discrepancies can be found in areas of sparse data, such as Central Africa, reflecting the uncertainty of the prediction. The long sequence of CMs does not have any particular order; they are exchangeable [46]. Any number of them can be produced, given sufficient time. Because the ‘map view’ in row (a) de-emphasizes the short-range variation, the portion of each map within the red square east of Lake Victoria (the same square as in Figure 1) is shown in three dimensions. The histogram in row (b) was generated by extracting the value of a large number of CMs at a single pixel (located near Brazzaville, Democratic Republic of the Congo) and combining these values. Repeating this procedure for every pixel results in the ‘density field’ pictured on the right in row (b). This density field is less informative than the set of CMs. It contains the posterior of each pixel taken independently, but does not contain any information about their probabilistic dependencies (i.e. it does not incorporate the patterns of long- and short-range variation seen in the CMs). The density field can be reduced further to produce the summary maps in row (c) by taking the mean, median and mode (Figure 2(d,f)) at each pixel. These maps are indispensable visual aids, but they do not reflect the short-range variation seen in the dataset and row (a). In other words, none of the maps in row (c) is a credible candidate for the unknown, true map. Row (a) is the most complete representation of the posterior; any of the summaries pictured in rows (b) and (c) can be calculated from row (a), but not vice versa.
Samples of CMs are the conceptual key to the full range of probabilistic results that BG can produce, so we focus on them in this paper. However, they are usually not produced explicitly in practice because of their computational cost [9]. Computational shortcuts exist to produce many of the same results (see the Conclusions).
Predicting functions of the map
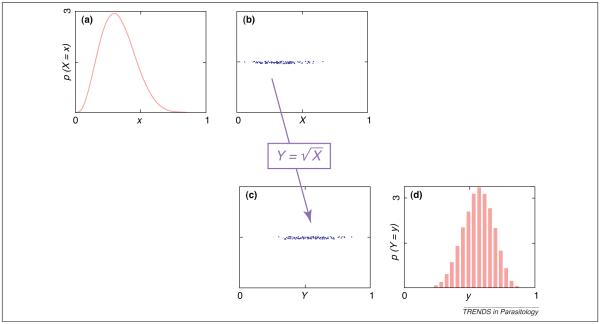
Consider once more the random number X whose probability distribution is shown in Figure 2. A useful feature of the candidate value-based representation is that it can be directly converted to an analogous representation for the probability distribution of any variable Y that depends on X, Y=f(X). Examples include the square of X and the logarithm of X. The procedure is simple: f is applied to each candidate value of X to obtain a candidate value of Y. If desired, these transformed values can be compiled into a histogram, which approximates the PDF of Y (Figure 4).
Figure 4.
Transformations of unknown variables. The probability distribution for variable X depicted in (a) as a probability density function can alternatively be represented by a set of candidate values (b), as in Figure 2. One advantage of this representation is that it can be easily converted to an equivalent representation for any variable Y=f(X) (c). This representation can be converted to a histogram (d), which approximates the probability density function of Y.
This benefit is also enjoyed by the candidate value-based representation of the posterior of the P. falciparum endemicity map (Figure 3). Suppose the population-weighted average endemicity in Tanzania were desired. If, hypothetically, the true map were known, this product could be approximated using standard geographic information systems (GIS) software by representing the map as a raster, multiplying it by a population raster (assuming it is known) of the same resolution, summing the result over all the pixels in Tanzania, and dividing by the total population. In reality, the true map is not available but CMs are. These can be converted into candidate values for population-weighted average endemicity in Tanzania by following the procedure in Figure 4. The raster operation just described (which plays the role of f) is applied to each of the CMs (X) to obtain a set of candidate values for the average endemicity (Y), which form a representation of its posterior (Figure 5). This can be presented directly as a histogram or summarized, for example as the mean, median or mode (Figure 2).
Figure 5.
Predicting volumetric quantities. Estimating population-weighted average endemicity in Tanzania. Each of a large number of CMs (a) is combined with a population raster [(b) shows the log of population density in Tanzania in 2007 according to the GRUMP product [47] to produce a sample from the posterior distribution of population-weighted average endemicity in Tanzania]. These values are collected to produce a histogram, which approximates the actual posterior.
The simplicity of candidate value-based prediction is deceptive, so it is worth emphasizing that it is a method for approximating the unique posterior prescribed by probability theory, based on the model (including priors) and the dataset, for any product that could be derived from the true map (if it were known). This simple, flexible procedure for making predictions is the primary advantage of BG.
‘The’ map and the role of GIS
It is not possible to visualize the posterior of a map as a PDF. As a useful alternative, BG analyses invariably present summary maps (Figure 3) [2,7,10-24]. Constructing these maps from the posterior is straightforward. If, hypothetically, the true map were known, endemicity at a given pixel could be extracted using a GIS. The procedure in the previous section can therefore be used to produce a posterior for endemicity (the CMs are X, extraction at a particular pixel is f, and the value of the map at the pixel is Y). The median, for example, of the distribution of endemicity at the pixel can be computed and recorded. The medians for all pixels of concern can be displayed as a map.
Summary maps are good overall pictures of the information contained in the data. However, they misrepresent the posterior in several important ways. The summary maps shown in Figure 3(c) lack the short-range variability seen in the data. Over longer scales, they give the incorrect impression that the endemicity is more spatially variable in areas of dense data coverage. The CMs are not subject to either shortcoming and indeed they look completely unlike the summary maps. The summary maps are not plausible candidates for the true map.
Nevertheless, a single summary map is usually presented, and users frequently perform further GIS-based analysis on it. This procedure often does not yield the desired results (Box 1). In addition, it introduces arbitrariness and ambiguity into the predictive analysis. For example, using the median in place of the mean changes the result. In the future, GIS software could evolve to facilitate flexible and correct predictive analysis by non-statisticians in the future. This possibility is discussed later. This possibility is discussed later.
Box 1. Using posterior summaries.
The posterior can be summarized by computing the posterior mean, median, interquartile range, standard deviation, etc. at each pixel in a grid, and displaying these values as a map. These summary maps have traditionally been presented as the end products of geostatistical analyses. For example, a map of the posterior median of the historical incidence of sickle-cell trait, HbS, in humans was presented [12]. They are useful as visual aids, but it is incomplete or incorrect to designate any one of them as ‘the map’ and feed it into a GIS-based analysis.
Suppose a geneticist or historian wanted to use this analysis [12] to estimate the total number of HbS carriers in a region. In GIS, the procedure for producing this estimate would be to multiply the median map by a map of population and sum the product over all the pixels of a region. Because the median was mapped, the mathematical formula for this would be:
whereas the mathematical formula for the median of the target quantity would be
where Xi is HbS allele frequency at a pixel i and Pi is the population inhabiting that pixel.
Unfortunately, the two are not equal and can be rather different. To make this point more concrete, consider an example where there are n pixels, with Xi Pi independent and log-normally distributed [42] with parameters m and v in each. The median of the sum is approximately ev/2 times the sum of the medians for large n. This difference quickly becomes huge as v increases. Errors of this general type have occurred in the literature, but we focus here on best practices for the future.
The correct way to produce the desired estimate is to use the posterior to produce a representative sample of the CMs that are consistent with the data, compute ∑i Xi Pi for each of them, and compile these values into a histogram. This histogram approximates the posterior of ∑i Xi Pi, and can be used to estimate the median or any other posterior summary. If there are a large number of pixels in the region of interest, generating CMs can be extraordinarily expensive [9], but the cost can be mitigated in some cases [12].
It is true that
regardless of the dependence between the s [42]. The sum of the means is, in fact, equal to the mean of the sum. This does not imply that the mean is overall a better posterior summary than the median, only that the mean of the sum can be produced efficiently from the mean map using GIS software. Note that it is not possible to compute the full posterior (or the variance, quantiles, credible intervals, etc.) of ∑i Xi Pi from summary maps.
What BG can provide
Subject to practical constraints discussed in the next section, BG can provide the probability distribution (not the values) of any quantities that could be determined (or whose probability distribution could be determined) if the true map were known. This category includes anything that could be derived from the true map (if it were known) by GIS-based raster manipulations. For example, Diggle et al. [10] were interested in the truth of the statement ‘Loa loa prevalence exceeds 20%’ at each pixel in their region of concern in Cameroon. Because this truth value can only take two values (true and false), its probability distribution is defined by a single number: the probability of truth. Diggle et al. [10] computed this probability at each pixel and displayed it as a map.
Probability distributions are much more informative than estimates and confidence intervals, but also more complicated. One way to build intuition about them is to ask operational questions. What advice could one give control program managers about communities in the extracted pixel in Figure 3? It might help to think of the histogram in row B as representing a large population of prevalences, from which the true prevalence in each community in the pixel (in the 2–10-year-old age group, averaged over the year 2007 [2]) has been drawn at random.
It is usually necessary to summarize probability distributions at some point. An advantage of thinking operationally about probability distributions is that it highlights which summaries are relevant. To give helpful advice to the hypothetical control program manager, it would be necessary to describe the key feature of the histogram in Figure 3(b), which is its shape. Prevalence can be expected to be low in many communities, but will occasionally be high. This general observation could be quantified in many ways. For example, the probabilities that prevalence in any given community is below 10%, between 10% and 60%, and above 60% could be reported.
Practical considerations
BG predictive analysis has been discussed at an abstract level to facilitate exposition. Here this discussion is supplemented with an overview of the computational constraints that define BG in practice.
Generating candidate values for each pixel independently is relatively inexpensive and is done routinely by all BG software packages [25] (http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/geobugs.shtml). For per-pixel products such as the summary maps in Figure 3(c) and the density field in Figure 3(b), these values produce the same results as actual CMs.
However, they cannot be used to produce candidate values for volumetric quantities (VQs) such as the average endemicity in Tanzania. These can be produced using CMs (Figure 3(a)), which are very expensive to produce [9]. Fortunately, candidate values for VQs can often be produced without full CMs by trading precision for running time. Piel et al. [12] provided an example, for which bespoke code had to be written.
It is sometimes possible to perform incomplete predictive analysis for VQs without programming. The posterior mean of a VQ can be obtained from a mean map using GIS software if the VQ can be obtained by multiplying the value of the mapped quantity at a set of pixels by a matrix and adding a vector, as is the case with the sum in Box 1. If that is not the case, or if the mean map is not available (Box 1), estimates produced using summary maps do not have a simple relation to the actual candidate values.
Computers are constantly getting faster, and novel hardware [26] and algorithms [27–30] are lowering the computational barriers. Revolutionary developments in probabilistic computing are beginning to appear on the horizon [31]. It will probably not be long before generating global-scale CMs is routine. Users of BG products should understand the corners that they are cutting in the present so that they are prepared to make full use of the posterior when more powerful tools become available.
In the nearer future, GIS software could support mapping via per-pixel candidate values. Ideally a well-documented standard would be developed for computer representations of geostatistical posteriors to encourage interoperability. Once a standard is in place, developers could wrap existing raster functionality to allow users to produce maps by correctly incorporating many candidate values.
Currently, commissioners and users of BG depend on statisticians to calculate their answers. The right questions are usually of the form, ‘what is the probability that…?’ or ‘what is the probability distribution of…?’ Many questions that seem reasonable, such as, ‘what is the value of…?’ and ‘should the mean map or the median map be published?’ are unanswerable or odd from the perspective of BG. The distinction is confusing if BG is viewed as only a mapping technique, but makes sense when the posterior is understood as a large sample of CMs.
Further reading
Diggle’s Model-Based Geostatistics is the standard introduction to both Bayesian and non-Bayesian model-based geostatistics [32], and Crainiceau et al. [33] and Diggle et al. [11] presented some pioneering uses of BG in parasitology. Soares Magalhães et al. [7] reviewed BG for malaria and helminth infections. Goovaerts’ Geostatistics for Natural Resources Evaluation [34] is a standard introduction to classical geostatisics, another geostatistical paradigm. Pfeiffer et al. [35] introduced spatial epidemiology in general. Gelman et al. [36] and Basáñez et al. [8] provided practical introductions to Bayesian data analysis in general, Jaynes and Bretthorst [37] a more conceptual one. Berger [38] and Goldstein [39] compared the objective and subjective branches of Bayesian analysis. Freedman [40] argued for frequentist analysis and against the Bayesian view. Hájek [41] compared frequentist, Bayesian and other interpretations of probability.
It is worth noting that the concepts discussed in this paper apply to classical geostatistics and even nominally non-Bayesian model-based geostatistics. Similar to BG, these other geostatistical paradigms approach the problem of inferring a map from imperfect data by producing a probability distribution for it, from which CMs can be drawn [32,34]. The true map is unknown but is fixed, not the outcome of a repeatable random experiment (assuming that the data have been drawn from the same map that is to be predicted). The use of probability to quantify certainty of knowledge about fixed unknowns is the defining feature of Bayesian analysis. Because these other paradigms also treat the unknown map in an essentially Bayesian way, they enjoy the benefits described in this paper. However, they deal with other model parameters such as covariate effect sizes in a non-Bayesian way.
Acknowledgments
We would like to thank Katherine Battle, Rosalind Howes, Catherine Moyes, Abdisalan Noor, David Smith, Marianne Sinka, William Temperley and William Wint for their thoughtful comments on the manuscript.
Glossary
- Bayesian geostatistical analysis:
the process of using probability theory to determine a probability distribution that quantifies knowledge gained about an unknown map from imperfect data, and using that probability distribution to make predictions with appropriate precision.
- Candidate maps
the probability distribution that a Bayesian geostatistical analysis produces for an unknown map can be represented as a large sample of maps that explain the data, in which maps that do a better job of explaining the data are more likely to be represented. We call these candidate maps in this paper because each is a credible candidate for the unknown, true map; none of them are ruled out by the data. This term is not standard.
- Cartography
the science of using geographic information to make maps.
- Cartographic analysis
The study and analysis (e.g. comparison) of one or several maps.
- Credible interval of probability q
the interval between the quantile of probability q/2 and the quantile of probability 1-q/2.
- Geographic information system or GIS
a suite of tools allowing the cartography, management and analysis of spatial data.
- GIS software
a specific piece of software to use and develop tools for spatial analysis of data.
- Interquartile range
the credible interval with probability 0.5. There is a 50% chance that the value of a random variable is within its interquartile range.
- Likelihood
- the probability or probability density of the data, as a function of the values of any other variables in the model. The likelihood can often be modeled based on physical or sampling considerations. For unknown variable X and data Y, the likelihood is usually denoted [YǀX]. When X is an unknown map, the likelihood is usually written using probability notation for each individual datapoint. Datapoint Yi usually depends only on the value of the map X at a specific location zi, X(zi). Common likelihoods in BG include the normal likelihood, which describes uncertain observations of maps whose value at a point can be any number,
the binomial likelihood, which describes observations of maps of prevalences (whose value at each point must be between zero and one inclusive) via finite samples of sizes ni,
and the Poisson likelihood, which describes observations of maps of rates of event occurrence (whose value at each point must be nonnegative) via counting,
where ki can be, for example, the duration of observation or the size of a sample depending on the context. - Markov chain Monte Carlo
a popular and effective fitting algorithm [8], that is, an algorithm for drawing samples from posterior distributions. In Bayesian analysis, fitting algorithms should be clearly distinguished from actual models. Any fitting algorithm should produce approximately the same answer for a given model, dataset and goal (i.e. posterior samples vs posterior mode). However, they differ in performance characteristics and output format.
- Mean
the probability-weighted average of the possible values of a random variable. If many independent values are drawn from the probability distribution of a random variable, their limiting average is its mean. For random numbers, this quantity coincides with the physical balance point of the probability distribution (Figure 2). For unknown variable X, the prior mean is usually denoted E(X) and the posterior mean given data Y is usually denoted E(XǀY).
- Median
the quantile of probability 0.5. There is a 50% chance that a random number is larger than its median.
- Mode
the most probable value of a variable. Rarely presented in Bayesian analysis because it is relatively difficult to estimate from a Markov chain Monte Carlo output.
- Per-pixel prediction
any prediction that can be made by considering candidate values of an unknown map at individual locations independently, as opposed to entire CMs. Important examples are the summary maps such as those in Figure 4 and the maps of uncertainty metrics that often accompany them. Volumetric quantities such as population-weighted mean endemicity in Tanzania cannot be predicted in a per-pixel fashion. This term is not standard.
- Pixel
geographical unit defining the resolution of a map (e.g. a 1 km by 1 km square).
- Posterior
the probability distribution of any variable in a model after data have been incorporated. It can be obtained from the prior and the likelihood by means of Bayes’ Rule [8,36,37,41]. For unknown variable X and data Y, the posterior is usually denoted [XǀY].
- Posterior predictive
nearly synonymous with posterior. The optional ‘predictive’ designation usually indicates that the variable under consideration is ‘predicted data,’ for example, infection prevalence at an unsampled location.
- Prior
the probability distribution of any unknown variable in a model before data have been taken into account. In Bayesian statistics, there is no way to avoid specifying priors, but opinions vary widely on the best way to do it. Many methods exist for eliciting priors from expert judgments [43]. Several standard priors, which do not use prior information, have been developed to avoid the explicit subjectivity in expert opinion-based priors [44,45]. For unknown variable X, the prior is usually denoted [X].
- Quantile of probability q
for unknown number X, this is the value xq for which the probability that X<xq is equal to q. If many independent values are drawn from the probability distribution of X, q gives the limiting proportion that are below xq.
- Random maps
in Bayesian probability, ‘random’ means ‘unknown.’ In BG, a single true map is known to exist, but it cannot be determined uniquely from the data. It therefore remains random or unknown even when the data are taken into account.
- Raster
grid or layer of information composed of pixels, as opposed to a vector layer, which is made of points, lines and polygons.
- Realization
in BG, this is a synonym for our term ‘candidate map.’
References
- 1.Guerra CA, et al. Assembling a global database of malaria parasite prevalence for the Malaria Atlas Project. Malar. J. 2007;6:17. doi: 10.1186/1475-2875-6-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hay SI, et al. A world malaria map: Plasmodium falciparum endemicity in 2007. PLoS Med. 2009;6:e1000048. doi: 10.1371/journal.pmed.1000048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Guerra CA, et al. Mapping the global extent of malaria in 2005. Trends Parasitol. 2006;22:353–358. doi: 10.1016/j.pt.2006.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hay SI, et al. Urbanization, malaria transmission and disease burden in Africa. Nat. Rev. Microbiol. 2005;3:81–90. doi: 10.1038/nrmicro1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hay SI, et al. From predicting mosquito habitat to malaria seasons using remotely sensed data: practice, problems and perspectives. Parasitol. Today. 1998;14:306–313. doi: 10.1016/s0169-4758(98)01285-x. [DOI] [PubMed] [Google Scholar]
- 6.Smith DL, et al. Standardizing estimates of the Plasmodium falciparum parasite rate. Malar. J. 2007;6:131. doi: 10.1186/1475-2875-6-131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Magalhães R.J. Soares, et al. The applications of model-based geostatistics in helminth epidemiology and control. Adv. Parasitol. doi: 10.1016/B978-0-12-385897-9.00005-7. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Basáñez M-G, et al. Bayesian statistics for parasitologists. Trends Parasitol. 2004;20:85–91. doi: 10.1016/j.pt.2003.11.008. [DOI] [PubMed] [Google Scholar]
- 9.Gething PW, et al. Quantifying aggregated uncertainty in Plasmodium falciparum malaria prevalence and populations at risk via efficient space-time geostatistical joint simulation. PLoS Comput. Biol. 2010;6:e1000724. doi: 10.1371/journal.pcbi.1000724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Diggle PJ, et al. Spatial modelling and the prediction of Loa loa risk: decision making under uncertainty. Ann. Trop. Med. Parasit. 2007;101:499–509. doi: 10.1179/136485913X13789813917463. [DOI] [PubMed] [Google Scholar]
- 11.Diggle P, et al. Childhood malaria in the Gambia: a case-study in model-based geostatistics. J. R. Stat. Soc. C: Appl. Stat. 2002;51:493–506. [Google Scholar]
- 12.Piel FB, et al. Global distribution of sickle cell gene and the geographical confirmation of the malaria hypothesis. Nat. Commun. 2010;1:104. doi: 10.1038/ncomms1104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gosoniu L, et al. Mapping malaria risk in West Africa using a Bayesian nonparametric non-stationary model. Comp. Stat. Data Anal. 2009;53:3358–3371. [Google Scholar]
- 14.Gosoniu L, et al. Bayesian modelling of geostatistical malaria risk data. Geospatial Health. 2006;1:127–139. doi: 10.4081/gh.2006.287. [DOI] [PubMed] [Google Scholar]
- 15.Gemperli A, et al. Mapping malaria transmission in West and Central Africa. Trop. Med. Int. Health. 2006;11:1032–1046. doi: 10.1111/j.1365-3156.2006.01640.x. [DOI] [PubMed] [Google Scholar]
- 16.Noor AM, et al. Spatial prediction of Plasmodium falciparum prevalence in Somalia. Malar. J. 2008;7:159. doi: 10.1186/1475-2875-7-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Noor AM, et al. The risks of malaria infection in Kenya in 2009. BMC Infect. Dis. 2009;9:180. doi: 10.1186/1471-2334-9-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Beck-Worner C, et al. Bayesian spatial risk prediction of Schistosoma mansoni infection in western Cote d’Ivoire using a remotely-sensed digital elevation model. Am. J. Trop. Med. Hyg. 2007;76:956–963. [PubMed] [Google Scholar]
- 19.Raso G, et al. An integrated approach for risk profiling and spatial prediction of Schistosoma mansoni-hookworm coinfection. Proc. Natl. Acad. Sci. U.S.A. 2006;103:6934–6939. doi: 10.1073/pnas.0601559103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Clements AC, et al. Bayesian spatial analysis and disease mapping: tools to enhance planning and implementation of a schistosomiasis control programme in Tanzania. Trop. Med. Int. Health. 2006;11:490–503. doi: 10.1111/j.1365-3156.2006.01594.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Clements AC, et al. Bayesian geostatistical prediction of the intensity of infection with Schistosoma mansoni in East Africa. Parasitol. 2006;133:711–719. doi: 10.1017/S0031182006001181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brooker S, Clements AC. Spatial heterogeneity of parasite co-infection: determinants and geostatistical prediction at regional scales. Int. J. Parasitol. 2009;39:591–597. doi: 10.1016/j.ijpara.2008.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Clements ACA, et al. Spatial risk assessment of Rift Valley fever in Senegal. Vector-Borne Zoonot. 2007;7:203–216. doi: 10.1089/vbz.2006.0600. [DOI] [PubMed] [Google Scholar]
- 24.Raso G, et al. Risk factors and spatial patterns of hookworm infection among schoolchildren in a rural area of western Cote d’ Ivoire. Int. J. Parasitol. 2006;36:201–210. doi: 10.1016/j.ijpara.2005.09.003. [DOI] [PubMed] [Google Scholar]
- 25.Christensen O, Ribeiro P., Jr GeoRglm-a package for generalised linear spatial models. R News. 2002;2:26–28. [Google Scholar]
- 26.Agullo E, et al. Numerical linear algebra on emerging architectures: the PLASMA and MAGMA projects. J. Phys.: Conf. Ser. 2009;180 DOI: 10.1088/1742-6596/180/1/012037. [Google Scholar]
- 27.Dietrich CR, Newsam GN. Fast and exact simulation of stationary Gaussian processes through circulant embedding of the covariance matrix. SIAM J. Stat. Comput. 1997;18:1088–1107. [Google Scholar]
- 28.Storkey AJ. Truncated covariance matrices and Toeplitz methods in Gaussian processes. Artificial Neural Networks. 1999:55–60. [Google Scholar]
- 29.Quinonero-Candela J, Rasmussen CE. A unifying view of sparse approximate Gaussian process regression. J. Machine Learn. Res. 2005;6:1939–1959. [Google Scholar]
- 30.Bach FR, Jordan MI. Predictive low-rank decomposition for kernel methods. Proceedings of the 22nd International Conference on Machine Learning; ACM Press; 2005. pp. 33–40. [Google Scholar]
- 31.Mansinghka VK. Natively Probabilistic Computation. Ph.D. Dissertation. Massachusetts Institute of Technology; 2009. [Google Scholar]
- 32.Diggle PJ, Ribeiro PJ., Jr . Model-Based Geostatistics. Springer; 2007. [Google Scholar]
- 33.Crainiceau CM, et al. Bivariate binomial spatial modeling of Loa loa prevalence in tropical Africa. J. Am. Stat. Assoc. 2008;103:21–47. [Google Scholar]
- 34.Goovaerts P. Geostatistics for Natural Resources Evaluation. Oxford University Press; 1997. [Google Scholar]
- 35.Pfeiffer DU, et al. Spatial Analysis in Epidemiology. Oxford University Press; 2008. [Google Scholar]
- 36.Gelman A, et al. Bayesian Data Analysis. Chapman & Hall/CRC; 2004. [Google Scholar]
- 37.Jaynes ET, Bretthorst GL. Probability Theory: The Logic of Science. Cambridge University Press; 2003. [Google Scholar]
- 38.Berger J. The case for objective Bayesian analysis. Bayesian Anal. 2006;1:385–402. [Google Scholar]
- 39.Goldstein M. Subjective Bayesian analysis: principles and practice. Bayesian Anal. 2006;1:403–420. [Google Scholar]
- 40.Freedman D. Some issues in the foundation of statistics. Foundations Sci. 1995;1:19–39. [Google Scholar]
- 41.Hájek A. Stanford Encyclopedia of Philosophy. The Metaphysics Research Lab Center for the Study of Language and Information; 2009. [Google Scholar]
- 42.Hogg RV, et al. Introduction to Mathematical Statistics. Pearson Education; 2005. [Google Scholar]
- 43.Hahn ED. Re-examining informative prior elicitation through the lens of Markov chain Monte Carlo methods. J. R. Stat. Soc. A. 2006;169:37–48. [Google Scholar]
- 44.Kass RE, Wasserman L. The selection of prior distributions by formal rules. J. Am. Stat. Assoc. 1998;93:412. previously 1996, Vol. 91, 1343. [Google Scholar]
- 45.Berger JO, et al. Objective Bayesian analysis of spatially correlated. J. Am. Stat. Assoc. 2003;98:779–1779. previously 2001, Vol. 96, 1361. [Google Scholar]
- 46.Jeffrey RC. Subjective Probability: The Real Thing. Cambridge University Press; 2004. [Google Scholar]
- 47.Balk DL, et al. Determining global population distribution: methods, applications and data. Adv. Parasitol. 2006;62:119–156. doi: 10.1016/S0065-308X(05)62004-0. [DOI] [PMC free article] [PubMed] [Google Scholar]