Molecular Dynamics Simulations on High-Performance Reconfigurable Computing Systems

Abstract

The acceleration of molecular dynamics (MD) simulations using high-performance reconfigurable computing (HPRC) has been much studied. Given the intense competition from multicore and GPUs, there is now a question whether MD on HPRC can be competitive. We concentrate here on the MD kernel computation: determining the short-range force between particle pairs. In one part of the study, we systematically explore the design space of the force pipeline with respect to arithmetic algorithm, arithmetic mode, precision, and various other optimizations. We examine simplifications and find that some have little effect on simulation quality. In the other part, we present the first FPGA study of the filtering of particle pairs with nearly zero mutual force, a standard optimization in MD codes. There are several innovations, including a novel partitioning of the particle space, and new methods for filtering and mapping work onto the pipelines. As a consequence, highly efficient filtering can be implemented with only a small fraction of the FPGA’s resources. Overall, we find that, for an Altera Stratix-III EP3ES260, 8 force pipelines running at nearly 200 MHz can fit on the FPGA, and that they can perform at 95% efficiency. This results in an 80-fold per core speed-up for the short-range force, which is likely to make FPGAs highly competitive for MD.

1. INTRODUCTION

Molecular dynamics simulation (MD) is a central method in high-performance computing (HPC) with applications throughout engineering and natural science. Acceleration of MD is a critical problem—there is a many order-of-magnitude gap between the largest current simulations and the potential physical systems to be studied. As such it has received attention as a target for supercomputers [Fitch et al. 2006], clusters [Bowers et al. 2006], and dedicated hardware [Komeiji et al. 1997; Shaw et al. 2007; Taiji et al. 2003], as well as coprocessing using GPUs [Rodrigues et al. 2008], Cell [Shi and Kindratenko 2008], and FPGAs [Alam et al. 2007; Azizi et al. 2004; Gu et al. 2006b; Hamada and Nakasato 2005; Kindratenko and Pointer 2006; Scrofano and Prasanna 2006; Villareal et al. 2007]. The last of these, MD with High Performance Reconfigurable Computing (HPRC), is our focus here. In particular, we demonstrate that MD with HPRC is not only cost-effective, but in fact an excellent fit. This result is surprising given the FPGA’s reputation for having difficulty with floating point intensive computations.

In this article we re-examine the short-range force computation which dominates MD. Although this problem has been addressed by many groups in the last few years, much of the design space remains unexplored. In addition, recent advances in FPGA hardware and in compiler technology appear to have shifted some basic trade-offs.

Our study has three parts. The first part considers the force pipeline. Our goal here is to maximize throughput—operating frequency and the number of pipelines that fit on the FPGA—while maintaining simulation quality. To do this, we explore various ways to perform the arithmetic, the modes in which to execute the operations, the levels of precision, and other optimizations. Some of the choices are as follows.

• Direct computation (Direct) versus table lookup with interpolation (LookUp)

• Interpolation order (for LookUp)

• Precision: single, double, custom

• Mode: floating point, hybrid fixed/floating point, custom

• Implementation: synthesized components, vendor cores, vendor compiler (e.g., Langhammer [2008])

• Various arithmetic reorderings

We find that direct computation, rather than table lookup, is now preferred, and that single precision floating point combined with higher precision fixed point leads to both excellent performance and high-quality simulations.

The second part considers filtering particle pairs. This issue emerges from the geometric mismatch between two shapes: (i) the cubes (or other polyhedrons) into which it is convenient to partition the simulation space and (ii) the spheres around each particle in which the short-range force is non-zero. If this mismatch is not addressed (e.g., only the standard cell-list method is used), then 85.5% of the particle pairs that are run through the force pipelines will be superfluous. While filtering is a critical issue, we believe that the only previously published results related to hardware implementations are from D.E. Shaw; these are with respect to their Anton processor [Larson et al. 2008].

Here, we find filtering implementation on FPGAs to provide a rich design space. Its primary components are as follows.

• Filter algorithm and precision

• Method of partitioning the cell neighborhood to balance load with respect to the Newton’s-3rd-Law optimization

• Method of mapping particle pairs to filter pipelines

• Queueing and routing between filter and force pipelines

We present new algorithms or methods for filtering, load balancing, and mapping, and find that nearly perfect filtering can be achieved with only a fraction of the FPGA’s logic.

The third part considers the integration of the new features specified by the other two parts. The particle mapping to the filter pipelines leads to changes in how cell lists are swapped on/off chip. Also, the filter pipelines generate neighbor lists which must be fed into the force pipelines. And having multiple force pipelines (8 or more) requires accumulation of forces on the other end. We find solutions to all of these issues that have simple control, match FPGA resources, and add only little overhead.

Our basic result is that for the Stratix-III EP3SE260, and for the best (as yet unoptimized) designs, 8 force pipelines running at nearly 200 MHz can fit on the FPGA. Moreover, the force pipelines can be run at high efficiency with 95% of cycles providing payload. As a result, the short-range force for the standard 90K NAMD benchmark can be computed in under 22 ms, or about a factor of 80 faster than its per-core execution time. Contributions are three-fold: (i) demonstrating that FPGAs are highly competitive for MD, (ii) substantially expanding the exploration of the MD force pipeline design space for FPGAs, and (iii) presenting the first study of particle-particle filtering on FPGAs and with it a number of innovations. The last of these may have implications to MD beyond HPRC.

The rest of this article is organized as follows: In the next section, we review the applicable parts of MD simulation. There follows the presentations of the three parts of our study, after which come results and some discussion. This article builds on work presented at HPRCTA08 [Chiu et al. 2008] and FPL09 [Chiu and Herbordt 2009] which concentrated on the force and filter pipelines, respectively. Besides combining and augmenting these pieces, we address here the substantial issues of their integration, as well as data movement throughout the application: host-accelerator, board-FPGA, and among components on the FPGA.

2. MD PRELIMINARIES

2.1 MD Review

MD is an iterative application of Newtonian mechanics to ensembles of atoms and molecules (see, e.g., Rapaport [2004] for details). MD simulations generally proceed in iterations each of which consists of two phases, force computation and motion integration. In general, the forces depend on the physical system being simulated and may include LJ, Coulomb, hydrogen bond, and various covalent bond terms:

$${\mathbf{F}}^{\mathit{total}}=F^{\mathit{bond}}+F^{\mathit{angle}}+F^{\mathit{torsion}}+F^{\mathit{H\; Bond}}+F^{\mathit{non}–\mathit{bonded}}$$ (1)

Because the hydrogen bond and covalent terms (bond, angle, and torsion) affect only neighboring atoms, computing their effect is O(N) in the number of particles N being simulated. The motion integration computation is also O(N). Although some of these O(N) terms are easily computed on an FPGA, their low complexity makes them likely candidates for host processing, which is what we assume here. The LJ force for particle i can be expressed as:

$${\mathbf{F}}_i^{\mathit{LJ}}=\sum _{j\ne i}\frac{{\mathit{\in }}_{\mathit{ab}}}{{\sigma }_{\mathit{ab}}^2}\left\{12{\left(\frac{{\sigma }_{\mathit{ab}}}{|r_{\mathit{ji}}|}\right)}^{14}-6{\left(\frac{{\sigma }_{\mathit{ab}}}{|r_{\mathit{ji}}|}\right)}^8\right\}{\mathbf{r}}_{\mathit{ji}}$$ (2)

where the ∈_ab and σ_ab are parameters related to the types of particles, that is, particle i is type a and particle j is type b. The Coulombic force can be expressed as:

$${\mathbf{F}}_i^C=q_i\sum _{j\ne i}\left(\frac{q_j}{|{\mathbf{r}}_{\mathit{ji}}{|}^3}\right){\mathbf{r}}_{\mathit{ji}}$$ (3)

A standard way of computing the nonbonded forces (LJ and Coulombic) is by applying a cut-off. Then the force on each particle is the result of only particles within the cut-off radius r_c. Since this radius is typically less than a tenth of the size per dimension of the system under study, the savings are tremendous, even given the more complex bookkeeping required.

The problem with cut-off is that, while it may be sufficiently accurate for the rapidly decreasing LJ force, the error introduced in the slowly declining Coulombic force may be unacceptable. A number of methods have been developed to address this issue with some of the most popular being based on Ewald Sums (see, e.g., Darden et al. [1993]) and multigrid (see, e.g., Izaguirre et al. [2005] and Skeel et al. [2002]). Here we use the standard convention of calling short-range the LJ force and the Coulombic force generated within a cut-off radius. We refer to the Coulombic force generated outside the cut-off radius as long-range. Since the long-range force computation is generally a small fraction of the total (see, e.g., Gu and Herbordt [2007] and Scrofano and Prasanna [2006]), we concentrate here on the short-range force.

2.2 Short-Range Force Computation

As just described, the short-range force computation has two parts, the LJ force and the rapidly converging part of the Coulomb force. The LJ force is often computed with the so-called 6-12 approximation given in Eq. (2). This has two terms, the repulsive Pauli exclusion and the van der Waals attraction. Both require coefficients specific to the component particles of the particle pair whose interaction is being evaluated. These can be combined with the other constants (physical and scaling) and stored in coefficient look-up tables. Thus, the LJ force can be expressed as

$$\frac{{\mathbf{F}}_{\mathit{ji}}^{\mathit{LJ}}(r_{\mathit{ji}}(a,b))}{{\mathbf{r}}_{\mathbf{ji}}}=A_{\mathit{ab}}|r_{\mathit{ji}}{|}^{-14}+B_{\mathit{ab}}|r_{\mathit{ji}}{|}^{-8}$$ (4)

where A_ab and B_ab are distance-independent coefficient look-up tables indexed with atom types a and b.

Returning now to the Coulomb force computation, we begin by rewriting Eq. (3) as

$$\frac{{\mathbf{F}}_{\mathit{ji}}^{\mathit{CL}}(r_{\mathit{ji}}(a,b))}{{\mathbf{r}}_{\mathbf{ji}}}=Q{Q}_{\mathit{ab}}{|r_{\mathit{ji}}|}^{-3},$$ (5)

where QQ_ab is a precomputed parameter (analogous to A_ab and B_ab). Because applying a cut-off here often causes unacceptable error, and also because the all-to-all direct computation is too expensive for large simulations, various numerical methods are applied to solve the Poisson equation that translates charge distribution to potential distribution. To improve approximation quality and efficiency, these methods split the original Coulomb force curve in two parts (with a smoothing function g_a(r)): a fast declining short range part and a flat long range part. For example:

$$\frac{1}{r}=(\frac{1}{r}-g_a(r))+g_a(r).$$ (6)

The short range component can be computed together with Lennard-Jones force using a third look-up table (for QQ_ab). The entire short range force to be computed is:

$$\frac{{\mathbf{F}}_{\mathit{ji}}^{\mathit{short}}}{{\mathbf{r}}_{\mathbf{ji}}}=A_{\mathit{ab}}{r}_{\mathit{ji}}^{-14}+B_{\mathit{ab}}{r}_{\mathit{ji}}^{-8}+{\mathit{QQ}}_{\mathit{ab}}(r_{\mathit{ji}}^{-3}+\frac{g_a^{\prime }(r)}{r}).$$ (7)

2.3 Computing Short-Range Forces with Table Look-Up

Since these calculations are in the “inner loop,” considerable care is taken in their implementation: even in serial codes, the LJ equation is often not evaluated directly, but rather with table look-up and interpolation. Previous implementations of HPRC MD have used table look-up for the entire LJ force as a function of particle separation [Azizi et al. 2004; Gu et al. 2006a]. The index used is |r_ji|² rather than |r_ji| so as to avoid the costly square-root operation. This method is efficient for uniform gases where only a single table is required [Azizi et al. 2004], but is less likely to be preferred in more general cases.

In more recent work [Gu et al. 2008], we use a different method: Instead of implementing the force pipeline with a single table lookup, we use three, one each for r⁻¹⁴, r⁻⁸ and $r_{\mathit{ji}}^{-3}+\frac{g_a^{\prime }(r)}{r}$. Equation (7) can be rewritten as a function of $r_{\mathit{ji}}^2$:

$$\frac{{\mathbf{F}}_{\mathit{ji}}^{\mathit{short}}(|{\mathit{r}}_{\mathit{ji}}{|}^2(a,b))}{{\mathbf{r}}_{\mathbf{ji}}}=A_{\mathit{ab}}{R}_{14}(|r_{\mathit{ji}}{|}^2)+B_{\mathit{ab}}{R}_8(|r_{\mathit{ji}}{|}^2)+{\mathit{QQ}}_{\mathit{ab}}{R}_3(|r_{\mathit{ji}}{|}^2),$$ (8)

where R₁₄, R₈, and R₃ are lookup tables indexed with |r_ji|².

The intervals in the tables are represented in Figure 1. Each curve is divided into several sections along the X-axis such that the length of each section is twice that of the previous. Each section, however, is cut into the same number of intervals N. To improve the accuracy, higher order terms can be used. When the interpolation is order M, each interval needs M + 1 coefficients, and each section needs N * (M + 1) coefficients:

$$F(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3$$ (9)

shows third order with coefficients a_i. Accuracy increases with both the number of intervals per section and the interpolation order. These issues are discussed in detail in Gu et al. [2008].

Fig. 1.

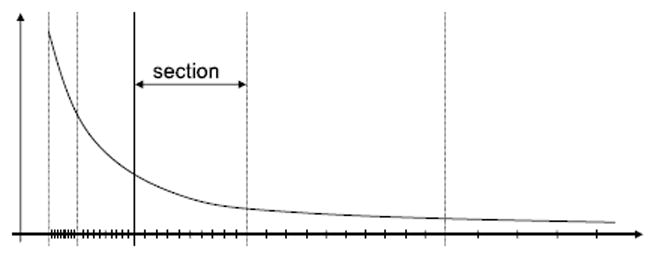
Table look-up varies in precision across r^−k. Each section has a fixed number of intervals.

2.4 Filtering Particle Pairs

While MD in general involves all-to-all forces among particles, a cut-off is commonly applied to restrict the extent of the short-range force to a fraction of the simulation space. Two methods are used to take advantage of this cut-off: cell lists and neighbor lists (see Figure 2). With cell lists, the simulation space is typically partitioned into cubes with edge-length equal to r_c. Non-zero forces on the reference particle P can then only be applied by other particles in its home cell and in the 26 neighboring cells (the 3x3x3 cell neighborhood). We refer the second particle of the pair as the partner particle. With neighbor lists, P has associated with it a list of exactly those partner particles within r_c. We now compare these methods.

Fig. 2.

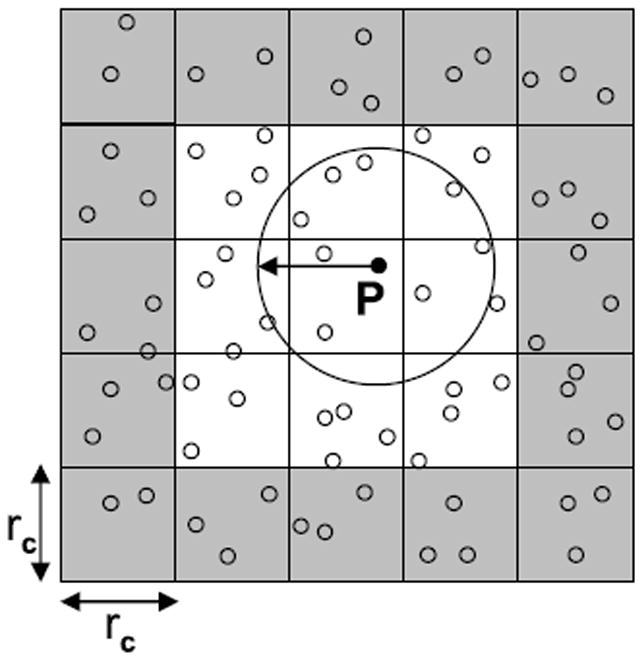
Shown is part of the simulation space about particle P. Its two dimensional cell neighborhood is shown in white; cells have edge size equal to the cut-off radius. The cut-off circle is shown; particles within the circle are in P’s neighbor list.

• Efficiency. Neighbor lists are by construction 100% efficient: only those particle pairs with non-zero mutual force are evaluated. Cell lists as just defined are 15.5% efficient with that number being the ratio of the volumes of the cut-off sphere and the 27-cell neighborhood.

• Storage. With cell lists, each particle is stored in a single cell’s list. With neighbor lists, each particle is typically stored in 400-1000 neighbor lists.

• List Creation Complexity. Computing the contents of each cell requires only one pass through the particle array. Computing the contents of each neighbor list requires, naively, that each particle be examined with respect to every other particle: the distance between them is then computed and thresholded. In practice, however, it makes sense to first compute cell lists anyway. Then, the neighbor lists can be computed using only the particles in each reference particle’s cell neighborhood.

From this last point, it appears that the creation of neighbor lists involves not only cell lists, but also a fraction of the force computation itself. At this point, why not finish computing the forces of those particles that are within the cut-off? Why save the neighbor list?

Most MD codes reuse the neighbor lists for multiple iterations and so amortize the work in their creation. But because particles move during each iteration, particles can enter and exit the cut-off region leading to potential error. The solution is to make the neighborlist cut-off larger than the force cut-off, for example, 13.5Å versus 12Å (see Figure 3). There is a trade-off between the increase in neighborhood size, and thus the number of particle pairs evaluated, and the number of iterations between neighbor list updates.

Fig. 3.

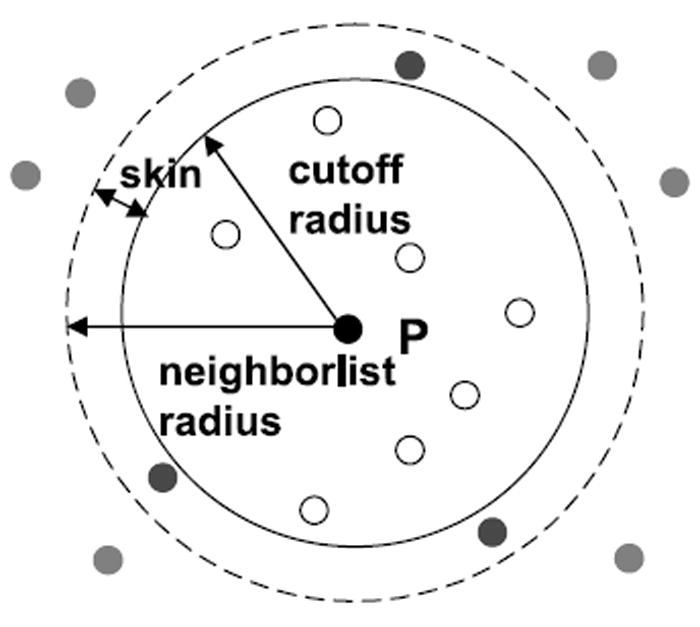
Neighborlists are often computed for a larger radius than the cutoff.

3. FORCE PIPELINE DESIGN AND OPTIMIZATION

3.1 Overview

In this section, we describe FPGA implementations of Eq. (7). All are pipelined and, on every cycle, input positions of particle pairs and output corresponding forces. There are numerous design axes as described in Section 1. The ones that reorder or change the pipeline components are as follows: the method of computation, Direct versus table lookup with interpolation (LookUp); for LookUp, order of interpolation; for Direct, whether the Altera FP Compiler is used or the FP cores directly; and whether integer is used for part of the computation.

The last two require further explanation. The Altera floating point compiler optimizes floating point datapaths by removing redundancy among operators and by making trade-offs in using various component types, for example, using hard or soft components as available [Langhammer 2008]. What is interesting here is that the use of the compiler results in a different datapath being optimal.

The second axis requiring explanation is float versus hybrid fixed/float. The problem arises in the force accumulation at the end of the pipeline. New forces are generated every cycle and must be added to the appropriate particles running totals. The floating point addition, however, requires more than a single cycle, although since it is pipelined it does not necessarily change throughput. But if the same particle’s force is referenced on successive cycles a hazard results. There are at least four solutions: (i) the pipeline can stall, (ii) particle processing can be orchestrated so that hazards are avoided, (iii) forces can be combined in a more complex structure, such as a reduction tree, or (iv) the force can be saved in integer format rather than floating point. In the last alternative, addition takes only a single cycle. Integer operations are also more efficient than floating point, and if done carefully, result in no loss of precision. The GROMACS code and the Protein Explorer, for example, both use mixed fixed/floating point [Taiji et al. 2003; van der Spoel et al. 2005].

In the rest of this section, we show how these alternatives cause the force pipeline to vary. Results are presented in Section 6.

3.2 Direct Computation

The flow of Direct is shown in Figure 4 with detail given in Figure 5. Note that the first two computations, adjusting for periodic boundary conditions and obtaining r², can be done in fixed point. In that case, r² must be converted to floating point before being combined with the coefficients (on the smoothing side) and divided (on the Coulomb + LJ side). The conversion at the output is similar.

Fig. 4.

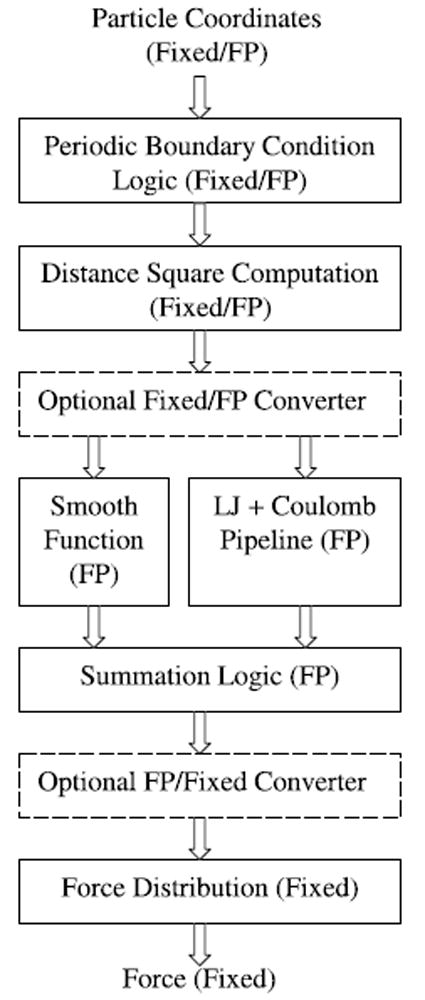
Functional block diagram of the short-range particle-particle datapath.

Fig. 5.

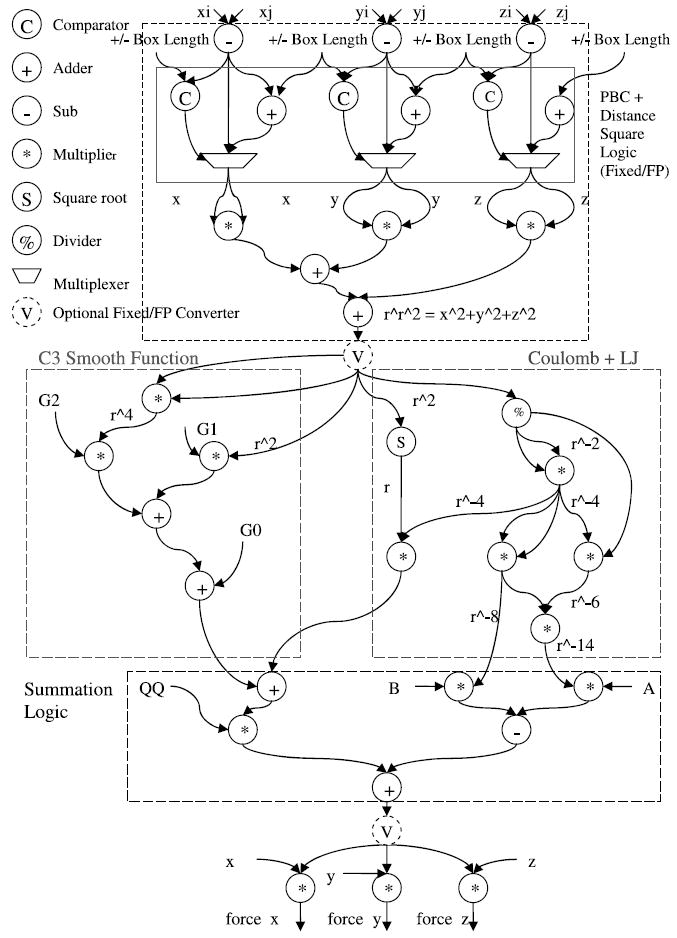
Shown is the detailed datapath for the direct computation. For hybrid integer/floating point, the computation is the same, but with data before the first conversion and after the second being integer.

Figure 6 shows the Coulomb-plus-LJ block that is used with the compiler. An inverse square root replaces the original square root and divide saving logic and improving performance. This works because of the favorable convergence properties of the inverse square root.

Fig. 6.

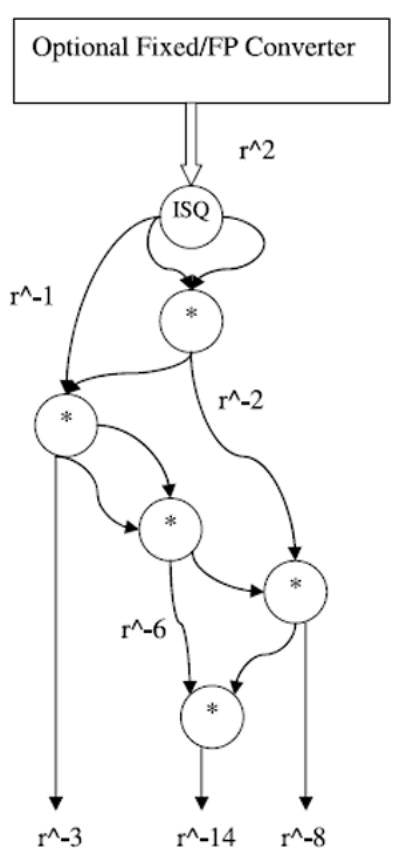
The Coulomb + LJ block (from Figure 5) modified for the FP Compiler optimization.

3.3 Table Lookup with Interpolation

We now describe the interpolation pipeline (see Figure 7). Assuming that the interpolation function is third order, it necessarily has the format

$$F(x)=((C_3(x-a)+C_2)(x-a)+C_1)(x-a)+C_0,$$

where x ≡ r² = input, a = the index of the interval from the beginning of the section (see Figure 1), and x − a = the offset into the interval. The coefficients C_{0, … ,} C₃ are unique to each interval, and are retrieved by determining the section and interval. Proper encoding makes trivial the extraction of the section, interval, and offset.

Fig. 7.

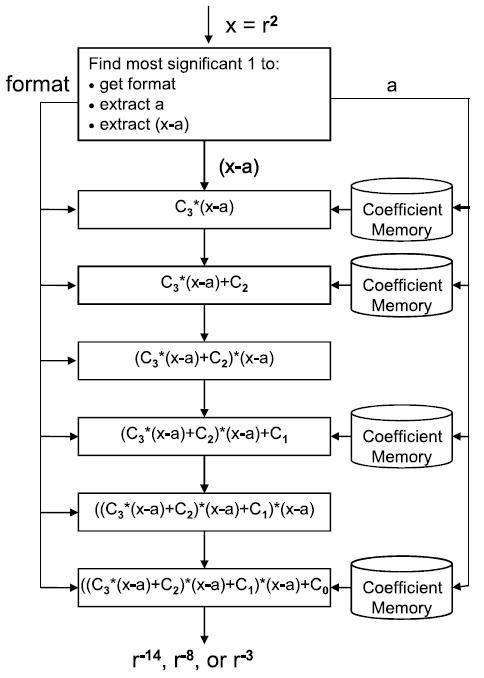
The interpolation pipeline: the position of the leading 1 determines the operand format in the interpolation pipeline.

Figure 8 contains the replacement in Figure 5 needed to implement LookUp. For lower order interpolation, fewer stages are needed.

Fig. 8.

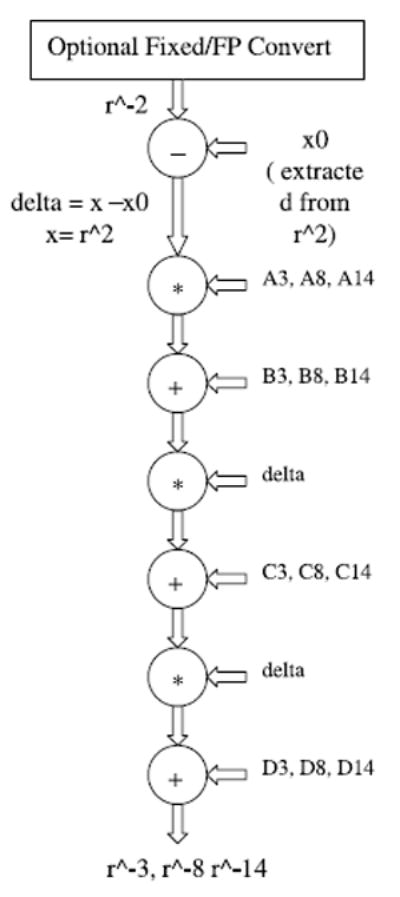
The Coulomb + LJ block (from Figure 5) modified for Table Lookup with Interpolation. Interpolation is 3rd order. Represented are three computations being done at once.

4. FILTER PIPELINE DESIGN AND OPTIMIZATION

We begin by assuming cell lists with processing concentrating on one home cell at a time. With no filtering or other optimization, forces are computed between all pairs of particles i and j, where i must be in the home cell but j can be in any of the 27 cells of the cell neighborhood, including the home cell. By filtering, we mean the identification of particle pairs where the mutual short-range force is zero. A perfect filter successfully removes all such pairs. The efficiency of the filter is the fraction of undesirable particle pairs removed. The extra work due to imperfection is the ratio of undesirable pairs not removed to the desirable pairs.

We evaluate three methods, two existing and one new, which trade off filter efficiency for hardware resources. As motivated in Sections 3 and 6, we store particle positions in three Cartesian dimensions, each in 32-bit integer. Filter designs have two parameters, precision and geometry.

1. Full Precision. Precision = full, Geometry = sphere. This filter computes r² = x² + y² + z² and compares whether $r^2<r_c^2$ using full 32-bit precision. Filtering efficiency is nearly 100%. Except for the comparison operation, this is the same computation that is performed in the force pipeline.

2. Reduced.Precision = reduced, Geometry = sphere. This filter, used by D.E. Shaw [Larson et al. 2008], also computes $r^2=x^2+y^2+z^2$, $r^2<r_c^2$, but uses fewer bits and so substantially reduces the hardware required. Lower precision, however, means that the cut-off radius must be increased (rounded up to the next bit) so filtering efficiency goes down: for 8 bits of precision, it is 99.5% for about 3% extra work.

3. Planar. Precision = reduced, Geometry = planes. A disadvantage of the previous method is its use of multipliers, which are the critical resource in the force pipeline. This issue can be important because there are likely to be 6 to 10 filter pipelines per force pipeline. In this method we avoid multiplication by thresholding with planes rather than a sphere (see Figure 9 for the 2D analog). The formulae are as follows:

   $$\begin{array}{l}—\left|x\right|<r_c,\left|y\right|<r_c,\left|z\right|<r_c\\ —\left|x\right|+\left|y\right|<\sqrt{2}{r}_c,\left|x\right|+\left|z\right|<\sqrt{2}{r}_c,\left|y\right|+\left|z\right|<\sqrt{2}{r}_c\\ —\left|x\right|+\left|y\right|+\left|z\right|<\sqrt{3}{r}_c\end{array}$$

With 8 bits, this method achieves 97.5% efficiency for about 13% extra work.

Fig. 9.

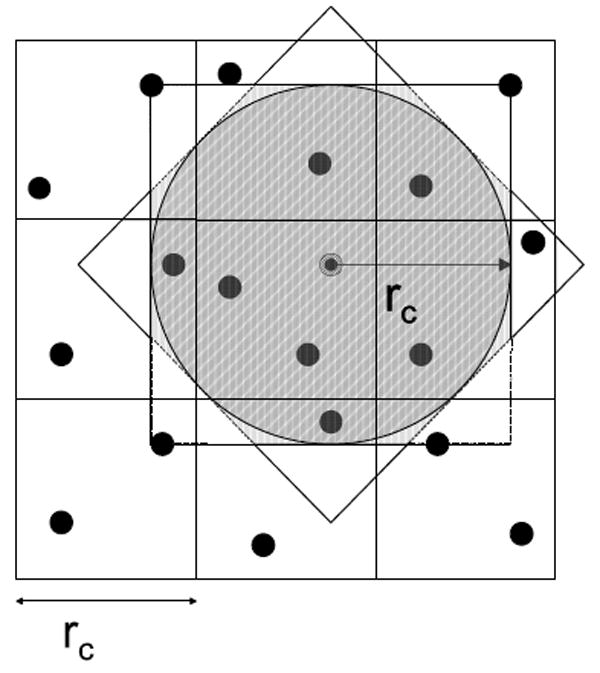
Filtering with planes rather than a sphere – 2D analogue.

Analysis

Table I summarizes the cost (LUTs, registers, and multipliers) and quality (efficiency and extra work) of the three filtering methods. Since multipliers are a critical resource, we also show the two “sphere” filters implemented entirely with logic. The cost of a force pipeline (from Section 3) is shown for scale.

Table I.

Comparison of Three Filtering Schemes with Respect to Quality and Resource Usage

Filtering Method	LUTs/Registers	Multipliers	Filter Eff.	Extra Work
Full precision	341/881 0.43%	12 1.6%	100%	0%
Full prec. - logic only muls	2577/2696 1.3%	0 0.0%	100%	0%
Reduced precision	131/266 0.13%	3 0.4%	99.5%	3%
Reduced prec. - logic only muls	303/436 0.21%	0 0.0%	99.5%	3%
Planar	164/279 0.14%	0 0.0%	97.5%	13%
Force pipe	5695/7678 5.0%	70 9.1%	NA	NA

A force pipeline is shown for reference. Percent utilization is with respect to the Altera Stratix-III EP3SE260.

The most important result is the relative cost of the filters to the force pipeline. Depending on implementation and load balancing method (see Section 5.4), each force pipeline needs between 6 and 9 filters to keep it running at full utilization. We refer to that set of filters as a filter bank. Table I shows that a full precision filter bank takes from 80% and 170% of the resources of its force pipeline. The reduced (logic only) and planar filter banks, however, require only a fraction: between 17% and 40% of the logic of the force pipeline and no multipliers at all. Since the latter is the critical resource, the conclusion is that the filtering logic itself (not including interfaces) has negligible effect on the number of force pipelines that can fit on the FPGA.

We now compare the reduced and planar filters. The Extra Work column in Table I shows that for a planar filter bank to obtain the same performance as logic-only-reduced, the overall design must have 13% more throughput. This translates, for example, to having 9 force pipelines when using planar rather than 8 for reduced. The total number of filters remains constant. The choice of filter therefore depends on the FPGA’s resource mix.

5. MD SYSTEM DESIGN

5.1 Architecture of Target Systems

We briefly state our assumptions about the target HPRC architecture: They are typical for current products; details of appropriate FPGA-based systems can be found, for example, in Hauck and DeHon [2008] and VanCourt and Herbordt [2009].

• The overall system consists of a host PC or workstation with an accelerator board plugged into a high-speed socket (e.g., PCI Express). The host runs the main application program and communicates with the accelerator through function calls.

• The accelerator board consists of a high-end FPGA, memory, and a bus interface. On-board memory is tightly coupled to the FPGA either through several interfaces (e.g., 6 × 32-bit) or a wide bus (128-bit).

• Besides configurable logic, the FPGA has dedicated components such as independently accessible multiport memories (e.g., 1000 × 1 KB) and a similar number of multipliers. FPGAs in HPRC typically run at 200 MHz, although with optimization substantially higher operating frequencies can be achieved. We assume that 10%-15% of the FPGA’s logic is dedicated to system (nonapplication) functions such as memory controllers.

5.2 Host/Accelerator Partitioning

The filtering problem was introduced in Section 2.4 and filter designs given in Section 4. In this section, we present coprocessor-specific considerations and answer the basic question of why perform filtering on the FPGA at all.

We begin with cell list computation: it is very fast and the data generated small (both O(N)) so it is generally done on the host along with the motion integration. Cell lists are downloaded to the coprocessor every iteration along with the new particle positions. The neighbor list computation, however, is much more expensive: if done on the host it could mitigate any advantage of coprocessing. Moreover, the size of the aggregate neighbor lists is often hundreds of times that of the cell lists, which makes their transfer impractical. As a consequence, neighbor list computation, if it is done at all, must be done on the coprocessor. But even on the coprocessor storage is still a concern.

We now look at MD operation starting with cell lists. For reference we examine the NAMD benchmark NAMD2.6 on ApoA1. It has 92,224 particles, a bounding box of 108Å × 108Å × 78Å, and a cut-off radius of 12Å. This yields a simulation space of 9 × 9 × 7 cells with an average of 175 particles per cell with a uniform distribution. On the FPGA, the working set is typically a single (home) cell and its cell neighborhood for a total of (naively) 27 cells and about 4,725 particles.

In actuality, Newton’s 3rd Law (N3L) is used to reduce this number. That is, since each particle-particle interaction is mutual, it is calculated once per particle pair and recorded for both particles. To effect the reduction in work, home cell particles are only matched with particles of part of the cell neighborhood, and with, on average, half of the particles in the home cell. We refer to the subset of cells in the cell neighborhood that are processed together with (and including) the home cell as the cell set. For the 14- and 18-cell sets presented in Section 5.4, the average number of particles to be examined (for each particle in the home cell) is 2,450 and 3,150, respectively. Given current FPGA technology, any of these cell sets (14, 18, or the original 27 cells) easily fits in the on-chip BRAMs.

Neighbor lists for a home cell do not fit on the FPGA. For example, the aggregate of the neighbor lists for 175 home cell particles is over 64,000 particles (one half of 732 for each of the 175 particles; 732 rather than 4,725 because of increased efficiency of neighbor lists over cell lists).

The memory requirements are therefore very different for the two methods. For cell lists, we swap cells onto and off of the FPGA as needed. Because of the high level of reuse, this is commonly done in the background (see Section 5.3). In contrast, neighbor list particles must be streamed from off-chip. This has worked when there are one or two force pipelines operating at 100 MHz [Kindratenko and Pointer 2006; Scrofano et al. 2006], but is problematic for current HPRC systems. For example, the Stratix-III/Virtex-5 generation of FPGAs supports 8 force pipelines operating at 200MHz leading to a bandwidth requirement of over 20 GB/s. While high-end FPGAs support this easily, memory interfaces in commercial systems generally do not.

From this discussion, it follows that use of neighbor lists calls for an “on-FPGA” solution, but that this itself appears to be impracticable due to memory and transfer requirements. At the same time, however, the 6x potential increase in efficiency cannot be abandoned.

One way to improve efficiency is to reduce the cell size: the smaller the cell size, the finer the granularity, and the larger the fraction of the cell neighborhood volume guaranteed to be useful. With a cell edge of r_c/2 and a 5³ set, efficiency increases to 26.8%. With more aggressive clipping of the corner cells, efficiency increases a bit more but so does the control complexity. More important is that reducing cell size also reduces reuse and still leaves much inefficiency. While reducing cell size is viable, there are better options.

The solution we propose is to use neighbor lists, but to compute them every iteration, generating them continuously and consuming them almost immediately. In this scenario, the use of neighbor lists can be viewed as filtering out the zero-force particle pairs: the filter pipelines feed the force pipelines with minimal buffering in between (see Figure 10).

Fig. 10.

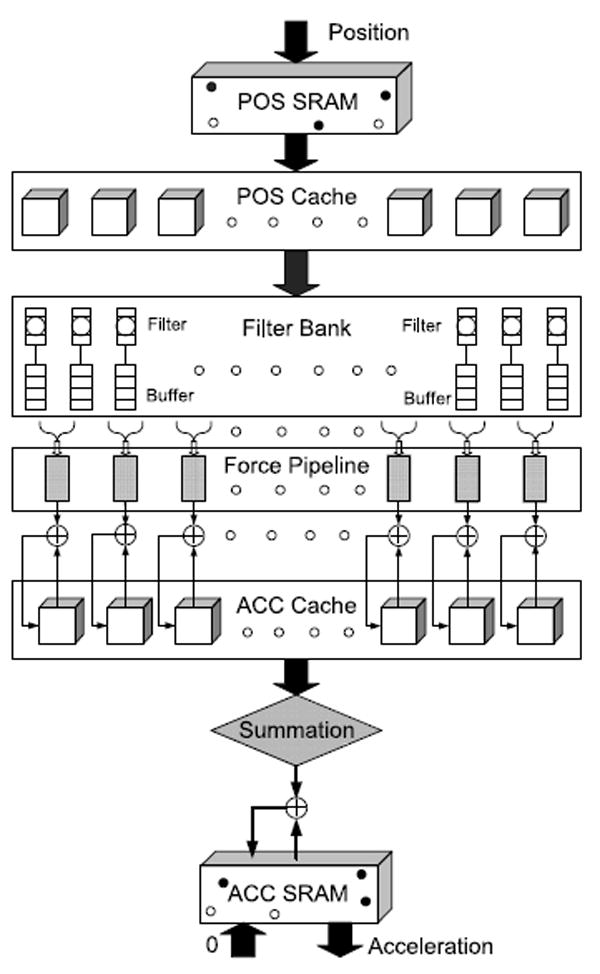
Schematic of the HPRC MD system.

5.3 Overall Design and Board-Level Issues

In this section, we describe the overall design (see Figure 10), especially how data are transferred between host and accelerator and between off-chip and on-chip memory. Details of transfers from stage to stage are presented in the succeeding subsections. For reference, we assume our current implementation of 8 force and 72 filter pipelines.

Host-Accelerator Data Transfers

At the highest level, processing is built around the timestep iteration and its two phases: force calculation and motion update. During each iteration, the host transfers position data to, and acceleration data from, the coprocessor’s on-board memory (POS SRAM and ACC SRAM, respectively). With 32-bit precision, 12 bytes are transferred per particle. While the phases are necessarily serial, the data transfers require only a small fraction of the processing time. For example, in Section 6 the short-range force calculation takes about 22 ms for 100-K particles and increases linearly with particle count through the memory capacity of the board. The combined data transfers of 2.4 MB take only 2-3ms. Moreover, since simulation proceeds by cell set, processing of the force calculation phase can begin almost immediately as the data begin to arrive.

Board-Level Data Transfers

Force calculation is built around the processing of successive home cells. Position and acceleration data of the particles in the cell set are loaded from board memory into on-chip caches, POS and ACC, respectively. When the processing of a home cell has completed, ACC data is written back. Focus shifts and a neighboring cell becomes the new home cell. Its cell set is now loaded; in our current scheme this is usually nine cells per shift. The transfers are double buffered to hide latency.

The time to process a home cell T_proc is generally greater than the time T_trans to swap cell sets with off-chip memory. Let a cell contain an average of N_cell particles. Then, T_trans = 324 × N_cell/ B (9 cells, 32-bit data, 3 dimensions, 2 reads and 1 write, and transfer bandwidth of B bytes per cycle). To compute T_proc, assume P pipelines and perfect efficiency. Then, $T_{\mathit{proc}}=N_{\mathit{cell}}^2\times 2\pi /3P$ cycles. This gives the following bandwidth requirement: B > 155 * P/N_cell. For P = 8 and N_cell = 175, B > 7.1 bytes per cycle. For many current FPGA processor boards, B ≥ 24. Some factors that increase the bandwidth requirement are faster processor speeds, more pipelines, and lower particle density. A factor that reduces the bandwidth requirement is better cell reuse.

On-Chip Data Transfers

Force computation has three parts, filtering particle pairs, computing and accumulating the forces (accelerations) themselves, and combinining the accumulated accelerations. In the design of the on-chip data transfers, the goals are simplicity of control and minimization of memory and routing resources.

Processing of a home cell proceeds in cohorts of reference particles that are processed simultaneously, either 8 or 72 at a time (either one per filter or one per force pipeline, see Section 5.5). This allows a control with a single state machine, minimizes memory contention, and simplifies accumulation. For this scheme to run at high efficiency, two types of load-balancing are required: (i) the work done by various filter banks must be similar and (ii) filter banks must generate particle pairs having non-trivial interactions on nearly every cycle. Details are given in the next subsections.

POS Cache to Filter Pipelines

Cell set positions are stored in 54-108 BRAMS, that is, 1-2 BRAMs per dimension per cell. This number depends on the BRAM size, cell size, and particle density. Reference particles are always from the home cell, partner particles can come from anywhere in the cell set. Given the flexibility in accessing the BRAMs there are a number of ways to organize these accesses (see, e.g., Figure 13).

Fig. 13.

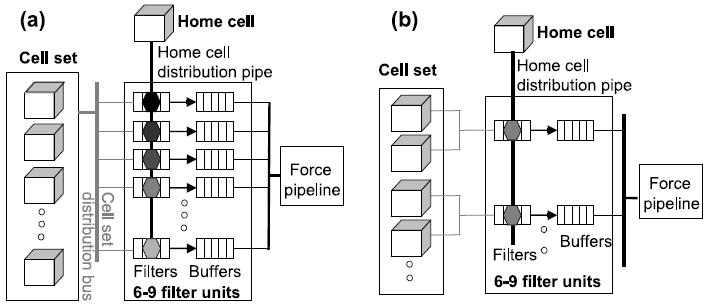
Two mappings of particle pairs onto filters. (a) Particle Mapping: Filters each hold a different reference particle. Particles in cell set are broadcast one per cycle. (b) Cell Mapping: Same reference particle held by all filters in a bank. Each filter is responsible for 2-3 cells.

Filter Pipelines to Force Pipelines

Various transfer schemes are described in Section 5.6.

Force Pipelines to ACC Cache

To support N3L, two copies are made of each computed force. One is accumulated with the current reference particle. The other is stored by index in one of the large BRAMs on the Stratix-III. Accumulation is described in Section 5.7.

5.4 Balancing Neighbor List Sizes

For efficient access of particle memory and control, and for smooth interaction between filter and force pipelines, it is preferred to have each force pipeline handle the interactions of a single reference particle at a time. This preference becomes critical when there are a large number of force pipelines and a much larger number of filter pipelines. Moreover, it is highly desirable for all of the neighborlists being created at any one time (by the filter banks) to be transferred to the force pipelines simultaneously (buffering mechanisms are described in Section 5.6). It follows that each reference particle should have a similar number of partner particles (neighbor list size).

The problem addressed in this subsection is that the standard method of choosing a reference particle’s partner particles leads to a severe imbalance in neighbor list sizes. How this arises can be seen in Figure 11(a), which illustrates the standard method of optimizing for N3L. So that a force between a particle pair is computed only once, only a “half shell” of the surrounding cells is examined (in 2D, this is cells 1–4 plus Home). For forces between the reference particle and other particles in Home, the particle ID is used to break the tie, with, for example, the force being computed only when the ID of the reference particle is the higher. In Figure 11(a), particle B has a much smaller neighborlist than A, especially if B has a low ID and A a high.

Fig. 11.

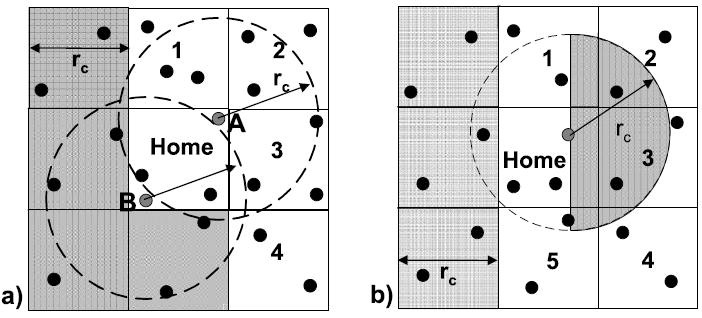
Shown are two partitioning schemes for using Newton’s 3rd Law. In (a), 1-4 plus home are examined with a full sphere. In (b), 1-5 plus home are examine, but with a hemisphere (shaded part of circle).

In fact neighborlist sizes vary from 0 to 2L, where L is the average neighborlist size. The significance is as follows: Let all force pipelines wait for the last pipeline to finish before starting work on a new reference particle. Then, if that (last) pipeline’s reference particle has a neighborlist of size 2L, then the latency will be double that if all neighbor lists were size L. This distribution has high variance (see Figure 12), meaning that neighbor list sizes greater than, say, $\frac{3}{2}L$ are likely to occur. A similar situation also occurs in other MD implementations, with different architectures calling for different solutions [Anderson et al. 2008; Snir 2004].

Fig. 12.

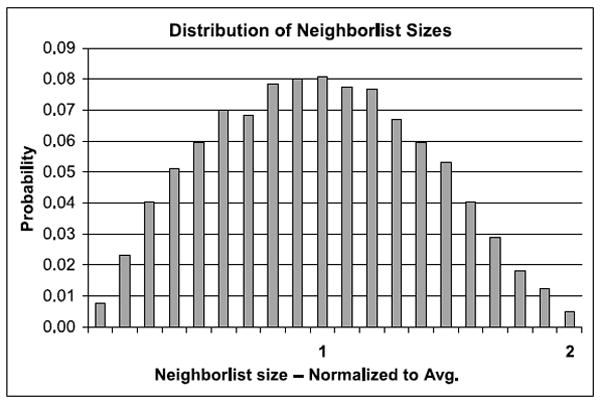
Distribution of neighborlist sizes for standard partition as derived from Monte Carlo simulations.

One way to deal with this load imbalance is to overlap the force pipelines so that they work independently. While viable, this leads much more complex control.

An alternative is to change the partitioning scheme. Our new N3L partition is shown in Figure 11(b). There are three new features. The first is that the cell set has been augmented from a half shell to a prism. In 2D, this increases the cell set from 5 cells to 6; in 3D, the increase is from 14 to 18. The second is that, rather than forming a neighbor list based on a cutoff sphere, a hemisphere is used instead (the “half-moons” in Figure 11(b)). The third is that there is now no need to compare IDs of home cell particles.

We now compare the two partitioning schemes. There are two metrics: the effect on the load imbalance and the extra resources required to prevent it.

1. Effect of Load Imbalance. We assume that all of the force pipelines begin computing forces on their reference particles at the same time, and that each force pipeline waits until the last force pipeline has finished before continuing to the next reference particle. We call the set of neighbor lists that are thus processed simultaneously a cohort. With perfect load balancing, all neighbor lists in a cohort would have the same size, the average L. The effect of the variation in neighbor list size is in the number of excess cycles—before a new cohort of reference particles can begin processing—over the number of cycles if each neighborlist were the same size. The performance cost is therefore the average number of excess cycles per cohort. This in turn is the average size of the biggest neighbor list in a cohort minus the average neighbor list size. We find that, for the standard N3L method, the average excess is nearly 50%, while for the “half-moon” method it is less than 5%.

2. Extra Resources. The extra work required to achieve load balance is proportional to the extra cells in the cell set: 18 versus 14, or an extra 29%. This drops the fraction of neighbor list particles in the cell neighborhood from 15.5% to 11.6%, which in turns increases the number of filters needed to keep the force pipelines fully utilized (overprovisioned) from 7 to 9. For the reduced and planar filters, this is not likely to reduce the number of force pipelines.

5.5 Mapping Particle Pairs to Filter Pipelines

From the previous sections, we converge on an efficient design for filtering particle pairs.

• During execution, the working set (data held on the FPGA) consists of the positions and accelerations of particles in a cell set; that is, a single home cell and its 17 neighbors (in the “half moon” scheme);

• Particles from each cell are stored in a set of BRAMs: this is currently one or two BRAMs per coordinate, depending on the cell size, for a total of 108-216;

• The N3L partition specifies 7-9 filter pipelines per force pipeline;

• FPGA resources in the Stratix-III/Virtex-5 generation yield 8-10 force pipelines; and

• Force pipelines handle at most a small number of reference particles at a time (and their N3L partners).

We now address the mapping of particle pairs to filter pipelines. There are a (perhaps surprisingly) large number of ways to do this; finding the optimal mapping is in some ways analogous to optimizing loop interchanges with respect to a cost function. Figure 13 shows two possibilities. In particle mapping (a), each filter is responsible for a different reference particle. Each cycle, a single partner particle from the cell set is broadcast to all of the filters (in all of the filter banks). In cell mapping (b), each filter bank is collectively responsible for a different reference particle. Each filter within a bank processes the reference particle with respect to partners from its own subset of 2 or 3 cells. The issues are as follows:

Force Pipeline Efficiency

Overall performance is proportional to the efficiency of the force pipelines, that is, the fraction of cycles that they deliver “payload” (pairs with non-zero forces). Since there are no stalls, the efficiency is thus proportional to the fraction of cycles that they input (are issued) payload particle pairs from their filter banks.

Payload Generation Rate

Given sufficient filters, a filter bank will generate payload pairs at an average rate of greater than one per cycle. The variance may be high, however, which can substantially degrade efficiency.

Distribution of Payload Particle Pairs

While the number of payload particle pairs from a given cell set—and even from any reference particle (from Section 5.4)—has a small variance, the number and distribution of payload pairs generated by any particular filter can vary wildly. For example, in Figure 11(b), let two filters (in a bank) each handle the same reference particle, but let the partner particles be from different cells, say 3 and 5. Each filter examines the same number of pairs, but the first filter passes most of its input while the second passes almost none.

Queueing Particle Pairs

A simple (but costly) solution is to: (i) append a large queue to each filter and (ii) implement a flexible router from these queues to the force pipeline. The two mappings lend themselves to multiple more practical queueing methods, the choice of which depends on the resources available on the FPGA.

In the next section we present two queueing strategies, whole neighborlist and continuous. We evaluate them with respect to the two particle mapping strategies for performance (force pipeline efficiency) and hardware cost (queue size and complexity).

5.6 The Filter Pipeline – Force Pipeline Interface

If there are sufficient BRAMs, then particle mapping can be used to generate neighborlists in their entirety; they are consumed in the same way. Details are as follows.

• A phase begins with a new and distinct reference particle being associated with each filter.

• Then, on each cycle, a single particle from the 18-cell set is broadcast to all of the filters.

• Each filter’s output goes to its own set of BRAMs.

• The output of each filter is exactly the neighborlist for its associated reference particle.

• Double buffering enables neighborlists to be generated by the filters at the same time that the previous phase’s neighborlists are being drained by the force pipelines.

Advantages of this method include:

• Nearly perfect load balance among the filters (from the “half-moon” partition);

• Little overhead: each phase consists of over 3000 cycles before a new set of reference particles must be loaded;

• Nearly perfect load balancing among the force pipelines: each operates successively on a single reference particle and its equal-sized neighborlist; and

• Simple queueing and control: neighborlist generation is decoupled from force computation.

One disadvantage of the whole neighborlist method is that it requires hundreds of BRAMs. Although there are a thousand or more on some high-end FPGAs, this is still a concern. Another disadvantage is fragmentation. The number of phases necessary to process the particles in a single home cell is ⌈|particles-in-home-cell| / |filters|⌉. For small cells or low-density simulations, the loss of efficiency can become significant. There are, however, several reasonable solutions.

• Increase the number of filters and further decouple neighbor list generation from consumption. The reasoning is that as long as the force pipelines are busy, some inefficiency in filtering is acceptable.

• Overlap processing of two home cells. This increases the working set from 18 to 27 cells for a modest increase in number of BRAMs required. One way to implement this is to add a second distribution bus.

• Another way to overlap processing of two home cells is to split the filters among them. This halves the phase granularity, and so the expected inefficiency, without significantly changing the amount of logic required for the distribution bus.

For the rest of this section, we examine more direct transfers of data from filters to force pipelines. Figure 13 shows the basic queueing used in both mappings: Some number of filters N _filters in a filter bank feed a single force pipeline. Each filter has a queue to which it outputs its data. As described in Section 5.3, the force pipelines should be as independent from one another as possible. This is to constrain the complexity of the routing between filter and force stages and between force stage and ACC Cache.

At a high-level, this is a typical queueing problem with N _filters servers where each has known arrival and departure rates. An arrival is the generation of a particle pair that has passed the filter criteria; a departure is when a payload pair is consumed by the force pipeline. Also, the goal is to minimize idle time (when all of the queues are empty) and hardware cost. The latter includes queue size, but also complexity of the control and of the concentrator logic that routes from the filter queues to the force pipeline.

There are also a number of differences, however. These restrict the utility of stochastic analysis, but also point to implementation methods.

1. Execution Proceeds in Phases. For particle mapping, the filter bank processes a cohort of N _filters reference particles in a phase. For cell mapping, it processes a single reference particle.

2. Uniformity. The total number of arrivals per reference particle varies only slightly within a phase (for particle mapping) and among phases (for both mappings).

3. Nonuniformities. The N _filters queues can have highly non-uniform departure rates and/or high variation in departure rates during a phase. Depending on the position of the reference particle in the home cell and on the cell of its partner, the a priori probability of a departure can be anything from 0 to 1.

Some design considerations are as follows: To minimize queue size, there are several mechanisms including under provisioning (by keeping N _filters small) and throttling (when queues are full). Even if these are used, however, performance is improved by smoothing and balancing the departure rates (arrivals at the force pipelines). Here are three ways that help do this.

Fetch Order

Especially for particle mapping, departure rates for each filter vary considerably during a phase. For example, in Figure 11(b), the filter (of the particle shown) has a departure rate near 0 when cell 4 is processed, but greater than .5 for cell 3. This variation can be smoothed by randomizing the order in which the partner particles are fetched from the cell set. A simple way to approximate this is to fetch particles from cells round-robin rather than cell-at-a-time.

Mapping Combinations of Cells

For cell mapping, different cells in the cell set vary widely in the probability that their particles will be part of a neighbor list. For example, in Figure 11(b), the Home cell and cell 3 are much more likely to provide payload partner particles than the corner cells (2 and 4). Pairing cells appropriately, for example, one with much payload potential with one that has little, helps equalize the arrival rates.

Concentrator Logic

Complex logic can completely smooth non-uniformities among filter queue arrivals (within a cycle) by transferring them to the queues with the most space. Logic that provides a nearly the same effectiveness but with minimal hardware cost is shown in Figure 14. Each filter independently enqueues particle pairs that have passed the selection criteria. An arbiter determines transfer to the force pipeline based on the following logic.

Fig. 14.

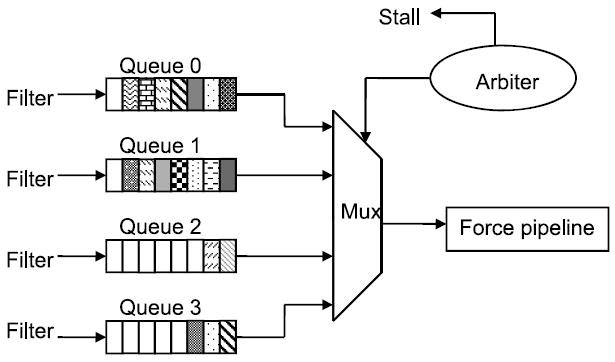
Concentrator logic between filters and force pipeline.

1. First priority is given to queues that are within one of being full. This is sufficient to prevent data from being dropped. If multiple queues are nearly full, then priority is rotated round-robin.

2. Otherwise, priority is given to queues that are not empty. Again, priority is rotated round-robin.

3. If multiple queues are nearly full, then the filters are throttled. Note that throttling by itself does not reduce efficiency; the key performance consideration is that the force pipelines always be active.

Another design consideration is whether to over- or under-provision and whether to throttle filter pipeline input to reduce the queue size needed to prevent overflow. Having a smaller or larger number of filters under- or over-provisions the force pipeline. The advantage of under-provisioning is that simple hardware is adequate for correct execution. The advantage of the over-provisioning is high utilization of the force pipelines: with nine or more filters in the Perfect/“half-moon” design option the force pipelines are almost always busy. In this case the design requires either larger queues or that the filters be throttled.

Table II shows various configurations with no throttling. The maximum queue size is that required to prevent overflow with very high probability. The utilization is the average fraction of cycles that the force pipelines are busy. “Cell mapped” requires smaller queues because it has shorter phases: each filter bank processes one reference particle at a time rather than N _filters. Even the largest queues require much less storage than the whole neighborlist method.

Table II.

Queue Size Requirement and Utilization are Shown for Various Configurations with No Throttling

# of filters	particle mapped				cell mapped
	6	7	8	9	6	9
Queue size	10	18	36	80	6	36
Utilization	69.7%	81.2%	92.5%	99.3%	69.6%	98.3%

We now examine the effect of throttling. In this design, the filters all halt when any is in danger of overflow. Since the force pipelines consume every cycle, this happens when multiple queues are within one of full. Figure 15 shows the effect of queue size, number of filters (queues), and mapping on utilization. Even with over provisioning, utilization can be less than 100% because of nonuniformities in arrivals, and because of start-up and tear-down effects. The key result is that with slight over provisioning, that is, 9 filters, particle mapped yields 99.2% utilization for a (small) queue size of 8. Particle mapped is slightly better than cell mapped because of its more uniform arrivals and longer phase.

Fig. 15.

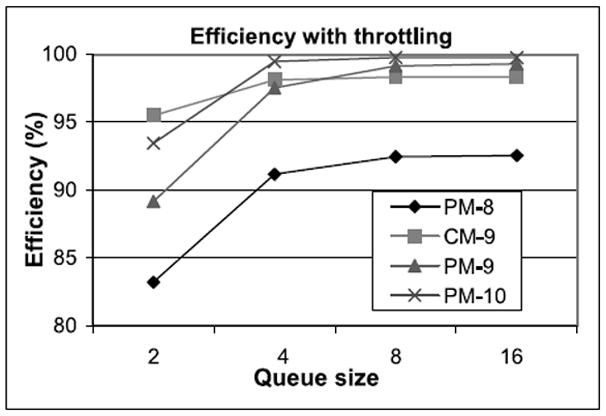
Graph shows the effect of queue size on utilization for various numbers of filters (queues) and mappings of particles onto filters. PM is particle mapped, CM is cell mapped.

5.7 Accumulating and Combining the Accelerations

The final processing steps are accumulating and combining the accelerations generated by the force pipelines. Unlike position data, which is read only, acceleration data is read/write. That is, during the processing of a home cell, each particle’s acceleration accumulates over this and other cells in the cell set; it is not complete until all 27 cells in the neighborhood have taken a turn as the home cell. Thus for each new home cell, the running total of accumulated accelerations of the cell set are read onto the chip in a way analogous to the position data.

One design constraint is that each force pipeline handles at most a small number of reference particles P_i at a time. This enables the total forces on the P_is to be accumulated in registers. Accumulating the mutual forces on the P_is’ N3L partner particles (P _js), however, is more complex as their positions span the cell set. To prevent BRAM access contention, the following strategy is used. Partner updates are written to BRAMs associated uniquely with each force pipeline. When processing of a home cell is completed, the partner data from the various pipeline-specific BRAMs are merged.

This method is depicted in Figure 16. In (a), the running accumulation for a single pipeline during cell processing is shown. We describe this for particle mapping, cell mapping is analogous. Recall that each of the N _force force pipelines has N _filters filters and that each filter processes a unique reference particle at a time. Also that reference particles are always from the home cell, but that partner particles come from the entire cell set. For each force pipeline, there are N _filters accumulators for the N _filters reference particles being processed at a time. There are also N _force force caches, one for each pipeline. Each force cache has an accumulator for each particle in the entire cell set.

Fig. 16.

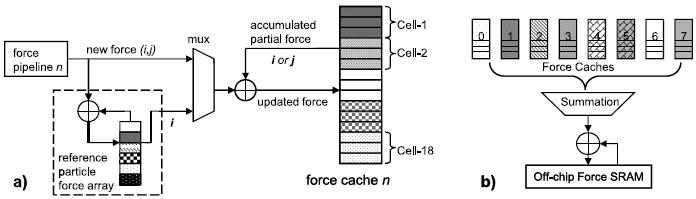
Mechanism for accumulating per particle forces. (a) shows the logic for a single pipeline for both the reference and partner particles. (b) shows how forces are accumulated across multiple pipelines.

Processing proceeds as follows: A new home cell and its acompanying cell set (positions and accelerations) are loaded. From the home cell, a cohort of reference particles is loaded into the filters. Forces are now computed with respect to all of the cell set particles and sent to the accumulators. Each force (for particle pair i, j) is added to both the register corresponding to reference particle i and to the jth slot in that force pipeline’s force cache. The accesses to the force cache BRAMs are pipelined: the js are sent a few cycles ahead so that the current accumulated values are available “just in time.” When the cohort of reference particles has been processed, the reference particle accumulators in the force array are combined with those in the force cache. When the home cell has been processed, the N _force force caches are combined (see Figure 16(b); the basic design first appeared in Gu [2008]). This operation is performed during swapping out, so its latency is completely hidden.

6. RESULTS

6.1 Overview

We use NAMD [Phillips et al. 2002] and ProtoMol [Matthey 2004] as reference codes, both to determine the number of short-range particle-particle interactions computed per iteration as well as the microprocessor time (per iteration per core). NAMD scales well with multiple cores and multiple processors up to hundreds of processors.

We refer to the NAMD benchmark NAMD2.6 on ApoA1. It has 92,224 particles, a bounding box of 108Å × 108Å × 78Å, and a cut-off radius of 12Å. By instrumenting the codes, we determine that on average 33.4M non-trivial particle-particle computations are performed per iteration. This agrees very closely with the 33.75M computations expected from the analysis in Section 5.2. According to a study by Stone et al. [2007], this benchmark is executed at 1.78 seconds per iteration on a single core of an Intel core 2 quad-core 2.66 GHz processor.

The rest of this section is organized as follows: In the next two sections, we evaluate the force pipelines proposed in Section 3. We do this first for resource utilization and then for simulation quality. In the final subsection, we describe current status of the overall implementation and implications for MD on HPRC.

6.2 Performance Comparisons of Force Pipeline Design Alternatives

Results are through post place-and-route (PaR) using the standard Altera tool chain. We assume the Stratix-III EP3SE260. This method is sufficient to give precisely the resource usage and the number of pipelines. For operating frequency, true implementations are often slightly lower. On the other hand, the floating point cores (and code compiled using the Altera Floating Point Compiler or FPC) are specified to run at more than 250 MHz, so with some optimization higher performance than what we have achieved so far could be realized. We first present the best design; it is characterized as follows.

• Direct computation (no table look-up)

• Hybrid fixed and floating point

• Single precision except for force accumulation (36 bit)

• Generated using FPC

1. Hybrid versus Single Precision versus Double Precision. Figure 17 shows resource usage for a number of arithmetic modes and force pipeline designs. Hybrid uses 32-bit fixed point for displacement and 36-bit fixed point for force accumulation. Single and double refer to use of floating point throughout. SemiFP is described in detail in previous work [Gu et al. 2008]; it has 35 bits of precision. Not shown here is that LookUp requires significant use of BRAMs (to hold the tables) while Direct does not.

   We observe that while Stratix-III FPGAs have substantial floating point support, this does not result in direct scaling from single to double precision. The increase in resources required is 2.5× - 3× for logic, but 4× - 4.5× for the multipliers. Also, the operating frequency is reduced, but the quality improves.

2. Effect of Arithmetic Implementation. Figure 18 shows the resource usage of various implementations but this time emphasizing single precision and the variation in interpolation order in LookUp.

   Direct computation (DC) uses less than 10% of the DSP units and far less of the remaining logic. The 3rd order LookUp uses a similar fraction of DSP units, but substantially more logic. Reducing the interpolation order to 2nd and 1st allows the implementation of perhaps another pipeline or two, but may not be worth the decrease in simulation quality. Overall, this is a surprising result. In previous studies we found LookUp to be superior to Direct. We attribute the change to advances in floating point support in both the FPGA hardware and the tool chain (cores and floating point compiler).

3. Floating Point Compiler versus Core Only. The effect of using the Altera Floating Point Compiler is shown in Figure 19. This computation (short-range force pipeline) does not take advantage of most of the compiler optimizations, but still results in a substantial reduction in non-DSP logic. This is especially helpful for saving logic for the filter pipelines.

Fig. 17.

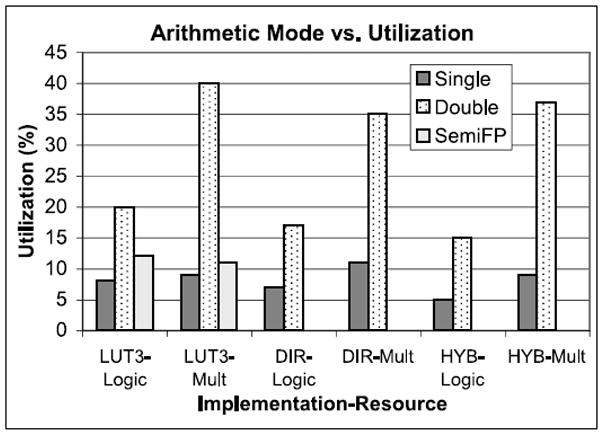
Resource utilization in registers and logic for the Stratix-III. LUT3 is LookUp with 3rd order interpolation. DIR is Direct. HYB refers to Direct with partial fixed point.

Fig. 18.

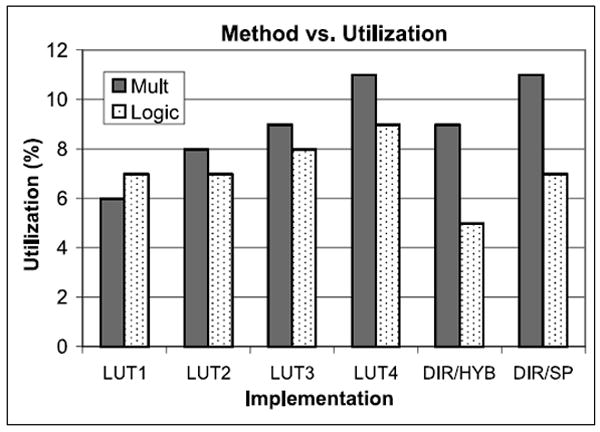
Resource utilization in registers and logic for the Stratix-III. The LUT number refers to the order of the interpolation. LUT implementations are for single precision FP.

Fig. 19.

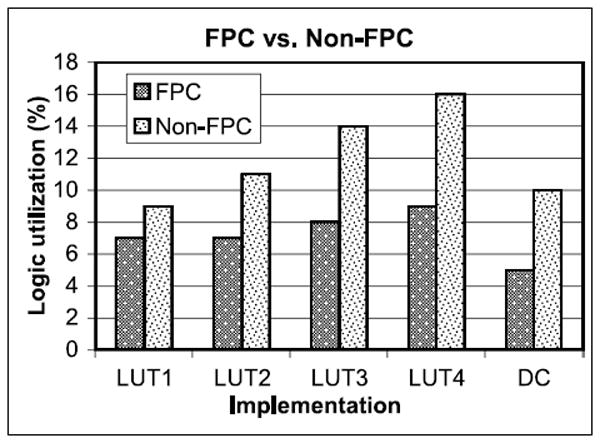
Effect of using the Altera FPC on logic utilization. For single pipeline, single precision. Same configurations as in Figure 18.

6.3 Quality Comparisons of Design Alternatives

Direct evaluations of MD simulation quality, such as through validation with wet-lab experiments, are often impractical. Thus surrogates are often used. One type measures the errors with respect to a reference computation. Another type monitors the simulation output to confirm that a physical invariant, such as the total energy, actually is so. Here we use two of each type.

1. Error per Individual Particle-Particle Force Computation. Figure 20 shows the relative average error for the individual particle-particle force computations for the various pipeline implementations. The reference is direct computation using double precision (DC Double, error = 0). We generate the particle pairs by randomly selecting particle positions between the cut-off and exclusion radii. For single precision LookUp, error becomes worse for higher orders. This is because of the higher precision required for those tables.

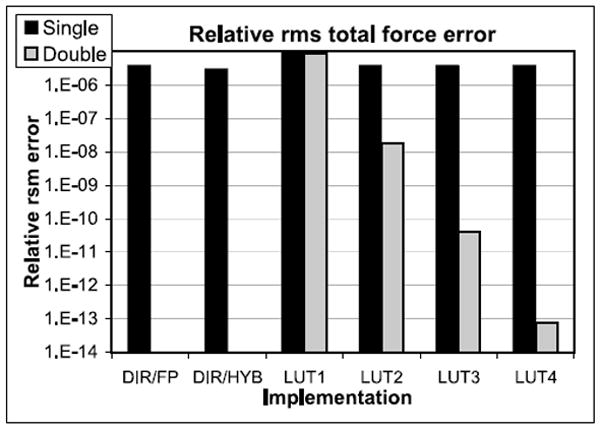
2. Error per Total Force on a Particle per Iteration. Figure 21 shows the relative rms force error of the total force on a particle (see, e.g., Shan et al. [2005]; Skeel et al. [2002]; Wolff and Rudd [1999]). The reference is direct computation using double precision (DIR/DP, error = 0). All exceed the quality criteria given in Shaw et al. [2007].

3. Energy Fluctuation. We simulated BPTI with 14K particles and 26 particle types. After 37K time steps (see Figure 22), the energy fluctuations [Amisaki et al. 1995] for direct force computation are 2.48×10⁻⁴ and 2.62×10⁻⁴ for double precision and single precision, respectively. The ratios of the fluctuations between total energy and kinetic energy are 0.0402 and 0.0422; both are better than the .05 suggested in van der Spoel [2004].

4. Energy Drift. The final quality measure we refer to as “energy drift.” We simulated 400 Argon atoms (as per the ProtoMol test case); the results are shown in Figure 23. Note that while the double precision direct computation remains stable, both simulations with 1st order LookUp appear to drift. That is, not only is there an envelope within which the energy fluctuates, the envelope itself fluctuates. This behavior may be less likely to be acceptable.

Fig. 20.

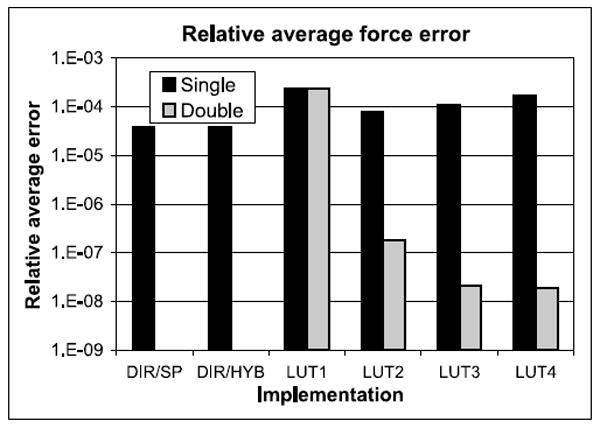
Relative average force error for the particle-particle force computation for various implementations and precisions. DIR is direct computation, LUTn refers to LookUp of various orders.

Fig. 21.

Relative average force error for the total force on a particle per iteration for various implementations and precisions. DIR is direct computation, LUTn refers to LookUp of various orders.

Fig. 22.

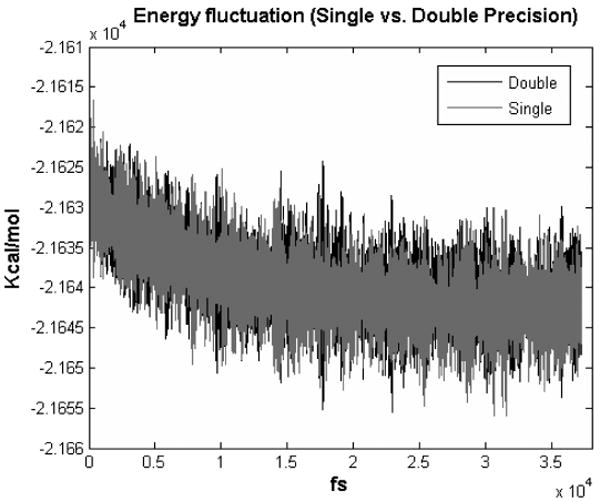
Energy profile of BPTI with 14K particles.

Fig. 23.

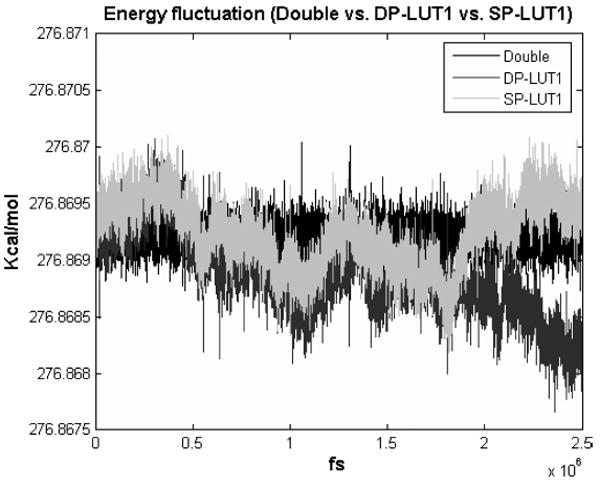
Energy profile of argon with 400 particles.

6.4 Current Status

We have investigated designs with respect to two high-end FPGAs from the 65nm process generation, the Altera Stratix-III SL340 and the Altera Stratix-III SE260. The two devices differ as follows: The SL340 has 30% more logic elements and 20% more BRAMs while the SE260 has 33% more multipliers (see Altera Corporation [2009] for details). For both FPGAs, the best designs have the following characteristics.

• The force pipelines use direct computation, rather than table lookup; hybrid 32/36-bit fixed point and single precision floating point; and are assembled and optimized with the Altera Floating Point Compiler.

• The filter pipelines use reduced precision and spherical geometry.

• N3L partitioning is done via the augmented 18-cell “half-moon” scheme.

• Particle pairs are mapped to filter pipelines via particle mapping (Figure 13(a)).

• Filter banks consist of nine filter pipelines for slight over provisioning.

For other FPGAs, planar filtering may be preferred. For queueing method, the choice depends on the balance between BRAMs on the one hand and logic and DSP units on the other. For the SL340, queueing full neighbor lists works well; for the SE260, continuous queueing is preferred (queue size = 8 with throttling). The configurations conservatively fit 7 and 8 force pipelines for the SL340 and the SE260, respectively, while still leaving ample room ancillary logic. More aggressive designs are possible, for example, by using logic for multipliers; then 9 force pipelines fit on the SE260 and 8 on the SL340. In all cases the force pipelines run at over 95% efficiency. The efficiency can be improved by implementing methods proposed in Section 5.6.

PAR results are shown in Table III. For BRAM utilization the percentages represent the numbers of BRAMs of which any part is used; most are used at less than 40% of capacity. This fraction depends only on particles per cell, not problem size. For multipliers, the SE260 8 pipeline design uses almost all of them; this is clearly the critical resource. The reason that the 9 pipeline version uses fewer multipliers is because there some multipliers are built with logic. All results in Table III are with no optimization below the architecture level.

Table III.

Resource Utilization for Configurations Optimized Variously for Two Altera Stratix-III FPGAs

Configuration	Logic ALUTs/Registers	Multipliers	Memories M9K/M144K	Max Frequency
SE260 – 8 force pipelines	78% (43%/71%)	99%	87% (75%/100%)	196 MHz
SE260 – 9 force pipelines	93% (53%/85%)	98%	97% (95%/100%)	190 MHz
SL340 – 6 force pipelines	53% (18%/41%)	85%	97% (94%/100%)	216 MHz
SL340 – 7 force pipelines	69% (24%/52%)	99%	100% (100%/100%)	198 MHz
SL340 – 8 force pipelines	100% (40%/75%)	100%	100% (100%/100%)	122 MHz

Our implementations are currently running in simulation. They have also been validated with multiple serial reference codes using methods outlined in other work [Gu 2008; Gu et al. 2008].

These results can be interpreted as follows: A system based on the 8 pipeline SE260 design system can execute the short-range force calculation in the ApoA1 benchmark in under 22 ms. This performance represents an 80-fold per-core speed-up over the result shown in [Stone et al. 2007]. Since NAMD scales well, this represents a 20-fold speed-up over a quadcore implementation. While the NAMD benchmark report is a little dated, its microprocessor is comparable in process technology to that of the Stratix-III FPGAs used here (65 nm). For other MD simulations having similar particle density, the FPGA performance scales linearly with the number of particles up to the memory capacity of the FPGA board, or several tens of millions particles. For simulations having much lower density, transfer of cell sets on/off chip becomes the bottleneck (see Section 5.3). This limitation, however, is a function of current HPRC systems rather than the FPGAs themselves. Most current HPRC board designs use only a small fraction of the FPGA’s available bandwidth.

7. SUMMARY AND DISCUSSION

We have presented a new implementation of MD for FPGA-based accelerators. We have thoroughly explored the design space of force pipeline implementations with respect to both performance and numerous measures of quality. We have presented a study of filtering that is the first for FPGAs and one of only very few for hardware implementations of MD. The results show that FPGAs are highly competitive with respect to the short-range force computation in MD simulations.

We summarize the results for the force pipeline. From Figure 18, we see that direct computation is somewhat favorable to table lookup with interpolation, except when 1st order is used. The reduction in accuracy, however, may not be acceptable (see Figure 23). Moreover, the use of BRAMs is a serious drawback given the overall multistage design. Other results are a demonstration of the Altera floating point compiler, and numerous observations with respect to datapath design parameters. The most important of these is probably that simulation quality of the single precision and hybrid (fixed point/single precision) implementations is comparable to that of full double precision.

In the filtering part of this study, we find that high quality filtering can be achieved with only a small amount of logic. We present a geometric filtering scheme that is preferable for FPGA implementation. We also present a new partitioning method for optimizing with respect to Newton’s 3rd Law. This is essential for the design presented here, but could also find application in other hardware implementations of MD. And finally, the scheme of mapping particle pairs to filter pipelines also appears to be new.

An important comparison is with Anton, the ASIC-based MD system from Shaw et al. [2007] that is designed to support hundreds of MD processor chips. The overall performance difference is that Anton runs at four times the clock frequency and holds four times as many force pipelines per chip. There are several design differences. For partitioning, rather than use either the standard “half shell” method or the “half-moon” method proposed here, Anton uses a novel “Neutral Territory” scheme. This especially minimizes interprocessor communication costs. Another consequence is that fewer filters per force pipeline are needed (normalized for throughput). For mapping particle pairs onto force pipelines, Anton uses a scheme similar to the “particle mapping” used here.

The design choices in Anton are not all preferred for single chip FPGA versions (in the current FPGA chip architecture). Some of the architectural differences that lead to different design choices are as follows: single chip versus multiple chip; limitations of FPGA routing logic and its implications in control complexity; chip density and therefore the acceleration (20x speed-up per chip versus 320x); and the number and type of the FPGA’s hard components, especially BRAMs and multipliers. The effect of the FPGA’s architecture on HPRC MD design choices are described throughout this article.

We now briefly discuss implications of this work for HPRC MD simulations as a whole. We have addressed here the short-range non-bonded force computation and associated overhead. There are typically three other significant computations in MD simulations: bonded forces, long-range non-bonded forces, and motion integration. Bonded forces and motion integration are generally computed every timestep while the long-range force may be computed every fourth timestep or even less frequently.

Can the entire MD simulation be performed with the configuration described in Section 5.1 with no slowdown due to these other computations? All of the force computations in a timestep can be overlapped with each other immediately; overlapping motion integration with the forces is also possible, but more complex as it requires pipelining partial results between phases (force and motion). We have obtained timings with respect to the same 92K ApoA1 benchmark for a single core of a 3.0 GHz quadcore Xeon processor running ProtoMol 2.1.1. Motion integration takes 22 ms per timestep while the bonded force calculation takes 43 ms. If four cores are used, straightforward partitioning allows most of this latency to be hidden. In the same configuration, the long range force using PME takes over 200ms (see Phillips [2007] for a similar result). Running with four cores every fourth timestep takes this off the critical path (maintaining agreement with a previous conclusion [Scrofano and Prasanna 2006]). A likely alternative is to also accelerate the long range force computation: Hardy et al. have demonstrated a GPU version with speed-up of over 20x [Hardy et al. 2009].