A General Assignment Method for Oriented Sample (OS) Solid-state NMR of Proteins Based on The Correlation of Resonances through Heteronuclear Dipolar Couplings in Samples Aligned Parallel and Perpendicular to the Magnetic Field

Abstract

A general method for assigning oriented sample (OS) solid-state NMR spectra of proteins is demonstrated. In principle, this method requires only a single sample of a uniformly ¹⁵N-labeled membrane protein in magnetically aligned bilayers, and a previously assigned isotropic chemical shift spectrum obtained either from solution NMR on micelle or isotropic bicelle samples or from magic angle spinning (MAS) solid-state NMR on unoriented proteoliposomes. The sequential isotropic resonance assignments are transferred to the OS solid-state NMR spectra of aligned samples by correlating signals from the same residue observed in protein-containing bilayers aligned with their normals parallel and perpendicular to the magnetic field. The underlying principle is that the resonances from the same residue have heteronuclear dipolar couplings that differ by exactly a factor of two between parallel and perpendicular alignments. The method is demonstrated on the membrane-bound form of Pf1 coat protein in phospholipid bilayers, whose assignments have been previously made using an earlier generation of methods that relied on the preparation of many selectively labeled (by residue type) samples. The new method provides the correct resonance assignments using only a single uniformly ¹⁵N-labeled sample, two solid-state NMR spectra, and a previously assigned isotropic spectrum. Significantly, this approach is equally applicable to residues in alpha helices, beta sheets, loops, and any other elements of tertiary structure. Moreover, the strategy bridges between OS solid-state NMR of aligned samples and solution NMR or MAS solid-state NMR of unoriented samples. In combination with the development of complementary experimental methods, it provides a step towards unifying these apparently different NMR approaches.

1. Introduction

Oriented Sample (OS) solid-state NMR spectroscopy is well suited for studies of biological supramolecular structures, such as virus particles and membranes, that immobilize the constituent macromolecules and provide a mechanism through their diamagnetic anisotropy for them to be aligned in the magnetic field of an NMR spectrometer. The atomic-resolution structures of several coat proteins in virus particles and a number of helical membrane proteins in phospholipid bilayers [1-8] have been determined in this way. In protein structure determination by OS solid-state NMR spectroscopy, the frequencies of the heteronuclear dipolar couplings and anisotropic chemical shifts associated with individual sites, typically the amide nitrogen and hydrogen of the peptide bonds, are measured from narrow single-line resonances that are resolved in multidimensional solid-state NMR spectra. The measured frequencies from these anisotropic spin interactions are orientationally dependent and therefore can be converted in a straightforward manner into angular constraints for the calculation of the three-dimensional protein structures.

Despite the strength of the method in obtaining angular constraints for all sites relative to a single external axis [9], most examples have been relatively small proteins. The application of the OS solid-state NMR to larger membrane proteins has been hindered mainly by limitations of the resonance assignment procedures. Efficient resonance assignment schemes that “walk” down the polypeptide backbone generally rely on the use of 100% uniformly ¹³C and ¹⁵N labeled samples. In solution NMR and MAS solid-state NMR, the rapid reorientation or rotation of the proteins average out the homonuclear ¹³C/¹³C dipolar couplings; however, this is not the case in stationary sample, such as single crystals or magnetically aligned bilayers, where the dense network of homonuclear ¹³C/¹³C dipolar couplings interferes with most solid-state NMR experiments. Methods for applying solid-state NMR to stationary samples uniformly labeled with ¹³C are in early stages of development. The current principal assignment method, the shotgun approach [10], relies on the periodicity of the regular protein secondary structures, α-helix [11, 12] or β-sheet [13], and the ability to readily label proteins by residue type when they are expressed in bacteria grown on minimal media containing only one type of amino acid that is isotopically labeled. This approach is limited by the need to prepare multiple samples, though the calculations for non-periodic tertiary structures are being improved. Spectroscopic methods based on dilute spin exchange [14-17] can be used to assign resonances in uniformly labeled samples, but even in its recently improved forms, its application to membrane proteins is limited by its relatively low sensitivity [18]. More powerful assignment methods are needed to extend OS solid-state NMR to larger, uniformly labeled proteins and to accelerate the rate of structure determination.

Robust sequential assignment methods have been established in solution NMR [19] and in MAS solid-state NMR [20-22] largely through the use of 100% uniformly ¹³C and ¹⁵N labeled samples that are tractable because of the averaging of the ¹³C/¹³C homonuclear dipolar couplings by the natural or experimentally induced isotropic motions. Both types of experiments yield resonances characterized by one or more isotropic chemical shift frequencies. As a result, the isotropic chemical shift assignments for proteins are frequently available, and here we demonstrate that they can be integrated into OS solid-state NMR experiments as part of a general assignment strategy. Notably, the development of a method that integrates these different NMR methods can take advantage of their individual strengths, as the ease of resolving resonances and obtaining angular constraints in OS solid-state NMR is combined with the established assignment methods in solution NMR and MAS solid-state NMR. A limitation is that the protein resonances must have similar isotropic chemical shifts in the lipids that constitute the micelle or isotropic bicelles samples used in solution NMR, or unoriented and possibly frozen liposomes in MAS solid-state NMR, and the liquid crystalline bilayers used in OS solid-state NMR. In favorable cases, the limitation can be partially alleviated by performing a q-titration experiment [23] to extrapolate from micelles or isotropic bicelles to the liquid crystalline bilayer environment used in OS solid-state NMR experiments.

Here we demonstrate that the isotropic chemical shifts can be “back calculated” from OS solid-state NMR spectra obtained from samples aligned with their bilayer normals parallel and perpendicular to the magnetic field [24]. Since the isotropic chemical shift frequencies vary from site-to-site in a protein they provide a unique “tag” for each residue. Consequently, they can serve as the carrier of assignment information between experimental OS solid-state NMR spectra and assigned solution NMR or MAS solid-state NMR spectra. The method for transferring the isotropic chemical shift assignments to stationary aligned samples relies on identifying those heteronuclear dipolar coupling frequencies in parallel alignment that are exactly twice as large as those in the perpendicular alignment. This is possible because the isotropic values for dipolar couplings are zero at all sites. The method utilizes only chemical shift and heteronuclear dipolar coupling data, which can be measured by two- or three- dimensional versions of heteronuclear correlation (HETCOR) and separated local field (SLF) experiments. The results obtained in this way can be readily augmented by assignment information from other experiments and spin interactions.

The membrane protein examples used to illustrate the assignment method are in magnetically aligned bilayers. While they naturally align with their normals perpendicular to the field, they can be “flipped” to the parallel alignment through the addition of lanthanide ions [25] that bind weakly to the phospholipids changing their magnetic susceptibility. Alternatively, there are phospholipids that naturally align with their normals parallel to the field [26]. The experiments are equally applicable to membrane proteins in lipid bilayers that are mechanically aligned on glass plates, since they can be physically arranged in the sample coil so that the bilayer normals are either parallel or perpendicular to the direction of the magnetic field [27-29]. In this article we demonstrate the principles of this new assignment method using simulated spectra, and its experimental application to two well-characterized examples of membrane proteins. This method has the potential to be applied to larger and more complex membrane proteins as the measurements of chemical shifts and heteronuclear dipolar couplings associated with ¹³C nuclei and higher field magnets are employed, and automated computer programs substitute for the step-by-step procedures used in these initial examples.

2. Results

Principles and Simulated Spectra

In both MAS solid-solid state NMR of powder samples and solution NMR of liquid samples, the angular dependencies of the anisotropic chemical shift and dipolar spin interactions are eliminated by motional averaging, which results in the isotropic values of the chemical shifts determining the observed frequencies of individual resonances in the NMR spectra. In contrast, the angular dependence of the chemical shift interaction is retained in stationary samples, including the uniaxially aligned samples used for protein structure determination by OS solid-state NMR spectroscopy. The observed resonance frequencies are determined by the directions and magnitudes of the principal elements of the chemical shift tensor relative to the magnetic field; this is obvious in powder patterns, which result from the sum of the frequencies from all orientations, and in the rotation patterns of single crystals, which can be obtained around multiple axes and used to characterize the chemical shift tensors. A useful property is that the magnitudes of the principal values available from either powder patterns or rotation patterns of single crystals by themselves provide sufficient information to determine the isotropic chemical shift frequency for any site. OS solid-state NMR of aligned membrane proteins differs in that only two orthogonal orientations are available; current technology enables samples to be prepared with their bilayer normals parallel or perpendicular to the magnetic field. It is possible to work with the perpendicular orientation because the proteins typically undergo fast axial diffusion about the bilayer normal in liquid crystalline phospholipid bilayers; the resulting single-line resonances complement those observed with the parallel alignment where molecular motion is not required [30].

To calculate the isotropic value of the chemical shift from aligned samples, the resonance frequencies measured for both the parallel and perpendicular alignments are combined. The use of magnetically aligned bilayers provides two major advantages. First, the protein-containing bilayers can be “flipped” between alignments with the bilayer normals perpendicular or parallel to the field by the addition of lanthanide ions, which enables the use of the same sample for the acquisition of both types of spectra. In general, the paramagnetic ions interact with the lipid head groups and do not perturb the proteins, although controls are always advisable. Second, the proteins undergo rapid uniaxial rotational diffusion about the normals of liquid crystalline bilayers at a frequency that is fast compared to the relevant NMR timescales determined by the frequency spans of the chemical shifts and heteronuclear dipolar couplings (approximately 100 kHz at a ¹H resonance frequency of 700 MHz), and this results in Equation (1), the so-called “bicelle equation” [8, 31-33], which greatly simplifies the calculations of the isotropic values compared with the situation in a rigid lattice:

$${\delta }_{iso}^i=\frac{{\delta }_{\parallel }^i+2{\delta }_{\perp }^i{S}_{rel}}{2S_{rel}+1}$$ (1)

In equation (1), δ_iso is the isotropic chemical shift frequency and δ_∥ and δ_⊥ are the anisotropic chemical shift frequencies observed in parallel and perpendicular bilayer samples, respectively. S_rel accounts for the small differences in order parameters [34] observed for the lipids and proteins in the two alignments; it is a global parameter, since the same value can be applied to all the residues in the same sample.

In principle, the isotropic chemical shift frequency of a resonance can be calculated from three measureable parameters, δ_∥, δ_⊥, and S_rel. In practice, however, since δ_∥ and δ_⊥ frequencies from many residues are observed in the same spectra of uniformly ¹⁵N labeled samples, it is generally not possible to identify which pair of δ_∥ and δ_⊥ frequencies belongs to the same residue by inspection. Here we demonstrate that the heteronuclear dipolar couplings measured for the resonances in the parallel and perpendicular samples can be used to identify those signals that come from the same site in the two spectra. To reiterate the principle of the method, this is feasible because the dipolar couplings always have an isotropic value of zero, and their magnitudes differ by exactly a factor of two between the parallel and perpendicular alignments. In practice, this means that the heteronuclear dipolar coupling frequencies observed in SLF spectra always “flip” around zero, and differ by a factor of 2S_rel between the parallel and perpendicular sample alignments, as is represented by the “bicelle equation” for dipolar couplings:

$$D_{\parallel }^i+2D_{\perp }^i{S}_{rel}=0$$ (2)

D_∥ and D_⊥ are the dipolar coupling frequencies of a resonance from a single site in samples aligned with their bilayer normals parallel and perpendicular to the magnetic field, respectively. In practice, it is advisable to make a list of all signals observed in both parallel and perpendicular spectra ranked according to the magnitudes of their dipolar coupling frequencies. A signal of the same rank in the lists obtained with the two alignments corresponds to the resonance from the same site, which provides a practical method to unambiguously identify the pairs of δ_∥ and δ_⊥ frequencies from each residue from experimental data. This ranking method is demonstrated in the second experimental example of a uniformly ¹⁵N labeled sample. Note that since the small correction factor, S_rel, is a global parameter, adjusting its value does not affect the rank-ordered list..

The last parameter required for Equation (1) is S_rel. After ranking the frequencies by their magnitudes, the dipolar couplings of all pairs of correlated resonances can be averaged to obtain an accurate value of the S_rel using Equation (3):

$$S_{rel}=\frac{1}{N}\sum _{i=1}^N\left(-\frac{D_{\parallel }^i}{2D_{\perp }^i}\right)$$ (3)

Alternatively, S_rel can be determined from a separate experiments that measure the order parameters of either the protein backbone or the phospholipids in the planar bilayers. We have found that a small error in S_rel value usually has negligible effect on the outcome of this assignment method, and therefore S_rel can also be assigned an empirical value of 0.9 without penalty to the assignment process. S_rel together with the pair of δ_∥ and δ_⊥ frequencies measured for each residue gives the isotropic chemical shifts from Equation (1).

A favorable feature of the “bicelle equation” is that the calculation of isotropic chemical shifts is immune to referencing errors. For example, a referencing error of the ¹⁵N chemical shifts in the solid-state NMR spectra on the parallel bicelle sample would result in the addition of a factor ε_∥ to the δ_∥ values of all residues. According to Equation (1), a factor of $\frac{{∊}_{\parallel }}{2S_{rel}+1}$ would consequently be added to all of the δ_iso values. Since S_rel is determined by comparing dipolar coupling values, it is unaffected by the referencing error and remains the same for all residues. Therefore, the same factor $\frac{{∊}_{\parallel }}{2S_{rel}+1}$ is added to δ_iso for all residues, and this factor can be removed by applying a systematic shift to all δ_iso values using the following procedure. After δ_iso values of all residues are obtained from solid-state NMR spectra, we calculate their average value. Similarly, we calculate the average of the isotropic chemical shifts observed in the corresponding solution NMR spectra or MAS solid-state NMR spectra. The difference between these two average values is applied as a universal correction factor to the calculated δ_iso of all residues. Note that systematic differences between isotropic chemical shift frequencies measured from solution NMR and solid-state NMR spectra have been observed previously [35], and there are a number of plausible reasons for this variation, including differences in referencing standards and methods, magnetic susceptibility of the samples, sample temperature, etc. As a result, a universal correction factor is likely to be required even when careful referencing methods are used in all experiments. Similarly, the accuracy of the resonance correlations would not be affected by solution NMR referencing errors, which often occur when the ¹H chemical shift is compared to the frequency of a water resonance instead of from an internal standard such as DSS (4,4-dimethyl-4-silapentane-1-sulfonic acid). Thus, we have found it necessary in practical applications to proteins to take into account both referencing errors and any systematic differences in chemical shifts by applying a correction factor to all δ_iso values.

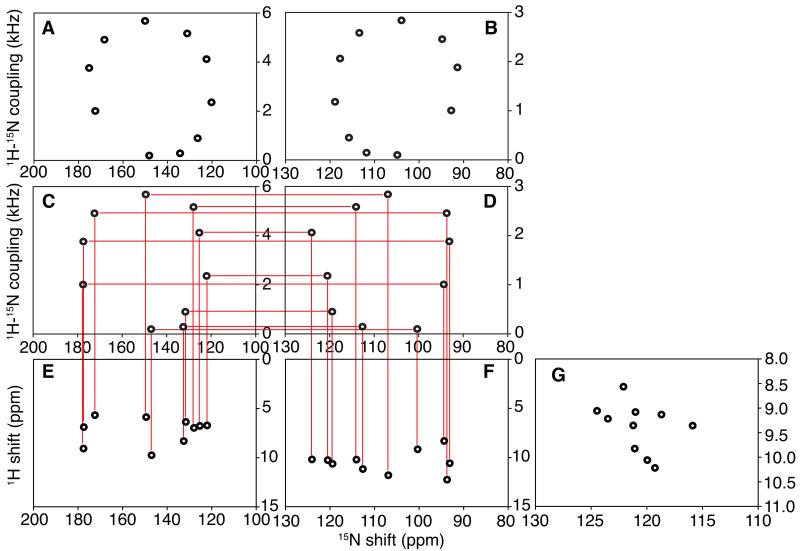
This approach to assigning resonances in the OS solid-state NMR spectra of membrane proteins is illustrated schematically in Figure 1 using simulated two-dimensional ¹H/¹⁵N SLF and HETCOR spectra from an ideal trans-membrane helix with a 40° tilt angle relative to the bilayer normal. By using only ten signals with their frequencies marked by “dots”, the characteristic polarity index slant angle (PISA) wheels [11, 12] can be readily recognized in the SLF spectra in Figure 1A and 1B. They appear as “ideal” helical wheels because they are simulated using the same isotropic chemical shift values (and the same consensus chemical shift tensors) for the ¹H and ¹⁵N nuclei in all ten residues. A more realistic situation is simulated by the pair of spectra in Figure 1C and 1D where the isotropic chemical shifts vary significantly among the residues as well as from the “ideal” value calculated from the “consensus” chemical shift tensors. The site-to-site variations in the positions of resonances induced by differences in the chemical shift frequencies can significantly distort the PISA wheels observed in high field OS solid-state NMR spectra. Significantly, the heteronuclear dipolar couplings are invariant, and retain the feature that their frequencies differ by exactly a factor of two between these two spectra, which enables the correlation between pairs of resonances in the spectra of samples aligned with their bilayer normals parallel (Figure 1C) and perpendicular (Figure 1D) to the magnetic field. The scale for the dipolar coupling frequency is between 0 kHz and 6 kHz for the parallel spectrum shown in Figure 1A and 1C, which is exactly twice that of the 0 kHz to 3 kHz scale for the perpendicular spectrum in Figure 1B and 1D. As discussed above, even though the value of S_rel is reduced from 1.0 to experimentally determined values in the range of 0.8 to 0.9 in membrane protein samples, it is still feasible to establish correlations by drawing horizontal lines between pairs of resonances at the same position in Figure 1C and 1D, after applying the same scaling factor, S^rel, to the data obtained from samples in the parallel and perpendicular alignments. Additional chemical shift dimensions can be added to the established dipolar correlation. For example, the amide ¹H frequencies observed in ¹H/¹⁵N HETCOR spectra (Figure 1E and F) can be linked to the two SLF spectra through their associated ¹⁵N chemical shifts. For simplicity, only two-dimensional HETCOR spectra [36] are shown in Figure 1 to illustrate the method. However, HETCOR can be combined with SLF spectroscopy in a three-dimensional experiment [37, 38], which was used in the second experimental example of a uniformly ¹⁵N labeled protein. By utilizing the isotropic chemical shift frequencies of both ¹H and ¹⁵N in an amide site, a two-dimensional ¹H/¹⁵N chemical shift correlation spectrum can be generated, as shown in Figure 1G, which has the same spectral frequencies as a heteronuclear correlation spectrum obtained on the same protein by solution NMR or MAS solid-state NMR. This is under the assumption that all of the amide sites have similar environmental and structural influences on their chemical shifts, which is frequently the case when similar lipids are used to prepare the samples. Bicelles are characterized by q, the molar ratio of the long chain (DMPC) to the short chain (DHPC) phospholipids. Low q (<1) DMPC:DHPC isotropic bicelles are used for solution NMR and high q (>2.5) magnetically-alignable DMPC:DHPC bilayers for OS solid-state NMR. A concern and potential limitation of the method is when isotropic chemical shift assignments obtained by solution NMR are used, since membrane proteins may adopt different conformations in different lipid environments. To recognize these differences and minimize the possibility of assignment errors, we routinely perform “q titration” solution NMR experiments as demonstrated in the second experimental example of a uniformly ¹⁵N labeled protein, where data from low q samples are used to extrapolate the chemical shifts to the high q samples used in OS solid-state NMR experiments. This problem is generally not present with assignments made by MAS solid-state NMR on proteoliposomes with only long-chain lipids.

Figure 1.

Spectral representations of numerical simulations that illustrate the method of dipolar coupling correlated isotropic chemical shift analysis described in the text. A., C., and E. are spectra from “flipped samples” with their bilayer normals parallel to the magnetic field. B., D., and F. are spectra from standard samples with their bilayer normals perpendicular to the magnetic field. A. and B. are SLF spectra simulated for an ideal 10-residue helix, where all amide sites have the same isotropic chemical shift. C. and D. are SLF spectra for the same helix with randomized chemical shift tensors as described in the text. The isotropic value of the heteronuclear dipolar coupling is zero. E. and F. are HETCOR spectra that can be correlated to the SLF spectra through the ¹⁵N chemical shift frequencies. G. Is the spectral representation of the ¹⁵N and ¹H isotropic chemical shift values calculated from the two HETCOR spectra.

Example of Resonance Assignments of a Selectively ¹⁵N Labeled Protein

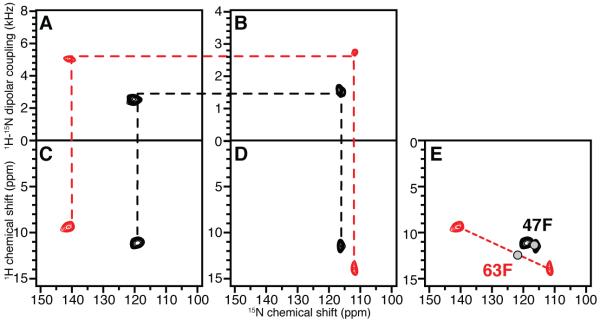
MerE is a 78-residue mercury transport membrane protein with two trans-membrane helices. ¹⁵N-Phe labeled MerE provides a simple example to demonstrate the assignment of resonances by combining heteronuclear dipolar coupling correlations with a previously assigned isotropic solution NMR spectrum. MerE has three phenylalanine residues: F 47, F 63 and F 74. Like most mobile residues located near the N- or C- termini of a membrane protein in phospholipid bilayers, the resonance from F 74 near the C-terminus is not observed in any of the one- or two-dimensional solid-state NMR spectra, presumably because the local backbone motions average out the dipolar interactions used for cross-polarization. Thus, ¹⁵N-Phe labeled MerE provides two resonances; they are known to come from phenylalanine residues, but have not previously been assigned to specific residues. The experimental solid-state NMR spectra in Figure 2 were obtained from protein-containing bilayer samples aligned with their normals parallel (Figure 2A and 2C) and perpendicular (Figure 2B and 2D) to the magnetic field. Both the isotropic ¹H and ¹⁵N chemical shift frequencies were determined from these experimental solid-state NMR spectra using the procedures described above, and were compared with the resonance frequencies and assignments observed in the solution NMR spectrum. The positions of the two gray “dots” in Figure 2E represent the solution NMR chemical shifts, and the assignments to Phe 47 and Phe 63 made using standard solution NMR triple-resonance methods are noted. The red and black “dots” correspond to the chemical shifts derived from the heteronuclear dipolar correlated signals in Figure 2A – 2D. This assigns the signals with the larger ¹H-¹⁵N dipolar couplings to Phe 63 and those with the smaller couplings to Phe 47. Based on the PISA wheel observed in the SLF spectrum of uniformly ¹⁵N labeled MerE (data not shown), the resonance assigned to Phe 63 is in a tilted trans membrane helix, while that for Phe47 is outside the wheel region, as expected for a residue in an irregular inter-helical loop structure. Therefore, the experimental assignments are consistent with the topological prediction of the two residues based on hydrophathy plots and a large body of both solution NMR and solid-state NMR data (not shown).

Figure 2.

Example of resonance assignments using experimental data from ¹⁵N-Phe-labeled MerE in magnetically aligned bilayers. A. and B. SLF spectra. C. and D. HETCOR spectra. A. and C. Sample with the bilayer normals parallel to the magnetic field. B. and D. Sample with the bilayer normals perpendicular to the magnetic field. The two resonances (red and black) observed in the experimental spectra are correlated by the dashed lines across the four spectra. E. The red and black dots represent the isotropic chemical shifts of the two residues calculated from the experimental solid-state NMR spectra in A. – D.. The two gray “dots” represent the resonance frequencies observed in an experimental two-dimensional HSQC solution NMR spectrum.

Example of Resonance Assignments of a Uniformly ¹⁵N Labeled Protein

The assignment method was demonstrated above with a membrane protein whose OS solid-state NMR spectra contain only two resonances for clarity. However, the method is intended for applications to uniformly ¹⁵N labeled proteins with many resonances, where there is the greatest need for more powerful assignment methods. While some aspects of the procedure can be carried out using two-dimensional spectra, especially for smaller proteins, the goal is to develop a general method that is applicable to uniformly labeled samples of larger membrane proteins, which requires three-dimensional spectra. The application of this method to uniformly labeled proteins is demonstrated here with the well-characterized example of the membrane bound form of the 46-residue Pf1 coat protein. The spectra of Pf1 coat protein in magnetically aligned bilayers have been assigned using the previous generation of OS solid-state NMR methods, which relied on the use of multiple selectively labeled samples and the shotgun method [10, 23].

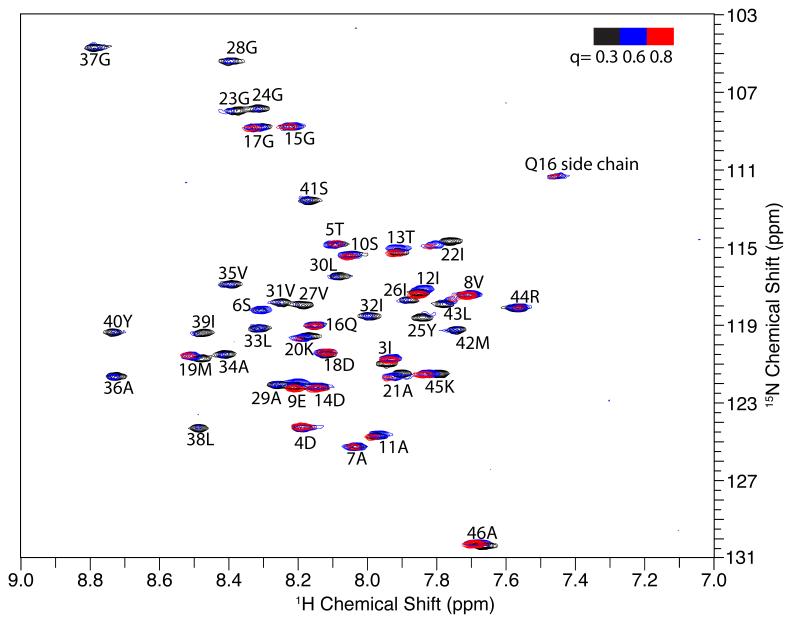
The first step is to perform a “q titration” experiment in solution NMR (Figure 3) where “q” is systematically increased by adding long chain lipid to the sample. The q-titration experiment takes the protein from fast-tumbling micelles to slower-tumbling isotropic bicelles with a larger fraction of long chain lipids thought to make the environment more like a bilayer. The q-titration experiment serves two purposes. First, resonances from residues in the trans-membrane helices and other structured regions of the protein can be readily recognizes, since their signals have dramatically reduced intensities (due to broader line widths) in the samples with higher q values. This is because the protein has a slower overall correlation time when the q is increased, and it selectively affects the relaxation of resonances from regions with structures, whose effective correlation time slows along with that of the isotropic bicelles as the q is raised. Mobile residues are also affected by increasing the q, but to a much smaller extent, because the local backbone motions reduce the impact of the slower overall correlation times of the protein-containing bicelles. In the membrane-bound form of Pf1 coat protein, the signals from residues 23 through 43 are weak in q = 0.6 bicelles and completely disappear in q = 0.8 bicelles. This is typical behavior for residues in trans-membrane helices in monotopic and polytopic membrane proteins. The second purpose of performing a q-titration experiment is to monitor changes in chemical shifts as the lipid environment of the protein goes from that of a micelle (q = 0) to that of magnetically alignable bilayers (q > 2.5). This is critical because the isotropic chemical shifts calculated from solid-state NMR spectra correspond to those of q = 3.2 DMPC:DHPC bilayers, whereas those observed in solution NMR spectra correspond to micelles (q = 0) or isotropic bicelles (q < 1). In order to minimize any errors in correlating the isotropic chemical shifts from these two similar but not identical samples, it is essential to optimize the lipid compositions and monitor the changes as a function of q. For Pf1 coat protein in 14-O-PC/6-O-PC bilayers, only small chemical shift changes were observed in the samples between q = 0.3 to q = 0.8, which allows us to utilize the chemical shift values measured in q = 0.3 bicelles for the assignment process..

Figure 3.

The bicelle q titration experiment of the membrane-bound form of Pf1 coat protein. The three superimposed HSQC solution NMR spectra (red, blue and black) were obtained from samples of Pf1 coat protein in isotropic bicelles with different q values, as colored coded in the upper right hand corner. The resonance assignments are marked for each resonance. The signal intensity of residues 23 to 43 drops below detection levels towards q=0.8 bicelles, and serve to define the residues in the trans-membrane helix.

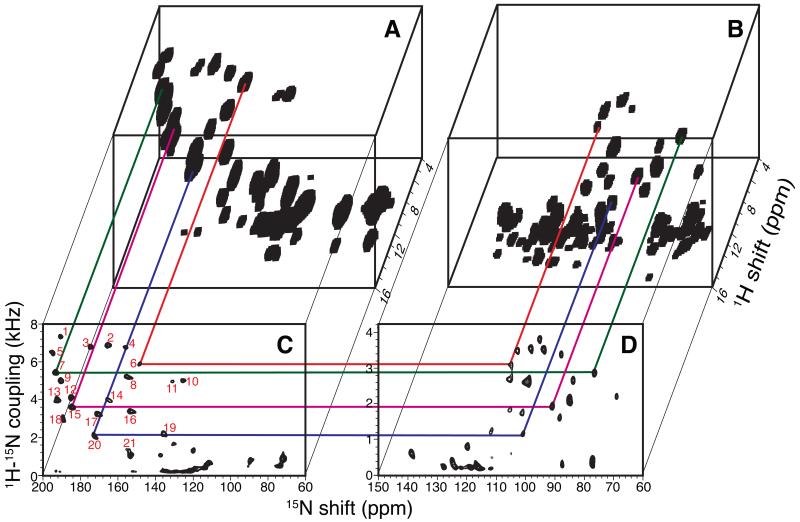
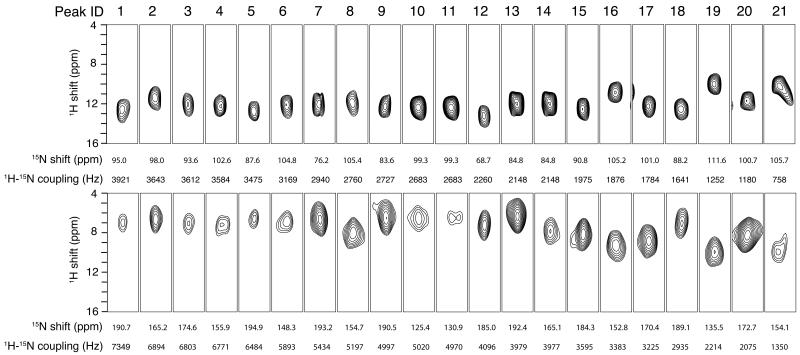
Two-dimensional SLF spectra and three-dimensional HETCOR/SLF spectra acquired from samples aligned both perpendicular and parallel to the field are arranged for ease of comparisons in Figure 4. A strip plot representation of the three-dimensional spectra in Figure 4 is presented in Figure 5. In the initial trial, 20 signals were identified that had dipolar coupling frequencies > 2 kHz, which generally differentiates resonances associated with residues in trans-membrane helices (larger couplings) from those in irregular non-helical regions (smaller couplings). There is one less resonance than expected, since the q-titration experiment showed that residues 23 – 43 are in a stable helical conformation. With further analysis, the signal labeled 21 (Figure 4C) was selected from several additional candidates near the helical region of the spectrum and assigned to residue 25. The assignment procedure is described in details below.

Figure 4.

Solid-state NMR spectra of uniformly ¹⁵N-labeled Pf1 coat protein in magnetically aligned bilayers. A. and C. The bilayer normals are parallel to the magnetic field. B. and D. The bilayer normals are perpendicular to the magnetic field. A. and B. Three-dimensional HETCOR/SLF spectra. C. and D. Two-dimensional SLF spectra. The 21 resonances in the helical wheel region are numbered in the order of the magnitude of their dipolar coupling frequencies (red number in panel C). Four representative correlations are shown in colored lines.

Figure 5.

Strip plots extracted from the three-dimensional HETCOR/SLF spectra (Figure 4A and 4B) obtained for uniformly ¹⁵N-labeled Pf1 coat protein in two differently aligned bicelles. Top: The bilayer normals are perpendicular to the magnetic field. Bottom: The bilayer normals are parallel to the magnetic field.

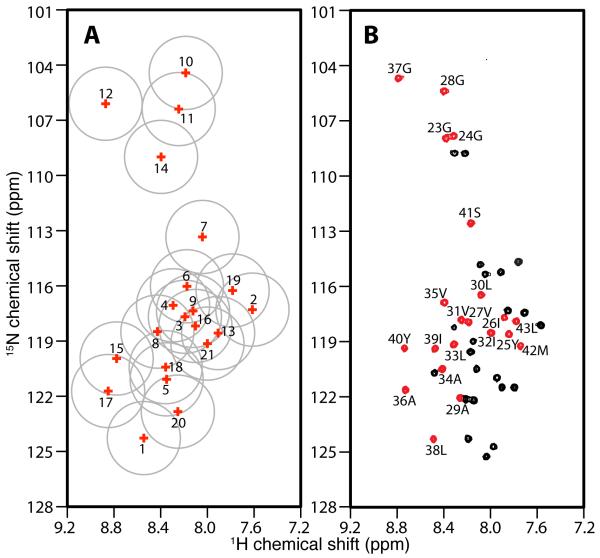
The assignment process starts with the correlation of the 20 resonances in each of the SLF spectra through their heteronuclear dipolar couplings (Figures 4C and 4D). All the signals in the trans-membrane helical region of the spectrum can be readily correlated, although peaks 9, 10 and 11 (Figure 4C) are not resolved in the dipolar coupling dimension. The correlation of these three peaks was accomplished by noting that peak 9 is well separated from peaks 10 and 11 in the ¹⁵N chemical shift frequency dimension. Due to the limited range of isotropic ¹⁵N chemical shift frequencies, peak 9 can be correlated with some confidence to the peak at 84 ppm in the perpendicular sample (Figure 4D). Consequently, peaks 10 and 11 can both be correlated to the peak at 102 ppm (Figure 4D). The signal at 102 ppm has about twice the intensity of the others, suggesting that it represents two overlapped resonances. After the dipolar correlation, the isotropic chemical shifts can be derived from these data for comparison with the isotropic chemical shifts present in the solution NMR heteronuclear chemical shift correlation spectrum (Figure 6 and Table 1).

Figure 6.

Spectral representations of the correlation of isotropic ¹⁵N and ¹H chemical shifts. A. Solid-state NMR data obtained from samples of Pf1 coat protein in magnetically aligned bilayers. B. Solution NMR data obtained from samples of Pf1 coat protein in isotropic bicelles (q=0.3). A. The isotropic chemical shifts of all 21 peaks in the helical wheel region are calculated and labeled with their peak numbers based on the magnitudes of their heteronuclear dipolar couplings. The grey circles indicate the estimated uncertainty in their positions. B. An experimental two-dimensional HSQC spectrum. The peaks colored in red are from residues in the trans-membrane helical region of the protein. The resonances assignments are marked.

Table 1.

Summary of data for the assignment and isotropic chemical shift calculations of uniformly ¹⁵N-labeled Pf1 coat protein. The solution NMR data are aligned with the solid-state NMR data according to the final assignments described in the text

Solid-state NMR										Solution NMR
Pea k ID	Parallel Bicelle			Perpendicular Bicelle			Srel	Isotropic value		Residu e numbe r	Isotropic value
	DC	15N	1H	DC	15N	1H		15N	1H		15N	1H
1	734 9	190.6 5	6.9 9	392 1	94.95	12.6 4	0.93 7	124.2 7	8.5 4	38	124.2 8	8.4 9
2	689 4	165.2 3	6.6 5	364 3	98.03	11.3 8	0.94 6	117.2 9	7.6 1	42	119.2 2	7.7 4
3	680 3	174.5 8	7.0 7	361 2	93.55	12.0 5	0.94 2	117.6 8	8.1 9	27	117.9 4	8.1 9
4	677 1	155.8 6	7.2 0	358 4	102.5 9	12.1 3	0.94 5	117.0 6	8.2 9	31	117.8 0	8.2 5
5	648 4	194.9 2	6.6 0	347 5	87.61	12.5 6	0.93 3	121.0 8	8.3 5	34	120.4 8	8.4 1
6	589 3	148.3 3	7.0 6	316 9	104.7 6	12.0 5	0.93 0	116.0 2	8.1 7	35	116.8 6	8.3 9
7	543 4	193.2 3	6.7 0	294 0	76.24	12.0 5	0.92 4	113.3 4	8.0 4	41	112.5 5	8.1 7
8	519 7	154.6 6	8.0 1	276 0	105.3 6	11.9 1	0.94 1	118.4 9	8.4 3	39	119.3 6	8.4 7
9	499 7	190.5 2	6.5 2	272 7	83.58	12.2 9	0.91 6	117.3 6	8.1 2	30	116.4 5	8.0 8
10	502 0	125.4 3	6.5 2	268 3	99.29	12.3 5	0.93 6	104.4 3	8.1 9	28	105.3 8	8.4 0
11	497 0	130.8 7	6.7 3	268 3	99.29	12.3 5	0.92 6	106.3 9	8.2 5	24	107.8 0	8.3 1
12	409 6	185.0 4	7.2 3	226 0	68.71	13.0 9	0.90 6	106.1 0	8.8 7	37	104.6 9	8.7 9
13	397 9	192.3 9	6.3 6	214 8	84.83	12.0 2	0.92 6	118.5 7	7.9 1	26	117.6 8	7.8 8
14	397 7	165.0 5	7.8 6	214 8	84.83	11.9 7	0.92 6	108.9 9	8.4 0	23	107.9 3	8.3 8
15	359 5	184.2 9	8.1 4	197 5	90.75	12.4 3	0.91 0	119.9 5	8.7 8	40	119.3 4	8.7 3
16	338 3	152.7 6	9.3 0	187 6	105.1 7	10.7 5	0.90 2	118.1 8	8.1 0	32	118.5 1	8.0 0
17	322 5	170.3 4	8.8 5	178 4	100.9 9	12.1 6	0.90 4	121.7 2	8.8 5	36	121.6 1	8.7 3
18	293 5	189.1 0	7.0 7	164 1	88.21	12.4 0	0.89 4	120.4 2	8.3 6	33	119.1 3	8.3 1
19	221 4	135.5 0	9.9 8	125 2	111.5 9	9.88	0.88 4	116.2 5	7.7 8	43	117.8 8	7.7 8
20	207 5	172.7 1	8.3 0	118 0	100.7 0	11.5 7	0.87 9	122.8 3	8.2 5	29	122.0 5	8.2 6
21	135 0	154.0 6	9.9 5	758	105.7 3	10.2 3	0.89 1	119.1 4	8.0 0	25	118.5 7	7.8 4

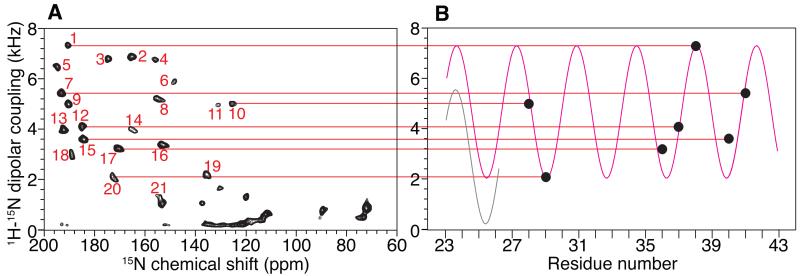
Next, the isotropic chemical shifts calculated from the parallel and perpendicular solid-state NMR spectra are compared to those measured in the experimental solution NMR spectrum. This enables some signals that are well separated from others to be assigned by inspection. Seven signals labeled 10, 12, 7, 15, 17, 20 and 1 are assigned to residues 28, 37, 41, 40, 36, 29 and 38, respectively. These assignments are valuable in their own right, but they also serve as anchor points to determine the phase of the dipolar wave associated with the regular helical secondary structure [39-41]. Meanwhile, the amplitude of the wave can be determined with some confidence from the largest and smallest values of the heteronuclear dipolar couplings that are observed in the helical region of the spectrum (Figure 7).

Figure 7.

Dipolar wave analysis of the dipolar coupling frequencies measured for the residues in the transmembrane helix region of Pf1 coat protein. A. SLF spectrum of magnetically aligned bilayers with their normals parallel to the magnetic field. The peaks are labeled in the order of increasing magnitude of their dipolar coupling. B. The seven unambiguously assigned residues are used to fit a dipolar wave (magenta color) following the procedure described previously[39-41]. The black dots represent the magnitudes of the dipolar couplings of the seven residues, and they are correlated through red lines to their respective peaks in the SLF spectrum. The separate dipolar wave in light grey is fitted to residues 23 to 25 to indicate a plausible distortion at the N-terminal end of the helix.

The rest of the resonance assignments follow readily from these two sources of information: the direct comparison of isotropic chemical shifts (Figure 6) and the dipolar wave analysis (Figure 7). By sequentially assigning the other fourteen resonances, any perturbation from the dipolar wave can be detected, which by itself provides strong evidence of any incorrect assignments. Based on the resonances assigned to residues 40 and 41, there are two possible candidates (resonances 2 and 13) for the signal from residue 42; however, only the dipolar coupling observed for signal 2 is consistent with the dipolar wave analysis. For residue 43, both peaks 19 and 13 are candidates. In the parallel SLF spectrum, the PISA wheel [11, 12] goes in the clockwise direction; in reading the dipolar wave from left to right (Figure 7B), the peaks on the rising part of the sine wave are located on the left side of the SLF spectrum (Figure 7A) in the ¹⁵N chemical shift region between 170 ppm and 200 ppm. Therefore, signal 13 can be ruled out, and signal 19 is assigned to residue 43. Three resonances, 5, 8 and 18, are candidates for residue 39 on the basis of their isotropic chemical shifts. However, 5 and 18 are on the “wrong side” of the PISA wheel, leaving resonance 8 as the only viable choice. For residue 35, the resonances labeled 3, 4, 6, 8 and 9 are all potential candidates. Resonances 3 and 9 can be ruled out by the PISA wheel analysis, and resonance 8 is already assigned; resonances 4 and 6 are too close to be distinguished by the dipolar wave analysis. This ambiguity is addressed later. For residue 34, the only possibilities are resonances 5 and 18. They are far apart in the dipolar wave analysis, and clearly residue 34 should be assigned to resonance 5. For residue 33, resonance 18 is the closest one in isotropic chemical shift. In addition, in the vicinity of resonance 18, all the other signals are already assigned. Therefore, we assign resonance 18 to residue 33. Next, we searched for a resonance to assign to residue 32. There are several unassigned candidates, including resonances 3, 9, 13 and 16. Signal 21, which would be possible otherwise, is excluded for residue 33 as discussed later. Among the four plausible candidates, resonance 3 and 9 are ruled out by the dipolar wave analysis, and resonance 13 is on the wrong side of PISA wheel. Therefore, resonance 16 is assigned to residue 32. The resonances labeled 3, 4, 6 and 9 are candidates for assignment to residue 31. Except for resonance 9, the three other signals cannot be ruled out by dipolar wave analysis. The ambiguity remains until we proceed to residue 30. Resonance 9 is readily assigned to residue 30, since the only other candidate, resonance 6, is located on the “wrong side” of the PISA wheel. The ambiguity is now narrowed to resonances 4 and 6 for residues 31 and 35. By careful comparison of their positions in the dipolar wave, resonance 4 is more likely to be from residue 31 and resonance 6 from residue 35. This is also consistent with the isotropic chemical shift comparison, where residue 31 is clearly closer to resonance 4 than to 6. The validity of the dipolar wave fitting is further confirmed by recognizing that, in the middle of the helix, residues 26 to 39 nearly perfectly match the expected positions on the dipolar wave. The signals for residues 29 and 28 are already assigned, and residue 27 can be readily assigned to resonance 3 and residue 26 to resonance 13. However, this leaves no signal available for the next residue in the helix, residue 25. In attempting to proceed with this analysis through residues 23 and 24, we find that neither of the candidate resonances, 11 or 14, fit to dipolar wave. This has structural implications, since it indicates that the dipolar wave describing the initial 7 anchoring residues is does not fit to this region of the protein. This is not entirely unexpected, since residues 23, 24, and 25 are near the end of the helix where structural distortions are most likely to be found.

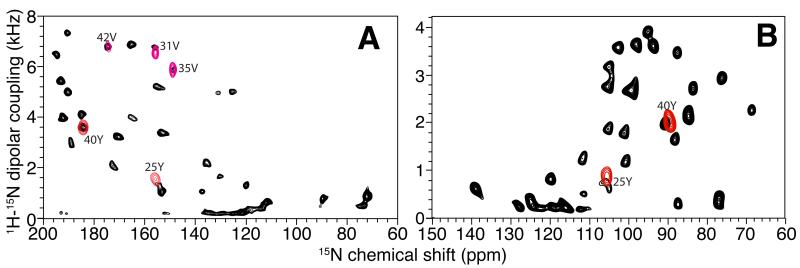
Assigning residues 23, 24, and 25 requires a careful analysis of the dipolar wave fitting and a search for an additional signal in the vicinity of the helical region of the SLF spectra. This leads to the identification of resonance 21 (Figure 4C), whose calculated isotropic chemical shift is close to that of residue 25. The assignment of resonance 21 to residue 25 is confirmed by an experimental SLF spectrum on a selectively ¹⁵N-Tyr labeled sample (Figure 8). This assignment differs from our previously reported assignment for this residue [23, 42]. Note that resonance 21 could be assigned to other residues if only isotropic chemical shifts are considered. For example, residue 32 would be a good alternative candidate since it is the closest one in isotropic chemical shift. Indeed, residues 32 and 25 were previously noted to have overlapping resonances in earlier spectra [23]. However, it is now established that in the vicinity of residue 32, the dipolar wave fitting has minimal errors, and therefore, assigning residue 32 to peak 21 would result in an erroneous distortion of the dipolar wave. In contrast, we already know that residues 23 and 24 (assigned to resonances 11 and 14, respectively) are significantly lower in frequency than predicted from the initial dipolar wave fitting; thus, there is a distinct possibility that the resonance from residue 25 is shifted down relative to the dipolar wave. A second dipolar wave can be generated for this region of the helix that has approximately the same amplitude and phase, but is systematically shifted down on the frequency scale (Figure 7B). This leads to the assignment of residue 23 to resonance 14, and of residue 24 to resonance 11. These two assignments cannot be confirmed by isotropic chemical shift analysis due to the close proximity of their resonances in the two-dimensional solution NMR spectrum. Neither can the assignments be confirmed by preparing selectively labeled samples since both are glycines. Therefore, the assignment of residue 23 and 24 presented here is based on the most likely result from the dipolar wave analysis, and it agrees with our previous assignment [23].

Figure 8.

The resonance assignment of Tyr 25 confirmed using spectra from a ¹⁵N-Tyr labeled sample of Pf1 coat protein. A. and B. SLF spectra. A. Bilayers with their normals parallel to the magnetic field. B. Bilayers with their normals perpendicular to the magnetic field. The SLF spectra of selectively ¹⁵N-Tyr labeled Pf1 (red signals) are superimposed on the corresponding spectra of uniformly ¹⁵N-labeled Pf1 (black signals). The assignments of the two Tyr resonances are marked.

3. Discussion

Using only a single uniformly ¹⁵N labeled sample and a previously assigned isotropic spectrum, the vast majority of resonances in the OS solid-state NMR spectrum of the membrane-bound form of Pf1 coat protein could be assigned to specific residues. While isotropic chemical shift assignments can be obtained readily in solution NMR and MAS solid-state NMR using only uniformly ¹³C and ¹⁵N labeled samples, in the method demonstrated here, they are calculated indirectly for OS solid-state NMR spectra based largely on matching the magnitudes of heteronuclear dipolar couplings in parallel and perpendicular aligned samples. The few examples of uncertainties and ambiguities that altered one earlier resonance assignment and may affect a few more are not surprising in the first applications of new methods. Most importantly, the experimental data from two different membrane proteins enabled us to demonstrate the practical application of a general assignment scheme that has the potential to enable the study of larger membrane proteins and to accelerate the entire process of structure determination in membrane bilayers.

There are many opportunities for the further development of this assignment method and extension to larger membrane proteins. First, as multidimensional ¹H/¹³C/¹⁵N triple-resonance OS solid-state NMR experiments are improved [43-45], the method can be extended to include many additional chemical shifts and dipolar couplings, such as ¹³C_α and ¹³C_β chemical shifts and ¹⁵N-¹³C_α and ¹H-¹³C dipolar couplings. The incorporation of additional chemical shift frequencies will increase the accuracy of the correlations among the various NMR spectra (solution NMR, OS solid-state NMR, and MAS solid-state NMR), and the additional heteronuclear dipolar coupling dimensions will enable confident correlation of peaks in more crowded regions of the spectra from larger proteins. Secondly, for larger membrane proteins, such as G-protein coupled receptors with seven trans-membrane helices, the line widths of signals prohibit their resolution and assignment in isotropic bicelle samples by existing solution NMR methods. Thus, an attractive alternative is to utilize MAS solid-state NMR methods, which have the potential to provide full or partial assignments of the isotropic spectra, and enable the structure determination to proceed on the basis of the angular constraints measured for the assigned resonances is the OS solid-state NMR spectra.

The demonstration of this assignment method that combines isotropic and anisotropic frequencies of resonances is not only a useful advance for protein structure determination by OS solid-state NMR, but also provides an example of one of the many potential ways to integrate all types of NMR data on membrane proteins, including solution NMR of micelles and isotropic bicelles, OS solid-state NMR of aligned bilayers, and MAS solid-state NMR of unoriented bilayers. Another example is the determination of angular constraints in the conventional applications of MAS solid-state NMR. The constraints are usually determined by analyzing powder patterns from unoriented samples [46], which become complicated when more than one resonance contribute to the signal, and therefore in dealing with uniformly labeled large proteins, the resolution often needs to be provided by other dimensions, leading to a significant increase in experimental time. In contrast, in OS solid-state NMR, each resonance’s signal appears as a single peak, and both chemical shift and dipolar coupling dimensions provide simultaneously angular constraints and resolution. In this case, the method described in the article can bring the angular constraints from OS solid-state NMR to complement the other structural information obtained in MAS solid-state NMR.

4. Experimental Methods

Sample Preparation

Uniformly ¹⁵N-labeled Pf1 coat protein samples were prepared as previously described [5]. Purified bacteriophage particles were dissolved in a mixed organic solution (50% trifluoroethanol, 0.1% trifluoroacetic acid and 49.9% water). The resulting DNA precipitate was pelleted by centrifugation. The solvent was partially removed by flowing nitrogen gas over the clear supernatant, and then the sample was lyophilized. In order to completely remove any residual trifluoroacetic acid, water was repeatedly added to the protein powder and the sample lyophilized again. NMR samples were reconstituted from the protein powder.

We have previously described the preparation of magnetically aligned protein-containing bilayers for OS solid-state NMR spectroscopy [25, 27, 47]. The phospholipids, 1,2-di-O-hexyl-sn-glycero-3-phosphocholine (6-O-PC) and 1,2-di-O-tetradecyl-sn-glycero-3-phosphocholine (14-O-PC), which are the non-hydrolyzable ether-linked analogues of 1,2-Dihexanoyl-sn-Glycero-3-Phosphocholine (DHPC) and 1,2-Dimyristoyl-sn-Glycero-3-Phosphocholin (DMPC), were used to enhance long-term stability. The lipids were obtained from Avanti Polar Lipids (www.avantilipids.com). Samples of Pf1 coat protein in q = 3.2 perpendicular bilayers were prepared by solubilizing the protein in an aqueous solution containing 100 μl water and 80 ul stock of 100 mg/ml short-chain lipid (6-O-PC). After adjusting the pH to approximately 6.7, the solution was then added to 40 mg long-chain lipid (14-O-PC) in powder form, followed by extensive vortexing and temperature cycling (0°C/45°C). The opaque initial mixture becomes transparent upon mixing, indicating the formation of an orientable bilayer phase. The pH is then adjusted to exactly 6.7 when the sample is fluid at 0°C. 160 μl of the protein-containing bilayer solution is then transferred into a 5 mm flat-bottomed tube (New Era Enterprises (www.newera-spectro.com)), which was then sealed with a rubber cap and wrapped in a layer of plastic film. After the acquisition of spectra on the perpendicular sample, the same sample was “flipped” into a parallel alignment in order to minimize any batch-to-batch differences in sample preparation. To “flip” the bilayers, the sample tube was cooled on ice and the fluid solution was transferred to a microcentrifuge tube. 5 μl of 100 mM YbCl₃·6H₂O in water was added to the sample, followed by several temperature cycles and pH adjustment to 6.7. The sample was then returned to the 5 mm tube used for the NMR experiments.

The sample of Pf1 coat protein used for the solution NMR experiments was prepared by solubilizing 0.5 mg of the protein in 50 mM 6-O-PC, 10mM MES at pH 6.7. The bicelle q titration experiments were performed on the same sample by successively adding 14-O-PC to the sample tube to achieve the desired molar ratios of long-chain and short-chain lipids.

The MerE expression, purification and sample preparation is similar to the procedure of MerFt protein described previously [8]. The 78-residue MerE[48] gene was synthesized and cloned into pET-31b(+) vector (Novagen, USA), which was incorporated into E.coli strain C41(λDE3) (Avidis, www.avidis.fr) through transformation. In case of preparation of the ¹⁵N-Phe-labeled sample, ¹⁵N-Phe and the other 19 unlabeled amino acids were added to 1 liter of M9 medium. Expression of the fusion protein was induced by adding 1 mM IPTG to the culture when the OD₆₀₀ reached 0.6, and the culture was then incubated for another 8 hours at 37°C. The collected cells were disrupted using a probe sonicator, and the inclusion body was isolated by centrifugation. The MerE fusion protein was solubilized in 6M guanidine hydrochloride (GuHCl) and purified using Ni-NTA affinity chromatography. The fusion protein was then cleaved by cyanogen bromide (CNBr) at the Met sites and purified by size exclusion chromatography in the presence of SDS. The final protein powder was obtained after exhaustive dialysis and lyophilization.

NMR Spectroscopy

The solution NMR experiments were performed on a Varian VNMR 500 MHz spectrometer equipped with a standard HCN triple-resonance probe. All experiments were performed at 60°C. The HSQC spectra were acquired using the pulse sequence gNhsqc[49] from BioPack (Varian Inc.) with 1024 complex t1 points and 128 complex t2 points. Data were processed using NMRPipe [50], and the spectra were referenced to the water peak whose chemical shift value at the given temperature was determined by NMRPipe. The assignments of the Pf1 coat protein resonances were adapted from those previously obtained for the protein in DHPC micelles [23], and the assignment of MerE was accomplished through standard triple-resonance experiments on uniformly ¹³C and ¹⁵N labeled protein in DHPC micelles (unpublished data).

The solid-state NMR experiments were performed on a 700 MHz spectrometer with Bruker Avance console equipped with a home-built strip-shield double-resonance probe [51] and a set of “thin” room temperature shim coils with a limited number of gradients. Magnet drift was compensated by a linear ramp of current to the Z₀ coil. Field drift was less than 0.1 ppm per day during the experiments. All of the solid-state NMR experiments were performed at 42°C. All two-dimensional SLF spectra were obtained using the SAMPI4 pulse sequence [36, 52] with 1 ms CP-MOIST [53] for ¹H-¹⁵N cross-polarization and SPINAL-16 [54, 55] for heteronuclear decoupling during data acquisition.

For the MerE protein, the two-dimensional HETCOR experiments [36] utilized 4 SAMPI4 periods to perform semi-selective coherence transfer in samples aligned perpendicular to the field and 2 periods for samples aligned parallel to the field. For both SLF and HETCOR experiment, the B₁ field strength was between 47 kHz and 50 kHz on the ¹⁵N and ¹H channels under matched conditions, and between 75 kHz and 79 kHz on the ¹H channel during ¹H chemical shift evolution. Typically, 40 real t1 points were signal averaged for 400 – 1000 scans for the SLF spectra; and 64 – 128 complex points were signal averaged for 100 – 200 scans for the HETCOR spectra.

For Pf1 coat protein, in both two-dimensional SLF experiments and three-dimensional HETCOR/SLF experiments [38], the B₁ field strength was 50 kHz on the ¹⁵N and ¹H channels under matched conditions, and between 70 kHz and 72 kHz on the ¹H channel during ¹H chemical shift evolution. 32 complex t1 points, 40 real t2 points and 512 complex t3 points were acquired for the three-dimensional HETCOR/SLF spectra. 80 real t1 points and 512 complex t2 points were acquired for the two-dimensional SLF spectra. 128 transients were signal averaged for the two-dimensional experiments and 16 – 32 scans were signal averaged for the three-dimensional experiments. The recycle delays were typically 6 sec for the three-dimensional experiments and 4 sec for the two-dimensional experiments. The ¹⁵N and ¹H chemical shifts were referenced externally to ¹⁵N-labeled solid ammonium sulfate defined as 26.8 ppm and internally to H₂O defined as 4.7 ppm at 42°C. The NMR data were processed and displayed using the programs NMRPipe [50], NMRView [56] and Sparky [57]. The theoretical scaling factor for both the HETCOR [37, 38] and SAMPI4 [36] experiments were utilized in the data processing and plotting.

Numerical Simulations

The PISA wheels shown in Figure 1 were simulated using in-house MATLAB (The MathWorks) script following a previously described procedure [31]. The torsion angles of α-helix were Φ = −64° and Ψ = −43°. The order parameter used in the calculations was 0.8, which is typical for magnetically aligned protein-containing bilayers. The principal values of the consensus chemical shift tensors for the ¹⁵N amide sites were σ₁₁ = 64, σ₂₂ = 77 and σ₃₃ = 217 ppm, and were σ₁₁ = 3, σ₂₂ = 8 and σ₃₃ = 17 ppm for the corresponding ¹H amide sites.. To simulate the SLF and HETCOR spectra for proteins, the chemical shift tensors were varied randomly from site to site. For each residue along the helix, all six of the principal values listed above were varied using a normal distribution around the value with standard deviation of 6 ppm for the ¹⁵N amide chemical shift and 0.6 ppm for the ¹H chemical shift. The newly generated values were then used as input for the same MATLAB script used to simulate the SLF and HETCOR spectra. The isotropic chemical shift frequencies were calculated using Equation (1) with S_rel = 1.

Isotropic Chemical Shift Calculations

The data shown in Table 1 were calculated as follows: S_rel was defined as the ratio of the heteronuclear dipolar coupling between parallel and perpendicular alignments, divided by two. It was calculated separately for each pair of correlated peaks, and the average value was found to be 0.92 using Equation (3). Each S_rel value was used for the isotropic chemical shift calculation of the corresponding residue; alternatively, the averaged S_rel of 0.92 were also used, giving a similar result (data not shown). Differences between the results were well below the experimental errors. For the Pf1 coat protein, the isotropic chemical shifts of all the residues were averaged, and we found that the values from solid-state NMR experiments were 3.97 ppm larger for ¹⁵N and 2.13 ppm larger for ¹H than those observed in the solution NMR spectra. These two values were applied as the universal correction factor to all the resonances, and the resulting predicted isotropic chemical shifts are listed in Table 1. Similar discrepancies may occur for other sets of experiments and protein samples, and a systematic frequency correction is required to assure the accuracy of isotropic chemical shift correlations and measurements. The correlation between OS solid-state NMR and solution NMR is shown Figure 6, and the estimated values for the maximal discrepancy between the chemical shifts calculated from solid-state NMR and observed in solution NMR are 1.5 ppm for ¹⁵N and 0.3 ppm for ¹H. More rigorous estimates of the errors will be possible in the future as more datasets become available. For the ¹⁵N-Phe selectively labeled MerE sample, a similar calculation procedure was utilized. Universal correction factors of 1.4 ppm in ¹⁵N and 3.3 ppm in ¹H were applied to the solution NMR data.