NEW EFFICIENT ESTIMATION AND VARIABLE SELECTION METHODS FOR SEMIPARAMETRIC VARYING-COEFFICIENT PARTIALLY LINEAR MODELS

Abstract

The complexity of semiparametric models poses new challenges to statistical inference and model selection that frequently arise from real applications. In this work, we propose new estimation and variable selection procedures for the semiparametric varying-coefficient partially linear model. We first study quantile regression estimates for the nonparametric varying-coefficient functions and the parametric regression coefficients. To achieve nice efficiency properties, we further develop a semiparametric composite quantile regression procedure. We establish the asymptotic normality of proposed estimators for both the parametric and nonparametric parts and show that the estimators achieve the best convergence rate. Moreover, we show that the proposed method is much more efficient than the least-squares-based method for many non-normal errors and that it only loses a small amount of efficiency for normal errors. In addition, it is shown that the loss in efficiency is at most 11.1% for estimating varying coefficient functions and is no greater than 13.6% for estimating parametric components. To achieve sparsity with high-dimensional covariates, we propose adaptive penalization methods for variable selection in the semiparametric varying-coefficient partially linear model and prove that the methods possess the oracle property. Extensive Monte Carlo simulation studies are conducted to examine the finite-sample performance of the proposed procedures. Finally, we apply the new methods to analyze the plasma beta-carotene level data.

1. Introduction

Semiparametric regression modeling has recently become popular in the statistics literature because it keeps the flexibility of nonparametric models while maintaining the explanatory power of parametric models. The partially linear model, the most commonly used semiparametric regression model, has received a lot of attention in the literature; see Härdle, Liang and Gao [9], Yatchew [32] and references therein for theory and applications of partially linear models. Various extensions of the partially linear model have been proposed in the literature; see Ruppert, Wand and Carroll [26] for applications and theoretical developments of semiparametric regression models. The semiparametric varying-coefficient partially linear model, as an important extension of the partially linear model, is becoming popular in the literature. Let Y be a response variable and {U, X, Z} its covariates. The semiparametric varying-coefficient partially linear model is defined to be

$$Y={\alpha }_0(U)+{\mathbf{X}}^T\mathit{\alpha }(U)+{\mathbf{Z}}^T\mathit{\beta }+\epsilon ,$$ (1.1)

where α₀(U) is a baseline function, α(U) = {α₁(U),…, α_d1(U)}^T consists of d₁ unknown varying coefficient functions, β = (β₁,…, β_d2)^T is a d₂-dimensional coefficient vector and ε is random error. In this paper, we will focus on univariate U only, although the proposed procedure is directly applicable for multivariate U. Zhang, Lee and Song [33] proposed an estimation procedure for the model (1.1), based on local polynomial regression techniques. Xia, Zhang and Tong [31] proposed a semilocal estimation procedure to further reduce the bias of the estimator for β suggested in Zhang, Lee and Song [33]. Fan and Huang [5] proposed a profile least-squares estimator for model (1.1) and developed statistical inference procedures. As an extension of Fan and Huang [5], a profile likelihood estimation procedure was developed in Lam and Fan [18], under the generalized linear model framework with a diverging number of covariates.

Existing estimation procedures for model (1.1) were built on either least-squares- or likelihood-based methods. Thus, the existing procedures are expected to be sensitive to outliers and their efficiency may be significantly improved for many commonly used non-normal errors. In this paper, we propose new estimation procedures for model (1.1). This paper contains three major developments: (a) semiparametric quantile regression; (b) semiparametric composite quantile regression; (c) adaptive penalization methods for achieving sparsity in semiparametric composite quantile regression.

Quantile regression is often considered as an alternative to least-squares in the literature. For a complete review on quantile regression, see Koenker [17]. Quantile-regression-based inference procedures have been considered in the literature; see, for example, Cai and Xu [2], He and Shi [10], He, Zhu and Fung [11], Lee [19], among others. In Section 2, we propose a new semiparametric quantile regression procedure for model (1.1). We investigate the sampling properties of the proposed method and their asymptotic normality. When applying semiparametric quantile regression to model (1.1), we observe that all quantile regression estimators can estimate α(u) and β with the optimal rate of convergence. This fact motivates us to combine the information across multiple quantile estimates to obtain improved estimates of α(u) and β. Such an idea has been studied for the parametric regression model in Zou and Yuan [35] and it leads to the composite quantile regression (CQR) estimator that is shown to enjoy nice asymptotic efficiency properties compared with the classical least-squares estimator. In Section 3, we propose the semiparametric composite quantile regression (semi-CQR) estimators for estimating both nonparametric and parametric parts in model (1.1). We show that the semi-CQR estimators achieve the best convergence rates. We also prove the asymptotic normality of the semi-CQR estimators. The asymptotic theory shows that, compared with the semiparametric least-squares estimators, the semi-CQR estimators can have substantial efficiency gain for many non-normal errors and only lose a small amount of efficiency for normal errors. Moreover, the relative efficiency is at least 88.9% for estimating varying-coefficient functions and is at least 86.4% for estimating parametric components.

In practice, there are often many covariates in the parametric part of model (1.1). With high-dimensional covariates, sparse modeling is often considered superior, owing to enhanced model predictability and interpretability [7]. Variable selection for model (1.1) is challenging because it involves both nonparametric and parametric parts. Traditional variable selection methods, such as stepwise regression or best subset variable selection, do not work effectively for the semiparametric model because they need to choose smoothing parameters for each sub-model and cannot cope with high-dimensionality. In Section 4, we develop an effective variable selection procedure to select significant parametric components in model (1.1). We demonstrate that the proposed procedure possesses the oracle property, in the sense of Fan and Li [6].

In Section 5, we conduct simulation studies to examine the finite-sample performance of the proposed procedures. The proposed methods are illustrated with the plasma beta-carotene level data. Regularity conditions and technical proofs are given in Section 6.

2. Semiparametric quantile regression

In this section, we develop the semiparametric quantile regression method and theory. Let ρ_τ (r) = τr − rI (r < 0) be the check loss function at τ ∈ (0, 1). Quantile regression is often used to estimate the conditional quantile functions of Y,

$$Q_{\tau }(u,\mathbf{x},\mathbf{z})=\underset{a}{\text{argmin}}E\{{\rho }_{\tau }(Y-a)|(U,\mathbf{X},\mathbf{Z})=(u,\mathbf{x},\mathbf{z})\}.$$

The semiparametric varying-coefficient partially linear model assumes that the conditional quantile function is expressed as Q_τ (u, x, z) = α_0,τ (u) + x^T α_τ (u) + z^T β_τ.

Suppose that {U_i,X_i,Z_i,Y_i}, i = 1, …, n, is an independent and identically distributed sample from the model

$$Y={\alpha }_{0,\tau }(U)+{\mathbf{X}}^T{\mathit{\alpha }}_{\tau }(U)+{\mathbf{Z}}^T{\mathit{\beta }}_{\tau }+{\epsilon }_{\tau },$$ (2.1)

where ε_τ is random error with conditional τ th quantile being zero. We obtain quantile regression estimates of α_0,τ (·), α_τ (·) and β_τ by minimizing the quantile loss function

$${\displaystyle \sum _{i=1}^n}{\rho }_{\tau }\{Y_i-{\alpha }_0(U_i)-{\mathbf{X}}_i^T\mathit{\alpha }(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\}.$$ (2.2)

Because (2.2) involves both nonparametric and parametric components, and because they can be estimated by different rates of convergence, we propose a three-stage estimation procedure. In the first stage, we employ local linear regression techniques to derive an initial estimates of α_0,τ (·), α_τ (·) and β_τ. Then, in the second and third stages, we further improve the estimation efficiency of the initial estimates for β_τ and (α_0,τ (·),α_τ (·)), respectively.

For U in the neighborhood of u, we use a local linear approximation

$${\alpha }_j(U)\approx {\alpha }_j(u)+{\alpha }_j^{\prime }(u)(U-u)\triangleq a_j+b_j(U-u)$$

for j = 0,…, d₁. Let {ã_0,τ, b̃_0,τ, ã_τ, b̃_τ, β̃_τ} be the minimizer of the local weighted quantile loss function

$${\displaystyle \sum _{i=1}^n}{\rho }_{\tau }\{Y_i-a_0-b_0(U_i-u)-{\mathbf{X}}_i^T\{\mathbf{a}+\mathbf{b}(U_i-u)\}-{\mathbf{Z}}_i^T\mathit{\beta }\}{K}_h(U_i-u),$$

where a = (a₁,…, a_d1)^T, b = (b₁,…, b_d1)^T, K(·) is a given kernel function and K_h(·) = K(·/h)/h with a bandwidth h. Then,

$$\begin{array}{cc}{\tilde{\alpha }}_{0,\tau }(u)={\tilde{a}}_0,\hfill & {\tilde{\mathit{\alpha }}}_{\tau }(u)={\tilde{\mathbf{a}}}_{\tau }.\hfill \end{array}$$

We take {α̃_0,τ (u), α̃_τ (u), β̃_τ} as the initial estimates.

We now provide theoretical justifications for the initial estimates. First, we give some notation. Let f_τ (·|u, x, z) and F_τ (·|u, x, z) be the density function and cumulative distribution function of the error conditional on (U, X, Z) = (u, x, z), respectively. Denote by f_U(·) the marginal density function of the covariate U. The kernel K(·) is chosen as a symmetric density function and we let

$$\begin{array}{cc}{\mu }_j={\displaystyle \int }{u}^{j}K(u)du\text{and}{\nu }_j={\displaystyle \int }{u}^j{K}^2(u)\mathit{\text{du}},\hfill & j=0,1,2,\dots .\hfill \end{array}$$

We then have the following result.

THEOREM 2.1. Under the regularity conditions given in Section 7, if h →0 and nh → ∞ as n → ∞, then

$$\sqrt{\mathit{\text{nh}}}\left[\left(\begin{array}{c}\hfill {\tilde{\alpha }}_{0,\tau }(u)-{\alpha }_{0,\tau }(u)\hfill \\ \hfill {\tilde{\mathit{\alpha }}}_{\tau }(u)-{\mathit{\alpha }}_{\tau }(u)\hfill \\ \hfill {\tilde{\mathit{\beta }}}_{\tau }-{\mathit{\beta }}_{\tau }\hfill \end{array}\right)-\frac{{\mu }_2{h}^2}{2}\left(\begin{array}{c}\hfill {\alpha }_{0,\tau }^{″}(u)\hfill \\ \hfill {\mathit{\alpha }}_{\tau }^{″}(u)\hfill \\ \hfill \mathbf{0}\hfill \end{array}\right)\right]\stackrel{𝔇}{\to }N\left(\mathbf{0},\frac{{\nu }_0\tau (1-\tau )}{f_U(u)}{\mathbf{A}}_1^{-1}(u){\mathbf{B}}_1(u){\mathbf{A}}_1^{-1}(u)\right),$$ (2.3)

where A₁(u) = E[f_τ (0|U, X, Z) (1, X^T, Z^T)^T (1, X^T, Z^T)|U = u] and B₁(u) = E[(1, X^T, Z^T)^T (1, X^T, Z^T)|U = u].

Theorem 2.1 implies that β̃_τ is a $\sqrt{\mathit{\text{nh}}}$ -consistent estimator—this is because we only use data in a local neighborhood of u to estimate β_τ. Define $Y_{i,\tau }^{*}=Y_i-{\tilde{\alpha }}_{0,\tau }(U_i)-{\mathbf{X}}_i^T{\tilde{\mathit{\alpha }}}_{\tau }(U_i)$ and compute an improved estimator of β_τ by

$${\widehat{\mathit{\beta }}}_{\tau }=\underset{\mathit{\beta }}{\text{argmin}}{\displaystyle \sum _{i=1}^n}{\rho }_{\tau }(Y_{i,\tau }^{*}-{\mathbf{Z}}_i^T\mathit{\beta }).$$ (2.4)

We call it the semi-QR estimator of β_τ. The next theorem shows the asymptotic properties of β̂_τ.

THEOREM 2.2. Let ${\mathit{\xi }}_{\tau }(u,\mathbf{x},\mathbf{z})=E[f_{\tau }(0|U,\mathbf{X},\mathbf{Z})\mathbf{Z}(1,{\mathbf{X}}^T,\mathbf{0})|U=u]\times {\mathbf{A}}_1^{-1}(u){(1,{\mathbf{x}}^T,{\mathbf{z}}^T)}^T$. Under the regularity conditions given in Section 7, if nh⁴→0 and nh²/ log(1/h)→∞ as n → ∞, then the asymptotic distribution of β̂_τ is given by

$$\sqrt{n}({\widehat{\mathit{\beta }}}_{\tau }-{\mathit{\beta }}_{\tau })\stackrel{𝔇}{\to }N(0,{\mathbf{S}}_{\tau }^{-1}{\mathbf{\Xi }}_{\tau }{\mathbf{S}}_{\tau }^{-1}),$$ (2.5)

where S_τ = E[f_τ (0|U,X,Z)ZZ^T] and Ξ_τ = τ(1 − τ)E[{Z − ξ_τ (U,X,Z)}{Z − ξ_τ (U,X,Z)}^T].

The optimal bandwidth in Theorem 2.1 is h ~ n^−1/5. This bandwidth does not satisfy the condition in Theorem 2.2. Hence, in order to obtain the root-n consistency and asymptotic normality for β̂_τ, undersmoothing for α̃_0,τ (u) and α̃_τ (u) is necessary. This is a common requirement in semiparametric models; see Carroll et al. [3] for a detailed discussion.

After obtaining the root-n consistent estimator β̂_τ, we can further improve the efficiency of α̃_0,τ (u) and α̃_τ (u). To this end, let {â_0,τ, b̂_0,τ, â_τ, b̂_τ} be the minimizer of

$${\displaystyle \sum _{i=1}^n}{\rho }_{\tau }\{Y_i-{\mathbf{Z}}_i^T{\widehat{\mathit{\beta }}}_{\tau }-a_0-b_0(U_i-u)-{\mathbf{X}}_i^T\{\mathbf{a}+\mathbf{b}(U_i-u)\}\}{K}_h(U_i-u).$$

We define

$$\begin{array}{cc}{\widehat{\alpha }}_{0,\tau }(u)={\widehat{\alpha }}_{0,\tau },\hfill & {\widehat{\mathit{\alpha }}}_{\tau }(u)={\widehat{\mathbf{a}}}_{\tau }.\hfill \end{array}$$ (2.6)

THEOREM 2.3. Under the regularity conditions given in Section 7, if h→0 and nh → ∞ as n → ∞, then

$$\sqrt{\mathit{\text{nh}}}\left[\left(\begin{array}{c}\hfill {\widehat{\alpha }}_{0,\tau }(u)-{\alpha }_{0,\tau }(u)\hfill \\ \hfill {\widehat{\mathit{\alpha }}}_{\tau }(u)-{\mathit{\alpha }}_{\tau }(u)\hfill \end{array}\right)-\frac{{\mu }_2{h}^2}{2}\left(\begin{array}{c}\hfill {\alpha }_{0,\tau }^{″}(u)\hfill \\ \hfill {\mathit{\alpha }}_{\tau }^{″}(u)\hfill \end{array}\right)\right]\stackrel{𝔇}{\to }N\left(\mathbf{0},\frac{{\nu }_0\tau (1-\tau )}{f_U(u)}{\mathbf{A}}_2^{-1}(u){\mathbf{B}}_2(u){\mathbf{A}}_2^{-1}(u)\right),$$ (2.7)

where A₂(u) = E[f_τ (0|U,X,Z)(1,X^T)^T (1, X^T)|U = u] and B₂(u) = E[(1, X^T)^T (1, X^T)|U = u].

Theorem 2.3 shows that α̂_0,τ (u) and α̂_τ (u) have the same conditional asymptotic biases as α̃_0,τ (u) and α̃_τ (u), while they have smaller conditional asymptotic variances than α̃_0,τ (u) and α̃_τ (u), respectively. Hence, they are asymptotically more efficient than α̃_0,τ (u) and α̃_τ (u).

3. Semiparametric composite quantile regression

The analysis of semiparametric quantile regression in Section 2 provides a solid foundation for developing the semiparametric composite quantile regression (CQR) estimates. We consider the connection between the quantile regression model (2.1) and model (1.1) in the situations where the random error ε is independent of (U,X, Z). Let us assume that Y = α₀(U) + X^T α(U) + Z^T β + ε, where ε follows a distribution F with mean zero. In such situations, Q_τ (u, x, z) = α₀(u) + c_τ + x^T α(u) + z^T β, where c_τ = F⁻¹(τ). Thus, all quantile regression estimates [α̂_τ (u) and β̂_τ for all τ] estimate the same target quantities [α(u) and β] with the optimal rate of convergence. Therefore, we can consider combining the information across multiple quantile estimates to obtain improved estimates of α(u) and β. Such an idea has been studied for the parametric regression model, in Zou and Yuan [35], and it leads to the CQR estimator that is shown to enjoy nice asymptotic efficiency properties compared with the classical least-squares estimator. Kai, Li and Zou [13] proposed the local polynomial CQR estimator for estimating the nonparametric regression function and its derivative. It is shown that the local CQR method can significantly improve the estimation efficiency of the local least-squares estimator for commonly used non-normal error distributions. Inspired by these nice results, we study semiparametric CQR estimates for model (1.1).

Suppose {U_i,X_i,Z_i,Y_i, i = 1, …, n} is an independent and identically distributed sample from model (1.1) and ε has mean zero. For a given q, let τ_k = k/(q + 1) for k = 1, 2, …, q. The CQR procedure estimates α₀(·), α(·) and β by minimizing the CQR loss function,

$${\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-{\alpha }_{0k}(U_i)-{\mathbf{x}}_i^T\mathit{\alpha }(U_i)-{\mathbf{z}}_i^T\mathit{\beta }\}.$$

To this end, we adapt the three-stage estimation procedure from Section 2.

First, we derive good initial semi-CQR estimates. Let {ã₀, b̃₀, ã, b̃, β̃} be the minimizer of the local CQR loss function

$${\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-a_{0k}-b_0(U_i-u)-{\mathbf{X}}_i^T\{\mathbf{a}+\mathbf{b}(U_i-u)\}-{\mathbf{Z}}_i^T\mathit{\beta }\}{K}_h(U_i-u),$$

where a₀ = (a₀₁, …, a_0q)^T, a = (a₁, …, a_d1)^T and b = (b₁, …, b_d1)^T. Initial estimates of α₀(u) and α (u) are then given by

$$\begin{array}{cc}{\tilde{\alpha }}_0(u)=\frac{1}{q}{\displaystyle \sum _{k=1}^q}{\tilde{\alpha }}_{0k},\hfill & \tilde{\mathit{\alpha }}(u)=\tilde{\mathbf{a}}.\hfill \end{array}$$ (3.1)

To investigate asymptotic behaviors of α̃₀(u), α̃(u) and β̃, let us begin with some new notation. Denote by f (·) and F(·) the density function and cumulative distribution function of the error, respectively. Let c_k = F⁻¹(τ_k) and C be a q × q diagonal matrix with C_jj = f (c_j). Write c = C1, c = 1^T C1 and

$${\mathbf{D}}_1(u)=E\left[\right(\begin{array}{ccc}\hfill C\hfill & \hfill {\mathbf{\text{cX}}}^T\hfill & \hfill {\mathbf{\text{cZ}}}^T\hfill \\ \hfill {\mathbf{\text{Xc}}}^T\hfill & \hfill c{\mathbf{\text{XX}}}^T\hfill & \hfill c{\mathbf{\text{XZ}}}^T\hfill \\ \hfill {\mathbf{\text{Zc}}}^T\hfill & \hfill c{\mathbf{\text{ZX}}}^T\hfill & \hfill c{\mathbf{\text{ZZ}}}^T\hfill \end{array}\left)\right|U=u].$$

Let τ_kk′ = τ_k ∧ τ_k′ − τ_kτ_k′ and let T be a q × q matrix with the (k, k′) element being τ_kk′. Write t = T1, t = 1^T T1 and

$${\mathbf{\Sigma }}_1(u)=E\left[\right(\begin{array}{ccc}\hfill T\hfill & \hfill {\mathbf{\text{tX}}}^T\hfill & \hfill {\mathbf{\text{tZ}}}^T\hfill \\ \hfill {\mathbf{\text{Xt}}}^T\hfill & \hfill t{\mathbf{\text{XX}}}^T\hfill & \hfill t{\mathbf{\text{XZ}}}^T\hfill \\ \hfill {\mathbf{\text{Zt}}}^T\hfill & \hfill t{\mathbf{\text{ZX}}}^T\hfill & \hfill t{\mathbf{\text{ZZ}}}^T\hfill \end{array}\left)\right|U=u].$$

The following theorem describes the asymptotic sampling distribution of {ã₀, b̃₀, ã, b̃, β̃}.

THEOREM 3.1. Under the regularity conditions given in Section 7, if h → 0 and nh → ∞ as n → ∞, then

$$\sqrt{\mathit{\text{nh}}}\left[\right(\begin{array}{c}\hfill {\tilde{\mathbf{a}}}_0-{\mathit{\alpha }}_0(u)\hfill \\ \hfill \tilde{\mathbf{a}}-\mathit{\alpha }(u)\hfill \\ \hfill \tilde{\mathbf{\beta }}-{\mathit{\beta }}_0\hfill \end{array})-\frac{{\mu }_2{h}^2}{2}(\begin{array}{c}\hfill {\mathit{\alpha }}_0^{″}(u)\hfill \\ \hfill \mathit{\alpha }″(u)\hfill \\ \hfill \mathbf{0}\hfill \end{array}\left)\right]\stackrel{𝒟}{\to }N(\mathbf{0},\frac{{\nu }_0}{f_U(u)}{\mathbf{D}}_1^{-1}(u){\mathbf{\Sigma }}_1(u){\mathbf{D}}_1^{-1}(u)),$$

where α₀(u) = (α₀(u)+c₁,…, α₀(u) + c_q)^T and β₀ is the true value of β.

With the initial estimates in hand, we are now ready to derive a $\sqrt{n}$ -consistent estimator of β by

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-{\tilde{a}}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathbf{a}}(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\},$$ (3.2)

which is called the semi-CQR estimator of β.

THEOREM 3.2. Under the regularity conditions given in Section 7, if nh⁴ → 0 and nh²/ log(1/h)→∞ as n → ∞, then the asymptotic distribution of β̂ is given by

$$\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\stackrel{𝔇}{\to }N\left(0,\frac{1}{c^2}{\mathbf{S}}^{-1}\mathbf{\Delta }{\mathbf{S}}^{-1}\right),$$ (3.3)

where S = E(ZZ^T) and $\mathbf{\Delta }={\displaystyle {\sum }_{k=1}^q{\displaystyle {\sum }_{k\prime =1}^q{\tau }_{\mathit{\text{kk}}\prime }}}E[\{\mathbf{Z}-{\mathit{\delta }}_k(U,\mathbf{X},\mathbf{Z})\}{\{\mathbf{Z}-{\mathit{\delta }}_{k\prime }(U,\mathbf{X},\mathbf{Z})\}}^T]$, with δ_k(u, x, z) being the kth column of the d₂ × q matrix

$$\mathbf{\delta }(u,\mathbf{x},\mathbf{z})=E[\mathbf{Z}({\mathbf{c}}^T,c{\mathbf{X}}^T,\mathbf{0})|U=u]{\mathbf{D}}_1^{-1}(u){(I_q,{\mathbf{1}}^T\mathbf{x},{\mathbf{1}}^T\mathbf{z})}^T.$$

Finally, β̂ can also be used to further refine the estimates for the nonparametric part. Let {â₀, b̂₀, â, b̂} be the minimizer of

$${\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}[Y_i-{\mathbf{Z}}_i^T\widehat{\mathit{\beta }}-a_{0k}-b_0(U_i-u)-{\mathbf{X}}_i^T\{\mathbf{a}+\mathbf{b}(U_i-u)\}]K_h(U_i-u),$$

where a₀ = (a₀₁, …, a_0q)^T. We then define the semi-CQR estimators for α₀(u) and α(u) as

$$\begin{array}{cc}{\widehat{\alpha }}_0(u)=\frac{1}{q}{\displaystyle \sum _{k=1}^q}{\widehat{\alpha }}_{0k},\hfill & \widehat{\mathit{\alpha }}(u)=\widehat{\mathbf{a}}.\hfill \end{array}$$ (3.4)

We now study the asymptotic properties of α̂₀(u) and α̂(u). Let

$$\begin{array}{c}{\mathbf{D}}_2(u)=E\left[\right(\begin{array}{cc}\hfill C\hfill & \hfill {\mathbf{\text{cX}}}^T\hfill \\ \hfill {\mathbf{\text{Xc}}}^T\hfill & \hfill c{\mathbf{\text{XX}}}^T\hfill \end{array}\left)\right|U=u],\hfill \\ {\mathbf{\Sigma }}_2(u)=E\left[\right(\begin{array}{cc}\hfill T\hfill & \hfill {\mathbf{\text{tX}}}^T\hfill \\ \hfill {\mathbf{\text{Xt}}}^T\hfill & \hfill t{\mathbf{\text{XX}}}^T\hfill \end{array}\left)\right|U=u].\hfill \end{array}$$

THEOREM 3.3. Under the regularity conditions given in Section 7, if h→0 and nh →∞as n→∞, the asymptotic distributions of α̂₀(u) and α̂(u) are given by

$$\sqrt{\mathit{\text{nh}}}({\widehat{\alpha }}_0(u)-{\alpha }_0(u)-\frac{1}{q}{\displaystyle \sum _{k=1}^q}{c}_k-\frac{{\mu }_2{h}^2}{2}{\alpha }_0^{″}(u))\stackrel{𝒟}{\to }N(0,\frac{{\nu }_0}{f_U(u)}\frac{1}{q^2}{\mathbf{1}}^T{[{\mathbf{D}}_2^{-1}(u){\mathbf{\Sigma }}_2(u){\mathbf{D}}_2^{-1}(u)]}_{11}\mathbf{1})$$

and

$$\sqrt{\mathit{\text{nh}}}(\widehat{\mathit{\alpha }}(u)-\mathit{\alpha }(u)-\frac{{\mu }_2{h}^2}{2}\mathit{\alpha }″(u))\stackrel{𝒟}{\to }N(0,\frac{{\nu }_0}{f_U(u)}{[{\mathbf{D}}_2^{-1}(u){\mathbf{\Sigma }}_2(u){\mathbf{D}}_2^{-1}(u)]}_{22}),$$

where [·]₁₁ denotes the upper-left q × q submatrix and [·]₂₂ denotes the lower-right d₁ × d₁ submatrix.

REMARK 1. α(u) and β represent the contributions of covariates. They are the central quantities of interest in semiparametric inference. Li and Liang [21] studied the least-squares-based semiparametric estimation, which we will refer to as “semi-LS” in this work. The major advantage of semi-CQR over the classical semi-LS is that semi-CQR has competitive asymptotic efficiency. Furthermore, semi-CQR is also more stable and robust. Intuitively speaking, these advantages come from the fact that semi-CQR utilizes information shared across multiple quantile functions, whereas semi-LS only uses the information contained in the mean function.

To elaborate on Remark 1, we discuss the relative efficiency of semi-CQR relative to semi-LS. Note that E(Y|U) = α₀(U) + E(X|U)^T α(U) + E(Z|U)^T β. It then follows that Y = E(Y|U) + {X − E(X|U)}^T α(U) + {Z − E(Z|U)}^T β + ε. Without loss of generality, let us consider the situation in which E(X|U) = 0 and E(Z|U) = 0. Then, all D₁(u),D₂(u),Σ₁(u) and Σ₂(u) become block diagonal matrices. Thus, from Theorem 3.3, we have

$$\sqrt{\mathit{\text{nh}}}({\widehat{\alpha }}_0(u)-{\alpha }_0(u)-\frac{1}{q}{\displaystyle \sum _{k=1}^q}{c}_k-\frac{{\mu }_2{h}^2}{2}{\alpha }_0^{″}(u))\stackrel{𝒟}{\to }N(0,R_1(q)\frac{{\nu }_0}{f_U(u)})$$

and

$$\sqrt{\mathit{\text{nh}}}(\widehat{\mathit{\alpha }}(u)-\mathit{\alpha }(u)-\frac{{\mu }_2{h}^2}{2}\mathit{\alpha }″(u))\stackrel{𝒟}{\to }N(0,R_2(q)\frac{{\nu }_0}{f_U(u)}{E}^{-1}({\mathbf{\text{XX}}}^T|U=u)),$$

where

$$R_1(q)=\frac{1}{q^2}{\mathbf{1}}^T{C}^{-1}T{C}^{-1}\mathbf{1}=\frac{1}{q^2}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{k\prime =1}^q}\frac{{\tau }_{\mathit{\text{kk}}\prime }}{f(c_k)f(c_{k\prime })}$$

and

$$R_2(q)=\frac{t}{c^2}=\frac{{\displaystyle {\sum }_{k=1}^q}{\displaystyle {\sum }_{k\prime =1}^q}{\tau }_{\mathit{\text{kk}}\prime }}{{\{{\displaystyle {\sum }_{k=1}^q}f(c_k)\}}^2}.$$

Note that

$$\mathit{\delta }(u,\mathbf{x},\mathbf{z})=E({\mathbf{\text{ZX}}}^T,\mathbf{0}|U=u)E{\left[\right(\begin{array}{cc}{\mathbf{\text{XX}}}^T\hfill & {\mathbf{\text{XZ}}}^T\hfill \\ {\mathbf{\text{ZX}}}^T\hfill & {\mathbf{\text{ZZ}}}^T\hfill \end{array}\left)\right|U=u]}^{-1}{({\mathbf{1}}^T\mathbf{x},{\mathbf{1}}^T\mathbf{z})}^T$$

with all columns of δ(u, x, z) the same. Thus, Δ = tΔ₀ with Δ₀ = E[{Z − δ₁(U,X,Z)}{Z − δ₁(U,X,Z)}^T]. It is easy to show that E{δ₁(U,X,Z)Z^T} = 0 and we then have

$${\mathbf{\Delta }}_0=E[E({\mathbf{\text{ZZ}}}^T|U)\times {\{E({\mathbf{\text{ZZ}}}^T|U)-E({\mathbf{\text{ZX}}}^T|U)E{({\mathbf{\text{XX}}}^T|U)}^{-1}E({\mathbf{\text{XZ}}}^T|U)\}}^{-1}E({\mathbf{\text{ZZ}}}^T|U)].$$

Therefore,

$$\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\stackrel{𝒟}{\to }N(0,R_2(q){\mathbf{S}}^{-1}{\mathbf{\Delta }}_0{\mathbf{S}}^{-1}).$$ (3.5)

If we replace R₂(q) with 1 in equations (23) and (24), we end up with the asymptotic normal distributions of the semi-LS estimators, as studied in Li and Liang [21]. Thus, R₂(q) determines the asymptotic relative efficiency (ARE) of semi-CQR relative to semi-LS. By direct calculations, we see that the ARE for estimating α(u) is R₂(q)^−4/5 and the ARE for estimating β is R₂(q)⁻¹. It is interesting to see that the same factor, R₂(q), also appears in the asymptotic efficiency analysis of parametric CQR [35] and nonparametric local CQR smoothing [13]. The basic message is that, with a relatively large q (q ≥ 9), R₂(q) is very close to 1 for the normal errors, but can be much smaller than 1, meaning a huge gain in efficiency, for the commonly seen non-normal errors. It is also shown in [13] that lim_q→∞R₂(q)⁻¹ ≥ 0.864 and hence lim_q→∞R₂(q)^−4/5 ≥ 0.8896, which implies that when a large q is used, the ARE is at least 88.9% for estimating varying-coefficient functions and at least 86.4% for estimating parametric components.

REMARK 2. The baseline function estimator α̂₀(u) converges to α₀(u) plus the average of uniform quantiles of the error distribution. Therefore, the bias term is zero when the error distribution is symmetric. Even for nonasymmetric distributions, the additional bias term converge to the mean of the error, which is zero for a large value of q. Nevertheless, its asymptotic variance differs from that of the semi-LS estimator by a factor of R₁(q). The study in Kai, Li and Zou [13] shows that R₁(q) approaches 1 as q becomes large and R₁(q) could be much smaller than 1 with a smaller q (q ≤ 9) for commonly used non-normal distributions.

REMARK 3. The factors R₁(q) and R₂(q) only depend on the error distribution. We have observed from our simulation study that, as a function of q, the maximum of R₂(q) is often closely approximated by R₂ (q = 9). Hence, if we only care about the inference of α(u) and β, then q = 9 seems to be a good default value. On the other hand, R₁ (q = 5) is often close to the maximum of R₁(q) based on our numerical study and hence q = 5 is a good default value for estimating the baseline function. If prediction accuracy is the primary interest, then we should use a proper q to maximize the total contributions from R₁(q) and R₂(q). Practically speaking, one can choose a q from the interval [5, 9] by some popular tuning methods such as K-fold cross-validation. However, we do not expect these CQR models to have significant differences in terms of model fitting and prediction because, in many cases, R₁(q) and R₂(q) vary little in the interval [5, 9].

4. Variable selection

Variable selection is a crucial step in high-dimensional modeling. Various powerful penalization methods have been developed for variable selection in parametric models; see Fan and Li [7] for a good review. In the literature, there are only a few papers on variable selection in semiparametric regression models. Li and Liang [21] proposed the nonconcave penalized quasi-likelihood method for variable selection in semiparametric varying-coefficient models. In this section, we study the penalized semiparametric CQR estimator.

Let p_λn(·) be a pre-specified penalty function with regularization parameter λ_n. We consider the penalized CQR loss

$${\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-{\tilde{\alpha }}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathit{\alpha }}(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\}+\mathit{\text{nq}}{\displaystyle \sum _{j=1}^{d_2}}{p}_{{\lambda }_n}(|{\beta }_j|).$$ (4.1)

By minimizing the above objective function with a proper penalty parameter λ_n, we can get a sparse estimator of β and hence conduct variable selection.

Fan and Li [6] suggested using a concave penalty function since it is able to produce an oracular estimator, that is, the penalized estimator performs as well as if the subset model were known in advance. However, optimizing (4.1) with a concave penalty function is very challenging because the objective function is nonconvex and both loss and penalty parts are nondifferentiable. Various numerical algorithms have been proposed to address the computational difficulties. Fan and Li [6] suggested using local quadratic approximation (LQA) to substitute for the penalty function and then optimizing using the Newton–Raphson algorithm. Hunter and Li [12] further proposed a perturbed version of LQA to alleviate one drawback of LQA. Recently, Zou and Li [34] proposed a new unified algorithm based on local linear approximation (LLA) and further suggested using the one-step LLA estimator because the one-step LLA automatically adopts a sparse representation and is as efficient as the fully iterated LLA estimator. Thus, the one-step LLA estimator is computationally and statistically efficient.

We proposed to follow the one-step sparse estimate scheme in Zou and Li [34] to derive a one-step sparse semi-CQR estimator, as follows. First, we compute the unpenalized semi-CQR estimate β̂⁽⁰⁾, as described in Section 3. We then define

$$G_n(\mathit{\beta })={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-{\tilde{\alpha }}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathit{\alpha }}(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\}+\mathit{\text{nq}}{\displaystyle \sum _{j=1}^{d_2}}{p}_{{\lambda }_n}^{\prime }(|{\beta }_j^{(0)}|)|{\beta }_j|.$$

We define β̂^OSE = argmin_β G_n(β) and call this the one-step sparse semi-CQR estimator. Indeed, this is a weighted L₁ regularization procedure.

We now show that the one-step sparse semi-CQR estimator β̂^OSE enjoys the oracle property. This property holds for a wide class of concave penalties. To establish the idea, we focus on the SCAD penalty from Fan and Li [6], which is perhaps the most popular concave penalty in the literature. Let ${\mathit{\beta }}_0={({\mathit{\beta }}_{10}^T,{\mathit{\beta }}_{20}^T)}^T$ denote the true value of β, where β₁₀ is a s-vector. Without loss of generality, we assume that β₂₀ = 0 and that β₁₀ contains all nonzero components of β₀. Furthermore, let Z₁ be the first s elements of Z and define

$$\mathit{\lambda }(u,\mathbf{x},\mathbf{z})=E[{\mathbf{Z}}_1({\mathbf{c}}^T,{c\mathbf{X}}^T,\mathbf{0})|U=u]{\mathbf{D}}_1^{-1}(u){(I_q,{\mathbf{1}}^T\mathbf{x},{\mathbf{1}}^T\mathbf{z})}^T.$$

THEOREM 4.1 (Oracle property). Let p_λ(·) be the SCAD penalty. Assume that the regularity conditions (B1)–(B6) given in the Appendix hold. If $\sqrt{n}{\lambda }_n\to \mathrm{\infty }$, λ_n →0, nh⁴ →0 and nh²/ log(1/h)→∞ as n → ∞, then the one-step semi-CQR estimator β̂^OSE must satisfy:

1. sparsity, that is, ${\widehat{\mathit{\beta }}}_2^{\text{OSE}}=0$, with probability tending to one;

2. asymptotic normality, that is,

   $$\sqrt{n}({\widehat{\mathit{\beta }}}_1^{\text{OSE}}-{\mathit{\beta }}_{10})\stackrel{𝒟}{\to }N(0,\frac{1}{c^2}{\mathbf{S}}_1^{-1}\mathbf{\Lambda }{\mathbf{S}}_1^{-1}),$$ (4.2)

   where ${\mathbf{S}}_1=E({\mathbf{Z}}_1{\mathbf{Z}}_1^T)\mathit{\text{ and }}\mathbf{\Lambda }={\displaystyle {\sum }_{k=1}^q{\displaystyle {\sum }_{k\prime }^q{\tau }_{\mathit{\text{kk}}\prime }}}E[\{{\mathbf{Z}}_1-{\mathit{\lambda }}_k(U,\mathbf{X},\mathbf{Z})\}{\{{\mathbf{Z}}_1-{\mathit{\lambda }}_{k\prime }(U,\mathbf{X},\mathbf{Z})\}}^T]$ with λ_k(u, x, z) being the kth column of the matrix λ(u, x, z).

Theorem 4.1 shows the asymptotic magnitude of the optimal λ_n. For a given data set with finite sample, it is practically important to have a data-driven method to select a good λ_n. Various techniques have been proposed in previous studies, such as the generalized cross-validation selector [6] and the BIC selector [27]. In this work, we use a BIC-like criterion to select the penalization parameter. The BIC criterion is defined as

$$\text{BIC}(\lambda )=\text{log}\left({\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-{\tilde{\alpha }}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathit{\alpha }}(U_i)-{\mathbf{Z}}_i^T{\widehat{\mathit{\beta }}}^{\text{OSE}}(\lambda )\}\right)+\frac{\text{log}(n)}{n}{\mathit{\text{df}}}_{\lambda },$$

where df_λ is the number of nonzero coefficients in the parametric part of the fitted model. We let λ̂_BIC = argmin BIC(λ). The performance of λ̂_BIC will be examined in our simulation studies in the next section.

REMARK 4. Variable selection in linear quantile regression has been considered in several papers; see Li and Zhu [22] and Wu and Liu [30]. The developed method for sparse semiparametric CQR can be easily adopted for variable selection in semiparametric quantile regression. Consider the penalized check loss

$${\displaystyle \sum _{i=1}^n}{\rho }_{\tau }\{Y_i-{\tilde{\alpha }}_{0,\tau }(U_i)-{\mathbf{X}}_i^T{\tilde{\mathit{\alpha }}}_{\tau }(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\}+n{\displaystyle \sum _{j=1}^{d_2}}{p}_{{\lambda }_n}(|{\beta }_j|).$$ (4.3)

For its one-step version, we use

$${\displaystyle \sum _{i=1}^n}{\rho }_{\tau }\{Y_i-{\tilde{\alpha }}_{0,\tau }(U_i)-{\mathbf{X}}_i^T{\tilde{\mathit{\alpha }}}_{\tau }(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\}+n{\displaystyle \sum _{j=1}^{d_2}}{p}_{{\lambda }_n}^{\prime }(|{\beta }_j^{(0)}|)|{\beta }_j|,$$ (4.4)

where β̂⁽⁰⁾ denotes the unpenalized semiparametric quantile regression estimator defined in Section 2. We can also prove the oracle property of the one-step sparse semiparametric quantile regression estimator by following the lines of proof for Theorem 4.1. For reasons of brevity, we omit the details here.

5. Numerical studies

In this section, we conduct simulation studies to assess the finite-sample performance of the proposed procedures and illustrate the proposed methodology on a real-world data set in a health study. In all examples, we fix the kernel function to be the Epanechnikov kernel, that is, $K(u)=\frac{3}{4}(1-u^2)+$, and we use the SCAD penalty function for variable selection. Note that all proposed estimators, including semi-QR, semi-CQR and one-step sparse semi-CQR, can be formulated as linear programming (LP) problems. In our study, we solved these estimators by using LP tools.

EXAMPLE 1. In this example, we generate 400 random samples, each consisting of n = 200 observations, from the model

$$Y={\alpha }_1(U)X_1+{\alpha }_2(U)X_2+{\beta }_1{Z}_1+{\beta }_2{Z}_2+{\beta }_3{Z}_3+\epsilon ,$$

where α₁(U) = sin(6πU), α₂(U) = sin(2πU), β₁ = 2, β₂ = 1 and β₃ = 0.5. The covariate U is from the uniform distribution on [0, 1]. The covariates X₁,X₂,Z₁,Z₂ are jointly normally distributed with mean 0, variance 1 and correlation 2/3. The covariate Z₃ is Bernoulli with Pr(Z₃ = 1) = 0.4. Furthermore, U and (X₁,X₂,Z₁,Z₂,Z₃) are independent. In our simulation, we considered the following error distributions: N(0, 1), logistic, standard Cauchy, t-distribution with 3 degrees of freedom, mixture of normals 0.9N(0, 1) + 0.1N(0, 10²) and log-normal distribution. Because the error is independent of the covariates, the least-squares (LS), quantile regression (QR) and composite quantile regression (CQR) procedures provide estimates for the same quantity and hence are directly comparable.

Performance of β̂_τ and β̂

To examine the performance of the proposed procedures with a wide range of bandwidths, three bandwidths for LS were considered, h = 0.085, 0.128, 0.192, which correspond to the undersmoothing, appropriate smoothing and oversmoothing, respectively. By straightforward calculation, as in Kai, Li and Zou [13], we can produce two simple formulas for the asymptotic optimal bandwidths for QR and CQR: h_CQR = h_LS · R₂(q)^1/5 and h_QR,τ = h_LS ·{τ(1−τ)/f [F⁻¹(τ)]}^1/5, where h_LS is the asymptotic optimal bandwidth for LS. We considered only the case of normal error. The bias and standard deviation based on 400 simulations are reported in Table 1. First, we see that the estimators are not very sensitive to the choice of bandwidth. As for the estimation accuracy, all three estimators have comparable bias and the differences are shown in standard deviation. The LS estimates have the smallest standard deviation, as expected. The CQR estimates are slightly worse than the LS estimates.

Table 1.

Summary of the bias and standard deviation over 400 simulations

		Bias(SD)
h	Method	β̂1	β̂2	β̂3
0.085	LSE	−0.012 (0.128)	0.008 (0.121)	−0.009 (0.171)
	CQR9	−0.009 (0.131)	0.009 (0.125)	−0.007 (0.172)
	QR0.25	−0.017 (0.163)	0.009 (0.161)	−0.151 (0.237)
	QR0.50	−0.012 (0.155)	0.011 (0.151)	−0.007 (0.198)
	QR0.75	−0.007 (0.165)	0.005 (0.158)	0.122 (0.216)
0.128	LSE	−0.009 (0.121)	0.005 (0.117)	−0.008 (0.164)
	CQR9	−0.010 (0.127)	0.008 (0.121)	−0.005 (0.163)
	QR0.25	−0.010 (0.159)	0.003 (0.152)	−0.082 (0.227)
	QR0.50	−0.008 (0.154)	0.011 (0.147)	−0.004 (0.193)
	QR0.75	−0.012 (0.163)	0.003 (0.161)	0.071 (0.207)
0.192	LSE	−0.007 (0.128)	0.001 (0.123)	−0.008 (0.169)
	CQR9	−0.009 (0.131)	0.005 (0.127)	−0.005 (0.169)
	QR0.25	−0.006 (0.169)	−0.004 (0.169)	−0.061 (0.230)
	QR0.50	−0.005 (0.153)	0.006 (0.152)	−0.007 (0.191)
	QR0.75	−0.012 (0.170)	0.007 (0.171)	0.049 (0.225)

In the second study, we fixed h = 0.128 and compared the efficiency of QR and CQR relative to LS. Reported in Table 2 are RMSEs, the ratios of the MSEs of the QR and CQR estimators to the LS estimator for different error distributions. Several observations can be made from Table 2.When the error follows the normal distribution, the RMSEs of CQR are slightly less than 1. For all other non-normal distributions in the table, the RMSE can be much greater than 1, indicating a huge gain in efficiency. These findings agree with the asymptotic theory. For QR estimators, their performance varies and depends heavily on the level of quantile and the error distribution. Overall, CQR outperforms both QR and LS.

Table 2.

Summary of the ratio of MSE over 400 simulations

	RMSE
Method	β̂1	β̂2	β̂3
Standard normal
CQR9	0.920	0.932	1.011
QR0.25	0.585	0.594	0.460
QR0.50	0.621	0.631	0.724
QR0.75	0.554	0.528	0.561
Logistic
CQR9	1.044	1.083	1.016
QR0.25	0.651	0.664	0.502
QR0.50	0.826	0.871	0.799
QR0.75	0.661	0.732	0.527
Standard Cauchy
CQR9	15,246	106,710	52,544
QR0.25	8894	56,704	24,359
QR0.50	19,556	137,109	66,560
QR0.75	8223	62,282	26,210
t-distribution with df = 3
CQR9	1.554	1.546	1.683
QR0.25	1.000	0.948	0.819
QR0.50	1.354	1.333	1.451
QR0.75	0.935	1.059	0.859
0.9N(0, 1)+ 0.1N(0, 102)
CQR9	5.752	4.860	5.152
QR0.25	3.239	3.096	2.300
QR0.50	5.430	4.730	4.994
QR0.75	3.790	2.952	2.515
Log-normal
CQR9	3.079	3.369	3.732
QR0.25	5.198	5.361	3.006
QR0.50	2.787	2.829	3.139
QR0.75	0.819	0.868	0.823

Performance of α̂_τ and α̂

We now compare the LS, QR and CQR estimates for α by using the ratio of average squared errors (RASE). We first compute

$$\text{ASE}=\left\{\frac{1}{n_{\text{grid}}}{\displaystyle \sum _{m=1}^{d_1}}{\displaystyle \sum _{k=1}^{n_{\text{grid}}}{\{{\widehat{a}}_m(u_k)-a_m(u_k)\}}^2}\right\},$$

where {u_k: k = 1, …, n_grid} is a set of grid points uniformly placed on [0, 1] with n_grid = 200. RASE is then defined to be

$$\text{RASE}(\widehat{g})=\frac{\text{ASE}({\widehat{g}}_{\text{LS}})}{\text{ASE}(\widehat{g})}$$ (5.1)

for an estimator ĝ, where ĝ_LS is the least-squares-based estimator.

The sample mean and standard deviation of the RASEs over 400 simulations are presented in Table 3, where the values in the parentheses are the standard deviations. The findings are quite similar to those in Table 2. We see that CQR performs almost as well as LS when the error is normally distributed. Also, its RASEs are much larger than 1 for other non-normal error distributions. The efficiency gain can be substantial. Note that for the Cauchy distribution, RASEs of QR and CQR are huge—this is because LS fails when the error variance is infinite.

Table 3.

Summary of the RASE over 400 simulations

	Normal	Logistic	Cauchy	t3	Mixture	Log-normal
CQR9	0.968 (0.104)	1.040 (0.134)	12,872 (176719)	1.428 (1.299)	3.292 (1.405)	2.455 (1.498)
QR0.25	0.666 (0.160)	0.720 (0.203)	7621 (110692)	0.958 (0.647)	2.029 (1.003)	3.490 (3.224)
QR0.50	0.771 (0.184)	0.881 (0.206)	13,720 (187298)	1.274 (1.166)	3.155 (1.323)	2.155 (1.674)
QR0.75	0.681 (0.191)	0.713 (0.201)	5781 (87909)	0.896 (0.325)	1.953 (0.905)	0.824 (0.679)

EXAMPLE 2. The goal is to compare the proposed one-step sparse semi-CQR estimator with the one-step sparse semi-LS estimator. In this example, 400 random samples, each consisting of n = 200 observations, were generated from the varying-coefficient partially linear model

$$Y={\alpha }_1(U)X_1+{\alpha }_2(U)X_2+{\mathit{\beta }}^T\mathbf{Z}+\epsilon ,$$

where β = (3, 1.5, 0, 0, 2, 0, 0, 0)^T and the covariate vector (X₁, X₂, Z^T)^T is normally distributed with mean 0, variance 1 and correlation 0.5^|i−j| (i, j = 1,…, 10). Other model settings are exactly the same as those in Example 1. We use the generalized mean square error (GMSE), as defined in [21],

$$\text{GMSE}(\widehat{\mathit{\beta }})={(\widehat{\mathit{\beta }}-\mathit{\beta })}^{T}E({\mathbf{\text{ZZ}}}^T)(\widehat{\mathit{\beta }}-\mathit{\beta }),$$ (5.2)

to assess the performance of variable selection procedures for the parametric component. For each procedure, we calculate the relative GMSE (RGMSE), which is defined to be the ratio of the GMSE of a selected final model to that of the unpenalized least-squares estimate under the full model.

The results over 400 simulations are summarized in Table 4, where the column “RGMSE” reports both the median and MAD of 400 RGMSEs. Both columns “C” and “IC” are measures of model complexity. Column “C” shows the average number of zero coefficients correctly estimated to be zero and column “IC” presents the average number of nonzero coefficients incorrectly estimated to be zero. In the column labeled “U-fit” (short for “under-fit”), we present the proportion of trials excluding any nonzero coefficients in 400 replications. Likewise, we report the probability of trials selecting the exact subset model and the probability of trials including all three significant variables and some noise variables in the columns “C-fit” (“correct-fit”) and “O-fit” (“over-fit”), respectively.

Table 4.

One-step estimates for variable selection in semiparametric models

Method	RGMSE Median (MAD)	No. of zeros		Proportion of fits
		C	IC	U-fit	C-fit	O-fit
Standard normal
One-step LS	0.335 (0.194)	4.825	0.000	0.000	0.867	0.133
One-step CQR	0.288 (0.213)	4.990	0.000	0.000	0.990	0.010
Logistic
One-step LS	0.352 (0.197)	4.805	0.000	0.000	0.870	0.130
One-step CQR	0.289 (0.206)	4.975	0.000	0.000	0.975	0.025
Standard Cauchy
One-step LS	0.956 (0.249)	2.920	0.795	0.595	0.108	0.297
One-step CQR	0.005 (0.021)	5.000	0.295	0.210	0.790	0.000
t-distribution with df = 3
One-step LS	0.346 (0.179)	4.803	0.000	0.000	0.860	0.140
One-step CQR	0.183 (0.177)	4.987	0.000	0.000	0.988	0.013
0.9N(0, 1)+0.1N(0, 102)
One-step LS	0.331 (0.190)	4.848	0.000	0.000	0.883	0.117
One-step CQR	0.060 (0.083)	4.997	0.000	0.000	0.998	0.003
Log-normal
One-step LS	0.303 (0.182)	4.845	0.000	0.000	0.887	0.113
One-step CQR	0.111 (0.118)	4.990	0.000	0.000	0.990	0.010

From Table 4, we see that both variable selection procedures dramatically reduce model errors, which clearly show the virtue of variable selection. Second, the one-step CQR performs better than the one-step LS in terms of all of the criteria: RGMSE, number of zeros and proportion of fits, and for all of the error distributions in Table 4. It is also interesting to see that in the normal error case, the one-step CQR seems to perform no worse than the one-step LS (or even slightly better). We performed the Mann–Whitney test to compare their RGM-SEs and the corresponding p-value is 0.0495. This observation appears to be contradictory to the asymptotic theory. However, this “contradiction” can be explained by observing that the one-step CQR has better variable selection performance. Note that the one-step CQR has significantly higher probability of correct-select than the one-step LS, which also tends to overselect. Thus, the one-step LS needs to estimate a larger model than the truth, compared to the one-step CQR.

EXAMPLE 3. As an illustration, we apply the proposed procedures to analyze the plasma beta-carotene level data set collected by a cross-sectional study [24]. This data set consists of 273 samples. Of interest are the relationships between the plasma beta-carotene level and the following covariates: age, smoking status, quetelet index (BMI), vitamin use, number of calories, grams of fat, grams of fiber, number of alcoholic drinks, cholesterol and dietary beta-carotene. The complete description of the data can be found in the StatLib database via the link lib.stat.cmu.edu/datasets/Plasma_Retinol.

We fit the data by using a partially linear model with U being “dietary beta-carotene.” The covariates “smoking status” and “vitamin use” are categorical and are thus replaced with dummy variables. All of the other covariates are standardized. We applied the one-step sparse CQR and LS estimators to fit the partially linear regression model. Five-fold cross-validation was used to select the bandwidths for LS and CQR. We used the first 200 observations as a training data set to fit the model and to select significant variables, then used the remaining 73 observations to evaluate the predictive ability of the selected model.

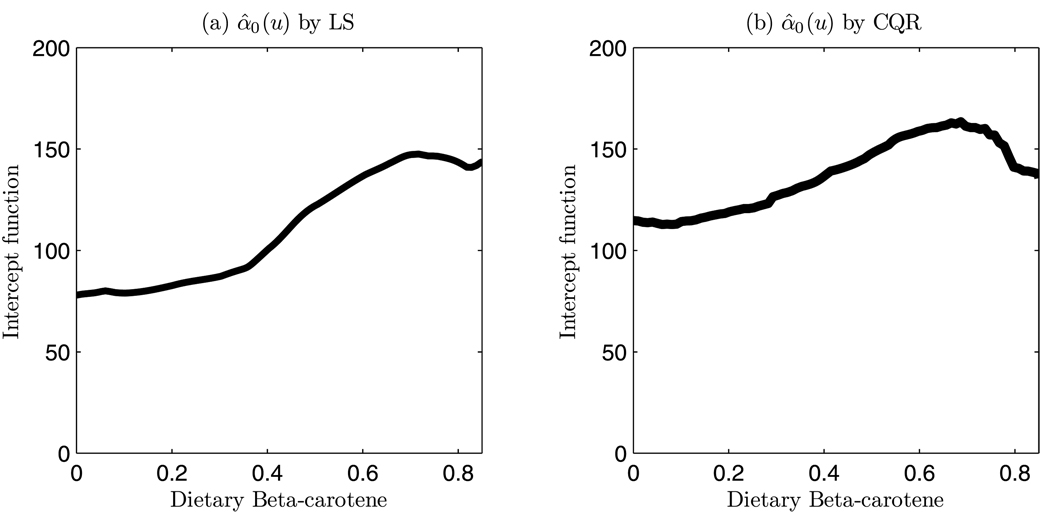
The prediction performance is measured by the median absolute prediction error (MAPE), which is the median of {|y_i − ŷ_i|, i = 1, 2,…, 73}. To see the effect of q on the CQR estimate, we tried q = 5, 7, 9. We found that the selected Z-variables are the same for these three values of q and their MAPEs are 58.52, 58.11, 62.43, respectively. Thus, the effect of q is minor. The resulting model with q = 7 is given in Table 5 and the estimated intercept function is depicted in Figure 1. From Table 5, it can be seen that the CQR model is much sparser than the LS model. Only two covariates, “fiber consumption per day” and “fairly often use of vitamin” are included in the parametric part of the CQR model. Meanwhile, the CQR model has much better prediction performance than the LS model, whose MAPE is 111.28.

Table 5.

Selected parametric components for plasma beta-carotene level data

	${\widehat{\beta }}_{\text{LS}}^{\text{OSE}}$	${\widehat{\beta }}_{\text{CQR}}^{\text{OSE}}$
Age	0	0
Quetelet index	0	0
Calories	−100.47	0
Fat	52.60	0
Fiber	87.51	29.89
Alcohol	44.61	0
Cholesterol	0	0
Smoking status (never)	51.71	0
Smoking status (former)	72.48	0
Vitamin use (yes, fairly often)	130.39	30.21
Vitamin use (yes, not often)	0	0
MAPE	111.28	58.11

Fig. 1.

Plot of estimated intercept function of dietary beta-carotene: (a) the estimated intercept function by LS method; (b) the estimated intercept function by CQR method with q = 7.

6. Discussion

We discuss some directions in which this work could be further extended. We have focused on using uniform weights in composite quantile regression. In theory, we can use nonuniform weights, which may provide an even more efficient estimator when a reliable estimate of the error distribution is available. Koenker [16] discussed the theoretically optimal weights. Bradic, Fan and Wang [1] suggested a data-driven weighted CQR for parametric linear regression, in which the weights mimic the optimal weights. The idea in Bradic, Fan and Wang [1] can be easily extended to the semi-CQR estimator, which will be investigated in detail in a future paper.

Penalized Wilcoxon rank regression has been considered independently in Leng [20] and Wang and Li [29] and found to achieve a similar efficiency property of CQR for variable selection in parametric linear regression. We could also generalize rank regression to handle semiparametric varying-coefficient partially linear models. In a working paper, we show that rank regression is exactly equivalent to CQR using q = n − 1 quantiles with uniform weights. This result indicates that CQR is more flexible than rank regression because we can easily use flexible nonuniform weights in CQR to further improve efficiency, as in Bradic, Fan and Wang [1]. Obviously, CQR is also computationally more efficient than rank regression. We note that in parametric linear regression models, rank regression has no efficiency gain over least-squares for estimating the intercept. This result is expected to hold for estimating the baseline function in the semiparametric varying-coefficient partially linear model.

When the number of varying coefficient components is large, it is also desirable to consider selecting a few important components. This problem was studied in Wang and Xia [28], where a LASSO-type penalized local least-squares estimator was proposed. It would be interesting to apply CQR to their method to further improve the estimation efficiency.

7. Proofs

To establish the asymptotic properties of the proposed estimators, the following regularity conditions are imposed:

• (C1)the random variable U has bounded support Ω and its density function f_U(·) is positive and has a continuous second derivative;
• (C2)the varying coefficients α₀(·) and α(·) have continuous second derivatives in u ∈ Ω;
• (C3)K(·) is a symmetric density function with bounded support and satisfies a Lipschitz condition;
• (C4)the random vector Z has bounded support;
• (C5)
  for the semi-QR procedure,

  1. F_τ (0|u, x, z) = τ for all (u, x, z), and f_τ (·|u, x, z) is bounded away from zero and has a continuous and uniformly bounded derivative;
  2. A₁(u) defined in Theorem 2.1 and A₂(u) defined in Theorem 2.3 are nonsingular for all u ∈ Ω;
• (C6)
  for the semi-CQR procedure,

  1. f (·) is bounded away from zero and has a continuous and uniformly bounded derivative;
  2. D₁(u) defined in Theorem 3.1 and D₂(u) defined in Theorem 3.3 are non-singular for all u ∈ Ω.

Although the proposed semi-QR and semi-CQR procedures require different regularity conditions, the proofs follow similar strategies. For brevity, we only present the detailed proofs for the semi-CQR procedure. The detailed proofs for the semi-QR procedure was given in the earlier version of this paper. Lemma 7.1 below, which is a direct result of Mack and Silverman [23], will be used repeatedly in our proofs. Throughout the proofs, identities of the form G(u) = O_p(a_n) always stand for sup_u∈Ω |G(u)| = O_p(a_n).

LEMMA 7.1. Let (X₁,Y₁),…, (X_n,Y_n) be i.i.d. random vectors, where the Y_i’s are scalar random variables. Assume, further, that E|Y|^r < ∞ and that sup_x ∫ |y|^r f (x, y)dy < ∞, where f denotes the joint density of (X,Y). Let K be a bounded positive function with bounded support, satisfying a Lipschitz condition. Then,

$$\underset{\mathbf{x}\in D}{\text{sup}}\left|n^{-1}{\displaystyle \sum _{i=1}^n}\{K_h({\mathbf{X}}_i-\mathbf{x})Y_i-E[K_h({\mathbf{X}}_i-\mathbf{x})Y_i]\}\right|=O_p\left(\frac{{\text{log}}^{1/2}(1/h)}{\sqrt{\mathit{\text{nh}}}}\right),$$

provided that n^2ε−1h→∞for some ε <1 −r⁻¹.

Let η_i,k = I (ε_i ≤ c_k)−τ_k and ${\eta }_{i,k}^{*}(u)=I\{{\epsilon }_i\le c_k-r_i(u)\}-{\tau }_k$, where $r_i(u)={\alpha }_0(U_i)-{\alpha }_0(u)-{\alpha }_0^{\prime }(u)(U_i-u)+{\mathbf{X}}_i^T\{\mathit{\alpha }(U_i)-\mathit{\alpha }(u)-\mathit{\alpha }\prime (u)(U_i-u)\}$. Furthermore, let ${\tilde{\mathit{\theta }}}^{*}=\sqrt{\mathit{\text{nh}}}{\{{\tilde{a}}_{01}-{\alpha }_0(u)-c_1,\dots ,{\tilde{a}}_{0q}-{\alpha }_0(u)-c_q,{\{\tilde{\mathbf{a}}-\mathit{\alpha }(u)\}}^T,{\{\tilde{\mathit{\beta }}-{\mathit{\beta }}_0\}}^T,h\{{\tilde{b}}_0-{\alpha }_0^{\prime }(u)\},h{\{\tilde{\mathbf{b}}-\mathit{\alpha }\prime (u)\}}^T\}}^T\text{ and }{\mathbf{X}}_{i,k}^{*}(u)={\{{\mathbf{e}}_k^T,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T,(U_i-u)/h,{\mathbf{X}}_i^T(U_i-u)/h\}}^T$, where e_k is a q-vector with 1 at the kth position and 0 elsewhere.

In the proof of Theorem 3.1, we will first show the following asymptotic representation of {ã₀, b̃₀, ã, b̃, β̃}:

$${\tilde{\mathit{\theta }}}^{*}=-f_U^{-1}(u){\{{\mathbf{S}}^{*}(u)\}}^{-1}{\mathbf{W}}_n^{*}(u)+O_p(h^2+{\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}}),$$ (7.1)

where S* (u) = diag{D₁(u), cµ₂B₂(u)} and

$${\mathbf{W}}_n^{*}(u)=\frac{1}{\sqrt{\mathit{\text{nh}}}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^{n}K}\{(U_i-u)/h\}{\eta }_{i,k}^{*}(u){\mathbf{X}}_{i,k}^{*}(u).$$

The asymptotic normality of {ã₀, b̃₀, ã, b̃, β̃} then follows by demonstrating the asymptotic normality of ${\mathbf{W}}_n^{*}(u)$.

PROOF OF THEOREM 3.1. Recall that {ã₀, ã, β̃, b̃₀, b̃} minimizes

$${\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}[Y_i-a_{0k}-b_0(U_i-u)-{\mathbf{X}}_i^T\{\mathbf{a}+\mathbf{b}(U_i-u)\}-{\mathbf{Z}}_i^T\mathit{\beta }]K_h(U_i-u).$$

We write $Y_i-a_{0k}-b_0(U_i-u)-{\mathbf{X}}_i^T\{\mathbf{a}+\mathbf{b}(U_i-u)\}-{\mathbf{Z}}_i^T\mathit{\beta }=({\epsilon }_i-c_k)+r_i(u)-{\mathrm{\Delta }}_{i,k}$, where ${\mathrm{\Delta }}_{i,k}={\{{\mathbf{X}}_{i,k}^{*}(u)\}}^T{\mathit{\theta }}^{*}/\sqrt{\mathit{\text{nh}}}$. Then, θ̃* is also the minimizer of

$$L_n^{*}({\mathit{\theta }}^{*})={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u)[{\rho }_{{\tau }_k}\{({\epsilon }_i-c_k)+r_i(u)-{\mathrm{\Delta }}_{i,k}\}-{\rho }_{{\tau }_k}\{({\epsilon }_i-c_k)+r_i(u)\}],$$

where K_i(u) = K{(U_i − u)/h}. By applying the identity [14]

$${\rho }_{\tau }(x-y)-{\rho }_{\tau }(x)=y\{I(x\le 0)-\tau \}+{\displaystyle {\int }_0^y}\{I(x\le z)-I(x\le 0)\}\mathit{\text{dz}},$$ (7.2)

we have

$$\begin{array}{cc}{L}_n^{*}({\mathit{\theta }}^{*})\hfill & ={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u)\left\{{\mathrm{\Delta }}_{i,k}[I\{{\epsilon }_i\le c_k-r_i(u)\}-{\tau }_k]+{\displaystyle {\int }_0^{{\mathrm{\Delta }}_{i,k}}}[I\{{\epsilon }_i\le c_k-r_i(u)+z\}-I\{{\epsilon }_i\le c_k-r_i(u)\}]\mathit{\text{dz}}\right\}\hfill \\ \hfill & ={\{{\mathbf{W}}_n^{*}(u)\}}^T{\mathit{\theta }}^{*}+{\displaystyle \sum _{k=1}^q}{B}_{n,k}^{*}({\mathit{\theta }}^{*}),\hfill \end{array}$$

where

$$B_{n,k}^{*}({\mathit{\theta }}^{*})={\displaystyle \sum _{i=1}^n}{K}_i(u){\displaystyle {\int }_0^{{\mathrm{\Delta }}_{i,k}}}[I\{{\epsilon }_i\le c_k-r_i(u)+z\}-I\{{\epsilon }_i\le c_k-r_i(u)\}]\mathit{\text{dz}}.$$

Since $B_{n,k}^{*}({\mathit{\theta }}^{*})$ is a summation of i.i.d. random variables of the kernel form, it follows, by Lemma 7.1, that

$$B_{n,k}^{*}({\mathit{\theta }}^{*})=E[B_{n,k}^{*}({\mathit{\theta }}^{*})]+O_p({\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}}).$$

The conditional expectation of ${\displaystyle {\sum }_{k=1}^q{B}_{n,k}^{*}({\mathit{\theta }}^{*})}$ can be calculated as

$${\displaystyle \sum _{k=1}^q}E[B_{n,k}^{*}({\mathit{\theta }}^{*})|U,\mathbf{X},\mathbf{Z}]={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u){\displaystyle {\int }_0^{{\mathrm{\Delta }}_{i,k}}}[F(c_k-r_i(u)+z)-F(c_k-r_i(u))]\mathit{\text{dz}}=\frac{1}{2}{({\mathit{\theta }}^{*})}^T\left(\frac{1}{\mathit{\text{nh}}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u)f(c_k-r_i(u))\{{\mathbf{X}}_{i,k}^{*}(u)\}{\{{\mathbf{X}}_{i,k}^{*}(u)\}}^T\right){\mathit{\theta }}^{*}+O_p({\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}})\triangleq \frac{1}{2}{({\mathit{\theta }}^{*})}^T{\mathbf{S}}_n^{*}(u){\mathit{\theta }}^{*}+O_p({\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}}).$$

Then,

$$\begin{array}{cc}{L}_n^{*}({\mathit{\theta }}^{*})\hfill & ={\{{\mathbf{W}}_n^{*}(u)\}}^T{\mathit{\theta }}^{*}+{\displaystyle \sum _{k=1}^q}E[B_{n,k}^{*}({\mathit{\theta }}^{*})]+O_p({\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}})\hfill \\ \hfill & ={\{{\mathbf{W}}_n^{*}(u)\}}^T{\mathit{\theta }}^{*}+{\displaystyle \sum _{k=1}^q}E\{E[B_{n,k}^{*}({\mathit{\theta }}^{*})|U,\mathbf{X},\mathbf{Z}]\}+O_p({\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}})\hfill \\ \hfill & ={\{{\mathbf{W}}_n^{*}(u)\}}^T{\mathit{\theta }}^{*}+\frac{1}{2}{({\mathit{\theta }}^{*})}^{T}E[{\mathbf{S}}_n^{*}(u)]{\mathit{\theta }}^{*}+O_p({\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}}).\hfill \end{array}$$

It can be shown that $E[{\mathbf{S}}_n^{*}(u)]=f_U(u){\mathbf{S}}^{*}(u)+O(h^2)$. Therefore, we can write L_n(θ*) as

$$L_n^{*}({\mathit{\theta }}^{*})={\{{\mathbf{W}}_n^{*}(u)\}}^T{\mathit{\theta }}^{*}+\frac{f_U(u)}{2}{({\mathit{\theta }}^{*})}^T{\mathbf{S}}^{*}(u){\mathit{\theta }}^{*}+O_p(h^2+{\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}}).$$

By applying the convexity lemma [25] and the quadratic approximation lemma [4], the minimizer of $L_n^{*}({\mathit{\theta }}^{*})$ can be expressed as

$${\tilde{\mathit{\theta }}}^{*}=-f_U^{-1}(u){\{{\mathbf{S}}^{*}(u)\}}^{-1}{\mathbf{W}}_n^{*}(u)+O_p(h^2+{\text{log}}^{1/2}(1/h)/\sqrt{\mathit{\text{nh}}}),$$ (7.3)

which holds uniformly for u ∈ Ω. Meanwhile, for any point u ∈ Ω, we have

$${\tilde{\mathit{\theta }}}^{*}=-f_U^{-1}(u){\{{\mathbf{S}}^{*}(u)\}}^{-1}{\mathbf{W}}_n^{*}(u)+o_p(1).$$ (7.4)

Note that S* (u) = diag{D₁(u), cµ₂B₂(u)} is a quasi-diagonal matrix. So,

$$\sqrt{\mathit{\text{nh}}}\left(\begin{array}{c}\hfill {\tilde{\mathbf{a}}}_0-{\mathit{\alpha }}_0(u)\hfill \\ \hfill \tilde{\mathbf{a}}-\mathit{\alpha }(u)\hfill \\ \hfill \tilde{\mathit{\beta }}-{\mathit{\beta }}_0\hfill \end{array}\right)=-f_U^{-1}(u){\mathbf{D}}_1^{-1}(u){\mathbf{W}}_{n,1}^{*}(u)+o_p(1),$$ (7.5)

where ${\mathbf{W}}_{n,1}^{*}(u)=\frac{1}{\sqrt{\mathit{\text{nh}}}}{\displaystyle {\sum }_{k=1}^q{\displaystyle {\sum }_{i=1}^n{K}_i(u)}}{\eta }_{i,k}^{*}(u){({\mathbf{e}}_k^T,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T)}^T$. Let

$${\mathbf{W}}_{n,1}^{\#}(u)=\frac{1}{\sqrt{\mathit{\text{nh}}}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u){\eta }_{i,k}{({\mathbf{e}}_k^T,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T)}^T.$$

Note that

$$\text{Cov}({\eta }_{i,k},{\eta }_{i,k\prime })={\tau }_{\mathit{\text{kk}}\prime },\text{ Cov}({\eta }_{i,k},{\eta }_{j,k\prime })=0\text{ if }i\ne j.$$

By some calculations, we have that $E[{\mathbf{W}}_{n,1}^{\#}(u)]=\mathbf{0}\text{ and Var}[{\mathbf{W}}_{n,1}^{\#}(u)]\to f_U(u){\nu }_0{\mathit{\sum }}_1(u)$. By the Cramér–Wold theorem, the central limit theorem for W_n,1(u) holds. Therefore,

$${\mathbf{W}}_{n,1}^{\#}(u)\stackrel{𝒟}{\to }N(\mathbf{0},f_U(u){\nu }_0{\mathbf{\Sigma }}_1(u)).$$

Moreover, we have $\text{Var}[{\mathbf{W}}_{n,1}^{*}(u)-{\mathbf{W}}_{n,1}^{\#}(u)|U,\mathbf{X},\mathbf{Z}]\le \frac{q^2}{\mathit{\text{nh}}}{\displaystyle {\sum }_{i=1}^n{K}_i^2(u){({\mathbf{e}}_k^T,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T)}^T({\mathbf{e}}_k^T,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T){\text{max}}_k\{F(c_k+|r_i|)-F(c_k)\}=o_p(1)}$, thus

$$\text{Var}[{\mathbf{W}}_{n,1}^{*}(u)-{\mathbf{W}}_{n,1}^{\#}(u)]=o(1).$$

So, by Slutsky’s theorem, conditioning on {U,X,Z}, we have

$${\mathbf{W}}_{n,1}^{*}(u)-E[{\mathbf{W}}_{n,1}^{*}(u)]\stackrel{𝒟}{\to }N(\mathbf{0},f_U(u){\nu }_0{\mathbf{\Sigma }}_1(u)).$$ (7.6)

We now calculate the conditional mean of ${\mathbf{W}}_{n,1}^{*}(u)$:

$$\begin{array}{cc}\frac{1}{\sqrt{\mathit{\text{nh}}}}E[{\mathbf{W}}_{n,1}^{*}(u)|U,\mathbf{X},\mathbf{Z}]\hfill & =\frac{1}{\mathit{\text{nh}}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u)\{F(c_k-r_i(u))-F(c_k)\}{({\mathbf{e}}_k^t,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T)}^T\hfill \\ \hfill & =-\frac{1}{\mathit{\text{nh}}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{K}_i(u)r_i(u)f(c_k)\{1+o(1)\}{({\mathbf{e}}_k^t,{\mathbf{X}}_i^T,{\mathbf{Z}}_i^T)}^T\hfill \\ \hfill & =-\frac{{\mu }_2{h}^2}{2}{f}_U(u){\mathbf{D}}_1(u)\left(\begin{array}{c}\hfill {\mathit{\alpha }}_0^{″}(u)\hfill \\ \hfill \mathit{\alpha }″(u)\hfill \\ \hfill \mathbf{0}\hfill \end{array}\right)+o_p(h^2).\hfill \end{array}$$ (7.7)

The proof is completed by combining (7.5), (7.6) and (7.7).

PROOF OF THEOREM 3.2. Let $\mathit{\theta }=\sqrt{n}(\mathit{\beta }-{\mathit{\beta }}_0)$. Then,

$$Y_i-{\tilde{a}}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathbf{a}}(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }={\epsilon }_i-c_k-\{{\tilde{a}}_{0k}(U_i)-{\alpha }_0(U_i)-c_k\}-{\mathbf{X}}_i^T\{\tilde{\mathbf{a}}(U_i)-\mathit{\alpha }(U_i)\}-{\mathbf{Z}}_i^T(\mathit{\beta }-{\mathit{\beta }}_0)={\epsilon }_i-c_k-{\tilde{r}}_{i,k}-{\mathbf{Z}}_i^T\mathit{\theta }/\sqrt{n},$$

where ${\tilde{r}}_{i,k}=\{{\tilde{a}}_{0k}(U_i)-{\alpha }_0(U_i)-c_k\}+{\mathbf{X}}_i^T\{\tilde{\mathbf{a}}(U_i)-\mathit{\alpha }(U_i)\}$. Then,

$$\widehat{\mathit{\theta }}=\text{argmin}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}(Y_i-{\tilde{a}}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathbf{a}}(U_i)-{\mathbf{Z}}_i^T\mathit{\beta })$$

is also the minimizer of

$$L_n(\mathit{\theta }={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}\{{\rho }_{{\tau }_k}({\epsilon }_i-c_k-{\tilde{r}}_{i,k}-{\mathbf{Z}}_i^T\mathit{\theta }/\sqrt{n})-{\rho }_{{\tau }_k}({\epsilon }_i-c_k-{\tilde{r}}_{i,k})\}.$$

By applying the identity (7.2), we can rewrite L_n(θ) as follows:

$$\begin{array}{cc}{L}_n(\mathit{\theta })\hfill & ={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}\left\{\frac{{\mathbf{Z}}_i^T\mathit{\theta }}{\sqrt{n}}[I({\epsilon }_i\le c_k)-{\tau }_k]+{\displaystyle {\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+{\mathbf{Z}}_i^T\mathit{\theta }/\sqrt{n}}}[I({\epsilon }_i\le c_k+z)-I({\epsilon }_i\le c_k)]\mathit{\text{dz}}\right\}\hfill \\ \hfill & ={\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\eta }_{i,k}{\mathbf{Z}}_i\right)}^T\mathit{\theta }+B_n(\mathit{\theta }),\hfill \end{array}$$

where $B_n(\mathit{\theta })={\displaystyle {\sum }_{k=1}^q{\displaystyle {\sum }_{i=1}^n{\displaystyle {\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+{\mathbf{Z}}_i^T\mathit{\theta }/\sqrt{n}}[I({\epsilon }_i\le c_k+z)-I({\epsilon }_i\le c_k)]\mathit{\text{dz}}}}}$. Let us now calculate the conditional expectation of B_n(θ):

$$E[B_n(\mathit{\theta })|U,\mathbf{X},\mathbf{Z}]={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\displaystyle {\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+{\mathbf{Z}}_i^T\mathit{\theta }/\sqrt{n}}}[\mathit{\text{zf}}(c_k)\{1+o(1)\}]\mathit{\text{dz}}=\frac{1}{2}{\mathit{\theta }}^T\left(\frac{1}{n}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}f(c_k){\mathbf{Z}}_i{\mathbf{Z}}_i^T\right)\mathit{\theta }-{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}f(c_k){\tilde{r}}_{i,k}{\mathbf{Z}}_i\right)}^T\mathit{\theta }+o_p(1).$$

Define R_n(θ) = B_n(θ) − E[B_n(θ)|U,X,Z]. It can be shown that R_n(θ) = o_p(1). Hence,

$$\begin{array}{cc}{L}_n(\mathit{\theta })\hfill & ={\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\eta }_{i,k}{\mathbf{Z}}_i\right)}^T\mathit{\theta }+E[B_n(\mathit{\theta })|U,\mathbf{X},\mathbf{Z}]+R_n(\mathit{\theta })\hfill \\ \hfill & =\frac{1}{2}{\mathit{\theta }}^T{\mathbf{S}}_n\mathit{\theta }+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\eta }_{i,k}{\mathbf{Z}}_i\right)}^T\mathit{\theta }-{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}f(c_k){\tilde{r}}_{i,k}{\mathbf{Z}}_i\right)}^T\mathit{\theta }+o_p(1),\hfill \end{array}$$

where ${\mathbf{S}}_n=\frac{1}{n}{\displaystyle {\sum }_{k=1}^q{\displaystyle {\sum }_{i=1}^{n}f(c_k){\mathbf{Z}}_i{\mathbf{Z}}_i^T}}$. By (7.3), the third term in the previous expression can be expressed as

$$\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}f(c_k){\tilde{r}}_{i,k}{\mathbf{Z}}_i=\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}\frac{f(c_k)}{f_U(U_i)}{\mathbf{Z}}_i{\left(\begin{array}{c}{\mathbf{e}}_k\hfill \\ {\mathbf{X}}_i\hfill \\ \hfill \mathbf{0}\hfill \end{array}\right)}^T\times {\mathbf{D}}_1^{-1}(U_i)\left(\frac{1}{\mathit{\text{nh}}}{\displaystyle \sum _{k\prime =1}^q}{\displaystyle \sum _{i\prime =1}^n}{\eta }_{i\prime ,k\prime }^{*}(U_i)\left(\begin{array}{c}{\mathbf{e}}_{k\prime }\hfill \\ {\mathbf{X}}_{i\prime }\hfill \\ {\mathbf{Z}}_{i\prime }\hfill \end{array}\right)K_{i\prime }(U_i)\right)+O_p(h^{3/2}+{\text{log}}^{1/2}(1/h)/\sqrt{{\mathit{\text{nh}}}^2})=\frac{1}{\sqrt{n}}{\displaystyle \sum _{k\prime =1}^q}{\displaystyle \sum _{i\prime =1}^n}{\eta }_{i\prime ,k\prime }{\mathit{\delta }}_{k\prime }(U_{i\prime },{\mathbf{X}}_{i\prime },{\mathbf{Z}}_{i\prime })+O_p(n^{1/2}{h}^2+{\text{log}}^{1/2}(1/h)/\sqrt{{\mathit{\text{nh}}}^2})=\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\eta }_{i,k}{\mathit{\delta }}_k(U_i,{\mathbf{X}}_i,{\mathbf{Z}}_i)+o_p(1),$$

where

$$\mathit{\delta }(U_i,{\mathbf{X}}_i,{\mathbf{Z}}_i)=E[\mathbf{Z}({\mathbf{c}}^T,{c\mathbf{X}}^T,\mathbf{0})|U=U_i]{\mathbf{D}}_1^{-1}(U_i){(I_q,{\mathbf{1}}^T{\mathbf{X}}_i,{\mathbf{1}}^T{\mathbf{Z}}_i)}^T.$$

Therefore,

$$\begin{array}{cc}{L}_n(\mathit{\theta })\hfill & =\frac{1}{2}{\mathit{\theta }}^T{\mathbf{S}}_n\mathit{\theta }+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\eta }_{i,k}\{{\mathbf{Z}}_i-{\mathit{\delta }}_k(U_i,{\mathbf{X}}_i,{\mathbf{Z}}_i)\}\right)}^T\mathit{\theta }+o_p(1)\hfill \\ \hfill & \triangleq \frac{1}{2}{\mathit{\theta }}^T{\mathbf{S}}_n\mathit{\theta }+{\mathbf{W}}_n^T\mathit{\theta }+o_p(1).\hfill \end{array}$$

It can be shown that S_n = E(S_n)+o_p(1) = cS + o_p(1). Hence,

$$L_n(\mathit{\theta })=\frac{c}{2}{\mathit{\theta }}^T\mathbf{S}\mathit{\theta }+{\mathbf{W}}_n^T\mathit{\theta }+o_p(1).$$

Since the convex function $L_n(\mathit{\theta })-{\mathbf{W}}_n^T\mathit{\theta }$ converges in probability to the convex function $\frac{c}{2}{\mathit{\theta }}^T\mathbf{S}\mathit{\theta }$, it follows, by the convexity lemma [25], that the quadratic approximation to L_n(θ) holds uniformly for θ in any compact set Θ. Thus, it follows that

$$\widehat{\mathit{\theta }}=-\frac{1}{c}{\mathbf{S}}^{-1}{\mathbf{W}}_n+o_p(1).$$ (7.8)

By the Cramér–Wold theorem, the central limit theorem for W_n holds and $\text{Var}({\mathbf{W}}_n)\to \mathbf{\Delta }={\displaystyle {\sum }_{k=1}^q{\displaystyle {\sum }_{k\prime =1}^q{\tau }_{\mathit{\text{kk}}\prime }}}E\{\mathbf{Z}-{\mathit{\delta }}_k(U,\mathbf{X},\mathbf{Z})\}{\{\mathbf{Z}-{\mathit{\delta }}_{k\prime }(U,\mathbf{X},\mathbf{Z})\}}^T$. Therefore, the asymptotic normality of β̂ is followed by

$$\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\stackrel{𝒟}{\to }N\left(0,\frac{1}{c^2}{\mathbf{S}}^{-1}\mathbf{\Delta }{\mathbf{S}}^{-1}\right).$$

This completes the proof.

PROOF OF THEOREM 3.3. The asymptotic normality of α̂₀(u) and α̂(u) can be obtained by following the ideas in the proof of Theorem 3.1.

PROOF OF THEOREM 4.1. Use the same notation as in the proof of Theorem 3.2. Minimizing

$${\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}{\rho }_{{\tau }_k}\{Y_i-{\tilde{a}}_{0k}(U_i)-{\mathbf{X}}_i^T\tilde{\mathbf{a}}(U_i)-{\mathbf{Z}}_i^T\mathit{\beta }\}+\mathit{\text{nq}}{\displaystyle \sum _{j=1}^d}{p}_{{\mathrm{\lambda }}_j}^{\prime }\left(\left|{\beta }_j^{(0)}\right|\right)|{\beta }_j|$$

is equivalent to minimizing

$$\begin{array}{cc}{G}_n(\mathit{\theta })\hfill & ={\displaystyle \sum _{k=1}^q}{\displaystyle \sum _{i=1}^n}\{{\rho }_{{\tau }_k}({\epsilon }_i-c_k-{\tilde{r}}_{i,k}-{\mathbf{Z}}_i^T\mathit{\theta }/\sqrt{n})-{\rho }_{{\tau }_k}({\epsilon }_i-c_k-{\tilde{r}}_{i,k})\}+\mathit{\text{nq}}{\displaystyle \sum _{j=1}^d}{p}_{{\mathrm{\lambda }}_j}^{\prime }\left(\left|{\beta }_j^{(0)}\right|\right)(|{\beta }_j|-|{\beta }_{0j}|)\hfill \\ \hfill & =\frac{c}{2}{\mathit{\theta }}^T\mathbf{S}\mathit{\theta }+{\mathbf{W}}_n^T\mathit{\theta }+\mathit{\text{nq}}{\displaystyle \sum _{j=1}^d}{p}_{{\mathrm{\lambda }}_j}^{\prime }\left(\left|{\beta }_j^{(0)}\right|\right)(|{\beta }_j|-|{\beta }_{0j}|)+o_p(1),\hfill \end{array}$$

where $\mathit{\theta }=\sqrt{n}(\mathit{\beta }-{\mathit{\beta }}_0)\text{ and }{\tilde{r}}_{i,k}=\{{\tilde{a}}_{0k}(U_i)-{\alpha }_0(U_i)-c_k\}+{\mathbf{X}}_i^T\{\tilde{\mathbf{a}}(U_i)-\mathit{\alpha }(U_i)\}$. Similar to the derivation in the proof of Theorem 5 in Zou and Li [34], the third term above can be expressed as

$$\mathit{\text{nq}}{\displaystyle \sum _{j=1}^d}{p}_{{\lambda }_j}^{\prime }(|{\beta }_j^{(0)}|)(|{\beta }_j|-|{\beta }_{0j}|)\stackrel{𝒫}{\to }\{\begin{array}{cc}0,\hfill & \text{if}{\mathit{\beta }}_2={\mathit{\beta }}_{20},\hfill \\ \mathrm{\infty },\hfill & \text{otherwise}.\hfill \end{array}$$ (7.9)

Therefore, by the epiconvergence results [8, 15], we have ${\widehat{\mathit{\beta }}}_2^{\text{OSE}}\stackrel{𝒫}{\to }0$ and the asymptotic results for ${\widehat{\mathit{\beta }}}_1^{\text{OSE}}$ holds.

To prove sparsity, we only need to show that ${\widehat{\mathit{\beta }}}_2^{\text{OSE}}=0$ with probability tending to 1. It suffices to prove that if β_0j = 0, then $P({\widehat{\beta }}_j^{\text{OSE}}\ne 0)\to 0$. By using the fact that $|\frac{{\rho }_{\tau }(t_1)-{\rho }_{\tau }(t_2)}{t_1-t_2}|\le \text{max}(\tau ,1-\tau )<1$, if ${\widehat{\beta }}_j^{\text{OSE}}\ne 0$, then we must have $\sqrt{n}{p}_{{\lambda }_j}^{\prime }(|{\beta }_j^{(0)}|)<\frac{1}{n}{\displaystyle {\sum }_{i=1}^n|Z_{\mathit{\text{ij}}}|}$. Thus, we have $P({\widehat{\beta }}_j^{\text{OSE}}\ne 0)\le P(\sqrt{n}{p}_{{\lambda }_j}^{\prime }(|{\beta }_j^{(0)}|)<\frac{1}{n}{\displaystyle {\sum }_{i=1}^n|Z_{\mathit{\text{ij}}}|})$. However, under the assumptions, we have $\sqrt{n}{p}_{{\lambda }_j}^{\prime }(|{\beta }_j^{(0)}|)\to \mathrm{\infty }$. Therefore, $P({\widehat{\beta }}_j^{\text{OSE}}\ne 0)\to 0$. This completes the proof.