Statistical Fusion of Continuous Labels: Identification of Cardiac Landmarks

Abstract

Image labeling is an essential task for evaluating and analyzing morphometric features in medical imaging data. Labels can be obtained by either human interaction or automated segmentation algorithms. However, both approaches for labeling suffer from inevitable error due to noise and artifact in the acquired data. The Simultaneous Truth And Performance Level Estimation (STAPLE) algorithm was developed to combine multiple rater decisions and simultaneously estimate unobserved true labels as well as each rater's level of performance (i.e., reliability). A generalization of STAPLE for the case of continuous-valued labels has also been proposed. In this paper, we first show that with the proposed Gaussian distribution assumption, this continuous STAPLE formulation yields equivalent likelihoods for the bias parameter, meaning that the bias parameter—one of the key performance indices—is actually indeterminate. We resolve this ambiguity by augmenting the STAPLE expectation maximization formulation to include a priori probabilities on the performance level parameters, which enables simultaneous, meaningful estimation of both the rater bias and variance performance measures. We evaluate and demonstrate the efficacy of this approach in simulations and also through a human rater experiment involving the identification the intersection points of the right ventricle to the left ventricle in CINE cardiac data.

1. Introduction

Characterization of the morphometric features of the heart to assess its clinical condition (e.g., coronary heart disease, arrhythmia, traumatic injury) necessitates the labeling and delineation of structures of interest. Typically, short axis images showing the cross section of the heart perpendicular to long axis connecting the heart apex and base are delineated to locate the left ventricle and the right ventricle [1]. Many approaches to the clinical and scientific analysis of heart motion employ human experts to: (1) delineate the epicardium (the outer contour of the left ventricle), (2) delineate the endocardium (the inner contour of the left ventricle), and (3) identify the two insertion points where the right ventricle connects to the left. Naturally, the raters will introduce errors, generate ambiguous interpretation of structures, and (occasionally) make careless mistakes. Hence, performance level assessment is an important aspect of interpreting reported structures. Of course, identification of the true labels is of central importance as well [2].

The Simultaneous Truth And Performance Level Estimation (STAPLE) algorithm enables fusion of labeled datasets created by a number of raters or automated methods [3]. The statistical approach involves maximum likelihood function calculation by expectation maximization (EM) algorithm [4]. The method iteratively constructs the estimated truth and estimated performance parameters in E-step and M-step repeatedly until convergence, which works well for volumetric multi-atlas multi-label process [5], in the case where the rater performance is characterized by sensitivity and specificity related to the probability whether he could assign a voxel with its underlying true label.

The STAPLE algorithm can efficiently characterize multi-rater data for volumetric datasets such as the volume of the myocardium. However, label fusion for insertion points is not well captured by volumetric labels. The locations of the two RV (right ventricle) insertion points are indicated by directional vectors with continuous scalar elements in a K-dimensional vector space (usually K=2 in 2-D images). As a result, discrete volumetric label analysis is not a reasonable approximation for finding the truth and performance in continuous landmark identification.

Previous methods have been proposed to handle a one-dimensional continuous space (a single scalar) [6], with rater decisions assumed to follow Gaussian distribution—a reasonable assumption for the prior distribution. However, using an analogous implementation of EM algorithm as in the classic STAPLE approach, the continuous version of STAPLE algorithm yields an equal likelihood for any bias parameter, which means that this approach cannot be used to fully evaluate rater performance (i.e., if bias is considered part of rater performance). Since the identification of points in space represents a 2D or 3D continuous variable and since the existing approach does not handle rater bias correctly, a new continuous STAPLE algorithm must be developed.

Herein, we present an extension of the expectation maximization algorithm for continuous landmark identification, with Gaussian distribution priors and maximum a posteriori function evaluation, in order to achieve a combined result of the locations of RV insertion points from various rater decisions. As we will see, by adding another prior for the performance parameters and performing a pre-estimation process, the rater bias will update and finally converge to a reasonable evaluation result.

2. Theory

2.1 EM Algorithm for ML Estimation

Suppose we have hired R raters to perform the task of locating landmarks (e.g., the RV insertion points in short-axis CINE cardiac images). Let there be N true landmarks in a K-dimensional space. We assume each rater has constant bias and variance when locating all different landmarks.

Therefore, the truth matrix is

$$\mathit{\text{T}}=\left[\begin{array}{c}{\mathit{\text{t}}}_1^T\\ ⋮\\ {\mathit{\text{t}}}_i^T\\ ⋮\\ {\mathit{\text{t}}}_N^T\end{array}\right]={\left[\begin{array}{cccc}{t}_{11}& t_{12}& \cdots & t_{1K}\\ ⋮& ⋮& \cdots & ⋮\\ t_{i1}& t_{i2}& \cdots & t_{iK}\\ ⋮& ⋮& \cdots & ⋮\\ t_{N1}& t_{N2}& \cdots & t_{NK}\end{array}\right]}_{N\times K}{t}_{ik}\in ℝ$$ (1)

Each rater j gives a 2-D decision matrix point by point, and the 3-D N × K × R decision matrix is

$${\mathit{\text{D}}}_j=\left[\begin{array}{c}{\mathit{\text{d}}}_{j1}^T\\ ⋮\\ {\mathit{\text{d}}}_{ji}^T\\ ⋮\\ {\mathit{\text{d}}}_{jN}^T\end{array}\right]={\left[\begin{array}{cccc}{d}_{j11}& d_{j12}& \cdots & d_{j1K}\\ ⋮& ⋮& \cdots & ⋮\\ d_{ji1}& d_{ji2}& \cdots & d_{\mathit{\text{jiK}}}\\ ⋮& ⋮& \cdots & ⋮\\ d_{jN1}& d_{jN2}& \cdots & d_{\mathit{\text{jNK}}}\end{array}\right]}_{N\times K}{\mathit{\text{d}}}_{\mathit{\text{jik}}}\in ℝ,j=1,\dots ,R$$ (2)

Each rater's performance level is evaluated by θ_j = {μ_j, Σ_j}, where μ_j is a vector denoting the average bias of rater j and Σ_j is his K × K covariance matrix. Under a Gaussian distribution, we can model the probability density function (pdf) of rater j's decision for point i as

$$f({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i,{\mathit{\mu }}_j,{\mathbf{\sum }}_j)=\frac{1}{{(2\pi )}^{K/2}\sqrt{det({\mathbf{\sum }}_j)}}{e}^{-\frac{1}{2}{({\mathit{\text{d}}}_{ji}-({\mathit{\text{t}}}_i+{\mathit{\mu }}_j))}^T{{\mathbf{\sum }}_j}^{-1}({\mathit{\text{d}}}_{ji}-({\mathit{\text{t}}}_i+{\mathit{\mu }}_j))}$$ (3)

Now with θ = {θ₁, …, θ_j, …, θ_R}, by EM algorithm we will update θ⁽ⁿ⁾ as the result of the n-th iteration and finally get θ and T simultaneously.

As developed in the classic STAPLE paper [3], the expectation of the log likelihood function, i.e.,

$$Q_{ML}(\mathit{\theta }\mid {\mathit{\theta }}^{(n)})=E(lnf(\mathit{\text{D}},\mathit{\text{T}}\mid \mathit{\theta })\mid \mathit{\text{D}},{\mathit{\theta }}^{(n)})={\int }_{{ℝ}^{N\times K}}ln(f(\mathit{\text{D}},\mathit{\text{T}}\mid \mathit{\theta })f(\mathit{\text{T}}))f(\mathit{\text{T}}\mid \mathit{\text{D}},{\mathit{\theta }}^{(n)})d\mathit{\text{T}}$$ (4)

is to be maximized. Here we assume the distribution of truth ln f(T) is constant, such that it is the same as maximizing

$${\int }_{{ℝ}^{N\times K}}ln(f(\mathit{\text{D}}\mid \mathit{\text{T}},\mathit{\theta })f(\mathit{\text{T}}))f(\mathit{\text{T}}\mid \mathit{\text{D}},{\mathit{\theta }}^{(n)})d\mathit{\text{T}}$$ (5)

Assuming independence among different raters and among different landmarks, the first term in the integrand of (5) is just the Gaussian we assumed. The second term is

$$f(\mathit{\text{T}}\mid \mathit{\text{D}},{\mathit{\theta }}^{(n)})=\frac{f(\mathit{\text{T}},\mathit{\text{D}}\mid {\mathit{\theta }}^{(n)})}{f(\mathit{\text{D}}\mid {\mathit{\theta }}^{(n)})}=\frac{f(\mathit{\text{D}}\mid \mathit{\text{T}},{\mathit{\theta }}^{(n)})f(\mathit{\text{T}})}{{\int }_{{ℝ}^{N\times K}}f(\mathit{\text{D}}\mid \mathit{\text{T}}\prime ,{\mathit{\theta }}^{(n)})f(\mathit{\text{T}}\prime )d\mathit{\text{T}}\prime }=\frac{f(\mathit{\text{D}}\mid \mathit{\text{T}},{\mathit{\theta }}^{(n)})}{{\int }_{{ℝ}^{N\times K}}f(\mathit{\text{D}}\mid \mathit{\text{T}}\prime ,{\mathit{\theta }}^{(n)})d\mathit{\text{T}}\prime }=\prod _{\text{i}}\prod _{\text{j}}\frac{f({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i,{\mathit{\theta }}_j^{(n)})}{{\int }_{{ℝ}^K}f({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i^{\prime },{\mathit{\theta }}_j^{(n)})d{\mathit{\text{t}}}_i^{\prime }}$$ (6)

The weight of each landmark can be defined as

$$\begin{array}{c}{W}_i^{(n)}({\mathit{\text{t}}}_i)=\prod _{\text{j}}\frac{f({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i,{\mathit{\theta }}_j^{(n)})}{{\int }_{{ℝ}^K}f({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i^{\prime },{\mathit{\theta }}_j^{(n)})d{\mathit{\text{t}}}_i^{\prime }}\\ =\frac{1}{{(2\pi )}^{K/2}\sqrt{det({\mathit{\text{A}}}_i^{(n)})}}{e}^{-\frac{1}{2}{({\mathit{\text{t}}}_i-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})}^T{\mathit{\text{A}}}_i^{-1(n)}({\mathit{\text{t}}}_i-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})}\end{array}$$ (7)

where ${\mathit{\text{A}}}_i^{(n)}={({\sum }_{\text{j}}{{\mathbf{\sum }}_j}^{-1(n)})}^{-1}$ and ${\mathit{\text{b}}}_i^{(n)}={\sum }_j{{\mathbf{\sum }}_j}^{-1(n)}({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n)})$. After sufficient number of iterations, ${\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)}\to {\mathit{\text{A}}}_i^{(\infty )}{\mathit{\text{b}}}_i^{(\infty )}$, which is the estimated true position of landmark i.

This completes the so-called E-step. For the M-step, we need to update the performance parameters ${\mathit{\mu }}_j^{(n)}$ and Σ_j⁽ⁿ⁾ in each iteration. From (5) we have

$$\{{\mathit{\mu }}^{(n+1)},{\mathbf{\sum }}^{(n+1)}\}=argmax\sum _i\sum _j{\int }_{{ℝ}^K}lnf({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i,{\mathit{\theta }}_j)W_i^{(n)}({\mathit{\text{t}}}_i)d{\mathit{\text{t}}}_i$$ (8)

For each rater,

$$\begin{array}{c}\{{\mathit{\mu }}_j^{(n+1)},{{\mathbf{\sum }}_j}^{(n+1)}\}=argmax\sum _i{\int }_{{ℝ}^K}lnf({\mathit{\text{d}}}_{ji}\mid {\mathit{\text{t}}}_i,{\mathit{\theta }}_j)W_i^{(n)}({\mathit{\text{t}}}_i)d{\mathit{\text{t}}}_i\\ =argmax\sum _i{\int }_{{ℝ}^K}\left[-\frac{1}{2}lndet({\mathbf{\sum }}_j)-\frac{1}{2}{\left({\mathit{\text{d}}}_{ji}-({\mathit{\text{t}}}_i+{\mathit{\mu }}_j)\right)}^T{{\mathbf{\sum }}_j}^{-1}\left({\mathit{\text{d}}}_{ji}-({\mathit{\text{t}}}_i+{\mathit{\mu }}_j)\right)\right]W_i^{(n)}({\mathit{\text{t}}}_i)d{\mathit{\text{t}}}_i\\ ≕argmax{F}_j\end{array}$$ (9)

To find the maximum point of F_j, take the partial derivatives and set them to zero,

$$\begin{array}{c}\frac{\partial F_j}{\partial {\mathit{\mu }}_j}=0,\frac{\partial F_j}{\partial {\mathbf{\sum }}_j}=0\\ \therefore \{\begin{array}{c}{\mathbf{\mu }}_j^{(n+1)}=\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})\\ {\mathbf{\sum }}_j^{(n+1)}=\frac{1}{N}\sum _i[{\mathit{\text{A}}}_i^{(n)}+({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n+1)}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)}){({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n+1)}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})}^T]\end{array}\end{array}$$ (10)

Use these new parameters in E-step of next iteration for a new estimate of the truth, which is then used in calculation of newer parameters until convergence. Convergence is guaranteed by the nature of EM algorithm [7].

2.2 Bias Update Failure

By examining Equation (10) in detail, we see:

$${\mathit{\mu }}_j^{(n+1)}=\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})=\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{t}}}_i^{(n)})$$ (11)

Replacing ${\mathit{\mu }}_j^{(n+1)}$ by $\frac{1}{\text{N}}{\mathbf{\sum }}_i{\mathit{\mu }}_j^{(n+1)}$ yields

$$\frac{1}{N}\text{∑}_i{\mathit{\text{t}}}_i^{(n)}=\frac{1}{N}\text{∑}_i({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n+1)})$$ (12)

While the right side appears to be related to j, the left side is independent of j, which means that regardless of having different raters this quantity is always going to be the same after each iteration. We should also note that ${\mathit{\text{A}}}_i^{(n)}$ is actually not dependent on i. As a result, by plugging in the definition of ${\mathit{\text{A}}}_i^{(n)}$ and ${\mathit{\text{b}}}_i^{(n)}$ into Equation (11) we can deduce that

$$\begin{array}{c}{\mathit{\mu }}_j^{(n+1)}=\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{t}}}_i^{(n)})\\ =\frac{1}{N}\sum _i{\mathit{\text{d}}}_{ji}-\frac{{\mathit{\text{A}}}_i^{(n)}}{N}\sum _{i,j}{\mathbf{\sum }}_j^{-1(n)}({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n)})\\ =\frac{1}{N}\sum _i{\mathit{\text{d}}}_{ji}-\frac{{\mathit{\text{A}}}_i^{(n)}}{N}\sum _j{\mathbf{\sum }}_j^{-1(n)}\sum _i{\mathit{\text{t}}}_i^{(n-1)}\\ =\frac{1}{N}\sum _i{\mathit{\text{d}}}_{ji}-\frac{{\mathit{\text{A}}}_i^{(n)}}{N}{\mathit{\text{A}}}_i^{-1(n)}\sum _i{\mathit{\text{t}}}_i^{(n-1)}\\ =\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{t}}}_i^{(n-1)})=\cdots =\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{t}}}_i^{(0)})={\mathit{\mu }}_j^{(1)}\end{array}$$ (13)

Therefore, the first iteration (initialization) is going to determine the bias and it will not change from then on. Unless we are able to initialize the iteration with the correct bias, there will always be constant error from the truth.

This phenomenon can be interpreted in two ways. Intuitively, as each rater generates his “cluster” of points by making multiple decisions, the relative positions of all clusters is going to form a pattern. While the pattern shape is reflected in the variance, which can be evaluated by the EM algorithm, the pattern position can be located anywhere in the space. Corresponding to any point as truth in the space, there is a set of biases, which is acting equally in giving us the maximum likelihood function, as long as the pattern shape is not changed. There was no assumption to determine whether the true point location should be within the clusters or outside of them. Mathematically, according to [8], the EM algorithm is guaranteed to converge to a local optimum, while here any bias indicates a constant local optimum. This means that any bias is equivalent in characterizing the maximum of the likelihood function.

Since any bias will maximize the likelihood function, more assumptions are needed to further restrict the estimated bias.

2.3 EM Algorithm for MAP Estimation

Let us add a Gaussian prior for the bias parameter as follows

$$p({\mathit{\theta }}_j)=p({\mathit{\mu }}_j)=\frac{1}{\sqrt{2\pi {\sigma }_{{\mathit{\mu }}_j}^2}}{e}^{-\frac{1}{2{\sigma }_{{\mathit{\mu }}_j}^2}{({\mathit{\mu }}_j-{\mathit{\mu }}_{{\mathit{\mu }}_j})}^T({\mathit{\mu }}_j-{\mathit{\mu }}_{{\mathit{\mu }}_j})}$$ (14)

where μ_μj and σ_μj are the mean and standard deviation of rater j's bias parameter.

Now we seek to maximize the log of the a posteriori function [9-11]

$$Q_{\mathit{\text{MAP}}}(\mathit{\theta }\mid {\mathit{\theta }}^{(n)})=Q_{ML}(\mathit{\theta }\mid {\mathit{\theta }}^{(n)})+lnp(\mathit{\theta })$$ (15)

In equation (9), function F_j now becomes

$$F_j=\sum _i{\int }_{{ℝ}^K}\left[-\frac{1}{2}lndet({\mathbf{\sum }}_j)-\frac{1}{2}{\left({\mathit{\text{d}}}_{ji}-({\mathit{\text{t}}}_i+{\mathit{\mu }}_j)\right)}^T{{\mathbf{\sum }}_j}^{-1}\left({\mathit{\text{d}}}_{ji}-({\mathit{\text{t}}}_i+{\mathit{\mu }}_j)\right)\right]W_i^{(n)}({\mathit{\text{t}}}_i)d{\mathit{\text{t}}}_i+lnp({\mathit{\theta }}_j)$$ (16)

The E-step is the same as above but the M-step becomes

$$\{\begin{array}{c}{\mathit{\mu }}_j^{(n+1)}={(\mathit{\text{I}}+\frac{{\mathbf{\sum }}_j^{(n+1)}}{N{\sigma }_{{\mathit{\mu }}_j}^2})}^{-1}(\frac{1}{N}\sum _i({\mathit{\text{d}}}_{ji}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})+\frac{{\mathbf{\sum }}_j^{(n+1)}}{N{\sigma }_{{\mathit{\mu }}_j}^2}{\mathit{\mu }}_{{\mathit{\mu }}_j})\\ {\mathbf{\sum }}_j^{(n+1)}=\frac{1}{N}\sum _i[{\mathit{\text{A}}}_i^{(n)}+({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n+1)}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)}){({\mathit{\text{d}}}_{ji}-{\mathit{\mu }}_j^{(n+1)}-{\mathit{\text{A}}}_i^{(n)}{\mathit{\text{b}}}_i^{(n)})}^T]\end{array}$$ (17)

so that the constant bias problem no longer exists and we can get a meaningful solution for the MAP biases.

To perform this technique, μ_μj, ${\sigma }_{{\mathit{\mu }}_{\mathit{\text{j}}}}^2$ has to be determined in advance. Here we suggest two ways of doing this:

1. The Weak Prior – to assign the most probable values to them. Usually the rater may not deviate too far from the truth and their biases are very close to the zero vector. It is reasonable to let μ_μj be zero and σ_μj be large (e.g., 10 voxels etc.). As long as σ_μj is large enough, the estimated result will be good. However, if one rater has too large of a bias, which might happen when he misunderstands the labeling instructions or deliberately performs badly, the weak prior will probably cause the later EM iteration to misinterpret his large bias as a large variance.

2. The Data Adaptive Prior – to use a pre-estimation process to obtain a coarse estimate of the truth before EM iterations. The pre-estimation takes all rater decisions for one landmark and calculates a weighted average of its position iteratively, then uses the average rater deviation from the coarse truth as μ_μj. In each iteration, the distance of the rater decision from the current averaged coarse truth is computed, whose inverse is going to act as a weight of this rater in next iteration. Therefore, if the rater constantly deviates from the majority decisions, his decision will not affect the coarse truth very much and his pre-estimated bias μ_μj is going to be large, which distinguishes his large bias for later EM iterations.

3. Results

3.1 Rater Performance Simulations

To simulate the truth and rater performance, a random pattern with 50 point locations is drawn from a uniform independent 2-D random distribution in the range of [0, 100], which is represented in Figure 1 by circles. Meanwhile, 20 raters with manually chosen biases and variances are generated (Table 1 shows the first 4 rater parameters), as well as their performances (dots in Figure 1) on identifying all of the 50 points. The performances in this experiment are actually the deviations of the point position vectors from the 50 generated true locations and are drawn randomly from a 2-D Gaussian distribution density with means and variances the same as rater parameters. For visualization purposes 4 of the rater performances are shown with different symbols. It is easily seen the “triangle rater” (No.3 in Table 1) has a large bias and therefore his decision pattern is shifted toward the upper right corner, while the “x rater” (No.4 in Table 1) has a large variance and therefore his decision pattern is seriously scattered around.

Figure 1.

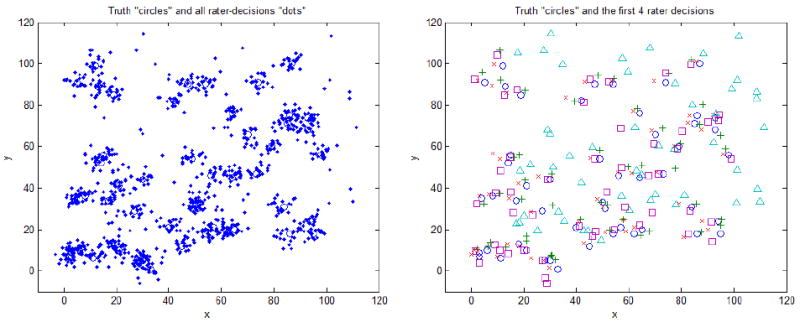
Simulated truth (circles) and rater decisions (dots) on the left and four of the raters' decisions denoted by different symbols (+, square, triangle, x). There are 50 points and 20 raters simulated. The “triangle rater” (No.3 below) has a large bias. Therefore his decision pattern is shifted toward the upper right corner.

Table 1.

The first four simulated rater performance parameters (biases and variances). Rater 3 has a large bias and rater 4 has a large variance.

Raters	1	2	3	4
Bias	[1,2]	[-3,1]	[15,15]	[-1,-1]
Variance

Figure 2 shows the estimated truth denoted by stars via EM ML estimation as in classic STAPLE comparing to the estimated truth using EM MAP estimation with data adaptive prior. In ML approach, since bias is not correctly updated, although the estimated distribution pattern is correct, this entire pattern is shifted by a certain amount dependent on initialization. In MAP approach however, the bias is dragged into the iteration process and everything is updating and converging to a reasonable result. The estimated parameters and the mean square errors are shown in Table 2 and 3, from which one can also observe the obvious correction introduced by EM MAP estimation.

Figure 2.

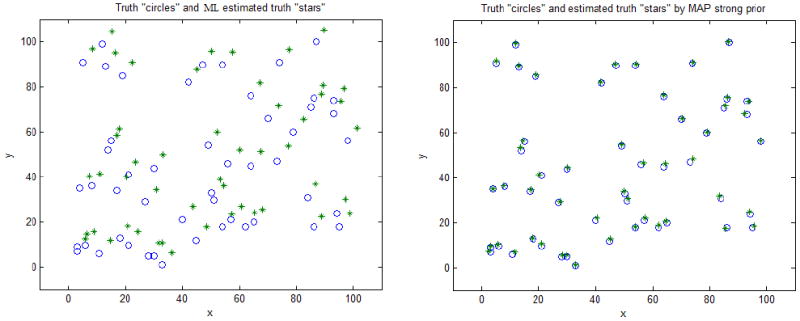
Estimated truth denoted by stars using EM ML estimation as in classic STAPLE (left) comparing to estimated truth using EM MAP estimation with data adaptive prior (right). In ML approach, the estimated distribution pattern seems to be correct, but is shifted to the upper right. In MAP approach, the bias gets properly estimated and everything is converging to a reasonable result.

Table 2.

Estimated first four rater performance parameters and the mean square errors in classic EM ML estimation. The bias is seriously deviated from the generated bias in Table 1 while the variance is quite close and characterized as a good approximation.

Raters	1	2	3	4	Total MSE
Estimated bias	[-2.3151, -3.2919]	[-6.2681, -4.7745]	[11.6347, 9.2363]	[-4.1992, -6.0098]	29.2464
Estimated variance					33.6249
Estimated truth					47.0750

Table 3.

Estimated first four rater performance parameters and the mean square errors in EM MAP estimation with data adaptive prior. The bias is closer to the generated bias comparing to the previous result, and the MSE is much smaller, which corrects the mistakes in ML approach.

Raters	1	2	3	4	Total MSE
Estimated bias	[0.9429, 1.8244]	[-3.0101, 0.3419]	[14.8927, 14.3526]	[-0.9412, -0.8934]	2.8105
Estimated variance					33.6249
Estimated truth					5.7861

3.2 Real Data Testing on Identification of RV Insertion Points

The high-resolution CINE MRI short axis images of the heart of a pig are obtained in a steady-state free suppression (SSFP) acquisition with breath holds on a commercial Philips 3T-Achieva whole body system. With 6 raters hired to identify 82 RV insertion points in 41 randomly selected slices, the ML MAP estimation process with data adaptive prior is implemented to analyze the underlying truth and rater performance level. From the 41 slices, the estimated results of 3 of them are shown in Figure 3, where the red “x” demonstrates all rater decisions, and the green “o” shows the EM MAP Continuous STAPLE fusion comparing to an expert's decision (yellow “x”) regarded as the underlying truth. The 3 examples are selected specifically to demonstrate cases in various practical situations. In the first image, although one rater deviates too much to the right, the fusion corrects his mistake and the estimated truth is put on the correct spot, almost hitting the expert decision. In the second image, when the raters' decisions are scattered around, fusion brings the result closer to the expert decision. In the last image, every rater deviates a certain amount to the same direction from the expert, inevitably causing the fusion also to deviate, while it is still brought close to the expert as much as possible by the estimation process.

Figure 3.

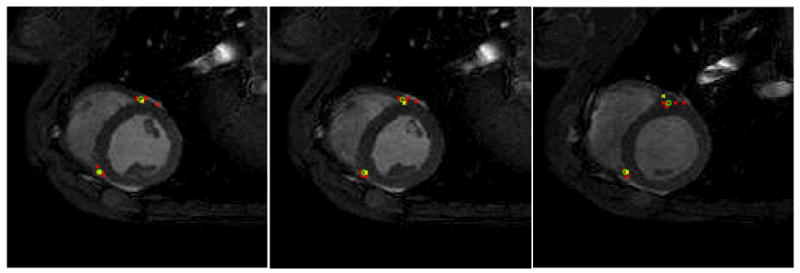
With 6 raters hired to identify 82 RV insertion points in 41 randomly selected pig heart slices, the analyzed results of 3 of the slices are shown, where the red “x” are all rater decisions, and the green “o” show the MAP Continuous STAPLE fusion comparing to an expert's decision (yellow “x”). In the first image, the fusion corrects the one rater's mistake that has deviated too much. In the second image, fusion brings the result closer to the expert decision than the scattered rater decisions. In the last image, although rater deviations cause the fusion also to deviate, it is still close to the expert decision.

4. Conclusion

This paper extends the classic STAPLE approach to continuous label spaces under a Gaussian distribution prior assumption. First, we described the EM algorithm for ML estimation in multi-dimensional continuous spaces. Then we stated the problem of the constant bias and demonstrated if nothing was to be done to prevent it, the result was going to deviate in any direction uncontrollably. Finally we suggested a solution by switching to MAP estimation and presented two techniques to obtain priors for the performance parameters.

It is essential to note that for a deviated pattern resulted from ML estimation, the unexpected shifting will not be easily predicted. The shifting depends on initialization and different initializations will cause different shifted positions (reflected in bias). However the estimated landmark distribution pattern, which reflects the relative positions among landmarks, is determined by the EM iterations, and it will not be affected by initialization (reflected in variance). Although the pattern is fixed by EM, the shifting cannot be ignored as it determines the real location, which is why classic ML estimation should be considered wrong in this case, or at least not sufficient.

With the MAP prior added, the bias problem is eventually fixed so that it can be considered a proper solution. For convenience, one could consider assigning only reasonable values for the bias mean and bias standard deviation as a weak prior, which is not only time-preserving but also appropriate as the raters usually do not have very large biases (large bias can only be achieved by a constant error). However, when a large bias case does appear, as a rater deliberately shifts his decision for whatever reason, the weak prior will be affected by this rater and not give as good result as a data adaptive prior obtained by weighted average pre-estimation process. The two approaches for getting MAP prior should be carefully considered before doing the analysis.

Future work includes finding a continuum between the two MAP priors, or any other possible relationship. Different priors will also affect the value of the likelihood function, as some prior will give larger likelihood value than others. Whether there exists a certain prior able to maximize the likelihood function among various priors is worth to explore. Moreover, when there is missing, partial, or repeated data existing, by simply ignoring the missing “holes” and recounting the repeated performances, this approach is no longer converging to the expected result. Comparing to the STAPLER solution developed recently [12], the approach is not robust enough since it requires too tight restrictions for rater performance times. A better solution to deal with the missing, partial, and repeated data in a continuous landmark space is still yet to be found.