A Stochastic Kinematic Model of Class Averaging in Single-Particle Electron Microscopy

Abstract

Single-particle electron microscopy is an experimental technique that is used to determine the 3D structure of biological macromolecules and the complexes that they form. In general, image processing techniques and reconstruction algorithms are applied to micrographs, which are two-dimensional (2D) images taken by electron microscopes. Each of these planar images can be thought of as a projection of the macromolecular structure of interest from an a priori unknown direction. A class is defined as a collection of projection images with a high degree of similarity, presumably resulting from taking projections along similar directions. In practice, micrographs are very noisy and those in each class are aligned and averaged in order to reduce the background noise. Errors in the alignment process are inevitable due to noise in the electron micrographs. This error results in blurry averaged images. In this paper, we investigate how blurring parameters are related to the properties of the background noise in the case when the alignment is achieved by matching the mass centers and the principal axes of the experimental images. We observe that the background noise in micrographs can be treated as Gaussian. Using the mean and variance of the background Gaussian noise, we derive equations for the mean and variance of translational and rotational misalignments in the class averaging process. This defines a Gaussian probability density on the Euclidean motion group of the plane. Our formulation is validated by convolving the derived blurring function representing the stochasticity of the image alignments with the underlying noiseless projection and comparing with the original blurry image.

1 Introduction

The field of microscopy consists of a very broad set of techniques used to visualize the surface, shape or interior structure of small objects. The main categories include optical, scanning probe, and electron microscopy. We begin with a broad overview of these different methods, and summarize some of the efforts within the robotics community to contribute to the advancement of microscopy. We then focus on our contribution, which is a method to increase the clarity in a particular method of microscopy called single-particle electron microscopy.

1.1 A General Overview of Microscopy Techniques

The mechanism of optical microscopy is relatively simple since it uses visible light and optical lenses. However, its resolution is usually limited to 0.2 μm due to the diffraction limit of visible light. Scanning probe and electron microscopy shows higher resolution down to atomic resolution. Scanning tunneling microscopy (STM) [4] and atomic force microscopy (AFM) [3] are instantiations of the scanning probe microscopy. In STM, the tunneling current between a scanning tip and the surface of objects is measured. This current induced by the quantum tunneling effect is a function of the distance between the probe tip and the surface of an object. The microscopic surface shape is computed from this current. In AFM, the sharp tip of a cantilever is kept in close proximity to the surface of the specimen and forces between the probe tip and the surface is maintained using feedback controllers, while the probe scans the surface. Electron microscopy (EM) uses electrostatic and electromagnetic lenses and electron beams to create high-resolution images of a specimen. Since the de Broglie wavelength of an electron is much shorter than that of visible light, higher resolution can be achieved in electron microscopy. In scanning electron microscopy (SEM), the electron beam scans a sample in a raster pattern and the resulting image is a high-resolution image of a sample's surface. In transmission electron microscopy (TEM), electrons are transmitted through and interact with the interior of samples. Then the electrons form an image on a detector, which shows the microscopic internal structure of samples as a projection modified by the transfer function of the microscope.

Robotics technologies and methodologies have been applied to microscopy in various ways. For example, a micro-nano control system has been designed for microscopic operation and has been attached to inverted microscopes for cell processing [10]. The mechanism of AFM intrinsically requires feedback control at the nanoscale and usually uses piezo-electric actuators to maintain constant contact forces. Schitter et al. [29] designed a new feedback controller for fast scanning AFM. Requicha et al. [26] developed algorithms and software for nano-manipulation with AFM and presented it to the robotics community. Martel et al. [21] designed a three-leg micro robot for nano-operation with STM. Kratochvil et al. [14] proposed a model-based method for visual tracking in SEM. In the present work, stochastic methods developed by the authors in the context of robot kinematics and motion planning are modified and applied to TEM.

1.2 Single-Particle Electron Microscopy

In single-particle electron microscopy, the goal is to reconstruct the three-dimensional (3D) density of biomolecular complexes from projection data obtained by TEM as shown in Fig. 1. Experimentally, many essentially identical copies of a complex of interest are embedded in a thin support layer. In cryo EM, the support layer consists of vitrified buffer formed by flash-cooling a solution. This specimen preparation is also done using a robot called a vitrification robot [9]. In the technique of negative staining the support layer consists of a dense metallic salt, and the density of the biomolecular complex is so much lower than the surrounding that it can be considered a void.

Figure 1.

Scheme of single-particle electron microscopy (a) Projections of identical randomly oriented macromolecular structures are obtained using an electron microscope. (b) The 3D structures are reconstructed from 2D electron micrographs.

If we consider the support layer to be in the x-y plane in the lab frame, then an electron beam takes projections of the density of the embedded biomolecular complexes along the z direction. In principle, the three-dimensional shape of the complex can be reconstructed using these projection images. The difference between this problem and computed tomography is that the projection angles are unknown a priori.

Typically the signal-to-noise ratio (SNR) in electron micrographs is extremely low [8]. In order to increase SNR, Jiang et al. [11] applied a bilateral filter to electron micrographs. As an indirect way of denoising, Mielikainen et al. [23] denoised sinograms of electron micrographs. In our work, instead of considering each electron micrograph, we will consider a group of images corresponding to the same (or quite similar) projection directions which are grouped together into a class and averaged to produce an averaged image called a class average. We use existing software to perform the classification. By averaging, the random noise in the background has a tendency to cancel, and the features of interest in the projections reinforce each other as the number of superimposed projections becomes large. This class averaging technique is useful for the 2D analysis of electron micrographs [8] as well as in 3D reconstruction [18, 19].

In most 3D EM reconstruction algorithms, an initial 3D density is derived and then iteratively refined [20,30–32,34]. To obtain a preliminary 3D density, the experimental single-particle images are aligned and classified. The images in each class are then averaged to yield characteristic views, and the 3D projection angles of each view are computed [8]. Once an initial 3D density is reconstructed, the steps of alignment, classification, angle assignment, and 3D reconstruction can be iterated to convergence, to yield a final density. Image alignment is a crucial step in both the classification and structure refinement steps, and the efficiency and accuracy of the alignment can therefore affect the overall performance of the 3D reconstruction process.

1.3 Our Stochastic Model

To image bio-macromolecular complexes, the electron dose is minimized to prevent damaging the specimen. This results in images with low signal-to-noise ratios. The high background noise complicates image alignment resulting in blurring relative to the true underlying image of interest. Consider the following image model:

$$\rho (x,t)={\rho }_0(g_t^{-1}\cdot \mathrm{x})+n(\mathrm{x},t),$$ (1)

where ρ is a single noisy image that is observed, ρ₀ is the underlying clear image which is sought, n is additive background noise with the mean m, g_t is a rigid-body transformation in SE(2) (the Lie group describing the translational and rotational motion on the plane) describing image alignment, $\mathbf{x}\in {\mathbb{R}}^2$ is the planar position of points in each image, and $t\in {\mathbb{Z}}^{+}$ is an artificial time variable used to order the images. The dot, ·, denotes the action of SE(2) on the plane ${\mathbb{R}}^2$:

$$g\cdot \mathbf{x}={(x\text{cos}\theta -y\text{sin}\theta +c_x,x\text{sin}\theta +y\text{cos}\theta +c_y)}^T$$ (2)

where $\mathbf{x}={(x,y)}^T\in {\mathbb{R}}^2$ and g is shorthand for

$$g(c_x,c_y,\theta )=\left(\begin{array}{ccc}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill & \hfill c_x\hfill \\ \hfill \sin \theta \hfill & \hfill \cos \theta \hfill & \hfill c_y\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill R\hfill & \hfill \mathbf{c}\hfill \\ \hfill 0^T\hfill & \hfill 1\hfill \end{array}\right).$$

The rigid-body misalignment of the t^th image is g_t = g(c_x(t), c_y(t), θ(t)) where c_x(t) and c_y(t) are respectively the translational misalignments in the x and y directions, and θ(t) is the rotational misalignment around the z axis.

If there were no noise term, then the appropriate matching of two images, ρ(x, t) and ρ(x, t′), occurs at g_t = g_t′ and the average is $(\rho (\mathbf{x},t)+\rho (\mathbf{x},t^{\prime }))∕2={\rho }_0\left(g_t^{-1}\mathbf{x}\right)$. However, if noise is present in the images, then the matching of many data images produces various g_t. The average will be of the form

$$\frac{1}{N}\sum _{t=1}^N\rho (\mathrm{x},t)\approx \frac{1}{N}\sum _{t=1}^N{\rho }_0(g_t^{-1}\cdot \mathrm{x})+m={\int }_{\mathrm{SE}\left(2\right)}\left(\frac{1}{N}\sum _{t=1}^N\delta (g_t^{-1}\circ g)\right){\rho }_0(g^{-1}\cdot \mathrm{x})dg+m,$$ (3)

where m is the mean of the noise, δ(g) is the Dirac impulse function, and the operation ffi denotes the group operation of SE(2). The integral over SE(2) is over c_x, $c_y\in \mathbb{R}$ and θ ∈ [0, 2π], and the volume element is dg = dc_xdc_ydθ. This dg is the associated invariant integration measure for SE(2) [7]. The first equality assumes that the noise term approximately becomes a spatially invariant constant during the average process. The second equality shows that this averaging process can be viewed as a convolution on the group of rigid-body motions of the plane, SE(2). The right hand side of the second equality in (3) is essentially the addition of the blurred version of ρ₀(x) depending on the distribution of members of the set {g_t} and the mean intensity of the background noise.

In the limit of a large number of images, the effect of the weighted sum of shifted Dirac δ functions under the integral in (3) is the same as that of an appropriate blurring kernel. This is not unique to the case of blurring over SE(2). For example, let $f(c_x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi \sigma }}\text{exp}[-{(c_x-\mu )}^2∕2{\sigma }^2]$ be a Gaussian distribution on the real line with mean μ and variance σ². This will also be written as f(c_x) for short. If c_x is sampled from f(c_x), then the law of large numbers dictates that for any well-behaved function ϕ(x),

$$\underset{N\to \infty }{\text{lim}}\frac{1}{N}\sum _{t=1}^N\varphi (x-c_x\left(t\right))=\underset{N\to \infty }{\text{lim}}{\int }_{\mathbb{R}}\left(\frac{1}{N}\sum _{t=1}^N\delta (y-c_x\left(t\right))\right)\varphi (x-y)dy={\int }_{\mathbb{R}}f\left(y\right)\varphi (x-y)dy,$$

where y is a dummy variable of integration, which can be replaced with c_x. This equality is not the same as saying that the sum of δ functions is equal to the blurring kernel, f(c_x). Rather, the average of many shifted copies of ϕ(x), each of the form ϕ(x−c_x(t)) with c_x(t) drawn independently and identically distributed according to the probability law defined by f(c_x), is equivalent to a convolution of f(·) and ϕ(·).

The replacement of sums over a large number of samples with integrals with respect to the probability densities from which samples are drawn is done all the time in the field of statistics. For example, if ψ₁(x) = x, the computed sample mean $\frac{1}{N}{\sum }_{t=1}^N{\psi }_1\left(x_t\right)$ approaches the true mean of f(x), ${\int }_{\mathbb{R}}f\left(x\right){\psi }_1\left(x\right)dx$. Or if ψ₂(x) = (x − μ)², then the sample variance approaches the actual covariance of f(x). Both statements being true in the limit as N → ∞.

Now we return to the specific topic of class averaging. In order to find the underlying image, ρ₀(x), we should solve the following inverse problem: Given a blurred image, γ(x), that describes the average of many experimentally-obtained projection images of a class, and given an estimate of the probability density function f(g) describing the error distribution in the alignment of these projection images, we seek to find the deblurred image ρ₀(x). This is expressed as the solution to the problem:

$${\int }_{\mathrm{SE}\left(2\right)}f\left(g\right){\rho }_0(g^{-1}\cdot \mathrm{x})dg+m=\gamma \left(\mathrm{x}\right),$$ (4)

where m is the mean of the additive background noise. Deconvolution over SE(2) is a direct tool for solving (4) [6, 16, 36]. However, the first step is to identify the blurring function, f(g), and how it relates to the experimental noise parameters. In this paper, we focus on characterizing the blurring function f(g) and estimating its parameters.

Relevant work appears in [2], in which the authors developed an algorithm to estimate the variances of translational and/or rotational misalignments using a Fourier-harmonic representation as well as the Fourier transform. While they assumed the misalignments are Gaussian, in our work we will derive the equations for misalignment distributions without the assumption of Gaussian distributions for misalignments, when the alignment is achieved by matching the mass centers and the principal axes of the experimental images. We then will rigorously show that the translational misalignment distribution is Gaussian and the rotational misalignment distribution can be modeled as a folded Gaussian, if the background noise is Gaussian.

2 Image alignment and class-averaged images

A standard way to align two images, ρ₁(x) and ρ₂(x), is by solving the following minimization problem:

$$\underset{g\in \mathrm{SE}\left(2\right)}{\text{min}}(\sum _i\Vert {\rho }_1\left({\mathrm{x}}_i\right)-{\rho }_2(g^{-1}\cdot {\mathrm{x}}_i){\Vert }^2).$$ (5)

Here the sum is taken over all pixels in the image plane. Even though there is substantial mathematical and computational machinery that has been developed to solve (5) [13, 27, 35], we use a simple alternative method to align two images; our alignments are achieved by matching the mass centers and the principal axes of the images. To implement this alignment method, each image is translated, rotated, and clipped by a circular window so that the resulting image has its center at the geometric center of the circular window and has a diagonal inertia matrix. The translation is implemented using cubic spline interpolation. The images are rotated by the three-shear-based rotation method [15].

This alignment method will give a quasi-optimal solution to (5). Although this alignment method still leads to blurred class averages, this method has the advantage that we can estimate the amount of blurriness using the information about the background noise. This will be explained in detail in Section 4. Here it is important to note that our alignment method is not meant to compete against existing alignment methods used for 3D reconstruction. Rather, our method can be used as a supporting tool. Importantly, as discussed below, we can apply our findings to aligned images that may be obtained by existing software tools such as EMAN [20], IMAGIC [32], SPIDER [30], and XMIPP [31].

Unlike matching the centers of mass of images, aligning the principal axis has an ambiguity, since an image has two equivalent principal axes whose directions are opposite to each other. In order to avoid this ambiguity, an additional process to choose a better direction of the principal axis is used. After the center matching, we rotate an image to align it to previously aligned images using the principal axis of the image. If the rotation angle is θ, then we check two possibilities: rotation by θ or θ + π. For these two cases, we measure the image difference between the average of previously aligned images and the image being aligned. We choose a rotation angle which results in lower image difference. The rotation of the first image can be either angle. This process to choose one angle from two candidates works well for the examples that will be presented in Section 5.

An application of this alignment method will be demonstrated using experimental single-particle EM images of purified, recombinantly expressed α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA)-selective ionotropic glutamate receptor in negative stain [22]. These receptors were composed of four GluA2 subunits that contained a glutamine at the Q/R site (GluA2-Q). The intact receptor has a relative molar mass of approximately 400kDa and dimensions of 190Å × 115Å × 100Å [22].¹ Receptors were stained with 2% (w/v) uranyl acetate and visualized on Kodak SO-163 film under low-dose conditions (< 10e⁻/Ų) at a magnification of 48,600× on a JEOL JEM-1010 electron microscope in the Rippel EM Facility at Dartmouth College. Negatives with minimal drift/astigmatism were identified and digitized using a Nikon Coolscan 8000 at 4000dpi (effective pixel size, 1.31Å). Particles were picked and processed using the EMAN package [20]. The individual images are 64×64 pixels with a pixel size of 5.24Å. The images were high passed filtered at 250Å and low passed filtered at 10.5Å. The contrast transfer function of the microscope was corrected and the phase flipping was applied to the individual images as described in [22].

The EM images are classified by EMAN and Fig.2(a) shows one image of a class. The SNR of this image is 0.45. We first align the class images by translating, rotating, and clipping using a circular window so that the resulting image has its center at the geometric center of the circular window and has the diagonal inertia matrix. Initially the size of the window is chosen to be radius=24 pixels. Fig. 2(c) is the edge detection of Fig. 2(b). The edge detector algorithm developed by Canny [5] is used. Based on this edge picture, the size of the window can be reduced to radius=19 pixels. As shown in Fig. 2(d), we can obtain a clearer class average with the smaller window, because a smaller amount of background noise will be included.

Figure 2.

An example of averaging in one class using different window sizes. (a) A single 64 × 64 image from a class. (b) A class average with a circular window (r = 24 pixels) after the proposed alignment method was applied. (c) The edge of (b) shows the size of the window can be reduced to r = 19 pixels. (d) A class average with a circular window (r = 19 pixels) that still contains the whole specimen.

3 Statistical analysis of background noise in EM images

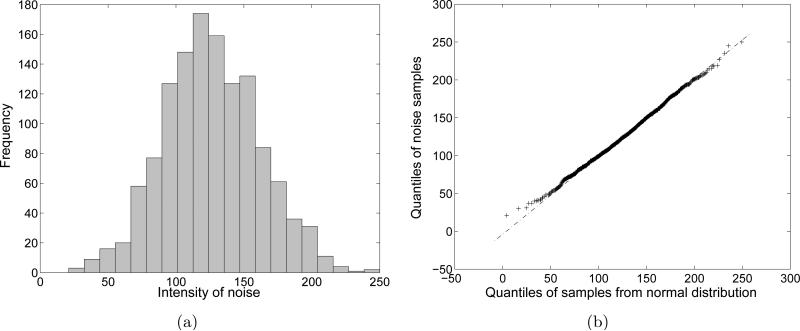
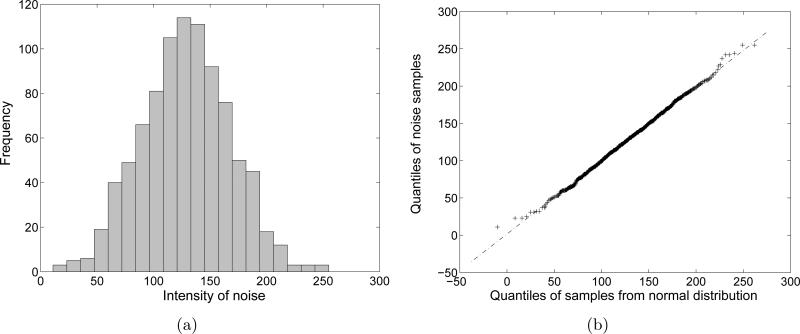
In this section, we analyze the background noise using experimental data which were used in Section 2. First of all, we sample the background noise around the edge of one noisy EM image. The number of samples is 1280. The histogram and the normal quantile-quantile (Q-Q) plot are shown in Fig. 3. The mean and the standard deviation of the distribution are 126.2789 and 35.4348, respectively. In order to plot the normal quantile-quantile plot, we drew 10000 samples from a normal distribution whose mean and standard deviation are the same as those of the noise samples. The normal quantile-quantile plot in Fig. 3(b) shows that relationship between the quantiles of the actual noise and the quantiles of the normal distribution. Since the Q-Q plot shows the linear relationship between the two sets of quantiles, treating the noise as Gaussian is justified. In addition, we sample the background noise at a specific position along the different images. The number of samples is 1000. The histogram and the normal quantile-quantile plot are shown in Fig. 4. As in Fig. 3, the noise samples form a Gaussian distribution.

Figure 3.

Statistics of background noise samples around the edge of a single EM image. (a) Histogram of the background noise samples. (b) A normal Q-Q plot of the background noise samples.

Figure 4.

Statistics of background noise samples at a specific pixel position from many EM images. (a) Histogram of the background noise samples. (b) A normal Q-Q plot of the background noise samples.

We also test the covariance between the noise samples. We consider a pixel and all nearest neighbors in images as the 3 × 3 patch:

$$Z=\left(\begin{array}{ccc}\hfill z_1\hfill & \hfill z_2\hfill & \hfill z_3\hfill \\ \hfill z_4\hfill & \hfill z_5\hfill & \hfill z_6\hfill \\ \hfill z_7\hfill & \hfill z_8\hfill & \hfill z_9\hfill \end{array}\right).$$ (6)

Here z₅ denotes the sample of the intensity of the central pixel, and all other z_i are samples of intensities of the surrounding pixels. Let us consider a vector

$$\mathbf{z}={\left(z_1{z}_2{z}_3{z}_4{z}_5{z}_6{z}_7{z}_8{z}_9\right)}^T.$$

We can sample z for the same location in different images. For example, the covariance matrix for 1000 samples of z is computed as

$$\sum =1000\times \left(\begin{array}{ccccccccc}\hfill 1.248\hfill & \hfill 0.896\hfill & \hfill 0.4533\hfill & \hfill 0.9136\hfill & \hfill 0.6943\hfill & \hfill 04147\hfill & \hfill 0.4377\hfill & \hfill 0.3501\hfill & \hfill 0.2997\hfill \\ \hfill 0.896\hfill & \hfill 1.3987\hfill & \hfill 0.9525\hfill & \hfill 0.7418\hfill & \hfill 1.0317\hfill & \hfill 0.7946\hfill & \hfill 0.455\hfill & \hfill 0.4953\hfill & \hfill 0.4723\hfill \\ \hfill 0.4533\hfill & \hfill 0.9525\hfill & \hfill 1.3424\hfill & \hfill 0.4292\hfill & \hfill 0.7756\hfill & \hfill 0.989\hfill & \hfill 0.3009\hfill & \hfill 0.4184\hfill & \hfill 0.5204\hfill \\ \hfill 0.9136\hfill & \hfill 0.7418\hfill & \hfill 04292\hfill & \hfill 1.3081\hfill & \hfill 0.9399\hfill & \hfill 0.4918\hfill & \hfill 0.9165\hfill & \hfill 0.6595\hfill & \hfill 0.3961\hfill \\ \hfill 0.6943\hfill & \hfill 1.0317\hfill & \hfill 0.7756\hfill & \hfill 0.9399\hfill & \hfill 1.4131\hfill & \hfill 1.0245\hfill & \hfill 0.7502\hfill & \hfill 0.986\hfill & \hfill 0.7912\hfill \\ \hfill 0.4147\hfill & \hfill 0.7946\hfill & \hfill 0.989\hfill & \hfill 0.4918\hfill & \hfill 1.0245\hfill & \hfill 1.4195\hfill & \hfill 0.4497\hfill & \hfill 0.7563\hfill & \hfill 1.0863\hfill \\ \hfill 0.4377\hfill & \hfill 0.455\hfill & \hfill 0.3009\hfill & \hfill 0.9165\hfill & \hfill 0.7502\hfill & \hfill 0.4497\hfill & \hfill 1.3606\hfill & \hfill 0.962\hfill & \hfill 0.5196\hfill \\ \hfill 0.3501\hfill & \hfill 0.4953\hfill & \hfill 0.4184\hfill & \hfill 0.6595\hfill & \hfill 0.986\hfill & \hfill 0.7563\hfill & \hfill 0.962\hfill & \hfill 1.4303\hfill & \hfill 1.0534\hfill \\ \hfill 0.2997\hfill & \hfill 0.4723\hfill & \hfill 0.5204\hfill & \hfill 0.3961\hfill & \hfill 0.7912\hfill & \hfill 1.0863\hfill & \hfill 0.5196\hfill & \hfill 1.0534\hfill & \hfill 1.5745\hfill \end{array}\right),$$ (7)

when we use the EM images that were used in Section 2. Using five correlation coefficients between the samples z_i, we have a model for the covariance matrix as

$$\sum ={\sigma }^2\left(\begin{array}{ccccccccc}\hfill 1\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_5\hfill \\ \hfill {\nu }_1\hfill & \hfill 1\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_4\hfill \\ \hfill {\nu }_3\hfill & \hfill {\nu }_1\hfill & \hfill 1\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_5\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_3\hfill \\ \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_4\hfill & \hfill 1\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_4\hfill \\ \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill 1\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill \\ \hfill {\nu }_4\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_1\hfill & \hfill 1\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill \\ \hfill {\nu }_3\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_5\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_4\hfill & \hfill 1\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_3\hfill \\ \hfill {\nu }_4\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill 1\hfill & \hfill {\nu }_1\hfill \\ \hfill {\nu }_5\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_4\hfill & \hfill {\nu }_2\hfill & \hfill {\nu }_1\hfill & \hfill {\nu }_3\hfill & \hfill {\nu }_1\hfill & \hfill 1\hfill \end{array}\right).$$ (8)

With the assumption of isotropic noise, the coefficients are defined as

$$\begin{array}{cc}\hfill {\nu }_1& =\text{COR}(z_1,z_2)=\text{COR}(z_1,z_4)=\text{COR}(z_2,z_3)=\text{COR}(z_2,z_5)=\text{COR}(z_3,z_6)=\text{COR}(z_4,z_5)=\text{COR}(z_4,z_7)=\text{COR}(z_5,z_6)=\text{COR}(z_5,z_8)=\text{COR}(z_6,z_9)=\text{COR}(z_7,z_8)=\text{COR}(z_8,z_9),\hfill \\ \hfill {\nu }_2& =\text{COR}(z_1,z_5)=\text{COR}(z_2,z_4)=\text{COR}(z_2,z_6)=\text{COR}(z_3,z_5)=\text{COR}(z_4,z_8)=\text{COR}(z_5,z_7)=\text{COR}(z_5,z_9)=\text{COR}(z_6,z_8),\hfill \\ \hfill {\nu }_3& =\text{COR}(z_1,z_3)=\text{COR}(z_1,z_7)=\text{COR}(z_2,z_8)=\text{COR}(z_3,z_9)=\text{COR}(z_4,z_6)=\text{COR}(z_7,z_9),\hfill \\ \hfill {\nu }_4& =\text{COR}(z_1,z_6)=\text{COR}(z_1,z_8)=\text{COR}(z_2,z_7)=\text{COR}(z_2,z_9)=\text{COR}(z_3,z_4)=\text{COR}(z_3,z_8)=\text{COR}(z_4,z_9)=\text{COR}(z_6,z_7),\hfill \\ \hfill {\nu }_5& =\text{COR}(z_1,z_9)=\text{COR}(z_3,z_7),\hfill \end{array}$$

where

$$\text{COR}(z_i,z_j)=\frac{\text{cov}(z_i,z_j)}{\sqrt{\text{var}\left(z_i\right)\text{var}\left(z_j\right)}},$$

and cov(z_i, z_j) and var(z_i) denote the covariance and the variance, respectively.

By matching (7) and (8), we have

$$\sigma =37.2587,{\nu }_1=0.7054,{\nu }_2=0.5369,{\nu }_3=0.3503,{\nu }_4=0.3049,{\nu }_5=0.2165.$$

With these parameter values, the normalized lease squared error between (7) and (8) is 0.0615.

We can increase the size of the sampling patch (6). For instance, if we use a 5 × 5 patch for sampling, we need to employ nine additional correlation coefficients. From the sample covariance matrix, these additional correlations are determined as less than 0.1. If we ignore small correlations less than 0.1, the covariance model (8) is enough. This compromise is reasonable, because more correlation coefficients complicate the computation. Therefore, we will use the covariance model (8) for estimating of the blurring function in the next section.

4 Estimation of the misalignment and the blurring function

In this section, we derive the equations for the means and variances of the misalignments in translation and rotation under the assumption that the noise is additive and Gaussian, and the noisy images share the same underlying clear image. As mentioned in Section 2, the noisy images in a class are aligned so that they have their mass centers at the center of the circular window and have diagonal inertia matrices. This alignment method is expected to give a near-optimal solution to (5). Even though this solution may not be truly optimal, and therefore can lead to more blurring effects on the class average, this alignment method has the advantage that we can quantitatively estimate the blurring function as will be shown in Section 4.2 – 4.4. And therefore, in principle the blurring effects associated with this alignment scheme can be removed by deconvolution on SE(2).

4.1 Higher moments of Gaussian distributions

When we identify the blurring function in the class averaging process, the main task is to estimate the parameters of the blurring function which is a distribution function of the misalignment. In the derivation of the equation for the parameters, calculation of higher moments of Gaussian functions is the crucial component.

We consider the additive ergodic Gaussian noise, n(x, t) in (1), the mean and the variance of which are m and σ², respectively;

$${\langle n(\mathbf{x},t)\rangle }_S=m\text{and}{\langle n(\mathbf{x},t)\rangle }_T=m$$ (9)

and

$${\langle {(n(\mathbf{x},t)-m)}^2\rangle }_S={\sigma }^2\text{and}{\langle {(n(\mathbf{x},t)-m)}^2\rangle }_T={\sigma }^2,$$

where 〈·〉_T and 〈·〉_S denote the average in the “time” and the space domains, respectively. Note that the mean intensity, m, in the EM images is not zero as seen in Section 3. It corresponds to a gray color and its value is around 128 (the middle intensity) in 8-bit gray scale images.

For two pixel locations, x_i and x_j, consider noise samples, n_i ≡ n(x_i, t) and n_j ≡ n(x_j, t). The covariance between (n_i − m) and (n_j − m) is 〈(n_i − m)(n_j − m)〉_T = ν_ijσ², where ν_ij is the correlation between (n_i − m) and (n_j − m). Using this, we have

$$\langle n_i{n}_j\rangle =\langle (n_i-m)(n_j-m)\rangle +m\langle n_i\rangle +m\langle n_j\rangle -m^2={\nu }_{ij}{\sigma }^2+m^2.$$ (10)

For convenience, henceforth we will use the description 〈·〉 instead of 〈·〉_T , because we only need the expectation in the “time” domain.

As seen in Section 3, there are seven cases for ν_ij as

$${\nu }_{ij}=\{\begin{array}{cc}1\hfill & \text{if}{\mathbf{x}}_i={\mathbf{x}}_j\hfill \\ {\nu }_1\hfill & \text{if}(i,j)\in S_1\hfill \\ {\nu }_2\hfill & \text{if}(i,j)\in S_2\hfill \\ {\nu }_3\hfill & \text{if}(i,j)\in S_3\hfill \\ {\nu }_4\hfill & \text{if}(i,j)\in S_4\hfill \\ {\nu }_5\hfill & \text{if}(i,j)\in S_5\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (11)

where ν_ij are the correlation coefficients between n_i and n_j which are noise samples at x_i and x_j, respectively. The sets S_k (k = 1, 2, ..., 5) are defined as

$$\begin{array}{c}\hfill S_1=\{(i,j)\mid {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2=1\},\hfill \\ \hfill S_2=\{(i,j)\mid {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2=2\},\hfill \\ \hfill S_3=\{(i,j)\mid {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2=4\},\hfill \\ \hfill S_4=\{(i,j)\mid {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2=5\},\hfill \\ \hfill S_5=\{(i,j)\mid {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2=8\}.\hfill \end{array}$$ (12)

Note that the distance between two adjacent grid points is set to be one.

The third order moment of Gaussian random variables is zero as

$$\langle (n_i-m)(n_j-m)(n_k-m)\rangle =0.$$

Using the linearity of the average operator, we compute

$$\langle (n_i-m)(n_j-m)(n_k-m)\rangle =\langle n_i{n}_j{n}_k\rangle -m\langle n_i{n}_j\rangle -m\langle n_i{n}_k\rangle -m\langle n_j{n}_k\rangle +m^2\langle n_i\rangle +m^2\langle n_j\rangle +m^2\langle n_k\rangle -m^3=0.$$

Therefore

$$\langle n_i{n}_j{n}_k\rangle =m{\sigma }^2({\nu }_{ij}+{\nu }_{ik}+{\nu }_{jk})+m^3.$$ (13)

The fourth order moment of Gaussian random variables is computed as

$$\langle (n_i-m)(n_j-m)(n_k-m)(n_1-m)\rangle ={\sigma }^4({\nu }_{ij}{\nu }_{kl}+{\nu }_{ik}{\nu }_{jl}+{\nu }_{il}{\nu }_{jk}).$$ (14)

In analogy with the way that (13) was derived, we expand (14) as

$$\begin{array}{c}\hfill \langle (n_i-m)(n_j-m)(n_k-m)(n_l-m)\rangle =\langle n_i{n}_j{n}_k{n}_l\rangle -m\langle n_i{n}_j{n}_k\rangle -m\langle n_i{n}_j{n}_l\rangle \hfill \\ \hfill -m\langle n_i{n}_k{n}_l\rangle -m\langle n_j{n}_k{n}_l\rangle +m^2(\langle n_i{n}_j\rangle +\langle n_i{n}_k\rangle +\langle n_i{n}_l\rangle +\langle n_j{n}_k\rangle +\langle n_j{n}_l\rangle +\langle n_k{n}_l\rangle )\hfill \\ \hfill -m^3(\langle n_i\rangle +\langle n_j\rangle +\langle n_k\rangle +\langle n_l\rangle )+m^4.\hfill \end{array}$$ (15)

Using (10), (13), (14) and (15), we have

$$\langle n_i{n}_j{n}_k{n}_l\rangle ={\sigma }^4({\nu }_{ij}{\nu }_{kl}+{\nu }_{ik}{\nu }_{jl}+{\nu }_{il}{\nu }_{jk})+m^2{\sigma }^2({\nu }_{ij}+{\nu }_{ik}+{\nu }_{il}+{\nu }_{jk}+{\nu }_{jl}+{\nu }_{kl})+m^4.$$ (16)

4.2 Distribution of translational misalignment

We denote the clean (without noise) image by ρ₀(x) and we assume that the mass center of ρ₀(x) is placed at (0, 0):

$$\frac{\sum _i{\mathbf{x}}_i{\rho }_0\left({\mathbf{x}}_i\right)}{\sum _i{\rho }_0\left({\mathbf{x}}_i\right)}=0.$$ (17)

Here ${\mathbf{x}}_i\in {\mathbb{R}}^2$ denotes the position of the i^th pixel in the image. For convenience, when we consider an N × N image, the origin of the coordinate system is placed at the center of an N × N square grid and each pixel is assigned to one grid point. The distance between two adjacent grid points is set to be unit length, and the coordinates of pixels can be written as

$${\mathbf{x}}_i={(x_i,y_i)}^T={(p-(N+1)∕2,q-(N+1)∕2)}^T,$$ (18)

where i = N(p − 1) + q for p, q = 1, 2, ..., N. Let us consider a circular window whose center is placed at (0, 0). The summation of the coordinates of the grid points enclosed by the window can be calculated as

$$\sum _{i\in W}{\mathbf{x}}_i=\sum _{i\in W}{(x_i,y_i)}^T=0,$$ (19)

where W denotes a set of grid points enclosed by the circular window. We used the geometric symmetry of the circular window for this calculation. Similarly, we have

$$\sum _{i\in W}{x}_i,y_i=0.$$ (20)

We will often use (19) and (20) in the upcoming calculations. For convenience, we will use the expression ${\sum }_i$ instead of ${\sum }_{i\in W}$, because all summations should be done in the circular window domain afterwards.

As stated in (1), the noisy images can be modeled as

$$\rho (\mathbf{x},t)={\rho }_0\left(R^T\left(t\right)(\mathbf{x}-\mathbf{c}\left(t\right))\right)+n(\mathbf{x},t),$$ (21)

where R(t) is the 2 × 2 rotation matrix and c(t) is a 2D translation vector. R(t) and c(t) respectively represent the rotational and translational parts of the rigid-body alignment of the images, g_t. In this paper, this alignment is achieved by matching the mass centers and the principal axes of the images.

When we average many noisy images, the noise term will vanish and the underlying clean image will be intensified. However, due to the effect of R(t) and c(t), the averaged image is blurred. Here we first determine the distribution of c(t) in the case of the additive Gaussian background noise.

Since c(t) is determined so that the mass center of the windowed noisy image is placed at the origin, we have

$$\begin{array}{c}\hfill 0=\sum _i{\mathbf{x}}_i\rho ({\mathbf{x}}_i,t)=\sum _i{\mathbf{x}}_i{\rho }_0\left(R^T({\mathbf{x}}_i-\mathbf{c}\left(t\right))\right)+\sum _i{\mathbf{x}}_{i}n({\mathbf{x}}_i,t)\hfill \\ \hfill =\sum _i{R}^T{\mathbf{y}}_i{\rho }_0\left({\mathbf{y}}_i\right)+\mathbf{c}\left(t\right)\sum _i{\rho }_0\left({\mathbf{y}}_i\right)+\sum _i{\mathbf{x}}_{i}n({\mathbf{x}}_i,t)=\mathbf{c}\left(t\right)\sum _i{\rho }_0\left({\mathbf{x}}_i\right)+\sum _i{\mathbf{x}}_{i}n({\mathbf{x}}_i,t).\hfill \end{array}$$

We used the change of variables, y_i = R^T (x_i − c) and the fact that ${\sum }_i{\mathbf{y}}_i{\rho }_0\left({\mathbf{y}}_i\right)=0$. Therefore, the translational misalignment can be written as

$$\mathbf{c}\left(t\right)={(c_x\left(t\right),c_y\left(t\right))}^T=-\frac{\sum _i{\mathbf{x}}_i{n}_i}{\sum _i{\rho }_0\left({\mathbf{x}}_i\right)},$$ (22)

where n_i = n(x_i, t). It is obvious that c_x(t) is Gaussian distributed, because it is a weighted sum of Gaussian variables. c_y(t) also is Gaussian distributed.

The mean of c(t) is computed as

$$\langle \mathbf{c}\rangle =-\frac{\sum _i\langle n_i\rangle {\mathbf{x}}_i}{\sum _i{\rho }_0\left({\mathbf{x}}_i\right)}=-\frac{m\sum _i{\mathbf{x}}_i}{\sum _i{\rho }_0\left({\mathbf{x}}_i\right)}=0,$$

since ${\sum }_i{\mathbf{x}}_i=0$. The covariance of c(t) is computed as

$$\begin{array}{c}\hfill \langle {\mathbf{cc}}^T\rangle =\frac{\sum _{i,j}\langle n_i{n}_j\rangle {\mathbf{x}}_i{\mathbf{x}}_j^T}{M^2}=\frac{\sum _{i,j}({\nu }_{ij}{\sigma }^2+m^2){\mathbf{x}}_i{\mathbf{x}}_j^T}{M^2}\hfill \\ \hfill =\frac{{\sigma }^2}{M^2}\sum _{i,j}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T+\sum _{i,j}{m}^2{\mathbf{x}}_i{\mathbf{x}}_j^T=\frac{{\nu }_s{\sigma }^2}{M^2}\sum _i{\mathbf{x}}_i{\mathbf{x}}_j^T,\hfill \end{array}$$ (23)

where ν_s = (1 + 4ν₁ + 4ν₂ + 4ν₃ + 8ν₄ + 4ν₅) and $M={\sum }_i{\rho }_0\left({\mathbf{x}}_i\right)$. We used (10), (19) and the calculation of ${\sum }_{i,j}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T$ which is derived in detail in Appendix A. The variances of the components of c(t) = (c_x(t), c_y(t))^T are

$$\langle c_x^2\rangle =\frac{{\nu }_s{\sigma }^2}{M^2}\sum _i{x}_i^2\text{and}\langle c_y^2\rangle =\frac{{\nu }_s{\sigma }^2}{M^2}\sum _i{y}_i^2.$$ (24)

Considering (18) and the circular window centered at the origin, it follows that ${\sum }_i{x}_i^2={\sum }_i{y}_i^2$. Therefore we have $\langle c_x^2\rangle =\langle c_y^2\rangle$. The off-diagonal term in (23) is computed as

$$\langle c_x{c}_y\rangle =\frac{{\nu }_s{\sigma }^2}{M^2}\sum _i{x}_i{y}_i=0.$$ (25)

We cannot directly compute $M={\sum }_i{\rho }_0\left({\mathbf{x}}_i\right)$, because we do not have ρ₀(x_i) yet. This can be estimated using

$$\langle \sum _i\rho ({\mathbf{x}}_i,t)\rangle =\sum _i{\rho }_0\left({\mathbf{x}}_i\right)+\sum _i\langle n({\mathbf{x}}_i,t)\rangle =\sum _i{\rho }_0\left({\mathbf{x}}_i\right)+mG,$$

where m is the mean of the background noise and G is the number of grid points enclosed by the circular window. Therefore, $M=\langle {\sum }_i\rho ({\mathbf{x}}_i,t)\rangle -mG$.

For example, the variances of the translational misalignments for the case of Fig. 2(d) is 1.2090. Again, the length of the adjacent pixels was set to be one.

4.3 Distribution of rotational misalignment

In this subsection, we determine the distribution of rotational misalignment. The inertia matrix of the noisy image ρ(x_i, t) is defined as

$$J\left(t\right)=\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T\rho ({\mathbf{x}}_i,t).$$

Using (21), this inertia matrix can be rewritten as

$$\begin{array}{c}\hfill J\left(t\right)=\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T{\rho }_0\left(R^T\left(t\right)({\mathbf{x}}_i-\mathbf{c}\left(t\right))\right)+\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^{T}n({\mathbf{x}}_i,t)\hfill \\ \hfill =\frac{1}{M}\sum _i(R\left(t\right){\mathbf{x}}_i+\mathbf{c}\left(t\right)){(R\left(t\right){\mathbf{x}}_i+\mathbf{c}\left(t\right))}^T{\rho }_0\left({\mathbf{x}}_i\right)+\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^{T}n({\mathbf{x}}_i,t)\hfill \\ \hfill =R\left(t\right)J_0{R}^T\left(t\right)+\mathbf{c}\left(t\right)\mathbf{c}{\left(t\right)}^T+\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^{T}n({\mathbf{x}}_i,t)\hfill \end{array}$$

where $J_0=\frac{1}{M}{\sum }_i{\mathbf{x}}_i{\mathbf{x}}_i^T{\rho }_0\left({\mathbf{x}}_i\right)$ and $M={\sum }_i{\rho }_0\left({\mathbf{x}}_i\right)$.

Since the rotation, R(t), is determined so that J(t) is diagonal, J(t) can be written as

$$J\left(t\right)=\left(\begin{array}{cc}\hfill L_1\left(t\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L_2\left(t\right)\hfill \end{array}\right)=R\left(t\right)J_0{R}^T\left(t\right)+\mathbf{c}\left(t\right)\mathbf{c}{\left(t\right)}^T+\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^{T}n({\mathbf{x}}_i,t).$$ (26)

If ||θ|| << 1 and

$$J_0=\left(\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2\hfill \end{array}\right),$$

then

$$\begin{array}{c}\hfill R\left(t\right)J_0{R}^T\left(t\right)=\left(\begin{array}{cc}\hfill \cos \theta \left(t\right)\hfill & \hfill -\sin \theta \left(t\right)\hfill \\ \hfill \sin \theta \left(t\right)\hfill & \hfill \cos \theta \left(t\right)\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2\hfill \end{array}\right)\left(\begin{array}{cc}\hfill \cos \theta \left(t\right)\hfill & \hfill \sin \theta \left(t\right)\hfill \\ \hfill -\sin \theta \left(t\right)\hfill & \hfill \cos \theta \left(t\right)\hfill \end{array}\right)\hfill \\ \hfill \approx \left(\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill ({\lambda }_1-{\lambda }_2)\theta \left(t\right))\hfill \\ \hfill ({\lambda }_1-{\lambda }_2)\theta \left(t\right))\hfill & \hfill {\lambda }_2\hfill \end{array}\right).\hfill \end{array}$$

The mean of J(t) is

$$\begin{array}{c}\hfill \langle J\rangle =\left(\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill ({\lambda }_1-{\lambda }_2)\langle \theta \rangle \hfill \\ \hfill ({\lambda }_1-{\lambda }_2)\langle \theta \left(t\right)\rangle \hfill & \hfill {\lambda }_2\hfill \end{array}\right)+\langle {\mathbf{cc}}^T\rangle +\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T\langle n_i\rangle \hfill \\ \hfill =\left(\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill ({\lambda }_1-{\lambda }_2)\langle \theta \rangle \hfill \\ \hfill ({\lambda }_1-{\lambda }_2)\langle \theta \rangle \hfill & \hfill {\lambda }_2\hfill \end{array}\right)+\frac{{\nu }_s{\sigma }^2+mM}{M^2}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T=\left(\begin{array}{cc}\hfill \langle L_1\rangle \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \langle L_2\rangle \hfill \end{array}\right),\hfill \end{array}$$ (27)

where ν_s = (1 + 4ν₁ + 4ν₂ + 4ν₃ + 8ν₄ + 4ν₅). Since ${\sum }_i{\mathbf{x}}_i{\mathbf{x}}_i^T$ is diagonal, it is clear that 〈θ〉 = 0. We can also estimate (λ₁ − λ₂) as

$$({\lambda }_1-{\lambda }_2)=\langle L_1\rangle -\langle L_2\rangle .$$ (28)

Looking at the off-diagonal component of (26), we have

$$({\lambda }_1-{\lambda }_2)\theta \left(t\right)=-c_x\left(t\right)c_y\left(t\right)-\frac{1}{M}\sum _i{x}_i{y}_{i}n({\mathbf{x}}_i,t).$$ (29)

The mean of θ(t) is computed as

$$\langle \theta \rangle =-\frac{1}{({\lambda }_1-{\lambda }_2)}\langle c_x{c}_y\rangle -\frac{1}{M({\lambda }_1-{\lambda }_2)}\sum _i{x}_i{y}_i\langle n_i\rangle =0,$$

using (20) and (25). The variance of θ(t) is computed as

$$\langle {\theta }^2\rangle =\frac{1}{{({\lambda }_1-{\lambda }_2)}^2}\left(\langle c_x{c}_y{c}_x{c}_y\rangle +\frac{1}{M^2}\sum _{ij}\langle n_i{n}_j\rangle x_i{y}_i{x}_j{y}_j+\frac{2}{M}\sum _i{x}_i{y}_i\langle n_i{c}_x{c}_y\rangle \right).$$

Using (16), (22), (41), (42) and (43), we have

$$\langle c_x{c}_y{c}_x{c}_y\rangle =\frac{1}{M^4}\sum _{i,j,k,l}\langle n_i{n}_j{n}_k{n}_l\rangle x_i{y}_j{x}_k{y}_l=\frac{{\nu }_s^2{\sigma }^4}{M^4}\sum _i{x}_i^2\sum _j{y}_j^2,$$

where ν_s = (1 + 4ν₁ + 4ν₂ + 4ν₃ + 8ν₄ + 4ν₅). In addition, using (10) and (44), we compute

$$\frac{1}{M^2}\sum _{i,j}\langle n_i{n}_j\rangle x_i{y}_i{x}_j{x}_j=\frac{{\nu }_s{\sigma }^2}{M^2}\sum _i{x}_i^2{y}_i^2.$$

Using (13), (22) and (43), we have

$$\begin{array}{c}\hfill \langle n_i{c}_x{c}_y\rangle =\frac{1}{M^2}\sum _{j,k}\langle n_i{n}_j{n}_k\rangle x_j{y}_k\hfill \\ \hfill =m{\sigma }^2\left(\sum _j{\nu }_{ij}{x}_j\sum _k{y}_k+\sum _j{x}_j\sum _k{\nu }_{ik}{y}_k+\sum _{j,k}{\nu }_{jk}{x}_j{y}_k\right)+m^3\sum _{j,k}{x}_j{y}_k=0.\hfill \end{array}$$ (30)

Finally, the variance of the rotation misalignment is computed as

$$\langle {\theta }^2\rangle =\frac{K}{{({\lambda }_1-{\lambda }_2)}^2}\left(K\sum _i{x}_i^2\sum _{j1}{y}_j^2+\sum _i{x}_i^2{y}_i^2\right),$$ (31)

where K = (1 + 4ν₁ + 4ν₂ + 4ν₃ + 8ν₄ + 4ν₅)σ²/M². For example, the variances of the rotational misalignments for the case of Fig. 2(d) is 0.0238(rad²).

Consider again the rotational misalignment, θ(t);

$$\theta \left(t\right)=A\left(t\right)+B\left(t\right),$$

where

$$A\left(t\right)=\frac{1}{({\lambda }_2-{\lambda }_1)}{c}_x\left(t\right)c_y\left(t\right)\text{and}B\left(t\right)=\frac{1}{M({\lambda }_2-{\lambda }_1)}\sum _i{x}_i{y}_i{n}_i.$$

The two random variables A(t) and B(t) are uncorrelated due to (30). And the mean of A(t) is zero due to (25). For the case shown in Fig. 2(d), the variance of A(t) is 0.00078(rad²). This means that sampling value from A(t) is very close to zero. Therefore the distribution of θ(t) can be treated as a Gaussian because B(t) is a Gaussian.

4.4 Estimation of the blurring function

As mentioned in Section 1.3, the blurring function f(g) in (4) is the probability density function describing the distribution of misalignments. We have shown that the translational misalignments (c_x and c_y) form Gaussian distributions and the distribution of the rotational misalignment (θ) can be approximated by a Gaussian distribution.

It is interesting to check if the three random variables c_x, c_y and θ are uncorrelated to one another. It is obvious that c_x and c_y are uncorrelated from (25). The covariance 〈c_xθ〉 is computed as

$$\langle c_x\theta \rangle =-\frac{1}{({\lambda }_1-{\lambda }_2)}\langle c_x{c}_x{c}_y\rangle -\frac{1}{M({\lambda }_1-{\lambda }_2)}\sum _i{x}_i{y}_i\langle c_x{n}_i\rangle .$$

Then we compute

$$\langle c_x{c}_x{c}_y\rangle =-\frac{1}{M^3}\sum _{i,j,k}{x}_i{x}_j{y}_k\langle n_i{n}_j{n}_k\rangle =-\frac{1}{M^3}\sum _{i,j,k}{x}_i{x}_j{y}_k(m{\sigma }^2({\nu }_{ij}+{\nu }_{ik}+{\nu }_{jk})+m^3)=0.$$

In addition, we have

$$\sum _i{x}_i{y}_i\langle c_x{n}_i\rangle =-\frac{1}{M}\sum _{i,j}{x}_i{y}_i{x}_j\langle n_j{n}_i\rangle =\frac{{\sigma }^2}{M}\sum _{i,j}{\nu }_{ij}{x}_i{y}_i{x}_j=0.$$

using (46). Therefore, we have 〈c_xθ〉 = 0. This means that c_x and θ are uncorrelated. Using the similar calculation we can easily show that c_y and θ are uncorrelated.

Since c_x, c_y and θ are uncorrelated Gaussian random variables, the joint distribution can be computed as

$$f(c_x,c_y,\theta ;{\tau }_1,{\tau }_2)=p_1(c_x,{\tau }_1)p_1(c_y,{\tau }_1)p_2(\theta ,{\tau }_2),$$ (32)

where p₁(x, τ) is a Gaussian function on a real line as

$$p_1(x,\tau )=\frac{1}{\sqrt{2\pi \tau }}{e}^{-x^2∕2\tau },$$ (33)

and p₂(θ, τ) is a folded normal distribution on the circle as

$$p_2(\theta ,\tau )=\sum _{n=-\infty }^{\infty }{p}_1(\theta -2\pi n,\tau )=\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}\tau }{e}^{ik\theta }.$$ (34)

The small values of τ₁ and τ₂ are computed separately to describe different amounts of translational and rotational error, as well as to account for the fact that the units of measurement are different for translations and rotations. The two parameters can be estimated as

$${\tau }_1=K\sum _i{x}_i^2$$ (35)

and

$${\tau }_2=\frac{K}{{({\lambda }_1-{\lambda }_2)}^2}\left(K\sum _i{x}_i^2\sum _j{y}_j^2+\sum _i{x}_i^2{y}_i^2\right),$$ (36)

where K = (1 + 4ν₁ + 4ν₂ + 4ν₃ + 8ν₄ + 4ν₅)σ²/M², σ² is the variance of the background noise, and ν_i are the correlation coefficients between background noise samples. The definition of ν_i appeared in Section 3. The term (λ₁ − λ₂) can be estimated using (28).

As mentioned in Section 2, we note that an image has two equivalent principal axes whose directions are opposite to each other. We choose a better orientation from two candidates by comparing the aligned images and the image that is being aligned. In the examples that will be presented in Section 5, this method to choose one angle from two candidates works successfully. This rationalized the use of the unimodal distribution for the rotation angles in (34).

5 Numerical validation

5.1 Numerical validation with synthetic data

In this section, we numerically verify that the function in (32) with the parameters in (35) and (36) is a reasonable model for the blurring function with which the class averaging process is formulated as the SE(2)-convolution in (4). Specifically we will compare two class-averaged images obtained by SE(2)-convolution and by averaging many aligned class images.

Fig. 5 shows one example of comparison. We prepare a 256 × 256 test image of GroEL/ES (PDB code: 1AON) as shown in Fig. 5(a). To obtain this image, we assign small three-dimensional Gaussian densities for C_α with standard deviation 1.6Å A and then compute a projection. Next, by adding the Gaussian noise to Fig. 5(a), we obtain a noisy image as shown in Fig. 5(b). To account for the properties of EM image formation, we generate the spatially correlated noise using a method explained in Appendix C. For simple demonstration, we consider the case of ν₁ ≠ = 0 and ν₂ = ν₃ = ν₄ = ν₅ = 0.

Figure 5.

Comparison of two blurred images. (a) Clear projection of GroEL/ES (PDB code:1AON). This is a projection of the small Gaussian functions (std=1.6Å) assigned at all C_α's. (b) Addition of Gaussian noise and (a). The SNR is 0.1914. The mean and standard deviation of the noise are 128 and 64, respectively. The correlation between adjacent noise samples is 0.3. (c) Class average obtained by averaging 1000 noisy images using the proposed alignment method. (d) Class average obtained by SE(2)-convolution in (4) of the clear image (a) and the blurring function in (32).

With different noise samples, we generate many noisy images. Then the noisy images are aligned and averaged using the method described in Section 2. The alignment is achieved by matching the centers of mass and principal axes of images. Out of two candidates for rotational alignments (θ or (θ + π) from (29) ), one angle is chosen which results in lower image difference between the average of previously aligned images and the image being aligned. We use a circular window whose size is radius= 80 (pixel). Fig. 5(c) is an average of 1000 noisy images. A blurred image obtained by SE(2)-convolution in (4) of the clear image Fig. 5(a) with the blurring function in (32) is also shown in Fig. 5(d). The parameters (35) and (36) for the blurring function are estimated using the mean and variance of the background noise. In the example in Fig. 5, the mean, standard deviation and correlation of the background noise are m = 128, σ = 64 and ν₁ = 0.3, respectively.

The SE(2)-convolution is implemented using the convolution theorem and Hermite-function-based image modeling. The detailed method appears in [25]. Even though the main work in [25] is SE(2)-deconvolution with discrete images, SE(2)-convolution is also introduced to formulate the deconvolution problem. (See equations (36) and (37) in [25].)

For tests for more various cases, we consider four test cases shown in Table 1. For each case defined in Table 1, various numbers of test noisy images are used for class average. Table 2 shows the normalized least squared errors (NLSEs) between two class-averaged images obtained by SE(2)-convolution and by averaging aligned noisy images. For example, the NLSE between Fig. 5(c) and Fig. 5(d) is 0.0742 (Case 4 with 1000 images). Note that the NLSE between the underlying clear image (Fig. 5(a)) and the class average obtained by our alignment method (Fig. 5(c)) is 0.2282, and the NLSE between the underlying clear image and the class average obtained by the SE(2)-convolution (Fig. 5(d)) is 0.2058. The NLSE of two images, ρ₁(x) and ρ₂(x), is defined as [17]

$$\text{NLSE}=\sqrt{\frac{\sum _i{[{\rho }_1\left({\mathbf{x}}_i\right)-{\rho }_2\left({\mathbf{x}}_i\right)]}^2}{\sum _i{\left[{\rho }_1\left({\mathbf{x}}_i\right)\right]}^2}}.$$

The summation for the NLSEs in Table 2 is taken over a circular window that was used for alignment because the essential feature of the images are enclosed by the window. Cross correlations between the two class-averaged images are also reported in Table 3. The cross correlations quantify similarity between two images. The cross correlation of two images, ρ₁(x) and ρ₂(x), is defined as

$$\mathrm{CC}=\frac{\sum _i{\rho }_1\left({\mathbf{x}}_i\right){\rho }_2\left({\mathbf{x}}_i\right)}{\sqrt{\sum _i{\left[{\rho }_1\left({\mathbf{x}}_i\right)\right]}^2\sum _i{\left[{\rho }_2\left({\mathbf{x}}_i\right)\right]}^2}}.$$

The summation for the cross correlation in Table 3 is also taken over a circular window that was used for alignment. Note that Fig. 5(c) and 5(d) have the gray background which is corresponding to the mean of the background noise of each EM images. Therefore in computation of the NLSEs and the cross correlation, the mean intensity was subtracted from the images shown Fig. 5(d) and Fig. 5(c).

Table 1.

Statistical parameters of background noise for four test cases. The first row shows the standard deviations of background noise. The second row shows correlations between two adjacent samples from background noise. The third row shows the signal-to-noise ratio of the synthetic data images. The mean intensity of background noise is 128 for all cases.

	Case 1	Case 2	Case 3	Case 4
SD	32	64	32	64
Correlation	0	0	0.3	0.3
SNR	0.7656	0.1914	0.7656	0.1914

Table 2.

NLSEs between class average images obtained by SE(2)-convolution and by averaging aligned class images.

Number of images	Case 1	Case 2	Case 3	Case 4
100	0.0963	0.1927	0.1128	0.2122
500	0.0482	0.0899	0.0543	0.0982
1000	0.0377	0.0681	0.0429	0.0742

Table 3.

Cross correlation coefficients between class-averaged images obtained by SE(2)-convolution and by averaging aligned noisy images.

Number of images	Case 1	Case 2	Case 3	Case 4
100	0.9954	0.9818	0.9936	0.9780
500	0.9988	0.9960	0.9985	0.9952
1000	0.9993	0.9977	0.9991	0.9972

Table 2 shows that as the number of class images is increased, the difference between two class-averaged images obtained by SE(2)-convolution and by averaging aligned noisy images is decreased. In addition, Table 3 shows similarities between two class-averaged images increases accordingly. Fig. 5, Table 2 and Table 3 verifies the model for class averaging in (4) and the estimates for parameters in (35) and (36).

Since the number of images in a class is finite, the additive background noise cannot be completely canceled. The mean of the residual noise is the same as the mean of the background noise in EM images and the variance is reduced in the averaging process. Specifically, the residual noise follows a normal distribution $\mathcal{N}(m,\sigma ∕\sqrt{N})$, when the background noise in EM images follows a normal distribution $\mathcal{N}(m,\sigma )$ and the N images are averaged. This residual noise may cause a problem in the deconvolution producing artifacts in the resulting image.

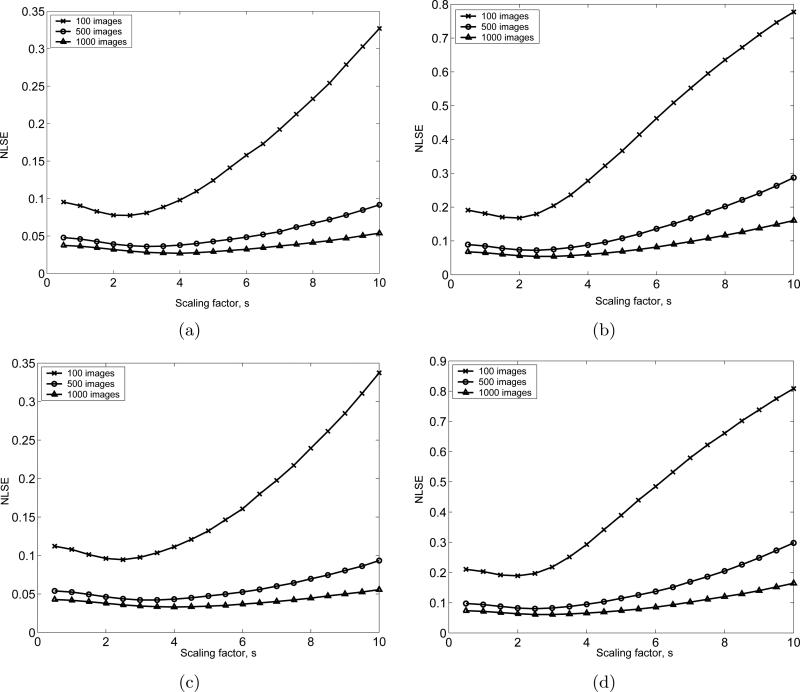
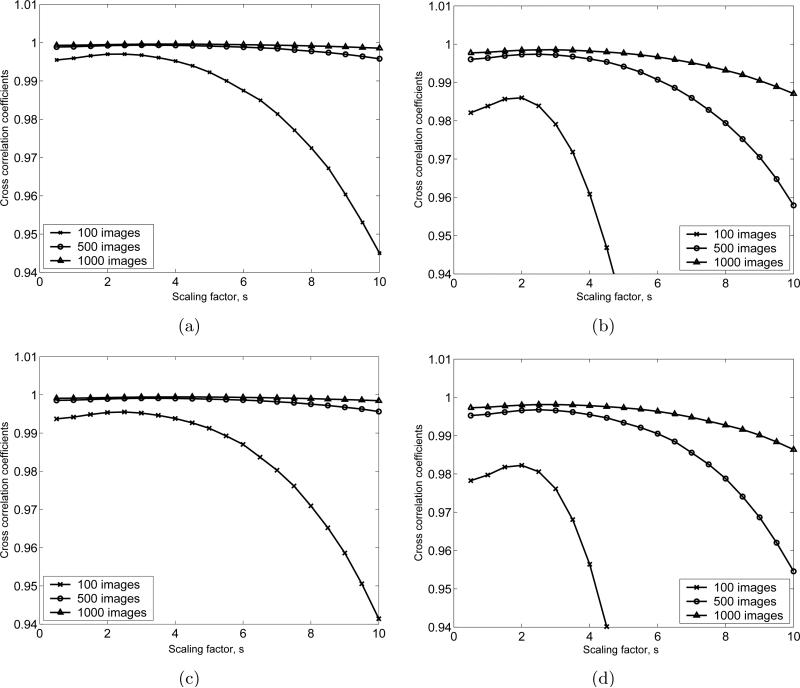
Consider the gray area around the GroEL/ES structure in Fig. 5(c). In order to reduce the residual noise in this area, we consider the pixels whose intensities are between ($m-s\sigma ∕\sqrt{N}$) and ($m+s\sigma ∕\sqrt{N}$), where s is a scaling factor, N images are averaged, and m and σ are the mean and the standard deviation of the background noise, respectively. Then we assign the mean intensity of the background noise to those pixels. Using this postprocessing, we can obtain a class average that is closer to the ideal class average. We apply this postprocessing technique to all cases shown in Table 1 with various values of the scaling factors. The image differences between the SE(2)-convolution-generated class average and the post-processed class average obtained by averaging and flattening are shown in Fig. 6. Fig. 7 shows the cross correlation coefficients (image similarities) for the same test images that are used in Fig. 6. Based on Fig. 6 and 7, the optimal value for s is chosen to be s = 2.5.

Figure 6.

NLSEs between the class average obtained by SE(2)-convolution and the class average after flattening the residual noise for the 4 cases defined in Table 1 with different numbers of images that are averaged. (a), (b), (c) and (d) are respectively the numerical test results for Case 1,2,3 and 4 defined in Table 1. For each case, 100, 500 and 1000 test images are used.

Figure 7.

Cross correlation coefficients between the class average obtained by SE(2)-convolution and the class average after flattening the residual noise for the 4 cases defined in Table 1 with different numbers of images that are averaged. (a), (b), (c) and (d) are respectively the numerical test results for Case 1,2,3 and 4 defined in Table 1. For each case, 100, 500 and 1000 test images are used.

5.2 Realignment of initially aligned images

Unlike the synthetic data, there is no reference underlying image in the experimental CTF-corrected images. In order to obtain a candidate underlying image, we re-align the noisy images to have a better averaged image that can be viewed as a reference underlying image.

First, we try to re-align the EM images to maximize the Frobenius norm of the resulting averaged image using the method in [24]. It can be formulated as

$$\underset{{\tilde{g}}_1,{\tilde{g}}_2,\cdots ,{\tilde{g}}_N}{\min }{\Vert \frac{1}{N}\sum _t\tilde{\rho }({\tilde{g}}_t^{-1}\cdot \mathbf{x},t)-m\Vert }^2$$ (37)

where $\tilde{\rho }(\cdot )$ is a class image aligned by matching the center of mass and principal axis, g̃_t = g(d_x(t), d_y(t), ϕ(t)) is the small re-alignment such that g̃_t ○ g_t is the total alignment of the original t^th image, m is the mean of the background noise and the action of g̃_t on x is defined in (2). This maximization process forces the spatially-distributed pixels to gather. In order to implement (37), translations and rotations are updated with iterative piecewise search.

For discrete search for these variables, the candidates for the variables are respectively

$$\begin{array}{c}\hfill d_x^{\left(1\right)}\left(t\right)=-{\sigma }_x\text{or}0\text{or}{\sigma }_x,\hfill \\ \hfill d_y^{\left(1\right)}\left(t\right)=-{\sigma }_y\text{or}0\text{or}{\sigma }_y,\hfill \\ \hfill {\varphi }^{\left(1\right)}\left(t\right)=-{\sigma }_{\theta }\text{or}0\text{or}{\sigma }_{\theta },\hfill \end{array}$$

where the superscript (·)⁽¹⁾ denotes the first iteration, ${\sigma }_x={\sigma }_y=\sqrt{{\tau }_1}$ and ${\sigma }_{\theta }=\sqrt{{\tau }_2}$. Note that the variables τ₁ and τ₂ were estimated in Section 4.4 to specify the blurring function. In the first iteration, we determine these variables for t = 1, 2, ..., N in a serial manner. For finer adjustments, the candidates for the variables in the j^th iteration are respectively

$$\begin{array}{c}\hfill d_x^{\left(j\right)}\left(t\right)=-\frac{{\sigma }_x}{2^{j-1}}\text{or}0\text{or}\frac{{\sigma }_x}{2^{j-1}},\hfill \\ \hfill d_y^{\left(j\right)}\left(t\right)=-\frac{{\sigma }_y}{2^{j-1}}\text{or}0\text{or}\frac{{\sigma }_y}{2^{j-1}},\hfill \\ \hfill d^{\left(j\right)}\left(t\right)=-\frac{{\sigma }_{\theta }}{2^{j-1}}\text{or}0\text{or}\frac{{\sigma }_{\theta }}{2^{j-1}}.\hfill \end{array}$$

With N_t iterations, the resulting transform g̃_t for the t^th image is computed as

$${\tilde{g}}_t={\tilde{g}}_t^{\left(N_t\right)}\circ {\tilde{g}}_t^{(N_t-1)}\cdots {\tilde{g}}_t^{\left(2\right)}\circ {\tilde{g}}_t^{\left(1\right)}$$ (38)

where ${\tilde{g}}_t^{\left(k\right)}=g(d_x^{\left(k\right)}\left(t\right),d_y^{\left(k\right)}\left(t\right),{\varphi }^{\left(k\right)}\left(t\right))$.

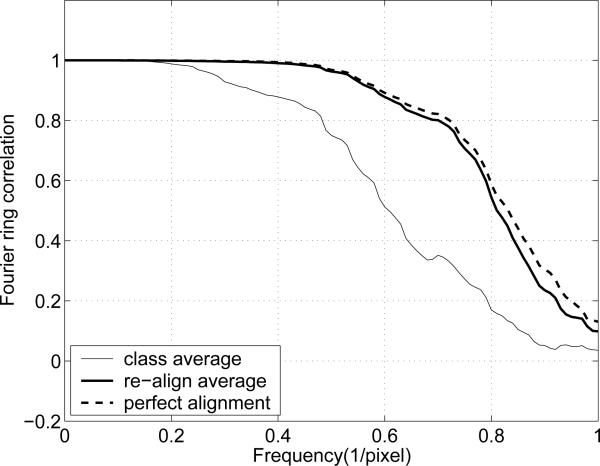
After five iterations with the example shown in Fig. 5, a new average with the re-aligned class images is obtained. To assess the quality of the result, we plot the Fourier ring correlation (FRC). The FRC provides the normalized cross correlation coefficients over corresponding rings in Fourier domain [28, 33]. The FRC for two images, ρ₁ and ρ₂, is defined as

$$FRC\left(r\right)=\frac{\sum _{{\mathbf{r}}_{i\in r}}{\widehat{\rho }}_1\left({\mathbf{r}}_i\right){{\widehat{\rho }}_2}^{\ast }\left({\mathbf{r}}_i\right)}{\sqrt{\sum _{{\mathbf{r}}_{i\in r}}\mid {\widehat{\rho }}_1\left({\mathbf{r}}_i\right){\mid }^2\cdot \sum _{{\mathbf{r}}_{i\in r}}\mid {\widehat{\rho }}_2\left({\mathbf{r}}_i\right){\mid }^2}}$$

where $\widehat{\rho }\left({\mathbf{r}}_i\right)$ is the complex structure factor at position r in Fourier space, and the * denotes complex conjugate. r_i is Fourier-space voxels that are contained in the ring with radius r.

In Fig. 8 the thin continuous curve is the FRC between the original reference image (Fig. 5(a)) and the class average (Fig. 5(c)). The thick continuous curve is the FRC between the original reference image and the new class average with the re-aligned images. The dashed curve is the FRC between the original reference image and the average of the ideally aligned class images. As shown in Fig. 8, the re-alignment process substantially recovers the misalignment, since the FRC for the new average is close to that of the ideal average. The NLSE and the cross correlation between the ideal average (Fig. 5(a)) and the re-alignment result are 0.0258 and 0.9997, respectively.

Figure 8.

Fourier ring correlations. The SNR of each test image is 0.1914.

5.3 Validation with experimental data

In this section we validate the SE(2)-convolution model of image blurring on real experimental data in two different ways. First, we illustrate that the class image of the glutamate receptor obtained by the CMPA method matches well to an image generated by convolution-blurring of an optimally re-aligned class average, with SE(2) blurring kernel obtained using the methods that are the main topic of this paper. Unlike in numerical studies, in the context of experimental data there is no baseline truth image available, and so the optimally re-aligned class average is used in place of the baseline truth. We also illustrate another point here, which is that SE(2)-convolution can be used to describe the blurring effects of other alignment methods (not only CMPA), even though it may not be obvious how to compute a priori the covariances of the associated blurring kernel for other alignment methods. As an example of this, we consider the alignment generated by EMAN. We then re-align the EMAN-aligned images using the methods of Section 5.2 to gain a slight improvement. We then show how the original EMAN alignment can be viewed as a subtle blurring of the re-aligned class image.

Fig. 9(a) shows the class averages obtained by our alignment method to match the center of mass and principal axis. Like the experiments with synthetic data in Section 5.1, we determine a better alignment angle out of two candidates due to the fact that an image has two equivalent principal axes.

Figure 9.

(a) A class average obtained by our alignment method to match the center of mass and principal axis. (b) A new class average after re-aligning class images. This new average is obtained by re-aligning the class images to maximize the Frobenius norm of the resulting average and then averaging the re-aligned images. (c) Class-averaged images obtained by SE(2)-convolution of (b) with the blurring kernel. (d) The difference images between (a) and (c). The pixel intensities of this difference image are amplified by a factor of 5, and then are inverted for better visualization.

Applying the re-alignment method to Fig. 9(a), we obtain a new class average as shown in Fig. 9(b). Through this re-alignment process, the new alignments for each misaligned image are generated. Since the re-alignment process is expected to bring near-optimal alignments, this re-alignment information reflects the inverse of the blurring process that our alignment method brings.

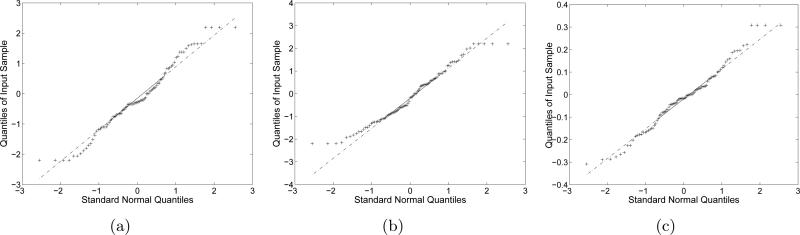
Table 4 shows the theoretical and empirical variances of alignments in Fig. 9. The theoretical variances are computed using the estimation formulas (24) and (31). The empirical variances are computed using the re-alignment information that is essentially rotations and translations that the class images undergo during re-alignment. Fig. 10 shows the normal Q-Q plot of the rotations and translations. Table 4 and Fig. 10 verifies that the Gaussian-based blurring function can be applied the alignment method to match the center of mass and principal axis. Fig. 9(c) shows the convolution of the image in Fig. 9(b) and the blurring functions with the theoretical variances in Table 4. To implement this SE(2)-convolution, we used the formulation in [25]. The NLSE between Fig. 9(a) and 9(c) is 0.1990. The NLSEs between Fig. 9(a) and Fig. 9(b), and between Fig. 9(b) and Fig. 9(c) are 0.2317 and 0.2627, respectively. The difference images between Fig. 9(a) and 9(c) is shown in Fig. 9(d). The NLSEs between the images in Fig. 9 verify the model for the blurring function in (32).

Table 4.

Theoretical and empirical variances for the re-alignments in Fig. 9.

	Theoretical variance	Empirical variance
$\langle c_x^2\rangle$	1.2090	1.2575
$\langle c_y^2\rangle$	1.2090	1.4349
〈 θ 2 〉	0.0238	0.0200

Figure 10.

Normal Q-Q plots for re-alignments. The class images that were aligned by our alignment method are aligned again to maximize the Frobenius norm of the resulting averaged image. (a) x-axis translation re-alignments, (b) y-axis translation re-alignments, (c) rotation re-alignments. (a), (b) and (c) are test results with the re-alignments in Fig. 9.

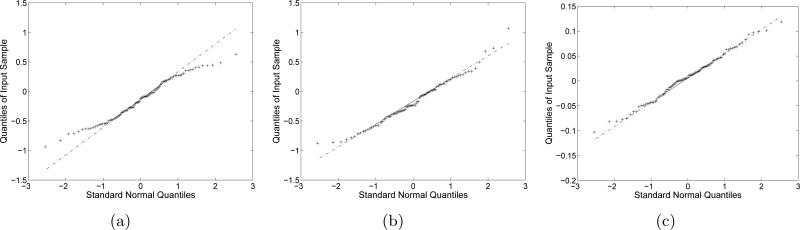
Fig. 11(a) shows the class average obtained by EMAN. Applying the re-alignment process to EMAN-aligned images results in Fig. 11(b). Table 5 shows the variances of re-alignments and Fig. 12 shows the normality of the re-alignments. Fig. 11(c) shows the convolution of the image in Fig. 11(b) and the blurring functions with the empirical variances in Table 5. The fact that these variances are very small is consistent with the original and realigned images being difficult to distinguish by the naked eye. The variances for x − y translations and rotation are computed as 〈(d_x(t))²〉, 〈(d_y(t))²〉 and 〈(ϕ(t))²〉, respectively. d_x(t), d_y(t) and ϕ(t) are obtained in (38) during realignment.

Figure 11.

(a) A class average obtained by EMAN. (b) A new class average after re-aligning class images. This new average is obtained by re-aligning the class images to maximize the Frobenius norm of the resulting average and then averaging the re-aligned images. (c) Class-averaged images obtained by SE(2)-convolution of (b) with the blurring kernel. (d) The difference images between (a) and (c). The pixel intensities of this difference image are amplified by a factor of 5, and then are inverted for better visualization.

Table 5.

Variances of re-alignment with EMAN results for the re-alignments in Fig.11.

	Empirical variance
$\langle c_x^2\rangle$	0.1319
$\langle c_y^2\rangle$	0.1456
〈 θ 2 〉	0.0022

Figure 12.

Normal Q-Q plots for re-alignments. The class images that were aligned by EMAN. (a) x-axis translation re-alignments, (b) y-axis translation re-alignments, (c) rotation re-alignments. (a), (b) and (c) are test results with the re-alignments in Fig. 11.

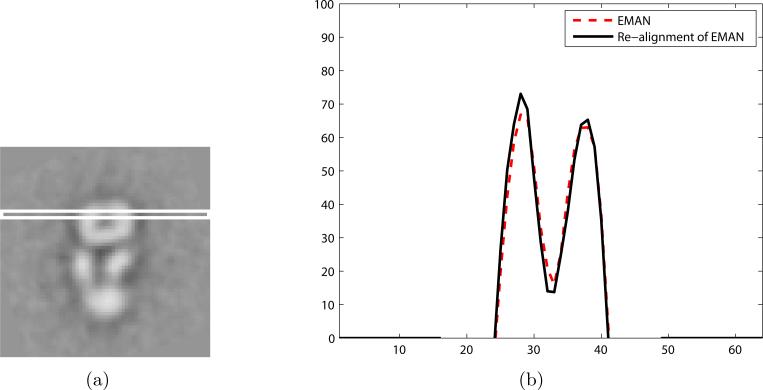
The NLSE between the two images in Fig. 11(a) and 11(c) is 0.1162. The difference image between Fig. 11(a) and 11(c) is shown in Fig. 11(d). The NLSEs between Fig. 11(a) and Fig. 11(b), and between Fig. 11(b) and Fig. 11(c) are 0.1381 and 0.1715, respectively. Fig. 13 shows the qualitative comparison between the class averages obtained by EMAN and re-alignment. Fig. 13(a) illustrates the location of the slice through the image where we compare the intensities of the original and re-aligned EMAN images. We can get the sharper profile using our re-alignment technique. The NLSEs between the images in Fig. 11 and the two profiles in Fig. 13(b) verifies that the re-alignment technique gives a slightly better class image and that the model for the blurring function in (32) can be used for the EMAN alignment method. Our goal in this example was not to introduce a method for improved alignment of class images, but rather only to illustrate that SE(2) covariances can be computed for any alignment method when a set of rigid-body transformations between each image in a class and a baseline image for the class are both given.

Figure 13.

Qualitative comparison between the class averages obtained by EMAN and re-alignment. (a) A white box denotes the sampling area. (b) Comparison between the profile sampled from Fig. 11(a) and 11(b) on the sampling area. For better visualization, the background intensity is suppressed to zero in (b).

Finally we apply the post-processing technique to the experimental data to reduce the residual noise that were developed in Section 5.1. Based on the numerical study in Section 5.1, we use s = 2.5 as a baseline value when selecting the threshold for experimental images. However, due to the fact that experimental images contain noise that is not exactly Gaussian, and the pixel sizes are different from those in Section 5.1, we would expect that the best value of s would be somewhere in the range 2 ≤ s ≤ 3. Fig. 14 illustrates the effect of various values of s on cleaning up the images. In practice an initial value of s would be chosen and a 3D density would be computed from deblurred versions of these cleaned up projections. Then the value of s would be updated during iterations in which the computed 3D density is projected and compared to each class. However, the steps of deblurring/deconvolution and 3D density reconstruction are not the subject of this paper and will be addressed in subsequent papers. Our emphasis here is the quantitative analysis of noise characteristics in EM images, which is a step toward developing improvements to existing methods for 3D density determination.

Figure 14.

Reduction of the residual noise. (a) to (d) are the results of the noise reduction applied to Fig. 2(d) with the scaling factor, s = 1.5, 2, 2.5 and 3, respectively.

Fig. 14 shows the postprocessing results of Fig. 2(d) with various scaling values. Ideally, the residual noise outside of the biomacromolecule structure should be eliminated by the postprocessing method without affecting the visual information of the structure of the biomacromolecule. As the scaling factor is increased, more residual noise is eliminated, but more structural information is also lost. Based on the trade-off in visual quality shown Fig. 14, we conclude that the value of the scaling factor determined numerically in Fig. 6 (s=2.5) is a reasonable choice.

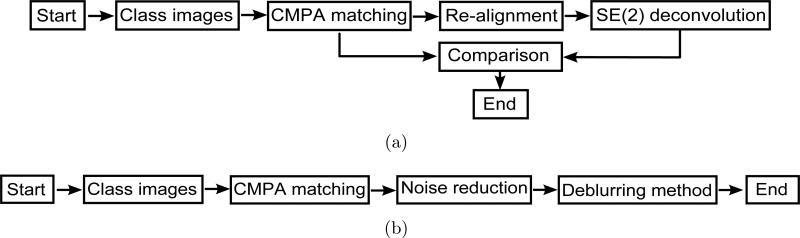
Fig. 15 shows the flows of the processes. Fig. 15(a) shows the process for validation of the blurring function and the associated SE(2)-convolution. The process of matching the center of mass and principal axis (CMPA) is denoted by CMPA matching. By this process, Fig 9(a) is generated. Using re-alignment process, we generate Fig. 9(b). Fig. 9(c) is a result of SE(2)-convolution. We compare Fig 9(a) and 9(c) to verify our blurring function and its parameters which are computed in (35) and (36). Fig. 15(b) shows the process for generating a better class average using the alignment result. The noise reduction process shown in Fig. 14 is applied to the result of alignment, and then the deblurring method is used to generate a better class average. The deblurring method for this purpose is available in [25].

Figure 15.

Diagrams for processes

6 Conclusion

In this work, we investigated the stochasticity of the class averaging process which is one important step in single-particle electron microscopy. After matching mass centers and principal axes of classified CTF-corrected images, class averages are computed. In the averaging process, the background noise is reduced. However, the alignment of the images cannot be exact due to the background noise. This misalignment leads to blurring in the averaged image.

Based on the observation that the distribution of the background noise can be estimated as a Gaussian, we derived the equations for the means and variances of the translational and rotational misalignments in class average. The means are zero and the variances are functions of the mean and variance of the background noise. Using the mean and variance of the misalignment, we derived an estimate for the blurring function. The blurring function can be defined as the multiplication of a 2D Gaussian function and a 1D folded Gaussian function on the circle. We performed numerical validation for the estimated blurring function by comparing the class averages obtained by SE(2)-convolution and by averaging many simulated noisy EM images. Using the experimental data which is processed by EMAN, we also verify that the SE(2)-convolution with the blurring kernel based on Gaussian functions is a good mathematical model for averaging of class images aligned by other alignment method.

Since the blurred class-averaged image can be defined by the SE(2)-convolution of the blurring function and the underlying clear image, the next step will be to deblur the class average by deconvolution methods. Mathematical approaches for deconvolution on SE(2) have been suggested in the literature including [6, 16, 36]. The actual implementation with the consideration of the specific case where the blurring function can be modeled in the form of (32) appears in [25].

Appendix A

Computation of ${\sum }_{i,j}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T$

The summation ${\sum }_{i,j}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T$ can be split into two parts for convenience as follows:

$$\sum _{i,j}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T=\sum _{(i,j)\in S_0}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T+\sum _{k=1}^5\sum _{(i,j)\in S_k}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T$$ (39)

where S₀ is a set of (i, j) where i = j and S_k (k = 1, 2, .., 5) are defined in (12).

The summation in S₁ can be computed as

$$\sum _{(i,j)\in S_1}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T={\nu }_1\sum _i\left({\mathbf{x}}_i\sum _{j\in S_1^i}{\mathbf{x}}_j\right),$$

where $S_1^i$ is a set of j where (i, j) ∈ S₁ for given i. If x_i is given as x_i = (x_i, y_i)^T, then we have

$$\sum _{j\in S_1^i}{\mathbf{x}}_j={(x_i+1,y_i)}^T+{(x_i-1,y_i)}^T+{(x_i,y_i+1)}^T+{(x_i,y_i-1)}^T=4{\mathbf{x}}_i.$$

Therefore, the summation in S₁ can be rewritten as

$$2\sum _{(i,j)\in S_1}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T=4{\nu }_1\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T.$$

Using similar calculations, we have

$$\sum _{i,j}{\nu }_{ij}{\mathbf{x}}_i{\mathbf{x}}_j^T=(1+4{\nu }_1+4{\nu }_2+4{\nu }_3+8{\nu }_4+4{\nu }_5)\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T$$ (40)

The components of the 2 × 2 matrix in (40) can be written as

$$\sum _{i,j}{\nu }_{ij}{x}_i{x}_j=(1+4{\nu }_1+4{\nu }_2+4{\nu }_3+8{\nu }_4+4{\nu }_5)\sum _i{x}_i^2,$$ (41)

$$\sum _{i,j}{\nu }_{ij}{y}_i{y}_j=(1+4{\nu }_1+4{\nu }_2+4{\nu }_3+8{\nu }_4+4{\nu }_5)\sum _i{y}_i^2,$$ (42)

and

$$\sum _{i,j}{\nu }_{ij}{x}_i{y}_j=(1+4{\nu }_1+4{\nu }_2+4{\nu }_3+8{\nu }_4+4{\nu }_5)\sum _i{x}_i{y}_i=0.$$ (43)

Using the similar manipulation, we also have

$$\sum _{i,j}{\nu }_{ij}{x}_i{y}_i{x}_j{y}_j=(1+4{\nu }_1+4{\nu }_2+4{\nu }_3+8{\nu }_4+4{\nu }_5)\sum _i{x}_i^2{y}_i^2.$$ (44)

We can also compute ${\sum }_{i,j}{\nu }_{ij}{x}_i{y}_i{x}_j$ using the manipulation in (39) as

$$\sum _{i,j}{\nu }_{ij}{x}_i{y}_i{x}_j=\sum _{(i,j)\in S_0}{\nu }_{ij}{x}_i{y}_i{x}_j+\sum _{k=1}^5\sum _{(i,j)\in S_k}{\nu }_{ij}{x}_i{y}_i{x}_j.$$ (45)

The first term of the right hand side in (45) is written as

$$\sum _{(i,j)\in S_0}{\nu }_{ij}{x}_i{y}_i{x}_j=\sum _i{x}_i^2{y}_i=0.$$

The second term of the right hand side in (45) with k = 1 is computed as

$$\sum _{(i,j)\in S_1}{\nu }_{ij}{x}_i{y}_i{x}_j=\nu \sum _i{x}_i{y}_i\sum _{j\in S_1^i}{x}_j=4{\nu }_1\sum _i{x}_i^2{y}_i=0.$$

We can show ${\sum }_{(i,j)\in S_k}{\nu }_{ij}{x}_i{y}_i{x}_j=0$ for k = 2, ..., 5 in a similar way. Therefore we have

$$\sum _{i,j}{\nu }_{ij}{x}_i{y}_i{x}_j=0.$$ (46)

Appendix B

Decomposition of the blurring kernel

On a plane parameterized by polar coordinates and on a circle, the Gaussian distribution densities are respectively²

$$f_1(r,\varphi )=\frac{1}{2\pi {\tau }_1}{e}^{-r^2∕2{\tau }_1}\text{and}{f}_2\left(\theta \right)=\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }.$$

We define the following functions on SE(2)

$$F_1(r,\varphi ,\theta )=\frac{1}{2\pi {\tau }_1}{e}^{-r^2∕2{\tau }_1}\delta \left(\theta \right)\text{and}{F}_2(r,\varphi ,\theta )=\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }\frac{\delta \left(r\right)}{2\pi r}\delta \left(\varphi \right).$$

We want to show that

$$(F_1\ast F_2)\left(g\right)=(F_2\ast F_1)\left(g\right)=f_1\left(g\right)f_2\left(g\right).$$

This allows us to decompose our blurring kernel into purely translational and purely rotational parts.

Proof

$$(F_1\ast F_2)\left(g\right)={\int }_{\mathrm{SE}\left(2\right)}{F}_1\left(h\right)F_2(h^{-1}\circ g)dh$$

and

$$(F_2\ast F_1)\left(g\right)={\int }_{\mathrm{SE}\left(2\right)}{F}_2\left(h\right)F_1(h^{-1}\circ g)dh.$$

By changing the variable k = h⁻¹ ○ g, we have

$$(F_1\ast F_2)\left(g\right)={\int }_{\mathrm{SE}\left(2\right)}{F}_1(g\circ k^{-1})F_2\left(k\right)dk={\int }_{\mathrm{SE}\left(2\right)}{F}_2\left(h\right)F_1(g\circ h^{-1})dh.$$

g and h can be parameterized as

$$g=g(r,\varphi ,\theta )=\left(\begin{array}{ccc}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill & \hfill r\cos \varphi \hfill \\ \hfill \sin \theta \hfill & \hfill \cos \theta \hfill & \hfill r\sin \varphi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$

and

$$h=h(R,\Phi ,ϴ)=\left(\begin{array}{ccc}\hfill \cos ϴ\hfill & \hfill -\sin ϴ\hfill & \hfill R\cos \Phi \hfill \\ \hfill \sin ϴ\hfill & \hfill \cos ϴ\hfill & \hfill R\sin \Phi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$

The multiplications are

$$h^{-1}\circ g=\left(\begin{array}{ccc}\hfill \cos (\theta -ϴ)\hfill & \hfill -\sin (\theta -ϴ)\hfill & \hfill r\cos (\varphi -ϴ)-R\cos (\Phi -ϴ)\hfill \\ \hfill \sin (\theta -ϴ)\hfill & \hfill \cos (\theta -ϴ)\hfill & \hfill r\sin (\varphi -ϴ)-R\sin (\Phi -ϴ)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$

and

$$g\circ h^{-1}=\left(\begin{array}{ccc}\hfill \cos (\theta -ϴ)\hfill & \hfill -\sin (\theta -ϴ)\hfill & \hfill r\cos \varphi -R\cos (\theta +\Phi -ϴ)\hfill \\ \hfill \sin (\theta -ϴ)\hfill & \hfill \cos (\theta -ϴ)\hfill & \hfill r\sin \varphi -R\sin \nabla (\theta +\Phi -ϴ)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$

Therefore,

$$\begin{array}{c}\hfill (F_1\ast F_2)\left(g\right)=\int F_2\left(h\right)F_1(g\circ h^{-1})dh\hfill \\ \hfill ={\int }_{\mathrm{SE}\left(2\right)}\left\{\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ikϴ}\frac{\delta \left(R\right)}{2\pi R}\delta \left(\Phi \right)\right\}\left\{\frac{1}{2\pi {\tau }_1}{e}^{-(R^2+r^2-2Rr\cos (\varphi -\theta -\Phi +ϴ))∕2{\tau }_1}\delta (\theta -ϴ)\right\}RdRd\Phi dϴ.\hfill \end{array}$$

Integration over Φ gives

$$\begin{array}{c}\hfill =\int \left\{\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }\frac{\delta \left(R\right)}{2\pi R}\delta \left(\Phi \right)\right\}\left\{\frac{1}{2\pi {\tau }_1}{e}^{-(R^2+r^2-2Rr\cos (\varphi -\Phi ))∕2{\tau }_1}\right\}RdRd\Phi \hfill \\ \hfill =\frac{1}{4{\pi }^2{\tau }_1}\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }\int \left\{e^{-(R^2+r^2-2Rr\cos (\varphi -\Phi ))∕2{\tau }_1}\frac{\delta \left(R\right)}{2\pi R}\delta \left(\Phi \right)\right\}RdRd\Phi .\hfill \end{array}$$

Using the fact that the δ(R)/(2πR) is a special delta function on a polar coordinate at singularity (R = 0), we have

$$(F_1\ast F_2)\left(g\right)=\frac{1}{4{\pi }^2{\tau }_1}\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }{e}^{-r^2∕2{\tau }_1}.$$

Similarly, we compute

$$\begin{array}{c}\hfill (F_2\ast F_1)\left(g\right)=\int F_2\left(h\right)F_1(h^{-1}\circ g)dh\hfill \\ \hfill ={\int }_{\mathrm{SE}\left(2\right)}\left\{\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ikϴ}\frac{\delta \left(R\right)}{2\pi R}\delta \left(\Phi \right)\right\}\left\{\frac{1}{2\pi {\tau }_1}{e}^{-(R^2+r^2-2Rr\cos (\varphi -\Phi ))∕2{\tau }_1}\delta (\theta -ϴ)\right\}RdRd\Phi dϴ.\hfill \\ \hfill =\frac{1}{4{\pi }^2{\tau }_1}\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }{e}^{-r^2∕2{\tau }_1}.\hfill \end{array}$$

Therefore, we showed that

$$(F_1\ast F_2)\left(g\right)=(F_2\ast F_1)\left(g\right)=f_1\left(g\right)f_2\left(g\right)==\frac{1}{4{\pi }^2{\tau }_1}\sum _{k=-\infty }^{\infty }{e}^{-\frac{k^2}{2}{\tau }_2}{e}^{ik\theta }{e}^{-r^2∕2{\tau }_1},$$

where

$$g=g(r,\varphi ,\theta )=\left(\begin{array}{ccc}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill & \hfill r\cos \varphi \hfill \\ \hfill \sin \theta \hfill & \hfill \cos \theta \hfill & \hfill r\sin \varphi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$

Appendix C

In this appendix, we generate the 2D correlated noise. The correlation between two adjacent noise samples is defined as ν. For simple simulation, we consider the case where ν₁ = μ, ν₂ = ν₃ = ν₄ = ν₅ = 0.

For N noise samples, each of which forms the Gaussian distribution, we can compute the N × N covariance matrix, Σ. This correlated noise samples can be generated by

$$\mathbf{y}=S\mathbf{x},$$

where $\mathbf{y}\in {\mathbb{R}}^N$ is N correlated samples, Σ = S² and $\mathbf{x}\in {\mathbb{R}}^N$ is N independent samplings from a Gaussian. If the size of N is large, it is not practical to compute S = Σ^1/2.

Alternatively, we generate the correlated noise as follows. It is natural to consider five independent random variables to define one pixel noise value, because one random variable contributes to generate one noise value and the other four adjacent noises. If each noise sample follows a normal distribution N(μ, σ) and the correlation between two adjacent noise samples is ν, then we can model the random variables at the position ‘1’ and ‘2’ in Fig. 16 as

$$P_1=\mu +\sigma (a{Z}_1+b{Z}_2+b{Z}_3+b{Z}_5+b{Z}_7)$$ (47)

$$P_2=\mu +\sigma (a{Z}_2+b{Z}_1+b{Z}_4+b{Z}_6+b{Z}_8)$$ (48)

where Z_i are independent random variables from a normal distribution N(0, 1).

Figure 16.

The pixel ‘1’ and ‘2’ are considered simultaneously. The correlation of two adjacent noise is ν.

Because the mean and variance of P₁ and P₂ are respectively μ and σ², we have a constraint, a² + 4b² = 1. Furthermore, since the covariance of P₁ and P₂ is νσ², we have another constraint as 2ab = ν. Using parametrization a = cosθ and 2b = sinθ, we simply have one solution to the constraints as

$$\theta ={\sin }^{-1}\left(2\nu \right)∕2,$$

$$a=\cos \theta \text{and}b=\left(\sin \theta \right)∕2.$$

This method is also easy to implement. A 2D correlated noise can be generated by linear combination of five 2D uncorrelated Gaussian noise using (47).